Modelling the Design of University Competitiveness

Dmytro H. Lukianenko

, Andriy V. Matviychuk

, Liubov I. Lukianenko

and Iryna V. Dvornyk

Kyiv National Economic University named after Vadym Hetman, 54/1 Peremogy Ave., Kyiv, 03680, Ukraine

Keywords:

Globalization, Competitiveness, Universities, Intellectual Capital, Innovations, Digital Transformation.

Abstract:

In the post-industrial knowledge economy, the key role in the generation and dissemination of innovations is

played by universities, where global intellectual capital is concentrated. Today, universities are becoming the

drivers of digital transformation of science, business, countries and society as a whole. In the latest paradigm

of development, based on the generalization of modern theoretical trends, the scientiﬁc and practical problems

as well as prospects for the development of universities are highlighted and the prerequisites, imperatives and

factors of their competitiveness are revealed. The research also focuses on modelling of university competi-

tiveness parameters with the clustering of countries on the basis of Kohonen maps and assessment of the level

of signiﬁcance of normalized parameters. The organizational design of a competitive model of the university

as well as key factors of its success in the system of open science, education and innovation are proposed.

1 INTRODUCTION

In the global highly competitive educational environ-

ment, under the inﬂuence of ultra-dynamic digital-

ization, traditional models and organizational struc-

tures of universities are being devalued. Innovative

network-type models are becoming relevant, and the

choice of breakthrough, catch-up or adaptation strate-

gies depends primarily on the competitive status of

the university in the global market of educational ser-

vices.

The global transformation of university education

raises new challenges for state authorities in the ﬁeld

of education and university administrations to ensure

their competitiveness in the international market of

educational services. In the context of increasing the

efﬁciency of the university management process in

modern globalization conditions, the tasks of assess-

ing its international competitiveness arise.

This problem has received close attention in scien-

tiﬁc research in recent years. Many publications are

focused on the analysis of generally accepted methods

for assessing the competitiveness of universities and

their ranking, comparing these methods, key indica-

https://orcid.org/0000-0002-3475-2126

https://orcid.org/0000-0002-8911-5677

https://orcid.org/0000-0001-6997-1575

https://orcid.org/0000-0002-2558-9654

tors, modelling principles and identifying their weak-

nesses.

Avralev and Eﬁmova (Avralev and Eﬁmova, 2015)

have conducted a survey of students over the years,

which showed that place in the university rankings is

an increasingly important criterion for students when

choosing a university. At the same time, most re-

searchers criticize the widely used rating systems.

Thus, Sayed (Sayed, 2019) demonstrates that accord-

ing to some of the world’s leading ranking systems,

a university may be at the top of the ranking, while

in others it may not be ranked at all. Many re-

searchers note (Anowar et al., 2015; Marginson and

van der Wende, 2016) that most of the global univer-

sity rankings focus primarily on research, while at the

same time not paying enough attention to the qual-

ity of teaching, student competences and learning out-

comes, social responsibility, etc.

At the same time, most scientists agree that the

main criteria that determine the competitiveness of

universities are research and teaching (Dimitrova and

Dimitrova, 2017; Sayed, 2019; Taylor and Braddock,

2008; Tee, 2016). In addition, some authors empha-

size the importance of other criteria, such as interna-

tional cooperation with university research networks,

involving foreign teachers and students, increasing

international citation (Avralev and Eﬁmova, 2013;

Chl

adkov

a et al., 2021; Deem et al., 2008), qual-

ity of pedagogical staff (Chl

adkov

a et al., 2021), so-

204

Lukianenko, D., Matviychuk, A., Lukianenko, L. and Dvornyk, I.

Modelling the Design of University Competitiveness.

DOI: 10.5220/0011933200003432

In Proceedings of 10th International Conference on Monitoring, Modeling Management of Emergent Economy (M3E2 2022), pages 204-214

ISBN: 978-989-758-640-8; ISSN: 2975-9234

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

cial and environmental responsibility (Lukman et al.,

2010), digitization of all university functioning pro-

cesses (Kucherova et al., 2021; Lukianenko et al.,

2020; Sannikova et al., 2021), expenditure on higher

education per student (Satsyk, 2014), employability

of graduates (Jur

skov

a et al., 2015b,a). The im-

portance of cooperation with business to improve the

competencies and employability of students and, as

a result, the competitiveness of the university, is em-

phasized in the papers (Jur

skov

a et al., 2015b; Lukia-

nenko et al., 2020; Stoimenova, 2019; Teixeira et al.,

2020).

As can be seen from the above review, all these

works are aimed either at the analysis and criticism of

known rating systems, or at the study of factors that

affect the competitiveness of universities, or, at most,

at the creation of own methods for calculating univer-

sity ratings, which are based on the simplest statistical

methods.

There are works in which advanced artiﬁcial intel-

ligence technologies are used to analyze and rank uni-

versities according to certain areas of activity. For ex-

ample, in (Kucherova et al., 2021) developed a fuzzy

logic model for assessment and ranking of universi-

ties’ websites by criterion of usability.

However, the analysis of developments in this di-

rection did not allow to identify studies on the mod-

eling of university competitiveness based on cutting-

edge artiﬁcial intelligence technologies, moreover,

which would not be based in the rating on the expertly

set weights of the evaluation criteria.

2 MODELING METHOD

Solving the task of evaluating the international com-

petitiveness of universities is associated with a num-

ber of speciﬁc problems, because competitiveness

does not have generally accepted evaluation indica-

tor, units or measurement scales. This is a subjec-

tive category that depends on many factors affecting

it. Moreover, the set of these factors and the degree

of inﬂuence of each of them are also not determined

by any objective circumstances and can be chosen by

analysts and researchers depending on their own un-

derstanding of the essence of the category “competi-

tiveness of universities”, the development of the ed-

ucational process, their own priorities, etc. All this

imposes a signiﬁcant imprint of subjectivism on the

formation of methods of their evaluation.

It is possible to reduce the dependence on the sub-

jective opinions of individual experts with the use of

special modeling methods capable of revealing regu-

larities in the structure of an array of heterogeneous

data, when there are no predetermined values of the

resulting indicator, such as for the international com-

petitiveness of universities.

Under such conditions, the clustering approach is

the most appropriate means of searching for hidden

regularities in sets of explanatory variables. The main

feature of this approach is that with its application,

objects that belong to one cluster are more similar to

each other than to objects that are included in other

clusters. As a result, it becomes possible to form

fairly homogeneous groups of researched objects that

are characterized by similar properties.

There is a wide range of cluster analysis methods:

K-means (Hartigan and Wong, 1979), K-medoids

(Kaufman and Rousseeuw, 1990), Principal Com-

ponent Analysis (Jolliffe, 2002), Spectral Clustering

(Von Luxburg, 2007), Dendrogram Method (Sokal

and Rohlf, 1962), Dendrite Method (Cali

nski and

Harabasz, 1974), Self-Organizing Maps – SOM (Ko-

honen, 1982, 2001), Density-Based Spatial Cluster-

ing of Applications with Noise – DBSCAN (Schubert

et al., 2017), Hierarchical DBSCAN – HDBSCAN

(Campello et al., 2013), Ordering Points to Identify

the Clustering Structure – OPTICS (Ankerst et al.,

1999), Uniform Manifold Approximation and Projec-

tion – UMAP (McInnes and Healy, 2018), Balanced

Iterative Reducing and Clustering Using Hierarchies

– BIRCH (Zhang et al., 1996), etc.

Each of these methods has its advantages and ar-

eas of application and tasks, where it reveals itself

in the best way. Experimental studies on compara-

tive analysis of the effectiveness of various cluster-

ing methods are described, in particular, in scientiﬁc

works (Kobets and Novak, 2021; Kobets and Yat-

senko, 2019; Subasi, 2020; Velykoivanenko and Ko-

rchynskyi, 2022).

Taking into account the capabilities of each of the

mentioned methods and the speciﬁcs of this study,

the Kohonen self-organizing maps toolkit was used

to cluster countries by the level of competitiveness of

universities, which, in addition to forming homoge-

neous groups of researched objects, provide a con-

venient tool for visual analysis of clustering results.

In particular, in contrast to other clustering methods,

the location of an object on the Kohonen map im-

mediately indicates to the analyst how developed the

investigated property is compared to others, because

the best and worst objects according to the analyzed

indicator are located in opposite corners of the self-

organizing map.

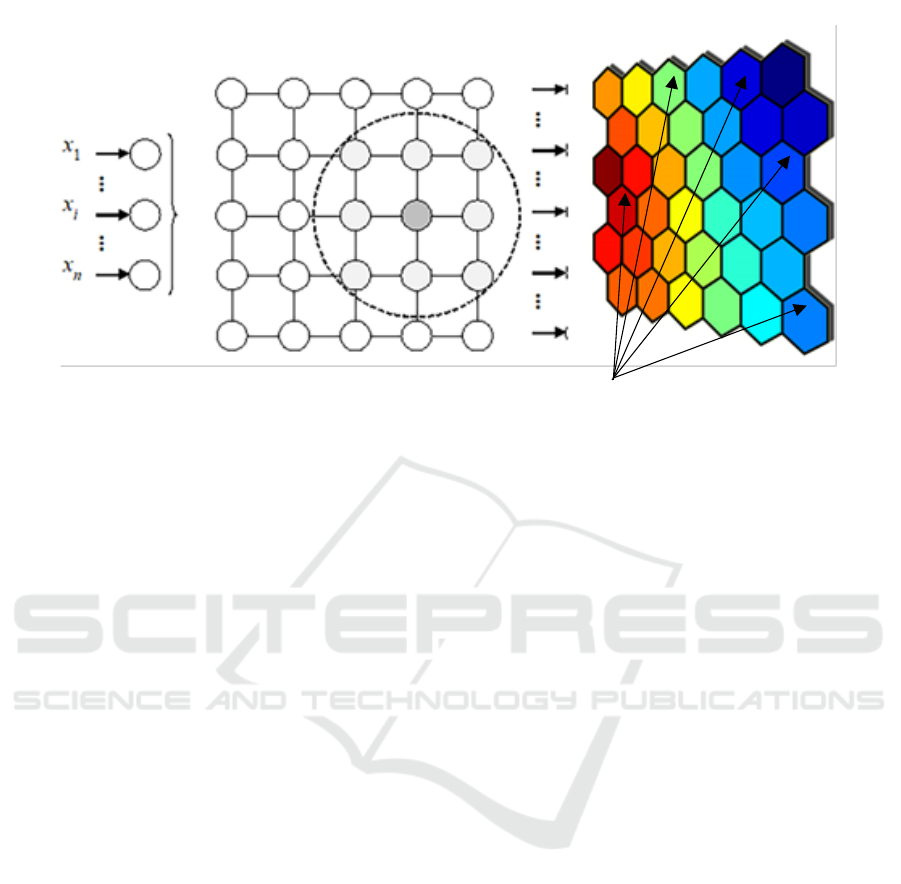
The result of constructing the Kohonen map is

a visual representation of a two-dimensional lattice

of neurons that reﬂect the organizational structure of

the countries of the world, forming clusters in which

Modelling the Design of University Competitiveness

205

countries are similar to each other according to the

group of indicators of evaluating the competitiveness

of universities (ﬁgure 1).

The Kohonen self-organizing algorithm is a clus-

tering method that reduces the dimension of multidi-

mensional data vectors. It can be used to visualize

clusters and to detect nonlinear patterns in input data

structures. The main feature of such neural networks

is unsupervised learning, when information about the

desired network response is not needed to correctly

set the parameters. In this study, self-organizing maps

are used to summarize a complex set of data and clus-

tering of countries by indicators that have the greatest

impact on the international competitiveness of univer-

sities.

Thus, each neuron of the Kohonen layer receives

information about the research object in the form of a

vector x, which consists of n explanatory variables (in

our case, these are the characteristics that determine

the competitiveness of universities). When a new data

vector arrives at the input layer of the network, all

neurons of the self-organization map participate in the

competition to be the winner. As a result of such a

competition, the winner is the neuron

o = argmin





x − w





(1)

that is more similar to the input data vector than oth-

ers, usually by Euclidean distance:



x − w



∑

i=1



− w



, j = 1, K (2)

where x is a vector of input data consisting of indi-

cators {x

, . . . , x

} that describe the objects un-

der study; x

is the vector of parameters of j

neu-

ron of the Kohonen map, which consists of elements

, . . . , w

}; K is the number of neurons of

the Kohonen map.

After determining the neuron-winner, we adjust

the vector of its parameters and its neighbors accord-

ing to the input vector:

(t + 1) = w

(t)+

α(t) · h

o j

(t) ·



x(t) − w

(t)



, j = 1, K (3)

where α(t) is the rate of learning (0 < α(t) ≤ 1),

which decreases with each learning epoch t; h

o j

(t) is

the strength of mutual inﬂuence for any pair of neu-

rons o and j, determined as a function (usually Gaus-

sian) of the distance between them on the map topol-

ogy:

o j

(t) = exp



−

∥r

− r

∥

2 · σ

(t)



(4)

where r

, r

are the two-dimensional vectors of coor-

dinates of geometric location of the neuron-winner o

and the j

neuron on the map; σ(t) is the effective

width of the topological neighborhood (a specially

chosen function of time that monotonically decreases

in the learning process).

In the process of self-organization of the Kohonen

map, the topological neighborhood narrows. This is

caused by a gradual decrease in the width of the func-

tion σ(t). The neuron-winner is located in the center

of the topological neighborhood. It affects neighbor-

ing neurons, but this effect decreases with increasing

distance to them according to (4). As a result, closely

located map nodes acquire similar characteristics.

The result of the learning process will be the

tuning of parameters of the Kohonen layer neurons,

which will correspond to different examples from the

training set. Thus, the self-organization of the struc-

ture of the Kohonen map is carried out, which ac-

quires the ability to combine multidimensional data

vectors in a cluster by identifying similar statisti-

cal characteristics in them. As a result, the ini-

tial high-dimensional space is projected onto a two-

dimensional map. Since self-organization maps are

characterized by the generalization property, they can

recognize input examples on which they have not pre-

viously been tuned – the new input data vector corre-

sponds to the map element to which it is mapped.

3 COLLECTION OF DATA FOR

MODELING

In order to correctly identify regularities in the de-

velopment of the scientiﬁc and educational sphere, it

is necessary to select the key properties that charac-

terize the processes under study, taking into account

the task. That is, it is necessary not only to choose

the maximum possible set of characteristics of the ob-

jects of study, but to form a set of those features that

describe the most signiﬁcant aspects of activity in the

context of the analysis. In this case, the selected fea-

tures will make it possible to group the studied ob-

jects or processes according to their similarity. That

is, if the task of analyzing the competitiveness of uni-

versities is being solved, then it is necessary to deter-

mine a set of characteristics of countries that will in-

ﬂuence this indicator. And as a result of clustering the

countries of the world according to these characteris-

tics, we will get a number of clusters, each of which

will group countries with a similar level of interna-

tional competitiveness of universities (since they will

have fairly close values of the characteristics that de-

termine this competitiveness).

Therefore, we will conduct an analysis of publicly

available databases that contain information on indi-

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

206

universities according to certain areas of activity. For

example, in (Kucherova et al., 2021) developed a fuzzy

logic model for assessment and ranking of universities'

websites by criterion of usability.

However, the analysis of developments in this

direction did not allow to identify studies on the

modeling of university competitiveness based on cutting-

edge artificial intelligence technologies, moreover,

which would not be based in the rating on the expertly set

weights of the evaluation criteria.

2 MODELING METHOD

Solving the task of evaluating the international

competitiveness of universities is associated with a

number of specific problems, because competitiveness

does not have generally accepted evaluation indicator,

units or measurement scales. This is a subjective category

that depends on many factors affecting it. Moreover, the

set of these factors and the degree of influence of each of

them are also not determined by any objective

circumstances and can be chosen by analysts and

researchers depending on their own understanding of the

essence of the category “competitiveness of

universities”, the development of the educational

process, their own priorities, etc. All this imposes a

significant imprint of subjectivism on the formation of

methods of their evaluation.

It is possible to reduce the dependence on the

subjective opinions of individual experts with the use of

special modeling methods capable of revealing

regularities in the structure of an array of heterogeneous

data, when there are no predetermined values of the

resulting indicator, such as for the international

competitiveness of universities.

Under such conditions, the clustering approach is the

most appropriate means of searching for hidden

regularities in sets of explanatory variables. The main

feature of this approach is that with its application,

objects that belong to one cluster are more similar to each

other than to objects that are included in other clusters.

As a result, it becomes possible to form fairly

homogeneous groups of researched objects that are

characterized by similar properties.

There is a wide range of cluster analysis methods: K-

means (Hartigan and Wong, 1979), K-medoids

(Kaufman and Rousseeuw, 1990), Principal Component

Analysis (Jolliffe, 2002), Spectral Clustering (Von

Luxburg, 2007), Dendrogram Method (Sokal and Rohlf,

1962), Dendrite Method (Caliński and Harabasz, 1974),

Self-Organizing Maps – SOM (Kohonen, 1982;

Kohonen, 2001), Density-Based Spatial Clustering of

Applications with Noise – DBSCAN (Schubert et al.,

2017), Hierarchical DBSCAN – HDBSCAN (Campello

et al., 2013), Ordering Points to Identify the Clustering

Structure – OPTICS (Ankerst et al., 1999), Uniform

Manifold Approximation and Projection – UMAP

(McInnes and Healy, 2018), Balanced Iterative Reducing

and Clustering Using Hierarchies – BIRCH (Zhang et al.,

1996), etc.

Each of these methods has its advantages and areas of

application and tasks, where it reveals itself in the best

way. Experimental studies on comparative analysis of the

effectiveness of various clustering methods are

described, in particular, in scientific works (Kobets and

Novak, 2021; Kobets and Yatsenko, 2019; Subasi, 2020;

Velykoivanenko and Korchynskyi, 2022).

Taking into account the capabilities of each of the

mentioned methods and the specifics of this study, the

Kohonen self-organizing maps toolkit was used to cluster

countries by the level of competitiveness of universities,

which, in addition to forming homogeneous groups of

researched objects, provide a convenient tool for visual

analysis of clustering results. In particular, in contrast to

other clustering methods, the location of an object on the

Kohonen map immediately indicates to the analyst how

developed the investigated property is compared to

others, because the best and worst objects according to

the analyzed indicator are located in opposite corners of

the self-organizing map.

The result of constructing the Kohonen map is a

visual representation of a two-dimensional lattice of

neurons that reflect the organizational structure of the

countries of the world, forming clusters in which

countries are similar to each other according to the group

of indicators of evaluating the competitiveness of

universities (see figure 1).

Figure 1: Visual representation of clusters on the self-organizing map (Matviychuk et al., 2019).

Neurons

Kohonen layer (self-organizing map)

Input layer

Clusters

Figure 1: Visual representation of clusters on the self-organizing map (Matviychuk et al., 2019).

cators that can inﬂuence the level of competitiveness

of universities.

Thus, the World Bank’s “World Development In-

dicators” database contains the ranking of the world’s

countries by the level of “Government expenditure on

education, total (% of GDP)” indicator (The World

Bank, 2022). The indicator is calculated annually

(for 266 countries) based on data from national statis-

tics and international organizations, including data

from the UN. Information on individual countries has

been available in this database since 1970, in the last

decade the data is presented quite fully, but only un-

til 2018 (later data by countries is much less). Other

indicators presented in this database are much poorer

and less related to higher education.

In the Human Development Reports of UNDP

(United Nations Development Programme, 2022)

there are data for 195 countries for 2021 according to

the indicators: “Human Development Index (HDI)”

(both in general and by male and female sexes, in ad-

dition, by this indicator also shows the dynamics and

increases in dynamics since 1990), “Government ex-

penditure on education, % of GDP”, “High-skill to

low-skill ratio”, “Research and development expendi-

ture, % of GDP” (during 2014-2018), “Ratio of edu-

cation and health expenditure to military expenditure”

(during 2010-2017), “Foreign direct investment, net

inﬂows, % of GDP”, “International student mobility,

% of total tertiary enrollment”, indicators of employ-

ment and unemployment both in general and among

young people, migrants, population by age group, etc.

The Global Competitiveness Index from the

World Economic Forum for 2019 (World Economic

Forum, 2019) can also be informative in assessing the

international competitiveness of the country’s univer-

sities. On this resource, this index is given for 141

countries. Later, in 2020, the Global Competitiveness

Index has been paused.

Another resource with information on competi-

tiveness is the annual reports of the European Com-

mission (European Commission, 2022), in particu-

lar in the areas of: “Competitiveness & Innovation”,

which contains separate reports and the following sec-

tions: “Global Innovation Index”, “Global Attractive-

ness Index”, “Global Talent Competitiveness Index”,

“Elcano Global Presence Index”, “Innovation Output

Indicator”; “Learning & Research”, which presents

reports: “European Skills Index”, “European Lifelong

Learning Indicators (ELLI-Index)”, “Higher Educa-

tion Rankings”, “Composite Learning Index”.

The work “Global Talent Competitiveness Index:

2019” (Lanvin and Monteiro, 2019) contains inte-

grated assessments and ranking places of countries for

a number of top-level indices, as well as for basic in-

dicators.

To assess the competitiveness of world universi-

ties, the resource (UNIVERSITAS 21, 2021) can be

useful, which provides fairly detailed country-level

aggregated information on the research and educa-

tional activities of universities in 50 countries for

2020. Here are the indicators grouped into four gen-

eralized categories – “Resources”, “Environment”,

“Connectivity”, “Output”. Each of these categories

consists of a set of basic indices, all of which are listed

in the header of the table 1.

In addition, we add to the database the overall

competitiveness score and rank number in the general

list (these indicators will not be taken into account

Modelling the Design of University Competitiveness

207

Table 1: Indicators of evaluation of international competitiveness of countries’ universities.

OVERALL

RANKING

RESOURCES

2020 SCORES

ENVIRONMENT

2020 SCORES

CONNECTIVITY

2020 SCORES

OUTPUT

2020 SCORES

Country

Rank 2020

Rank 2019

Score 2020

Score 2019

Government expenditure on tertiary

education as a percentage of GDP

Total expenditure on tertiary

education as a percentage of GDP

Total expenditure per student USD PPP

Expenditure in tertiary institutions

for R&D as a percent of GDP

Expenditure in tertiary institutions

for R&D per head of population

Proportion of female students

Proportion of female academic staff

Data quality

Qualitative index of environment

WEF Survey

Proportion of international students

Proportion of articles with international collaborators

Webometrics VISIBILITY index divided by population

Rating of knowledge transfer

between university and companies

Percentage of university research

publications co-authored with industry

Total number of documents produced

by higher education institutions

Total documents produced per head of population

Average impact of articles

Weighted Shanghai ranking scores for

universities per head of population

Shanghai scores for best three universities

Tertiary enrollment rates

Percentage of population aged 24-64

with a tertiary qualiﬁcation

Number of researchers in the nation per head of population

Unemployment rate of the tertiary

educated compared with school leavers

Argentina 40 38 46 45,1 56,7 48,4 13,8 13,4 4,7 100 97,1 100 67,8 51,3 9,1 52,4 7 54,1 19,5 2,1 6,2 45,9 2,6 13,1 90 61,6 14,9 30,9

Australia 9 8 82,2 80,9 37,7 70,6 42,9 64 51,2 100 91,3 100 98,1 81,9 78,9 72,8 56 68,1 41,4 15,9 85,3 84,3 76,8 39,3 100 79 55 32,6

Austria 12 12 79,3 77,2 81,9 64,8 48,7 68,6 63,7 100 84,7 100 72 68,3 63,1 86,9 54 84,8 100 3,3 49,4 86 57 22 85,1 56,5 62,5 31,3

Belgium 13 13 75,6 73,6 63,8 55,4 48,3 53 45 100 97,1 100 75,8 82,2 31,8 89,3 28,4 82,5 78,8 4,8 56,6 94,2 51,4 31,4 79,7 70,2 59,9 39,1

Brazil 41 40 45,6 44,1 49,9 66,5 37,9 n.a. n.a. 100 91,4 88,6 63,8 41,8 0,9 43,8 6,9 40,3 26,2 11,6 7,5 45,3 3,8 21,2 51,3 31,8 10,7 39,7

Bulgaria 45 44 42,7 41,8 32,3 40,3 17,8 4,3 1,6 100 97,9 93,2 53,1 54,7 16,8 57,5 10,9 46 44,3 0,8 14,6 55,2 3,3 2,7 71,2 38,1 25,8 45,2

Canada 7 6 83,2 81,9 62,5 86,8 62,9 63,6 53 100 88,6 90,9 73,3 87,1 47,4 68,8 69,2 86,3 59 17,2 62,6 82 44 42,9 88,2 100 51,8 33,7

Chile 31 32 54,3 51,3 48,4 100 22,3 14,8 6 100 85,1 100 81,4 54,8 1,4 81,6 14,3 62,3 28,3 2,2 16,1 63,4 8,2 11,8 88,5 43,5 6,1 30,2

China 26 27 56,8 54,7 42,5 50,7 20 15 4,4 100 n.a. 88,6 76,6 73 1,3 34,1 8,4 65,9 32 70,7 6,8 59,3 7,5 39,6 49,1 16,7 15 n.a.

Croatia 43 43 43,6 42,1 49,9 36,8 18 24,9 11,2 100 97,8 93,2 47,3 47 1,6 58,3 11 35,5 50,8 0,9 30,4 52,9 17,2 8 66,5 39,2 22,6 31,2

Czech Rep. 29 26 54,8 55,2 36,3 35,1 26,6 34,4 22,2 100 76,9 100 69,3 61,1 46,1 62 29,3 53,6 55,7 2,9 37 62,8 22 14,7 64,1 41,9 44,7 40,4

Denmark 3 5 85,7 82,5 80,4 62,7 44,9 100 91,4 100 88,6 95,5 67,4 80,6 39,5 85,3 47,5 89,2 85,2 4,3 100 97,1 83,3 38,8 80,6 65,7 95,7 21

Finland 8 9 82,8 80,4 80,8 61,9 46,6 68,5 54,6 100 100 100 81,6 93,8 30 82,3 64,7 90 77 2,9 70,8 86 72,2 23,9 88,2 78,1 81,3 41,3

France 17 17 68,6 67,6 57 53,6 43 44,3 35 100 87,9 100 73,1 69,6 37,4 77,7 23,8 70,3 68,8 13,5 28,2 75,6 28,9 40,6 65,6 63,7 53,8 39,8

Germany 16 16 70,5 69,6 51,3 44,9 46,3 51,2 46 97 78,6 100 61,6 86,8 30,8 67,8 38,6 87,9 76 21 34,2 79,1 32,9 39,7 70,2 50,2 61 37

Greece 37 37 47,4 47 35,1 26 10,9 31,8 15,5 97,1 68,6 93,2 26,9 49,2 12,5 68,7 35,2 43,7 61,5 2,5 31,2 73,3 21 14,1 100 54,8 38,2 36

Hong Kong 14 15 72,7 70,2 50,1 55,6 64,7 39,8 43,3 100 n.a. 90,9 97,2 76,7 42 54,3 48,2 82,5 35,8 3,5 63,7 95,9 54,9 26,3 74,3 50,9 41,4 41,4

Hungary 33 35 51,3 48,5 34,7 39,7 30 17,6 8,8 100 80,5 100 51,6 47 36,6 70,9 22,1 58,6 82,8 1,6 22,3 69,2 14,4 10,7 48,5 43,4 35,4 54,6

India 49 49 39,6 38,8 54,8 59,1 13 2,4 0,3 96,2 81,2 90,9 58,1 74,6 0,5 27,2 0,9 57,8 19 14,9 1,5 47,1 0,6 12,5 27,4 18,3 2,6 12,6

Indonesia 50 50 35 33,5 25,7 25 7,9 4,6 1 100 86,2 100 64,7 71,6 0,3 23,6 4,4 72,5 31,4 3,1 1,6 45,3 0 0 36,4 20,5 2,6 26,4

Iran 47 48 42,2 39,2 50,2 51,9 15 n.a. n.a. 92,1 62,2 81,8 67 52,8 1,6 33,7 5,1 52,1 10,6 7,3 12 51,7 5 15,2 69,6 36,9 8,1 n.a.

Ireland 19 19 66 64,7 28,7 29,6 35,2 25,2 33,7 100 90 100 68,6 87,6 32,6 75,1 60,1 88,2 63 2,4 64,8 80,8 47,6 18,7 77,8 81,1 49,8 36,8

Israel 18 18 67,4 67,3 39,4 52,1 29,6 50,9 34,6 100 n.a. 95,5 73,3 74,9 10,6 66,3 34,6 91,1 49,5 3,2 48,5 77,9 51,5 30,6 63,4 88 100 34,6

Italy 30 30 54,5 53,4 28,6 33 30,8 32,1 22,5 100 74,2 100 63,8 60 19,5 62,9 18 60,5 54,2 15,7 34,9 77,3 29,4 24,6 61,9 33,4 27,8 35,6

Japan 20 20 61,9 61,7 21,2 51,2 51 37,6 28,9 95,4 56,8 100 83,2 70,8 15,7 39 18,9 57 78 17,2 18,4 50,6 14,5 42,9 63,6 89,7 64,3 34,5

Korea 24 23 58 57,4 32,7 64,4 27,8 37,7 25,7 83,4 70,2 100 58 56,3 8,3 37,9 14,8 62,6 61,4 12,4 32,3 56,4 24,1 24,8 94,3 84,7 91,1 25,2

Malaysia 27 28 56,1 54,5 56,5 75,1 39,4 48 22,9 100 100 95,5 78,6 83,7 29,6 59,5 7,5 79,4 16,3 3,6 15,1 55,8 5,8 14 43,7 37,7 28,6 21,6

Mexico 48 47 41,7 41,1 47,2 50,5 19,5 12,7 4,1 100 n.a. 95,5 82,4 48,5 2,1 53 3,8 52,9 19,5 3 3,2 42,4 0,8 11,1 40,2 31,1 3 20,7

Netherlands 10 10 81,6 80,2 59,8 62,7 51,8 58,3 54,3 100 91,7 100 79,3 88 40,4 82,5 47,5 96,7 85,4 9 70,7 97,7 59,4 37,5 85 66,2 60,7 34,7

New Zealand 14 14 72,7 71,5 44,1 64,5 39,7 33,6 21,4 100 99,7 100 89,7 86,5 72 77,3 55,8 76,1 46,4 2,2 59,5 79,1 64,6 18,4 82 67,9 49,1 33,9

Norway 11 11 80,5 77,8 89,9 70,7 58,4 68,8 74,8 100 92,6 100 66,9 85,9 11,6 80,8 58,9 81 61,8 3,1 78,2 87,2 63 28,1 82 75,3 78,5 32,2

Poland 32 31 52,6 52,2 48,4 43,9 23,8 33,3 17,2 100 90 100 81,9 58,3 15,1 42,3 17,3 60,4 32,3 6,4 22,8 58,1 7,3 14,1 67,8 53,4 30,6 49,1

Portugal 25 25 57,6 56,8 39,4 42,6 29,3 55,3 31 100 88,6 100 60,9 71,7 23,5 71,9 33,9 64,5 41,5 3,6 47,2 66,9 26,7 18,7 63,9 43,1 52 33,7

Romania 44 45 43 41,7 32,9 42,8 28,9 5,2 2,4 100 100 95,5 76 45,2 17,7 36,6 10,2 54 32,1 2,3 15,9 50,6 2,7 5,9 48,2 29,6 10,8 45,8

Russia 35 35 49,1 48,5 37,3 42,5 22,5 9,8 4,6 100 100 100 70,2 60,1 15 36,2 8,4 43,9 20,1 8,8 8,3 47,7 2,9 21,7 81,9 97,9 34,6 47,7

Saudi Arabia 22 22 59,3 59,3 100 77,7 53,1 n.a. n.a. 96,3 81,7 79,5 50,5 69,3 17,1 100 3,9 68,9 29,6 3,1 12,7 76,7 7,8 24,8 69,7 41,2 n.a. 9,4

Serbia 42 41 44,2 43,4 55,8 48,7 17,4 32,9 8,8 100 93,1 90,9 42,3 52,9 16,3 62,1 8,5 52,1 23,7 1,1 20,5 53,5 9,3 7,4 66,5 37,2 25,2 28,7

Singapore 4 7 84,5 81,3 50,1 53,7 100 63,4 100 100 74,1 95,5 82 94 100 87,7 36,7 91,7 38,6 2,8 66,5 94,8 41,4 26,5 84,8 86,5 81,6 30,6

Slovakia 38 33 47,2 49,6 35,8 37 30,3 21,2 11,9 100 91,5 100 64,2 44,8 25,3 57,7 16,8 35,6 64,4 1 24,2 63,4 4,7 2,9 46,6 42,5 33,9 46,4

Slovenia 28 29 55,4 53,6 44,5 38,3 29,9 20,3 12,6 100 85,1 100 63,7 65,3 14,3 71,1 25,1 63,1 53,6 0,7 48,8 67,4 31,4 7,4 78,6 56,1 54,2 35,9

SAR 34 34 49,7 48,7 37,4 49,9 28,9 26,2 6,1 100 n.a. 88,6 86,7 45,3 11,9 68,6 3,7 54,8 36,9 3,7 8,6 69,8 5,8 18,6 22,4 12,4 6 100

Spain 23 24 58,6 57,3 41,6 45,9 33,5 32 21,6 100 86,9 100 69,9 59,5 11,9 61,6 30,7 57 46,2 12,7 37 65,7 29,9 22 88,9 64,4 34,8 39,7

Sweden 5 4 84,3 82,9 71,2 59,7 64,6 83,2 73,7 100 89,7 100 75,2 76,9 24,8 86,8 59,6 83,1 86,2 6,3 83,5 89,5 82,5 38,8 67 74,7 92 24,4

Switzerland 2 2 90,1 88,6 64,9 51,7 75,4 88 97,6 99,4 71 100 69,5 100 65,2 91,3 79,7 100 76,9 5,8 91,7 100 100 44,2 59,6 75,6 63,7 30,4

Taiwan 21 21 60,5 60,5 33,5 51,8 32,8 29,3 26,2 100 72 93,2 86,9 72,3 16,2 45,4 44,3 80 38,3 5,1 29,1 55,2 20,3 19,7 84,5 84,5 76,1 25

Thailand 46 46 42,3 41,2 32,1 34,8 13,7 13,7 4,2 100 100 95,5 71,9 60,1 4,8 57,8 10,2 65,5 34,7 2,1 4,3 53,5 1,8 11,3 49,3 28,1 14,7 18,2

Turkey 39 42 46,3 43,3 71,1 70,5 27,9 31,5 14,8 92 88 100 44,9 51,3 5,5 30,6 7,6 57,4 16,6 7,2 11,9 44,2 4,1 11,2 94,7 35,9 16,8 23,2

Ukraine 36 38 47,8 45,1 76,4 63,9 10,8 3,2 0,5 100 n.a. 90,9 60,6 62,4 11,6 41,2 8 45,8 60,4 1,3 4,2 33,1 0 0 83,4 84,4 12 58,3

UK 6 3 83,6 84,5 28,2 64,7 63,1 38,8 29,7 100 89,5 100 89,5 75,5 65,8 72,1 63,7 82,1 68,9 31,1 63,1 86 58,1 73,7 60 79,1 53,1 34,4

USA 1 1 100 100 42,6 91,2 80,1 35,7 37,7 100 98,2 100 100 90,8 19 45 100 92,3 58,4 100 41,2 78,5 43,4 100 88,2 81,9 51,6 48,7

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

208

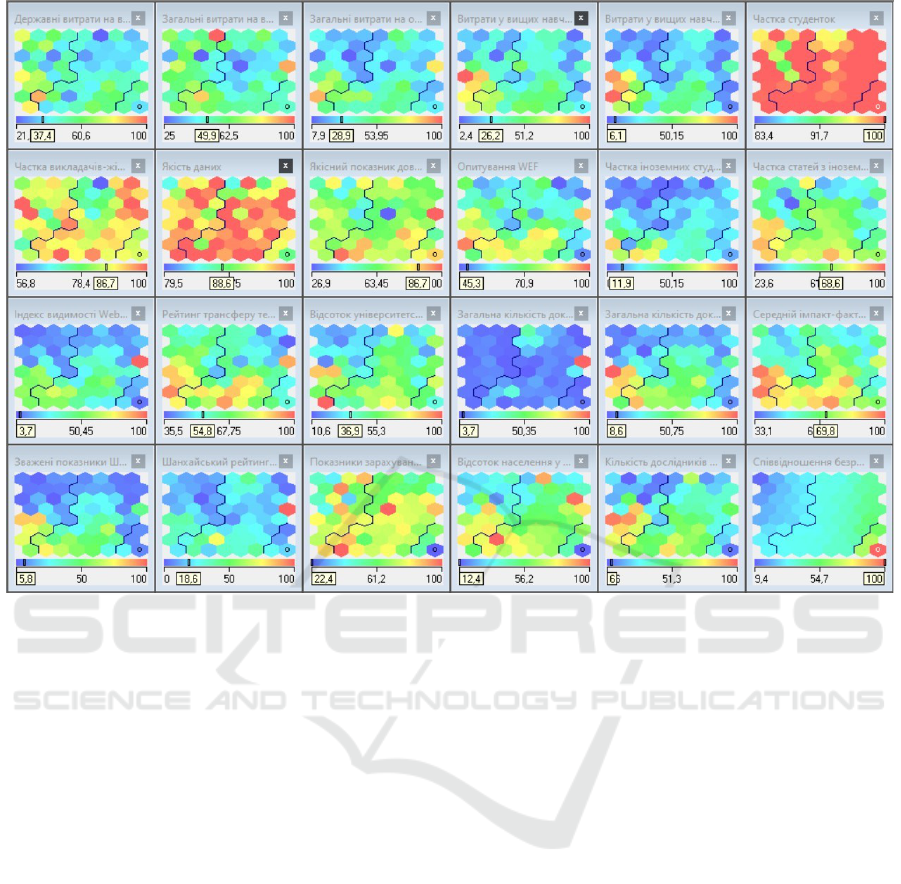
Figure 2: Kohonen topological maps for all indicators of university competitiveness assessment.

when clustering countries, but will serve as a refer-

ence when analyzing clusters).

To carry out clustering based on Kohonen maps,

it is necessary to avoid gaps in the data. Since there

are only 50 countries in this database, moreover, the

scores for each individual indicator for different coun-

tries are quite close to each other, so we will not divide

countries into groups and replace the blanks with the

corresponding average values for all countries. This

will not lead to distortions of the clustering results,

since the percentage of gaps in this database is very

small.

4 MODELING THE UNIVERSITY

COMPETITIVENESS

The construction of Kohonen self-organizing maps in

our study was carried out using the analytical plat-

form Deductor Studio Academic. In the process of

constructing a map, the task of ﬁnding its optimal di-

mension (number of neurons) arises, which is imple-

mented experimentally on the basis of statistical data.

The dimension of the self-organizing map was chosen

from various options according to the mean weighted

quantization error criterion, which reﬂects the aver-

age distance between the data vector given to the map

inputs and neurons’ parameters.

A hexagonal lattice of neurons with dimensions of

8 by 8 was determined as the most adequate structure

of a self-organizing map for this task according to a

given set of indicators (table 1). Self-organization oc-

curs over 1500 learning epochs.The map parameters

are initialized with small random variables. Gaussian

(4) was chosen as a function of the neighborhood of

neurons. Since all indicators for assessing the com-

petitiveness of universities are already presented on

an identical scale from 0 to 100, none of them will

have a decisive inﬂuence on the clustering process.

Therefore, it was decided to build Kohonen maps on

the original data without processing them. As a re-

sult of the process of self-organization, the countries

from the table 1 were distributed among three clus-

ters, which can be seen in ﬁgure 2.

As can be seen from the topological maps for all

indicators in ﬁgure 2, for the vast majority of them

there is no clear demarcation of their levels between

clusters. That is, their low, medium and high values

are evenly distributed throughout the map, which, to-

gether with the low levels of signiﬁcance of many in-

dicators (ﬁgure 3), does not contribute to the quality

of the countries segmentation process.

Modelling the Design of University Competitiveness

209

Indicator

Significance of the indicator

Cluster 1 Cluster 2 Cluster 3 In all

Proportion of female

students

Data quality

Total expenditure per

student USD PPP

Total expenditure on

tertiary education as a

percentage of GDP

Proportion of

international students

Proportion of female

academic staff

Proportion of articles

with international

collaborators

Given the low significance of a large number of

indicators selected for the study, a series of experiments

was conducted on the construction of Kohonen maps on

different sets of input variables, when various

combinations of the least influential factors were

alternately removed. However, each time the same low

quality of the distribution of countries by the levels of

university competitiveness evaluation indicators

remained. For example, for all clustering options,

Bulgaria, South Africa, Poland, the Russian Federation,

Romania, Slovakia, Hungary, and Croatia were located

next to Ukraine on Kohonen map, but the United States

was also a neighbor in this cluster. Of course, such

segmentation of countries cannot be considered

acceptable.

Therefore, it was decided to apply z-score

standardization to process the initial values of the

variables. As a result of forming a map on the full set of

standardized explanatory variables, 5 clusters were

obtained (see figure 4).

Figure 3: Levels of signiﬁcance of a number of indicators for evaluating the competitiveness of universities.

Given the low signiﬁcance of a large number of

indicators selected for the study, a series of experi-

ments was conducted on the construction of Koho-

nen maps on different sets of input variables, when

various combinations of the least inﬂuential factors

were alternately removed. However, each time the

same low quality of the distribution of countries by

the levels of university competitiveness evaluation in-

dicators remained. For example, for all clustering

options, Bulgaria, South Africa, Poland, the Russian

Federation, Romania, Slovakia, Hungary, and Croatia

were located next to Ukraine on Kohonen map, but

the United States was also a neighbor in this cluster.

Of course, such segmentation of countries cannot be

considered acceptable.

Therefore, it was decided to apply z-score stan-

dardization to process the initial values of the vari-

ables. As a result of forming a map on the full set

of standardized explanatory variables, 5 clusters were

obtained (ﬁgure 4).

Figure 4 shows that the levels of indicators change

when crossing from cluster to cluster, which indi-

cates a successful delimitation of countries based on

a given set of explanatory variables. Ukraine got to

the upper right corner of the Kohonen map next to

Argentina, Bulgaria, Poland, the Russian Federation,

Serbia, Turkey, Croatia, and Chile. Somewhat lower

in the same cluster were Brazil, India, Indonesia, Iran,

China, Malaysia, Mexico, South Africa, Romania,

Slovakia, and Thailand.

Austria, Denmark, the Netherlands, Norway, Sin-

gapore, Finland, Switzerland, Sweden are located in

the opposite corner of the map from Ukraine (bottom

left). The United States and Great Britain were lo-

cated in the upper left corner of the map. They are

surrounded by Australia, Hong Kong, Israel, Canada,

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

210

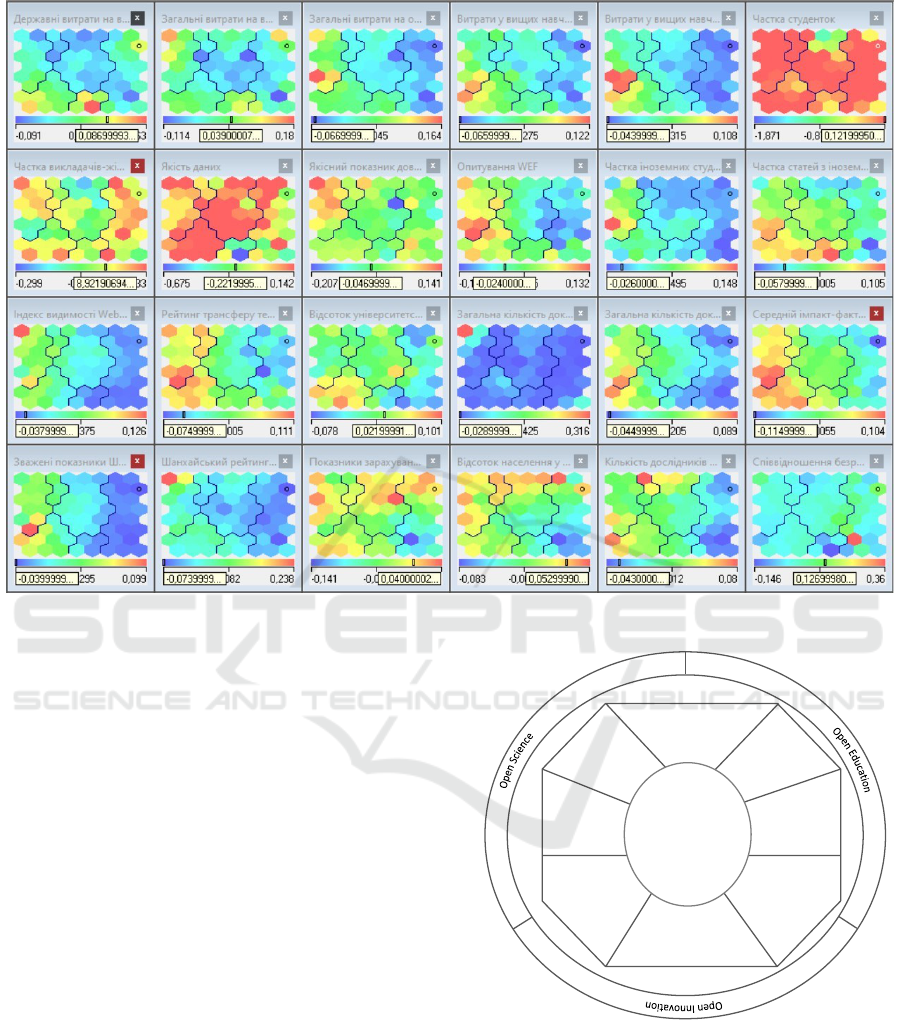
Figure 4: Kohonen topological maps according to the normalized indicators of university competitiveness assessment.

and Taiwan.

It should be noted that since, in accordance with

the given task, polar objects are located on the Ko-

honen map in opposite corners, this self-organization

of countries indicates that the competitiveness of

Ukrainian universities is currently quite far from the

competitiveness of universities in developed coun-

tries.

The analysis of the characteristics of the univer-

sities of the countries of the most developed cluster

makes it possible to determine the priority areas of de-

velopment and tasks that must be solved in order to in-

crease the international competitiveness of Ukrainian

universities.

Research and generalization of traditional, en-

trepreneurial, innovative and creative models of uni-

versities, their selection depending on objective en-

dogenous and exogenous conditions and imperatives

of the development of Ukrainian higher education

made it possible to substantiate the most adaptive

competitive model of the university, which is shown

in ﬁgure 5.

Critically important in the proposed model is the

development of strategic partnership in the triangle

“science – business – education”, public-private part-

nership and consolidated social responsibility.

Figure 5: Competitive model of the university.

CONCLUSIONS

The global transformation of university education raises

new challenges for state authorities in the field of

education and university administrations to ensure their

competitiveness in the international market of

educational services. In the context of increasing the

efficiency of the university management process in

modern globalization conditions, the tasks of assessing

its international competitiveness arise.

In today’s world, the ways of innovative behavior of

corporations, universities and other organizations must

take into account the need to act in conditions of political,

market and social turbulence, which necessitates the

constant generation of non-standard ideas, strategic

concepts, models and behaviors.

This research is aimed at developing a new

methodological approach to the study of such a poorly

formalized indicator as the competitiveness of

universities. Since competitiveness does not have

generally accepted evaluation indicator, units or

measurement scales, etc., it was decided to apply the

clustering approach for searching of hidden regularities

in the set of explanatory variables.

Accordingly, the article carried out a thorough

analysis of existing approaches to evaluating the

competitiveness of universities and identified unresolved

problems in this sphere. In addition, various methods of

clustering, their advantages and features were analyzed,

and the most appropriate method for solving the problem

was chosen.

The use of the Kohonen self-organizing map toolkit

was justified, which, in addition to forming

homogeneous groups of researched objects, provide a

convenient tool for visual analysis of clustering results.

In addition, the methodology of self-organizing maps

provides an analytical tool for searching the indicators

which are lagging the most, so that management actions

can be focused on increasing the competitiveness of

Ukrainian universities in the global market of educational

services.

As a result of the conducted research, a competitive

model of the university was formed during the analysis

of the competitive advantages of the universities of the

countries included in the most competitive cluster.

REFERENCES

Ankerst, M., Breunig, M., Kriegel, H.-P., and Sander, J. (1999).

OPTICS: Ordering points to identify the clustering

structure. ACM SIGMOD Record, 28(2):49-60.

http://dx.doi.org/10.1145/304182.304187.

Anowar, F., Helal, M.A., Afroj, S., Sultana, S., Sarker, F., and

Mamun, K.A. (2015). A Critical Review on World

University Ranking in Terms of Top Four Ranking

Systems. In K. Elleithy and T. Sobh (Eds.), Lecture Notes

Intelligence concentration

(professors, researchers,

students)

Academic quality

and integrity

Diversified

financial system

Innovation

management

Integration of

research and

teaching

Entrepreneurial

motivation and

behavior

Developed digital

infrastructure

Creative

thinking and

culture

Efficient

research and

development

Figure 5: Competitive model of the university.

5 CONCLUSIONS

The global transformation of university education

raises new challenges for state authorities in the ﬁeld

of education and university administrations to ensure

their competitiveness in the international market of

educational services. In the context of increasing the

Modelling the Design of University Competitiveness

211

efﬁciency of the university management process in

modern globalization conditions, the tasks of assess-

ing its international competitiveness arise.

In today’s world, the ways of innovative behavior

of corporations, universities and other organizations

must take into account the need to act in conditions of

political, market and social turbulence, which neces-

sitates the constant generation of non-standard ideas,

strategic concepts, models and behaviors.

This research is aimed at developing a new

methodological approach to the study of such a poorly

formalized indicator as the competitiveness of univer-

sities. Since competitiveness does not have generally

accepted evaluation indicator, units or measurement

scales, etc., it was decided to apply the clustering ap-

proach for searching of hidden regularities in the set

of explanatory variables.

Accordingly, the article carried out a thorough

analysis of existing approaches to evaluating the com-

petitiveness of universities and identiﬁed unresolved

problems in this sphere. In addition, various methods

of clustering, their advantages and features were an-

alyzed, and the most appropriate method for solving

the problem was chosen.

The use of the Kohonen self-organizing map

toolkit was justiﬁed, which, in addition to forming

homogeneous groups of researched objects, provide

a convenient tool for visual analysis of clustering re-

sults.

In addition, the methodology of self-organizing

maps provides an analytical tool for searching the in-

dicators which are lagging the most, so that manage-

ment actions can be focused on increasing the com-

petitiveness of Ukrainian universities in the global

market of educational services.

As a result of the conducted research, a compet-

itive model of the university was formed during the

analysis of the competitive advantages of the universi-

ties of the countries included in the most competitive

cluster.

REFERENCES

Ankerst, M., Breunig, M. M., Kriegel, H.-P., and Sander,

J. (1999). OPTICS: Ordering Points to Identify the

Clustering Structure. In Proceedings of the 1999 ACM

SIGMOD International Conference on Management

of Data, SIGMOD ’99, page 49–60, New York, NY,

USA. Association for Computing Machinery. https:

//doi.org/10.1145/304182.304187.

Anowar, F., Helal, M. A., Afroj, S., Sultana, S., Sarker,

F., and Mamun, K. A. (2015). A Critical Review

on World University Ranking in Terms of Top Four

Ranking Systems. In Elleithy, K. and Sobh, T., editors,

New Trends in Networking, Computing, E-learning,

Systems Sciences, and Engineering, pages 559–566,

Cham. Springer International Publishing. https://doi.

org/10.1007/978-3-319-06764-3 72.

Avralev, N. and Eﬁmova, I. (2015). University Rank-

ings as a Tool for Assessing the Quality of Educa-

tion in the Context of Globalization. Asian Social

Science, 11(10):292–298. https://doi.org/10.5539/ass.

v11n10p292.

Avralev, N. V. and Eﬁmova, I. N. (2013). University Rank-

ings as a Tool to Enhance Competitiveness, Cluster-

ing and Transnational Governance of Higher Educa-

tion in the Context of Globalization. Middle-East

Journal of Scientiﬁc Research, 16(3):357–361. https:

//www.idosi.org/mejsr/mejsr16(3)13/7.pdf.

Cali

nski, T. and Harabasz, J. (1974). A dendrite

method for cluster analysis. Communications

in Statistics, 3(1):1–27. https://doi.org/10.1080/

03610927408827101.

Campello, R. J. G. B., Moulavi, D., and Sander, J. (2013).

Density-based clustering based on hierarchical den-

sity estimates. In Pei, J., Tseng, V. S., Cao, L., Mo-

toda, H., and Xu, G., editors, Advances in Knowl-

edge Discovery and Data Mining, pages 160–172,

Berlin, Heidelberg. Springer Berlin Heidelberg. https:

//doi.org/10.1007/978-3-642-37456-2 14..

Chl

adkov

a, H., Sk

ypalov

a, R., and Bla

skov

a, V. (2021).

Strengthening the university competitiveness in the

Czech Republic. Tuning Journal for Higher Educa-

tion, 9(1):127–155.

Deem, R., Mok, K. H., and Lucas, L. (2008). Trans-

forming higher education in whose image? explor-

ing the concept of the ‘world-class’ university in eu-

rope and asia. Higher Education Policy, 21(1):83–97.

https://doi.org/10.1057/palgrave.hep.8300179.

Dimitrova, G. and Dimitrova, T. (2017). Competitiveness

of the universities: measurement capabilities. Trakia

Journal of Sciences, 15(1):311–316. https://doi.org/

10.15547/tjs.2017.s.01.055.

European Commission (2022). Statistical Au-

dits. https://knowledge4policy.ec.europa.eu/

composite-indicators/statistical-audits en.

Hartigan, J. A. and Wong, M. A. (1979). Algorithm AS

136: A K-Means Clustering Algorithm. Journal of the

Royal Statistical Society. Series C (Applied Statistics),

28(1):100–108. https://doi.org/10.2307/2346830.

Jolliffe, I. T. (2002). Principal Component Analysis.

Springer Series in Statistics. Springer, 2nd edition.

https://link.springer.com/book/10.1007/b98835.

Jur

skov

a, O., Ju

ıkov

a, M., and Kocourek, J. (2015a).

Brand Building of a University as an Integral Part of

the Educational Process. The Turkish Online Journal

of Educational Technology,(Special Issue for INTE

2015):100–105. http://tojet.net/special/2015 9 1.pdf.

Jur

skov

a, O., Ju

ıkov

a, M., and Kocourek, J. (2015b). In-

novation of Educational Process as a Factor of En-

hancing Competitiveness. The Turkish Online Jour-

nal of Educational Technology,(Special Issue 2 for

INTE 2015):301–305. http://www.tojet.net/special/

2015 7 2.pdf.

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

212

Kaufman, L. and Rousseeuw, P. J. (1990). Partitioning

Around Medoids (Program PAM), chapter 2, pages

68–125. Wiley Series in Probability and Statistics.

John Wiley & Sons, Ltd. https://doi.org/10.1002/

9780470316801.ch2.

Kobets, V. and Novak, O. (2021). EU countries clustering

for the state of food security using machine learning

techniques. Neiro-Nechitki Tekhnolohii Modelyuvan-

nya v Ekonomitsi, 2021(10):86–118.

Kobets, V. and Yatsenko, V. (2019). Inﬂuence of the

Fourth industrial revolution on divergence and con-

vergence of economic inequality for various coun-

tries. Neiro-Nechitki Tekhnolohii Modelyuvannya v

Ekonomitsi,2019(8):124–146.

Kohonen, T. (1982). Self-organized formation of topolog-

ically correct feature maps. Biological Cybernetics,

43(1):59–69. https://doi.org/10.1007/BF00337288.

Kohonen, T. (2001). Self-organizing maps, volume 30 of

Springer Series in Information Sciences. Springer

Berlin, Heidelberg, 3 edition. https://doi.org/10.1007/

978-3-642-56927-2.

Kucherova, H., Honcharenko, Y., Ocheretin, D., and Bil-

ska, O. (2021). Fuzzy logic model of usability of

websites of higher education institutions in the con-

text of digitalization of educational services. Neiro-

Nechitki Tekhnolohii Modelyuvannya v Ekonomitsi,

2021(10):119–135.

Lanvin, B. and Monteiro, F. (2019). Global Talent Com-

petitiveness Index 2019. INSEAD. https://nonews.co/

wp-content/uploads/2019/06/GTCI2019.pdf.

Lukianenko, D., Lukianenko, O., Mozghalli, O., Dvornyk,

I., and Oriekhov, M. (2020). Digital imperative of uni-

versity activities transformation. Financial and credit

activity: problems of theory and practice, 4(35):449–

458. https://doi.org/10.18371/fcaptp.v4i35.222478.

Lukianenko, D. and Strelchenko, I. (2021). Neuromodeling

of features of crisis contagion on ﬁnancial markets be-

tween countries with different levels of economic de-

velopment. Neiro-Nechitki Tekhnolohii Modelyuvan-

nya v Ekonomitsi, 2021(10):136–163.

Lukman, R., Krajnc, D., and Glavi

c, P. (2010). Uni-

versity ranking using research, educational and en-

vironmental indicators. Journal of Cleaner Produc-

tion, 18(7):619–628. https://doi.org/10.1016/j.jclepro.

2009.09.015.

Marginson, S. and van der Wende, M. (2016). To Rank

or To Be Ranked: The Impact of Global Rankings in

Higher Education. Journal of Studies in International

Education, 11(3-4):306–329. https://doi.org/10.1177/

1028315307303544.

Matviychuk, A., Lukianenko, O., and Miroshnychenko,

I. (2019). Neuro-fuzzy model of country’s invest-

ment potential assessment. Fuzzy economic review,

24(2):65–88. https://doi.org/10.25102/fer.2019.02.04.

McInnes, L. and Healy, J. (2018). UMAP: Uniform Mani-

fold Approximation and Projection for Dimension Re-

duction. https://doi.org/10.48550/arXiv.1802.03426.

Sannikova, I., Prikhodko, E., and Muhitdinov, A. (2021).

Assessment of the universities impact on global com-

petitiveness based on rankings. E3S Web Conferences,

296:08009.

Satsyk, V. (2014). Global Competitiveness of Universi-

ties: Key Determinants and Strategies (International

and Ukrainian cases). In Int. Conf. “The Education

and Science and their Role in Social and Industrial

Progress of Society”, 12-15 June 2014, Kyiv, Ukraine.

https://www.academia.edu/10233950.

Sayed, O. H. (2019). Critical Treatise on Univer-

sity Ranking Systems. Open Journal of Social

Sciences, 07(12):39–51. https://doi.org/10.4236/jss.

2019.712004.

Schubert, E., Sander, J., Ester, M., Kriegel, H., and Xu, X.

(2017). DBSCAN revisited, revisited: Why and how

you should (still) use DBSCAN. ACM Transactions

on Database Systems, 42(3):1–21. https://doi.org/10.

1145/3068335.

Sokal, R. and Rohlf, F. (1962). The comparison of den-

drograms by objective methods. Taxon, 11:33–40.

https://doi.org/10.2307/1217208.

Stoimenova, B. (2019). Regional innovation systems and

university competitiveness. International Journal of

Innovation, 7(2):227–239. https://doi.org/10.5585/iji.

v7i2.353.

Subasi, A. (2020). Clustering examples. In Practical

Machine Learning for Data Analysis Using Python,

pages 465–511. Elsevier. https://doi.org/10.1016/

b978-0-12-821379-7.00007-2.

Taylor, P. and Braddock, R. (2008). International Uni-

versity Ranking Systems and the Idea of Univer-

sity Excellence. Journal of Higher Education Policy

and Management, 29(3):245–260. https://doi.org/10.

1080/13600800701457855.

Tee, K. F. (2016). Suitability of performance indicators and

benchmarking practices in UK universities. Bench-

marking: An International Journal, 23(3):584–600.

https://doi.org/10.1108/BIJ-07-2014-0069.

Teixeira, A., Oliveira, A., Daniel, A., Preto, M., Br

as, G.,

and Rodrigues, C. (2020). The Impact of Universi-

ties on Regional Competitiveness: A Review of the

Main Theoretical and Methodological Approaches. In

Daniel, A., Teixeira, A., and Preto, M., editors, Exam-

ining the Role of Entrepreneurial Universities in Re-

gional Development, pages 67–92. IGI Global. https:

//doi.org/10.4018/978-1-7998-0174-0.ch004.

The World Bank (2022). World Development Indica-

tors. https://data.worldbank.org/indicator/SE.XPD.

TOTL.GD.ZS.

United Nations Development Programme (2022). Human

Development Reports. http://hdr.undp.org/en/content/

download-data.

UNIVERSITAS 21 (2021). Rankings Raw Data 2020.

https://universitas21.com/media/966.

Velykoivanenko, H. and Korchynskyi, V. (2022). Appli-

cation of Clustering in the Dimensionality Reduction

Algorithms for Separation of Financial Status of Com-

mercial Banks in Ukraine. Universal Journal of Ac-

counting and Finance, 10(1):148–160. https://doi.org/

10.13189/ujaf.2022.100116.

Modelling the Design of University Competitiveness

213

Von Luxburg, U. (2007). A tutorial on spectral clustering.

Statistics and computing, 17(4):395–416. https://doi.

org/10.1007/s11222-007-9033-z.

World Economic Forum (2019). Global Compet-

itiveness Index 4.0. http://reports.weforum.

org/global-competitiveness-report-2019/

competitiveness-rankings/.

Zhang, T., Ramakrishnan, R., and Livny, M. (1996).

BIRCH: an efﬁcient data clustering method for very

large databases. In Proceedings of the 1996 ACM

SIGMOD international conference on Management of

data, page 103–114. ACM. https://doi.org/10.1145/

233269.233324.

M3E2 2022 - International Conference on Monitoring, Modeling Management of Emergent Economy

214