Semi-Autogenous Grinding Mill (SAG) Overload Forecasting Using

Gram Penalized Matrices in a CNN

R. Hermosilla

1 a

, H. Allende

1 b

and C. Valle

2 c

Universidad T

ecnica Federico Santa Mar

ıa, Valpara

ıso, Chile

Universidad de Playa Ancha de Ciencias de la Educaci

on, Chile

Keywords:

Overload Forecasting, SAG Mill Overload, Multivariate Times-Series Forecasting, Image Encoding for

Time-Series, Time-Series CNN, CNN Explanation.

Abstract:

In mining, detecting overload conditions is an opportunity to perform SAG mill to optimal operating condi-

tions. With this in mind, several authors have prove using machine learning mechanisms to detect overloads.

Our proposal establishes and tests a series of techniques to detect and forecast these events. Finally, we will

look for an explanation of what the model considers for classiﬁcation improving the phenomenon knowledge.

Inspired by previous work and how operators classify overloads by analyzing behavior graphs of the most

relevant variables, we proposed a framework that includes selection, encoding, and ﬁltering improvement to

ﬁnally discover the importance of the characteristics observed by our model using explanation techniques.

Thus, using a group of novelty techniques, our advances exceed the results presented by other authors and by

ourselves in previous publications, opening the door to a model based on attention in the future.

1 INTRODUCTION

In the mining context, comminution is the process that

reduces the ore size. In the case of most Chilean min-

ing, to obtain smaller particles for the next step in the

copper extraction (ﬂotation).

Usually, this process includes crushing and grind-

ing equipment in a circuit composed of several stages.

SAG mill (semi-autogenous grinding) can process

large amounts of ore in the so-called primary grind-

ing stage. Usually, this process includes crushing and

grinding equipment in a circuit composed of several

steps. The efﬁcient use of SAG mills means an in-

crease in ore production.

A 1% increase in SAG mill treatment supposes

a proﬁt increase of up to US$160 MM per year and

between 200 and 400 tons of CO

emissions saving

under the same electricity consumption (Wakeﬁeld

et al., 2018; Pontt et al., 2012; Northey et al., 2013).

However, achieving these efﬁciency levels has the

risk of overload, a condition that limits the opera-

tion. Divers authors have tried to identify through

several techniques such as the theoretical analysis

https://orcid.org/0000-0002-6032-4811

https://orcid.org/0000-0002-9899-0051

https://orcid.org/0000-0001-7158-2069

of variables (Strohmayr and Valery, 2001; Powell

et al., 2009), use of predictive control ((Forbes and

Gough, 2003)), making simulation models (Varas

et al., 2019), through linear programming (C

esar and

Daniel, 2009) or using machine learning techniques

(Ko and Shang, 2011; McClure and Gopaluni, 2015;

Hermosilla et al., 2021).

In our research, we have established a mechanism

that allows the classiﬁcation and early detection (fore-

cast) of overloads as a multivariate binary classiﬁca-

tion model.

Inspired by the work performed in the generation

of encodings based on distance matrices (Bardinas

et al., 2018) and the analysis that expert metallur-

gists to determine the occurrence of overloads, we

have proposed a deep convolutional neural network

that uses the feature relationship using a multivariate

approach of Gram’s matrix as an encoder.

In other words, we proposed the generation of ma-

trices with angular differences of the feature pair ar-

rays as input for our model. Those matrices are penal-

ized with a temporary degradation ﬁlter that penalizes

the oldest data, trying to establish a mechanism for

differentiating the temporal data used in each encoded

time window, which has yielded promising results.

Finally, we uncover, through explanation mecha-

nisms, the combinations of variables/time that most

Hermosilla, R., Allende, H. and Valle, C.

Semi-Autogenous Grinding Mill (SAG) Overload Forecasting Using Gram Penalized Matrices in a CNN.

DOI: 10.5220/0011946800003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 391-396

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

391

affect the prediction of overloads.

The following chapters explain the overload phe-

nomenon and how we have approached a solution.

Section 2 explains the overload phenomenon and its

importance in the comminution process. Section 3

will delve into our proposal and how we address it

through a set of proposed methods. Section 4 shows

our results. Section 5 shows our conclusions and fu-

ture work.

2 OVERLOAD DETECTION AND

RELATED WORK

Maximizing ore treatment is one of the main goals of

a SAG mill operation. Though, this objective depends

on several factors that can inﬂuence the occurrence of

an overload event.

Factors such as the distribution of solids, hardness,

excessive load volume, particle size distribution, the

number of steel balls, and wear, among others, can

generate an overload condition.

2.1 Overload Types

In a SAG mill can found three kinds of overloads can

occur (Fig. 1).

In all cases of overload, mill loses the cataract

property generating a vicious circle that leads to

the ineffectiveness of the equipment. The volumetric

overload occurs when the SAG mill is overfed. Ore’s

hardness, size, or composition can produce this con-

dition.

When excess water attenuates the fall’s effect, it

is declared an overload by slurry pooling, affecting

the ore’s size reduction, producing accumulation and

next, a volumetric overload. When the pulp covers

the lifters, a freewheeling overload is declared. The

pulp on the lifters avoids the ore rising, inhibiting the

cascade.

Also, composition, distribution, and load ﬁll can

inﬂuence an overload occurrence. We can search this

behavior by observing the power consumed but only

at the beginning of an overload (Apelt et al., 2001),

without enough foreseeing.

The distinct factors and the complex relations of

the features underlying the overload make obtaining a

physical forecast overload system hard. However, es-

tablishing a model based on data that learn this com-

plex relationship is possible. Thus, our research fo-

cused on obtaining an overload forecast model based

Ore rises to the top of the mill, breaking on the impact

zone.

Figure 1: SAG mill overloads.

on a time-series classiﬁcation with a multivariate ap-

proach.

2.2 Related Work

According to our research, two approaches exist at

least to address the SAG mills’ overloads and under-

stand the problems associated with their operation.

One seeks to generate an adequate operation from

the control point of view, and the other focuses on

seeking the occurrence of overloads.

Among these investigations, ((Salazar et al.,

2014)) establish a control and prediction mechanism

for the behavior of the mill using a method called

Multiple Input/Multiple Output Predictive Control

Model (MIMO MPC).

The authors prove the relationship between the op-

erating variables based on load tonnage.

His work also allowed the establishment of simu-

lated operating conditions of an overload state, keep-

ing the controlled variables without relevant variation.

On the other hand, (Wang et al., 2020) allowed to

establish overload-free operating conditions through

the control of the speed of the mill, generating an op-

timal operating space describing the relationship be-

tween speed, ore quantity, and particle size.

However, one of the nearest research to our line of

study is published by (McClure and Gopaluni, 2015),

which experiments with techniques like KPCS, SVM,

and LLE to classify overloads (not predict them).

Likewise, our previously published research ad-

vanced toward constructing an overload prediction

framework using deep networks.

Now, we have improved results by better under-

standing the underlying phenomenon and the inclu-

ISAIC 2022 - International Symposium on Automation, Information and Computing

392

sion of elements, such as the degradation or penalty

ﬁlter.

In the previous work, we intuited could be ex-

plained the network in some way.

In this proposal, we have included a way to ex-

plain the network and analyze the results, allowing

contrasting the model’s decisions with experts’ opin-

ions.

3 OVERLOAD FORECASTING

PROPOSED METHOD

As we have pointed out, we propose approaching our

overload prediction problem through a multivariate

binary classiﬁcation model based on deep convolu-

tional neural networks.

So, we have to overcome several difﬁculties, such

as adequately selecting operation variables, generat-

ing a representative encode, or attending a highly un-

balanced scenario (less than 2% of the labeled data

corresponds to overloads).

Furthermore, we will add a ﬁlter that has given us

promising results penalizing past data and the applica-

tion of an interpretation method called Grad-CAM++

(Chattopadhay et al., 2018) to determine and check

the dependency of the selected relationships with our

target.

3.1 Base Deﬁnition

Let y = [y

, . . . , t

′

]

with T ∈ [1, . . . , T

′

] as the set

of values binaries that describe the overload condi-

tion every time t t (y

= 1 as an overload at time

t). We will assume the matrix T

′

× N as the matrix

X = [x

|. . . |x

′

]

that expresses the collection of vec-

tors x

formed by the N available and selected fea-

tures. That is, x

( j)

denotes the value of the j − th

characteristic at time t.

Expressed our approach as a multivariate time-

series problem that symbolizes a stochastic process,

we deﬁne our goal as overload forecasting y

t+k

, thus,

in k steps ahead of the current observation t. Given

that the associated distribution of the underlying pro-

cess is unknown, we assume our model will learn the

relationship of values observed previously to forecast

the overload occurrences. Then, we modeled the val-

ues’ ﬁt as p(y

t+k

, ..., x

t−w−1

) in w steps to the past.

3.2 Feature Selection by Pairs

We propose to train a deep convolution neural net-

work to learn the relationship of the available features

through a structure that includes pairing the variables

with the highest relationship with the overload.

Inspired by the classiﬁcation of overloads

achieved by metallurgical experts, we intend to select

those pairs that provide the most information regard-

ing our target.

We solved this using Conditional Mutual Informa-

tion (CMI) (Liang et al., 2019) to get a reduced num-

ber of pairwise relations, looking for pairs related to

adding the maximum information possible about our

target. We express CMI as follows:

I(x

(i)

, x

( j)

|y) = E

(i)

( j)

|y)

||P

(i)

|y)

⊗P

( j)

|y)

)],

(1)

where I(x

(i)

, x

( j)

|y) is the value expected respect to y,

of the relative entropy or Kullback-Leibler divergence

from conditional joint distribution P

(i)

( j)

|y)

the product ⊗ of conditional marginals P

(i)

|y)

and

( j)

|y)

Accordilyng, let deﬁne z

= (z

(1)

, z

(2)

) as a matrix

with features pairs x

(i)

and x

( j)

selected from rth bet-

ter CMI values (1).

Let z

= (z

(1)

, z

(2)

) as a matrix with features pairs

(i)

and x

( j)

selected from rth better CMI values (1).

Let

Z as an array with three dimensions w × w ×

R, with window length w and the number of selected

pairs R, each composed by ˜z

(i)

3.3 Encoder by Matrices Inspired in

Gram

Problems such as univariate time series have recently

been solved using gram matrices (Wang et al., 2022);

however, we will use it as a multivariate approach ap-

plying some changes. After selecting R pairs on top of

CMI ranking time series X using the technique min-

max scaler, we transform each pair z

, . . . , z

to the

space [−1, 1] as follow:

˜z

(i)

− min(z

(i)

)

max(z

(i)

) − min(z

(i)

)

, i = 1, 2, t = 1,

. . . , T, r = 1, . . . , R,

(2)

where minimum value min(z

(i)

) and maximum value

max(z

(i)

) of the ith selected feature.

Then, we transform ˜z

(i)

to polar coordinates throw

the cosine of the angle of the values, and obtaining the

radius ρ using the timestamp ts

, given by:

Semi-Autogenous Grinding Mill (SAG) Overload Forecasting Using Gram Penalized Matrices in a CNN

393

Figure 2: Image generated with GADF approach with R

pairs/channels.

(i)

= arccos(˜z

(i)

), −1 ≤ ˜z

(i)

≤ 1, (3)

max(ts)

, ts

∈ ts,

where the value of the timestamp is represented by ts

and the maximum value of all timestamps is wrote as

max(ts).

The next step in our process is to apply a Gramian

approach to the angle differences of each pair to ob-

tain a three-dimensional array G with w × w × R di-

mensions. Here, g

r(i, j)

represents each pixel in posi-

tion (i, j) of rth Gram’s matrix of G, as follows:

r(i, j)

= cos(θ

(1)

+ θ

(2)

r j

), i, j = 0, . . . , w − 1,(4)

where θ

(1)

and θ

(2)

r j

represents the transformed pair se-

lected previously. We can understand G as the render-

ing of an image with R channels, where each image

represents the angular variation of the top-R CMI’s

ranking selected pairs (Figure 2).

3.4 Penalization over Time

Sub-Matrices

As we can guess, overloads are a phenomenon that

increases as we get closer to the moment of their ap-

pearance. Also, after making our models, we veriﬁed,

using an explanation method (4.2), that in the cases

in which overloads occur, our model considered the

instants prior to the evaluated time to be more critical

(Figure 3). Based on these antecedents, we deﬁne a

ﬁlter that allows us to penalize those previous values

in each channel of the encoder.

Let f = [0, . . . , w − 1] deﬁne the ﬁlter F =

f + f

which will generate a ﬁlter of dimension w × w with

Figure 3: Importance by selected pairs over overload clas-

siﬁcation. Blue and red colors represent low and high im-

portance, respectively.

Figure 4: Filter applied in each channel.

values in R in the interval [0, 1] which we will ap-

ply to each of the channels R of the generated images

G (Figure 4). As we will see in chapter 4, this sim-

ple method allowed us to improve our model signiﬁ-

cantly.

3.5 Convolutional Neural Network

The set of images G are taken by a deep convolutional

neural network (Fig. 5), made up of convolutional

layers with n

ﬁlters of k

× k

size and 2 × 2 max-

pooling, followed by a batch normalization layer.

We added once more time the same set of convo-

lutional, max-pooling and batch normalization layers

(with the same hyperparameters). All the convolu-

tional layers have ReLU as an activation function and

zero padding.

Finally, the last layer is fully connected with a ﬂat-

ter layer, followed by n

nodes with Dropout dense

layer, to end with one single neuron as output for bi-

nary classiﬁcation using a sigmoidal activation func-

tion. Due to the highly imbalanced scenario found,

Figure 5: Convolutional Neural Network Architecture.

ISAIC 2022 - International Symposium on Automation, Information and Computing

394

we use focal binary crossentropy as a cost function

setting with class weights parameters.

4 EXPERIMENTS AND RESULTS

Obtaining a forecast with ten minutes of anticipation

is our primary goal. Considering a 30 seconds resolu-

tion, we set k = 20 in our target y

+k. Also, we deﬁne

w = 60 as the offset into the past, ergo 30 minutes.

We have a dataset with around 700k labeled

records strongly imbalanced (1.46% imbalanced ra-

tio), corresponding to nearly twelve months of data.

We selected 48 of 72 features linearly indepen-

dent. With these 48 features we start our process

of selecting the K = 10 top pairs corresponding to

{( f in, gru), (pot, dm ), (ton, dm ), ( f in, int), (gru, int),

(pre, vel), (pot, vel), (pot, pre), (pre, dm ), (int, pre)}

After selecting our top feauture pairs, we build the

G matrices using our Gram’s matrices approach. Due

to time-missing values, this process reduced the num-

ber of matrices to around 685k, reducing our imbal-

anced ratio to 1.38%.

We setted the network hyperparameters with n

256, n

= 128, n

= 512 nodes for each layer using the

grid search method. Using the same way we setted

× k

) = (k

× k

) = (3 × 3) for the kernels size.

We setted the optimizer as Adam with learning rate

(lr = 0.001).

To train we use a cross-validation technique pro-

posed by (Bergmeir and Ben

ıtez, 2012) for time se-

ries.

4.1 Evaluation Methods

Table 1 shows the average sensitivity, speciﬁcity, and

F1 score with the respective standard deviation to the

model based on LLE+LDA as suggested by (McClure

and Gopaluni, 2015), we have also included the re-

sults of our previously proposed model (Hermosilla

et al., 2021), and the results of this proposal, without

ﬁlter (⋆) and with penalization ﬁlter. As can be seen,

the proposed model with the applied ﬁlter exceeded

the previous results signiﬁcantly.

4.2 GradCAM++ CNN Explanation

The authors (Chattopadhay et al., 2018) proposed a

generalized method called Grad-CAM++ that is for-

mulated by explicitly modeling the contribution of

ﬁn: ﬁne granulometry, gru: coarse granulometry, dm :

milliseconds from the last maintenance, int: intermediate

granulometry, pre: pressure, vel: velocity, ton: total ton-

nage.

Figure 6: Example of cluster generated with a explanation

model based on GradCam++.

each pixel in the feature maps of a CNN to the ﬁ-

nal output. With this, it is possible to look at the el-

ements to which the network pays attention in each

case. To do this, they reformulate the structure of the

weight for c class in k layer of the network:

∑

i j

.relu

∂Y

∂A

i j

, (5)

where relu is the Rectiﬁed Linear Unit activation

function, α

i j

are the weights of the gradients for a

particular pixel i, j, and Y

are the values of the partic-

ular class to analyze. w

will capture the importance

of the activation map A

Using this method, we characterized the overloads

to understand feature pairs directly inﬂuencing the

target. Have been clustered the results to achieve

an analysis of the leading classiﬁcation groups of the

model.

In Figure 6, we can see an example of how the

model considers the pairs of channels 5, 6, 8, and 9

most relevant in the periods close to the overload oc-

currence.

Precisely channels 5 ({pre}, {vel}) and 6 ({pot},

{vel}) are relationships, which experts use to clas-

sify overloads. However, channels 8 and 9, with pairs

(pre, dm ), (int, pre), seem particularly relevant to the

model and offer an opportunity to use new relations to

the study of overload genesis.

An interesting observation is that even having pe-

nalized the times far from the moment t, in all cases,

the model highlights those instants as essential for the

classiﬁcation, which makes us suppose that the infor-

mation contained in the ﬁrst moments of the charac-

teristics matrix G is essential for forecasting.

Semi-Autogenous Grinding Mill (SAG) Overload Forecasting Using Gram Penalized Matrices in a CNN

395

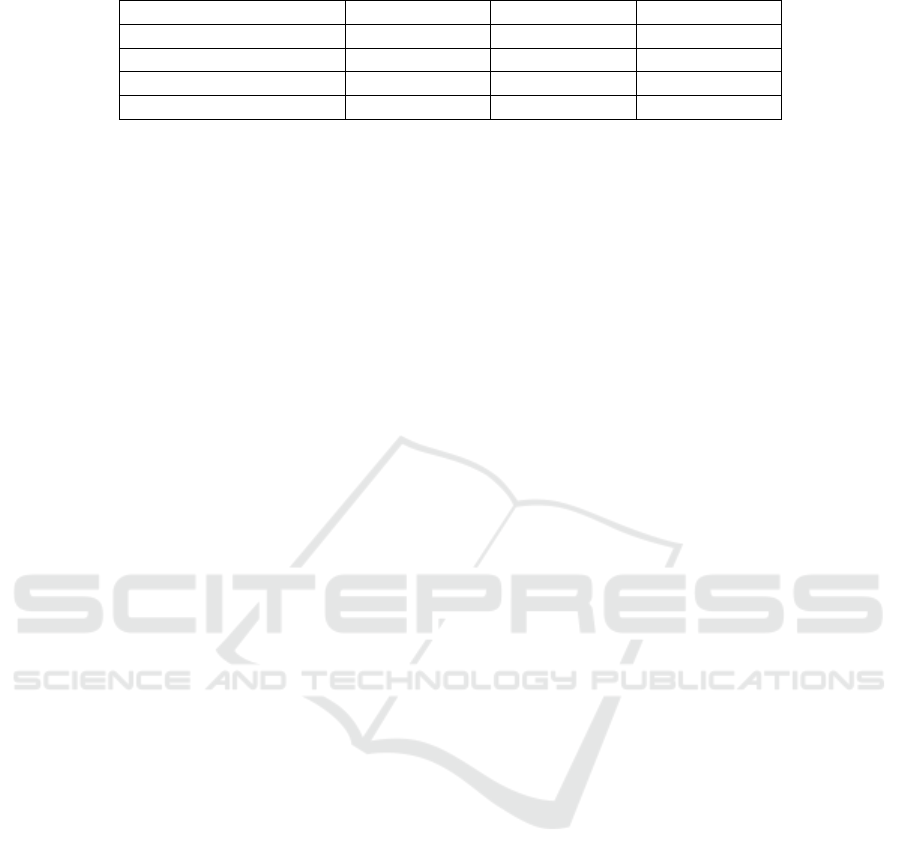
Table 1: Average and standard deviation over S test sets.

Model Sensitivity Speciﬁcity F1

LLE+LDA 0.555(±0.425) 0.453(±0.321) 0.440(±0.298)

Previous proposed model 0.643(±0.227) 0.894(±0.106) 0.609(±0.084)

Proposed model⋆ 0.653(±0.124) 0.889(±0.178) 0.742(±0.098)

Proposed model 0.871(±0.134) 0.838(±0.102) 0.859(±0.113)

5 CONCLUSIONS AND FUTURE

WORKS

In this work, we propose improving the methods to

arrive at an overload forecasting model in a complex,

multivariate, and highly unbalanced problem using a

Gram matrix-based encoding.

We take advantage of the beneﬁts of the CNNs to

generate a model that allows us to know the relation-

ships of these matrices with the overload.

The experimental results show that we have over-

come the approach in previous works and state of the

art.

Using an explanation method called Grad-

CAM++, we established some interesting study sets

for expert review, for example, the relationship be-

tween pressure and timing of equipment maintenance

and ﬁne grain size and pressure to explain some over-

loads.

Also, this behavior could allow us to increase the

forecast distance. In the future, we will integrate the

care information in the same network to generate a

model specialized mainly in those elements that most

inﬂuence the occurrence of overloads.

REFERENCES

Apelt, T., Asprey, S., and Thornhill, N. (2001). Inferential

measurement of sag mill parameters. Minerals engi-

neering, 14(6):575–591.

Bardinas, J., Aldrich, C., and Napier, L. (2018). Predict-

ing the operating states of grinding circuits by use of

recurrence texture analysis of time series data. Pro-

cesses, 6(2):17.

Bergmeir, C. and Ben

ıtez, J. M. (2012). On the use of cross-

validation for time series predictor evaluation. Infor-

mation Sciences, 191:192–213.

esar, G. Q. and Daniel, S. H. (2009). Multivariable model

predictive control of a simulated sag plant. IFAC Pro-

ceedings Volumes, 42(23):37–42.

Chattopadhay, A., Sarkar, A., Howlader, P., and Balasub-

ramanian, V. N. (2018). Grad-cam++: Generalized

gradient-based visual explanations for deep convolu-

tional networks. In 2018 IEEE winter conference on

applications of computer vision (WACV), pages 839–

847. IEEE.

Forbes, M. G. and Gough, B. (2003). Model predictive con-

trol of sag mills and ﬂotation circuits.

Hermosilla, R., Valle, C., Allende, H., Lucic, E., and Es-

pinoza, P. (2021). Semi-autogeonous (sag) mill over-

load forecasting. In Iberoamerican Congress on Pat-

tern Recognition, pages 392–401. Springer.

Ko, Y.-D. and Shang, H. (2011). Sag mill system di-

agnosis using multivariate process variable analy-

sis. The Canadian Journal of Chemical Engineering,

89(6):1492–1501.

Liang, J., Hou, L., Luan, Z., and Huang, W. (2019). Feature

selection with conditional mutual information consid-

ering feature interaction. Symmetry, 11(7):858.

McClure, K. and Gopaluni, R. (2015). Overload de-

tection in semi-autogenous grinding: A nonlinear

process monitoring approach. IFAC-PapersOnLine,

48(8):960–965.

Northey, S., Haque, N., and Mudd, G. (2013). Using sus-

tainability reporting to assess the environmental foot-

print of copper mining. Journal of Cleaner Pro-

duction, 40:118–128. Special Volume: Sustainable

consumption and production for Asia: Sustainability

through green design and practice.

Pontt, J., Valderrama, W., Olivares, M., Rojas, F., Robles,

H., L’Huissiers, S., and Leiva, F. (2012). Uso eﬁciente

de la energia en procesos mineros. Centro de automa-

tizacion para la industria minera, Chile.

Powell, M., Van der Westhuizen, A., and Mainza, A. (2009).

Applying grindcurves to mill operation and optimisa-

tion. Minerals Engineering, 22(7-8):625–632.

Salazar, J.-L., Vald

es-Gonz

alez, H., Vyhmesiter, E., and

Cubillos, F. (2014). Model predictive control of semi-

autogenous mills (sag). Minerals Engineering, 64:92–

96.

Strohmayr, S. and Valery, W. (2001). Sag mill circuit op-

timisation at ernest henry mining. In Proceedings of

the SAG 2001 Conference, Vancouver, BC, Canada,

volume 30.

Varas, P., Carvajal, R., and Ag

uero, J. C. (2019). State

estimation for sag mills utilizing a simpliﬁed model

with an alternative measurement. In 2019 IEEE

CHILEAN Conference on Electrical, Electronics En-

gineering, Information and Communication Technolo-

gies (CHILECON), pages 1–7. IEEE.

Wakeﬁeld, B., Lindner, B., McCoy, J., and Auret, L. (2018).

Monitoring of a simulated milling circuit: Fault diag-

nosis and economic impact. Minerals Engineering,

120:132–151.

Wang, J., Li, S., Ji, W., Jiang, T., and Song, B. (2022). A

t-cnn time series classiﬁcation method based on gram

matrix. Scientiﬁc Reports, 12(1):1–14.

Wang, X., Yi, J., Zhou, Z., and Yang, C. (2020). Optimal

speed control for a semi-autogenous mill based on dis-

crete element method. Processes, 8(2):233.

ISAIC 2022 - International Symposium on Automation, Information and Computing

396