On Detection and Classification of State Changes in Physical

Processes by Signal Processing Techniques

Dorel Aiordachioaie

Department of Electronics and Telecommunications,

Dunarea de Jos University of Galati, Romania

Keywords: Signal Processing, Time-Frequency Transform, Image Processing, Information Processing, Source

Identification, Entropy, Feature Selection and Extraction.

Abstract: The paper presents a comparation of some methods based on signal processing, for detection and classification

of the changes in the states of physical processes. The investigated processes generate mechanical vibrations,

which are properly managed for computer-based processing. As a case study, the incipient faults in bearings

are considered. Five signal processing methods are promoted, which are based on statistical processing, signal

modelling, spectral analysis, time-frequency image processing, and information modelling. Statistical

processing method considers ten features based on statistical moments of various orders. The method of signal

modelling involves models with parameters estimated by an Kalman estimator. The method of spectral

analysis considers the power spectrum of the vibration’s signals. The method based on time-frequency

analysis considers the short-time Fourier transform and Choi-Williams transform for feature extraction. The

information-based method is based on information source identification and processing. The classifier is based

on similarity comparation using a distance-based classifiers. The novelty/contribution of the paper is the

evaluation of the methods for change detection and diagnosis, all based on signal processing paradigm. Each

of the considered method has advantages and disadvantages and depends on available data. The involved

techniques could be applied also in process monitoring and conditioning.

1 INTRODUCTION

In the operation of production processes, defects in

various elements of the components may occur. Their

incipient detection and limitation of interruptions in

production are of major importance in engineering

practice. Fault detection refers to such

problems/defects in the context of physical and – very

often – industrial processes. However, the use of this

expression may be limiting or inappropriate, as

possibly giving rise to mis interpretation in certain

cases. For example, changing the state of a variable

in the process can also be achieved without being

defective, by changing the regime and/or the load in

the process under study.

Change detection based on the recording and

processing of a single signal, in the simplest case, is

done by checking the "dynamic" range of the signal

(peak-peak value) or, in more complex cases, on the

extraction of features and the application of change

detection methods.

By detecting the change of a state is meant the

activity of sensing/ identifying the change of a state

(usually undesirable) in the operation of a system.

The processed signals are taken from the process or

are obtained from the use of a model, through

simulation. Such signals can be vibration signals,

sound waves of different frequencies (e.g., audio,

ultrasonic), and even electrical signals from the

investigated system

There are processes in which harmonic signals are

available (by measurements) and affected by a

greater or lesser number of noises, so they have a

random behavior. If the changes in these signals

correspond to defects in action elements, process or

sensors, methods based on signal-model-based can be

applied. A representative example is the vibration

monitoring application which allows, by measuring

position, speed or acceleration, the detection of non-

equilibrium or defective bearings.

An example of a complex process, in which the

detection of change and the detection of defects and

diagnosis are important activities are the case of a

440

Aiordachioaie, D.

On Detection and Classiﬁcation of State Changes in Physical Processes by Signal Processing Techniques.

DOI: 10.5220/0011950800003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 440-445

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

wind turbine, where faults can be in the mechanical

part (external blades, reducer box) or in the electrical

part (generator, converter, transformer, etc.). Another

case is of a rolling mill, where the mechanical part is

important in the quality of the product and is the part

dominated in the generation of defects, sources of

vibration signals, (Precup et al., 2015), (Seeliger et

al., 2002).

In the field of Change Detection and Diagnosis

(CDD) methods, two categories are important,

(Zhang & Jiang, 2008). The methods based on

model, process and/or measured signals, and methods

based on measured data. From the various available

methods, in this work it will be considered the

analytical method, based on the processing of the

vibration signals. Other examples and details are

available through the references (Isermann, 2006),

(Patton, et al, 1989), (Venkatasubramanian, et al,

2008), (Ypma, 2001), (Zhang, 2010).

The structure of the detection method by

analyzing the signal model assumes a mathematical

model for the signal, one can calculate specific

parameters such as: amplitudes, phases, frequency

spectra and correlation functions, for the frequency

of the signal. By comparison with the features

observed in normal function, analytical syndromes

are generated. Signal models can be parametric

(amplitudes for certain frequencies or specific type

models) or nonparametric (frequency spectra or

statistical correlation functions), (Iserman, 2006).

The detection of the changes by methods of

processing their signatures can be solved by several

methods, some of which are direct (i.e. the signal is

processed directly and the processed values have

physical significance) or indirect (values are

processed transformed into different spaces from the

original ones, where the processed data may or may

not have physical significance, (Timusk, et al, 2008).

In direct methods, the observed values are directly

calculated by calculating statistical quantities (most

often) or gradient-based criteria. These methods are

often applied in process monitoring applications by

processing vibrations and audio signals. The methods

are simple to understand and simple to implement,

sometimes with very good results, but less good in the

case of non-stationary signals or time-varying or

interdependent events (defects).

Indirect methods, based on transformations, are

more complex, but the calculations for decision

making in the new spaces of observations are simpler.

Compared to direct methods, indirect methods give

better results. The following types of transformations

can be exemplified here: time-frequency

transformations and entropic transformations (based

on the evolution of entropy).

The signals can be processed in the time domain,

in the frequency domain or in the combined/mixed

time-frequency domain. Each of these areas has

advantages and disadvantages, so a robust solution

involves a combination of methods from the fields

presented, (Popescu et al, 2017).

The paper is organized in five sections. The next

section presents the general structure of the methods

used for data processing and a short analysis of data

used in the testing stage. Section 3 presents the

principles of the promoted methods. Section 4

presents some results of the computer-based

experiments. Finnally, the conclusion section ends

the paper.

2 THE STRUCTURE OF THE

METHODS

The problem of change detection and classification of

faults in bearings is considered. The data used for

experiments are from (CWR, 2022). There are four

classes of signals, associated to four

states/cases/faults: F0- free of faults, F1- fault in ball,

F2 – fault in inner ring, and F4-fault in outer ring. For

each state/fault, a record of 200,000 samples is

available, which corresponds to an observation

interval of ten [s]. The motor speed is 1797 rpm, and

the working conditions are without mechanical load.

A test vector is considered with frames of 5,000

samples for each record, which is explored with a

sliding window of length w, variable from 100 to

5,000 samples, depending on the performance of the

detection. The bigger window the less precise is the

point change detection.

The structure of the data processing is presented

in Fig.1. Data are pre-processed by filtering and

scaling to [-1,1] interval. The next block computes the

features, and the classifier estimates the state/fault.

The input waveforms are quite similar, so the most

important block is the feature selector. A primary

frequency analysis shows an overlapping in

frequency domain, which will generate difficulties for

a right classification. This is a reason to explore more

than a method for CDD, as in the case of the present

paper, and to promote combination of methods from

the same domain or from different domains.

Figure 1: The structure of data processing.

On Detection and Classiﬁcation of State Changes in Physical Processes by Signal Processing Techniques

441

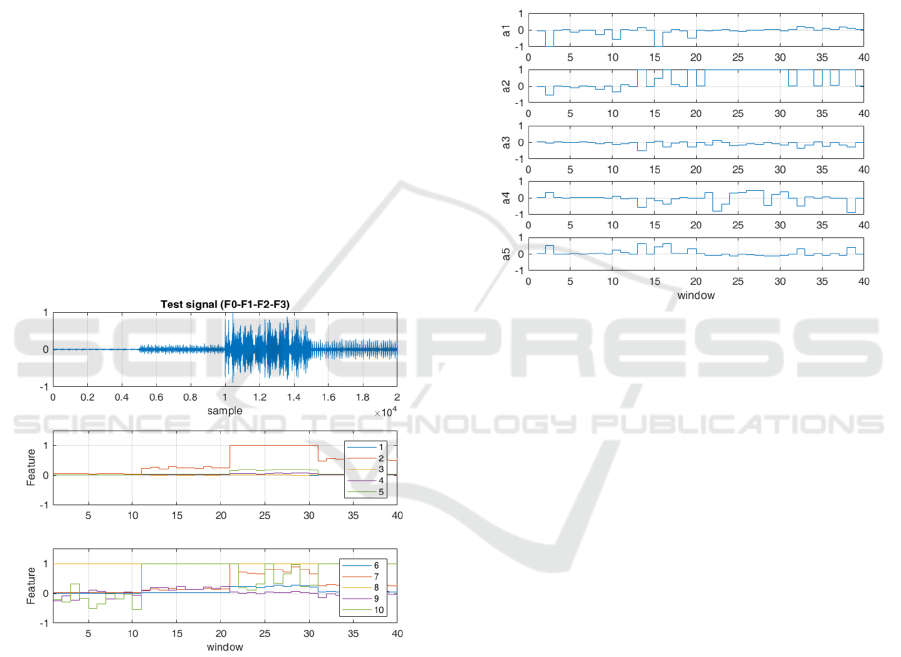
3 THE METHODS

Five methods are considered for this work. Some are

used as references, e.g., statistical method, and others

are based on advanced processing techniques, as

those based on time-frequency techniques.

3.1 The Statistical Method

The basic theory and the computation of the statistical

moments are presented in (Gustafson, 2007),

(Shanmugan and Breipohl, 1988), and (Barkat, 2005).

Examples of the method under various simulation

scenarios are presented in (Basseville, 1997),

(Aiordachioaie, 2013).

Ten statistical features are used: the mean, the

dynamic range, the median, the variance, the mean of

the absolute values, the root mean squares, the peak

value, the crest factor, the skewness, and the kurtosis.

Fig. 2 presents the evolution of the feature set, for

an observation window with 500 samples. The

evolution of the features indicates the moment of

change. The process diagnosis depends on the

performance of the classifier.

Figure 2: Features of the statistical method.

3.2 The Signal Modelling Method

The principle of the method is to design an

autoregressive moving average (ARMA) signal

model, (Kay, 1993), (Poor, 1994), (Bozic, 2021) and

to estimate its parameters in each observation

window. A change in one or more parameters

indicates a change in the structure of the process.

The equation of the ARMA (Ma, Mb) model is

𝑦



𝑛





∑

𝑎





𝑛



𝑦



𝑛𝑘











∑

𝑏





𝑛



𝑣



𝑛

𝑗









𝑣



𝑛



(1)

where y(n) is the modelled signal, and v(n) is

Gaussian white noise. A Kalman estimator is used for

the estimation of the parameters, (Haykin, 2002).

Fig. 3 presents an example of the first five

parameters of the ARMA(5,5) model, during the test

with windows (of length 500 sample). More details of

the used method are available in (Aiordachioaie,

2014).

Figure 3: Features of the signal model-based method.

3.3 The Spectral Analysis Method

For each sliding data window, a power spectrum is

computed and analysed. The features vector is

composed of eight features: the mean and the

variance in frequency, the third and fourth order

centred statistical moments, the median, the energy in

frequency domain, and the mean and the variance

over the amplitude values. The basic equations are

presented in (Aiordachioaie, 2022a).

Fig. 4 presents the evolution of the feature set,

over a test vector composed of 40 windows. The

evolution allows the detection of the changes in the

test vector.

The method based on the features of power

spectra is called SF (Spectral Features) and the

method based on power spectra only is referred a SD

(Spectral Direct) in Table 1. In the case of SD method,

the spectral lines could be labelled as direct features.

The SD method needs a higher resolution than SF.

ISAIC 2022 - International Symposium on Automation, Information and Computing

442

Figure 4: Evolution of the features in frequency domain.

3.4 Time-Frequency Analysis Method

The methods based on time-frequency transforms

(TFT) represent effective solutions for the detection

of change of in vibratory processes, since it is

detected the change in the frequency domain and the

moment of change in time domain, when they have

occurred. The approach is indicated for intermittent

and dynamic faults. Time-frequency analysis covers

a major area related to the non-stationary signals

(including transient ones) by the ability to detect and

to locate them.

Three most used methods are based on the short-

time Fourier transform (STFT), quadratic time-

frequency transform (e.g., Wigner transform) and

wavelet transform (WT). Some good references are

(Auger, 1991), (Boashash, et al, 2014), and (Cohen,

1989).

Let consider a signal x(t) and a sliding observation

window w(t). By discretization, a time-frequency

matrix is generated. The basic equations for the above

transforms are

𝑋



𝑛,

𝑓





∑

𝑥



𝑘



𝑤



𝑘𝑛



𝑒









(2)

for STFT, and

𝑊



𝑛,

𝑓





∑

𝑥



𝑘



𝑥

∗



𝑛𝑘



𝑒









(3)

for Wigner transform. In experiments, the Choi-

Williams transform (CWT) is used to decrease the

interference terms, (Barry, 1992), (Flandrin, et al,

1996). In the case of WT, the signal x(t) is

decomposed following the mother wavelet 𝜑, and the

coefficients a

define the matrix of interest, (Mallat,

1989), and (Daubechies, 1992).

An efficient approach is to consider the

coefficients of the TFT as elements of a digital image,

and thus to obtain a time-frequency image (TFI).

Each observation window generates a TFI, which is a

matrix or a 2D signal.

Seven features are considered for an image as: the

mean, the variance, the skewness, the kurtosis, the

coefficient of variations, the spectral flux, the

frequency of the maximum amplitude. The

computation expressions are available in

(Aiordachioaie, 2022b).

Fig. 5 presents a set of TFI based on STFT. It is

about windows 1, 13, 27 and 39 from the set of 40.

On the x axis the index of the window is presented,

and on y axis the frequency in Hz. The size of the TFI

is 6001x50 pixel.

Fig. 6 shows a set of four TFI based on CWT for

the same set of windows. The time variable is

considered on the x axis. The size of the TFI is

500x500 pixel. This approach has a higher precision

referred to the previous one. By analysing and

classifying the content of the image, the change and

diagnosis could be easily solved.

Figure 5: Time-frequency images for STFT.

Figure 6: Time-frequency images for CWT.

The Fig.7 and 8 presents the evolution of some

features for the methods of time-frequency

approaches. A change in the signal is detected by one

or more changes of the selected features.

On Detection and Classiﬁcation of State Changes in Physical Processes by Signal Processing Techniques

443

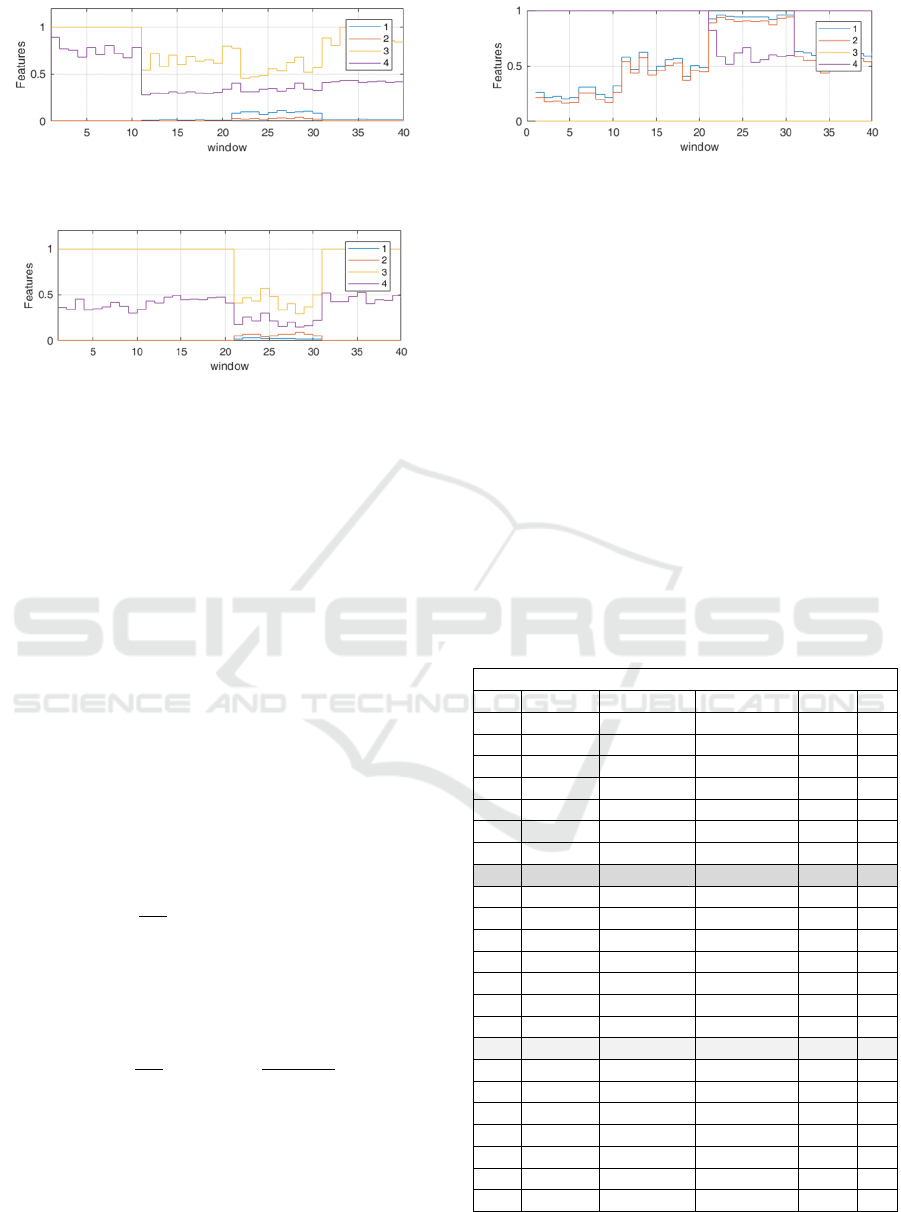
Figure 7: Feature evolution for STFT based method.

Figure 8: First four features for CWT based method.

3.5 The Information Processing

Method

Functions based on entropies is used for each data

window, e.g., Renyi entropy. A source identification

process is necessary before computation of the

entropies, to estimate the probabilities of the basic

elements. The approach can be applied directly to the

vibration signals (1D signals) or to time-frequency

images (2D signals) as in the present approach.

The set of the features has the Shannon entropy,

the Renyi entropy of order 2 and 3, (Baraniuk, 2001),

the multiscale entropy, (Humeau-Heurtier, 2016), the

crest factor, the variance of the probabilities, the

maximum amplitude of data, and the Lempel-Ziv

complexity (Aiordachioaie & Popescu, 2020),

(Karmeshu, 2003), and (Aiordachioaie, 2021).

The most used entropy is the Renyi entropy of

order α, defined as

𝐻𝑅





𝑋









𝑙𝑜𝑔



∑

𝑃







,𝛼1

(5)

where P

are the probabilities of the samples from the

set X. For an image I, a normalized expression is used

for Renyi entropy as

𝐻𝑅





𝑰









𝑙𝑜𝑔

∑∑







,



∑∑









,











(6)

Fig. 9 presents the first four features obtained by

using information-based approach. This method is

called “Info” in Table 1. The challenge is to properly

design the change detection criteria, in a trade-off

between the change point detection and

computational resource and complexity.

Figure 9: The information-based features.

4 EXPERIMENTS RESULTS

The above methods were evaluated with a vector

composed from four segments, one for a state/fault,

each of 5,000 samples.

The results of the classification/recognition rates

(RR) are presented in Table 1, for both used distances,

Euclidean and Manhattan. Three values of the length

w of the observation window were considered, i.e.,

500, 2,500 and 5,000 samples. The number of the

used features nf is also presented.

The low values of some methods are explained by

the non-stationarities of the test signals. The highest

values of classification rates were obtained by the

ARMA method, which needs at least 5,000 samples

to properly estimate the parameters of the model.

Table 1: Results of the classification.

R [%]

o. T

e Euclidean

anhattan w n

1. Stat 72.50 47.50 500 10

2. ARMA 67.50 52.50 500 10

3. SF 70.00 75.00 500 8

4. SD 80.00 90.00 500 w

5. STFT 75.00 50.00 500 7

6. CWT 40.00 40.00 500 7

7. Info 47.50 45.00 500 8

8. Stat 75.00 50.00 2500 10

9. ARMA 87.50 62.50 2500 10

10. SF 75.00 75.00 2500 8

11. SD 100 62.50 2500 w

12. STFT 50.00 50.00 2500 7

13. CWT 50.00 50.00 2500 7

14. Info 50.00 50.00 2500 8

15. Stat 75.00 50.00 5000 10

16. ARMA 100 50.00 5000 10

17. SF 75.00 75.00 5000 8

18. SD 75.00 50.00 5000 w

19. STFT 50.00 50.00 5000 7

20. CWT 50.00 50.00 5000 7

21. Info 50.00 50.00 5000 8

ISAIC 2022 - International Symposium on Automation, Information and Computing

444

5 CONCLUSIONS

The main objective of the work was to present a set

of CDD methods based on signal modelling

paradigm. The basic structure of the data processing

has two blocks: one for the computation of the

features and another one for classification, based on

distance functions. The block of feature selection

based, e.g., on feature variance and on the sensitivity

of CDD criterion is not considered here. The

complexity of the methods is not considered here.

Five methods were considered. Each method has

pros and cons, and a good approach is to combine

them to obtain the highest recognition rate.

A special attention was paid to time-frequency

representations, by developing and adapting features

from time or frequency domains.

The computer-based experiments indicate a need

to select the region of interest before computing the

features for CDD. This will be the next research step

to follow.

REFERENCES

Aiordachioaie, D., 2022a. On change detection and process

diagnosis based on information and frequency domain

models, AIP Conference Proceedings, 2570, 040020.

Aiordachioaie, D., 2022b. On Feature Selection from Time-

Frequency Images, 14th Int. Conf. on Electr., Comp.

and AI (ECAI), pp. 1-4.

Aiordachioaie, D., 2021. Industrial Process Diagnosis

based on Information and Time Domain Models, 13th

Int. Conf. on Electr., Comp. and AI (ECAI), pp. 1-4.

Aiordachioaie, D. and Popescu, Th.D., 2020, Aspects of

Time Series Anal. with Entropies and Complexity

Measures, Int. Symp. on Electr. & Tc (ISETC), pp. 1-4.

Aiordachioaie, D., 2014. On quick-change detection based

on process adaptive modelling and identification, Int.

Conf. on Develop. and Appl. Syst. (DAS), pp. 25-28.

Aiordachioaie, D., 2013. Signal Segmentation Based on

Direct Use of Statistical Moments and Renyi Entropy,

10th Int. Conf. on Electr., Computer and Computation

(ICECCO), Istanbul, Turkey, pp. 359-362.

Auger, F., 1991. Representations Temps-Frequence Des

Signaux Nonstationnaires: Synthese et Contributions,

PhD thesis, Ecole Centrale de Nantes, France.

Bozic, S.M., 1996. Digital and Kalman Filtering. An

introduction to discrete time-filtering and optimum

linear estimation, Halsted Pr., 2nd Edition.

Basseville, M., 1997. Statistical approaches to industrial

monitoring problems - Fault detection and isolation,

Proc. Of the SYSID’97, Kitakyushu, Japan.

Boashash, B., Azemi, G., and Khan, N.A., 2014. Principles

of time–frequency feature extraction for change

detection in nonstationary signals: appl. to newborn

EEG abnormality detection, PR, pp. 616-627.

Baraniuk, R.G., et al, 2001. Measuring time–frequency

information content using the Rényi entropies, IEEE

Trans. on IT, 47(4), pp. 1391-1409.

Barry, T. 1992. Fast calculation of the Choi-Williams time-

frequency distribution, IEEE Trans. on SP, 40(2), pp.

450-455.

Barkat, M., 2005. Signal Detection and Estimation, 2nd

Edition, Artec House.

CWR, Case Western Reserve Univ. Bearing Data Center,

2022. https://engineering.case.edu/bearingdatacenter.

Cohen, L., 1989. Time-Frequency Distributions - A

Review, Proceedings of the IEEE, 77(7), pp. 941–980.

Daubechies, I., 1992. Ten lectures on wavelets, CBMS-

NSF Conf. series in applied mathematics. SIAM Ed.

Flandrin, A.P.; Gonçalvès, P.; Lemoine, O., 1996. Time-

Frequency Toolbox for Use with MATLAB, CNRS

(France) / Rice Univ. (USA).

Gustafson, F., 2007. Statistical Signal Processing

Approaches to Fault Detection, ARC, 31, pp.41–54.

Haykin, S. 2002. Adaptive Filter Theory, 4th Edition,

Prentice Hall.

Humeau-Heurtier, A., (Editor) 2016.

Multiscale Entropy

Approaches and Their Applications, MDPI Entropy.

Isermann, R. 2006. Fault detection with signal models. In:

Fault-Diagnosis Systems. Springer, Berlin, Heidelberg.

Karmeshu, J., 2003. (Ed.). Entropy measures, maximum

entropy principle and emerging applications, New

York: Springer-Verlag.

Kay, S.M., 1993. Fundamentals of Statistical Signal

Processing: Estimation Theory, Prentice Hall.

Seeliger, A., Mackel, J., and Georges, D., 2002.

Measurement and Diagnosis of Process-Disturbing

Oscillations in High-Speed Rolling Plants, IMEKO

2002, Tampere, Finland

Shanmugan, K.S. and Breipohl, A.M., 1988. Random

Signals: Detection, Estimation and Data Analysis, John

Wiley & Sons, NY.

Timusk, M.; Lipsett, M.; Mechefske, C.K., 2008. Fault

detection using transient machine signals, Mechanical

Systems & SP, Vol. 22, pp. 1724-1749.

Patton, R.J.; Frank, P; Clark, R., 1989. Fault Diagnosis in

Dynamic Syst. – Theory and Application, Prentice Hall.

Precup, R.E., et al, 2015. An overview on fault diagnosis

and nature-inspired optimal control of industrial

process appl., Computers in Ind., 74, pp. 75-94.

Popescu, Th.D, Aiordachioaie D., and Manolescu, M.,

2017. Change detection in vibration analysis — A

review of problems and solutions, Proc of the ISEEE,

Galati, Romania, pp. 1-6.

Poor, H.V., 1994. An introduction to signal detection and

estimation, Springer.

Mallat, S., 1989. A theory for multiresolution signal

decomposition: the wavelet representation, IEEE

Pattern Anal. and Machine Intell., 11(7), pp 674–693.

Venkatasubramanian, V., Rengaswamy, R; Yin, K.;

Kavuri, S. N., 2008. A review of process fault detection

and diagnosis, Comp. & Chem. Eng., 27, pp. 293-311.

Ypma, A., 2001. Learning Methods for Machine Vibration

Analysis and Health Monitoring, PhDThesis, TU Delft.

Zhang, W., 2010. Fault detection, In-Tech.

On Detection and Classiﬁcation of State Changes in Physical Processes by Signal Processing Techniques

445