Computing Implementation of Globular Cluster Simulation for CSST

Zhongmu Li

1,*

, Yangyang Deng

1,2

and Tao Xia

1,3

Institute of Astronomy, Dali University, Dali 671003, China

Yunnan Observatories, Chinese Academy of Sciences, Kunming 650216, China

Shanghai Key Lab for Astrophysics, Shanghai Normal University, Shanghai 200234, China

Keywords: Computing Implementation, N-Body Simulation, Globular Cluster, CSST.

Abstract: Direct N-body simulation is hard to implement as the great demand on computational resources. It is strictly

relied on the configurations of hardware and software. The direct N-body simulation of star clusters are

important for many scientific projects including the China Space Station Telescope (CSST), because star

clusters are important celestial bodies of these projects. Such simulation is difficult to be done by normal

computers because of the large number of cluster member stars. This paper carries out the direct N-body

simulation of three globular cluster models for CSST. The cluster models take various star numbers, binary

fractions and chemical compositions. The simulation is realized via employing appropriate environment

configuration and an updated code, NbodyCP, which is based on NBODY6++GPU. The photometric data,

spatial and physical parameters of three clusters are finally calculated. It is shown that GPU computational

technique and the number of binaries dominate the computational efficiency of celestial bodies with a large

amount of member stars.

1 INTRODUCTION

China Space Station Telescope (CSST) is the largest

space-based optical telescope in China. It is expected

to put into service in 2024 (Zhan, 2021). As one of

the advanced study of CSST, the simulation of star

clusters is crucial because it can provide the

theoretical guidance and test for observations.

According to cluster age, number and spatial

distribution of member stars, star cluster are classified

into two types, globular and open clusters. The former

contains more than thousands of member stars and the

latter one includes only dozens to thousands of

member stars. Some globular clusters are thought as

the oldest celestial bodies, because they are as old as

the universe. It is likely to give some limitation on the

cosmic age and reveal the formation and evolution of

early universe. Besides, globular clusters are widely

distributed in the Milky Way and nearby galaxies

(e.g., M31, Large and Small Magellanic Clouds).

Therefore, globular cluster is the key object in CSST

study. The detailed simulation of globular clusters is

required to complete the map of celestial studies.

Due to the large number of member stars and the

complex stellar evolution process, the

implementation of direct N-body simulation of

globular cluster is relatively difficult. As well as the

limitation of the configurations and environment of

computational resource, it is hard to derive the

simulated results of several globular clusters within a

short period.

In consequence, this work concentrates on the

direct N-body simulation of globular clusters. We

compute the simulation of three globular cluster

models, from zero age to 13.7 giga year. The model

clusters are put in specific nearby galaxies and the

stellar magnitudes are transfer to the photometric

systems of CSST. Some other physical parameters

such as effective temperature and luminosity of

member stars are also obtained in the simulation.

2 N-BODY SIMULATION

2.1 Algorithm and Parallelization

In this work, we apply an improved N-body

simulation code, NbodyCP, which is especially

designed for calculating star clusters with multiple

populations by Prof. Zhongmu Li. The code is based

on NBODY6++GPU code (Wang et al, 2015),

modified by adding the simulation of multiple stellar

Li, Z., Deng, Y. and Xia, T.

Computing Implementation of Globular Cluster Simulation for CSST.

DOI: 10.5220/0011952600003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 471-475

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

471

population and improving the stellar evolution code

(Banerjee et al, 2020). The code has also been

designed to be used conveniently.

Similar to the descriptions of Wang et al (2015),

the combination of the fourth-order Hermite

integration and hierarchical time-steps methods is

applied to decide the calculating time-steps. In order

to decrease the computational time of forces among

particles, the Ahmad-Cohen neighbour scheme

(Ahmad and Cohen, 1973) is employed. The forces

are divided into two types according to the locations

of particles away from the neighbour radius. The

inner is irregular force (time-step is large) and the

outer is regular force (time-step is small). In addition,

the members of star clusters include close binaries,

triples and higher order systems, which are important

parts in dynamical process, requiring the precise

solution. The internal evolution processes of these

systems are treated differently using the algorithms in

Kustaanheimo & Stiefel (1965) (KS) and chain

regularization (Mikkola and Aarseth, 1993).

In addition, the hybrid parallelization is used in

NbodyCP code to implement the simulation of

million particles, similar to that in

NBODY6++GPU. In general, the integration of the

time-step of KS is calculated by CPU because the

time-step distribution is the smallest, then the time-

step of irregular force is parallelized by AVX/SSE

with OpenMP. The regular force time-step is

parallelized by GPUs with OpenMP as well. An

adjust block is existed after the calculation of regular

force time-step, is parallelized by GPUs. A node is

consisted of all the time-step blocks, and numerous

nodes constitute the entire code structure (for

computer cluster). Therefore, the NbodyCP code is

able to simulate the globular clusters in a relatively

short period.

2.2 Configuration and Environment

The simulation of this work is performed on three

servers. Different GPUs are used for computations on

these servers. The GPUs on these servers are NVIDIA

RTX A6000, NVIDIA GeForce RTX 3090 and

NVIDIA GeForce RTX 3080 respectively. The CPUs

of the servers are Intel Core i9-10900k and i9-11900k,

contain 20 or 16 cores. The basic frequency is 3.7 and

3.5 GHz separately. Other configurations of the three

servers, such as operating system, memory, compiler

and motherboard, are all the same. Table 1 lists the

descriptions of configurations and environments of

the three servers.

Table 1: Configurations and environments of different

servers.

Server 1 Server 2 Server 3

GPU RTX

A6000

GeForce

RTX 3090

GeForce

RTX 3080

CPU Core i9-

11900k,

3.5 GHz,

16 cores

Core i9-

10900k,

3.7 GHz,

20 cores

OS Ubuntu 20

Memory

4 × 32 GB, DDR4-3200

GPU

Compile

CUDA 11

Basic

Compile

gfortran

Motherboar

TUF GAMING Z590-PLUS WIFI

2.3 Model Input

We build three globular cluster models for our

globular cluster simulation. The three cluster models

contain 50,000, 100,000 and 100,000 member stars

respectively. They are named Model 1, Model 2 and

Model 3. Models 1 and 3 contain the initial binary

fraction of 0.1, while all member stars in Model 2 are

set to be single. As the significant role in cluster

dynamical evolution process, initial binary fraction

affects the computational efficiency significantly.

Note that all binary stars are randomly generated. The

metallicities of Models 1 and 2 are Z = 0.0001, and

that of Model 3 is Z = 0.0003, because most globular

clusters are detected to be metal-poor. The stellar

masses of three models are produced by the initial

mass function (IMF) of Kroupa (2001), covering a

range from 0.08 to 100 solar masses as described in

stellar evolution theory. Star members are set to

distribute as the Plummer sphere (Plummer, 1911).

The stellar evolutionary process is calculated by the

developed BSE code (Banerjee et al, 2020; Hurley et

al, 2002). Due to the universe age, the maximum

evolution age of cluster models is set to 13.7 giga year.

The first 8 rows of Table 2 summary the input

parameters of the three star cluster models.

ISAIC 2022 - International Symposium on Automation, Information and Computing

472

Table 2: Input parameters and computational times of three

models. Number, f

, M

max

and M

min

indicate star number,

binary fraction, upper and lower limits of stellar masses.

Age is the simulated physical age of star cluster and t is the

time spent in the simulation process. The unit of stellar mass

is solar mass.

Model 1 Model 2 Model 3

Numbe

50,000 100,000 100,000

0.1 0.0 0.1

0.0001 0.0003

IMF Krou

(

2001

)

max

100 M

⊙

min

0.08M

⊙

Stellar

evolution

code

BSE code (Banerjee et al, 2020; Hurley

et al, 2002)

Spatial

distribution

Plummer (1911)

e 13.7

8 days and

20 hours

18 days

and

20 hours

40 days

and

4 hours

Device Server 1 Server 2 Server 3

2.4 Results

After the computations of three models, the spatial,

kinetic, and evolutionary data of member stars are

obtained at different ages from the direct N-body

simulation. In detail, the three-dimension position

and velocity, stellar radius, core radius, effective

temperature, luminosity, stellar type, gravitational

acceleration and metallicity are precisely determined

in the evolutionary process. In order to derive the data

at a fixed time, we develop an interpolation program

to obtain the data at a given time. The detailed star

distribution and stellar evolution of three cluster

models can be tracked well (see examples in Figures

1 and 2) using the simulation data.

The time spent on the simulations of three models

are found to be significantly different. As can be seen

in the tenth row of Table 2, Model 1 spends 8 days

and 20 hours computing the integral process. Model

2 costs more than two times and Model 3 needs about

five times of that of Model 1. The comparison of

Models 2 and 3 suggests that binary fraction affect a

lot on the computing efficiency of cluster simulation,

because the largest difference between the two

simulations is the number of binaries. Star number

affects the computing time significantly as well.

Moreover, the minimal investment of time of Model

1 emphasizes the crucial impact on computing power

of GPU unit. Although the CPU-computing of Model

https://sec.center/YBC/

1 is weaker than those of Models 2 and 3, the time

spent decreases effectively.

3 TRANSFORMATION OF

MAGNITUDES AND

COORDINATES

In order to use the simulated results as a reference for

the observation of CSST, the related physical

parameters, such as effective temperature, luminosity,

mass and metallicity, are utilized to calculate the

magnitudes in CSST bands online

. Therefore the

stellar data is expanded to involve NUV, u, g, r, i, z and

y magnitudes. Figure 1 displays the example of

Hertzsprung-Russell and color-magnitude diagrams

(HRDs and CMDs) of Model 1. The evolution times

(i.e., ages) are 5 and 13 giga years. Because the HRD

and CMD are the ideal criteria of stellar evolutionary

computation, the diagrams verify the accuracy of our

simulation.

Besides, the simulated cluster center is 0 of a

local system in our simulation, so we put three

models to some locations of three nearby galaxies

(

M31, Large and Small Magellanic Clouds) to get

more useful mimic clusters. This helps to do some

advanced studies easily. The entire process is

implemented by the Astropy package

. Firstly, the

positions and radial velocities of the galaxies are

converted from the equatorial coordinate system to

the Cartesian coordinate system. Then a three-

dimensional coordinate in the range of galaxy radius

is randomly generated to be the coordinate of cluster

center, avoiding the overlap of cluster position. After

that, a linear superposition of the coordinates of

galaxies and cluster center is obtained. The combined

coordinates are finally converted back to the

equatorial coordinate system. Consequently, The

right ascensions (RAs), declinations (DECs), proper

motions, radial velocities and the distances from the

sun to the three model clusters in

galaxies M31,

Large and Small Magellanic Clouds are derived.

Figure 2 exhibits the example of distributions of

initial spatial positions and the final parameters that

will be observed by CSST. The expansion of cluster

scale is also shown in the figure.

https://www.astropy.org/

Computing Implementation of Globular Cluster Simulation for CSST

473

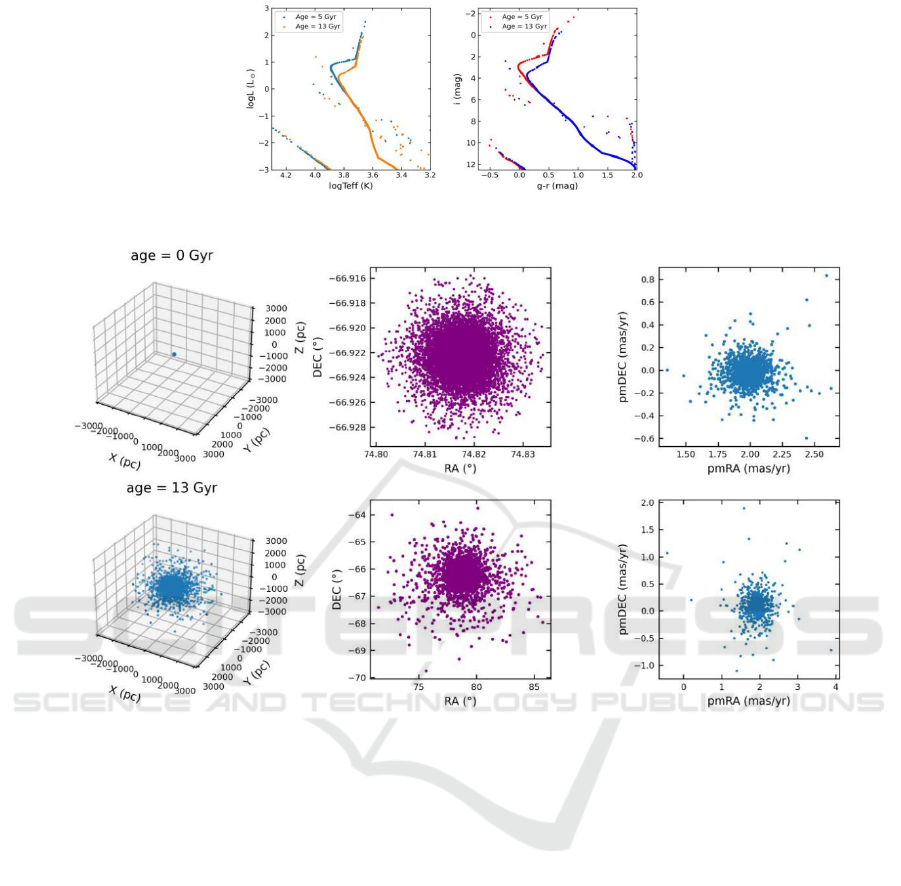
Figure 1. Examples of HRD and CMD for Model 1.

Figure 2. Examples of direct star distributions from N-body simulation, converted coordinates (RA, DEC) and proper motions

in RA and DEC. The selected data is from Model 1 which located in Large Magellanic Cloud.

4 CONCLUSIONS

This paper describes the direct N-body simulation of

three globular cluster models with various numbers of

stars, which can be used for the advanced studies of

CSST. The simulation is realized on three Linux

servers, on which the software and environment

configurations are set to be the same. However, the

configurations of CPU and GPU are different because

of the implementation of algorithms in the code is

affected obviously by the hardware.

The NbodyCP code (modified on the basis of

NBODY6++GPU by Prof. Zhongmu Li) and an

interpolation program are employed to obtain the

stellar evolutionary data at every 0.01 giga year. The

simulated data is converted to CSST bands and the

coordinates are transferred to some locations in three

nearby galaxies. As the result, the size of three

globular clusters are simulated to expand rapidly. The

stellar evolution process is consistent with the

previous theory as well.

By comparing the computational time with our

previous work (Deng, 2021), the simulated speed of

globular clusters has been significantly improved, as

the NBODY6++GPU code and GeForce 2080Ti are

used in the previous simulation. In addition, the

results confirm the important role of binary fraction

and GPU computing performance in N-body

simulation for a large number of particles. According

to the tests, the improvement of CPU basic frequency

and the factors above are needed in further

simulations.

ISAIC 2022 - International Symposium on Automation, Information and Computing

474

ACKNOWLEDGEMENTS

This work is supported by the National Natural

Science Foundation of China (No. 11863002),

Yunnan Academician Workstation of Wang Jingxiu

(202005AF150025), China Manned Space Project

with NO.CMS-CSST-2021-A08 and Sino-German

Cooperation Project (No. GZ 1284).

REFERENCES

Ahmad A., Cohen L., 1973, A numerical integration

scheme for the N-body gravitational problem, Journal

of Computational Physics, 12: 389-402.

Banerjee, S., Belczynski, K., Fryer, C. L., Berczik, P.,

Hurley, J. R., Spurzem, R., Wang L., 2020, BSE versus

StarTrack: Implementations of new wind, remnant-

formation, and natal-kick schemes in NBODY7 and

their astrophysical consequences, Astronomy &

Astrophysics, 439: A41-A63.

Deng, Y., Li, Z. and Chen, W., 2021, Simulation of

Formation of Binary Compact Objects in Globular

Cluster, Journal of Physics: Conference Series, 2068(1):

012049.

Hurley, J. R., Tout, C. A., Pols, O. R., 2002, Evolution of

binary stars and the effect of tides on binary populations,

Monthly Notices of the Royal Astronomical Society,

329(4): 897-928.

Kustaanheimo, P and Stiefel, E., 1965, Perturbation theory

of Kepler motion based on spinor regularization,

Journal f

r die reine und angewandte Mathematik, 218:

204-219.

Kroupa, P., 2001, On the variation of the initial mass

function, Monthly Notices of the Royal Astronomical

Society, 322(2): 231-246.

Mikkola, S., Aarseth, S. J., 1993, An Implementation of N-

Body Chain Regularization, Celestial Mechanics and

Dynamical Astronomy, 57(3):439-459.

Plummer, H. C., 1911, On the problem of distribution in

globular star clusters, Monthly Notices of the Royal

Astronomical Society, 71: 460-470.

Wang, L., Spurzem R., Aarseth, S., Nitadori, K., Berczik,

P., Kouwenhoven, M. B. N., Naab, T., 2015,

NBODY6++GPU: ready for the gravitational million-

body problem, Monthly Notices of the Royal

Astronomical Society, 450(4):4070-4080.

Zhan, H., 2021, The wide-field multiband imaging and

slitless spectroscopy survey to be carried out by the

Survey Space Telescope of China Manned Space

Program, China Science Bulletin, 66(11):1290-1298.

Computing Implementation of Globular Cluster Simulation for CSST

475