Evapotranspiration Prediction Using ARIMA, ANN and Hybrid

Models for Optimum Water Use in Agriculture: A Case Study of

Keiskammahoek Irrigation Scheme, Eastern Cape, South Africa

Mbulelo Phesa

, Yali Woyessa

and Nkanyiso Mbatha

Department of Civil Engineering, Walter Sisulu University, Buffalo City, 5214, South Africa

Department of Civil Engineering, Central University of Technology, Bloemfontein, South Africa

Department of Geography, University of Zululand, Kwadlangezwa, 3886, South Africa

Keywords: Evapotranspiration, Prediction, ARIMA, ANN, Forecasting, Keiskammahoek, Irrigation

Abstract: Evapotranspiration is the main limitation for irrigation development in developing countries and semi-arid

regions. Proper prediction of this variable is key for proper planning and positively contribute to daily

management of irrigation schemes. This study used 18 years (2001-2018) of remotely sensed data extracted

at Keiskammahoek Irrigation Scheme, Eastern Cape province of South Africa, a province that has been

declared drought disaster region forcing many irrigation schemes in this region to close some irrigated

sections in order to deal with reduced dam levels. This study used three prediction models, namely Auto-

Regressive Integrated Moving Average (ARIMA), Artificial Neural Networks (ANN), and Hybrid (ARIMA-

ANN) to predict ET for optimal water use in this irrigation scheme. The prediction models were evaluated

using four model performance statistics, namely Root Mean Square Error (RMSE), Mean Absolute

Percentage Error (MAPE), Mean Absolute Error (MAE), and the Pearson’s correlation of coefficient (R). The

results show that the hybrid (ARIMA-ANN) model outperformed both the ARIMA and ANN consecutively

with less values of the statistical performance evaluation showing RMSE = 33.80, MAE = 27.02, MAPE =

17.31, and R = 0.94 compared to higher values of ARIMA and ANN. In general, these prediction results show

the dominance of the Hybrid (ARIMA-ANN) model over ARIMA and ANN. These results will assist water

managers at Keiskammahoek Irrigation Scheme to plan effectively.

1 INTRODUCTION

The estimation and understanding of the terrestrial

water balance are part of viable water administration

systems. Considering the recent patterns of the impact

of climate change, these estimates will be of

increasing importance. One of the primary water-

balance calculation parameters is the reliable

estimation of evapotranspiration (ET). Therefore,

understanding of energy and water vapor fluxes in

certain sites is vital, particularly in a perspective of

authenticating climate change forecasting (Gwate,

Mantel, Pailmer, Gibson, & Munch, 2018). Thus,

precise prediction of ET flux is important for

agricultural development and water resource

https://orcid.org/0000-0002-9625-5045

https://orcid.org/0000-0002-1128-7321

https://orcid.org/0000-0001-9120-2481

management. However, in developing countries, like

South Africa, it is very difficult to obtain all the

relevant data to use in a widely applied Penman-

Montheith approach, therefore alternative reliable

and powerful prediction approaches are used to

examine the non-linear trends related to the predictor

variables for ET rate (Ghorbani, Kazempour, Chau,

Shamshirband, & Ghazvinei, 2018).

This study predicts evapotranspiration for optimal

water use in Keiskammahoek irrigation scheme

located in the Eastern Cape province of South Africa.

This province has been declared a drought disaster

region (Mahlalela, Blamey, Hart, & Reason, 2020,

Botai, et al., 2020, Graw, et al., 2017), which led to

Keiskammahoek Irrigation Scheme closing other

section of its irrigated site in order to deal with

276

Phesa, M., Woyessa, Y. and Mbatha, N.

Evapotranspiration Prediction Using ARIMA, ANN and Hybrid Models for Optimum Water Use in Agriculture: A Case Study of Keiskammahoek Irrigation Scheme, Eastern Cape, South Africa.

DOI: 10.5220/0012009000003536

In Proceedings of the 3rd International Symposium on Water, Ecology and Environment (ISWEE 2022), pages 276-286

ISBN: 978-989-758-639-2; ISSN: 2975-9439

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

reduced water levels on water reserves. This study,

therefore, used three widely used prediction tools

namely, ARIMA, ANNs and Hybrid (ARIMA-ANN)

model to predict ET and in order to assist

Keiskammahoek water managers to plan and manage

the irrigation scheme effectively.

According to (Ziervogel, et al., 2014), the increase

in annual temperatures in South Africa by at least 1.5

times of the average 0.65 degrees has led to climate

being a key concern. They further suggested that it

was posing a vital treat to South Africa’s water

reserves, food security, health, infrastructure, as well

as ecosystem services and biodiversity. The growing

impact of climate change has key consequences for

South Africa, particularly for the poor even though

there are programmes supporting an ambitious

renewable energy program, South Africa’s response

to climate change is hindered by hesitation in

policies(Chersich, et al., 2018). In the province of

Eastern Cape, South Africa livestock farming is very

crucial for livelihood and is considered as a wealth by

famers despite their education status (Mandleni &

Anim, 2011). According to the conclusion of (Todaro

& Smith, 2012), livestock farmers suffer a greater

impact from climate change. South Africa suffers

from scarcity of water as the demand for water

resources increases with the increase in population. If

the country wants to sustain economic development,

urgent needs must be in place to protect the quality of

the resources whilst striving to meet the problem of

water scarcity (Todaro & Smith, Economic

development, 2020).

Most of the land in this province is used for

agriculture with around 35% of households being

involved in agricultural activities, however the

extreme drought conditions over the past decades

have negative impact on these famers (Graw, et al.,

2017). In South Africa, irrigation accounts for over

55% of the total available consumptive freshwater

(Mishra & Singh, 2011). South Africa falls within the

semi-arid region where the evaporation rate is more

than the precipitation rate (Nkondo, Zyl, Keuris, &

Shrener, 2012).ET is one of the crucial elements of

the hydrological cycle; hence, it expedites the

furtherance of precipitation through the process of

condensation. It is also crucial for the transportation

of minerals and nutrients necessary for plant growth,

and it creates a favorable cooling method to plant

canopies in many climates through its direct

relationship with the Latent heat flux (LE) effect on

earth energy and water balance (Calzadilla, Zhu,

Rehdanz, Richard, & Ringler, 2014).

Therefore, ET remains to be one of the major

constraints for irrigation development in developing

countries and in semi-arid regions of the world

(Traore, Wang, & Kerh, 2008). Accurate prediction

of ET is key for agriculture as it informs proper

planning and contributes positively to the daily

management of the irrigation scheme. Moreover,

determining the perfect timing and amount of water

needed for irrigation is important for effective

management of water used by crops (Kishore &

Pushpalatha, 2017). Therefore, scheduling becomes

very critical in agriculture, as ET estimation will give

an assurance of the reliable daily run of the irrigation

scheme, design, and project planning (Kishore &

Pushpalatha, 2017). It is therefore crucial to

effectively predict ET in agriculture in order to attain

a comprehensive picture of the water cycle. (Dutta,

Smith, Grant, Pattey, & Desjardins, 2016) and for

effectively managing scarce resources for crop

production (Anapalli, Fisher, Reddy, Rajan, &

Pinnamaneni, 2019).

2 MATERIAL AND METHODES

2.1 The Study Area

Keiskammahoek Irrigation scheme is in

Keiskammahoek, a small town situated in the Eastern

Cape province of South Africa and located at Latitude

S 32°41ʹ14ʺ E 27°07ʹ48ʺ. The average temperature

ranges from 6.5º C in winter to 26.7º C in summer.

and an average rainfall of 502mm (Sanral, Gibb, &

Eoh, 2016).

Figure 1: Map of Keiskammahoek Irrigation Scheme.

Evapotranspiration Prediction Using ARIMA, ANN and Hybrid Models for Optimum Water Use in Agriculture: A Case Study of

Keiskammahoek Irrigation Scheme, Eastern Cape, South Africa

277

2.2 Autoregressive Integrated Moving

Average (ARIMA) Model

Autoregressive integrated moving average (ARIMA)

is one of the most widely used models because of its

statistical properties, and it can be used in different

ways, such as pure autoregressive (AR), pure moving

average, and combined ARIMA series (Kishore &

Pushpalatha, 2017). It is also called the Box-Jenkins

modeling approach and it is one of the most used time

series because of its flexibility, even though it cannot

predict nonlinear relationships as its linear correlation

structure is presumed among the time values (Zhang,

Zhang, & Li, 2016). In their study, Zhang, Zhang, &

Li, (2016) define ARIMA as the model that can be

decomposed into two parts, with the first part being

the “Integrated (I) component (d)”, representing the

quantity of distinguishing to be achieved on the

sequence to make it constant; the second is the

ARIMA model sequence that is rendered constant

through variation. ARIMA is regarded the most

effective forecasting tool, and it is widely used in

social science and for time series; it also depends on

the historical data as well as its past error relations for

predicting (Adebiyi, Adewumi, & Ayo, 2015). In the

study by Gautam & Sinha, (2016), ARIMA is

reported as the most appropriate modeling tool for

examination and predicting hydrological events.

They further explain the model as explaining the

linear mixture of the earlier state of a variable “(pure

AR component), and previous forecast error (pure

MA component)”. Therefore, in this study, the

ARIMA model will be one of the forecasting

techniques applied to this study to assist seek accurate

prediction of evapotranspiration at the

Keiskammahoek Irrigation scheme. The ARIMA

model can be mathematically explained as follows:

y =

0 + ∅1 yt-1 + ∅2yt-2 +……. ∅pyt-p

(1)

+ εt - ∅1εt-1 - ∅2 εt-2 ……∅qεt-

(2)

Where the terms 𝑦



and 𝜀



are the actual value and

the random error at a given time 𝑡 . The model

parameters are ∅



(

1,2,⋯,𝑝

)

𝜃



(0,1,2,⋯,𝑞)..

The model parameters p and q are integers and are

normally explained as orders of the model. The model

random errors 𝜀



, are predicted to be independently

and identically distributed with a mean of zero and a

constant variance of 𝜎



. The above equation is a

general equation that represents and necessitates

several essential special cases of the ARIMA family

of models. For example, if 𝑞=0, then this ARIMA

model becomes an AR model of order 𝑝. On the other

hand, when parameter 𝑝=0, this model reduces to

an MA model of order 𝑞. Therefore, the most

important part of designing the ARIMA model is to

determine the appropriate model order (𝑝,𝑞).

2.3 Artificial Neural Networks (ANN)

Model

ANN is a family of artificial intelligence techniques

which can predict any time series, including the

geophysical time series. ANNs are non-linear data-

driven networks that were designed and inspired by

the theory of neuroscience (Morimoto, Ouchi,

Shimizu, & Baloch, 2007), hence the name ‘neural’.

These are mathematical models based on the

capabilities of the human brain to predict and classify

problem domains. Khanna, Plyus, & Bhalla, (2014)

describe ANN as “the information processing

paradigm that is inspired by the way biological

nervous systems such as a brain process information”.

ANNs are fundamentally a semi-parametric

regression method with the capacity to estimate any

quantifiable function up to an unrestrained degree of

correctness (Parasuraman, Elshorbagy, & Carey,

2007). They have been widely adopted for predicting

and forecasting in diverse fields of research such as

finance, medicine, engineering, and sciences as well

as to solve an extraordinary range of problems (Maier

& Dandy, 2000). ANNs are specifically useful when

the relationships between both input and output

variables are discrete (Jha, 2007). These models have

been commended as favorable models in cases where

the variety of data is excessive and the relationship

among those variables is mainly unclearly understood

(Jha, 2007).

In this study, the single hidden layer feedforward

network was used as one of the techniques to predict

ET. Schultz, Wieland, & Lutze, (2000) explains a

single hidden feedforward network as the widely used

models for forecasting models for modelling and for

predicting time series. The model has three

processing layers which are linked by its acyclic and

distinguished by its connection between output (yt)

and inputs (y

t -1

. y

t-2

,.., y

t-p

. Schultz, Wieland, & Lutze,

(2000), gives the following model’s mathematical

association between input and output:

𝑦



=𝛼



+𝛼



𝑔𝛽



𝛽



𝑦







+𝜀









(3)

Where 𝛼



(𝑗=0,1,2,⋯,𝑞) and 𝛽



(

𝑖=

0,1,2,⋯,𝑝;𝑗=1,2,⋯,𝑞

)

are model limits which

ISWEE 2022 - International Symposium on Water, Ecology and Environment

278

are called the joining weights; p and q are the number

of inputs nodes and the number of the hidden nodes,

respectively. When designing these types of ANN,

the logistic function is often employed as the hidden

layer transfer function that is given by:

𝑔

(

𝑥

)

1+exp

(

−𝑥

)

(4)

It should be noted though that the ANN model

presented above performs a nonlinear functional

mapping from the past observations

(𝑦



,𝑦



,⋯,𝑦



) to the future value 𝑦



i.e.;

𝑦



𝑓

𝑦



,𝑦



,⋯,𝑦



,𝑤+𝜀



(5)

Where 𝑤 is a vector of all parameters and 𝑓 is a

function determined by the network structure and

connection weights (Schultz, Wieland, & Lutze,

2000).

• Training the Artificial Neural Networks

A multilayer perceptron (MLP) type of network

was used; hence, it is the most used form of a neural

network. Provided sufficient data, sufficient hidden

units, and sufficient time, an MLP can learn to

estimate almost any function to a precise degree (Jha,

2007).

2.4 Hybrid (ARIMA-ANN) Model

To ensure the accuracy of the results obtained from

two models that have already been used, namely Auto

Regressive Integrated Moving Average (ARIMA)

and Artificial Neural Networks (ANN), a hybrid

(ARIMA-ANN) model was used. As much as both

models can be satisfactory in modelling and

forecasting using time series, ARIMA are able to

detect linearity of the time series whilst the ANNs are

capable of detecting nonlinearity of the time series.

Therefore, each model alone cannot adequately

handle linear and nonlinear patterns; thus, by using

joint models, multifaceted autocorrelation structures

in data can be modelled precisely (Zhang G. P.,

2003). As an example, a study by Mallikarjuna &

Prabhakara, (2019), used Zhang hybrid model and

reported that neither ARIMA nor ANN is completely

appropriate for prediction of all the time series

because the real-world time series have both linear

and nonlinear correlation structures between

observations. Thus, in this study, they followed a

study by (Zhang G. P., 2003) and used both ARIMA

and ANN and developed a hybrid system which is

given by:

𝑦



=𝐿



+𝑁



(6)

Elwasify, (2015)

described what each of these

values represents as follows:

• 𝑦



- represents the observation of time series at

the time t,

• 𝐿



- represents the linear part of ARIMA

models, and

• 𝑁



- represents the nonlinear part of the ANN

models.

According to Zhang G. P., (2003), the first step is to

model using ARIMA for the linear component, and

the residual left from the liner data will contain the

nonlinear relationship and letting ET donate the

residual at time t from the linear model then et is

presented as follows:

𝑒



=𝑦



−𝐿



(7)

Where L

is the prediction value of time t from the

predicted relationship of the original ARIMA

formula. This residual is very crucial in the diagnosis

of the adequate linear models; hence, the linear model

is not adequate should there still be linear correlation

structures remaining on the residual. Currently, there

is no statistic for nonlinear autocorrelation connection

diagnosis and that causes that even when models have

been accepted by the diagnosis examination, it may

still be accurate enough for a nonlinear relationship to

be properly modelled and that means every nonlinear

pattern cannot be modelled by ARIMA. Modeling the

residual using ARIMA will assist to discover the

relationship in nonlinear correlation. Zhang G. P.,

(2003), suggests the models for residual as follows:

𝑒



𝑓

(

𝑒



−1,𝑒



−2,…..,𝑒



)

+𝜀



(10)

𝜀



is the random error whilst f is determined by

the nonlinear function using neural network, and if f

is not adequate, the error is not certainly random. It is

very crucial to determine the perfect model.

Therefore, by donating forecast from the residual

model, the combined forecast will be

=𝐿



+𝑁



(11)

This simply means that the first step will be to

utilise the ARIMA model to examine the linear part,

and the second step of the hybrid will be to develop

Evapotranspiration Prediction Using ARIMA, ANN and Hybrid Models for Optimum Water Use in Agriculture: A Case Study of

Keiskammahoek Irrigation Scheme, Eastern Cape, South Africa

279

the models using the residual from the first ARIMA

model; hence, the residual from ARIM will be having

nonlinear patterns and the results obtained from

neural networks will be used to estimate the model

error for ARIMA terms. The Hybrid model will

therefore have different features and will have much

power of ARIMA and ANN, which will determine

different patterns (Zhang P. G., 2003).

2.5 Model Performance

Normally, there are no standard norms for evaluating

the forecasting performance of a model and appraisal

with other benchmark models (Mbatha & Bencherif,

2020). To evaluate the performance of the three

models used in this study, namely ARIMA, ANNs,

and Hybrid, we compared the forecasted ET values

with their corresponding measured ET values

obtained from the study site using typical

performance metrics. According to Lewis C. D.,

(1982), there are many alternative models used over

the years to forecast the time series; therefore, one

needs to consider specific conditions in choosing the

appropriate model to be employed. For the purpose of

this study, It is crucial to check the model accuracy to

select the most appropriate model based on the ET

forecasted results. Below are the performance

measures used for RMSE, MAPE and MAE as

explained by (Lewis C. D., 1982). The Root Mean

Square Error was used in order to evaluate the

difference between the predicted ET results and the

original ET data. According to (Chai & Draxler,

2014), the RMSE model has been widely used in

many studies to examine the model performance.

Because of uncertainties reported by Willmott &

Matsuura, (2005), other models were applied. The

Mean Percentage Error (MAPE) statistic measure

was also applied in order to evaluate the quantity of

error in the forecasted values of ET.

This widely used Measure is used when the

amount of the predicted values remain higher than

zero (Myttenaere, Golden, Grand, & Rossi, 2016,

Khair, Fahmil, Hakim, & Rahim, 2017). The Mean

Absolute Error (MAE) was also applied. This

measure is calculated from an average error, and it is

frequently used to examine the vector to vector

models (Willmott & Matsuura, 2005). The model

accuracy was checked by the use or Pearson’s

correlation of coefficient. This model is explained by

Mukaka, (2012), as the method that is used to

evaluate the likely two-way linear connection

between two continuous variables. Zero value of the

Correlation coefficient indicates that there is no linear

association between the two variables. However,

between +1 or -1 indicate a perfect correlation and

this strength can be found anywhere between +1 and

-1. The positive value indicates the direct relationship

between two values and the negative value indicates

that there is an inverse relationship between two

values. Results and discussion.

3 RESULTS AND DISCUSSION

3.1 ARIMA Model Selection

The data from 2001 to 2018 was fitted to

AUTOARIMA using “R” and a portmanteau test

called Ljung-Box was done to test the excellence of

the time series model. According to Burns, (2002),

this test is mostly used, and should the significant

autocorrelation not be found on model residuals, the

model is considered perfect. If the values of

correlation of residuals for various time lags is not

significantly different from zero, the model is then

considered adequate for use in forecasting. On one

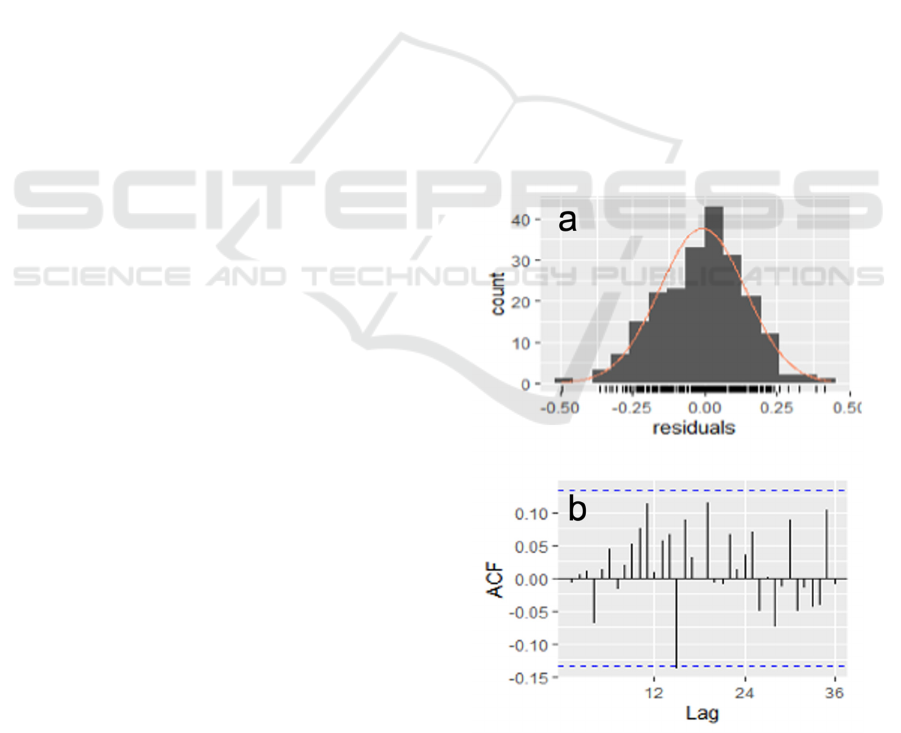
hand, Figure 2(a &b) shows the Akaike’s Information

Criteria (AIC) graph that indicates that there is no

significant correlation because all the bars do not

exceed

the dotted line 95% confidence levels and

Figure 2: Autocorrelation Function (ACF) and Histogram

of residuals of residual of Keiskammahoek Irrigation

Scheme as a ideal fitted model for data series of ET from

2001 to 2018.

ISWEE 2022 - International Symposium on Water, Ecology and Environment

280

according to (Widowati, Putro, Koshio, &

Oktaferdian, 2016), and (Gautam & Sinha, 2016) the

residue is random. The best selected ARIMA model

to forecast ET is ARIMA (1,0,0). On the other hand,

Figure 9(b) presents residuals which are evenly

dispersed. The normal distribution of residuals

indicates that the selected ARIMA model is free of

overfitting (Reza & Debnath, 2020).

3.2 ARIMA Model Training

The training of the ARIMA model was done by

selecting data from 2001 to 2015 as a training set of

data. One of the important aims of slitting data to

training and testing is to use the testing part of the

time series to check the sign of the variable’s

parameters, and to investigate whether they are

significant or not

3.3 ARIMA Forecasting

In this study, the training of the ARIMA model was

done by selecting data from 2001 to 2015 as a training

set of data. One of the important aims of slitting data

to training and testing is to use the testing part of the

time series to check the sign of the variable’s

parameters, and to investigate whether they are

significant or not.

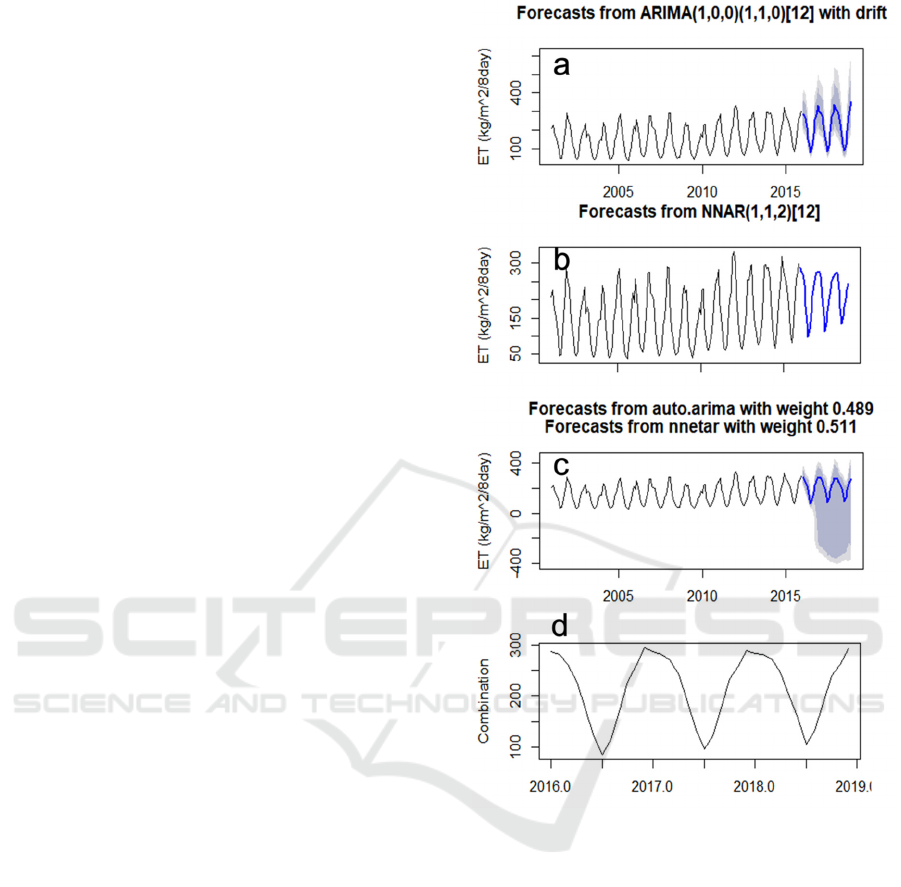
Figure 3(a-c) depicts the prediction results using

ARIMA, ANN and Hybrid models. After the training

of the models was done using 15 years time series

data from 2001 to 2015, the next step was to predict

ET using the remaining 3 year data from 2016 to

2018. Thus, the data set from 2016 to 2018 was used

as the testing part of the time series Prediction. This

was important in forecasting because the testing part

is forecasted and then forecasting results are

compared with the actual results. The black line

represents the training part of the time series data

(2001 to 2018) and the ET forecasted results (2016 to

2018) indicated by the blue line with the dark grey

and light-grey shadings, indicating the 80% and 95%

confidence levels of the forecasted time series. The

ARIMA model constructed for this data is the

ARIMA (1,0,0) and NNAR (1,1,2)(12) for ANNs.

The Zhang P. G., (2003) proposed this model

shown by figure 3(d) because of its the ability to

forecast both linear and nonlinear underlying

processes. The Kaiskammahoek irrigation scheme is

no exception to real world time series contains both

linear and nonlinear correlation structures. The black

line indicates the training data set for a 15-year period

(2001 to 2015); the blue line indicates the forecasted

results, and the grey shading indicating the 95%

Figure 3: Forecasted ET for 3-year period from 2016 to

2018 using the ARIMA (a), ANN (b), Hybrid (ARIMA-

ANN) (c) and the ever-aged models (d). The black line in

Figure 3 (a-c) represents the data from 2001 to 2015 and the

blue line presents the 3 year forecast, with 95% confidence

levels grey lines (a &c) and figure 3(d) with a black line

representing 3 years averaged (ARIMA, ANN and Hybrid)

models.

confidence levels for the three year period (2016 to

2018).

Consecutively Figure 3(d) shows the prediction of

3 combined ARIMA, ANN and Hybrid models

averaged using the summation methods. The black

line shows combined prediction part from 3 models

used from 2016 to 2018. This was done to see if the 3

averaged models could improve the forecast as such

has been proven by other researchers. This study has

employed 3 different model systems and showed its

Evapotranspiration Prediction Using ARIMA, ANN and Hybrid Models for Optimum Water Use in Agriculture: A Case Study of

Keiskammahoek Irrigation Scheme, Eastern Cape, South Africa

281

performances in terms of the correlation coefficient

“R”. However, it is always important to also average

the forecast in order to improve the forecast accuracy

(Bates & Granger, 2017, Clemen, 1989).

3.4 Correlation Statistics

To check the correlation of the prediction portion

person correlation (Lin, 1989), was employed with

ET predicted variables against the ET observed

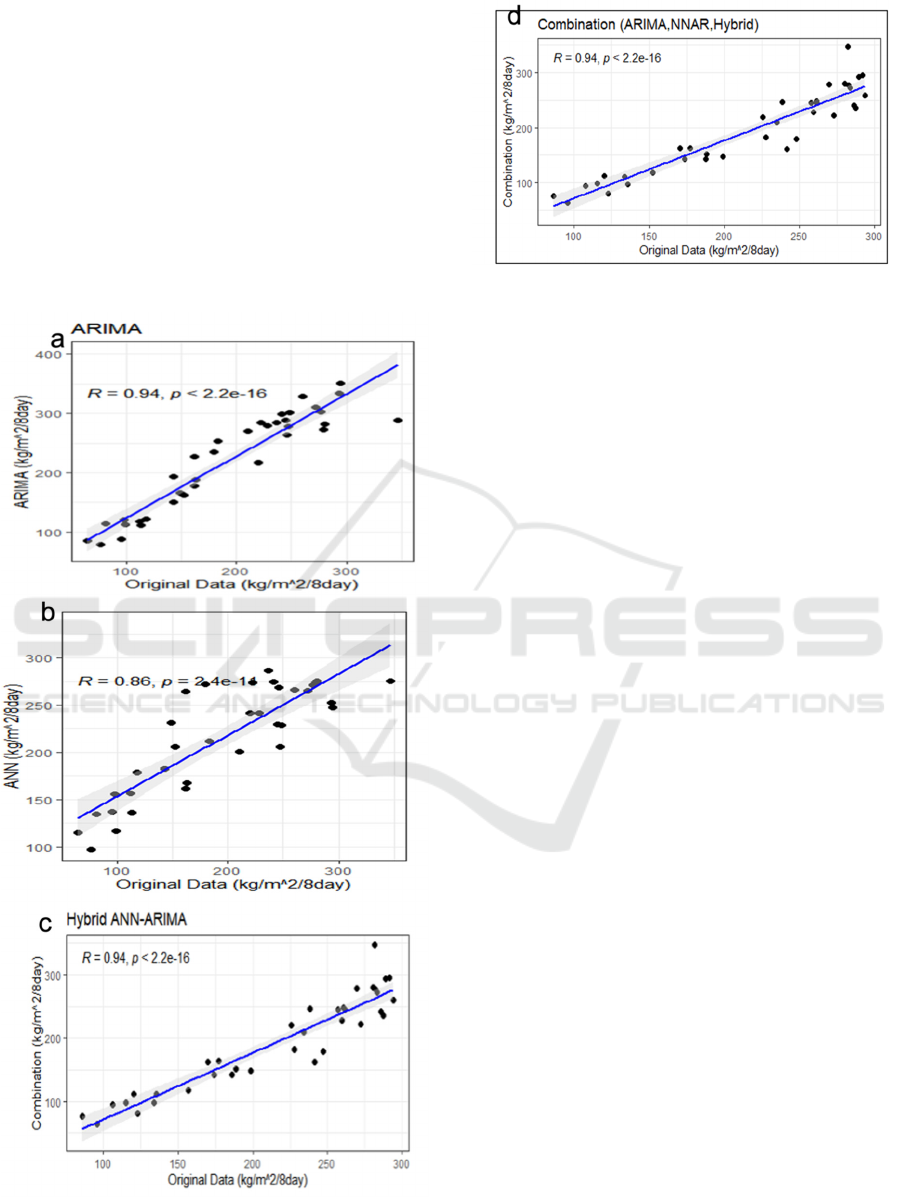
variables. Figure 3 (a-d) depicts the scatter diagram

of the original ET and forecasted ET, represented by

the black dots falling on the 45 line through the origin.

Figure 4: Scatter plot between observed and forecasted ET

show diagram of the actual ET versus the forecasted annual

ET using ARI-MA (1,0,0)(1,1,0)[12] (a), NNAR(1,1,2)[12]

(b), Hybrid (ARIMA-ANN's) (c) and the averaged (d)

models (with validation period, 2016 to 2018).

The correlation of the forecasted for all the 4

forecasting models applied shows a strong correlation

coefficient with ARIMA (R = 0.94), ANN (R= 0.86),

Hybrid (R = 94) and the averaged models with (R =

0.94). Based on the R values for all the 3 models and

the averaged model, it is evidence that there is higher

linear relationship between the forecasted results and

the original time series data. Correlation Coefficient

suggest other 3 used forecasting modelling ARIMA

and Hybrid to be more correlated compared to lower

value of ANN (0.86).

3.5 Model Comparison

Table 1 below shows the three models employed in

this study to forecast ET at Keiskammahoek

Irrigation Scheme, namely ARIMA, ANNs and

Hybrid (ARIMA-ANN), and average of the three

models. The model forecast capabilities are compared

by using model performance statistics such as Root

Mean Square Error (RMSE), Mean Absolute Error

(MAE), Mean Absolute Percentage Error (MAPE),

and Correlation Coefficient (R). The results presented

in this table indicate that Hybrid model outperforms

other models with RMSE = 33.80, MAE = 27.02,

MAPE = 17.31 and R = 0.93. It is also noticeable that

the Mean Absolute Percentage Error-values for

ARIMA and Hybrid seem similar, considering

ARIMA (MAPE = 17.26) and Hybrid (MAPE =

17.31). Since the hybrid model is made up of a

combination of ARIMA and ANNs, it is possible that

this model will perform better than the other models

because it is expected to be capable of capturing both

linearity and non-linearity in the time series. In terms

of the correlation coefficient, ARIMA seems to

outperform the others models, with a correlation

coefficient of R = 0.94.

ISWEE 2022 - International Symposium on Water, Ecology and Environment

282

Table 1: Comparison of the ARIMA, ANN, Hybrid and

Combined Models: RMSE, MAE, MPE, and R.

Models RMSE MAE MAPE R

ARIMA 37.58 32.37 17.26 0.94

ANN 44.18 35.88 24.35 0.86

Hybrid 33.80 27.02 17.31 0.94

Combined 34.68 28.00 18.15 0.94

These results are interesting as they agree with

results found by (Zhang P. G., 2003), who archives

higher accuracy of time series prediction through use

of Hybrid (ARIMA-ANN) models.

The three utilized models were further averaged

to see if prediction accuracy could be reached. It has

been shown in previous studies that combination of

multiple forecasting methods leads to increase of the

forecasting accuracy (Clemen, 1989). Therefore, in

this study, the predictions obtained from the three

models used were combined by using the summation

method. The results of the COMBINED models

indicated in Table 1 show better results of ARIMA

and NNAR. These observations are encouraging as

they are consistent with results of studies on the

combination of several time series forecasting

methods. Similar what is obtained in this study,

Hyndman & Athanasopoulos, (2018), also pointed

out that combining forecasts often lead closer to, or

better than, the best component method.

4 CONCLUSIONS

The possibility to predict evapotranspiration (ET) is

essential as it can affirm perfect planning, design and

operation of any irrigation scheme. Thus, the main

aim of this study was to predict evapotranspiration

(ET) at Keiskammaheok, Irrigation Scheme located

in the province of Eastern Cape of South Africa using

3 time series forecasting models, namely (ARIMA),

(ANN), and the Hybrid (ARIMA-ANN) models. The

18 years (2001-2018) remotely sensed ET data was

extracted from a cloud-built software called Moderate

Resolution Imaging Spectroradiometer (MODIS)

Tera/ Aqua 16-day dataset. Using four model models

performance measures, namely, Root Mean Square

Error (RMSE), Mean Absolute Error (MAE), Mean

Absolute Percentage Error (MAPE), and the

Correlation Coefficient (R). It could be concluded

that the Hybrid (ARIMA-ANN) guarantees the

steadfast ET prediction for Keiskammahoek

irrigation Scheme. The model outperformed other

models with less values (RMSE =33.80, MAR =

27.02, MAPE = 17.31 and R = 0.94). This indicates

that the combination of ARIMA and ANN is a better

option because such hybrid models are able to capture

both linearity and non-linearity in the time series of

ET, which in turn produce better results. This work

will assist the Keiskammahoek irrigation scheme

management to plan effectively.

Future work may include further checking other

variables in order to assess whether these reported

drought in this region like Normalized Different

Vegetation Index (NDVI) to assess vegetation state,

Normalized Deference Water Index (NDWI) which is

the availability of water in plants and Normalized

Difference Different Index (NDDI) in order to check

the drought state in the study site.

ACKNOWLEDGEMENTS

This author like to thank Department of Higher

Education and Training (DHET) for funding the

project under its prestigious program named New

Generation of Academics Program (nGAP), and the

Manufacturing, Engineering and Related Services

SETA (merSETA) under the Walter Sisulu

University Faculty of Science, Engineering and

Technology (FSET).

The authors also would like to thank all personnel

involved in the development of the Google Earth

Engine system and climate engine. We also thank the

providers of the important public data set in the

Google Earth Engine, in particular NASA, USGS,

NOAA, EC/ESA, and MERRA-2 model developers.

REFERENCES

Adebiyi, A. A., Adewumi, A. O., & Ayo, C. K. (2015).

Comparison of Arima and Artificial Neural Networks

Models for Stock Price Prediction. Jornal of Applied

Mathamatics.

Adler, J., & Parmryd, I. (2010). Quantifying colocalization

by correlation: The Pearson correlation coefficient is

superior to the Mander's overlap coefficient. Journal of

Quantitative Cell Science.

Anapalli, S., Fisher, D. K., Reddy, K. N., Rajan, N., &

Pinnamaneni, S. R. (2019). Modeling

evapotranspiration for irrigation water management in

a humid climate. Agricultural Water management,

105731.

Evapotranspiration Prediction Using ARIMA, ANN and Hybrid Models for Optimum Water Use in Agriculture: A Case Study of

Keiskammahoek Irrigation Scheme, Eastern Cape, South Africa

283

Arnold, G. J., Srinivasan, R., Muttiah, S. R., & Williams, J.

R. (1998). Large area hydrologic modeling and

assessment part I: Model development. Journal of the

American water resources Association.

Averbeke, V. W., M'Marete, C. K., Belete, A., & Igodan,

C. O. (1998). An investigation into food plot production

at irrigation schemes in central eastern cape. Eastern

Cape: Water Research Commission Report.

Bachour, R. (2013). Evapotranspiration modeling and

forecasting for efficient management of irrigation

command areas. Doctoral dissertation, Utah State

University.

Bates, M. J., & Granger, J. W. (2017). The combination of

Forecast. Journal of the Operational reaserch Society.

Bencherif, H., Toihir, A. M., Mbatha , N., Sivakuma, V.,

Preez, D. J., beque, N., & Coetzee, G. (2020). Ozone

Variability and Trend Estimates from 20-year of

Ground-Based and Satellite Observations at Irene

Station, South Africa. MDPI atmosphere.

Botai, C. M., Botai, J., Adeola, A. M., Wit, J. P.,

Ncongwane, K. P., & Zwane, N. N. (2020). Drought

Risk Analysis in the Eastern Cape Province of South

Africa: The Copula Lens. Water.

Burns, P. (2002). Robustness of Ljung-Box Test and its

Rank. www.burns-stat.com.

Calzadilla, A., Zhu, T., Rehdanz, K., Richard, S. T., &

Ringler, C. (2014). Climate change and agriculture:

Impacts and adaptation options in South Africa.

Elsevier, 24-48.

Chai, T., & Draxler, R. R. (2014). Root mean square error

(RMSE) or mean absolute error (MAE)? – Arguments

against avoiding RMSE in the literature. European

Geosciences Union, 1247-1250.

Chersich, M. F., Wright, C. Y., Venter, F., Rees, H., Fiona,

S., & Erasmus, B. (2018). Impacts of Climate Change

on Health and Wellbeing in South Africa. International

Journal of Enviromental Research and Public Health.

Clemen, R. T. (1989). Combination Forecast: A review and

annotated bibliography. International Journal of

Forecasting, 559-583.

Contreras, J., Esponola, R., Nogales, F., & Conejo, A. J.

(2003). ARIMA Models to Predict Next-Day

Electricity Prices. IEEE Transactions of Power

Systems.

Dang, X., Peng, H., Wang, X., & Zhang, H. (2008). Theil-

Sen Estimators in a Multiple Linear Regression Model.

Olemiss Edu.

Darmawan, Y., & Sofan, P. (2012). Comparison of the

vegetation indices to detect the tropical rain forest

changes using breaks for additive seasonal and trend

(BFAST) model. International Journal of Remote

Sensing and Earth Sciences, 21-34.

Dinpashoh, Y., Jhajharia, D., Pard-Fakheri, A., Singh, P.

V., & Kahya, E. (2011). Trends in reference crop

evapotranspiration over Iran. Elsevier, 422-433.

Dutta, B., Smith, W. N., Grant, B. B., Pattey, E., &

Desjardins, C. L. (2016). Model development in DNDC

for the prediction of evapotranspiration and water use

in temperate field cropping systems. Elsevier, 9-25.

Elwasify, A. I. (2015). A Combined Model between

Artificial Neural Networks and ARIMA Models.

International Journal of Recent Research in Commerce

Economics and Management, 134-140.

Gautam, R., & Sinha, A. K. (2016). Time series analysis of

refrence crop evapotranspiration for Bokaro District,

Jharkhand, India. Journal of Water and Land

Development, 51-56.

Ghorbani, M. A., Kazempour, R., Chau, K.-W.,

Shamshirband, S., & Ghazvinei, P. T. (2018).

Forecasting pan evaporation with an integrated

artificial neural network quantum-behaved particle

swarm optimization model: a case study in Talesh,

Northern Iran. Journal, 1(12), 724-737.

Graw, V., Ghazaryan, G., Dali, K., Gomez, A. D., Abdel-

Hamid, A., Jordaan, A., . . . Dubovyk, O. (2017).

Drought Dynamics and Gegetation Productivity in

Different Land Management Systems of Eastern Cape,

South Africa- A Remoste Sensing Perspective. MDI

sustainability.

Grinsted, A., Moore, J., & Jevrejeva, S. (2004). Application

of the cross wavelet transform and wavelet coherence

to geophysical time series. Nonlinear Processes in

Geophysics, 561-566.

Gwate, O., Mantel, S. K., Pailmer, A. R., Gibson, L. A., &

Munch, Z. (2018). Measuring and modelling

evapotranspiration in a South African grassland:

Comparison of two improved Penman-Monteith

formulations. WATER SA.

Hyndman, R. J., & Athanasopoulos, G. (2018). Forecasting

Principles and Practice. Australia: Monash University.

Jha, K. G. (2007). Artificial Neural Networks and Its

Applications.

Jovanovic, N., Mu, Q., Bugan, D. R., & Zhao, M. (2015).

Dynamics of MODIS evapotranspiration in South

Africa. Water South Africa, 79-90.

Khair, U., Fahmil, H., Hakim, S. A., & Rahim, R. (2017).

Forecasting Error Calculation with Mean Absolute

Deviation and Mean Absolute percentage Error.

Journal of Physics.

Khanna, R., Plyus, & Bhalla, P. (2014). Study of Artificial

Neural Network. International Journal of Research in

Information technology, 271-276.

Khoshhal, J., & Mokarram, M. (2012). Model fpr

Prediction of Evapotranspiration Using MLP Neural

Network. International Journal of environmental

Science, 3.

Kishore, V., & Pushpalatha, M. (2017). Forecasting

Evapotranspiration for Irrigation Scheduling using

Neural Networks and ARIMA. International Journal of

Applied Engineering Research, 10841-10847.

Lewis, C. D. (1982). Industrial and business forecasting

methods: A practical guide to exponential smoothing

and curve fitting. Butterworth-Heinemann.

Lin, L. I.-K. (1989). A Consordance Correlation Coefficient

to Evaluate Reproducibility. International Biometric

Society is collaborating with JSTOR to digitize,

preserve and extend access to Biometrics, 255-268.

Loua, R. T., Bencherif, H., Mbatha, N., Begue, N.,

Hauchecome, A., Bamba, Z., & Sivakumar, V. (2019).

ISWEE 2022 - International Symposium on Water, Ecology and Environment

284

Study on Temporal Variations of Surface Temperature

and Rainfall at Conakry Airport, Guinea: 1960–2016.

MDPI.

Loua, R. T., Bencherif, H., Mbatha, N., Begue, N.,

Hauchecome, A., Bamba, Z., & Sivakumar, V. (2019).

Study on Temporal Variations of Surface temperiture

and Rainfall at Nonakry Airport, Guinea:1960-2016.

MDPI Climate.

Mahlalela, P. T., Blamey, R. C., Hart, N. C., & Reason, C.

J. (2020). Drought in the Eastern Cape region of South

Africa and trends in rainfall characteristics. Climate

Dynamics.

Maier, H. R., & Dandy, G. C. (2000). Neural networks for

the prediction and forecasting of water resources

variables: a review of modelling issues and

applications. Elsevier, 101-124.

Mallikarjuna, M., & Prabhakara, R. R. (2019). Evaluation

of forecasting methods from selected stock market

returns. Springer .

Mandleni, B., & Anim, F. (2011). Climate Change

Awareness and decision on Adaption Measures by

Livestock Famers. 85rd Annual Confrence of the

Agricultutre Economics Society. Florida: Warwick

University.

Mbatha, N., & Bencherif, H. (2020). Time Series Analysis

and Forecasting Using a Novel Hybrid LSTM Data-

Driven Model Based on Empirical Wavelet Transform

Applied to Total Column of Ozone at Buenos Aires,

Argentina (1966–2017). MD{I-Atmosphere.

Mbatha, N., & Xulu, S. (2018). Time Series Analysis of

MODIS-Derived NDVI for the Hluhluwe-Imfolozi

Park, South Africa: Impact of Recent Intense Drought.

MDPI-CLimate.

Mishra, A. K., & Singh, V. P. (2011). Drought Modeling.

Elsevier, 157-175.

Morimoto, T., Ouchi, Y., Shimizu, M., & Baloch, M. S.

(2007). Dynamic optimization of watering satsuma

mandarin using neaural networks and genetic

algorithms. Elsevier.

Mukaka, M. M. (2012). Statistics Corner: A guide to

appropriate use of Correlation coefficient in medical

research. Malawi Medical Journal, 69-71.

Myttenaere, A. D., Golden, B., Grand, B. L., & Rossi, F.

(2016). Mean Absolute Percentage Error for regression

models. Elsevier.

Ng, K. E., & Chan, C. J. (2012). Geophysical Applications

of Partial Wavelet Coherence and Multiple Wavelet

Coherence. Journal of Atmospheric and Ocean

Technolgy, 1845-1853.

Nkondo, M. N., Zyl, F. V., Keuris, H., & Shrener, B.

(2012). Proposed National Water Resoiurce Strategy

2(NWRS 2): Summary. Managing water for an

equitable and sustainable future. Department of Water

Affairs, Republic of South Africa.

Parasuraman, K., Elshorbagy, A., & Carey, S. K. (2007).

Modelling the dynamics of the evapotranspiration

process using genetic programming. hydrological

Sciences Journal, 563-578.

Patel, J. N., & Balve, P. N. (2016). Evapotranspiration

estimation with Fuzzy Logic. Proceedings of 40th The

IRES International Conference (pp. 20-23).

International Journal of Mechanical Civil Engineering.

Pohlert, T. (2017). Non-Parametric Trend Tests and

Change-Point Detection.

Rahimi, S., Sefidkouhi, M. A., Raeini-Sarjaz, M., &

Valipour, M. (2015). Estimation of actual

evapotranspiration by using MODIS images (a case

study: Tajan catchment). Archives of Agronomy and

Soil Science, 695-709.

Ramoelo, A., Majozi, N., Mathieu, R., Jovanivoc, N.,

Nickless, A., & Dzikiti, S. (2014). Validation of Global

Evapotranspiration Produc (MOD16) using Flux Tower

Data in the African Savanna, South Africa. Remote

sensing, 7406-7423.

Raymond, S. (1991). On the statistical analysis of series of

observations.

Reza, A. D., & Debnath, T. (2020). An approach to make

comparison of ARIMA and NNAR Models for

Forecasting Price of Commodities. Research Gate.

Sanral, Gibb, & Eoh. (2016). Improvement of national route

N2 Section 14&15 from green river (KM 60.0) to

Zwelitsha intersection (KM 6.00) & the new breidbach

interchange (KM 9.8). Eastern Cape: department of

Environmental Affairs Republic of South Africa.

Schultz, A., Wieland, R., & Lutze, G. (2000). Neural

networks in agroecological modelling — stylish

application or helpful tool? Elsevier, 73-97.

Soh, Y. W., Koo, C. H., Huang, Y. F., & Fung, K. F. (2018).

Application of artificial intelligence models for the

prediction of standardized precipitation

evapotranspiration index (SPEI) at langat River Basin,

Malaysia. Computer and Electronics in Agriculture,

164-173.

Todaro, M. P., & Smith, S. C. (2012). Economic

Development. New York: Library of Congress

Cataloging .

Todaro, M. P., & Smith, S. C. (2020). Economic

development. In M. P. Todaro, & S. C. Smith. Pearson:

library of congress ctaloging.

Torrence, C., & Compo, G. P. (1998). A practical guide to

wavelet analysis. Bulletin of American Meteorological

Society, 61-78.

Torrence, C., & Gompo, G. P. (1997). A Practical Guide to

Wavelet Analysis. Bulletin of the American

Meteorological Society.

Traore, S., Wang, Y.-M., & Kerh, I. (2008). Modeling

Reference Evapotranspiration by Generalized

Regression Neural Network in Semiarid Zone of

Africa. WSEAS Transactions on information science &

applications, 991-1000.

Valipour, M., Banihabib, M. E., & Behbahani, S. M.

(2013). Comparison of the ARMA, ARIMA and the

autoregressive artificial neural network models in

forecasting the monthly inflow of Dez dam reservoir.

Journal of Hydrology, 433-441.

Widowati, Putro, P. S., Koshio, S., & Oktaferdian, V.

(2016). Implementation of RIMA model to asses

Seasonal Variability Macrobenthic Assemblages.

Elsevier, 277-284.

Willmott, & Matsuura. (2005).

Evapotranspiration Prediction Using ARIMA, ANN and Hybrid Models for Optimum Water Use in Agriculture: A Case Study of

Keiskammahoek Irrigation Scheme, Eastern Cape, South Africa

285

Willmott, C. J., & Matsuura, K. (2005). Advantages of the

mean absolute error (MAE) over the root mean square

error (RMSE) in assessing average model performance.

climate research clim res, 79-82.

Yang, F., White, M. A., Michaelis, A. R., Ichii, K.,

Hashimoto, H., Votava, P., . . . Nemani, R. R. (2006).

Prediction of Continental-Scale Evapotranspiration by

Combining MODIS and AmeriFlux Data Through

Support Vector Machine. IEEE Transactions on

Geoscience and remote sensing.

Yue, S., & Wang, Y. C. (2004). The Mann-Kendall Test

Modified by Effective Sample Size to Detect Trend in

Serially Correlated Hydrological Series. Springer Link,

201-218.

Zhang, G., Patuwo, E. B., & Hu, Y. M. (1998). Forecasting

with artificial neural networks: The state of the art.

Elsevier, 35-62.

Zhang, L., Zhang, G. X., & Li, R. R. (2016). Water Quality

Analysis and Prediction Using Hybrid Time Series and

Neural Network Models. J.Agri.Sci. Tech, 975-983.

Zhang, P. G. (2003). Time series forecasting using a hybrid

ARIMA and Neural network model. Elsevier, 159-175.

Ziervogel, G., New, M., Archer, G. v., Midgley, G., Taylor,

A., Mamann, R., . . . Warburton, M. (2014). Climate

change impacts and adaption in South Africa. WIREs

Climate Change .

ISWEE 2022 - International Symposium on Water, Ecology and Environment

286