Drill String Vibration Monitoring as an Element of Automatic Control of

Drilling

Vladimir Morkun

1 a

, Natalia Morkun

1 b

, Vitalii Tron

2 c

, Alona Haponenko

3 d

Iryna Haponenko

3 e

and Evhen Bobrov

3 f

Faculty of Engineering Sciences, Bayreuth University, Universit

atsstraße, 30, Bayreuth, 95447, Germany

Department of Automation, Computer Science and Technology, Kryvyi Rih National University,

11 Vitalii Matusevych Str., Kryvyi Rih, 50027, Ukraine

Research Department, Kryvyi Rih National University,

11 Vitalii Matusevych Str., Kryvyi Rih, 50027, Ukraine

Keywords:

Drilling, Vibration, Monitoring, Automatization, Ore, Mining.

Abstract:

The research is aimed at monitoring drill string vibrations as an element of automatic control of the drilling

process. To reduce negative impacts of vibrations occurring in the drill string at deep drilling of hard rocks, a

mathematical model is proposed to consider parameters of the drilling process and predict the penetration rate.

The following parameters are used as input variables when studying drilling data: weight-on-bit, rotations per

minute, torque, mechanical speciﬁc energy, longitudinal, transverse and torsional vibrations. In this study,

the rate of penetration is used as a resulting variable. Considering these parameters, a mathematical model of

the drilling process is formed on the basis of adaptive neural-fuzzy inference structures. The accuracy of this

model is 95.56 %.

1 INTRODUCTION

Deep drilling of hard rocks causes strong vibrations in

the drill string associated with a reduced rate of pene-

tration (ROP) and early failure of equipment (Cobern,

2003; Morkun et al., 2015c). The only available

method of limiting vibrations during drilling is to

change the rotary speed or weight-on-bit (WOB). Yet,

these changes often reduce drilling efﬁciency.

There are a number of vibration sources in a

drilling rig that can potentially reduce the mechani-

cal rate of penetration and cause vibrations damag-

ing sensors and clamps. These include, in particular,

shock vibrations from bit cones and blades (Morkun

et al., 2015c; Golik et al., 2015). There are sev-

eral cones on the bit which make the string vibrate

when moving. Vibration frequency is a multiple of

https://orcid.org/0000-0003-1506-9759

https://orcid.org/0000-0002-1261-1170

https://orcid.org/0000-0002-6149-5794

https://orcid.org/0000-0003-1128-5163

https://orcid.org/0000-0002-0339-4581

https://orcid.org/0000-0002-9275-3768

the speed of the bit blades.

Besides, in drilling there is a direct precession –

lateral vibration – caused by imbalance in the drill

string (Cobern, 2003; Morkun et al., 2015b). The

imbalance can occur due to peculiarities of machin-

ing drill collars or due to their curvature, these caus-

ing lateral vibrations along the drill string. The re-

verse precession is caused by friction between the

drill string and the borehole. If there is a sufﬁcient

contact effort and rotary speed, couplings begin to ro-

tate around the borehole counterclockwise with the

friequency that depends on the external diameter of

the couplings and that of the borehole. This creates

an imbalance effort on the drill string. Excitation is a

multiple of the motor speed multiplied by the number

of rotor blades.

In addition, the stabilizers have blades in contact

with the borehole (Cobern, 2003; Deng et al., 2021).

The resulting excitation is a multiple of the rotary

speed multiplied by the number of blades. Straight

blades cause greater vibration than inclined ones. The

stick-slip phenomenon is another source of vibration

caused by friction between couplings or stabilizers

and the borehole as a result of gravity along the drill

Morkun, V., Morkun, N., Tron, V., Haponenko, A., Haponenko, I. and Bobrov, E.

Drill String Vibration Monitoring as an Element of Automatic Control of Drilling.

DOI: 10.5220/0012009700003561

In Proceedings of the 5th Workshop for Young Scientists in Computer Science and Software Engineering (CSSE@SW 2022), pages 57-62

ISBN: 978-989-758-653-8; ISSN: 2975-9471

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

string (Cobern, 2003; Moharrami et al., 2021). This

phenomenon can make the element bit jammed. After

accumulating enough effort to release the drill string,

it resumes its rotation at a high angular speed.

The roller-cone bit is a kind of mechanism that,

when interacting with the borehole bottom, converts

rotation of the drill string or the borehole motor shaft

in longitudinal, torsional, and under certain condi-

tions, transverse vibrations (Novikov and Serikov,

2020; Bogomolov and Serikov, 2018). Strong vibra-

tions during machine operation can cause destruction

of drill collars and derrick elements, damage to bore-

hole motors and equipment, an increase in the bore-

hole diameter, early wear of the bit, reduction of the

mechanical penetration rate. With intensiﬁed vibra-

tions and no control of their level, the phenomenon

of resonance can occur, which in most cases results

in severe destruction of elements of drill collars and

the bit (Bogomolov and Serikov, 2018; Morkun et al.,

2015a).

Longitudinal and torsional vibrations are essen-

tially connected with speciﬁc design of roller-cone

bits and the principle of their operation (Novikov and

Serikov, 2020; Liu et al., 2021). Vibrations are of a

wavelike nature. They are classiﬁed into longitudinal,

transverse and torsional. They occur simultaneously

and depend on wavelike characteristics of the drill

string and devices included in its assembly (calibra-

tors, centrators, dampers, shock absorbers), bit size,

properties of drilled rocks, and drilling mode param-

eters.

The causes of vibrations include a stick-slip nature

of rock destruction, rough borehole bottom (Serikov

and Ginzburg, 2015; Morkun and Tron, 2014), inho-

mogeneity, fracturing and sharp intermittency in hard-

ness of drilled rocks, pressure differences under dif-

ferent support teeth of the bit (Novikov and Serikov,

2020; Serikov et al., 2016), uneven wear of teeth lead-

ing to formation of different contact areas with the

rock; the toothed working surface of the bit, pres-

sure pulsation in the discharge system (Vasiliev et al.,

2015; Morkun et al., 2014) and discrete tool feed.

2 MATERIALS AND METHODS

In paper (Sharma et al., 2021) a lumped mass drill rod

model that consists of two degrees of freedom was

suggested. The drill rod is represented by the equiva-

lent mass and rigidity for axial and torsional motions

(ﬁgure 1).

Equations of for axial and torsional motions the

drill string are as follows:

Figure 1: Simpliﬁed lumped model for axial and torsional

motion: a – axial motion; b – torsional motion (Sharma

et al., 2021).

m ¨x + c

˙x + k

(x − v

∗t) = −W OB (1)

θ + c

θ + k

(θ − Ω ∗t) = −T OB (2)

where m is the effective mass of the drill rod, x is the

axial displacement, J is the effective polar inertia mo-

ment, c

s the damping coefﬁcient during the axial

motion, c

is the damping coefﬁcient during torsional

motion, k

is the axial rigidity, k

is the torsional rigid-

ity, v

is the initial axial velocity, θ is the angular dis-

placement of the bit and Ω is the surface rotation rate

in radians per second (RPS). Axial and torsional mo-

tion equations (1) and (2) are related due to interaction

forces of the bit.

A method of direct quantitative determination of

various vibration forms with parameters that can be

easily transmitted to the surface was substantiated in

(Cobern, 2003). The system uses four accelerome-

ters and a magnetometer mounted on the drill string.

By using various combinations of accelerometer out-

put signals, it is possible to distinguish a whirl, a

stick slip, a rebound of the bit, and lateral vibrations

from each other. Three accelerometers are mounted

in the cuff at the angle of 120 degrees from each other

and oriented radially to be measured. The fourth ac-

celerometer is installed axially. The magnetometer is

also installed in one of the pockets. The pockets can

also accommodate WOB and TOB (time on bottom)

strain gauges providing a complete toolkit for bore-

hole diagnostics. Installing accelerometers radially

(ﬁgure 2) enables direct calculation of various vibra-

tion modes.

Radial accelerometers measure the centrifugal

force, which is directly related to the rotary speed

(Cobern, 2003). As a result, the rotary speed, the

stick-slip and the swirl can be directly calculated.

The magnetometer is used as a backup for measur-

ing the rotary speed. To measure axial vibration, only

a single-axis accelerometer is required. These param-

eters are calculated as follows.

CSSE@SW 2022 - 5th Workshop for Young Scientists in Computer Science Software Engineering

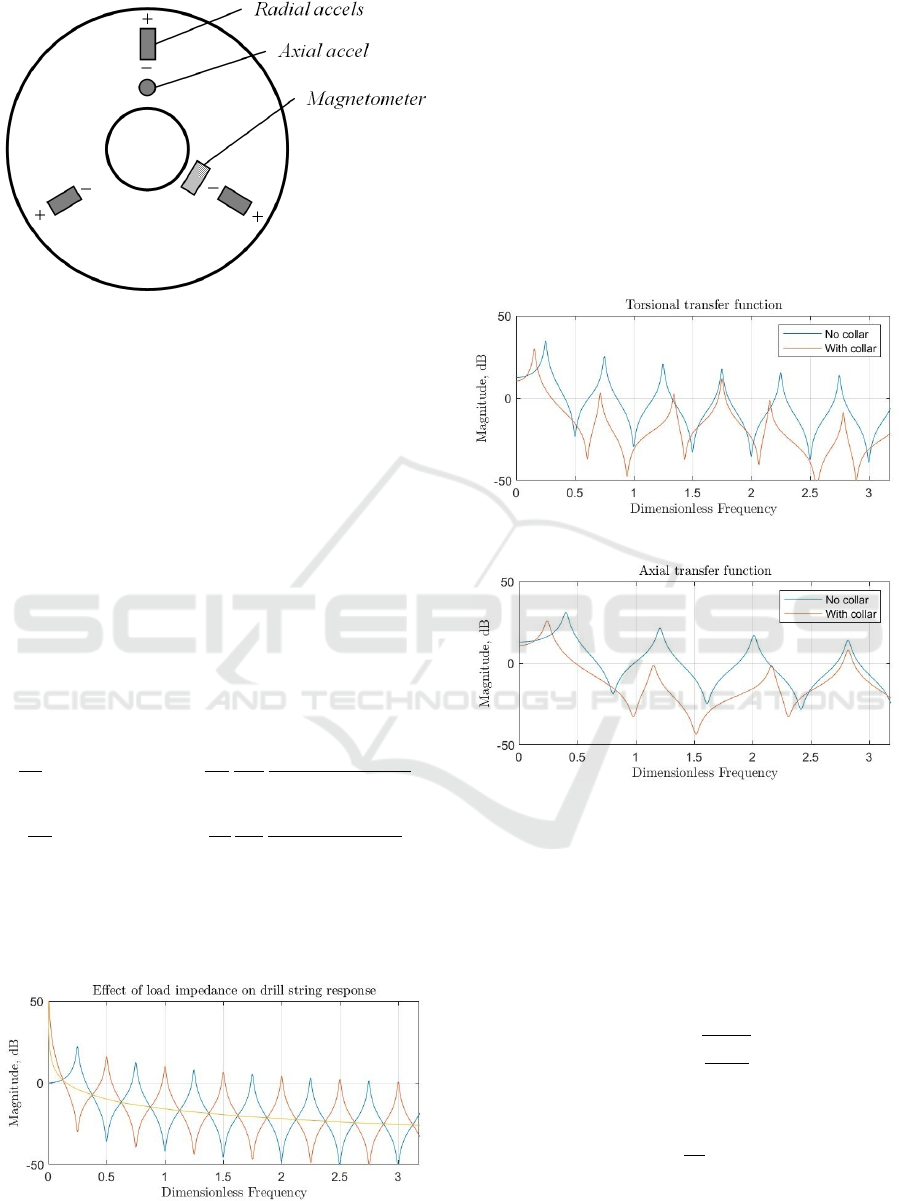
Figure 2: Drill collar sensors.

3 RESULTS AND DISCUSSION

Analysis of frequency characteristics of vibrations

during drill string operation indicates different fre-

quency ranges for individual technical components.

In particular, Cobern (Cobern, 2003) reveals that vi-

brations of components cause vibrations of the fol-

lowing frequency: bit rotation – 1000 Hz, stick-slip

motion of the bit – 10 Hz, direct precession – 10 Hz,

reverse precession – 100 Hz. Also, the vibrations pro-

duced by these sources differ signiﬁcantly in ampli-

tude.

Transfer functions in a closed form associating de-

formation of the drill string with displacement on the

bit in the dimensionless form are described by the fol-

lowing expressions:

( ¯s) = Ψ

( ¯s) = −

¯s

c,a

+ Z

L,a

tanhΓ

L,a

+ Z

c,a

tanhΓ

( ¯s) = Ψ

( ¯s) = −

¯s

c,t

+ Z

L,t

tanhΓ

L,t

+ Z

c,t

tanhΓ

Graphical results of modelling the above trans-

fer functions are obtained via software solutions de-

scribed in (Aarsnes and Aamo, 2016) and shown in

ﬁgure 3.

Figure 3: Drill collar sensors.

The bottom section of the drill string usually con-

sists of weighted drill collars, which can have a great

impact on dynamics of the drill string due to their ex-

tra inertia. In particular, transition from collars to cou-

plings in the drill string causes reﬂections in traveling

waves due to a change in the characteristic impedance

of the line.

The length of sections is included in propagation

operators, so they determine basic frequencies of an

individual section. Figure 4 demonstrates the impact

of a 200m drill collar on a 1200m drill string on trans-

fer functions.

(a)

(b)

Figure 4: Transfer function with and without drill collars:

a – torsional, b – axial.

To determine the rotary speed, we calculate the

centripetal acceleration A

(t) (Cobern, 2003):

(t) = (A

(t) + A

(t))



3 (3)

As A

(t) = ω

(t) − r, where r is the sensor radius, ω

is the angular rotary speed, radian/sec. From here:

ω (t) =

(t)

(4)

the instantaneous speed is determined by the expres-

sion:

RPM =



2π



· ω (t) (5)

The stick-slip effect is set by the maximum rotary

speed (Cobern, 2003):

= max (ω (t)) (6)

Drill String Vibration Monitoring as an Element of Automatic Control of Drilling

The reverse precession is determined by the peak

of the following expression (Cobern, 2003):

(t) = A

(t) + A

(t) cos(120 deg)+

(t) cos(240 deg)

Lateral vibration has two components. The x-axis

acceleration is equal to:

(t) =



(t) − A

(t)

cos(30)

−

(t) − A

(t)

cos(30)



(7)

The y-axis acceleration is determined by the for-

mula:

(t) =

(t) − A

(t)+

−A

(t) + A

(t)

sin(30)

−

−A

(t) + A

(t)

sin(30)

)

Thus, the value of lateral vibration is determined

by the vector sum (Cobern, 2003):

Lat

(t) =

(t)

+ A

(t)

(8)

Axial vibration can be directly measured with an

axial accelerometer.

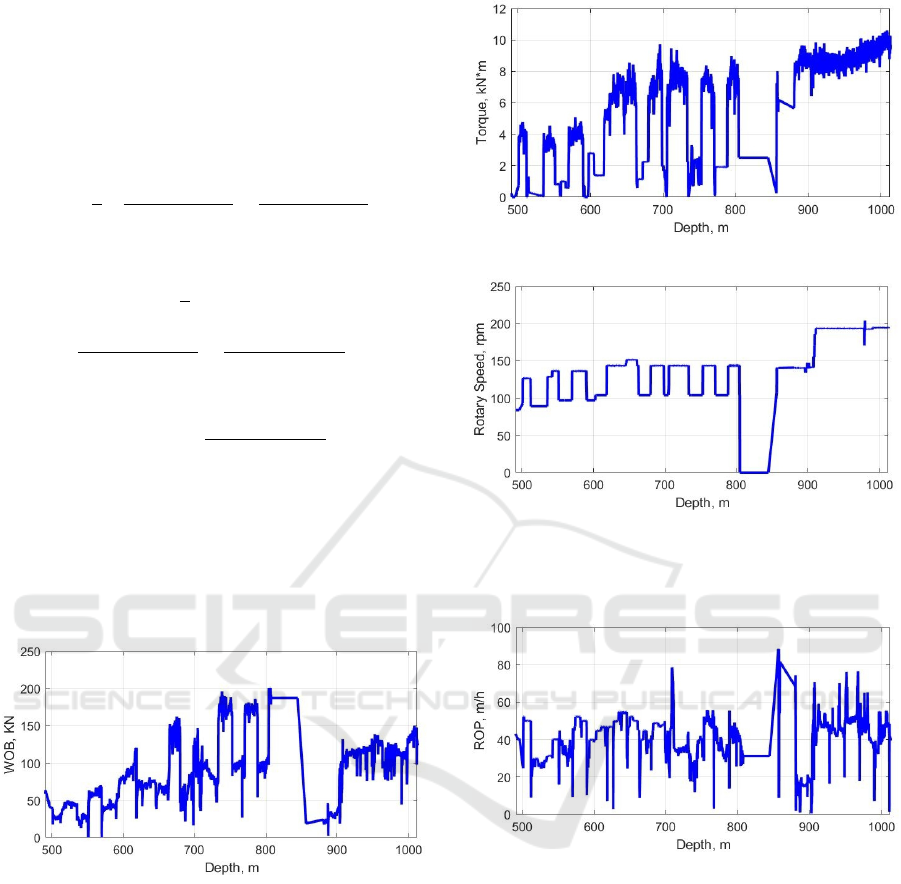
To verify the mathematical model, the data on drill

string operation published in (Tunkiel et al., 2021) is

used. On ﬁgure 5 shows the results of measuring the

weight-on-bit depending on the depth of the borehole.

Figure 5: Dependence of the weight-on-bit on the borehole

depth.

The graph of a dependence of the weight-on-bit on

the borehole depth demonstrates characteristic stick-

slip changes in the weight indicator which may be as-

sociated with alternation of various types of drilled

rocks. On ﬁgure 6 revealed a dependence of the

torque and the rotary speed on the borehole depth.

These dependences are also characterized by areas

with a stick-slip change in the indicator as in the case

with the WOB indicator.

On ﬁgure 7 it is shown the change of the resulting

indicator value (the ROP of the borehole) depending

on the depth.

When studying the data on the drilling process, the

above parameters are used as input variables: WOB,

(a)

(b)

Figure 6: Dependence of the torque and the rotary speed on

the borehole depth: a – torque, b – rotary speed.

Figure 7: Drilling parameters.

RPM, torque, MSE, longitudinal, transverse and tor-

sional vibrations. The resulting variable in this study

is the ROP of the borehole.

Considering the above parameters, a mathemati-

cal model of the drilling process is formed on the ba-

sis of adaptive neural-fuzzy inference structures (AN-

FIS). There are three input terms of membership func-

tions. The type of input membership functions is bell-

shaped. On ﬁgure 8 it is shown the results of veriﬁca-

tion of the resulted model.

The veriﬁcation results of the developed model on

the test sample (ﬁgure 8) conﬁrm its applicability to

practical use. The accuracy of this model is 95.56 %.

CSSE@SW 2022 - 5th Workshop for Young Scientists in Computer Science Software Engineering

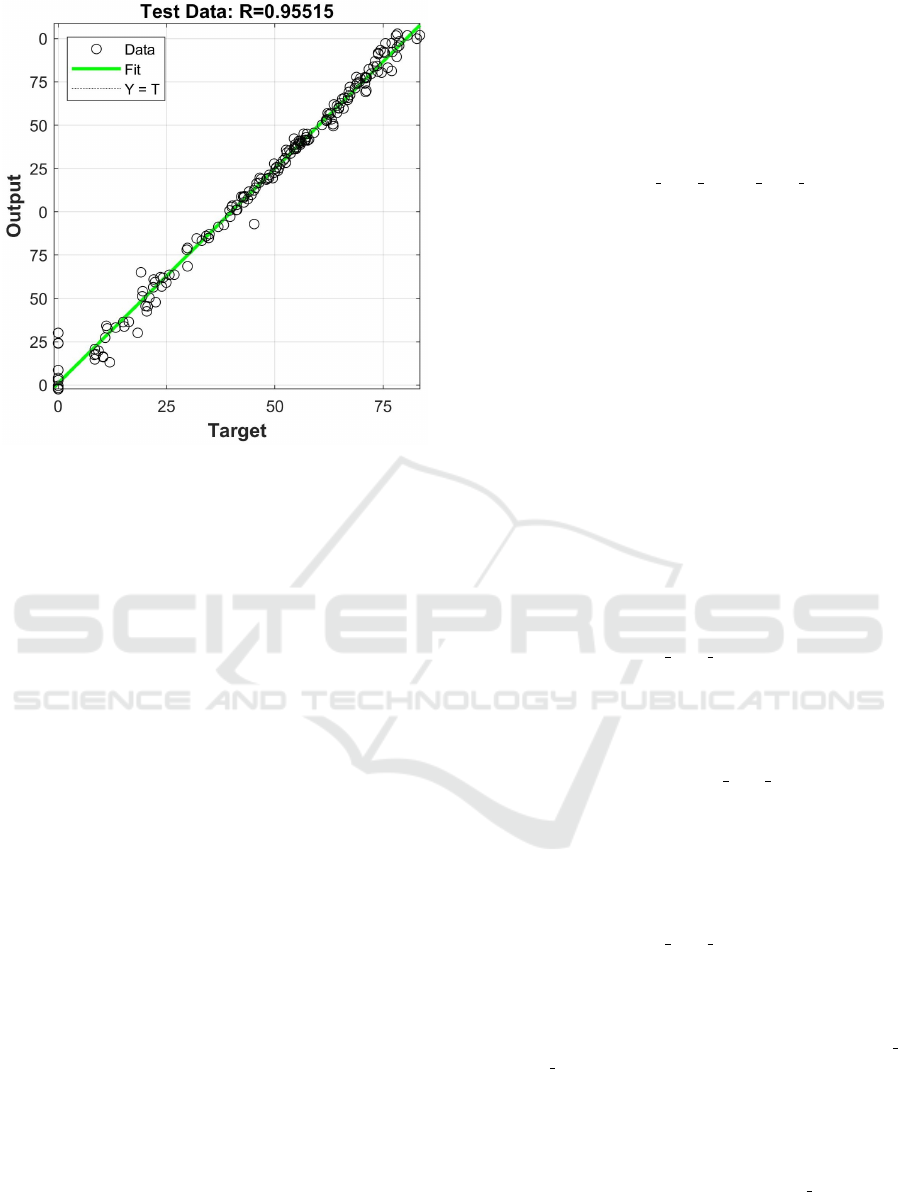
Figure 8: Modelling results.

4 CONCLUSIONS

To reduce negative impacts of vibrations occurring

in the drill string at deep drilling of hard rocks, a

mathematical model is proposed to consider param-

eters of the drilling process and predict the penetra-

tion rate. When studying the data on the drilling pro-

cess, the above parameters are used as input variables:

WOB, RPM, torque, MSE, longitudinal, transverse

and torsional vibrations. The resulting variable is the

ROP of the borehole. Considering the above param-

eters, a mathematical model of the drilling process is

formed on the basis of adaptive neural-fuzzy infer-

ence structures (ANFIS). The accuracy of the given

model makes 95.56 %.

REFERENCES

Aarsnes, U. J. F. and Aamo, O. M. (2016). Linear stabil-

ity analysis of self-excited vibrations in drilling using

an inﬁnite dimensional model. Journal of Sound and

Vibration, 360:239–259. https://doi.org/10.1016/j.jsv.

2015.09.017.

Bogomolov, R. M. and Serikov, D. Y. (2018). Vibration

damper-calibrator. Equipment and Technologies for

Oil and Gas Complex, 3:39–43. https://doi.org/10.

30713/1999-6934-2018-3-39-43.

Cobern, M. E. (2003). Downhole vibration monitoring &

control system. Final report, APS Technology. https:

//doi.org/10.2172/831129.

Deng, P., Zhang, A., Fu, K., and Li, H. (2021). Nonlin-

ear Vibration of a Time-Space Coupled Drill String

System Based on the Surface Morphology of Rock.

Journal of Sound and Vibration, 506:116153. https:

//doi.org/10.1016/j.jsv.2021.116153.

Golik, V., Komashchenko, V., Morkun, V., and

Zaalishvili, V. (2015). Enhancement of

lost ore production efﬁciency by usage of

canopies. Metallurgical and Mining Indus-

try, 7(4):325–329. https://www.metaljournal.

com.ua/assets/MMI 2014 6/MMI 2015 4/

047-GolikKomashchenkoMorkunZaalishvili.pdf.

Liu, Y., Li, Q., Qi, Z., and Chen, W. (2021). Defect sup-

pression mechanism and experimental study on lon-

gitudinal torsional coupled rotary ultrasonic assisted

drilling of CFRPs. Journal of Manufacturing Pro-

cesses, 70:177–192. https://doi.org/10.1016/j.jmapro.

2021.08.042.

Moharrami, M. J., de Arruda Martins, C., and Shiri, H.

(2021). Nonlinear integrated dynamic analysis of

drill strings under stick-slip vibration. Applied Ocean

Research, 108:102521. https://doi.org/10.1016/j.apor.

2020.102521.

Morkun, V., Morkun, N., and Pikilnyak, A. (2014). Mod-

eling of ultrasonic waves propagation in inhomoge-

neous medium using ﬁbered spaces method (k-space).

Metallurgical and Mining Industry, 6(2):43–48. https:

//www.metaljournal.com.ua/assets/Journal/a8.pdf.

Morkun, V., Morkun, N., and Tron, V. (2015a). Dis-

tributed control of ore beneﬁciation interrelated

processes under parametric uncertainty. Met-

allurgical and Mining Industry, 7(8):18–21.

https://www.metaljournal.com.ua/assets/Journal/

english-edition/MMI 2015 8/004Morkun.pdf.

Morkun, V., Morkun, N., and Tron, V. (2015b). Iden-

tiﬁcation of control systems for ore-processing

industry aggregates based on nonparametric kernel

estimators. Metallurgical and Mining Industry,

7(1):14–17. https://www.metaljournal.com.ua/assets/

Journal/english-edition/MMI 2015 1/3%20Morkun,

%20Tron.pdf.

Morkun, V., Morkun, N., and Tron, V. (2015c).

Model synthesis of nonlinear nonstationary dy-

namical systems in concentrating production

using Volterra kernel transformation. Met-

allurgical and Mining Industry, 7(10):6–9.

https://www.metaljournal.com.ua/assets/Journal/

english-edition/MMI 2015 10/001Morkun.pdf.

Morkun, V. and Tron, V. (2014). Automation of

iron ore raw materials beneﬁciation with the op-

erational recognition of its varieties in process

streams. Metallurgical and Mining Industry, 6(6):4–

7. https://www.metaljournal.com.ua/assets/MMI

2014 6/1-MorkunTron.pdf.

Novikov, A. S. and Serikov, D. Y. (2020). Some features of

the work of drill bits and practical techniques for their

use [Nekotorye osobennosti raboty burovykh dolot i

prakticheskie priemy pri ikh ispolzovanii]. Sphere. Oil

and Gas, 2:44–49. https://xn--80aaigboe2bzaiqsf7i.

xn--p1ai/upload/journal/sphereoilandgas 2020-2.pdf.

Serikov, D. Y. and Ginzburg, E. S. (2015). Increasing the

efﬁciency of destruction of medium and hard rocks

Drill String Vibration Monitoring as an Element of Automatic Control of Drilling

through the use of helical cones [Povyshenie effek-

tivnosti razrusheniia srednikh i tverdykh porod putem

ispolzovaniia kosozubogo vooruzheniia sharoshek].

Equipment and Technologies for Oil and Gas Com-

plex, 4:18–22. https://www.elibrary.ru/item.asp?id=

23868184.

Serikov, D. Y., Panin, N. M., and Ageeva, V. N. (2016).

Improvement of sealing systems for bearing assem-

blies of cone bits [Sovershenstvovanie sistem germeti-

zatcii podshipnikovykh uzlov sharoshechnykh dolot].

Construction of oil and gas wells on land and at

sea, 4:16–19. https://www.elibrary.ru/item.asp?id=

25849083.

Sharma, A., Al Dushaishi, M., and Nygaard, R. (2021).

Fixed Bit Rotary Drilling Failure Criteria Effect

on Drilling Vibration. In U.S. Rock Mechan-

ics/Geomechanics Symposium, volume All Days,

page 116–121. https://onepetro.org/ARMAUSRMS/

proceedings-pdf/ARMA21/All-ARMA21/

ARMA-2021-2083/2480289/arma-2021-2083.pdf.

Tunkiel, A. T., Sui, D., and Wiktorski, T. (2021). Reference

dataset for rate of penetration benchmarking. Journal

of Petroleum Science and Engineering, 196:108069.

https://doi.org/10.1016/j.petrol.2020.108069.

Vasiliev, A. A., Vyshegorodtseva, G. I., and Serikov,

D. Y. (2015). Study of the inﬂuence of the ﬂushing

scheme of a roller-cone drill bit on the bottom hole

cleaning [Issledovanie vliianiia skhemy promyvki

sharoshechnogo burovogo dolota na ochistku zaboia

skvazhiny]. Construction of oil and gas wells on land

and at sea, 5:25–28. https://www.elibrary.ru/item.

asp?id=23702308.

CSSE@SW 2022 - 5th Workshop for Young Scientists in Computer Science Software Engineering