Ultrasonic Cleaning of Ore Particles and Disintegration of Flocculation
Formations
Vladimir Morkun
1 a
, Natalia Morkun
1 b
, Vitalii Tron
2 c
, Oleksandra Serdiuk
2 d
,
Iryna Haponenko
3 e
and Alona Haponenko
3 f
1
Faculty of Engineering Sciences, Bayreuth University, Universit
¨
atsstraße, 30, Bayreuth, 95447, Germany
2
Department of Automation, Computer Science and Technology, Kryvyi Rih National University,
11 Vitalii Matusevych Str., Kryvyi Rih, 50027, Ukraine
3
Research Department, Kryvyi Rih National University,
11 Vitalii Matusevych Str., Kryvyi Rih, 50027, Ukraine
Keywords:
Ultrasonic Cleaning, Ore Particles, Disintegration, Flocculation, Ore Processing.
Abstract:
The research is aimed at increasing efficiency of magnetite concentrate flotation by cleaning the surface of
useful component particles through disintegrating ore flocculated formations. The generalized model of bub-
ble motion dynamics with time-dependent pressure and bubble size is presented. Computer modelling of
bubbles behaviour under the action of ultrasonic radiation is performed. The high-energy ultrasound power is
calculated to maintain cavitation modes in the iron ore slurry. The research into flocculation and defloccula-
tion considers the dependence of magnetic susceptibility on duration of magnetization. The modelling results
enable the conclusion that in order to improve quality of cleaning ore particles before flotation, it is advisable
to apply a spatial effect to the iron ore slurry by means of high-energy ultrasound of 20 kHz in the cavitation
mode modulated by high-frequency pulses of 1 MHz to 5 MHz.
1 INTRODUCTION
In the liquid medium, some physical, chemical and
physicochemical processes occur including cavita-
tion, radiation pressure and ultrasonic flows under the
influence of ultrasound (Gubin et al., 2017; Morkun
et al., 2014). Since liquids are sensitive to stretching
forces, therefore, under powerful ultrasonic oscilla-
tions, compression and liquefaction zones arise in the
liquid. During the wave phase, which creates lique-
faction, there are many gaps in the form of cavitation
bubbles in the liquid, which close abruptly in the sub-
sequent phase of compression.
Different effects of ultrasound on individual min-
erals, are used to achieve high dispersion (Soyama
and Korsunsky, 2022; Golik et al., 2015; Morkun
et al., 2017), for example, for grinding schistose min-
a
https://orcid.org/0000-0003-1506-9759
b
https://orcid.org/0000-0002-1261-1170
c
https://orcid.org/0000-0002-6149-5794
d
https://orcid.org/0000-0003-1244-7689
e
https://orcid.org/0000-0002-0339-4581
f
https://orcid.org/0000-0003-1128-5163
erals (graphite, molybdenite). The process of grind-
ing molybdenite under excessive static pressure re-
sults in manufacturing a product, the dispersion of
which is 2-3 times higher than that of the product ob-
tained under atmospheric pressure (Soyama and Kor-
sunsky, 2022).
Application of ultrasound to processing ore raw
materials has been an urgent research problem for a
long time. In particular, introduction of ultrasound
into the water system of ore processing provides spe-
cific activation based on two physical phenomena –
acoustic cavitation and acoustic wind (Ambedkar
et al., 2011; Ambedkar, 2012; Morkun et al., 2015a;
Morkun and Morkun, 2018). Gas discharge in acous-
tic cavitation is most preferable at lower frequency
within 20kHz-40kHz, while the acoustic wind domi-
nates at frequencies above 400kHz and1MHz in ultra-
sonic and megasonic systems, respectively (Ambed-
kar et al., 2011).
The experiment results in (Harrison et al., 2002)
reveal an increase in the clean coal yield from 3 % to
10 %, greater production of clean coal and a decrease
in the content of sulfur, mercury, ash and moisture in
the processed coal. These results are associated with
78
Morkun, V., Morkun, N., Tron, V., Serdiuk, O., Haponenko, I. and Haponenko, A.
Ultrasonic Cleaning of Ore Particles and Disintegration of Flocculation Formations.
DOI: 10.5220/0012009900003561
In Proceedings of the 5th Workshop for Young Scientists in Computer Science and Software Engineering (CSSE@SW 2022), pages 78-85
ISBN: 978-989-758-653-8; ISSN: 2975-9471
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

ultrasonic shock waves generated by bubble cavita-
tion that contributes to breaking natural relationships
between coal and ash-forming mineral impurities and
cleaning of coal particles from impurities. Cavitation
also enhances removal of unwanted particles of clay,
slime and oxidation products covering the surface of
coal.
Application of the above methods is a promis-
ing approach to improving efficiency of technologi-
cal processes of iron ore beneficiation (Morkun et al.,
2015b,c).
The research aims to increase efficiency of flota-
tion of magnetite concentrates by disintegrating ore
flocculated formations and cleaning particle surfaces.
To achieve the set aim, it is necessary to investigate
peculiarities of formation of cavitation modes in iron
ore slurry by applying high-energy ultrasound.
2 MATERIALS AND METHODS
Let us consider mathematical description of cavitation
processes in the heterogeneous medium. The gener-
alized model of bubble motion dynamics dependent
on the pressure time and the size of bubbles is pre-
sented as a Rayleigh-Plesset equation (Gubin et al.,
2017; Kozubkov
´
a et al., 2012). Solving the Rayleigh-
Plesset equation for a certain pressure value p
∞
(t) en-
ables obtaining the value of the bubble radius dR
b
(t)
dR
b
dt
=
s
2
3
p
vap
(t) − p
∝
(t)
ρ
1
, (1)
where R
b
is the bubble radius, µm; p
∝
is pressure in
the medium at perpetuity, Pa; p
vap
is vapour pressure,
Pa; ρ
1
is liquid density, kg/m
3
.
The results of Singhal et al. (Singhal et al., 2002)
suggests a cavitation model based on a complete cav-
itation model. The density of the mixture is defined
as
ρ = αρ
vap
+ (1 −α) ρ
1
, (2)
where α is the volumetric fraction of vapour; ρ
vap
is
vapour density, kg/m
3
; ρ
1
is liquid density, kg/m
3
.
The ratio between density of the mixture and the vol-
umetric fraction of vapour α has the form:
∂
∂t
(ρ) = −(ρ
1
−ρ
vap
)
∂
∂t
(α), (3)
where ρ is density of the mixture, kg/m
3
; α is the
volumetric fraction of vapour; ρ
vap
is vapour density,
kg/m
3
; ρ
1
is liquid density, kg/m
3
. The volumetric
fraction of vapour α is determined from f as
α = f
ρ
ρ
vap
. (4)
According to the cavitation model proposed in
(Schnerr and Sauer, 2001), the equation for the par-
ticle volumetric fraction of vapour α is obtained from
the expression
R =
∂
∂t
(ρ
vap
α) +
∂
∂x
j
(ρ
vap
αu
j
), (5)
where R is the evaporation rate, kg/h.
R =
ρ
vap
ρ
1
ρ

∂α
∂t
+
∂(u
j
α)
∂x
j

(6)
When substituting equation (5) in (6) we obtain
R =
ρ
vap
ρ
1
ρ
α(1 −α)
3
R
b
s
2
3
(p
vap
−p)
ρ
1
(7)
The bubble radius is determined from the expres-
sion
R
b
=

α
1 −α
3
4π
1
n
b

1
3
. (8)
Also in this model, the only parameter to be deter-
mined is the number of spherical bubbles in the vol-
ume of liquid n
b
.
Equation (7) is also used to simulate the conden-
sation process. The final form of the model is as fol-
lows:
if p ≤ p
vap
R
e
=
ρ
v
ρ
1
ρ
α(1 −α)
3
R
b
s
2
3
(p
vap
−p)
ρ
1
. (9)
if p ≥ p
vap
R
c
=
ρ
v
ρ
1
ρ
α(1 −α)
3
R
b
s
2
3
(p − p
vap
)
ρ
1
. (10)
If ultrasonic frequency is small (< 1MHz) and
pressure amplitude is much smaller than the atmo-
spheric static pressure (101 kPa), a bubble will be in
the state of stable cavitation (Hu, 2013), i.e. fluctu-
ate around its initial radius in the periodic mode pe-
riodically. This process should be described using
an empirical equation based on the simplified Keller-
Herring model (Carvell and Bigelow, 2011)
R
0
∼
=
3
{
MHz
}
µm
f
lin
0
, (11)
where R
0
is the radius of the bubble, µm; µ is the
shearing viscosity coefficient, f
lin
0
is ultrasonic fre-
quency, MHz.
It should be noted that at higher pressure, the bub-
ble reaction also largely depends on the ultrasonic
field pressure amplitude and, therefore, equation (11)
is no longer possible in this “inertial cavitation” sce-
nario.
Ultrasonic Cleaning of Ore Particles and Disintegration of Flocculation Formations
79

There are expressions in (Carvell and Bigelow,
2011) to calculate the optimal initial radius of the bub-
ble for maximum expansion depending on ultrasonic
frequency and pressure amplitude
R
optimal
=
1
√
0.0327F
2
+ 0.0679F + 16.5P
2
, (12)
where P is the pressure amplitude for the ultrasonic
sinusoidal wave, MPa; f is frequency, MHz; R
optimal
is the optimal bubble radius, µm.
For example, if f = 1MHz, P = 1MPa, the opti-
mal bubble radius is 0.2454m.
Calculation covers the frequency range, MHz,
pressure amplitudes, MPa and radii, µm used in mod-
elling (Hu, 2013) (table 1). It should be noted that
at f = 0.5MHz and pressure P = 8.0MPa the initial
radius is R = 30.75nm.
After converting dependence (12), we get a square
equation that includes the function of optimal fre-
quency for a certain size of bubbles from where F (R)
at the known pressure P can be determined from the
expression
F (R) =
−0.068 ±
q
0.068
2
−4 ·0.034 ·

6.5P
2
−
1
R

2 ·0.033
. (13)
where R
optimal
is the optimal bubble size, µm; F () is
frequency of high-energy ultrasound, MHz.
Consequently, the cavitation mode with the known
bubble size is formed by impacting the slurry with
high-energy ultrasound with F

R
optimal

frequency.
We denote the function of distributing bubbles
by size by f (R), then the value f (R)dR determines
the fraction of bubbles within the size range of R to
R + dR.
Table 2 demonstrates the value of the function
used in calculations.
The obtained dependences allow determining op-
timal frequency of high-energy ultrasound to main-
tain cavitation in the iron ore slurry depending on pa-
rameters of its components. Therefore, to form con-
trolled cavitation processes and acoustic flows in the
iron ore slurry, it is necessary to model dynamic ef-
fects of high-energy ultrasound in the heterogeneous
medium.
3 RESULTS AND DISCUSSION
Bubble behavior under the influence of ultrasonic ra-
diation is modelled by using a specialized software
package Bubblesim in MATLAB (Hoff et al., 2000).
Dynamics of air bubble sizes during the modelling
process is determined through the modified Rayleigh-
Plesset equation (Hoff, 2001):
¨aa +
3
2
˙a
2
+
p
0
+ p
i
(t) p
L
ρ
−
a
pc
˙p
L
= 0 (14)
where a is the bubble radius, m; p
0
is hydrostatic pres-
sure, Pa; p
i
is acoustic pressure, Pa; p
L
is pressure on
the bubble surface, Pa; ρ is fluid density, kg/m3; c is
the sound speed, m/s.
The following dependence is used to determine
the value of the bubble surface pressure p
L
:
p
L
= −4η
L
˙a
a
−(T
2
−T
1
) + p
g

a
e
a

3k
(15)
where ν
L
is the internal friction coefficient; T
1
, T
2
are
tension of the inner and outer bubble walls, respec-
tively; p
g
is internal pressure of gas bubbles, Pa; k is
the gas constant of the polytropic process.
The modelling results with nonlinear effects of
high-energy ultrasound considered are presented in
(figure 1): the driving pulse (figure 1, a), changes of
the bubble radius (figure 1, b), the signal spectrum
(figure 1, c).
During the study, the radiation pressure amplitude
is 0.3 MPa, while the ultrasound frequency changes
and makes 1 MHz, 3 MHz, 5 MHz.
To model the process of ultrasonic signal propa-
gation in the liquid medium when changing the sound
propagation rate and density, the 1st and 2nd-order
k-space method is used based on the 1st-order linear
equations (Tabei et al., 2002; Mast et al., 2001).
To apply the k-space method to the system of the
1st-order equations describing wave propagation, the
2nd-order k-space operator can be used by dividing it
into parts associated with each spatial direction. For a
two-dimensional case, this procedure is performed as
follows
∂p(r,t)
∂
(c
0
∆t)
+
x
≡
= F
−1
ik
x
e
ik
x
∆
x
/
2
sin

c
0
∆t k

2

c
0
∆t k

2
F (p (r,t))
!
; (16)
∂p(r,t)
∂
(c
0
∆t)
+
y
≡ F
−1
ik
y
e
ik
y
∆
y

2
sin

c
0
∆t k

2

c
0
∆t k

2
F (p (r,t))
!
;
∂p(r,t)
∂
(c
0
∆t)
−
x
≡ F
−1
ik
x
e
ik
x
∆
x
/
2
sin

c
0
∆t k

2

c
0
∆t k

2
F (p (r,t))
!
;
∂p(r,t)
∂
(c
0
∆t)
−
y
≡ F
−1
ik
y
e
ik
y
∆
y

2
sin

c
0
∆t k

2

c
0
∆t k

2
F (p (r,t))
!
;
CSSE@SW 2022 - 5th Workshop for Young Scientists in Computer Science Software Engineering
80

Table 1: Parameters of ultrasonic cavitation modes.
f, MHz
P, MPa
0.01 0.1 0.3 0.5 0.7 1.0 3.0 5.0 8.0
0.5 4.779 2.197 0.809 0.489 0.350 0.245 0.082 0.049 0.031
1.0 3.127 1.940 0.794 0.486 0.349 0.245 0.082 0.049 0.031
3.0 1.414 1.228 0.710 0.465 0.341 0.242 0.081 0.049 0.031
5.0 0.929 0.869 0.615 0.435 0.328 0.238 0.081 0.049 0.031
Table 2: Values of the function of distributing bubbles by size.
R,m ×10
−6
3 5 10 20 50
f (R),m
−1
0.0054 0.0273 0.0545 0.330 0.545
R,m ×10
−4
1.5 2.0 2.5 3.0 3.5
f (R),m
−1
×10
−3
49 21.2 10.9 6.5 4.1
so that

∂p (r,t)
∂
(c
0
∆t)
+
x
∂p (r,t)
∂
(c
0
∆t)
−
x
+
∂p (r,t)
∂
(c
0
∆t)
+
y
∂p (r,t)
∂
(c
0
∆t)
−
y

p(r,t) =
=

∇
(c
0
∆t)

2
p(r,t) (17)
Spatial-frequency components k
x
and k
y
are deter-
mined so that k
2
= k
2
x
+ k
2
y
. The use of equation op-
erators (16) in (15) enables formation of the 1st-order
k-space method which is equivalent to equation (14).
Application of exponential coefficients from equation
(16) requires evaluation of ultrasonic wave velocities
u
x
and u
y
at the grid points at intervals ∆x

2 and
∆y

2, respectively. The resulting algorithm has the
form
u
x
(r
1
,t
+
) −u
x
(r
1
,t
−
)
∆t
=
1
ρ(r
1
)
∂p (r,t)
∂
(c
0
∆t)
+
x
;
u
y
(r
2
,t
+
) −u
y
(r
2
,t
−
)
∆t
=
1
ρ(r
2
)
∂p (r,t)
∂
(c
0
∆t)
+
y
;
p(r,t + ∆t) − p(r,t)
∆t
=
= −ρ(r ) c(r)
2

∂u
x
(r
1
,t
+
)
∂
(c
0
∆t)
−
x
+
∂u
y
(r
2
,t
+
)
∂
(c
0
∆t)
−
y

(18)
where
r
1
≡

x + ∆x

2,y

, r
2
≡

x,y + ∆x

2

,
t
+
≡t + ∆t

2, t
−
≡t −∆t

2.
(19)
In equation (18), the coefficients c
0
and ρ
0
are
replaced spatially and transformed by values of the
sound speed and density c (r) and r (r) . Spatial dis-
tribution in equation (18) is implicitly introduced into
spatial derivatives of the operators considered. For
example, operators
∂
.
∂
(c
0
∆t)
+
x
and
∂
.
∂
(c
0
∆t)
−
x
determined by formula (16) correspond to derivatives
calculated after spatial shifts according to the Fourier
transformation shift property ∆x

2 and −∆x

2 , re-
spectively.
High-energy ultrasound power, which allows
maintaining cavitation modes in the iron ore slurry, is
calculated on the basis of the above results of studying
distribution of the ultrasonic pulse front by using HI-
FUSimulator v1.2 (Soneson, 2011). The calculation
results are given in figures 3, 4, 5, 6, 7.
The modelling results enable us to conclude that
in order to improve quality of cleaning ore particles
before flotation, it is advisable to apply a spatial effect
to the iron ore slurry by means of high-energy ultra-
sound of 20kHz in the cavitation mode modulated by
high-frequency pulses of 1 MHz - 5 MHz.
At the same time, the reasons for forming floc-
cules from particles of magnetite iron ore slurry,
which being beneficiated move relative to each other
and interact with their poles, include movement of
ferromagnetic particles in the magnetic field to re-
duce total magnetostatic energy (energy of free poles)
(Karmazin and Karmazin, 2005). This phenomenon
is an integral part of beneficiation of fine materials
with significant magnetic properties and directly af-
fects efficiency of beneficiation. The size of floccules
can vary from 2 to 1000 diameters of the particles
forming them.
The phenomenon of fluctuations of monopolar
blast furnace boundaries under the action of ultrasonic
waves propagating along them is explained by the fact
that ultrasound causes variable mechanical stresses in
iron particles, which leads to an increase in magnitude
of magneto-elastic energy U
d
generally determined
from the expression (Vlasko-Vlasov and Tikhomirov,
1991)
U
d
= −σ ·λ (20)
Ultrasonic Cleaning of Ore Particles and Disintegration of Flocculation Formations
81

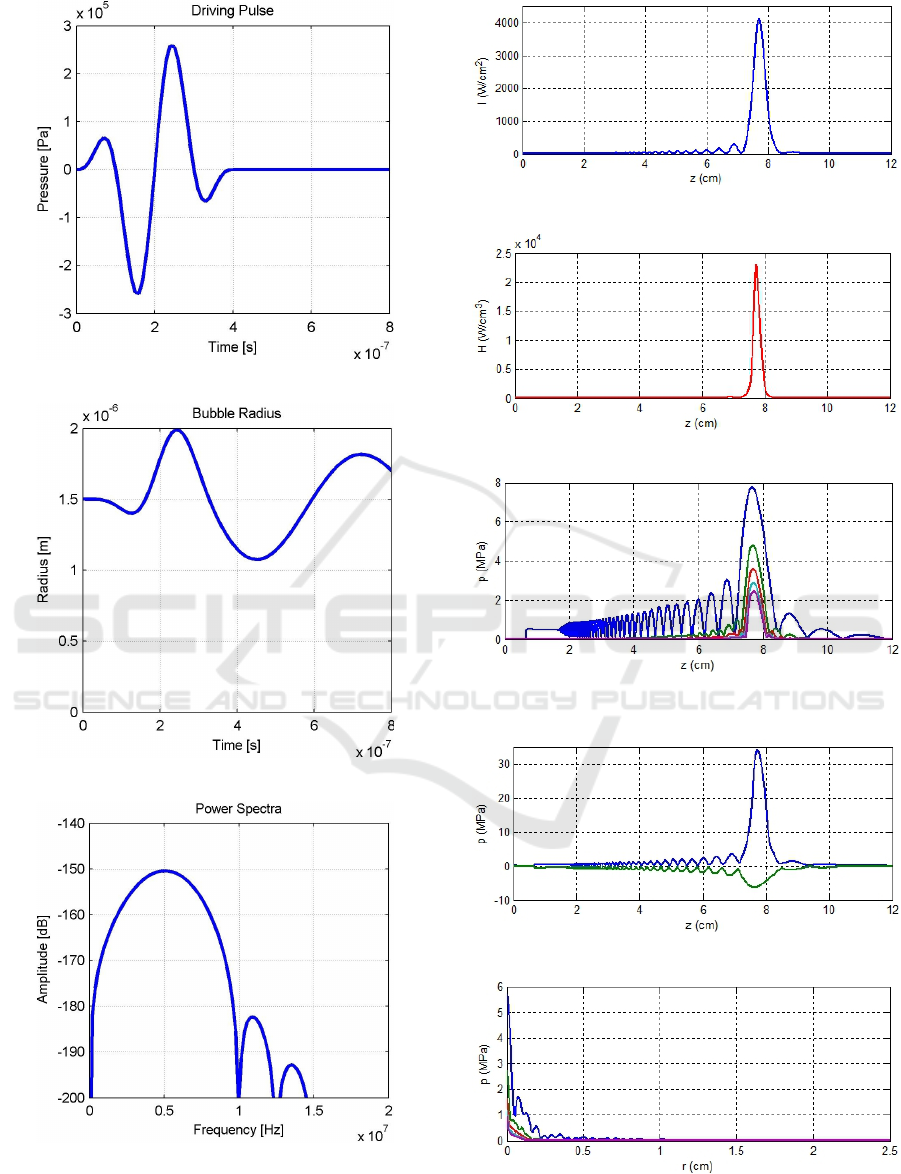
(a)
(b)
(c)
Figure 1: Modelling results of cavitation processes under
high-energy ultrasound.
Figure 2: Radial intensity in the ultrasound focus.
Figure 3: Intensity in the ultrasound focus.
Figure 4: Axial distribution of pressure of the first five har-
monics of ultrasonic radiation.
Figure 5: Axial pressure peaks in ultrasonic radiation.
Figure 6: Distribution of radial pressure of the first five har-
monics in the ultrasonic radiation focus.
CSSE@SW 2022 - 5th Workshop for Young Scientists in Computer Science Software Engineering
82

Figure 7: Shape of the ultrasonic wave along the radiation
axis at the distance (z=7.73 cm), which corresponds to the
peak intensity.
where λ is magnetostriction; σ is tension.
According to the Akulov anisotropy law, the ex-
pression for U
d
has the following form (Chikazumi,
2009):
U
d
= −σ· a
1
∑
i=1,2,3

S
2
i
β
2
i
−
1
3

+ a
2
∑
i̸= j

S
i
S
j
β
i
β
j

!
(21)
To observe the condition
∂(U
K
+U
D
+U
H
)
∂α
= 0 (22)
where U
K
is magnetic anisotropy energy of a crystal;
U
H
is energy of the external magnetic field.
According to expressions (20)–(22), if energy U
H
changes, magnetism of the particles increases.
Interaction of magnetic masses in flocculation is
described in accordance with the Coulomb law to
determine the strength of flocculated formations F
f
l
(Karmazin and Karmazin, 2005):
F
f l
= σ
f l
s = kχ
2
H
2
s
2

µ
0
r
2

(23)
where σ
f l
is the floccule strength, S is the area of the
floccule cross section, k is the coefficient specifying
the coordinate of the point of magnetic mass concen-
tration, ξ is magnetic susceptibility, H is intensity of
the magnetic field, r is the distance of interaction.
The strength of floccules is determined by the ex-
pression (Karmazin and Karmazin, 2005):
σ
f l
= kJ
2
.
(1 −χN)
2
(24)
where k is the proportionality coefficient; J is floccule
magnetization; N is the floccule demagnetization co-
efficient. This characteristic is also evaluated by the
expression of ferromagnetic energy:
F
f l
= −
dU
dx
= −
d (BHV )
dx
= −0.5BHV = −0.5 µH
2
s;
σ
f l
= 0.5µH
2
.
(25)
When studying flocculation and deflocculation,
one should consider the dependence of magnetic sus-
ceptibility γ
c
on duration of magnetization t.
The dependence of the flocculation degree Ψ and
the field intensity looks like (Karmazin and Kar-
mazin, 2005):
ψ = k
1
H
2
0
+ ∆ψδ(H −H
kr
)+
+ (1 + ψ
2
)(1 −exp(−k
2
(H −H
kr
))),
(26)
where H
0
is initial intensity of the magnetic field
which causes equilibral reversible flocculation; ∆ψ =
ψ
1
−ψ
2
is an increase in the flocculation degree due
to the avalanche process; ψ
1
−ψ
2
are flocculation de-
grees at the beginning and at the end of the avalanche
process, respectively, which are functions of concen-
tration, the formfactor, size and magnetic suscepti-
bility of flocculating particles; H
kr
is critical field
tension causing avalanche flocculation H
0
< H
kr
; k
1
,
k
2
are intensity coefficients presented as functions of
concentration, magnetic susceptibility, the formfac-
tor, the Reynolds parameter for the hydromechanical
mode of the medium motion, particle size dependent
on time [k
2
= f (C, N, ℵ, R
e
,d,t)] ; δ (H −H
kr
) is the
Dirac function from tension;
R
H
kr
+∆
H
kr
−∆
δ(H −H
kr
)dH =
1, where ∆ is a small number.
The dependence of size of the narrow fraction
particle extracted from the floccule (flocculation de-
gree) E obtained in (Karmazin and Karmazin, 2005;
Chikazumi, 2009), shows a significant dependence of
flocculation on the content of the ferromagnetic com-
ponent in the iron ore slurry:
E = 1 −e


−
r
0
v
0
t
R
R
f
r
0
exp
(
−kχd
(
r
−1
0
−r
−1
)
.
(3πµD
t
)
)
rdr


(27)
noindent where r
0
is the radius of the floccule; v
0
is
the speed of particles of a narrow fraction near the
surface of the floccule; t is flocculation time; D
t
is
the turbulent diffusion coefficient. It should be noted
that with decreased size, magnetic susceptibility of
the magnetic sharply decreases, and the coercive force
increases sharply, which is explained by approxima-
tion to the monodomain size of magnetite, that com-
plicating the flocculation process.
When implementing this approach, the ultrasonic
wave radiator should be able to vary frequency during
measurements in a fairly wide range. In practice, this
can be done by means of the ultrasonic phased array.
While developing its design, the influence of the dis-
tance between elements, wavelength and the number
of elements on controllability and efficiency of ultra-
sonic radiation are investigated. Optimal parameters
of the ultrasonic phased array are selected by indica-
tors that characterize its directional diagram (Morkun
et al., 2015b,c).
Analysis of the research results enables conclud-
ing that in order to increase efficiency of the flotation
Ultrasonic Cleaning of Ore Particles and Disintegration of Flocculation Formations
83

process by disintegrating flocculated ore formations,
it is advisable to exert a spatial effect on the iron ore
slurry including a combination of high-energy ultra-
sound and the pulsed magnetic field of descending in-
tensity.
The modelling results enable concluding that to
improve quality of ore particles cleaning before flota-
tion, it is advisable to apply a spatial effect to the
iron ore slurry. This includes a combination of high-
energy ultrasound of 20 kHz in the cavitation mode
modulated by high-frequency pulses within 1 MHz-
5 MHz and the pulsed magnetic field of descending
intensity. The next stage involves calculation of char-
acteristics of these effects and determination of the
device parameters to disintegrate flocculated ore for-
mations in the slurry flow on the basis of the ultra-
sonic phased array.
4 CONCLUSIONS
To increase efficiency of magnetite concentrates flota-
tion by disintegrating flocculated ore formations and
cleaning the particle surface, it is advisable to use
nonlinear effects of the high-energy ultrasonic field to
form and maintain cavitation processes and acoustic
flows in the iron ore slurry.
Investigation into cavitation patterns results in de-
pendences obtained to determine optimal frequency
of high-energy ultrasound aimed to maintain cavita-
tion processes in the iron ore slurry depending on pa-
rameters of its components.
Based on the modelling results, it is established
that in order to improve quality of ore particles clean-
ing before flotation, a spatial effect should be ex-
erted on the iron ore slurry, which includes a com-
bination of 20kHz high-energy ultrasound in the cav-
itation mode modulated by high-frequency pulses of
1 MHz-5 MHz and the pulsed magnetic field of de-
scending intensity.
REFERENCES
Ambedkar, B. (2012). Ultrasonic Coal-Wash for De-
Ashing and De-Sulfurization: Experimental Investi-
gation and Mechanistic Modeling. Springer Theses.
Springer Berlin, Heidelberg. https://doi.org/10.1007/
978-3-642-25017-0.
Ambedkar, B., Nagarajan, R., and Jayanti, S. (2011).
Investigation of High-Frequency, High-Intensity Ul-
trasonics for Size Reduction and Washing of
Coal in Aqueous Medium. Ind. Eng. Chem.
Res, 50(23):13210–13219. https://doi.org/10.1021/
ie200222w.
Carvell, K. J. and Bigelow, T. A. (2011). Dependence of op-
timal seed bubble size on pressure amplitude at ther-
apeutic pressure levels. Ultrasonics, 51(2):115–122.
https://doi.org/10.1016/j.ultras.2010.06.005.
Chikazumi, S. (2009). Physics of Ferromagnetism, vol-
ume 94 of International Series of Monographs on
Physics. Oxford University Press, Oxford, 2 edition.
Golik, V., Komashchenko, V., Morkun, V., and
Zaalishvili, V. (2015). Enhancement of
lost ore production efficiency by usage of
canopies. Metallurgical and Mining Indus-
try, 7(4):325–329. https://www.metaljournal.
com.ua/assets/MMI 2014 6/MMI 2015 4/
047-GolikKomashchenkoMorkunZaalishvili.pdf.
Gubin, G. V., Tkach, V. V., and Ravinskaya, V. O. (2017).
Application of ultrasound for cleaning the surface of
altered mineral particles before flotation [Primene-
nie ul’trazvuka dlja ochistki poverhnosti izmenennyh
mineral’nyh chastic pered flotaciej]. The quality of
mineral raw materials, 1:341–349.
Harrison, C. D., Raleigh, Jr., C. E., and Vujnovic, B. J.
(2002). The use of ultrasound for cleaning coal.
In Proceedings of the 19th Annual International
Coal Preparation Exhibition and Conference, vol-
ume 1, page 61–67. http://web.archive.org/web/
20190713150249if /http://www.bixbydental.com:
80/about/news/coalultrasound.pdf.
Hoff, L. (2001). Acoustic Characterization of Con-
trast Agents for Medical Ultrasound Imaging.
Springer Dordrecht. https://doi.org/10.1007/
978-94-017-0613-1.
Hoff, L., Sontum, P. C., and Hovem, J. M. (2000). Oscilla-
tions of polymeric microbubbles: Effect of the encap-
sulating shell. The Journal of the Acoustical Society
of America, 107:2272–2280. https://doi.org/10.1121/
1.428557.
Hu, Z. (2013). Comparison of Gilmore-Akulichev equa-
tion and Rayleigh-Plesset equation on the rapeu-
tic ultrasound bubble cavitation. Master’s the-
sis, Iowa State University. https://doi.org/10.31274/
etd-180810-3261.
Karmazin, V. V. and Karmazin, V. I. (2005). Magnetic,
electrical and special methods of mineral processing.
Publishing house MGTU.
Kozubkov
´
a, M., Rautov
´
a, J., and Bojko, M. (2012). Math-
ematical Model of Cavitation and Modelling of Fluid
Flow in Cone. Procedia Engineering, 39:9–18. XI-
IIth International Scientific and Engineering Confer-
ence ”Hermetic Sealing, Vibration Reliability and
Ecological Safety of Pump and Compressor Machin-
ery” - ”HERVICON-2011”. https://doi.org/10.1016/j.
proeng.2012.07.002.
Mast, T. D., Souriau, L. P., Liu, D.-L. D., Tabei, M., Nach-
man, A. I., and Waag, R. C. (2001). A k-space
method for large-scale models of wave propagation
in tissue. IEEE Transactions on Ultrasonics, Fer-
roelectrics, and Frequency Control, 48(2):341–354.
https://doi.org/10.1109/58.911717.
Morkun, V. and Morkun, N. (2018). Estimation of the
Crushed Ore Particles Density in the Pulp Flow Based
on the Dynamic Effects of High-Energy Ultrasound.
CSSE@SW 2022 - 5th Workshop for Young Scientists in Computer Science Software Engineering
84

Archives of Acoustics, 43(1):61–67. https://doi.org/10.
24425/118080.
Morkun, V., Morkun, N., and Pikilnyak, A. (2014). The
adaptive control for intensity of ultrasonic influence
on iron ore pulp. Metallurgical and Mining Industry,
6(6):8–11. https://www.metaljournal.com.ua/assets/
MMI 2014 6/2-MorkunPikilnyak.pdf.
Morkun, V., Morkun, N., and Tron, V. (2015a). Dis-
tributed closed-loop control formation for tech-
nological line of iron ore raw materials bene-
ficiation. Metallurgical and Mining Industry,
7(7):16-19. https://www.metaljournal.com.ua/assets/
Journal/english-edition/MMI 2015 7/003Vladimir%
20Morkun%2016-19.pdf.
Morkun, V., Morkun, N., and Tron, V. (2015b). Dis-
tributed control of ore beneficiation interrelated
processes under parametric uncertainty. Met-
allurgical and Mining Industry, 7(8):18–21.
https://www.metaljournal.com.ua/assets/Journal/
english-edition/MMI 2015 8/004Morkun.pdf.
Morkun, V., Morkun, N., and Tron, V. (2015c).
Model synthesis of nonlinear nonstationary dy-
namical systems in concentrating production
using Volterra kernel transformation. Met-
allurgical and Mining Industry, 7(10):6–9.
https://www.metaljournal.com.ua/assets/Journal/
english-edition/MMI 2015 10/001Morkun.pdf.
Morkun, V., Semerikov, S., Hryshchenko, S., and Slovak,
K. (2017). Environmental geo-information technolo-
gies as a tool of pre-service mining engineer’s training
for sustainable development of mining industry. In Er-
molayev, V., Bassiliades, N., Fill, H., Yakovyna, V.,
Mayr, H. C., Kharchenko, V. S., Peschanenko, V. S.,
Shyshkina, M., Nikitchenko, M. S., and Spivakovsky,
A., editors, Proceedings of the 13th International
Conference on ICT in Education, Research and In-
dustrial Applications. Integration, Harmonization and
Knowledge Transfer, ICTERI 2017, Kyiv, Ukraine,
May 15-18, 2017, volume 1844 of CEUR Workshop
Proceedings, pages 303–310. CEUR-WS.org. https:
//ceur-ws.org/Vol-1844/10000303.pdf.
Schnerr, G. H. and Sauer, J. (2001). Physical and Numerical
Modeling of Unsteady Cavitation Dynamics. In CMF-
2001, 4th International Conference on Multiphase
Flow. New Orleans, USA, May 27 - June 1, 2001.
https://www.researchgate.net/publication/296196752.
Singhal, A. K., Athavale, M. M., Li, H., and Jiang, Y.
(2002). Mathematical Basis and Validation of the
Full Cavitation Model. Journal of Fluids Engineering,
124(3):617–624. https://doi.org/10.1115/1.1486223.
Soneson, J. (2011). High intensity fo-
cused ultrasound simulator. https://www.
mathworks.com/matlabcentral/fileexchange/
30886-high-intensity-focused-ultrasound-simulator.
Soyama, H. and Korsunsky, A. M. (2022). A critical com-
parative review of cavitation peening and other sur-
face peening methods. Journal of Materials Process-
ing Technology, 305:117586. https://doi.org/10.1016/
j.jmatprotec.2022.117586.
Tabei, M., Mast, T. D., and Waag, R. C. (2002). A k-
space method for coupled first-order acoustic propa-
gation equations. The Journal of the Acoustical So-
ciety of America, 111(1):53–63. https://doi.org/10.
1121/1.1421344.
Vlasko-Vlasov, V. K. and Tikhomirov, O. A. (1991). Oscil-
lations of monopolar domain walls in the field of ultra-
sonic waves. Solid State Physics, 33(12):3498–3501.
https://journals.ioffe.ru/articles/22125.
Ultrasonic Cleaning of Ore Particles and Disintegration of Flocculation Formations
85