Research on Guidance Method of Hypersonic Vehicle Based on
Reinforcement Learning and Dynamic Surface Control
Yin Diao
1a
, Baogang Lu
2b
and Yingzi Guan
3c
1
Beijing Institute of Astronautical Systems Engineering, Beijing, China
2
Science and Technology on Space Physics Laboratory, Beijing, China
3
School of Astronautics, Harbin Institute of Technology, Harbin, China
Keywords: Hypersonic Vehicle, Reinforcement Learning, Dynamic Surface Control, Online Guidance.
Abstract: To meet the requirements of high-precision tracking of long-range hypersonic vehicle position and
minimization of terminal velocity deviation, this paper completes the online generation of guidance
commands based on dynamic surface control theory and reinforcement learning method. First, this paper
transforms the control problem of three-dimensional under-actuated system into a problem of two-
dimensional path-tracking and establishes the basic framework of the guidance system by using the control
method of dynamic surface path-tracking, and the online optimal adjustment of guidance parameters is then
accomplished through the online network of flight state deviation and reinforcement learning to achieve the
minimization of the integrated deviation of the process position and terminal velocity. The simulation results
show that the proposed guidance method can solve the high-precision position tracking problem of long-range
hypersonic vehicles effectively, and it can reduce the terminal velocity deviation. The algorithm computation
is small, which has good prospects for engineering applications.
1 INTRODUCTION
Hypersonic vehicles are fast, have long flight range,
and can achieve flexible mission maneuvers, but
modeling and perturbation deviations under complex
environmental conditions can seriously affect the
flight capability and mission execution effectiveness
of hypersonic vehicles. Once the optimal trajectory
satisfying the mission and constraints is planned
offline or online, a high-precision trajectory tracking
guidance system is the key to ensuring that the
hypersonic vehicle is effective.
For a nonlinear system with large perturbations
and strong uncertainties such as hypersonic vehicles,
the backstepping method can divide the higher-order
system into several lower-order subsystems based on
modeling deviations, and achieve the asymptotic
stability of the system through the rectification of the
subsystems that meet the Lyapunov stability
requirements (Xu et al, 2011). However, due to the
need to derive the virtual control quantities, it is easy
to lead to the problem of "complexity explosion". The
a
https://orcid.org/0000-0002-1102-2745
b
https://orcid.org/0000-0001-8277-1922
c
https://orcid.org/0000-0001-7925-2400
adaptive dynamic surface control (ADSC) method is
based on the backstepping method and solves the
"complexity explosion" problem by adding a first-
order low-pass filter (Swaroop et al, 1997), so it has
also been more widely used. The combination of
extended observer and dynamic inversion technology
improved the response speed and accuracy of attitude
control for hypersonic vehicles (Liu et al, 2015). The
Reference (Xu et al, 2014) designed a general
hypersonic vehicle longitudinal controller based on
adaptive dynamic surface method. In the literature
(Wu et al, 2021), a finite-time control strategy is
proposed by combining dynamic surface trajectory
tracking control with sliding mode attitude control.
The literature (Butt et al, 2010; Butt et al, 2013)
combined dynamic surface control theory with neural
networks for the design of tracking control systems,
which better dealt with the effect of nonlinear terms
in the system. After that, (Yu et al, 2014; Xu et al,
2016; Shin, 2017) used neural networks with different
structures to compensate the nonlinear terms, so as to
achieve accurate tracking of the states such as altitude
Diao, Y., Lu, B. and Guan, Y.
Research on Guidance Method of Hypersonic Vehicle Based on Reinforcement Learning and Dynamic Surface Control.
DOI: 10.5220/0012010400003612
In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 651-657
ISBN: 978-989-758-622-4; ISSN: 2975-9463
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
651

and speed. The literature (Hu et al, 2013) combined
dynamic surface control with a dynamic inverse
strategy to improve the robustness of the control
system against the effects of model uncertainty. The
literature (Aguiar et al, 2007) used a path tracking
method to transform the 3D underdriven trajectory
tracking problem into a 2D tracking control problem
and achieved a better tracking control effect using
dynamic surface control, but the control parameters
could not be adaptively adjusted to meet the demand
of long-range unpowered gliding trajectory tracking
under strong disturbance conditions.
Among the model-free reinforcement learning
methods, the actor-critic algorithm combines the
advantages of policy-based methods in terms of
continuous action space problem description and
value-based methods in terms of convergence speed,
and has therefore been extensively studied. In the
literature (Li et al, 2018), an optimization model for
hypersonic vehicle control parameters was designed
in the actor-critic framework. The Reference (Zhen et
al, 2019) designed a PID controller based on actor
critical network which adjusted parameters online.
The literature (Lillicrap et al, 2015) applied the
successful concept of Deep Q-Learning to the
continuous action domain and proposed an Actor-
Critic deep deterministic policy gradient (DDPG)
approach based on no model dependency, which
successfully solved several simulated physics tasks.
The literature (Cheng et al, 2019; Gao, 2019) applied
the DDPG method to complete the optimization of
hypersonic re-entry flight trajectories with terminal
altitude and velocity magnitude constraints using
velocity inclination as the action space, but did not
consider the process position tracking and terminal
constraint guidance requirements under perturbation
conditions.
In this paper, for the needs of high precision
position tracking and terminal velocity deviation
minimization of long-range hypersonic vehicles, the
basic framework of the guidance system is
established by adopting the path tracking idea and
ADSC theory, and converting the effects of earth
rotation and curvature into system modeling
deviations, while introducing the DDPG
reinforcement learning method to generate the
optimal adjustment network of guidance parameters
under perturbation conditions for online generation of
guidance commands, and finally, the effectiveness of
the proposed method is verified by simulation.
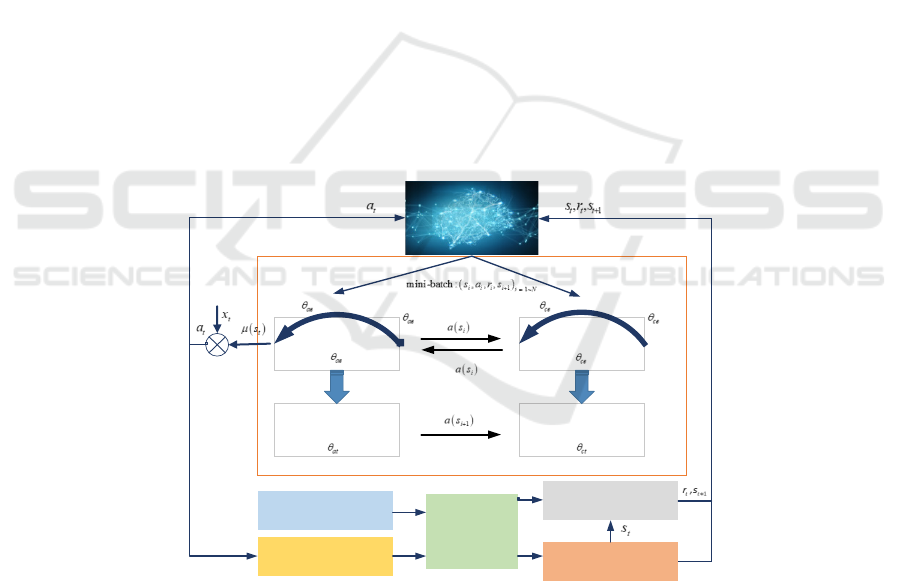
Actor eval-net
Actor target-net
Critic eval-net
Critic target-net
Update
Policy gradient
w.r.t
Soft-update
periodically
Soft-update
periodically
Actual dyn amics of
hyperson ic vehicle
Nominal instruction
Model control parameters
ADSC
Random sampling
OU noise
Ideal dynamics of hypersonic
vehicle
Replay buffer
Update
Policy gradient
w.r.t
Policy gradient
w.r.t
Figure 1: Guidance system training and online application framework based on DDPG.
2 OVERALL FRAMEWORK
The hypersonic vehicle guidance method based on
dynamic surface control and reinforcement learning
takes the adaptive dynamic surface control method
(ADSC) as the basic guidance framework and adopts
the angle of attack increment and velocity inclination
increment as the control commands for position
tracking; meanwhile,
i
s
is defined as the
reinforcement learning state expressed in terms of
instantaneous flight state and predicted terminal state,
i
a is the reinforcement learning action expressed in
terms of ADSC control matrix coefficients, and
i
r is
ISAIC 2022 - International Symposium on Automation, Information and Computing
652

the reward function, and the control parameters of
ADSC are continuously adjusted by the DDPG
method to finally obtain the optimal control
parameters that satisfy the path and terminal
constraints. The overall framework of the guidance
system is shown in Figure 1.
3 DYNAMIC SURFACE
CONTROL TRACKING
GUIDANCE METHODS
The reference trajectory is interpolated with the actual
x
position coordinates of the vehicle to obtain the
reference control program angle, which transforms
the three-dimensional trajectory tracking problem
into a two-dimensional path tracking problem. A
simplified model of the dynamics at half speed is used
in the calculation of the guidance command (Song et
al, 2016). The differences between the simplified and
real models are then considered in ADSC in the form
of model deviations. The form of the control system
used is:
1112
22 21
ccc
xfwx
x
fBuww
xfw
=+ =


=+ ++


=+




(1)
Where
1
w and
2
w are the model deviations, and the
variables in the control equation are:
[][ ]
[] [] [ ]
[][ ]
][ ]
[]
TT
1 11 12 2 21 22
TT T
12
TT
11 12
1 11 12 2 21 22
21 22
TT
ref ref 1 2
T
ref ref ref ref vref
ΔΔ
sin cos sin
v
cccc
c
ww ww
yz yz
bb
fff fff B
bb
yz
vv
γ
θθψ
==
===


===





==

=−
ww
xxuα
xwww
f
(2)
()
ref
ref
11
12
21 ref reff
22 tref veff
Dref
sin
cos sin
cos cos / sin /
sin sin cos cos sin /
cos sin /
v
LD
Lvv
r
rv
r
r
fv
fv
f
CqS mCqS mg
f
CqS m
CqS m
θ
θψ
θγ θ
θψ γ ψ γ
θψ

=

=−


=−−


=+


+

(3)
()
()
ref ref ref
11
12
21 tref reff Dref
22
sin / cos cos /
cos sin /
sin sin cos cos sin / cos sin /
cos cos sin sin sin /
r
DvLrr
rLref vref
L
r
ref v v v
Lref v vref v vref
r
bCqS m CqSm
bCqS m
b C qS m C qS m
bCqS m
αα
α α
θθγ
θγ
θψ γ ψ γ θψ
ψγ θψγ






=− +
=−
=++

=−
(4)
Where the subscripts c and ref denote the variables
on the reference trajectory, the control quantities
α Δ
and
v
γ
Δ are the differences from the reference angle
of attack and velocity inclination,
Dref
C and
Lref
C are
the aerodynamic coefficients on the reference
trajectory,
Dref
C
α
and
Lref
C
α
are the aerodynamic
derivatives on the reference trajectory.
Designing of guidance laws:
()
11
2111
22 22 2
212
1
22222
ˆ
ˆ
,(0) (0)
ˆ
c
cc
dd cd c
d
d
δ
−
=−


=− −−


+= =


=−


=−−−



exx
xgKew
τxx xx x
egx
uB x g Ke w
(5)
Where τ ,
1
K
,
2
K
are non-singular diagonal control
matrices.
Define filtering error:
1
22 2
dc c
x
xx δδτδ
−
=− =− −


(6)
The adaptive equations for the model error
ˆ
i
w and
the filtering error
ˆ
δ are:
Research on Guidance Method of Hypersonic Vehicle Based on Reinforcement Learning and Dynamic Surface Control
653

11
ˆ
ˆ
,(0)0
ˆˆ
,(0)0
ˆ
ˆ
i
iiiwi i
δ
δδδ




=− =
=− =



wwwQe K
Qe K
(7)
Where
i
Q ,
i
w
K
,
δ
K
are non-singular diagonal
matrices, and a sufficiently large
i
Q can make the
position tracking error
i
e sufficiently small, as
demonstrated in the literature (Swaroop et al, 1997).
However, for a long-range unpowered gliding
hypersonic vehicle, too large a
i
Q will lead to an
increase in the velocity error, which in turn will make
it difficult to maintain the flight state when
approaching the flight terminal due to practical
constraints such as flight angle of attack, and
eventually lead to a sharp increase in both position
and velocity deviations. Therefore, the optimal
control coefficients
i
Q need to be selected online for
different flight states and deviation conditions in
order to minimize the combined deviation of process
position and terminal velocity.
4 REINFORCEMENT LEARNING
BASED CONTROL
PARAMETER TUNING
METHOD
In this paper, an actor-critic-based DDPG
reinforcement learning architecture is built with a
vehicle as to the agent. Actor outputs actions
()
t
as
based on state decisions
t
s
, and critic evaluates Q
values based on state
t
s
and actions
t
a . The relevant
learning elements are:
[]
1
12
,,,, , , , , , ,
,, ,
,
160 / 40 /10
e
t f f fpre fpre
ttp tt
t
tfpre
v
ffpref
oxhv hvhv
so oo
aQQ
rhhvv
θψ ασ
−−
=




=


=
=− − − −

(8)
Considering the actual aerodynamic characteristics
and control requirements, the guidance system needs
to limit the actions and program angles:
[
]
[] [ ]
max
0.1, 3 , 1, 2
0,30 , 5/s, 70,70
i
Qi
αασ
∈=
∈° ° =° ∈−° °

(9)
To explore well in physical environments that have
momentum, Ornstein-Uhlenbeck (OU) noise
(Uhlenbeck et al, 1930) is added to the output of the
actions by the actor-network during reinforcement
learning training,
[
]
1
,,,
tttt
s
ars
+
is obtained by
interacting with the environment and stored in the
replay buffer. Every time the intelligence interacts
with the environment
e
p step by step, a sample is
randomly selected
N from the replay buffer for
training and updating the parameters of critic eval-net
ce
θ and actor eval-net
ae
θ using the Adam (Kingma et
al, 2014).
()
()
()
() ( )
ce
ae c
ct at
e
1
ce ce 1 1
1
ae ae
,,
,
t
tt
tt
ct t t tt
tt
at tt
rQs s Qsa
sQsa
θθ
θ
θθ
θθλ κ μ
θθλμ
+
++
+


=+ + −


=+∇ ∇
(10)
Where:
c
λ and
a
λ are the learning rates of critic eval-
net and actor eval-net, respectively,
t
r is the current
reward value, and
κ is the discounting factor. When
eval-net is updated
t
p times, the DDPG algorithm
periodically soft-update target-net.
()
()
1
ct ct
1
at
ce
at ae
1+
1+
tt
tt
θττθ
ττθ
θ
θθ
+
+
=


=

−

−
(11)
The actor eval-net parameters
()
ae
s
θ after the
training can be used to adjust the control parameters
of the hypersonic vehicle during guided flight online.
5 REINFORCEMENT LEARNING
BASED CONTROL
PARAMETER TUNING
METHOD
5.1 Simulation Conditions
The simulation uses a publicly available CAV model
with a mass of 907 kg, an aerodynamic reference area
of 0.48 m², and the mission parameters shown in
Table 1.
The simulation step and guidance period are both
taken as 100 ms, and the control parameter update and
environment interaction period is 1 s. The structure of
actor-net is set to
[
]
11 5,20, 20,10, 2× , and the
ISAIC 2022 - International Symposium on Automation, Information and Computing
654

structure of critic-net is set to
[
]
11 5 2,20, 20,10,1×+ .
The training hyperparameters are shown in Table 2.
Table 1: List of vehicle mission parameters.
Parameters
Parameter
value
Initial
parameters
Hei
g
ht/k
m
60
S
p
eed/
(
m/s
)
5,500
Fli
g
ht
p
ath an
g
le/
(
°
)
-1
Heading angle/(°) 90
Design range/km 4300
Terminal
parameters
Height/k
m
28
S
p
eed/
(
m/s
)
1,840
Remainin
g
ran
g
e/k
m
50
Table 2: Super parameter setting of RL training.
Item Value
e
p 5
N 32
a
λ 0.000 1
c
λ 0.002
κ 0.99
t
p 5
τ 0.001
0
κ ( OU noise) 0.15
0
η
( OU noise) 0.15
Table 3: Status deviations and environmental disturbances.
Deviations Value
Initial of height
0
h (m) -100~100
Initial of velocity
0
v (ms
-1
) -20~20
Initial of flight path angle
0
γ

(°) -1~1
Resistance coefficient (%) -10~10
Lift coefficient (%) -10~10
Atmospheric density (%) -10~10
5.2 Reinforcement Learning Training
Introducing normally distributed state biases and
environmental perturbations during reinforcement
learning training. The status deviations and
environmental disturbances are shown in Table 3.
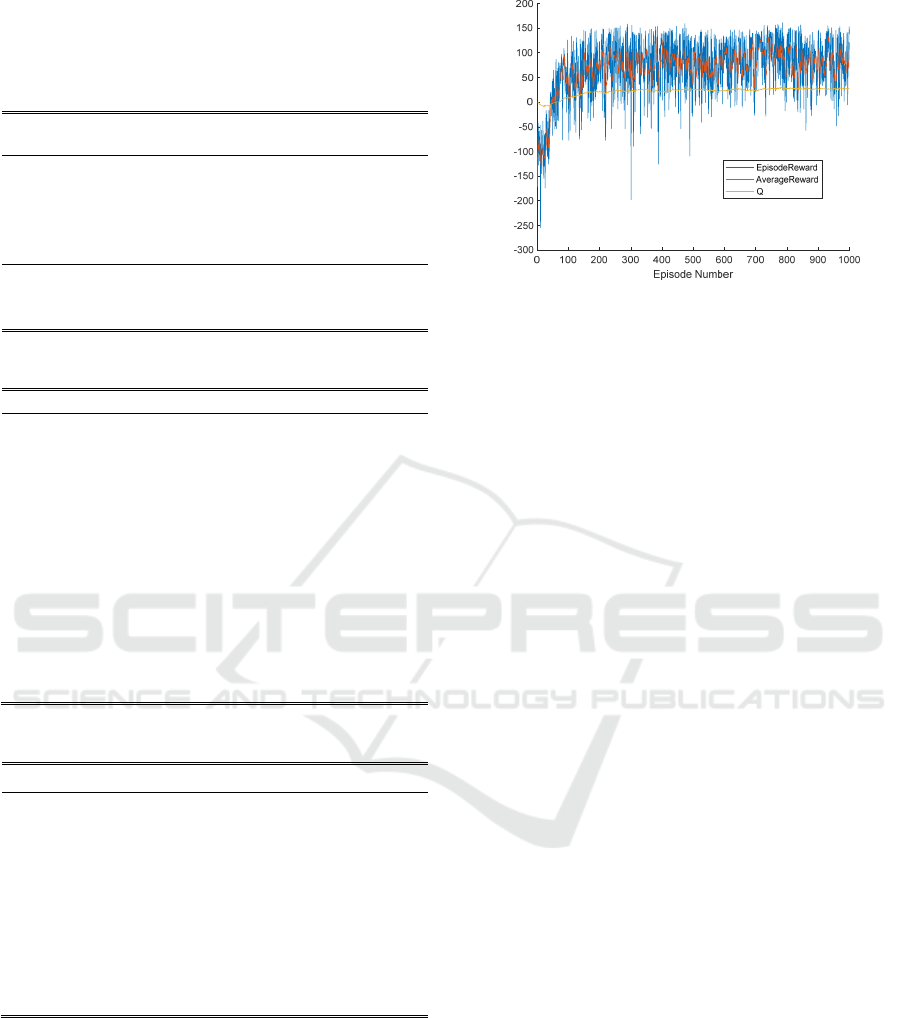
With 1000 training sessions, the reward function
gradually converges, as shown in Figure 2.
Figure 2: Curve of reward function in the process of
reinforcement learning and training.
5.3 Guidance Simulation Results
To verify the adaptability of the guidance method
proposed in this paper, given the limiting pull-off
condition.
00
0
100 m, 20m/s
0.5 , 10%
10% 10%
L
D
hv
C
C
γ
ρ
=± =±


=± ° =±


==



 
，
(12)
The ADSC guidance law and ADSC+DDPG
methods are used for guidance simulation,
respectively. The simulation results are shown in
Figures 3-8.
Under the two limit deviation conditions, the
maximum altitude deviations of ADSC+DDPG are
reduced by 28 m and 5023 m, respectively, compared
with the ADSC process when jumping out
x
according to the terminal position; the terminal
velocity deviation is reduced by 16.2 m/s and 101.1
m/s, respectively. This result proves the effectiveness
of the proposed guidance method.
6 CONCLUSIONS
In this paper, the basic framework of the guidance
system is established by using the idea of path
tracking and ADSC theory to address the needs of
high-precision position tracking and terminal velocity
deviation minimization for long-range hypersonic
vehicles, converting the effects of earth rotation and
curvature into system modeling deviations, and
introducing the DDPG reinforcement learning
method to generate the optimal adjustment network
of ADSC control parameters under perturbation
conditions for online generation of guidance
commands. Finally, the effectiveness of the proposed
method is verified by simulation.
Value
Research on Guidance Method of Hypersonic Vehicle Based on Reinforcement Learning and Dynamic Surface Control
655

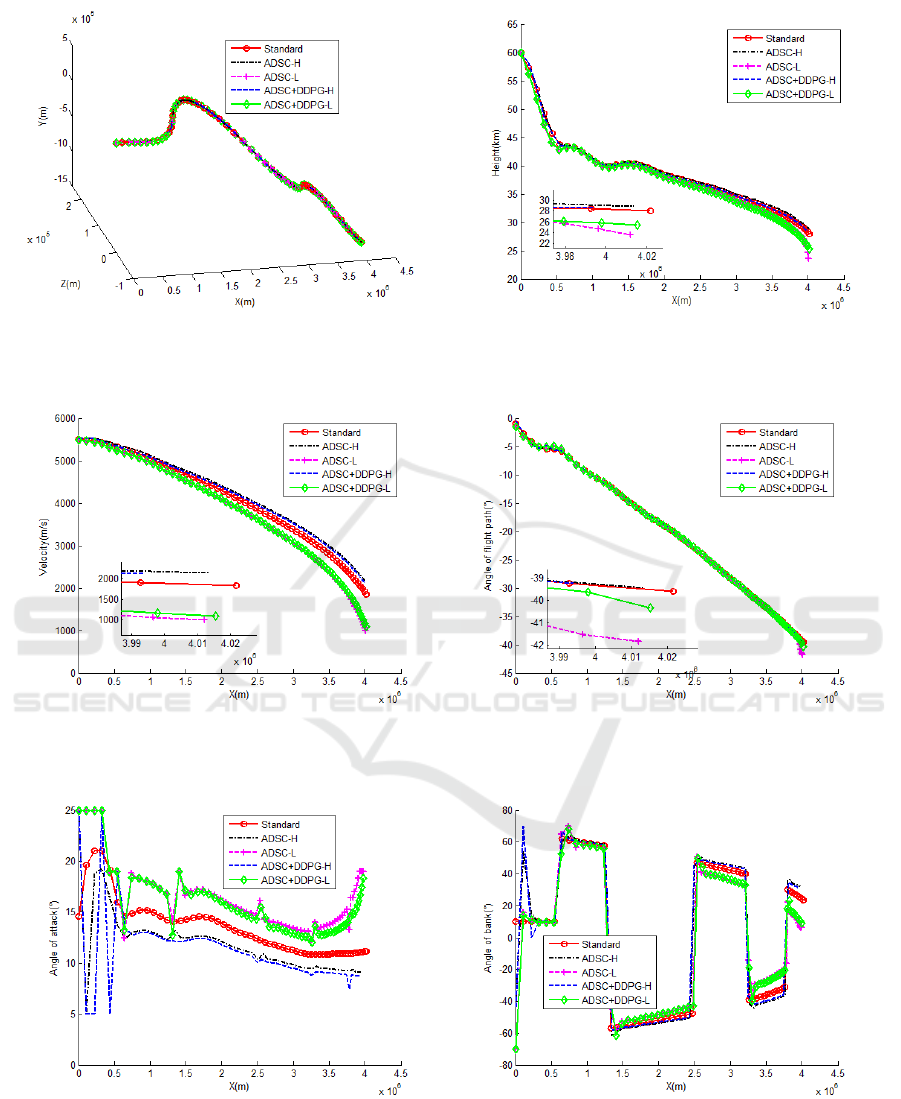
Figure 3: 3D trajectory versus time. Figure 4: Height versus time.
Figure 5: Velocity versus time. Figure 6: Flight path angle versus time.
Figure 7: Attack angle versus time. Figure 8: Bank angle versus time.
ISAIC 2022 - International Symposium on Automation, Information and Computing
656

ACKNOWLEDGEMENTS
The authors would like to thank the financial supports
of the open Fund of National Defense Key Discipline
Laboratory of Micro-Spacecraft Technology (Grant
No. HIT.KLOF.MST.2018028).
REFERENCES
Xu B., Sun F., Wang S., et al. (2011). Adaptive hypersonic
flight control via back-stepping and Kriging estimation.
In Proc. 2011 IEEE International Conference on
Systems, Man, and Cybernetics, pages 1603-1608.
IEEE.
Swaroop D., Gerdes J. C., Yip P. P., et al. (1997). Dynamic
surface control of nonlinear systems. In Proc. The 1997
American Control Conference, pages 3028-3034.
IEEE.
Liu X. D., Huang W. W., Yu C. M. (2015). Dynamic
surface attitude control for hypersonic vehicle
containing extended state observer. Journal of
Astronautics, 36(8):916-922.
Xu B., Sun F., Wang S., et al. (2014). Dynamic surface
control of hypersonic aircraft with parameter
estimation. Advances in Intelligent Systems and
Computing, 213:667-677.
Wu X., Zheng W., Zhou X., et al. (2021). Adaptive dynamic
surface and sliding mode tracking control for uncertain
QUAV with time-varying load and appointed-time
prescribed performance. Journal of the Franklin
Institute, 358(8):4178-4208.
Butt W. A., Yan L., Kendrick A. S. (2010). Dynamic
surface control for nonlinear hypersonic air vehicle
using neural network. In Proc. The 29th Chinese
Control Conference, pages 733-738. IEEE.
Butt W. A., Amezquita, et al. (2013). Adaptive integral
dynamic surface control of a hypersonic flight vehicle.
International Journal of Systems Science: The Theory
and Practice of Mathematical Modelling, Simulation,
Optimization and Control in Relation to Biological,
Economic, Industrial and Transportation Systems,
46(9/12):1717-1728.
Yu J., Chen J., Wang C., et al. (2014). Near space
hypersonic unmanned aerial vehicle dynamic surface
backstepping control design. Sensors & Transducers
Journal, 174(7):292-297.
Xu B., Zhang Q., Pan Y. (2016). Neural network based
dynamic surface control of hypersonic flight dynamics
using small-gain theorem. Neurocomputing,
173(JAN.15PT.3):690-699.
Shin J. (2017). Adaptive dynamic surface control for a
hypersonic aircraft using neural networks. IEEE
Transactions on Aerospace & Electronic Systems,
53(5):2277-2289.
Hu C. F., Liu Y. W. (2013). Fuzzy adaptive nonlinear
control of hypersonic vehicles based on dynamic
surfaces. Control and Decision Making, 28(12):1849-
1854.
Aguiar A. P., Hespanha J. P. (2007). Trajectory-tracking
and path-following of underactuated autonomous
vehicles with parametric modeling uncertainty. IEEE
Transactions on Automatic Control, 52(8):1362-1379.
Li R. F., Hu L., Cai L. (2018). Adaptive tracking control of
a hypersonic flight aircraft using neural networks with
reinforcement synthesis. Aero Weaponry, 2018(6):3-
10.
Zhen Y., Hao M. R. (2019). Research on intelligent PID
control method based on deep reinforcement learning.
Tactical missile technology
, 2019 (5):37-43.
Lillicrap T. P., Hunt J. J., Pritzel A., et al. (2015).
Continuous control with deep reinforcement learning.
arXiv e-prints, arXiv:1509.02971.
Cheng Y., Shui Z. S., Xu C., et al. (2019). Cross-cycle
iterative unmanned aerial vehicle reentry guidance
based on reinforcement learning. In Proc. 2019 IEEE
International Conference on Unmanned Systems, pages
587-592.
Gao J. S. (2019). Research on trajectory optimization and
guidance method of lift reentry vehicle. Doctoral
Dissertation, Huazhong University of science and
technology.
Song C., Zhou J., Guo J. G., et al. (2016). Guidance method
based on path tracking for hypersonic vehicles. Acta
Astronautica, 37(4): 435-441.
Uhlenbeck, George E. and Ornstein, L. S. (1930). On the
theory of the brownian motion. Physical Review,
36(5):823.
Kingma D., Ba J. (2014). Adam:a method for stochastic
optimization. arXiv preprint, arXiv:1412.6980.
Research on Guidance Method of Hypersonic Vehicle Based on Reinforcement Learning and Dynamic Surface Control
657