A Microscope Image Auto-Focus Method Based on Colorful-Gradient

Po-Yi Li

, Chia-Jen Liu

, Cheng-Kuan Lin

3,∗

and Yu-Chee Tseng

Department of Biological Science and Technology, National Yang Ming Chiao Tung University, Taiwan

Institute of Emergency and Critical Care Medicine, School of Medicine, National Yang Ming Chiao Tung University,

Taiwan

Department of Computer Science, National Yang Ming Chiao Tung University, Taiwan

Keywords:

Auto-Focus Measurement, Gradient-Based Operators, Image Processing.

Abstract:

Blood testing has always been an important indicator for judging patients’ states and various types of lesions.

The typical way to observe the blood sample is by having medical personnel operate the conventional micro-

scope and classify the white blood cells in a patient’s blood sample. However, such a long period of observation

may cause visual fatigue. As a result, we built an automated microscope system to ensure the efﬁciency of the

observation. In addition, focus measurement has always been a huge topic in the auto-focus method, which

we implemented in the system. We proposed an automatic focus algorithm based on the gradient operator

and colorfulness value to ﬁt with the automated microscope system. The color-gradient operator is compared

to conventional operators such as Laplacian-based, Wavelet-based, and DCT energy-based. By taking advan-

tage of the three components in the color-gradient operator, the standard of determining a microscope image

consists of both sharpness and colorfulness. The experimental results showed that the proposed microscope

automatic focus algorithm is signiﬁcantly stable in all real-life blood cell microscope image dataset scenarios.

Such performance is discussed in speciﬁc situations that happened only in microscope auto-focus measure-

ments.

1 INTRODUCTION

Clinically, blood testing has always been one of the

critical indicators for judging the state of patients and

various types of lesions. For example, by count-

ing and classifying white blood cells in a patient’s

blood sample, you can know whether the patient has

leukemia and the type of leukemia. In addition, var-

ious indexes of white blood cells are also closely re-

lated to Covid-19. In 198 COVID-19 patients, the re-

search of Tong et al. shows that the survivors’ lym-

phocytes, basophils, and eosinophils levels were sig-

niﬁcantly higher than those of non-survivors (Tong

et al., 2021). Blixt et al. observed that the most con-

valescent COVID-19 patients have robust and durable

B and T cell immunity (Blixt et al., 2022). There-

fore, improving the detection efﬁciency and accuracy

of white blood cells is very important, which will help

to judge the patient’s status accurately.

In the ﬁeld of leukemia-related disease, acute

myeloid leukemia (AML) accounted for a large pro-

portion. Practically, medical personnel spends hours

∗

Corresponding author.

of microscope observation on patients’ blood sample

to identify their health. However, looking straight

into the microscope for hundreds or even thousands

of samples often cause visual fatigue or lower overall

efﬁciency. Therefore, many manufacturers of micro-

scope accessories have launched series for automatic

photography to solve the fatigue of repetitive oper-

ation behavior. Taking the Lionheart LX/FX series

of automated microscopes launched by BioTek as an

example, it costs about 40, 000 to 70, 000 US dollars

per device. Nonetheless, the whole product line of

the digital microscope DM B series launched by Le-

ica also costs about 5, 000 to 10, 000 US dollars. As

we can see, although the fatigue problem of medical

personnel has been solved at ﬁrst glance, such an au-

tomated photographic microscope is too expensive for

many medical institutions with relatively insufﬁcient

funds.

To solve the problems which people met in real

life, we came up with the idea of building an au-

tomated photography microscope system having the

following features: (1) modulized structure, (2) lower

price, (3) ability to analyze the image. The main idea

is to build a retroﬁt modular system that can easily in-

Li, P., Liu, C., Lin, C. and Tseng, Y.

A Microscope Image Auto-Focus Method Based on Colorful-Gradient.

DOI: 10.5220/0012017800003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 693-698

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

693

stall on a conventional microscope which most med-

ical institutions own. At the same time, we have to

make sure that the price of this module is affordable,

which makes us abandon the method of installing an

auto-focus digital camera on top of the microscope.

We, however, chose the Raspberry Pi High-Quality

Camera as our image collector.

Such a choice has to pay the price: There is no

auto-focus system in the pi camera; we have to control

the adjustment wheel on the microscope with motors

and take several photos while scrolling it. As a result,

we’ll get a set of images that involve different heights

from the microscope stage to the microscope objec-

tive, which means we have to ﬁgure out the way to

pick out the non-blurry image from the set. However,

there were quite a few differences between the daily

photos and cell images captured with a microscope.

And that’s the primary purpose of the algorithm we

designed and implemented in this paper.

In Section 2, we introduce related works for mi-

croscope auto-focus. Section 3 describes our micro-

scope image auto-focus method based on Colorful-

Gradient and propose our Colorful-gradient auto-

focus algorithm (CGAF). And we analyze the experi-

mental results in Section 4. Finally, we conclude this

paper in Section 5.

2 RELATED WORKS

In this section, we review several previous studies of

focus measurement. We search for how people solve

the blurry image ﬁltering problem nowadays. A fo-

cus measure is a stated quantity used to calculate the

pixel sharpness locally. Sharpness is a general term

for every focus measurement score to be taken as a

sharpness value. To calculate it, several focus opera-

tors are proposed by different researchers. In the re-

search of Pertuz et al. (Pertuz et al., 2013), six main

groups of sharpness operators were used in the work.

We pick four of them as our competitors to evaluate

our performance. The four sharpness operator groups

are shown in the following lines.

1 Gradient-Based Operators: This group of focus

measures uses the ﬁrst image derivative or gradi-

ent to measure the focus level. Considering the

images as a function f of the intensity value of

pixels(x, y), the gradient g can be computed by:

g =



∂ f

∂x





∂ f

∂y



(1)

This is also one of the most commonly used fo-

cus measurements. However, there is an assump-

tion that this operator is based on: focused images

present more sharp edges than blurred ones. This

also means that it is pretty sensitive to the sharp

edges in an image.

2 Laplacian-Based Operators: These operators

are similar to the Gradient-based operator group.

These focus measures are based on the second

derivative of an image. Considering the images as

a function f of the intensity value of pixels(x, y),

the Laplacian can be computed by the equation

below, which is usually deﬁned as divergence of

the gradient of a function f :

∆ f (x, y) = div(grad( f )) (2)

Group members such as Energy of Laplacian and

Variance of Laplacian have been used as a fo-

cus measure for auto-focus in many pieces of re-

search. A focus measure based on an alternative

deﬁnition of the Laplacian, known as the modiﬁed

Laplacian, showed the ability to become a focus

measurement value (Nayar and Nakagawa, 1994).

To conclude, Laplacian has shown a remarkable

ability to deal with accurate shape recovery, mak-

ing us later pick the Laplacian-based operator as

our ﬁrst experimental option.

3 Wavelet-Based Operators: These operators are

based on the discrete wavelet transform coef-

ﬁcients. Thus, these coefﬁcients are used to

compute the focus amount of an image. How-

ever, these kinds of operators have primarily been

based on the statistical properties of the discrete

wavelet transform (DWT) coefﬁcients. It is a fo-

cus measurement for auto-focus computing from

the sub-bands of a higher-level discrete wavelet

transform which is basically the sum of wavelet

coefﬁcients (Yang and Nelson, 2003).

4 DCT-Based Operators: This group of operators

utilizes the discrete cosine transform coefﬁcients

to calculate the degree of focus. The discrete co-

sine transform is now part of many images and

video encoding algorithms. The sum of the AC

components of the DCT was proved to be equal

to the variance of the image intensity and can be

used as a focus measure (Baina and Dublet, 1995).

Shen and Chen proposed a ratio between DC and

AC components in the DCT as a new focus mea-

surement method (Shen and Chen, 2006). Lee et

al. applied the DCT to 8 × 8 image sub-blocks

in order to measure focus (Lee et al., 2009). To

improve the computation time, they picked only 5

out of 63 AC coefﬁcients to compute the AC en-

ergy, which made the whole calculation faster and

was named DCT reduced energy ratio.

Based on this literature review section, we started

everything from the one with higher accuracy of

ISAIC 2022 - International Symposium on Automation, Information and Computing

694

shape recovery, the Laplacian-based operator. How-

ever, we faced problems due to these high-accuracy

features and the particular situation while processing

microscopy images. Nonetheless, six different focus

measurement operators are ﬁnally chosen as compo-

nents in the simulation section. We will compare our

method of this research to others while processing the

same set of images.

3 METHODS

Picking a clear image is vital in our project. After

placing one patient’s blood samples onto the micro-

scope stage, we control the stage’s height with motors

and get a cluster of images that contains photos with

the variable focus of the same sample. Then, this clus-

ter of images will transfer to our server to begin pro-

cessing the clear image selection calculation. Finally,

when we get a single most explicit image, we run our

AI model to classify cells in the images and even an-

alyze the image with pre-trained medical knowledge.

The complete process can be ﬁnished while the med-

ical personnel is having a nice sleep, and a detailed

report will be shown on the user’s computer at the

end. However, in this research, we focus our method-

ology on the focus measurement instead of the whole

microscope project.

Most auto-focus methods are based on a sharpness

function that delivers a real-valued image quality es-

timate. However, a threshold has to be set to classify

whether the target image is blurry or not. Meanwhile,

the most commonly used method for ﬁltering blurry

images is the Gradient-based operator or Laplacian-

based operator calculation of an image. As a result,

in our early pipeline design, there was only one com-

ponent: “calculate the sharpness value.” After facing

different problems, we devised a new pipeline solu-

tion for the microscope image focus measurement.

1 Sharpness Measurement: Using the second

derivative of an image, we could get the areas

of rapidly changing intensity in the image (Pech-

Pacheco et al., 2000). The Laplacian operator is

often used for edge detection. Furthermore, this

algorithm is based on the assumption that if a

picture has high variance, then it has a broader

frequency response range, representing a typical,

well-focused picture. But if the picture has a

slight variance, it has a narrower frequency re-

sponse range, which means that the number of

edges in the picture is low. As we know, the blur-

rier the picture is, the fewer it has edges. At the

beginning of our experiment, we thought it would

be straightforward to pick a clear image since

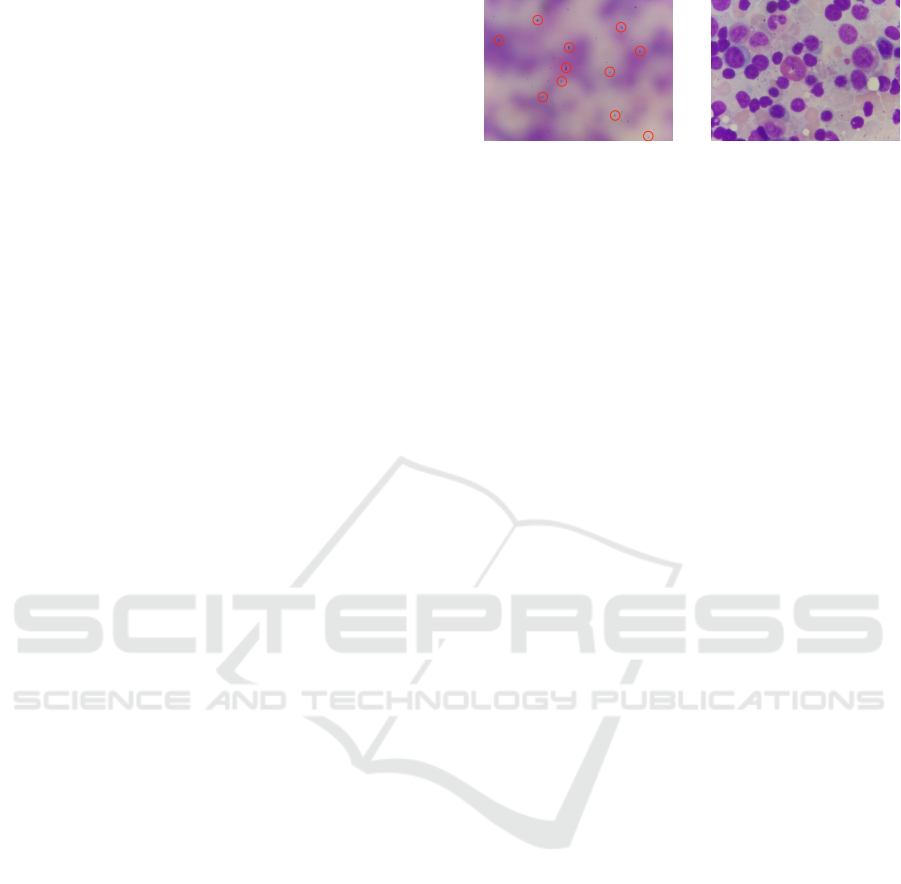
(a) (b)

Figure 1: Fixing impurities on the microscope makes the

program regard a blurry image as a clear image with several

sharp edges of impurities target.

Laplacian-based operators have been regarded as

the most effective way to get this job done. How-

ever, compared to the standard image in our daily

life, there were too many impurities in the micro-

scope image (Figure 1). Every impurity on the

image will be recognized as several rapidly chang-

ing intensity areas. This would make the Lapla-

cian transform value quite similar between pho-

tos since every image uses the same microscope

lenses, and there will be the same impurities in

the same position. The red circle in Figure 1(a)

shows the impurities in the image. Figure 1(b) is

the clear image of this set of images, which we

expected the program to pick.

However, we still needed information on the

sharpness value of the image. We then tried the

Gradient-based operator, which only calculates

the ﬁrst derivative of the image. Formally, an im-

age gradient is deﬁned as a directional change in

image intensity. Finally, we got a more accurate

result compared to the Laplacian-based operator.

Figure 2 illustrates the sharpness value calculated

with both Laplacian and gradient-based operators,

the clearest image in this set is the 35-th (image

ids). In this ﬁgure, the x-axis coordinate shows the

image of a set, which also stands for the different

distances between the microscope stage and the

microscope objective (descending power). The y-

axis corresponds to the sharpness value of both

Gradient-based and Laplacian-based operators.

2 Colorfulness Measurement: Although sharp-

ness seems to be the most efﬁcient method for

blur detection, we found that since impurities are

black dots of various sizes when the image is be-

ing transformed into grayscale in the sharpness

calculation process, machines cannot tell the im-

purities or the cells are precisely the main tar-

gets it should focus on. This resulted in mak-

ing the wrong decision about a clear image. We

come up with a different aspect of blur detec-

tion in this case-Colorfulness calculation. The

whole point of the colorfulness calculation is that

we want to ﬁlter the total blur image with only

A Microscope Image Auto-Focus Method Based on Colorful-Gradient

695

Figure 2: Comparison between Gradient-based sharpness

value and Laplacian-based sharpness value.

impurities. These kinds of images share a com-

mon feature: they lack other colors except black

and white. Haslera and S

usstrunk the colorfulness

calculation (Haslera and S

usstrunk, 2003). First,

they split the image into RGB color values, R, G,

and B. Then, they immediately calculate

rg = R − G (3)

yb =

2R + 2G

− B (4)

Following up, they calculated both the standard

deviation of rg, σ

, the standard deviation of yb,

, the mean value of rb, µ

, and the mean value

of yb, µ

, to ﬁt the ﬁnal Colorfulness function

Color f ulness f unction = σ

rgyb

+ 0.3 × µ

gryb

(5)

where

rgyb

+ σ

(6)

rgyb

+ µ

(7)

We set it as a double-check value which makes

sure that the high sharpness of a single image is

not just caused by the impurities on the micro-

scope lenses. Figure 3 shows the difference be-

tween adding colorfulness to the sharpness value

or not. The index of the image stands for the

microscope stage’s height, as when the index in-

crease, the stage height goes higher and higher

to the microscope objective. If the colorfulness

value is not considered, the program will pick the

second image as the clearest due to the impurity

problem. On the other hand, colorfulness did help

check this kind of mistake by making the correct

clear image have a higher score by adding a higher

colorfulness value on the sharpness value.

3 CIE Lab Color Space: Combining colorfulness

and sharpness to calculate the focus value seems

Figure 3: Showing how the colorfulness value helped in the

situation of impurities problems.

Figure 4: A general look of a set of images with a color cast

problem.

to be the most accurate method to identify the

clear microscope image. However, the illuminator

under the stage can sometimes cause serious color

cast problems, as shown in Figure 4. Noticed that

it should be a set of images from blurry to non-

blurry, but several of them suddenly had a color

casting problem with a blue tone. Considering

that we were using colorfulness as one of our cen-

tral scoring values, the program may give a very

high score to the color cast image in the aspect

of colorfulness. As a result, we modiﬁed the col-

orfulness calculation function with CIE Lab color

space to check for the image’s color cast degree.

The distance between colors in the color space is

consistent with its perceived difference, so it is

more reasonable to detect the color cast image un-

der it.

4 Pipeline Processing: Finally, we designed a new

process to solve the microscope image autofocus,

considering that there will be undodgeable im-

purities on the lens and illuminator accidentally

causing the color cast problem. As Figure 5 shows

below, when an image is inputted to the opera-

tor, we will start calculating the sharpness value,

colorfulness value, and color cast score parallelly.

Afterward, we multiply the reciprocal number of

the color cast score by the colorfulness value and

ISAIC 2022 - International Symposium on Automation, Information and Computing

696

Figure 5: The overall workﬂow of the Color-gradient focus

value calculation.

add the original sharpness value on it to get the

ﬁnal focus value of the colorful-gradient opera-

tor. Algorithm 1 shows the detail of our method.

To begin, three lists will be declared (Sharpness,

Colorful, ColorCast) for storing sharpness value,

colorfulness value, and color cast score, respec-

tively. Secondly, we read the image to the vari-

able “im” to start calculating the three main com-

ponents in three color-gradient functions (S, CF,

CC) with three sub-functions (SCal, CCal, CCCal).

After traversing the directory, we scale all the val-

ues with a min-max scaler and get the focus value

with the proposed function. Finally, the index of

the image with the highest focus value will return

as an output.

4 EXPERIMENTAL RESULTS

To have a better look at the colorful-gradient opera-

tor’s ability, we set up a few other operators to com-

pare the performance of picking the non-blurry image

from a set of images. The testing process included 18

directories of images, each of them containing multi-

ple images from blurry to non-blurry images, which

are all taken in real-life patients’ blood samples. For

these 18 cases of images, there are 12 cases taken on

microscopes with impurities on the lens, and 6 cases

are taken on a microscope with a clean lens. We com-

pare our method, color gradient (C

), with Gradient-

based (G

), Laplacian-based (L

), wavelet summary

), wavelet variance (W

), DCT ratio (D

), and DCT

reduced ratio (D

). As Table 1 shows below, the col-

orful gradient is doing a great job in the 12 cases with

impurities. The most explicit image in every case is

accurately picked by it. However, most of the other

operators could not have a stable performance while

facing impurities problems. On the other hand, when

it comes to cases without the interference of impuri-

Algorithm 1: Colorful-gradient auto-focus algorithm

(CGAF).

Input: A list of strings (path of every image

in the image directory), Input =

[path

, path

, ··· , path

Output: A index of the most explicit image.

1 begin

2 Sharpness ← [];

3 Color f ul ← [];

4 ColorCast ← [];

5 len = length(Input);

6 while len > 0 do

7 im ← ImageToArray(Input[len − 1]);

8 Append SCal(im) to Sharpness;

9 Append CCal(im) to Color f ul;

10 Append CCCal(im) to ColorCast;

11 len ← len − 1;

12 end

13 SS ← MinMaxScaler(Shar pness);

14 CS ← MinMaxScaler(Color f ul);

15 CCS ← MinMaxScaler(ColorCast);

16 Focus ← ColorGradient(SS,CS,CCS);

17 return FindMaxValueIndex(Focus);

18 end

Table 1: The benchmark with impurity interference

# steps, s C

s < 1 12 6 2 1 7 5 0

5 ≤ s < 15 0 3 3 1 1 5 5

15 ≤ s < 35 0 0 0 1 0 0 2

s ≥ 35 0 3 7 4 4 2 3

ties, as Table 2 showed, all of the operators can nearly

pick the clearest image by an error of about three steps

on average. We can still observe that the colorful-

gradient operator is very stable, regardless of whether

the impurities are interfering.

Not only can the colorful gradient handle the im-

purities cases, but it can also deal with a color cast

that often happens in microscope images. One of

the 12 cases with impurities interference also has a

severe color casting problem, as shown in Figure 5

(Notice that to have an easier understanding of the

color cast problem, we did not show all of the images

in Figure 6. We picked images with an interval of

three started from the fourth image). A standard mi-

croscope image of blood cells should be purple due

to the dye fusing in the sample for more straight-

Table 2: The benchmark without impurity interference

# steps, s C

s < 1 5 3 1 0 1 0 0

5 ≤ s < 5 1 3 5 6 5 6 5

s ≥ 5 0 0 0 0 0 0 1

A Microscope Image Auto-Focus Method Based on Colorful-Gradient

697

Figure 6: Benchmark comparison between other operators

and the Color-gradient operator.

forward observation. However, we can see several

photos in the set have a color casting to blue (exam-

ple 1 ∼ 5.jpg), which made all of the operators pick

the example 2.jpg, which is the wrong one with the

color cast problem. Figure 6 is a line chart of all the

operators calculating this color cast case. Because of

the blue color casting, all lines suddenly peak when

the image index is number 2. Even if the process ﬁ-

nally meets the actual clear image, number 52 in the

set, the peak can only be a local maximum instead of

a global maximum for all the other operators, leading

to a wrong answer. Once again, the colorful gradient

operator is still the only one that survives in this color

casting case.

The ﬁnal simulation with python code ﬁles is all

open sources on the internet. Please refer to the

URL: https://github.com/Pockylee/Colorful-gradient

for a deeper understanding of the colorful-gradient

operator algorithm.

5 CONCLUSIONS

We proposed a new focus measurement operator con-

sidering three aspects: sharpness, colorfulness, and

color cast. Unlike most sharpness operators nowa-

days, colorful-gradient cannot only do the regular im-

age focus measurement job well, but it can also easily

deal with microscopy cases. According to the real-

life data collected from medical institutes, we found

the two main factors of making microscopy images

harder to do focus measurement. First, the impurity

on the lens is an undodgeable problem, especially in

medical institutions located in remote areas. Second,

the color cast problems are caused by the illuminator

of a conventional microscope. After all, we tested the

operators with real-life data and constructed a bench-

mark to show the difference between the colorful-

gradient operator and others. With the focus algo-

rithm we propose, we can perform excellently on the

microscope image focus detection cases. We had al-

ready implemented this algorithm onto the automated

microscope system. However, the current algorithm is

not fast enough to make a real-time adjustment with

the microscope stage adjust wheel. We can only take

one photo on every slight rotation (step) of the adjust-

ment wheel; after gathering all of the images of the

sample, we send them to the server to ﬁnd the perfect

height for the microscope stage. As a result, we can

start from a higher height instead of taking the photo

from the bottom, which wastes much time.

REFERENCES

Baina, J. and Dublet, J. (1995). Automatic focus and

iris control for video cameras. In Fifth International

Conference on Image Processing and its Applications,

pages 232–235.

Blixt, L., Bogdanovic, G., Buggert, M., Gao, Y., Hober,

S., Healy, K., Johansson, H., Kjellander, C., Mravina-

cova, S., Muschiol, S., Nilsson, P., Palma, M., Pin, E.,

Smith, C. I. E., Stromberg, O., Chen, M. S., Zain, R.,

Hansson, L., and

Osterbor, A. (2022). Covid-19 in

patients with chronic lymphocytic leukemia: clinical

outcome and b- and t-cell immunity during 13 months

in consecutive patients. Leukemia, 36(2):476–481.

Haslera, D. and S

usstrunk, S. (2003). Measuring colour-

fulness in natural images. In SPIE - the International

Society for Optical Engineering, volume 5007, pages

87–95.

Lee, S.-Y., Yoo, J.-T., Kumar, Y., and Kim, S.-W. (2009).

Reduced energy-ratio measure for robust autofocus-

ing in digital camera. IEEE Signal Processing Letters,

16(2):133–136.

Nayar, S. K. and Nakagawa, Y. (1994). Shape from focus.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 16(8):824–831.

Pech-Pacheco, J. L., Cristobal, G., Chamorro-Martinez, J.,

and Fernandez-Valdivia, J. (2000). Diatom autofocus-

ing in brightﬁeld microscope: a comparative study. In

the 15th International Conference on Pattern Recog-

nition (ICPR-2000), volume 3, pages 314–317.

Pertuz, S., Puig, D., and Garcia, M. A. (2013). Analysis of

focus measure operators for shape-from-focus. Pat-

tern Recognition, 46:1415–1432.

Shen, C.-H. and Chen, H. H. (2006). Robust focus measure

for low-contrast images. In 2006 Digest of Technical

Papers International Conference on Consumer Elec-

tronics, number 69-70.

Tong, X., Cheng, A., Yuan, X., Zhong, X., Wang, H., Xu,

W. Z. X., and Li, Y. (2021). Characteristics of periph-

eral white blood cells in covid-19 patients revealed.

BMC Infectious Diseases, 21(1):1236.

Yang, G. and Nelson, B. J. (2003). Wavelet-based autofo-

cusing and unsupervised segmentation of microscopic

images. In 2003 IEEE/RSJ International Conference

on Intelligent Robots and Systems (IROS 2003) (Cat.

No.03CH37453), pages 2143–2148.

ISAIC 2022 - International Symposium on Automation, Information and Computing

698