The Best Decision-Making Scheme Based on Bitcoin and Gold Stock

Market

Jingru Zeng, Yufei Wang

and Xiyu Zheng

International College Wuhan University of Science and Technology, Wuhan, China

Keywords: Unstable Assets, Bull and Bear Market Judgment Model, Risk Model, Time Series Prediction Model, Xgboost

Regression Model.

Abstract: Market traders frequently buy or sell their volatile assets, Bitcoin and gold, in order to maximize their returns,

and each purchase and sale of these two assets requires a commission. In order to study this economic

management problem, we made certain assumptions and established a prediction model to achieve the best

rete of returns. We construct bull and bear market judgment models, risk models and time series prediction

models to help traders make the best decisions every day in order to maximize profits. Find the total assets in

the hands of traders as of 9/10/2021. To demonstrate the feasibility of our strategy, we use XGboost regression

model to fit the predicted data and the real data. After determining the sensitivity of the model and analyzing

the impact of market price fluctuations on our model, we communicated our decisions, models, and results to

traders in the form of memos. In summary, when you have $1000 on September 11, 2016, through our model

based on five years’ market data, you will have $184659.88 on September 10, 2021.

1 INTRODUCTION

Market traders often buy or sell their volatile assets -

bitcoin and gold - to maximize their returns. Each

purchase or sale of these two assets requires a

commission, and while gold is not open every day,

bitcoin can be bought and sold daily. The trader would

have a principal of $1,000 on November 9, 2016, and

would use that money to invest and trade gold and

bitcoin over a five-year period from November 9,

2016, to September 10, 2021, to maximize their

returns. We categorize this problem as a quantitative

economic investment strategy analysis problem

(Tang, 2021), quantitative investment is a type of

trading with quantitative statistical analysis tools at its

core and programmed trading (Guo, 2014; Hou,

2021). We use data from the past five days to predict

the future day's gold and bitcoin prices and build a

dynamic programming model to determine the

objective function (Gou, 2022). Specifically, our

work starts with data preprocessing of the trading

market amounts for the last five years of trading, and

since traders cannot determine the market stock

movements for the day after, we form our total model

Corresponding author

part by building three models: a bull and bear market

model, a risk forecasting model and a time series

forecasting model. It is used to forecast the economic

conditions of the market stocks on a 5-day basis. This

model is used to determine daily trading decisions

and to calculate total assets on hand on 10/9/21. Next

is to use our regression model using machine learning

XGboost to learn all the transaction amounts over the

five years and fit them to the data obtained from our

model to test the accuracy of the decision model.

Finally starting with the commission collection for

each trade, we determine the sensitivity of the trade

and analyze the impact of price fluctuations on us.

2 RELATED WORK

As we provide traders with a daily decision-making

solution, it is important to forecast the direction of the

market. It is difficult to predict the trend of the stock

market because of the many factors and complex

relationships that influence it. In this regard, we have

made progress in understanding the development of a

good prediction model by consulting the literature on

338

Zeng, J., Wang, Y. and Zheng, X.

The Best Decision-Making Scheme Based on Bitcoin and Gold Stock Market.

DOI: 10.5220/0012030400003620

In Proceedings of the 4th International Conference on Economic Management and Model Engineering (ICEMME 2022), pages 338-344

ISBN: 978-989-758-636-1

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

stock market prediction models. Based on the neural

network integration theory, we developed a stock

market forecasting model. The "Basic Data Model",

"Technical Indicator Model" and "Macro Analysis

Model" were developed and finally a simple average

was used to create an integrated system (Zhang,

2003). The corresponding BP algorithm network

forecasting model and ARCH (1) and GARCH (1,1)

forecasting models are also developed to forecast the

volatility of the closing price of the Shenzhen Stock

Index at each weekend using the actual data of the

Shenzhen stock market in China (Pang, 2006). In

addition, a stock-specific forecasting estimation

method is proposed based on a specific state space

form consisting of a combination of trend, smooth

autoregressive and nonlinear heteroscedastic random

variables (Wang, 2010). Drawing on the advantages

of spatial reconstruction techniques and visual data

analysis techniques for expressing the patterns and

characteristics of complex systems, graphical

methods for forecasting stock market trends based on

minute-by-minute stock market trading information

have been proposed (Hu, 2014). A stock-specific

forecasting estimation method is proposed based on a

specific state space form consisting of a combination

of trend, smooth autoregressive and nonlinear

heteroskedastic random variables (Zhu, 2006). The

new XGBoost-ARIMA hybrid forecasting model is

also suitable for forecasting about daily average data

(Liu, 2022).

In order to optimize various forecasting

models, the Realized GARCH model is a good

choice. In addition, the study ignores the impact of

the information contained in the exchange volume on

the stock price volatility, which may lead to biased

estimation of the model parameters. Stochastic

volatility models based on Poisson distribution can

not only effectively solve the problem of

underutilization of volume information by traditional

practices (Sun, 2019). The analysis and judgment of

the stock market is also crucial to the proposed

decision. Using parametric and semiparametric

methods, we judge and predict the bull and bear

market cycles of the stock market (Ye, 2021). In the

case that short selling is not allowed, a log-optimal

portfolio model with conditional value-at-risk as the

risk measure can be established based on the

conditional value-at-risk proposed by Rockefeller

(Moazeni, 2015). In order to optimize various

forecasting models, the Realized GARCH model is a

good choice. In addition, the study ignores the impact

of the information contained in the exchange volume

on the stock price volatility, which may lead to biased

estimation of the model parameters (Shi, 2019).

new multifractal volatility forecasting model was

constructed based on the HAR model, taking into

account the intra-day effects of high frequency stock

market data and the measurement error of realized

volatility to revise the existing multifractal volatility

indicator construction method. The models were

evaluated using the Diebold-Mariano test and the

"model confidence setting" test (Yuan, 2020).

3 EXPERIMENT

According to the daily price of gold and bitcoin in the

past five years, this method forecasts the price of gold

and bitcoin in a certain period of time, and finally

makes the most profitable measure according to the

assumption of bull and bear market. From the table,

we find that the prices of gold and bitcoin are

increasing in the general situation, and the prices

themselves are related to the prices of the previous

year; In the short term, it will be affected by the local

market policies and other uncertain factors and will

increase or decrease. According to the above two

characteristics, we choose to use AR autoregressive

model to simulate and forecast the amount of money

we need in the time period according to the known

data. First of all, we need to test the data to see if they

are stable, if not, then we need to make small changes

and debug them until the conditions are met. We use

the method called Daniel test, which is mainly around

the Spearman correlation coefficient. Spearman

correlation coefficient 𝑞



and statistical

variables 𝑇 The formula is as follows:

𝑞



=1−



(



)



(

𝑡−𝑅



)







(1)

𝑇=





√











(2)

After knowing the above two quantities, we can

start the test.

For a set of data, there will be the rank of the time

series (sort the data from small to large, and the rank

of each data is its serial number). We use MATLAB's

own algorithm to calculate the rank of the data.𝑅𝑡 ;

For significant levels𝛼From the time series (the

matrix of data in the file), calculate (t_0, 𝑅𝑡 ), t_0 =

1,2, …, the correlation coefficient of n. If | T | ≤ t_0,

then the sequence is stationary; Conversely, if | T | ≥

t_0, it is not stationary and 𝑞𝑠 > 0, showing an upward

trend. The specific operation is shown below:

clc, clear;

[a]=xlsread('BCHAIN-MKPRU','B3:B1827');

a=a';

Rt=tiedrank(a);

n=length(a); t=1:n;

The Best Decision-Making Scheme Based on Bitcoin and Gold Stock Market

339

Qs=1-6/n*(n^2-1)*sum((t-Rt).^2);

T=Qs*sqrt(n-2)/sqrt(1-Qs^2);

t_0=tinv(0.995,n-2);

To debug data, we take to do the first-order

difference operation, that is, the new sequence 𝑏



𝑎



−𝑎



, then you can easily get 𝑎



=𝑏



+𝑎



and here a𝑎



is the prediction value we calculated,

𝑏



is the new sequence we will 𝑎



for change to get,

that is, to meet the use of smooth time series

conditions of the sequence, here We subject the new

series to another Daniel's test.

b=diff(a);

[Tb,t_00]=spearman(b);

The Spearman function is the function that we

check whether the sequence is stationary. To put it

simply, we will summarize our previous work and see

them written into a new function.

function [T,t_0]=spearman(a)

a=a'; a=a(:); a=a';

Rt=tieddrank(a);

n=length(a); t=1:n;

Qs=1-6/n*(n^2-1)*sum((t-Rt).^2);

T=Qs*sqrt(n-2)/sqrt(1-Qs^2);

t_0=tinv(0.995,n-2);

The debugged data is the precondition of AR

autoregressive model. At this time, we put the

debugged data into the model.

According to the theory, we know that the formula

of AR autoregressive model is as follows:

𝑦



=𝑐



𝑦



+𝑐



𝑦



+⋯+𝑐



𝑦



+𝜀



(3)

It can be clearly seen that the regression equation

𝑦



is composed of the first p terms and the last 𝜀



(i.e.,

the random perturbation term with a mean of 0), and

the theory of this AR autoregressive model is that the

data of the t

year is expressed with the data of the

previous p years, and finally the AR(p) is formed, and

this p, we use the AIC criterion to seek, and finally

our p = 6, as follows.

m=ar(b,6,'1s');

bhat=predict(m,[b';1000:]);

ahat=[a(1),a+bhat'];

delat=abs((ahat(end-1)-a)./a);

There are several unknown representations above:

m is a vector composed of c_1, c_2, ..., will find him,

we can get to the expression of the function AR (p),

the completion of the expression will mean that we

can find the new sequence b, and then we will

calculate the ahat (the first few fitted values and the

n+1 predicted value, the first fitted value may have a

difference with the But the final delat is the algorithm

for calculating the relative error, where our relative

error is very small, probably only about 0.00008), and

the final result is our predicted value.

We need to judge whether it is the best way to

judge whether it is the best way to make a profit by

buying or selling gold in the bull market or in the bull

market every day. After making this judgment,

according to the price of the previous few days, judge

whether to trade on the same day. The specific

judgment methods of the model are as follows.

We assume that if the average amount of the

current cycle is higher than 20% of the previous

cycle, it is considered as a "bull market", and we will

sell it in full. Assuming that the average amount in the

current cycle is less than 80% of the previous cycle,

we consider it a "bear market" and we will buy gold

or bitcoin. Based on the average amount of each

period obtained from the previous data analysis,

Establish the judgment model of "bear market" and

"bull market" in each cycle.

NUM=xlsread('C:\Users\wyf\Documents\

WeChat Files\wxid_uknuh3yjrrhv22\

File\2022-

02\333.xlsx');

a=NUM'

a=round(a);

disp(a);

for ii=2:length(a)

if a(1,ii)>=1.05*a(1,ii-1)

disp('This was the bull market.')

elseif a(1,ii-1)*0.95>=a(1,ii)

disp('This was the bull market.')

else

continue

end

Second, we need to judge whether traders will

buy, hold or sell gold and bitcoin on a certain day.

Here, we simply use MATLAB to realize our

hypothesis. First of all, let's assume that a certain day

is an unknown day in the 21

century, then we input

the number into MATLAB and bring it into the code.

We can get the conclusion that a = 1\0\2.

Assuming that the date we input is September 20,

2017, we can clearly see that this day is the 368

day

from September 12, 2016, and the final conclusion is

a = 0 (buy). We use the data given in the title and

further optimize it to form a new table and bring it

into MATLAB. The specific operation code is shown

in the following:

clc, clear;

y=input('input years:');

m=input('input months:');

t=input('input dates:');

date=(y-2016)*360+(m-9)*30+(t-12);

[NUM]=xlsread('BCHAIN-MKPRU',1);

b=NUM(date-4:date);

ave=mean(v)

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

340

if b-ave>=0.2*ave

a=1;

elseif ave-b>=0.2*ave

a=0;

else

a=2;

end

4 RESULTS AND EVALUATION

In this section, we will show the results of our model.

The first is our data detection results. If the two Excel

data mentioned above are not stable, AR

autoregression is not possible. According to the

programming results, |T| ≥ t_0, and 𝑞



0.Therefore, we have verified our previous idea that

it is unstable, so our later step is to make the data

stable, and then run the AR autoregressive model.

Secondly, we put the above debugged data into the

programming system of AR model. In the middle, we

interspersed the verification that the debugged data is

stable. Taking bitcoin as an example, its result is t =

0.000000 million+42.696604080418390i, t_0 =

2.578528918212297, which obviously satisfies |T| ≤

t_0. Therefore, the new sequence B created is the

data sequence satisfying AR autoregressive model.

Finally, sequence B is brought into the MATLAB

programming function of AR autoregressive model.

The result is that the price of bitcoin on September

10, 2021 is $46161, while the price of gold is

$1796.5.

Finally, the most important result is the result of

solving the problem. While judging the bull and bear

market, we combine the results of each cycle with the

price of gold bitcoin to calculate the final profit we

get. Here we start with three assumptions about how

to allocate the $1000.

4.1 Suppose You Cost All $1000 for

Gold

Purchase price: $1324.6

Selling price (assuming last day sell): $1796.5

Ultimate Assets: $1356.3

4.2 Suppose You Cost All $1000 for

Bitcoin

Purchase price: $621.65

Selling price (assuming last day sell): $ 46161

Ultimate Assets: $74255.6

4.3 Suppose You Cost $500 for Gold

and $500 for Bitcoin

Bitcoin purchase price: $621.65

Bitcoin selling price (assuming last day): $46161

Gold buying price: $1324.6

Gold selling price (assuming last day): $1796.5

Ultimate Assets: $86734.7

We decided to start the investment plan in the

form of 50% investment, that is, half of the money to

buy gold, half of the money to buy bitcoin. In this

way, we can get the most cost, which is our best

trading plan.

We choose to put the average bitcoin price of the

previous five-day line and the average price of gold

on the 15th day line into MATLAB for analysis.

Using the code of "the price of the day and the

judgment of the previous cycle", we classify the

needs of buying, selling and holding, and then further

calculate and distribute the money in proportion. The

specific operation is as follows:

[NUM]=xlsread('liangbaihebing(1)',1,'C2:C1827'

);

NUM(isnan(NUM(:,1))==1)=[];

NUM=NUM';

A=A';

l=length(NUM);

i=1;

while(i<=1)

if NUM(i)-NUM(i+1)>=0.1*NUM(i)

a=1;i=i+1;

elseif NUM(i+1)-NUM(i)>=0.1*NUM(i+1)

a=0:i=i+1;

else

a=2;i=i+1;

end

A(i)=a;

end

According to the above method, the final result is:

from September 10, 2016 to September 10, 2021, the

final amount is $184659.88.

In the previous model part, we established AR

autoregressive model to predict the future stock price

trend of bitcoin and gold. Through the establishment

of risk model and bull bear market model, we got our

best plan. In order to prove the feasibility of the

strategy, it is necessary to test the fitting degree

between the time series prediction and the reality.

With the return of XGboost, we simulated the trend

of bitcoin and gold and compared it with the actual

situation.

Since the amount of data is too large (more than

1000 lines), and the results of each simulation will

change due to the debugging of simulation parameters

The Best Decision-Making Scheme Based on Bitcoin and Gold Stock Market

341

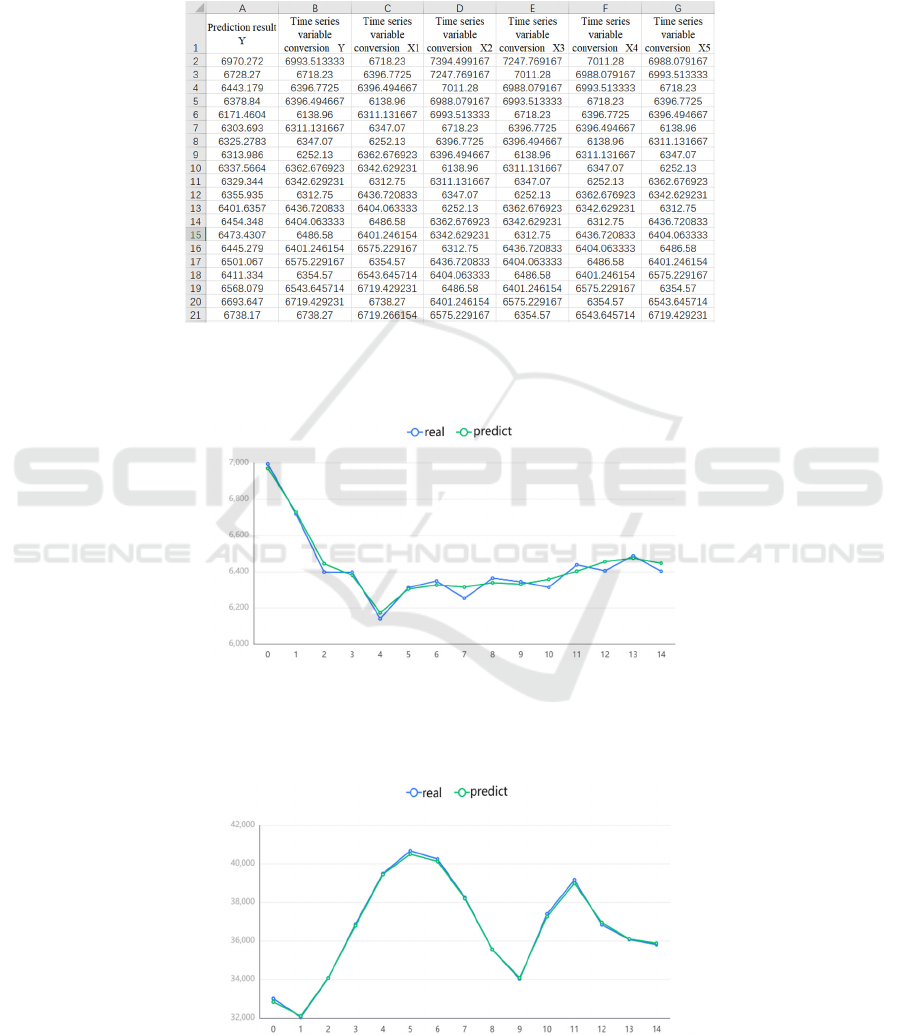
of XGboost regression, we consider the operation of

the program, that is, bitcoin is divided into two parts

by 5/31/19, that is, the first 993 days and the last 833

days. Gold is divided into the first 1000 days and the

last 266 days by 8/24/20.

The first analysis is the two parts of Bitcoin. First,

we can see the first 993 days, as shown in the Figure

below, which is the quantitative Y of time series

analysis and some data of X1, X2, X3, X4 and X5

(due to the large number of data, we can’t show them

one by one).

Figure 1: XGboost model testing data (partial).

Then the regression simulation of 993 before

Bitcoin is:

Figure 2: First 993 days for Bitcoin.

Using the same analysis method, we also get the

fit between the predicted value and the actual value of

the second half of Bitcoin:

Figure 3: The last 833 days for Bitcoin.

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

342

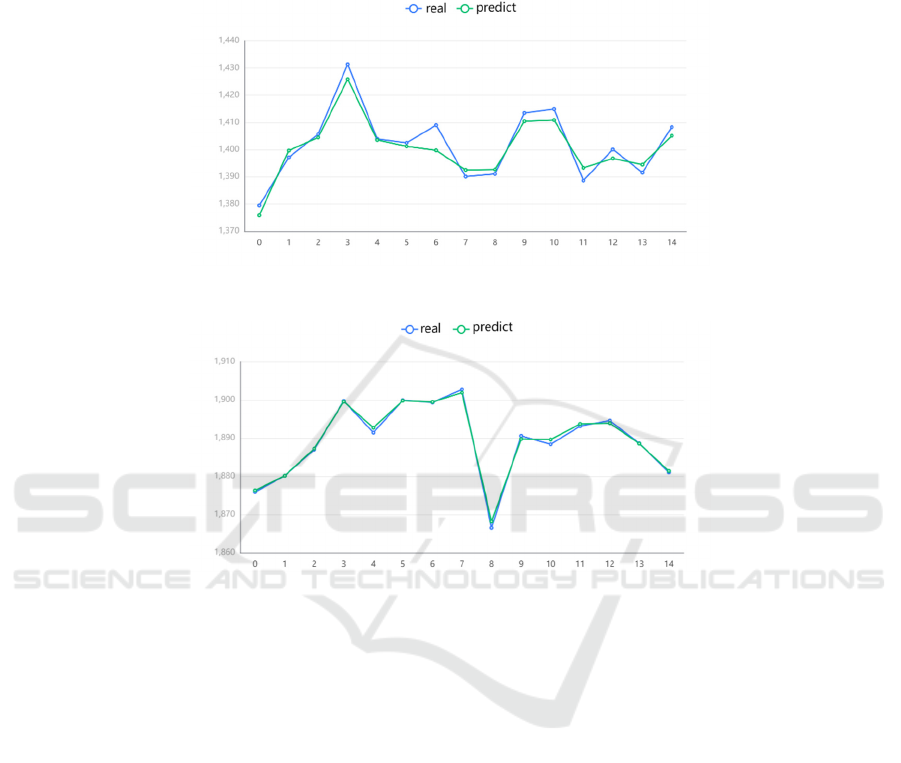
Through this fitting, we can clearly see that

although there is a slight deviation in the first half of

the forecast trend, it will not be very serious. The error

range is controlled around 100, which has no obvious

impact on our final results. The second half of the

simulation is perfect, which shows that our timing

forecast is very suitable for the market trend of

Bitcoin. The next step is the simulation of gold. The

simulation of gold is as Fig.3 and Fig.4.

Figure 4: First 993 days for gold.

Figure 5: The last 833 days for gold.

As can be seen from the two fitting curves in the

above chart, although there are some deviations in the

trend prediction of the first half of gold, the maximum

value is not more than 10. Combined with the

simulation of the second half, it can be said that our

simulation results are very impressive. To sum up, our

decision-making model is very precise and

reasonable.

5 DISCUSSION AND

CONCLUSION

Based on the data of gold and bitcoin trading markets

in the past five years, we have constructed the

judgment model, risk model and time series

prediction model of bull and bear markets to help

traders make the best decisions every day in five

years, so as to maximize profits. From September 10,

2016 to September 9, 2021, the total assets held by

traders increased from $1000 to $184659. At the same

time, XGboost regression model is used to fit the

predicted data and the real data, and the better fitting

results are obtained. The advantages of our decision-

making are obvious. The three models

comprehensively analyze the fluctuation of stock

market price. When verifying the fitting degree of

time series prediction, we choose XGboost to fit to

achieve better results. But unfortunately, the risk

indicators in the model still need to be considered

comprehensively. In a word, our decision-making

model provides a good reference for traders' decision-

making.

REFERENCES

Guo Xicai. The development and supervision of

quantitative investment[J]. Jiangxi Social Sciences, vol.

3, pp. 58-62, 2014.

Hou Xiaohui, Wang Bo. Quantitative investment based on

fundamental analysis: Research Review and

The Best Decision-Making Scheme Based on Bitcoin and Gold Stock Market

343

prospect[J]. Journal of Northeast Normal University,

vol. 3, pp. 124-131, 2021.

Hu Min, Sun Yufeng. Visual prediction of stock market

trend based on state evolution[J]. Journal of computer

aided design and graphics, vol. 02, pp. 302-313, 2014.

Liu Yongmin, Luo Haoyi, Xie Tieqiang. PM based on

XGboost Arima method_(2.5) research and application

of mass concentration prediction model[J]. Journal of

safety and environment, vol.3, pp. 1-13, 2022.

Moazeni S, Powell W B, Hajimiragha A H. Mean-

Conditional Value-at-Risk Optimal Energy Storage

Operation in the Presence of Transaction Costs[J].

IEEE Transactions on Power Systems, vol. 30(3), pp.

1222-1232, 2015.

Pang Sulin, Xu Jianmin, Li Rong. The empirical

comparison of BP algorithm and symmetric arch model

for Stock Market Volatility Prediction[J]. Control

theory and response, vol. 04, pp. 658-662, 2006.

Shi Yanlin, AI Chunrong. The intra week characteristics of

volatility in China’s stock market and its prediction

model[J]. System theory and practice, vol. 04, pp. 935-

945, 2019.

Sun Yanlin, Chen Shoudong, Liu Yang, Stock Price

Volatility Prediction Based on stock market and foreign

exchange volume information[J]. System theory and

practice, vol. 04, pp. 935-945, 2019.

Wang Wenbo, Fei Fusheng, Yi Xuming. Prediction of

China's stock market based on EMD and neural

network[J]. System theory and practice, vol. 06, pp.

1027-1033, 2010.

Xianwei Gou. Analysis of Quantitative Economic

Investment Strategy[J]. Scientific Journal of Intelligent

Systems Research, vol. 4(4), pp.34-54, 2022.

Ye Lu, Wang Zhizheng. Identification and prediction of bull

and bear market in Chinese stock market [J] Statistics

and decision making, vol. 37(20), pp. 161-165, 2021.

Yuan Ying, Chen Shoudong, Liu Xin. Research on

multifractal modeling and prediction of China’s stock

market [J]. System theory and practice, vol. 09, pp.

2269-2281, 2020.

Zihe Tang and Yanqi Cheng and Ziyao Wang. Quantified

Investment Strategies and Excess Returns: Stock Price

Forecasting Based on Machine Learning[J]. Academic

Journal of Computing & Information Science, vol. 4,

pp.24-34,2021.

Zhang Xiuyan, Xu Benben. Stock market forecasting model

based on neural network integrated system[J]. System

theory and practice, vol. 09, pp. 67-70, 2003.

Zhu Yu, Shi Zhongke. The spatial trend method of stock

market[M], vol. 05, 2006, pp. 567-570.

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

344