The Analytic Hierarchy Process Evaluation and Linear Regression

Model of the Global Equity

Xi Yang

, Lu Meng and Yunze Xue

College of Water Conservancy and Civil Engineering, Zhengzhou University, Zhengzhou, China

Keywords: Global Fair, Asteroid Mining, Analytic Hierarchy Process, Global Equity.

Abstract: This thesis establishes a model based on analytic hierarchy process (AHP) to measure global equity. First of

all, there are a large number of countries in the world, and in order to simplify the calculation, several

representative countries have been selected. By comparing the overall situation of each continent, such as

GDP, with the countries within the continent, the countries that can represent the continent are selected and

adjusted according to the specific circumstances such as the total number of countries. For example, China,

India and Japan are selected in Asia, the United States, Brazil and Argentina are selected in the Americas,

Australia is selected in Australia, and South Africa and Egypt are selected in Europe and The United Kingdom

and Germany are selected. The inputs and needs of these countries are then identified and the situation in each

country is sorted using analytic hierarchy and tools such as MATLAB, SAS, LINGO, etc. Finally, the order

of inputs and requirements is fitted and analyzed. It is then concluded that the global equity level is 60%. We

qualitatively address every step of asteroid mining and finally identify its possible impact on global equity.

Through analytic hierarchy, the global equity for asteroid mining is infrastructure, science and technology

research and development, beneficiary funding, and high-end technologies. Based on the above modeling data

analysis results, the main parameters and mechanisms of asteroid impact global equilibrium are determined.

Targeted policy recommendations are then made based on key impact parameters so that asteroid mining can

truly benefit all and promote global equity.

1 INTRODUCTION

Since 1967, when Outer Space Treaty (Si, 2018) was

signed by the vast majority of the world's nations, it

has guided and restricted the exploration and

development (Jiang, 2021) of outer space resources

for the sake of global equity (Qu, 2022). But is this

international commitment to fairness sustainable? In

other words, we need to develop a model for

measuring global fairness. In that case, our biggest

difficulty is to define global fairness, select

appropriate analysis methods to analyze and rate 224

countries around the world, and finally draw

conclusions through complex programming. Because

we only select the asteroid mining case for analysis

among many outer space resources, we need to

combine the actual asteroid mining cases in various

countries around the world with the global equity

measurement model we created for specific analysis,

and then conclude the specific factors that asteroid

mining affects global equity. The biggest difficulty

during this period is the difficulty of collecting a large

amount of data and programming, which requires us

to make concerted efforts to overcome. In addition,

we need to take into account global development

patterns (Wu, 2021) to develop policies that

encourage the asteroid mining sector to move towards

global equity. These are all the difficulties we may

meet before the study, and we need to work together

to solve them.

Fairness is an eternal topic in human society, and

the understanding of fairness (Wang, 2016; Li, 1995;

Cheng, 2014) has given us a preliminary

understanding of the definition of fairness through the

research of Wang Dongtong, Wang Yiduo, Li Riqin

and others. For the topic of global equity, there have

been many articles that have carried out in-depth

research, such as in global education, Li Hanying,

David Echolaina, Dai Weifen, Chen Jiawen (Li,

2012; David, 2018; Dai, 2018; Chen, 2017) and

others elaborated that the current global education

level is in a relatively unfair stage, but through the

implementation of a number of policies has achieved

good development. In terms of global response to

Yang, X., Meng, L. and Xue, Y.

The Analytic Hierarchy Process Evaluation and Linear Regression Model of the Global Equity.

DOI: 10.5220/0012030500003620

In Proceedings of the 4th International Conference on Economic Management and Model Engineering (ICEMME 2022), pages 345-354

ISBN: 978-989-758-636-1

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

345

climate issues, Sun yaohua, Chen Hua (Fairness and

Justice in the Global Governance System, 2014; Sun,

2013; Chen, 2012; Wang, 2011; Liu, 2012; He, 2009)

and others have discussed the issue of global equity

in environmental governance. And the issue of global

equity in economic globalization has also been

studied in depth by Liu Qijun, Udo Kreickemeier,

Douglas Nelson and others. (Liu, 2002; Liu, 2002;

Udo Kreickemeier, 2010; Udo Kreickemeier) With

the increasing progress of science and technology and

the development of the mining industry, human

beings have begun to study how to carry out mining

operations on asteroids in order to extract better, more

efficient and clean resources. (Zhang, 2020) For the

development of the industry and the technology of

mining, Jiang Kai, Chen Xiaolong (Jiang, 2022; Li,

2022; Chen, 2022; Qiang, 2022; Li, 2022) and others

have made plans and predictions for the technical

development and safety intelligence of mining pages.

Through the application of a variety of technologies,

humans have found various resources on multiple

asteroids. (Flying to an asteroid in search of treasure

in space, 2013; Chen, 2013; Zhu, 2012; Sun, 2013)

Due to the gap between countries in economy and

technology, the asteroid mining industry will

inevitably affect global equity issues. (Qu, 2022;

Zhang, 2015; Oriental Star, 2017; Asteroid

Exploration, 2017; Lv, 2021) In general, the

development of the asteroid mining industry has been

rewarded and developed accordingly through the

different inputs and efforts of each country, thus

further affecting the fair status quo of various

countries around the world.

In this paper, global fairness will first be defined,

then a hierarchical matrix of global countries be built

through the construction of Markov model, and then

GDP and other indicators for cluster analysis of 224

countries be selected in the world. Then, ratings will

be calculated based on multi-objective decision

making (MODM) with fuzzy evaluation. The

modeling analysis and collected data will be

calculated and analyzed by MATLAB, SAS, LINGO

and other programming software, and the preliminary

results will be obtained. After that, the development

of the asteroid mining industry will be simulated and

a reasonable development plan be come up. Based on

the previous model analysis, analytic hierarchy

Process (AHP) will be used to assign weights to

qualitatively analyze and ultimately be found out

what impact asteroid mining will have on global

equity. Based on the above results of modeling data

analysis, the main parameters and mechanisms of

asteroid impact global parity will be determined. We

will propose targeted policy recommendations based

on key impact parameters and make asteroid mining

truly beneficial to all and promote equitable

development globally. Finally, the strengths and

weaknesses of the model will be objectively

evaluated, and the exact direction for model

improvement and horizontal and vertical extension of

the model be provided.

2 MODEL CONSTRUCTION

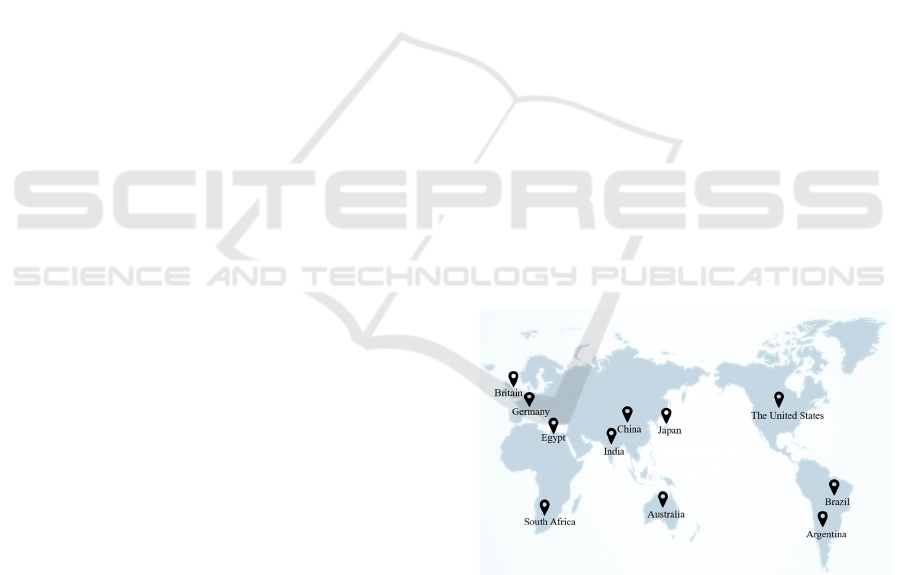
In order to identify some highly representative

countries on a global scale (which can cover all

national levels around the world), we select indicators

such as GDP, population, population density and so

on the basis of each continent, compare and fit the

countries within each continent with the overall

situation of the continent, select representative

countries within each continent according to the

results of the analysis, and draw preliminary

conclusions. We take the different realities that exist

on the six continents into account, such as the total

population, the total number of countries, etc., to

adjust the representative countries. In the end, 11

countries are selected. They are the United States in

North America, Brazil and Argentina in South

America, Australia in Australia, India, China and

Japan in Asia, South Africa and Egypt in Africa, and

the United Kingdom and Germany in Europe. (Due to

the length of this article, we will not repeat it here and

explain it graphically).

Figure 1: Map of the selected country.

2.1 The AHP Model of Global Equity

2.1.1 Model of Inputs by Countries

We selected per capita investment in the five aspects

of "infrastructure construction, education,

environmental protection, social equality and poverty

reduction" to form the second tier of the analytic

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

346

hierarchy method. We compared the five indicators in

the second tier to obtain the following pairwise

comparison matrix.













11/221/31/4

21111/2

1/2111/21/3

31211/2

42321

(1)

After solving for the maximum eigenvalue of A,

program solutions using MATLAB software, and

then we get the solution yields the maximum

eigenvalue λ

max

=5.2145 and normalized weight

vectors as following.

()

0.01750.2292 .0.01732163.00.5197 ，，，，

The weight of each criterion in the second tier is

determined in the same way by all countries of the

third tier. Set P

to the decision-making tier's pairwise

comparison matrixes in turn are W

, W













33331/343431/21

1/31111/511111/41/3

1/31111/571111/41/3

35551767624

1/4111/71/711111/41/3

1/3

1111/611111/41/3

1/41111/711111/41/3

1/31111/611111/41/3

24441/2444413

13331/433331/31

(2)

Solve for the maximum eigenvalue of A, program

solutions using MATLAB software, and then we get

the solution yields the maximum eigenvalue

max

=11.6600 and normalized weight vectors as

following.

ω=(0.0766,0.2439,0.0199,0.0155,0.0199,0.0255,

0.4263,0.0566,0.0193,0.0193.0.1904)

Later, the largest feature root and normalized

weight vector of W

, W

and W

pairwise

comparison matrix were found by the same method,

the consistency test was accepted, and all paired

comparison matrices passed the consistency test.

Furthermore, five normalized feature vectors Wi can

be used as a weighting of the third tier (national P

) to

the second tier of each data.

Table 1: Calculation Results of The Third Tier to The Second Tier.

1 2 3 4 5

0.0038 0.0256 0.1068 0.2790 0.6540

0.5197

0.2163

0.0173

0.2292

0.0175

0.2781 0.0645 0.1272 0.1048 0.1546

0.2275 0.0467 0.1088 0.1142 0.8400

0.0135 0.1624 -0.0079 0.1306 0.1200

0.0128 0.1723 -0.0394 0.0014 0.9874

0.0033 0.0538 0.0524 0.0815 -0.3331

0.1337 0.4291 0.3065 0.0972 0.1547

0.0049 0.0327 0.0025 0.0247 0.9436

0.0036 -0.0478 0.0051 0.0245 0.2110

0.1581 0.0110 0.0744 0.0633 0.6720

0.1606 0.0496 0.2635 0.0788 0.3640

11.2539 12.9060 11.3717 11.5112 12.9820

In summary, the above operation is equivalent to

multiplying a matrix composed of ω

by the weight

vector Φ

, thus obtaining the comprehensive weight

of the third tier to the first tier ω. It can be calculated

by calculation as following.

The Analytic Hierarchy Process Evaluation and Linear Regression Model of the Global Equity

347

ω=(0.0848,0.1874,0.1711,0.0740,0.0608,0.0271,

0.1926,0.0318,0.0009,0.1121,0.1232)

This represents the proportion of inputs in each

country in the selected data. From this, we order the

countries’ inputs down from P

(Japan) to P

(the

United States) to P

(Australia) to P

(Germany) to

(the United Kingdom) to P

(China) to P

(Brazil) to

(Argentina) to P

(India) to P

(South Africa) to

(Egypt). X

and Y

correspond to the countries in

this sequence. And the X

value is incremented from

1 to 11.

2.1.2 Model of Requites by Countries

Among the data from countries, we collected and

used five data, including "GDP, forest cover, safety

index, poverty rate, and number of PhDs per million

people", to estimate the international requites

countries received. By comparing the five items of

data in the second tier, we can get the pairwise

comparison matrix B.













12222/1

2/11223/1

2/12/1133/1

2/12/13/116/1

23361

(3)

Solve for the maximum eigenvalue of A, program

solutions using MATLAB software, and then we get

the solution yields the maximum eigenvalue

max

=5.1787 and normalized weight vectors as

following.

ω=(0.5682,0.0128,0.0558,0.0600,0.30321)

Using the same method, we can determine the

weight of each criterion in the second tier by all

countries in the third tier, then Q

, Q

can

be obtained as shown in Table 2.

Table 2: Calculation Results of The Third Tier to The Second Tier.

1 2 3 4 5

0.0766 0.0927 0.0156 0.0940 0.0779

0.5682

0.0128

0.0558

0.0600

0.3032

0.2439 0.2069 0.0112 0.1324 0.2432

0.0199 0.2669 0.3164 0.3483 0.1400

0.0155 0.0535 0.0112 -0.0131 0.1430

0.0199 0.0074 0.0163 0.0178 0.0500

0.0255 -0.0336 0.0089 0.0010 0.1360

0.4263 0.1170 0.0019 0.1155 0.0846

-0.0566 0.0181 0.0039 0.0088 0.1522

0.0193 0.0272 0.0879 0.0564 0.1113

0.0193 0.1220 0.0508 0.0576 0.0987

0.1904 0.1220 0.4759 0.1812 0.0354

11.6600 12.0307 11.7355 11.2727 11.6988

In summary, the above operation is equivalent to

multiplying a matrix composed of ω

by the weight

vector Φ

, thus obtaining the comprehensive weight

of the third tier to the first tier ξ

. It can be calculated

by calculation as following.

=(0.0748,0.2235,0.0957,0.0527,0.0285,0.0559,

0.2764,0.0150,0.0533,0.0487,0.1579)

This represents the proportion of requites in each

country in the selected data. From this, we order the

countries' inputs down from P

(Japan) to P

(the

United States) to P

(Germany) to P

(Australia) to

(China) to P

(India) to P

(Egypt) to P

(Brazil) to

(the United Kingdom) to P

(Argentina) to

(South Africa). At this point, it can be concluded

that the value of Y

is the ranking value of the

corresponding country in terms of requites.

2.1.3 Comparative Models of Inputs and

Requites to Countries

Through the above summary, we solve the values of

and Y

, and the conclusions are as follows:

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

348

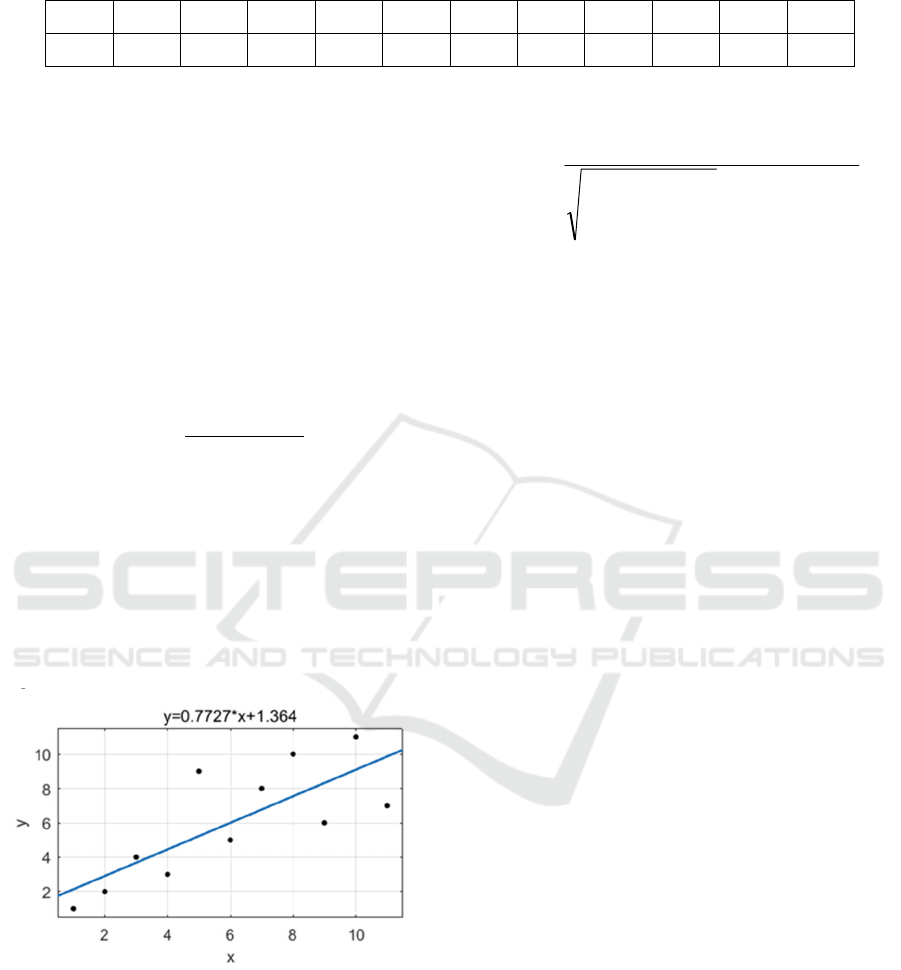
Table 3: Comparative Data on Inputs and Requites.

1 2 3 4 5 6 7 8 9 10 11

1 2 4 3 9 5 8 10 6 11 7

By comparing the input with the requite, a

conclusion can be drawn as to whether fairness is

achieved. We established a Cartesian coordinate

system for input X and requite Y, and mark the (X

) values in the figure. Then, the linear regression

(Qi, 2019) (LR) equation between the input X and

requite Y can be expressed as:

𝑦

𝑎

𝑥𝑏 (4)

Where the 𝑎 and b



are the coefficients of slope

and intercept, respectively. The coefficients of slope

𝑎 can be obtained based on the least square method as

following.

𝑎



∑























∑

















(5)

In addition, the intercept b



in the linear regression

(LR) equation can also be obtained based on the

average point (x, y) as following.

𝑏𝑦



𝑎

𝑥



(6)

After programming using the MATLAB software,

the line between the input X and requite Y from the

linear regression (LR) can be plotted as shown in

Figure 2.

Fig 2. The line of linear regression equation.

From the comparison of input and requite, it can

be seen that if the X and Y fitted correlation index is

1, then it is in an absolutely fair state, and if the fitted

correlation index is 0, then it is in an absolutely unfair

state. The degree of fit can be calculated from the

formula (7):













−













−





−

−−

ynyxnx

yxnyx

(7)

Then we can calculate "r" equals 0.5971. It can be

seen that the correlation coefficient of this regression

line fitting is at a moderate level. At this point, we can

measure that global equity is 60% fair.

2.2 A Model of the Impact of Asteroid

Mining on Global Equity

2.2.1 Impact on Inputs

In order to clarify the impact of each project on the

input, we take the infrastructure, scientific and

technological research and development, and

personnel training as the third tier of the analytic

hierarchy method, and take the specific data on the

input of various countries as the second tier. Compare

the items in the third tier in pairs to form a pairwise

comparison matrix C













12/15/1

213/1

531













12/12

215

2/15/11













114

113

4/13/11













12/15/1

213/1

531













122/1

2/113/1

231

(8)

We can calculate the weight vector as following.

(0.4512,0.3527,0.1920)

It is concluded that the impact of infrastructure

construction, scientific and technological research

and development, and personnel training on input are

ranked as infrastructure construction, scientific and

technological research and development, and

personnel training respectively. At this point, the

impact on the "Input" aspect is derived.

The Analytic Hierarchy Process Evaluation and Linear Regression Model of the Global Equity

349

2.2.2 Impact on Requites

The benefit funds, harvest resources, and high-end

technology are taken as the third tier of the analytic

hierarchy method, and the specific data on the

requites of each country is taken as the second tier.

Compare the items in the third tier in pairs to form a

pair comparison matrix D

１

＝













12/16/1

213/1

631

２

＝













12/12

214

2/14/11

３

＝













142

4/112/1

2/121

４

＝













125/1

2/113/1

531

５

＝













133

6/113/1

3/161

(9)

We can get the weight vector

(0.4122,0.2135,0.3742)

. So the ranking of the

impact on "Requite" is derived as benefit funds, high-

end technology, and harvest resources.

3 RESULTS AND DISCUSSIONS

3.1 The Results of Evaluation

According to the world's existing large-scale mineral

mining programs (Liu, 2020), large private

enterprises or state-owned enterprises are responsible

for mining, and under the supervision and

management of the government, resources are

rationally allocated and benefited from. However,

due to the particularity of asteroid mining, the huge

demand for funds, and the high requirements for

scientific research capabilities, management levels,

distribution schemes, etc., it is impossible for

countries or enterprises to mine alone.

Based on the above analysis, we have summarized

the following solutions: Cooperation among

governments to facilitate the participation of private

enterprises and international institutions, with

technical support provided by enterprises with strong

scientific research capabilities, and jointly funded by

private enterprises, national governments and

international cooperation agencies, in order to

facilitate the development of the asteroid mining

industry. In addition, after satisfying both a

reasonable and equitable distribution, the various

benefits of the minerals themselves and the minerals

on the asteroid should also be provided by providers

of funds and technologies in the asteroid mining

industry, so as to comply with the basic concept of

global equity.

So far, we have simulated the basic scenario of

asteroid mining. Based on previously established the

model to measure global equity, the following

conclusions can be drawn: Asteroid mining will affect

the investment of countries, such as increased

investment in infrastructure construction, increased

investment in education, etc., and it will also affect

the requites of countries, such as GDP growth, the

increase in the number of doctoral students per

million people. These changes will affect global

equity to some extent.

In summary, many countries are in a situation of

high investment and low return. Asteroid mining is a

high-input industry, and its benefits flow more to

higher-level countries, that is, it will affect the fitting

correlation coefficient of X

and Y

. Based on the

established model, countries' "Input" rankings will

remain, while "Requite" rankings will be disrupted,

that is, the global inequities will be added.

3.2 Suggestions and Recommendations

We've got the factors that affect global equity in

asteroid mining. The asteroid mining industry affects

the input situation of countries by influencing global

infrastructure construction and scientific and

technological research and development, and affects

the requite of countries by influencing global benefit

funds and high-end technology. In turn, it also

influences the state of global fairness. Based on the

above analysis, this paper gives the following

analysis suggestions:

 Policy Recommendation I: Countries around

the world should consciously abide by the laws and

regulations on the allocation of space resources. At

the same time, countries should monitor each other

and firmly oppose any violation of the concept of

"global equity".

 Policy Recommendation II: The United

Nations organization should judge the contribution of

each country to all humanity in the world, and

distribute the various benefits of space resources,

including minerals themselves, to each country fairly

(Li, 2013). At the same time, the United Nations

should uphold the concept of "Input" and "Requite"

synchronization to better maintain global equity.

 Policy Recommendation III: For those

countries that have made outstanding contributions to

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

350

the cause of space resource exploration, the United

Nations Organization should give them additional

rewards and use this to inspire people to move higher

and thus creating more wealth for mankind (Zhang,

2022).

 Policy Recommendation IV: In terms of

inputs, because capital inputs in infrastructure,

scientific and technological research and

development and other fields are more likely to affect

global equity, countries should join hands, cooperate

with the division of labor, and try to balance the

capital inputs in each field.

 Policy Recommendation V: In terms of

requites, because the benefits of benefit funds, high-

end science and technology and other fields are more

likely to affect global equity, all countries should

strictly abide by the distribution of benefits of the

United Nations organization and resolutely oppose

hegemonism (Cao, 2019).

 Policy Recommendation VI: The premise for

the benefit of all mankind is not to endanger the

planet on which humanity depends and to maintain

respect and equal treatment for everyone in the world,

so that the rich mineral resources obtained by

asteroids must not produce weapons of great mass

destruction or products with extremely high-risk

factors without the permission of the United Nations.

On the contrary, these mineral resources should be

rationally utilized to maximize the progress of human

society and promote scientific development.

 Policy Recommendation VII: The abundant

scarce mineral resources of the earth on the asteroid

should be rationally exploited and distributed. We

must not exploit the scarce and expensive resources

on the earth on a large scale on the asteroid, such as

diamonds, gold, etc., thus causing a financial crisis

(Lian, 2021) on the earth and undermining the peace

of the earth.

3.3 Error Analysis

In the model of global equity, for the factors affecting

the input and requite of countries around the world,

we just selected five evaluation indicators for analysis

by hierarchical analysis, so increasing the number of

evaluation indicators will make the calculation results

of our model more accurate. In addition, we just

collect relevant data for one year, but due to the

different rates of development across countries

around the world, the data is changing rapidly, and if

more data can be collected and analyzed, the accuracy

of the model will be improved. In the model of the

impact of asteroid mining on global equity, the

influencing factors of the asteroid mining industry on

global equity are just selected in six aspects, and if the

data can be specific, the influencing factors can be

more accurately reflected.

Since the model for measuring global fairness

constructed by this team is a measure of "global

fairness", so all the data have been determined and the

sensitivity cannot be directly obtained. The value of a

single indicator can only be changed under the

condition that the data of other indicators is

unchanged, so as to obtain the rate of change of the

model results. Or we can use the values of previous

years, compare them with this result, and evaluate the

sensitivity in the light of the global fairness of the

actual situation.

3.4 Model Evaluation

3.4.1 Advantages

a. This model has reasonable conjectures and

assumptions about the evaluation and prediction of

the problem.

b. This model adopts a scientific and reasonable

method in the selection of representative countries,

which greatly improves the reliability of data and

results.

c. We use analytic hierarchy in the model

solution many times, which greatly improved the

effectiveness, reliability and feasibility of decision-

making.

d. This model uses the method of linear

regression to innovatively solve the problem of

comparison and analysis between two sets of data.

e. We use a variety of mathematical and drawing

software such as MATLAB, SPSS and EXCEL to

create models and write articles to make the results

obtained by the model.

3.4.2 Disadvantages

a. Due to the particularity of the analytic hierarchy

method, from the establishment of the hierarchical

model to the giving of the pairwise comparison

matrix, it is easy to be affected by the subjective

feelings of the operator, resulting in different people

having different results, so the results obtained by this

method cannot be accepted by all readers.

b. When measuring global equity, the model

built by our team uses ranking to measure the selected

metrics, not in terms of more specific weights, and

has reduced in accuracy.

The Analytic Hierarchy Process Evaluation and Linear Regression Model of the Global Equity

351

3.5 Model Extension

The model for measuring global equity is extensive,

and if specific data can be collected, it can be used to

obtain the state of global fairness at any time. And

through this model, we can understand the many

factors affecting global equity and their proportions,

and adjust various factors to achieve a more equitable

state. For example, the development of the asteroid

mining industry can be adjusted through this model to

achieve better results. This model is popular, through

simple data analysis, using simple analytic hierarchy

to convert data into rankings, simplifying the

difficulty of data operation, making the model easy to

understand and disseminate. This model can not only

be used for the judgment and measurement of

fairness, but also can be used for other practical

problems that need to be compared, which has strong

practical significance.

3.6 Model Improvements

We should expand the model it has built to cover a

wider range of areas. For example, we rely on only a

few aspects of the data to represent the whole, easy to

lead to the error of partial generalization. Therefore,

the model should be more careful in selecting the

influencing factors of "Input" and "Requite", and

choose more convincing indicators that can make the

model more accurate and understandable. In addition,

this model should also be how much improvement in

data collection and processing, because the model in

the process of data collection, by many aspects of the

inhibition, resulting in the model used data is not

enough to summarize all aspects.

Another limitation of this model is that multiple

sets of data that can be calculated and draw

conclusions need to come from the same year, so it is

not easy and convenient to process data from multiple

years. Therefore, the model needs to be further

refined in this area to enable it to calculate whether

two, three or more years at the same time meet the

global fairness standard.

4 CONCLUSION

In conclusion, we construct the Markov model,

establish the hierarchical matrix method of global

countries, select GDP and other indicators for cluster

analysis of 224 countries in the world, then use multi-

objective decisions based on fuzzy evaluation

(MODM) to calculate the score, and finally use

MATLAB, SAS, LINGO and other programming

tools to analyze the data. To conclude that only 60%

of global equity is fair. In the case of asteroid mining,

which is a high-input industry, the benefits flow more

to the top countries. Based on the established model,

the "Input" ranking of countries will remain the same,

while the "Return" ranking of countries will be

disrupted, that is, global inequality will increase.

Then, we plan how the development of asteroid

mining will correspond to the change of input and

return of each country, then use the analytic hierarchy

process to express and rank the factors of weight

change, and get the specific factors that affect the

global rights and interests of asteroid mining. The

analytic hierarchy process is used to represent the

weight of changing factors, and the specific factors

that affect the global equity of asteroid mining are

infrastructure, scientific research and development,

beneficiary funds and high-end technology. Based on

the above modeling data analysis results, the main

parameters and mechanism of asteroid impact on

global equality are determined. We make targeted

policy recommendations based on key impact

parameters to make asteroid mining truly beneficial

to all and promote global equity.

We can extend the model we will build in the

future to cover a wider range of domains. We should

be more cautious in choosing the influencing factors

of "Input" and "Return", and choose more convincing

indicators to make the model more accurate and

understandable. In addition, the model should also be

improved in data collection and processing, so it

needs to be further refined in this area to be able to

calculate whether two, three or more years at the same

time meet global equity standards.

ACKNOWLEDGEMENTS

First of all, we would like to thank MathWorks,

because the MATLAB programming software

developed by the company is indispensable for the

topic selection in the early stage, writing in the middle

stage and concluding in the late stage. In addition, we

would like to thank CNKI for providing strong

support for the references and massive data search we

need. Secondly, we also want to thank our team of

three people for their strong cooperation and

assistance. In terms of mid-term writing, YANG Xi

was responsible for mathematical modeling and made

excellent modeling with the model. XUE Yunze was

responsible for programming analysis. And then

MENG Lu was responsible for typesetting. The

excellent completion of the paper is not possible

without every one of us, so we would like to thank

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

352

everyone for their best efforts. Finally, we would like

to thank the teachers who take the time out of their

busy schedules to participate in the evaluation and

evaluation of this paper, and express our most

heartfelt thanks to all of them!

REFERENCES

Asteroid Exploration. Let China Move from a Space Power

to a Great Power[J]. Infrared, 2017, 38(08):50.

CAO Yingwang Mao Zedong's Exposition of TheOry of

Opposing Hegemonist Thought [J]. Mao Zedong

Research, 2019(05): 55-65.

CHENG Cheng. What is fairness? [J]. Textile Report,

2014(10): 37-38.

CHEN Hua, ZHU Dajian, ZOU Li. Spatial study of carbon

dioxide emissions from major countries around the

world: based on ecology-equity-efficiency models[J].

Journal of Northeastern University (Social Science

Edition), 2012,14(02):119-124.

CHEN Xiaolong. Analysis of Mining Technology and

Construction Safety Management in Coal Mine

Engineering[J]. Energy and Energy Conservation,

2022(06):55-56+59.

CHEN Ke. Go to space to "pan for gold"[J]. Environment,

2013(04):77-79.

CHEN Jiawen. Is there really progress in educational equity

on a global scale? People's Education, 2017(10): 9.

David Echolena, Zhang Dan. Quality and Equity:

UNESCO's Goals and Pathways for Global Education

Governance: A Dialogue between David Echolaina and

Dan Zhang [J]. Journal of East China Normal

University (Educational Science Edition),

2018,36(02):139-147+159.

DAI Weifen, NIU Ying, YAN Beibei. A Study on the

Development Trend of Teacher Education under the

Goal of Educational Excellence and Equity: A Review

Based on the 3rd Global Teacher Education Summit[J].

Teacher Education Research, 2018,30(03):103-107.

Fairness and Justice in the Global Governance System[J].

National Governance, 2014(02):1.

Flying to an asteroid in search of treasure in space[J].

Heilongjiang Science, 2013(11):15.

HE Jiankun, TENG Fei, LIU Bin. Actively promote the

global response to climate change under the principle of

equity[J]. Journal of Tsinghua University (Philosophy

and Social Sciences Edition), 2009, 24(06): 47-53+158.

JIANG Kai On the prospect of the development of outer

space resources[J]. Economist, 2021(03): 81-82.

JIANG Kai. Research on mine mining technology safety

management methods[J]. Xinjiang Nonferrous

Metals,2022,45(04):59-60+62.

LI Yueqin, LI Fengsheng. On the Relationship between

Fairness and Efficiency: From different definitions of

fairness[J]. Quest, 1995(02): 39-41.

LI Hanying. Global Education Reform: Equity, Quality and

Development: A Review of the Fourth World

Comparative Education Forum[J]. Comparative

Education Research,2012,34(01):87-90.

LIU Mingming. The equitable distribution of carbon

emission space in the context of global climate change:

taking the basic political position of the Durban

Conference on Equitable Access to Sustainable

Development as an analytical approach[J]. Law

Review, 2012, 30(04): 78-84.

LIU Qijun. Economic Globalization, Efficiency and

Equity[J]. Social Sciences, 2002(06):30-34.

LIU Qijun. An Analysis of the Relationship between

Efficiency and Fairness in the Process of Economic

Globalization[J]. Journal of Social Sciences of Jilin

University, 2002(04):85-90.

LI Haijun, LIANG Wei, PU Chenggang. Construction and

Discussion on the Construction and Discussion of

Innovative Model for Intelligent Mining Talent

Training in the New Era[J]. Guizhou Agricultural

Mechanization, 2022(02):43-45.

LI Haijun, LIANG Wei, PU Chenggang. Construction and

Discussion on the Construction and Discussion of

Innovative Model for Intelligent Mining Talent

Training in the New Era[J]. Guizhou Agricultural

Mechanization, 2022(02):43-45.

LV Xiaoying, Li Xiande. Markov zone system conversion

vector autoregressive model analysis of the

interrelationship between economic, social and political

globalization[J]. Gansu Social Sciences, 2021(03): 205-

212.

LIU Zhiyuan, Zhou Huimin. Study on the selection of

large-scale gold mining scheme based on economic

comparison method[J]. China Metal Bulletin,

2020(05): 289-290.

LI Juan. A Brief Analysis of Marxist Theory of Fair

Distribution[J]. Enterprise Herald, 2013(01): 259-260.

LIAN Fei. A Study on The Early Warning of Financial

Crisis in Emerging Market Countries: An Empirical

Test Based on the Logit Model[J]. Journal of

Technoeconomics and Management, 2021(07): 67-71.

Oriental Star. Asteroids and their detection and

development[J]. International Space, 2017(07):48-55.

QIANG Kejun. Research on Mining Technology and

Construction Safety in Mining Engineering[J].

Metallurgical Management, 2022(09):94-96.

QU Xiangjie, ZHANG Xinxin, TIAN Xue. Global equity

model of asteroid mining rights allocation based on

demand-level analysis method[J]. Equipment

Manufacturing Technology, 2022(01): 82-85.

QU Xiangjie, ZHANG Xinxin, TIAN Xue. Global equity

model of demand-level analysis method and asteroid

mining right allocation[J]. Equipment Manufacturing

Technology, 2022(01):82-85.

QI Long. Algorithm research on solving linear regression

equations using least squares[J]. Computer Products

and Circulation, 2019(09): 230.

SI Wenwen. Outer Space Treaty[J]. China Investment,

2018(17): 94-95.

SUN Yaohua, ZHONG Weizhou. Global Climate Change,

Greenhouse Gas Emission Reduction and Fair and Just

Development: An Analysis Based on the Perspective of

The Analytic Hierarchy Process Evaluation and Linear Regression Model of the Global Equity

353

Economics[J]. Comparison of Economic and Social

Systems, 2013(05):80-90.

SUN Ying. Go to the asteroid to mine? [J]. China

Mechanical and Electrical Industry, 2013(04):11.

Udo Kreickemeier, Douglas Nelson, Liao Jia. Fair Wages,

Unemployment and Technological Change in the

Global Economy[J]. Economic Data Translation Series,

2010(04):50-65.

Udo Kreickemeier, Douglas Nelson, Liao Jia Fair wages,

unemployment and technological change in the global

economy[J]. Economic Data Translation Series,

2010(04): 50-65.

WU Fei. A comparative study on the development model of

scientific and technological innovation in major cities

around the world[J]. Statistical Science and Practice,

2021(05): 23-26.

WANG Dongdong. The Difficulty of Defining

"Fairness"[J]. Communist Party Member (Hebei),

2016(17): 13-1033.

WANG Yiduo. On the Operability Definition of the

Concept of Fairness[J]. Journal of Southwest

University for Nationalities (Humanities and Social

Sciences Edition), 2005(10):198-202.

WANG Yi, HUANG Yu. Equity and Uncertainty: Key

Issues in Global Carbon Emission Allocation[J].

Chinese Resources and Environment,

2011,21(S2):271-275.

ZHANG Kefei, LI Huaizhan, WANG Yunjia, DENG

Kazhong, LI Changgui, WANG Qianxin, LIU Xinhua,

XIE Yaoshe, DUAN Yabo, YANG Yang. Development

status, opportunities and challenges of space mining[J].

Journal of China University of Mining and

Technology,2020,49(06):1025-1034.

ZHU Enyong, SUN Guojiang, GUO Linli. Analysis of

Asteroid Surface Sampling Technology[J]. China

Aerospace, 2012(02):32-35.

ZHANG Zhenjun. The US Congress has accelerated a new

round of commercial space legislation-the ownership of

resources obtained by asteroid mining has aroused

widespread concern[J]. China Aerospace, 2015(06):8-

10.

ZHANG Qiaoqi. Discussion on the application of incentive

mechanism in enterprise human resource

management[J]. Enterprise Reform and Management,

2022(11): 67-68.

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

354