Performance of the Delta-Hedging Strategies Based on the Heston

Model and the Black Scholes Model on Meta Platforms

Yehong Li

School of Materials Science and Engineering, South China University of Technology,

Panyu District, Guangdong Province, China

Keywords: Heston Model, Black Scholes Model, Delta-Hedging.

Abstract: This paper researches the performance of the Delta-Hedging strategies and compares the different results

between the Black Scholes (BSM) model and the Heston model. In this study, parameters in two models are

calibrated separately by utilizing data on ten options on the stock of Meta Platforms. Then, after the two

models have been built, the price of the options and options’ delta values can be calculated. The delta hedging

portfolios are composed of one share of a call option and delta shares of the underlying stock. Finally, the

results of different strategies are compared. The sum of squared errors (SSE) of the BSM model is higher than

the SSE of the Heston model. It means that the Heston model prices the options more precisely than the Black

Scholes model. In addition, both two models can transfer the risk of fluctuating prices by implementing delta-

hedging strategies. This paper is helpful for investors to build their portfolios by using different models in

option pricing.

1 INTRODUCTION

Risk management is a significant topic of companies’

investment. Many companies utilize derivatives

instruments to transfer the risks and fix the profit they

could make. For the commodity suppliers,

implementing hedging strategies can avoid the risk of

fluctuating prices, and then the suppliers produce and

sell their products for making a relatively fixed profit.

Hedging strategy is also a popular way in the field of

investment. Investors can compose a portfolio by

purchasing a set of stocks and shorting index futures

to gain excess profits. When the hedging strategies are

implemented, using different models to price the

options may have different results. Fischer Black

derived a theoretical formula to price the options in

1973, and this Black-Scholes model has become one

of the most important models in option pricing. In the

BSM model, the volatility is assumed to be a constant

number, but the volatility in the real options market is

arbitrary (Black, 1973). Then, stochastic volatility

models were researched. Heston built up a stochastic

volatility model and derived a formula for calculating

a call option price. Since then, option pricing and risk

hedging become interesting topics in the financial

field (Heston, 1993).

To illustrate, Xiong used three delta hedging

strategies on Shanghai Stock Exchange 50 ETF and its

options, and they proved that three strategies can

significantly reduce investment losses (Xiong, 2017).

And Jerbi, Y used neural networks (NNs) to model a

European call option price and found that the NNs

method performed fairly well in option pricing (Jerbi,

2020). Similarly, JAG Cervera used artificial neural

networks to calibrate a call option price efficiently

(Cervera, 2019). Furthermore, D Lamberton

researched some properties of the American option

price and extended some results in the BS model to the

Heston model (Lamberton, 2019). Euch, O. E.

composed the portfolios by the forward variance curve

and the asset, which is theoretically perfect hedging

(Euch, 2018). In addition, L Goudenège utilized the

Heston model and the BSM model in valuing

Guaranteed Minimum Withdrawal Benefit and

presented the numerical results (Goudenège, 2019).

With the rapid development of the metaverse, the

stock of Meta Platforms has caused many investors’

concerns, since Meta Platforms is one of the biggest

companies in the field of the metaverse. However, the

performance of pricing options on the Meta Platforms’

stock is rarely discussed. Therefore, this paper focuses

on this matter.

366

Li, Y.

Performance of the Delta-Hedging Strategies Based on the Heston Model and the Black Scholes Model on Meta Platforms.

DOI: 10.5220/0012033200003620

In Proceedings of the 4th International Conference on Economic Management and Model Engineer ing (ICEMME 2022), pages 366-371

ISBN: 978-989-758-636-1

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

This paper is structured as follows: Section 2

shows the data and methods. Section 3 shows the

results of delta-hedging strategies in different models,

and also discusses the results. Section 4 concludes this

paper.

2 DATA AND METHODS

2.1 Data

The data is all from Yahoo Finance

(https://finance.yahoo.com). Meta Platforms’ stock is

chosen as the underlying stock in this paper since its’

options have a huge trading volume, so enough trading

data can be used to calibrate the parameters. The Data

of the underlying stock is collected from June 8th,

2022 to July 11th, 2022. The data of the options are

collected from June 24th, 2022 to July 11th, 2022. In

the BSM model, these data are used for calibrating

implied volatility for the underlying stocks. In the

Heston model, these data are used for calibrating three

parameters. Then, the option prices and delta values

can be calculated by using the two models. Finally,

two delta hedging strategies are constructed for a call

option of Meta Platforms’ stock from June. 27th,

2022, to July. 11th, 2022.

Table 1: The 10 options of the meta platforms

Call options chosen for calibration

META

22072

2C001

70000

META

22072

2C001

75000

META

22072

2C001

80000

META

22072

2C001

85000

META

220722

C0019

0000

Put options chosen for calibration

META

22072

2P001

65000

META

22072

2P001

55000

META

22072

2P001

50000

META

22072

2P001

45000

META

220722

P0014

0000

Table 2: The option of the Meta Platforms’ stock for

hedging.

Call option selected for hedging

Meta Platforms META220722C00165000

In detail, the options contracts that are collected to

calibrate parameters in different models for Meta

Platforms’ stock are shown in the table Ⅰ. And the

contract of the American call option selected for Meta

Platforms for delta hedging is shown in the table Ⅱ.

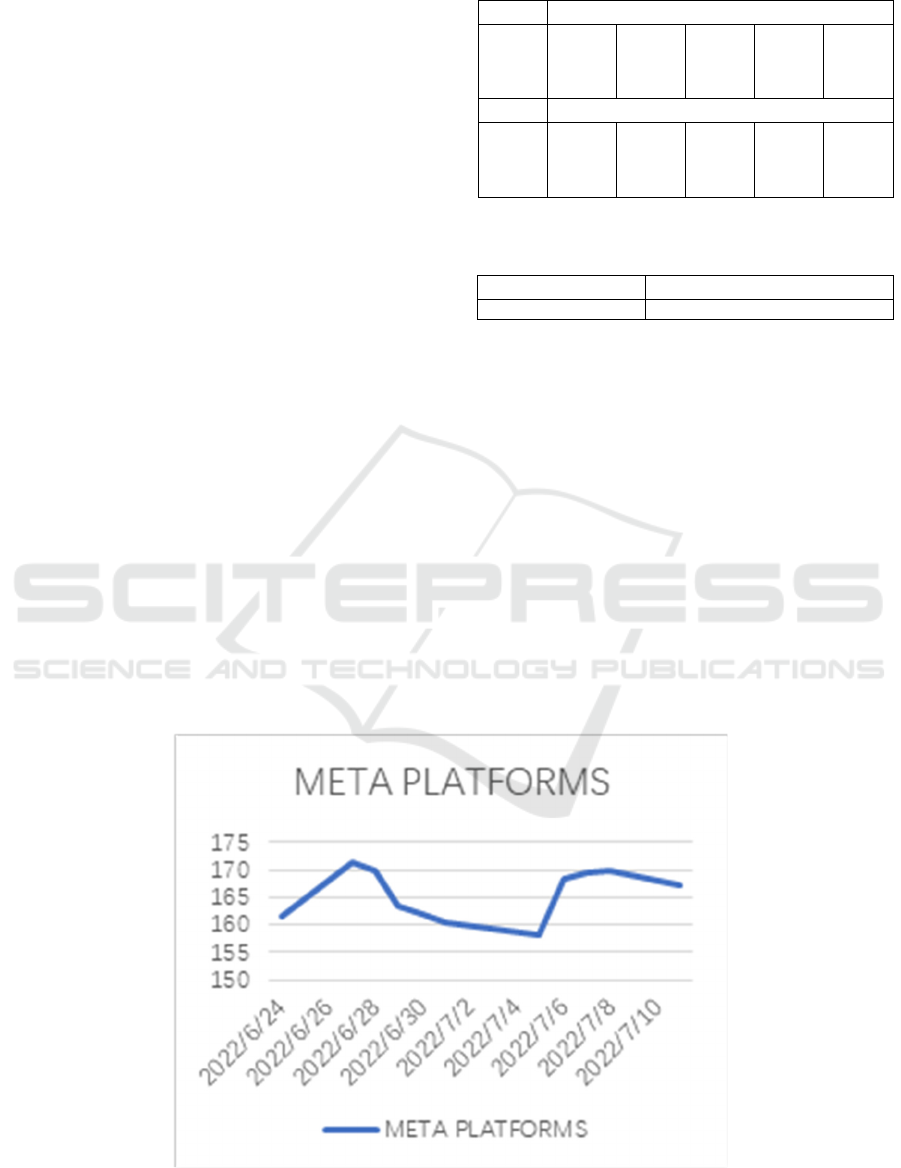
Also, the stock price trend for Meta Platforms is

shown in the Figure 1.

As shown above, the stock price of Meta Platforms

has been volatile from June 24th, 2022, to July 11th,

2022. In detail, Meta Platforms’ stock price

experienced a slip from June 27th, 2022, to July 5th,

2022, but it bounced back to the previous range on

July 8th.

The descriptive statistics of the rate of return of

Meta Platforms’ stock from June 24th, 2022, to July

11th, 2022, are shown below. As can be seen, Meta

Platforms’ stock has a large size range.

Figure 1: The price trend of Meta.

Performance of the Delta-Hedging Strategies Based on the Heston Model and the Black Scholes Model on Meta Platforms

367

Table 3: Descriptive Statistics.

Mean Median Variance Max Mini

value 0.007 -0.008 0.001 0.064 -0.037

2.2 Methods

In this study, two models are used for options pricing.

There are three steps in researching this project. The

first step is to calibrate the parameters in two models.

For the BSM model, Meta Platforms’ volatility is

calibrated by utilizing the open price of Meta

Platforms’ stock and the open price of ten options on

the underlying stock. For the Heston model, three

parameters are calibrated. Secondly, after the

parameters in models are calculated, the theoretical

price of call options and options’ delta values can be

calibrated in both models separately. Finally, two

delta hedging strategies are composed of one share of

a call option on Meta Platforms’ stock and delta shares

of the underlying stock. In comparison, one trading

strategy without hedging is also composed. The results

are shown and discussed in Section 3.

Some assumptions are proposed as follows: 1. The

dividend rate of underlying stock D=0; 2. The options

are American options, but they are treated as European

Options. Therefore, the options theoretical price can

be calibrated by the formula in the Heston model and

the BS formula; 3. In the Heston model, ρ equals 0,

which is the correlation between two Brownian

Motions.

In the BSM model, the stock price is described by

a geometric Brownian motion, which is shown in the

formula (1), where σ stands for the implied volatility,

stands for a Brownian motion. Furthermore, the

call and put options prices are calibrated by the Black-

Scholes formula (2) and (3), where N(d

) stands for

the normal distribution of d

. d

and d

can be

calculated by the formula (4) and formula (5) (Black,

1973), where T-t is the time to maturity, S

is the open

price of the stock at the time t, K is the strike price of

the option, and r is the interest rate, which is assumed

to be 3.13% in these models since the USA ten-years

Treasury bond yield on June 24th, 2022, equals to

3.13%.

𝑑𝑆



=𝜇𝑆



𝑑𝑡 + 𝜎𝑆



𝑑𝑊



(1)

C(t,S) = S



N(d



)−

()

N(d



)

(2)

(

t,S

)

= −S



(

−d



)



(





)

(

−d



)

(3)



log(





) + (r + 0.5σ



)(T − t)

√

T−t

(4)



log(





)+(r−0.5σ



)(T − t)

√

T−t



−σ

√

T−t

(5)

In the Heston model, the stock price is also

described by a geometric Brownian motion, but the

volatility is modelled by the Cox-Ingersoll-Ross (CIR)

process (Heston, 1993). The volatility can be

described by the formula (6) (Heston, 1993).

𝑑𝑉



=𝜅

(

𝜃−𝑉



)

𝑑



+ 𝜎



𝑉



𝑑𝑍



∗

(6)

Where 𝑍



∗

is another Brownian motion, and 𝜌 is

the correlation between 𝑍



∗

and W



, which is assumed

to be 0 in this model. Kappa 𝜅, theta 𝜃, and sigma 𝜎

are three parameters that need to be calibrated. Some

different methods are used for calculating the option

price by constructing different characteristic function.

One of the methods is shown in the formula below.

Because the correlation is assumed to be 0, the

characteristic function is given by formula (7)

(Simonsy):

𝜙

(

𝑢,𝑡

)

=𝐸[exp

(

𝑖𝑢log

(

𝑆



𝑆



,𝜎





]

=exp (𝑖𝑢(𝑙𝑜𝑔𝑆



+𝑟𝑡) ×exp (𝜂𝜅𝜃



(

𝜅−𝑑

)

𝑡

−2log

1−𝑔𝑒



1−𝑔

)

×exp(𝜎





𝜃



(

𝜅−𝑑

)

1−𝑒



1−

𝑔

𝑒



)

(7)

Where

𝑑=𝜅



−𝜃



(

−𝑖𝑢 − 𝑢



)

.

(8)

𝑔=

𝜅−𝑑

𝜅

𝑑

(9)

Carr, P utilized the fast Fourier transform in option

valuation. Referring to the method mentioned above,

a European call option price is calculated by the

formula (10) as below (Hunter, 2000):

𝐶



=𝑆



−



𝑆



𝐾𝑒



𝜋

𝑅𝑒[ exp

(

𝑖𝑢𝐾

)

∅



(𝑢





−

𝑖

)

𝑢



𝑑𝑢]

(10)

After the option prices are calculated, the sum of

squared errors is calculated for options on June 24th,

2022, by using the formula (11) below.

𝑆𝑆𝐸= 

(𝑃

𝑖

(

𝑎

)

−𝑃

𝑖

𝑚

)

𝑃

𝑖

𝑚

𝑀

𝑖

(11)

Where 𝑃



(

𝑎

)

represents the theoretical option

price in the BSM model or in the Heston model, 𝑃





represents options’ market price, and M is the number

of options, which equals to 10 in these models. In the

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

368

Black-Scholes model, the SSE is minimized to

calibrate the implied volatility. In the Heston model,

the calibration of the SSE is different. Since the

volatility is modelled by the CIR process, the SSE is

minimized to calibrate three parameters, which are

kappa 𝜅, theta 𝜃 and sigma 𝜎.

The data of the stock price from June 8th, 2022, to

June 23th, 2022 is utilized to calculate the daily yields

of the stock. Then the initial volatility of the

underlying stock v

can be estimated, which is

assumed to be the standard deviation of the daily

yields of the stock. v

equals to 0.2161 after

calibration. After the calibration of the parameters in

different models. Two delta hedging strategies are

composed by one share of a call option on Meta

Platforms’ stock and delta shares of the underlying

stock. Firstly, the stock price data from June 24th,

2022, to July 11th, 2022, and also the market price of

the option contracts chosen are collected. Secondly,

the theoretical prices of the call option can be

calculated on a daily basis by using the BS model and

the Heston model. Thirdly, the hedging portfolios are

composed by one unit of the call option, and delta

shares of the stocks. The delta value equals to N(d

)

for the BSM model. For the Heston model, the delta

value can be estimated by formula (12).

𝑑𝑒𝑙𝑡𝑎(𝑠)

𝐶

(

𝑠+∆𝑠

)

−𝐶(𝑠−∆𝑠)

2∆𝑠

(12)

Finally, the data of profit or loss is calculated by

implementing the delta-hedging strategies every day

from June 24th, 2022, to July 11th, 2022. The profit or

loss without hedging is also calculated. In detail, to

calculate the implied volatility in the Black Scholes

model, the Solver function in the Microsoft Excel

software is utilized by minimizing the sum of squared

errors. Also, a Python programme is cited (Jace,

2021). The function named optimize in the Python

module is used to minimize the SSE and calibrates the

parameters in the Heston model.

3 RESULTS AND DISCUSSION

3.1 Results

By minimizing the SSE, the parameters in two models

are calibrated. In the Black Scholes model, the

optimize sigma σ=0.498. The SSE equals to 0.799. In

the Heston model, the parameters are shown in the

table IV. The SSE equals to 0.772.

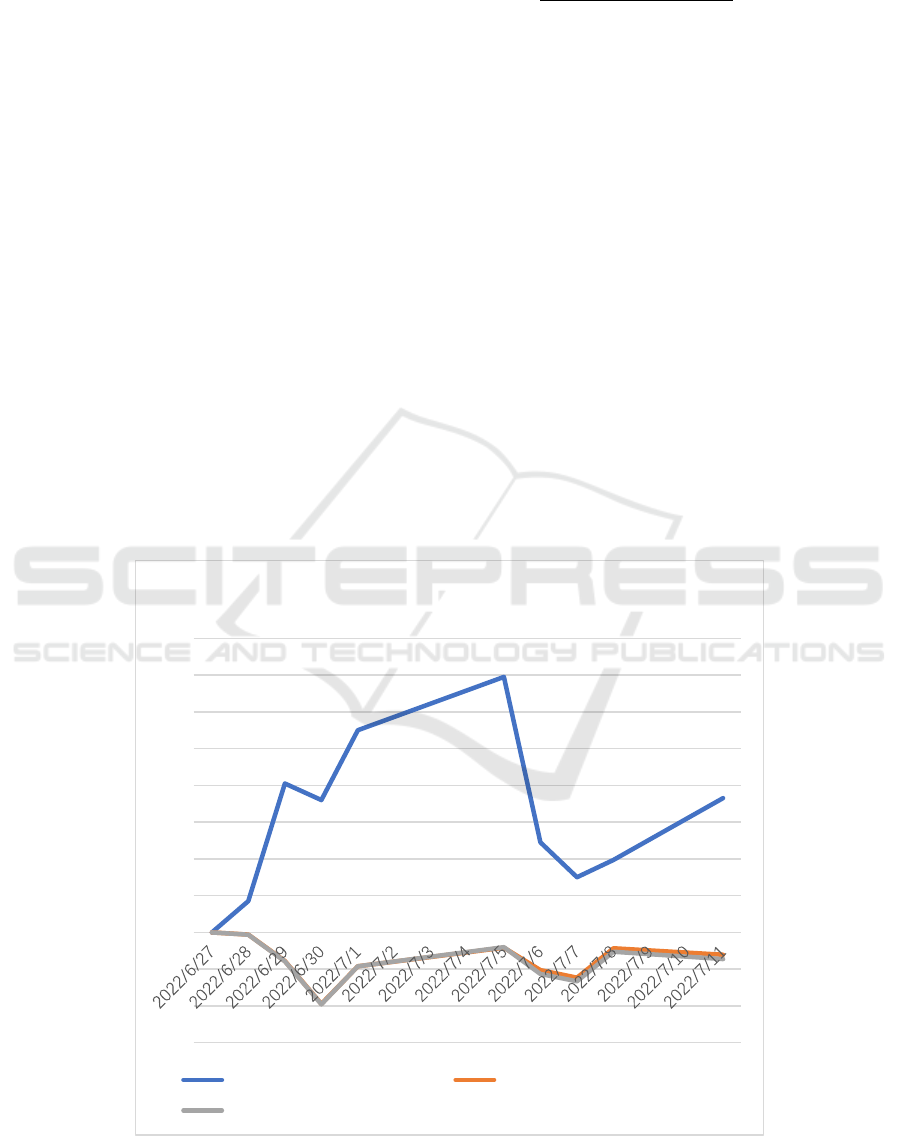
Figure 2: Comparision of profit/loss holding.

-3

-2

-1

Call option of Meta Platforms

without hedging hedging in the BS model

hedging in the heston model

Performance of the Delta-Hedging Strategies Based on the Heston Model and the Black Scholes Model on Meta Platforms

369

Table 4: The parameters of Heston Model.

𝝆 𝝈 𝜽 𝜿 𝑽

𝟎

value 0 0.0248 0.487 0.6839 0.2161

As shown in the Figure 2, the profit without

hedging always exceeds the profit with hedging in two

models. The trend of the profit with hedging in the

Black Scholes model is similar to that in the Heston

model. From June 27th, 2022 to July 11th, 2022, the

profit without hedging is $3.65, while the loss with

hedging by using the Heston model is $0.726. By

using the Black Scholes model, the loss with hedging

is $0.609.

3.2 Discussion

As shown in the Result section, the strategy of selling

the call option without hedging performs very well.

The reason is that the stock price of the Meta

Platforms decreased during that period. The market

price of the underlying stock fluctuates a lot. It

decreased from 171.32 to 167.07, from June 27th,

2022 to July 11th, 2022. Although this strategy makes

some profits, it does not mean that it has effectively

reduced the risk. In comparison, the performance of

hedging strategies performs well. The profit or loss

changes slightly on a daily basis.

In addition, the SSE in the BSM model is higher

than that in the Heston model. It shows that the Heston

model performs better than the BSM model in the

accuracy of option pricing.

There are some shortages in this paper. Firstly,

when calibrating the parameters in the Heston model

and the BSM model, the open price of the stock and

its options on June 24th, 2022 is used. These data are

discrete. If the continuous time series data is used, the

parameters in two models are revised in a period. The

theoretical options’ price and the delta values can also

be calculated with higher accuracy. Secondly, the

method that calculated the delta values in the Heston

model is not the precise way. In the Black Scholes

Model, the delta value equals to N(d

) and the delta

values are estimated by the formula (11) above. If the

formula of the delta values in the Heston model is

known, the delta value can be calculated in a more

precise way. Thirdly, some error in calculating the

options price is caused, because the American options

are considered the European Options. The American

option is a kind of path-dependent option. If the

formula to calculate an American option price is

known, the theoretical price and delta values of the

options can be calculated more accurate.

Finally, the correlation between the two Brownian

motions is assumed to be 0 in the Heston model. If the

correlation ρ is not 0, the formula for calibrating the

option price may be more complicated. However, the

option price can be calculated with higher accuracy.

4 CONCLUSION

This paper studies the performance of the delta-

hedging strategies on Meta Platforms by utilizing the

Heston model and the BSM model. Although

researchers have studied hedging strategies in the

Chinese option market. The topic this paper

researched has not been discussed before. Firstly, the

implied volatility is calibrated using the information

from five call options and five put options on the

shares of Meta Platforms in the BSM model. Three

parameters in the Heston model are also calibrated by

utilizing the same data. Then, after the Black Scholes

model and the Heston model are built, the prices of an

option and delta values of the option are calibrated

every day. Two strategies with hedging are composed,

including one share of a call option and delta shares of

the Meta Platforms’ stock. Finally, the performances

of the hedging strategies are compared. Compared

with the strategy without hedging, the hedging

strategies effectively avoid the risk of fluctuating

prices. Furthermore, when the Heston model is used to

calculate the option price and its delta values, the sum

of squared errors is lower than that when the Black

Scholes model is used. This paper proved that the

BSM model and the Heston model perform similarly

on Meta Platforms options. This result may help the

investors choose a proper delta hedging strategy to

avoid the risk and gain profits in the options market.

However, some assumptions are assumed to be

correct in Section 2, while these assumptions may not

perfectly accurate in the real financial market.

Therefore, the results of these two models deserve

more research and discussions in the future.

REFERENCES

Black, F. , & Scholes, M. S. . (1973). The pricing of options

and corporate liabilities. Journal of Political Economy,

81(3), 637-654.

Cervera, J. . (2019). Solution of the black-scholes equation

using artificial neural networks. Journal of Physics:

Conference Series, 1221, 012044-.

Euch, O. E. , & Rosenbaum, M. . (2018). Perfect hedging

in rough heston models. Annals of Applied Probability,

28(6), 3813-3856.

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

370

Heston, S. L. . (1993). A closed-form solution for options

with stochastic volatility with applications to bond and

currency options. Review of Financial Studies(2), 2.

Hunter, D. . (2000). Option valuation using the fast Fourier

transform.

Jace, Y. . (2021). Heston Model: pricing formulas and

calibration. https://github.com/Jace-Yang/heston-

model_pricing-formulas-and-calibration/

Jerbi, Y. , & Chaabene, S. . (2020). European call price

modelling using neural networks in considering

volatility as stochastic with comparison to the heston

model. Journal of Statistical Computation and

Simulation, 90(10), 1793-1810.

Lamberton, D. , & Terenzi, G. . (2019). Properties of the

american price function in the heston-type models.

Working Papers.

L Goudenège, Molent, A. , & Zanette, A. . (2019). Pricing

and hedging gmwb in the heston and in the black-

scholes with stochastic interest rate models.

Computational Management Science, 16(269).

Simonsy, J. E. . A Perfect Calibration! Now What? Wim

Schoutens.

Xiong, X. , & Liu, Y. . (2017). The dynamic hedging

strategy of sse 50etf options and empirical test. Journal

of Chongqing University of Technology (Natural

Science).

Performance of the Delta-Hedging Strategies Based on the Heston Model and the Black Scholes Model on Meta Platforms

371