Option Pricing and Risk Hedging in Current Financial Market:

A Case for Pfizer

Hang Zhang

Liberal Arts & Sciences, University of Connecticut, l22 Eastwood Rd, Storrs, CT, 06268, U.S.A.

Keywords: BS, BT, Option Pricing, Pfizer.

Abstract: The research background of this paper is that in stock option trading, the risk is weakened, and the profit

level is improved by means of hedging. This paper discusses and analyzes the differences in the hedging

results of stock options of the same company based on different option pricing models. The data adopts the

stock option trading data of Pfizer, and uses the historical data model, BS (black-Scholes) model, and BT

(Binomial Tree) model to construct an option pricing model and calibrate it, and finally perform delta

hedging. The results show that the historical data model shows the best results in the final hedging, the

hedging results of the BS model are in the middle level, while the hedging results of the BT model are not

satisfactory in this study. This research appears in stock option trading, and the investment behavior of

single company stock option as the target weakens the comprehensive risk and improves the comprehensive

profit level.

1 INTRODUCTION

Beginning in the second half of 2019, Covid-19

spread recklessly around the world, which has

brought huge negative impact on people's daily life

and production and construction. With the

development and production of vaccines and antiviral

drugs, people are working hard to fight and defeat the

virus. In this process, pharmaceutical companies

have become bridgeheads to overcome difficulties,

and have introduced a large amount of funds for

scientific research and development and drug

production. Therefore, in the post-epidemic era,

companies in the field of big health are generally

beneficial. As one of the top pharmaceutical

companies, Pfizer has become the most favored

company by investors in the pharmaceutical industry.

However, with the influx of more and more

investors, the phenomenon of blind investment and

follow-up buying continues to appear. People are

superstitious about the long-term benefits of the

pharmaceutical industry, while ignoring the objective

risks in stock option trading. Therefore, it is very

important to choose a suitable option pricing model

and a reasonable hedging strategy, which will help to

reduce risks and improve returns.

The research on stock option pricing model and

hedging strategy is not a new topic in the industry.

Around this center, in the current field, many

scholars have expressed their views on option pricing

models and their understanding of hedging strategies.

Li Xu, Shijie Deng, Valerie M. Thomas co-published

article and hold the idea that options that the impact

of market volatility on option prices is divided into

effectiveness and destructiveness (Xu, 2016).

Ghulam Sarwar wrote that there is contemporaneous

positive feedback between the volatility of the

exchange rate and the trading volume of call and put

options (Sarwar, 2003). The paper completed by Jie

cao and Bing Han pointed out that when using delta

to hedge stock options, as the heterogeneous

volatility of the underlying stock increases, returns

show a monotonically decreasing trend (Cao, 2013).

Research by Gurdip Bakshi and Nikunj Kapadia

found that delta-hedged portfolio returns are

correlated with changes in the volatility risk premium

(Bakshi, 2003). When Erik Ekström and Johan Tysk

studied stochastic volatility and the Black-Scholes

equation, they found that option prices are the only

classical solution to parabolic differential equations,

and this solution is bounded (Ekström, 2010). Yisong

Tian's research pointed out that the calibrated

binomial model can recalibrate the binary tree

through the skew parameter, this method allows the

Zhang, H.

Option Pricing and Risk Hedging in Current Financial Market: A Case for Pﬁzer.

DOI: 10.5220/0012033400003620

In Proceedings of the 4th International Conference on Economic Management and Model Engineering (ICEMME 2022), pages 381-386

ISBN: 978-989-758-636-1

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

381

location of barrier location nodes based on different

option form prices (Tian, 1999).

The propositions and findings of the above

scholars are worth studying and learning. On this

basis, this paper sets the research focus on the

differences in the performance of hedging strategies

based on different option pricing models when

investing in stock options of the same company.

Taking Pfizer's stock option positioning data as the

object, using historical data model, Black-Scholes

model and Binomial Tree model to construct and

calibrate three different option pricing models, and

then perform hedging on this basis, and finally

compare the results.

2 DATA COLLECTION

The data of this project is all from Yahoo Finance

(https://ca.finance.yahoo.com), and the stock price

data of Pfizer Inc. during the ten working days from

June 6 to June 17, 2022, and the transaction on June

17, the maturity time is unified There are five calls

and puts on July 1. In addition, option A selects a put

option on July 29 with a relatively late maturity date.

The reason why choose Pfizer Inc. is, Pfizer Inc. is a

stock that is publicly traded in the United States, and

its stocks have corresponding option trading

behavior. The selected options data and historical

stock prices are as follows in table 1.

Table 1: The 5 call and 5 put options chosen.

Call options

chosen

Put options

chosen

Pfizer

Inc.

PFE220701

C00045000

PFE220701

P00045000

PFE220701

C00046000

PFE220701

P00046000

PFE220701

C00046500

PFE220701

P00046500

PFE220701

C00047000

PFE220701

P00047000

PFE220701

C00047500

PFE220701

P00047500

Table 2: The Option A

Option A PFE220729P0050000

Figure 1: The historical stock price if Pfizer Inc.

This icon shows and indicates that Pfizer's stock

traded continuously during the trading day from June

7th to June 17th, and the stock traded at relatively

random prices.

3 METHODS

After selecting the above data, use the data to

construct three different option pricing models.

According to the different theoretical basis of the

models, the three models are divided into historical

data model, BS model, and BT model. The

construction ideas of the three models are roughly

similar, the difference is that the volatility is slightly

different. The historical data model uses historical

volatility, while the BS and BT models use implied

volatility.

The Black-Scholes model, also known as the

Black-Scholes-Merton (BSM) model, is one of the

most important concepts in modern financial theory.

This formula is based on consideration of the

theoretical value of derivatives of investment

instruments, other risk factors that affect value, such

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

382

as time, are also considered (Hayes, 2022). Since its

birth in 1973, it has been an important application

tool in the history of options contract pricing. The

binomial option pricing model, another important

method for option valuation, was developed in 1979.

The core of this model is the usage iteration process,

which allows arbitrary nodes or points in time within

the time span between the valuation date and the

option expiration date (Chen, 2019). In this study,

three different option pricing models are used to

complete the hedging of option A to minimize the

impact of errors on the final data.

After the option pricing model is established, the

model needs to be calibrated with data, and all three

models use 𝝈 calibration. In the calibration model

stage, the ideas of the three model calibrations are

relatively unified, but they tend to be diversified in

performance. The idea is to bring the variable 𝝈 into

one or more formulas that can reflect the size of the

error value and bring it in according to the collected

data to form a formula based on the data and the

value of 𝝈. The result of the reaction is that under

different data, the error The size of the value. After

that, set 𝝈 as the independent variable, set the

formula representing the error value and its result as

the dependent variable, perform the calibration

operation, and obtain the 𝝈 when the minimum error

value is obtained, which is the final purpose of this

step. Detailed model specifications are shown below.

In Historical Data Model, S represents the stock

price, and k represents the date, which starts from

June 6 to June 17. Then k+1 represents the second

day based of the k. First, use equation (1) to get the

logarithm values of stock prices on each date. Then

use equation (2) to calculate the difference of

logarithm values between every two days. All the

results of equation (2) are used to take the variance

value of equation (3). Because the trading of stocks

and options only occurs on trading days, assuming

that there are 251 trading days in a year, bring it into

equation (4) to get the final 𝝈 value.

A=log𝑆



(1)

R=log(𝑆



)−log𝑆



(2)

𝑉𝑎𝑟=𝑣𝑎𝑟(log (𝑆



)−log𝑆



)

(3)

𝜎=

√

𝑉𝑎𝑟 251

(4)

In BS Model, σ represents implied volatility, t

represents time to maturity, S(t) represents the stock

price, K represents the strike price of the option, and

r represents the interest rate, which is assumed to be

2.8% in this model (The Fed - Selected Interest Rates

(Daily), 2020). First use equation (5) and equation

(6) to calculate value of 𝑑



and 𝑑



which are the

required elements for further calculation. Equation

(7) and (8) calculate the call and put price of the

option, and the 𝑁

(

𝑑



)

represents the normal

distribution of 𝑑



, 𝑁

(

𝑑



)

represents the normal

distribution of 𝑑



. After getting the values of the call

and put options, put them into equation (9) to

calculate the SSE (Residual sum of squares) error. C

represents the call option prices, which calculate

from equation (7), P represents the put option prices,

which calculate from equation (8), and 𝑃



represents

the corresponding market values. At last, when the

SSE value is the smallest, the desired 𝜎 value can be

obtained.

𝑑



√

(𝑡)

ln

𝑆

(

𝑡

)

𝐾

+𝑟+



𝑡

(5)

𝑑



√

(t)

ln

𝑆

(

𝑡

)

𝐾

+𝑟−



𝑡

=𝑑



−σ

√

(6)

𝐶𝑡,𝑆

(

𝑡

)

=𝑆

(

𝑡

)

𝑁

(

𝑑



)

−𝐾𝑒



𝑁

(

𝑑



)

(7)

𝑃𝑡,𝑆

(

𝑡

)

=𝐾𝑒



𝑁

(

−𝑑



)

−𝑆

(

𝑡

)

𝑁(−𝑑



)

(8)

𝑆𝑆𝐸=

(𝑃



−𝑃





)



𝑃





(𝑃



−𝑃





)



𝑃





(9)

In the BT Model, u represents the up coefficient

in binomial tree, d represents the down coefficient, t

represents time to maturity, p represents option

prices, and r represents the interest rate, which is

assumed to be 2.8% in this model. Calculate the up

and down coefficients of each level of the binomial

tree according to equations (10) and (11). Then bring

each coefficient into equation (12) to get the prices of

the option. Using equation (13), the calculated option

price and the corresponding stock price are brought

in to calculate the SSE error, when the SSE value is

the smallest, the desired σ value can be obtained

(Muroi, 2022).

𝑢=𝑒



√



(10)

𝑑=

𝑢

(11)

𝑝=

𝑒



−𝑑

𝑢−𝑑

(12)

𝑆𝑆𝐸=

(𝑃



−𝑃





)



𝑃





(𝑃



−𝑃





)



𝑃





(13)

After the above calculation process, the obtained

𝝈 value can be the variable value used after the

model has been calibrated. After the model has been

calibrated, it can be combined with Option A for

hedging. All three models use the delta hedging

Option Pricing and Risk Hedging in Current Financial Market: A Case for Pﬁzer

383

method. In this step, the hedging process of the

historical data model and the BS model is the same,

and the BT model is slightly different. For BS model,

p(t) represents the portfolio value, and using equation

(14) to get each p(t), then using equation (15) to

finish the hedging process. The BT model will

additionally use equation (16) in the hedging phase,

where S represents the option price. Collect the

results of the three model hedges, compare them, and

draw a conclusion.

𝑝

(

𝑡

)

=𝑝

(

𝑡−1

)

+𝑁(𝑑



)(𝑆

(

𝑡

)

−𝑆

(

𝑡−1

)

(14)

𝐿𝑜𝑠𝑠 𝑤𝑖𝑡ℎℎ𝑒𝑑𝑔𝑖𝑛𝑔(𝑡)

=𝑆

(

𝑡

)

−𝐾−𝑝(𝑡)

(15)

𝐻𝑒𝑑𝑔𝑒 𝑟𝑎𝑡𝑖𝑜=

𝐷



−𝐷



𝑆



−𝑆



(16)

4 RESULTS

According to the numerical results, the three models

have played a practical role in the manifestation of

the hedging effect, and the historical data model has

the best final effect in the presentation of the results.

Table 3: The gain/loss of holding one unit of the option on Pfizer Inc.’s stock with hedging by historical data model.

Days T-t T_A Stock A(put) Delta_A(put) Sell/Buy stock Cash

2022/6/6 1 39 0.1553785 53.19 1.338987 -0.285192551 0.285192551 16.508378

2022/6/7 2 38 0.1513944 53.28 1.284773 -0.279170686 -0.006021865 16.189375

2022/6/8 3 37 0.1474104 54.06 1.053795 -0.24084287 -0.038327816 14.119179

2022/6/9 4 36 0.1434263 53.27 1.229061 -0.276060889 0.035218019 15.996818

2022/6/10 5 35 0.1394422 51.31 1.83916 -0.381873758 0.105812868 21.427861

2022/6/13 6 34 0.1354582 48.82 2.950776 -0.540372814 0.158499056 29.168176

2022/6/14 7 33 0.1314741 47.75 3.536934 -0.613388331 0.073015517 32.65792

2022/6/15 8 32 0.12749 47.88 3.427221 -0.607455173 -0.005933157 32.377484

2022/6/16 9 31 0.123506 47.69 3.5134 -0.623120722 0.015665548 33.128186

2022/6/17 10 30 0.1195219 47.38 3.679893 -0.647319738 0.024199016 34.278431

According to the table above, the result of

hedging using the historical data model shows that

the final loss is $0.071472 per unit.

Table 4: The gain/loss of holding one unit of the option on Pfizer Inc.’s stock with hedging by BS model.

Days T-t T_A Stock A(put) Delta_A(put) Sell/Buy stock Cash

2022/6/6 1 39 0.1553785 53.19 1.233434 -0.278295356 0.278295356 16.035964

2022/6/7 2 38 0.1513944 53.28 1.181519 -0.272043762 -0.006251594 15.704668

2022/6/8 3 37 0.1474104 54.06 0.958312 -0.232535959 -0.039507803 13.570628

2022/6/9 4 36 0.1434263 53.27 1.129156 -0.268778694 0.036242735 15.502792

2022/6/10 5 35 0.1394422 51.31 1.730362 -0.378709777 0.109931083 21.145086

2022/6/13 6 34 0.1354582 48.82 2.844506 -0.544474042 0.165764266 29.240056

2022/6/14 7 33 0.1314741 47.75 3.438411 -0.620624141 0.076150098 32.879485

2022/6/15 8 32 0.12749 47.88 3.329489 -0.614415597 -0.006208543 32.585888

2022/6/16 9 31 0.123506 47.69 3.418796 -0.630684062 0.016268465 33.365367

2022/6/17 10 30 0.1195219 47.38 3.589578 -0.655785007 0.025100944 34.558372

According to the table above, the result of

hedging using the BS model shows that the final loss

is $0.102301 per unit.

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

384

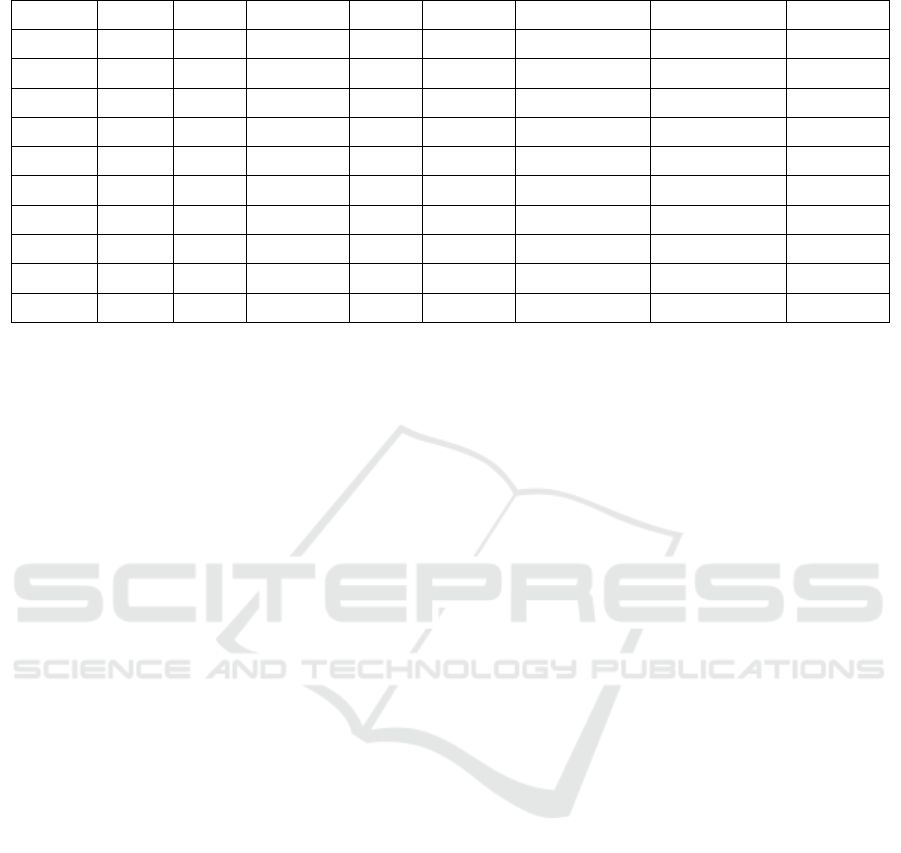
Table 5: The gain/loss of holding one unit of the option on Pfizer Inc.’s stock with hedging by BT model.

Days T-t T_A Stock A(put) Delta_A(put) Sell/Buy stock Cash

2022/6/6 1 39 0.1553785 53.19 0.733978 -0.232385794 0.232385794 13.094578

2022/6/7 2 38 0.1513944 53.28 0.694675 -0.22488392 -0.007501873 12.696339

2022/6/8 3 37 0.1474104 54.06 0.519476 -0.1794846 -0.04539932 10.243468

2022/6/9 4 36 0.1434263 53.27 0.659125 -0.220793512 0.041308912 12.445137

2022/6/10 5 35 0.1394422 51.31 1.19646 -0.355724826 0.134931314 19.369851

2022/6/13 6 34 0.1354582 48.82 2.320051 -0.570073709 0.214348883 29.836524

2022/6/14 7 33 0.1314741 47.75 2.960814 -0.66647809 0.096404381 34.443162

2022/6/15 8 32 0.12749 47.88 2.854744 -0.658574284 -0.007903806 34.06857

2022/6/16 9 31 0.123506 47.69 2.961679 -0.678597143 0.020022859 35.027261

2022/6/17 10 30 0.1195219 47.38 3.157355 -0.709127711 0.030530568 36.477707

According to the table above, the result of

hedging using the BT model shows that the final loss

is $0.278274 per unit.

5 DISCUSSION

As shown in the results section, the results of the

hedging strategy based on the historical data option

pricing model are the best, the results of the hedging

strategy based on the BS model are second only to

the former, and the results of the hedging strategy

based on the BT model are not satisfactory. The

methods of historical data and BS models in the

hedging stage are delta hedging, so the factor that

affects the hedging result is the definition of delta

value. In the evaluation method of delta, the

historical data model is obviously more accurate. The

values of the parameters of this model come from the

actual stock price and option data. The BS model is

subject to its formula principle, and the calculation

steps of many parameters are more responsible, and

the occurrence of errors can also be attributed to this.

When the BT model is established in the option

pricing model, the value of 𝝈 after calibration is

different from the value of the historical data model

and the BS model. At the same time, the hedging

process of the BT model is slightly different from the

above two models in steps, and the calculation steps

are slightly more. As the calculation steps increase,

the possibility of the existence of errors also

increases. The comprehensive analysis of the BT

model is unsatisfactory in the final hedging results

because of the large error of the 𝝈 value and the

added hedging step also increases the error.

6 CONCLUSION

This paper studies the use of different methods to

establish option pricing models for a single

company's stock, and conducts hedging, and analyzes

and discusses the different performances of different

pricing models in hedging. This paper selects the

options of Pfizer Inc. stock and uses historical data,

BS model, and BT model to establish option pricing

models. Use the Historical Volatility method to

calibrate the historical data model and use the

Implied Volatility method to calibrate the BS model

and BT model. After calibration, the historical data

model, the BS model, and the BT model use delta

hedging as the hedging method to complete the

hedging process. When comparing the results, the

hedging results of the historical data model

performed the best, with the smallest amount of loss

per unit. This study emphasizes that when hedging

stock options of the same company, hedging

strategies based on different option pricing models

perform differently, which is beneficial for investors

to flexibly use different hedging strategies and option

pricing models for portfolio investment.

REFERENCES

A. Hayes. What Is the Black-Scholes Model?

Investopedia, 2022.

https://www.investopedia.com/terms/b/blackscholes.as

p#:~:text=The%20Black%2DScholes%20model%2C

%20aka

E. Ekström, J. Tysk, J. The Black–Scholes equation in

stochastic volatility models. Journal of Mathematical

Analysis and Applications, 2010, 368(2), 498–507.

Option Pricing and Risk Hedging in Current Financial Market: A Case for Pﬁzer

385

G. Sarwar. The interrelation of price volatility and trading

volume of currency options. Journal of Futures

Markets, 2003, 23(7), 681–700.

https://doi.org/10.1002/fut.10078

G. Bakshi, N. Kapadia. Delta-Hedged Gains and the

Negative Market Volatility Risk Premium. The

Review of Financial Studies, 2003, 16(2), 527–566.

https://doi.org/10.1093/rfs/hhg002

J. Cao, B. Han. Cross section of option returns and

idiosyncratic stock volatility. Journal of Financial

Economics, 2013, 108(1), 231–249.

https://doi.org/10.1016/j.jfineco.2012.11.010

J. Chen. How the Binomial Option Pricing Model Works.

Investopedia, 2019.

https://www.investopedia.com/terms/b/binomialoption

pricing.asp

L. Xu, S. J. Deng, V.M. Thomas. Carbon emission permit

price volatility reduction through financial options.

Energy Economics, 2016, 53, 248–260.

https://doi.org/10.1016/j.eneco.2014.06.001

The Fed - Selected Interest Rates (Daily) - H.15 - May 22,

2020. URL: www.federalreserve.gov.

Y. S. Tian. A flexible binomial option pricing model.

Journal of Futures Markets, 1999, 19(7), 817–843.

https://doi.org/3.0.co;2-d">10.1002/(sici)1096-

9934(199910)19:7<817::aid-fut5>3.0.co;2-d

Y. Muroi, S. Suda. Binomial tree method for option

pricing: Discrete cosine transform approach.

Mathematics and Computers in Simulation, 2022, 198:

312-331.

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

386