Research on Logistics Warehouse Planning

Based on K-Means Algorithm Clustering Analysis

Hongwei Li

1,*

, Linbo Su

, Faming Da

and Lei Qin

College of Information and Communication National University of Defense Technology, Wuhan, China

Unit 96716, Ganzhou, China

15897248201@163.com, qinleinust@126.com

Keywords: K-Means Algorithm, Cluster Analysis, Logistics Warehouse Planning, The Center of Gravity Method.

Abstract: With the development of logistics industry, warehouse location planning has become a key link in logistics

network layout, and its rationality has an important impact on logistics cost and service level. K-means

algorithm is efficient and fast for analyzing and processing large sample data, but the randomness of K value

will lead to the reduction of clustering effect. In this paper, the optimal K value is selected by clustering

evaluation index CH, so as to improve the K-means algorithm. Through simulation, the optimal distribution

area is obtained, and then the center of gravity method is used for site selection. Finally, the actual location

of the warehouse is determined by combining the natural environment and infrastructure factors. The results

show that the improved K-Means clustering algorithm has practical significance for the planning of logistics

warehouse.

1 INTRODUCTION

In recent years, with the rapid development of the e-

commerce industry, the number of offline stores

keeps increasing, which means the quantity of

warehouse distribution and distribution routes keep

increasing, and the competition between enterprises

has shifted from the competition of business model to

the competition of logistics services. Therefore, how

to solve the logistics technology lag in reality, so as

to accelerate the logistics distribution speed and

shorten the distribution time, which has become the

source of competitive advantage of enterprises.

Warehouse or logistics center location is a very

important part of logistics network layout planning, it

can carry out strategic storage and allocation of

commodities, can bring objective economic benefits

for enterprises. Whether the location of the

warehouse is reasonable or not has an important

impact on the logistics cost and service level, which

is related to the long-term development of the

enterprise.

2 DEVELOPMENT STATUS AT

HOME AND ABROAD

Domestic and foreign scholars have made many

achievements in the study of logistics center location.

Taniguchi et al. mainly explored the scale and

selection of public logistics nodes by building a

bilevel programming model, and solved the model

with queuing theory and nonlinear programming

(Taniguchi, 1999). Yan Wentao and Qin Yanhong

studied the location of underground logistics nodes by

establishing a two-level programming model, and the

simulation results of real cases verified the feasibility

and rationality of this model (Yan, 2016).

Vlachopoulou et al. applied Geographic

Information System (GIS) to the location problem of

logistics nodes. Based on a variety of qualitative and

quantitative evaluation criteria, he ranked the

advantages and disadvantages of the existing

alternatives of distribution centers, so as to obtain the

optimal location scheme (Vlachopoulou, 2001). Shi

Hongwei and Wang Fanian constructed an

optimization model of logistics node layout after

analyzing the basic characteristics of each logistics

node, such as radiation range, spatial characteristics

and construction cost, and designed a suitable ant

Li, H., Su, L., Da, F. and Qin, L.

Research on Logistics Warehouse Planning Based on K-Means Algorithm Clustering Analysis.

DOI: 10.5220/0012034400003620

In Proceedings of the 4th International Conference on Economic Management and Model Engineering (ICEMME 2022), pages 445-450

ISBN: 978-989-758-636-1

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

445

colony algorithm to solve the problem for research

(Shi, 2010). Zhao Hairu, Chen Ling In order to reduce

logistics costs and improve distribution efficiency, a

multi-objective logistics node location model was

built with the minimum logistics system operating

cost and maximum customer time satisfaction as the

objective function (Zhao, 2016).

Wang Jiaju systematically expounded the

advantages and disadvantages of the center of gravity

method in the location of logistics centers and its

applicable scope, providing a theoretical basis for the

study of the location of logistics centers (Wang,

2008). Wang Feifei and Lin Wen improved the

limitations of the center of gravity method in the

location of logistics center, established a model and

obtained the best location, and finally verified the

correctness of the model through an example (Wang,

2014).

3 K-MEANS ALGORITHM

CLUSTERING ANALYSIS

Clustering is a process of classifying data members

based on similarity characteristics. K-Means

algorithm clustering analysis, also known as K-center

clustering, is a statistical analysis method that sums

the homogeneous continuous variables together

through an iterative process.

Distance is usually taken as the index of

similarity, and the data set

{, 1,2, }

Uui n==

divided into K classes

{, 1,2, }

Ccj K==

, and

each class

has a clustering center

. Calculate

the sum of squares of distances from each data point

to the clustering center in all clusters:

()

juc

Dc u m

=∈

=−



(1)

The clustering result is obtained by making

()Dc

minimum through iterative operation.

Because it has the advantages of fast convergence

speed and small computation, it is suitable for

analyzing and processing large sample data, which

can effectively reduce the computation time and

improve the operation efficiency.

For warehousing and logistics, the logistics

network is usually divided into different distribution

areas with each warehouse as the center and the

distribution distance as the radius. K-means

clustering algorithm divides regions according to

distance, and this method can be well applied to the

regional division of warehousing logistics. K in k-

means algorithm is the number of warehousing

logistics distribution regions.

In the k-means algorithm, the number K of

clusters is randomly selected (Xu, 2019). Although

such clustering algorithm is fast and simple, the

randomly selected value of K will affect the

clustering effect, thus leading to the decline of

clustering quality. A good clustering method can

generate clusters with good clustering, the samples

within clusters are very close and the clusters between

clusters are very large. The clustering evaluation

index CH (Calinski, 1974) mainly considers the

similarity degree of samples in the cluster and the

distancing degree of clusters. Between 2 and the

number of samples, the clustering evaluation index

CH is used to evaluate the clustering effect of each K

value, and the optimal cluster number K value is

calculated and evaluated, so as to determine the

number of warehouses.

4 K-MEANS ALGORITHM

CLUSTERING ANALYSIS

WITH DETERMINE K VALUE

Too large or too small cluster number K value will

affect the clustering effect of k-means algorithm, and

the determination of K value becomes the most

important problem to be solved by K-means

clustering algorithm.

4.1 Algorithm Steps

This paper mainly optimizes the first step of K-means

algorithm, and improves this shortcoming by

evaluating the best K value with clustering evaluation

index, so as to achieve a better clustering. The steps

are as follows:

1. Determine K value by clustering evaluation

index;

2. Calculate the distance between each data point

and each cluster center, and determine which cluster

center it belongs to if the distance between each data

point and a cluster center is small;

3. Recalculate the centers of K clusters, and the

arithmetic mean value of the points contained in the

cluster is the cluster center;

4. If the cluster center does not change, go to Step

5; Otherwise, go to Step 2.

5. Output the classification result of the dataset.

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

446

4.2 Implementation Process

The implementation flow of this K-means clustering

algorithm with a determined K value is as follows:

1. Select a search range for the number of clusters

min

, K

max

Assuming that there are n data samples, then the

maximum number of clustering clusters is

theoretically n, that is, the number of clustering

clusters when each point is infinitely far away is

max

=n; On the contrary, if n points are infinitely

close to each other, they are grouped into a cluster. In

general practical applications, the number of data

samples is between Kmin and Kmax, so the search

range for the number of clusters is determine as (K

min

max

2. In the range of (K

min

, K

max

), the optimal

clustering index value of clustering evaluation index

CH under different cluster number is obtained.

3. Analyze the application effect of clustering

evaluation index, and the clustering evaluation of data

samples is carried out combined with the actual

situation, so as to obtain the best clustering number.

4. According to the best clustering number

obtained, the K-means algorithm is used to cluster the

number of data samples.

5 SIMULATION RESULTS AND

ANALYSIS

Through the investigation and analysis of 59 cities in

East China, the coordinates of prefecture-level cities

in the following table are obtained. Where, the

horizontal coordinate X and vertical coordinate Y are

the distances converted according to the latitude and

longitude of each city respectively, and the task

quantity is determined according to the service area

of each city and the logistics demand of surrounding

users.

Table 1: Geographical coordinates of 59 cities.

City name

X-

coordinate

Y-

coordinate

Task

quantity

Zhangzhou 11764 2451 40

Xiamen 11807 2446 80

Quanzhou 11857 2493 50

Putian 11900 2547 40

Fuzhou, Fujian 11928 2609 70

Ningde 11951 2668 90

Sanming 11763 2627 70

Longyan 11700 2508 60

Nanping 11817 2665 40

Ganzhou 11491 2585 30

Ji’an 11498 2712 50

Wuhu 11842 3136 80

Maanshan 11849 3168 40

Nanjing 11878 3206 100

Shanghai 12146 3125 90

Nantong 12088 3199 80

Changzhou 11997 3182 70

Wuxi 12029 3150 90

Suzhou 12057 3130 50

Zhenjiang 11944 3221 40

Yichun 11440 2782 50

Xinyu 11491 2783 50

Nanchang 11585 2869 40

Fuzhou,

Jiangxi

11635 2797 40

Yingtan 11705 2827 60

Jingdezhen 11717 2928 50

Shangrao 11793 2847 60

Quzhou 11887 2895 70

Chuzhou 11831 3231 70

Hefei 11722 3183 60

Jiujiang 11599 2972 70

Huangshan 11832 2972 80

Jinhua 11964 2909 50

Huaibei 11694 3365 60

Xuzhou 11727 3421 70

Suqian 11826 3397 80

Huaian 11900 3362 70

Chizhou 11749 3067 60

Yancheng 12015 3335 50

Bengbu 11738 3292 60

Fuyang,

Anhui

11580 3290 80

Taizhou,

Jiangsu

11990 3246 70

Lishui 11992 2848 80

Wenzhou 12069 2801 80

Taizhou,

Zhejiang

12140 2867 60

Ningbo 12154 2988 60

Zhoushan 12218 3000 60

Shaoxing 12057 3004 70

Hangzhou 12021 3025 50

Jiaxing 12074 3076 60

Huzhou 12008 3090 70

Xuancheng 11875 3095 50

Tongling 11780 3097 70

Lianyungang 11921 3460 30

Pingxiang 11386 2763 40

Bozhou 11577 3386 60

Research on Logistics Warehouse Planning Based on K-Means Algorithm Clustering Analysis

447

Anqing 11705 3054 50

Huainan 11698 3264 50

Liuan 11650 3174 80

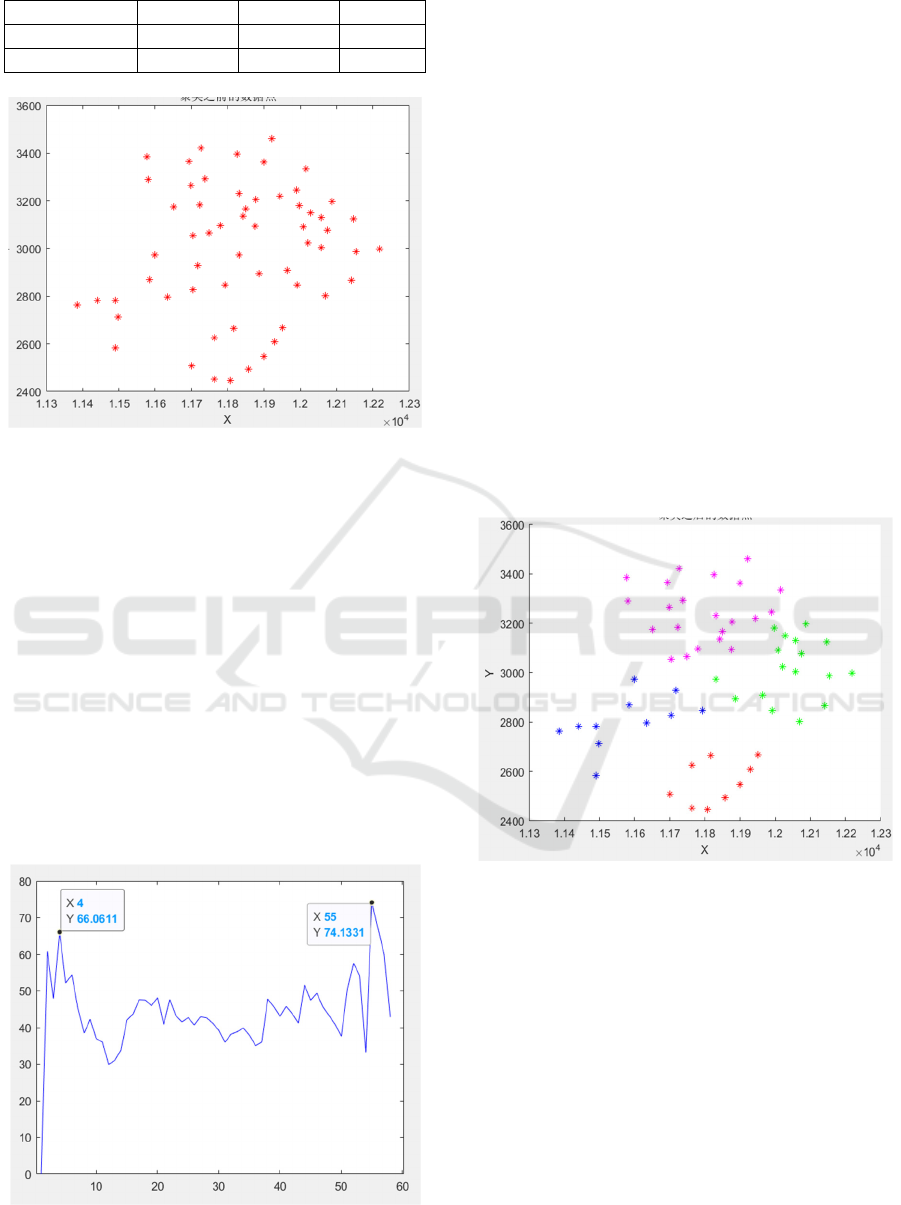
Figure 1: Data tracing points of the above 59 cities.

The coordinates of 59 cities in Table 1 were traced

to get Figure 1, from which the distribution of each

data point can be intuitively seen.

5.1 K-Means Clustering Algorithm

Figure 2 can be obtained by using K-Means clustering

evaluation scheme to simulate data samples. It can be

seen from Figure 2 that the clustering evaluation

index CH changes to a certain extent with the increase

of the cluster number, and there are two peaks, which

are the corresponding values when the cluster number

K=4 and K=55. However, the scheme with relatively

small k value is relatively economical in practice.

Therefore, K=4 is selected as the optimal clustering

number.

Figure 2: Cluster evaluation indicators.

According to the measurement, the area of 59

cities is about 480,000 square kilometers. According

to the optimal clustering number K=4, the area of a

single distribution area is about 120,000 square

kilometers.

On this basis, we assume the following

conditions:

1. The delivery time of transport vehicles is the

working time of logistics industry: 8:00-12:00,2:00-

6:00.

2. In order to ensure the efficiency of warehouse

operation, the transport vehicles must be completed

within one day and returned to prepare for the next

shipment. Therefore, considering the round-trip time,

the single trip time is calculated as 4 hours.

3. The average speed of transport vehicles is

generally 40-60km/h. Considering the problems such

as traffic jams and bad road conditions, the average

speed of vehicles is considered to be 50km/h.

When clustering cluster K=4, the 59 cities in

Table 1 are clustered and the following results are

obtained, as shown in Figure 3:

Figure 3: K-Means clustering.

According to the measurement, the distribution

area of each warehouse center is about 120,000

square kilometers, which is in line with the

distribution range of the warehouse. Therefore, the

selection of cluster number K=4 meets the

requirements of the actual warehouse establishment.

5.2 Center of Gravity Method for Site

Selection

The center of gravity method mainly considers the

transportation rate, transportation distance,

transportation volume and other parameters for site

selection. By calculating the transportation cost

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

448

between each distribution point and the logistics

center, the weighted value is minimized to obtain the

center of gravity of the distribution area, that is, the

theoretical location of the logistics center within the

distribution area. Assuming that the transportation

rate per unit distance is

, the straight-line distance

from the warehouse to the distribution point is

and the freight volume is

, then the transportation

cost of goods from the logistics center to the

distribution point is:

iiii

Hhdw=∗∗

(2)

Where,

()()

00iii

dxxyy=−+−

(3)

the coordinate of the logistics center is

()

,xy

and the coordinate of the distribution point is

()

. The total transportation cost of the logistics

center in the distribution area is:

() ( )( )

00 0 0

ii i i

Hxy h w x x y y

=××−+−



(4)

Where,

is the number of distribution points in

the distribution area. The value of function

()

,Hxy

is minimized by iterative operation, and

the obtained coordinate is the theoretical position of

the warehouse in the distribution area. Through

simulation, the following results are obtained, as

shown in Figure 4:

Figure 4: Theoretical locations of warehouses in each

distribution area.

In the figure, the theoretical coordinates of the

warehouse in the blue clustering area is:

(11597.95,2831.69), the theoretical coordinates of the

warehouse in the red clustering area is

(11845.11,2558.42), the theoretical coordinates of the

warehouse in the green clustering area is

(12049.63,3034.78), the theoretical coordinates of the

warehouse in the purple clustering area is

(11805.42,3228.25).

In addition to transportation costs, the location of

logistics centers also needs to consider factors such as

natural environment and infrastructure conditions.

1. Natural environmental factors

(1) Geological conditions. The warehouse should

be built in a place with high and relatively flat terrain

as far as possible. It should not be built in a place with

geological problems such as silt layer, quicksand

layer and loose soil layer. Otherwise, it may cause

serious consequences such as subsidence and

churning.

(2) Meteorological conditions. The main

meteorological conditions to consider when choosing

a warehouse location include temperature, humidity,

precipitation, frost and other indicators such as the

depth of the frozen soil.

(3) Hydrological conditions. When choosing a

warehouse location, avoid flood basins and

groundwater flooding areas.

2. Conditions of base facilities

(1) Traffic conditions. Logistics distribution

should have convenient transportation to meet the

needs of timely distribution and cost reduction, so the

location of the warehouse should be close to the main

traffic road or high-speed entrances and exits.

(2) Condition of public facilities. The location of

the warehouse needs good communication quality

and is not easy to be interfered with. The power

supply, water supply, heat supply and gas supply

capacity should be sufficient.

(3) Surrounding environment. The warehouse

should be securely spaced from other surrounding

buildings, and the site should be located in an open

area on the outskirts of the city, which may reduce the

occupation of the field.

Taking the above factors into consideration, the

actual location of the warehouse is selected near the

theoretical coordinate according to the actual

situation.

5.3 Result Analysis

It can be found that the experimental results are often

different from the actual results, mainly because:

1. The location of a logistics center needs to

consider many factors, such as the choice of

transportation mode, the guarantee range of the

warehouse, the local climate conditions, etc. In this

paper, when determining the number of cluster,

namely the number of warehouses, only the

Research on Logistics Warehouse Planning Based on K-Means Algorithm Clustering Analysis

449

automobile is considered as the means of

transportation, and the scope of warehouse guarantee

is given in an assumed way. The center of gravity

method adopted in this paper only considers the three

major factors of distance, transportation rate and

transportation volume, and is simply calculated by

mathematical method.

2. K-means clustering has certain limitations. It

has been mentioned in the paper that the k-means

clustering effect is greatly influenced by the initial

clustering number K value. In order to avoid this

influence, this paper uses CH clustering evaluation

index to evaluate a K value, although this method has

certain application value. However, any evaluation

system has its own disadvantages. The CH evaluation

system is obtained by comparing with the existing

more famous clustering indexes BWP and SIL. With

the continuous development of clustering research,

more complete clustering evaluation indexes will also

appear.

7 CONCLUSIONS

Based on K-Means clustering analysis, this paper

studies the planning of logistics warehouse. By

selecting the best value of the clustering evaluation

index CH as the best clustering number K, the k-

means algorithm is improved and the influence of the

randomness of K value on the clustering effect is

improved. After the clustering results are obtained

through the experimental simulation, the planned

quantity of the warehouse is determined by analyzing

the actual situation. Finally, the center of gravity

method is used for site selection, and the actual

location of the warehouse is determined by

combining the natural environment and

infrastructure. It can be seen from the result analysis

that this method has practical significance for the

planning of logistics warehouse.

ACKNOWLEDGEMENTS

This work was supported by National University of

Defense Technology under the Teaching and

Learning Funding Scheme.

REFERENCES

Calinski, T. & Harabasz, J. (1974). A Dendrite Method for

Cluster Analysis. J. Communications in Statistics. 1, 1-

27.

Shi, H. W. & Wang, F. N. (2010). A Clustering Model and

its Adaptive Ant Colony Algorithm in Logistics Service

Nodes layout Optimization. J. Industrial Engineering

and Management. 4, 10-14.

Taniguchi, E., Noritake, M., Yamada, T., Izumitani, T.

(1999). Optimal size and location planning of public

logistics erminals. J. Transportation Research.

35(PartE), 207-222．

Vlachopoulou, M., Silleos, G., Manthou, V. (2001).

Geographic Information Systems in Warehouse Site

Selection Decitions. J. Production Economics. 71, 205-

212．

Wang, J. J. (2008). Selecting the Site of Distribution Center

Based on Centroid Method. J. Journal of Yangtze

University. 4, 64-66.

Wang, F. F. & Lin, W. (2014). Study on Location Problem

of 3PL Distribution Centers Based on Improved

Gravity-Actor Analysis. J. Logistics Technology. 3,

185-187.

Xu, Y. C. & Dai, T. (2019). Solving Multiple Distribution

Center Location Allocation Problem Using K-Means

Algorithm and Center of Gravity Method. J. Logistics

Technology. 6, 69-73.

Yan, W. T. & Qin, Y. H. (2016). Research on Bi-level

Programming Model and Algorithm of Underground

Logistics Node Location. J. Chinese Journal of

Underground Space and Engineering. 4, 870-874.

Zhao, H. R. & Chen, L. (2016). Application of improved

MOPSO in logistics node location model. J. Computer

Engineering and Applications. 12, 239-245.

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

450