
A Game of Stakeholders in Evolutional Tourism
Tingting Ni
1,3
, Cheng Liu
2
, Junyi Wei
1,3,*
, Qin Yang
1
, Pan Zhao
4
and Gang Wang
5
1
Business and Tourism School, Sichuan Agricultural University, Sichuan, China
2
Department of Foundational Courses Dujiangyan Campus, Sichuan Agricultural University, Sichuan, China
3
National Forestry and Grassland Southwest Engineering Technology Research Center of Taxus, Sichuan, China
4
School of Literature, Journalism & Communication, Xihua University, Sichuan, China
5
College of Forestry, Sichuan Agricultural University, Sichuan, China
Keywords: Educational Tourism, Evolutionary Game.
Abstract: The popularization of the Internet and information technology redefined the form of education and eliminated
the educational barriers, which make educational tourism within reach. This paper constructs a hybrid strategy
model to study the benefit relations of subjects and equilibrium points among the government, schools, and
families under the background of education reform due to the rapid development of the Internet and the
compatibility of disciplines. The result shows that the government and family not only influence each other's
strategic choices but also affect the decision-making of schools. Specifically, reasonable rewards or subsidies
for schools and families can remarkably promote the construction of the educational system and participation
in educational tourism.
1 INTRODUCTION
In 2021, the government issue not only reduce the
pressure of homework and after-school training but
also required improving the quality of educational
resources, which included building professional
extracurricular activities and educational bases (Yan
Lin, 2021). However, now schools merely paying
attention to knowledge acquisition and emphasizing
discipline standards, fail to promote educational
travel that advocates all-around development.
Importantly, under the social background of
development diversification, families have more
freedom of choice, rather than the only choice from
school about educational tourism. The benefit
relations among the government, schools, and
families have ushered in a major restructuring. The
quality of educational travel in the future has attracted
extensive attention from all walks of life. In addition,
the rise of cloud computing has also facilitated the
popularity of educational tourism. More and more
families have begun to attach importance to
comprehensive development. As for this, it is
necessary to solve the benefit conflicts initiated by
educational travel subjects (Bo Ma, 2020).
2 LITERATURE REVIEW
To fully implement the effective way of
comprehensive practical education, scholars have
studied different aspects of educational tourism,
which mostly stay in qualitative analysis and less
quantitative analysis, being in contradiction with the
vigorous development in China. Foreign scholars
focus on the role of educational tourism, and the
existing research results show that educational
tourism has a positive impact on self-view (Roberson
and Donald N., 2018), practical education (Xiaoyan
Wang, 2017), and cross-cultural development (Hao
Zhang, 2017). The causes and countermeasures of
educational tourism summarized have been widely
recognized by the academic circles, which include a
lack of accurate understanding of educational value,
lack of strict planning, and so on (Meaux J B, Saviers
B and Traywick L, 2021). Some scholars have studied
different types, which demonstrated the practical
value. It can be found that scholars widely agree to
bring research and learning into the teaching system.
However, few schools effectively integrate
educational tourism into the teaching system.
Specifically, schools lack professional talents, mostly
cooperate with institutions to complete educational
activities and ignore students' subjective initiative
Ni, T., Liu, C., Wei, J., Yang, Q., Zhao, P. and Wang, G.
A Game of Stakeholders in Evolutional Tourism.
DOI: 10.5220/0012034700003620
In Proceedings of the 4th International Conference on Economic Management and Model Engineering (ICEMME 2022), pages 457-463
ISBN: 978-989-758-636-1
Copyright
c
2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
457

(Shujuan Yu, Yuan Wang and Huijun Wu., 2017).
which demonstrates the effective gain of schools,
government, and families in educational tourism.
Government participation or policy formulation plays
an important role, and tourism institutions will also
affect educational tourism (Lei Rong, 2021).
Moreover, the rapid development of the social
economy has shaken the cooperative relationship, put
forward new requirements for the government. The
government's support for families will change
enthusiasm of stakeholders. Therefore, the benefit
relations need to be reconsidered.
To sum up, the different demands of stakeholders
inevitably lead to contradictions, that is the game
between stakeholders under the background of reform
in education. Scholars mainly focus on students and
families. They are mostly empirical research and
qualitative analysis. The traditional research methods
fail to reflect the game relationship and conduct
analysis. Therefore, this paper studies the
stakeholders through the evolutionary game method,
which is not only conducive to expanding the
research ideas and enriching the application fields of
the evolutionary game but also conducive to
clarifying the contradictions between stakeholders
and the mutually compromised interest relations and
strategies, providing effective gains for the
implementation of educational reform and the
development of educational tourism.
3 ASSUMPTIONS & VARIABLE
The relevant parameters are shown as follows:
r
1
: Excellence reputation of government
regulation;
r
2
: Revenue from educational tourism;
r
3
: Acquired knowledge of family;
k
1
: Profit sharing coefficient of school, 0< k
1
<1;
k
2
: Cost coefficient of family, 0< k
2
<1;
k
3
: Acquired Knowledge coefficient, 0< k
3
<1;
c
1
: Cost of government regulation;
c
2
: Cost of constructing tourism system in
schools;
j: Government rewards for schools;
b: Government subsidies for the family;
f: Government fines on schools.
Assumption 1 Educational tourism stakeholders
in this paper refer to the government, schools, and
families. Three stakeholders are limited rationality,
limited access to information, and commitment to
maximizing their interests.
Assumption 2 The income of educational
tourism of schools comes from family, so the cost of
family educational tourism should be directly
proportional to the total income of educational
tourism, but less than the total income. Therefore, the
family cost coefficient k
2
is introduced.
Assumption 3 Schools are the main position for
the development of educational tourism. Particularly,
when schools cooperate with institutions, educational
tourism is mostly outsourced to institutions, which
makes students have a poor sense of experience and
could not systematically acquire knowledge.
Therefore, this paper introduces the knowledge
acquisition coefficient k
3
.
Assumption 4 There are two strategic choices for
government subjects: Supervision and Non-
Supervision. The policy set is S
1
= (X
1
, X
2
). In
particular, when the government carries out
supervision, it rewards schools that incorporate
educational tourism into the education program and
build a complete system. In addition, the government
punishes schools that fail to implement the policy,
and grant subsidies to family participating in
activities. When the government is non-supervision,
schools and families will not be rewarded or punished
for any strategy. But the government can gain a good
reputation through regulation.
Assumption 5 There are two strategic choices for
school subjects: Non-Cooperation and Cooperation.
The policy set is S
2
= (Y
1
, Y
2
). The difference lies in
whether to choose to cooperate with institutions and
whether to build an educational tourism system
independently. When a school chooses to cooperate
with the institutions, the income should be shared
with the institution. The cost of cooperation should be
borne by the institution. When the school does not
cooperate with institutions, the school needs to build
an educational tourism system, and schools bear all
costs without sharing the profits.
Assumption 6 There are two strategic choices for
family subjects: Participation and Non-Participation.
The policy set is S
4
= (W
1
, W
2
). When the family
chooses to participate, the cooperation between
schools and institutions will reduce the acquisition of
family knowledge. Besides, the cost of family
participation in educational tourism is directly
proportional to the income of schools. The main
income of family participation in educational tourism
is reflected by the acquired knowledge. When the
family chooses not to participate, no matter what
strategies the schools and institutions adopt, it will not
have an impact on the family, and the knowledge
acquired through educational tourism is 0.
For the three-party game subjects, the strategy
choice of any two parties will affect the income of the
third party. Hence, in the case of incomplete
ICEMME 2022 - The International Conference on Economic Management and Model Engineering
458

information symmetry, stakeholders being difficult to
determine whether their strategy is the best, only
adjusting the strategy through the continuous game.
Suppose that the probability of the government
choosing to supervise is x and the probability of
choosing not to supervise is 1-x; The probability of
choosing cooperation is y and the probability of
choosing noncooperation is 1−y; The probability of
families choosing to participate is z and the
probability of choosing not to participate is 1− z.
Thus, the different game payment matrix is shown in
Table 1.
Table 1: Parameter.
Strategy GR SR FR
H
( X
,
Y
,Z
) 𝑟
−𝑐
−
𝑗
−𝑏
𝑗
+r
−c
𝑟
−k
𝑟
+𝑏
H
(X
,
Y
,Z
) 𝑟
+
𝑓
−𝑐
−𝑏 k
r
−
𝑓
k
𝑟
−k
k
𝑟
+𝑏
H
(X
,
Y
,Z
) 𝑟
−𝑐
−
𝑗
𝑗
−c
0
H
( X
,
Y
, Z
) 𝑟
+
𝑓
−𝑐
−
𝑓
0
H
( X
,
Y
,Z
) 0 r
−c
𝑟
−k
𝑟
H
(X
,
Y
,Z
) 0 k
r
k
𝑟
−k
k
𝑟
H
( X
,
Y
,Z
) 0 −c
0
H
(X
,
Y
,Z
) 0 0 0
4 MODEL ANALYSIS
4.1 The Expected Return
When the government selects "Supervision (U11)",
otherwise "Non-supervision (U12)"; When the school
chooses "Non-cooperation (U21)", otherwise
"Cooperation (U22)"; When the family chooses
"Participation (U31)", otherwise " Non-participation
(U32)"; As follows:
𝑈
=𝑟
−𝑐
−𝑧𝑏−𝑦
(
𝑗−𝑓
)
;
𝑈
=𝑥𝑟
−𝑥𝑐
−𝑥𝑧𝑏−𝑥𝑦
(
𝑗−𝑓
)
;
𝑈
=𝑥𝑗+𝑧r
−c
;
𝑈
=𝑧𝑘
𝑟
−𝑥𝑓;
𝑈
=𝑦𝑈
+
(
1−𝑦
)
𝑈
;
𝑈
=𝑦
(
𝑟
−k
𝑟
)
+
(
1−𝑦
)(
k
𝑟
−
k
k
𝑟
)
+𝑥𝑏;
𝑈
=𝑦𝑧
(
𝑟
−k
𝑟
)
+
(
1−𝑦
)
𝑧
(
k
𝑟
−
k
k
𝑟
)
+𝑥𝑧𝑏.
4.2 Replicated Dynamic Equation
The replicated dynamic equation of government
"Supervision" is:
F
(
𝑥
)
=
=𝑥
(
1−𝑥
)
[𝑟
−𝑐
−𝑧𝑏−𝑦
(
𝑗−𝑓
)
]
(1)
1) If
y=
(
)
, F ’ ( x)=0, F(x)=0, x is in a
stable state from 0 to 1.
2) If
y≠
(
)
, w h e n F ( x)=0, then x=0 or
x=1. Derive F(x)=0, then F’(x)=(1-2x) [r
1
-c
1
-f-z (b+f)
- yj].
a. If
y>
(
)
,
(
)
|
<
0,
(
)
|
>0, therefore, x=0 is the government's
stability strategy.
b. If
y<
(
)
,
(
)
|
>
0,
(
)
|
<0, therefore, x=1 is the government's
stability strategy.
Similarly, perform the same operation on F
(
𝑦
)
and F
(
𝑧
)
as follows:
The replicated dynamic equation when the
school chooses "Non-Cooperation " is:
F
(
𝑦
)
=
𝑑𝑦
𝑑𝑡
=𝑦
(
1−𝑦
)
[𝑥
(
𝑗+𝑓
)
+𝑧𝑟
(1 − 𝑘
)−𝑐
] (2)
1) If z=
(
)
(
)
, F
(
𝑦
)
=0,F
(
𝑦
)
=0,𝑧 is in
a stable state from 0 to 1.
2) If z≠
(
)
(
)
, when F
(
𝑦
)
=0,then 𝑦=
0 or 𝑦 = 1 . Derive F
(
𝑦
)
=0, then F
(
𝑦
)
=(1−
2𝑦)[𝑥
(
𝑗+𝑓
)
+𝑧𝑟
(1 − 𝑘
)−𝑐
].
① If z>
(
)
(
)
,
(
)
|
<0,
(
)
|
>
0 , therefore, 𝑦=0 is the schools' evolutionary
stability strategy.
②If z<
(
)
(
)
,
(
)
|
>0,
(
)
|
<0,
therefore, 𝑦=1 is the schools' evolutionary stability
strategy.
A Game of Stakeholders in Evolutional Tourism
459

The replicated dynamic equation when the family
chooses " Participation " is:
F
(
𝑧
)
=
=z
(
1−z
)
[𝑦
(
𝑟
−k
𝑟
)
+
(
1−
𝑦
)(
k
𝑟
−k
k
𝑟
)
+𝑥𝑏] (3)
1) If 𝑥=
(
)(
)
(
)
, F
(
𝑧
)
=
0, F
(z) = 0, 𝑧 is in a stable state from 0 to 1.
2) If 𝑥≠
(
)(
)
(
)
, when
F
(
𝑧
)
=0,then 𝑧=0 or 𝑧=1. Derive F
(
𝑧
)
=0 ,
then F
(
𝑧
)
=
(
1−2z
)
[𝑦
(
𝑟
−k
𝑟
)
+
(
1−
𝑦
)(
k
𝑟
−k
k
𝑟
)
+𝑥𝑏].
① If 𝑥>
(
)(
)
(
)
,
(
)
|
<0,
(
)
|
>0, therefore, 𝑧=0 is the
family's evolutionary stability strategy.
② If 𝑥<
(
)(
)
(
)
,
(
)
|
>0,
(
)
|
<0, therefore, 𝑧=1 is the
family's evolutionary stability strategy.
4.3 Stability Analysis
Referring to Xiaolan Liu's dynamic stability analysis
and Jixiang Zhang's equilibrium points stability
analysis (Xiaoyan Wang, 2017). This paper only
studies the stability of 8 points. The trace (trJ) and
determinant (detJ) of the Jacobian matrix were
obtained by derivation of the partial derivative of in
F(x), F(y) and F(z) can judge the stability of the
equilibrium points. When is less than 0, it belongs to
the saddle point. When both are greater than 0, it is
the unstable point. When is greater than 0 and r is less
than 0, it belongs to the stable point. The 8
equilibrium points are calculated according to the
Jacobi matrix (Xiaoyan Wang, 2017), as shown in
Table 2. Ultimately, when j > r1, k2 + k1 < 1, k3r3 <
k1k2r2, and k2 r2 < r3.
① For the point 𝑃
, when 𝑟
−𝑐
−𝑓<
0 and 𝑘
𝑟
−𝑘
𝑘
𝑟
>0, the larger the value of
𝑘
𝑟
, and the smaller the value of 𝑘
𝑘
𝑟
, then the
more unstable the value of 𝑃
.
②For the point 𝑃
, when 𝑟
−𝑐
−𝑗<0,𝑗+
𝑓−𝑐
> 0 and 𝑘
𝑟
−𝑘
𝑘
𝑟
>0, the larger the
value of 𝑐
,𝑗 and 𝑓, and the smaller the value of 𝑟
,
𝑐
and 𝑘
𝑘
𝑟
, then the more unstable the value of
𝑃
.
③ For the point 𝑃
, when 𝑟
−𝑐
−𝑗>
0 and 𝑟
−𝑘
𝑟
>0, the larger the value of 𝑟
,
𝑐
and 𝑟
, and the smaller the value of 𝑗、𝑓 and 𝑘
𝑟
,
then the more unstable the value of 𝑃
.
④For the point 𝑃
, when 𝑟
−𝑐
−𝑓−𝑏>0,
(
1−𝑘
)
𝑟
−𝑐
> 0 and 𝑘
𝑟
−𝑘
𝑘
𝑟
>0 , the
larger the value of
𝑟
𝑎𝑛𝑑 𝑘
𝑟
, and the smaller the value of 𝑐
,𝑓,
𝑏, 𝑘
𝑎𝑛𝑑 𝑘
𝑘
𝑟
, then the more unstable the value
of 𝑃
.
⑤For the point 𝑃
, when 𝑗−𝑟
+𝑐
>0,𝑐
−
𝑗−𝑓>0 and 𝑟
−𝑘
𝑟
+𝑏>0 , the larger the
value of 𝑟
,𝑏,𝑐
𝑎𝑛𝑑 𝑐
,
and the smaller the value of 𝑟
, 𝑓 𝑎𝑛𝑑 𝑘
𝑟
, then
the more unstable the value of 𝑃
.
⑥ For the point 𝑃
, when 𝑐
−𝑟
+𝑓+𝑏>
0,𝑗+𝑓+
(
1−𝑘
)
𝑟
−𝑐
>0 and 𝑘
𝑘
𝑟
−
𝑘
𝑟
−𝑏>0, the larger the value of 𝑘
𝑘
𝑟
,𝑐
, 𝑓,
𝑏 , 𝑗 and 𝑟
, 𝑟
,𝑘
𝑟
,𝑏,𝑐
and 𝑘
, then the more
unstable the value of 𝑃
.
⑦ For the point 𝑃
, when 𝑟
−𝑐
−𝑗−𝑏>
0,
(
1−𝑘
)
𝑟
−𝑐
< 0 and 𝑘
𝑟
−𝑟
−𝑏>0, the
larger the value of 𝑐
, 𝑏, 𝑗 and 𝑟
, 𝑘
𝑟
,𝑟
, 𝑐
and
𝑘
, then the more unstable the value of 𝑃
.
⑧For the point 𝑃
, when 𝑐
−𝑟
+𝑓+𝑏>0,
𝑐
−
(
1−𝑘
)
𝑟
−𝑗−𝑓>0 and 𝑘
𝑟
−𝑟
−𝑏>
0, the larger the value of 𝑐
, 𝑏, 𝑐
and 𝑘
𝑟
, 𝑟
,𝑗, 𝑟
,
𝑏 and 𝑘
, then the more unstable the value of 𝑃
.
To sum up, the government tends to the
"Supervision" strategy, that is to pay more attention
to the government's reputation, improve the family's
knowledge acquisition, reduce the cost of school
construction of education system and the cost of
family participation in educational tourism, which
can promote the government's "Supervision"
strategy; The schools tend to the "Non-Cooperation"
strategy, that is, to improve the reward for colleges
and universities, reduce the proportion of profit
sharing when schools cooperate with institutions and
reduce the cost of building the research education
system, which can promote the construction of the
research education system; The family tends to the "
Participation "strategy, that is, to increase the
knowledge acquired by the family in educational
tourism and the allowance for educational tourism,
and reduce the profit sharing ratio and income when
schools cooperate with institutions, which can
promote family to choose to "Participation"
educational tourism.
ICEMME 2022 - The International Conference on Economic Management and Model Engineering
460

Table 2: Equilibrium point.
Equilibrium
point
trJ detJ
𝑃
(0,0,0)
(
𝑟
−𝑐
−
𝑓
)
−𝑐
+(𝑘
𝑟
−𝑘
𝑘
𝑟
)
(
𝑟
−𝑐
−
𝑓
)
(−𝑐
)(𝑘
𝑟
−𝑘
𝑘
𝑟
)
𝑃
(1,0,0)
(
−1
)(
𝑟
−𝑐
−𝑗
)
+
(
𝑗+
𝑓
−𝑐
)
+(𝑘
𝑟
−𝑘
𝑘
𝑟
+𝑏)
(
−1
)(
𝑟
−𝑐
−𝑗
)(
𝑗+
𝑓
−𝑐
)
(𝑘
𝑟
−𝑘
𝑘
𝑟
+𝑏)
𝑃
(0,1,0)
(
𝑟
−𝑐
−𝑗
)
+𝑐
+(𝑟
−𝑘
𝑟
)
(
𝑟
−𝑐
−𝑗
)
𝑐
(𝑟
−𝑘
𝑟
)
𝑃
(0,0,1)
(
𝑟
−𝑐
−
𝑓
−𝑏
)
+
[
(
1−𝑘
)
𝑟
−𝑐
]
+(𝑘
𝑟
−𝑘
𝑘
𝑟
)
(
𝑟
−𝑐
−
𝑓
−𝑏
)
[
(
1−𝑘
)
𝑟
−𝑐
]
(𝑘
𝑟
−𝑘
𝑘
𝑟
)
𝑃
(1,1,0)
(
𝑗−𝑟
+𝑐
)
+
(
𝑐
−𝑗−
𝑓
)
+(𝑟
−𝑘
𝑟
+𝑏)
(
𝑗−𝑟
+𝑐
)(
𝑐
−𝑗−
𝑓
)
(𝑟
−𝑘
𝑟
+𝑏)
𝑃
(1,0,1)
(
𝑐
−𝑟
+
𝑓
+𝑏
)
+
[
𝑗+
𝑓
+
(
1−𝑘
)
𝑟
−𝑐
]
+(𝑘
𝑘
𝑟
−𝑘
𝑟
−𝑏
)
(
𝑐
−𝑟
+
𝑓
+𝑏
)
[
𝑗+
𝑓
+
(
1−𝑘
)
𝑟
−𝑐
]
(𝑘
𝑘
𝑟
−𝑘
𝑟
−𝑏)
𝑃
(0,1,1)
(
𝑟
−𝑐
−𝑗−𝑏
)
−[
(
1−𝑘
)
𝑟
−𝑐
]
+(𝑘
𝑟
−𝑟
−𝑏)
(
𝑟
−𝑐
−𝑗−𝑏
)
[𝑐
−
(
1−𝑘
)
𝑟
](𝑘
𝑟
−𝑟
−𝑏)
𝑃
(1,1,1)
(
𝑐
−𝑟
+𝑗+𝑏
)
+[𝑐
−
(
1−𝑘
)
𝑟
−𝑗
−
𝑓
]+(𝑘
𝑟
−𝑟
−𝑏)
(
𝑐
−𝑟
+𝑗+𝑏
)
[𝑐
−
(
1−𝑘
)
𝑟
−𝑗
−
𝑓
](𝑘
𝑟
−𝑟
−𝑏)
Equilibrium
p
oint
trJ detJ
𝑃
(0,0,0)
(
𝑟
−𝑐
−
𝑓
)
−𝑐
+(𝑘
𝑟
−𝑘
𝑘
𝑟
)
(
𝑟
−𝑐
−
𝑓
)
(−𝑐
)(𝑘
𝑟
−𝑘
𝑘
𝑟
)
𝑃
(1,0,0)
(
−1
)(
𝑟
−𝑐
−𝑗
)
+
(
𝑗+
𝑓
−𝑐
)
+(𝑘
𝑟
−
𝑘
𝑘
𝑟
+𝑏)
(
−1
)(
𝑟
−𝑐
−𝑗
)(
𝑗+
𝑓
−𝑐
)
(𝑘
𝑟
−
𝑘
𝑘
𝑟
+𝑏)
𝑃
(0,1,0)
(
𝑟
−𝑐
−𝑗
)
+𝑐
+(𝑟
−𝑘
𝑟
)
(
𝑟
−𝑐
−𝑗
)
𝑐
(𝑟
−𝑘
𝑟
)
𝑃
(0,0,1)
(
𝑟
−𝑐
−
𝑓
−𝑏
)
+
[
(
1−𝑘
)
𝑟
−𝑐
]
+(𝑘
𝑟
−𝑘
𝑘
𝑟
)
(
𝑟
−𝑐
−
𝑓
−𝑏
)
[
(
1−𝑘
)
𝑟
−𝑐
]
(𝑘
𝑟
−𝑘
𝑘
𝑟
)
𝑃
(1,1,0)
(
𝑗−𝑟
+𝑐
)
+
(
𝑐
−𝑗−
𝑓
)
+(𝑟
−𝑘
𝑟
+𝑏)
(
𝑗−𝑟
+𝑐
)(
𝑐
−𝑗−
𝑓
)
(𝑟
−𝑘
𝑟
+𝑏)
𝑃
(1,0,1)
(
𝑐
−𝑟
+
𝑓
+𝑏
)
+
[
𝑗+
𝑓
+
(
1−𝑘
)
𝑟
−
𝑐
]
+(𝑘
𝑘
𝑟
−𝑘
𝑟
−𝑏)
(
𝑐
−𝑟
+
𝑓
+𝑏
)
[
𝑗+
𝑓
+
(
1−𝑘
)
𝑟
−
𝑐
]
(𝑘
𝑘
𝑟
−𝑘
𝑟
−𝑏)
𝑃
(0,1,1)
(
𝑟
−𝑐
−𝑗−𝑏
)
−[
(
1−𝑘
)
𝑟
−𝑐
]+
(𝑘
𝑟
−𝑟
−𝑏)
(
𝑟
−𝑐
−𝑗−𝑏
)
[𝑐
−
(
1−𝑘
)
𝑟
](𝑘
𝑟
−𝑟
−𝑏)
𝑃
(1,1,1)
(
𝑐
−𝑟
+𝑗+𝑏
)
+[𝑐
−
(
1−𝑘
)
𝑟
−𝑗−
𝑓
]+(𝑘
𝑟
−𝑟
−𝑏)
(
𝑐
−𝑟
+𝑗+𝑏
)
[𝑐
−
(
1−𝑘
)
𝑟
−𝑗
−
𝑓
](𝑘
𝑟
−𝑟
−𝑏)
A Game of Stakeholders in Evolutional Tourism
461
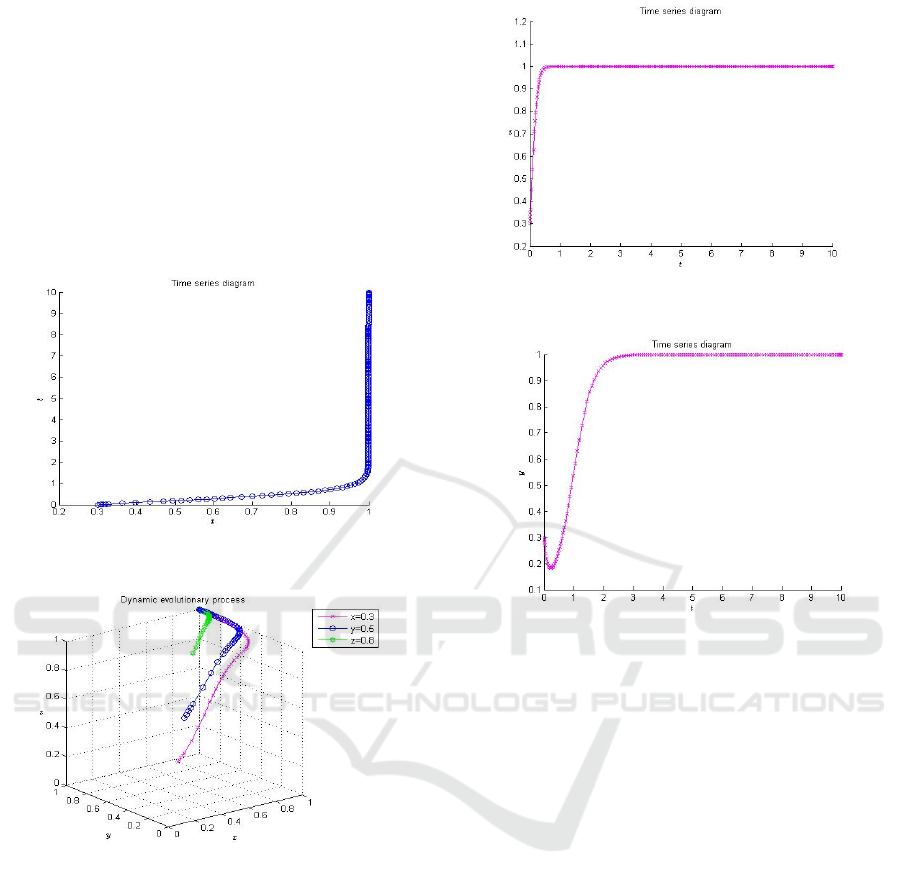
5 SIMULATION ANALYSIS
Considering the current situation of educational
tourism, we assign the variables (r1=10, r2=20, r3=20,
k1=0.3, k2=0.5, k3=0.8, c1=5, c2=10, j=2, f=1, b=1)
and draw a graph among tripartite evolutionary game
(Figure 1) and evolution scheme with time (Figure 2)
through Matlab. X-axis, Y-axis, and Z-axis mean
respectively the strategy choice of the government, the
school, and the family, which the better equilibrium
point is (1,1,1) in Figure 1.
Figure 1: Dynamic evolutionary process.
Figure 2: Time series diagram (t-x).
Figure 2, Figure 3, and Figure 4 mean the strategy
change over time among the government, the school,
and the family in Figure 2. For example, the
government would like to select “Supervision” and
the family would like to select “Non-cooperation”
under existing parameter values. In particular, the
school prefers to select “Participation” first and then
becomes “Non-participation” in Figure 3: Time series
diagram (t-y).
Figure 3: Time series diagram (t-y).
Figure 4: Time series diagram (t-z).
6 CONCLUSIONS
Educational tourism is an innovative form of
connection between theoretical learning and social
education. The results show that the government and
family not only influence each other's strategic
choices but also affect the decision-making of
schools. The government's reasonable setting of
rewards or subsidies for schools and families can
effectively promote the school's construction of
educational tourism education system and the
family's enthusiasm to participate in educational
tourism. The knowledge acquired by the family has a
positive impact on the government's supervision and
the school's construction of educational tourism
education system.
The government should implement the
responsibility decomposition and responsibility
boundary to prevent students from falling into the
vacuum of management. And the government should
ensure financial support and coordinate the resources
of all social parties. Schools should incorporate it into
the education plan and train professional teachers to
ICEMME 2022 - The International Conference on Economic Management and Model Engineering
462

build an assessment mechanism. Meantime, schools
should continue to carry out and improve educational
tourism according to students' needs, and the process
of educational reform. The family should correct their
views on educational tourism and recognize that
educational tourism could build a learning
community for students and effectively improve
students' social participation ability. And the family
should actively participate in the educational tourism
organized by the schools and complete the curriculum
evaluation.
In short, student harmonious development
requires the joint efforts of the three stakeholders
under the background of educational reform lies in
the cooperation and game among the government,
schools, and families.
ACKNOWLEDGEMENTS
The author(s) received the financial support of
Sichuan Development Research Centre of Study
Travel (YX22-08) and Sichuan Liangshan Science
and Technology Plan Projects (21ZDFY0152) for the
research, authorship, and/or publication of this article.
REFERENCES
Bo Ma. (2020). On the development of tourism in China --
the development of educational tourism theory.
Tourism Tribune, 35 (09): 1.
Hao Zhang. (2017). The soul of educational tourism is
practical education. People's education, 2017(23):16-
18.
Lei Rong. (2021). On path dependence in the promotion of
educational tourism. Forum on Education Research,
2021 (04): 61-65.
Meaux J B, Saviers B, Traywick L. (2021). Effects of study
abroad on cultural and interprofessional competencies.
Nurse Education Today, 103(2):104928.
Roberson, Donald N. (2018). Learning while traveling: The
school of travel. Journal of Hospitality Lsure Sport &
Tourism Education, 22:14- 18.
Shujuan Yu, Yuan Wang, Huijun Wu. (2017). Causes and
Countermeasures of educational tourism problems in
China. Journal of Teaching and Management, 2017
(19): 11-13.
Xiaoyan Wang. (2017). Give full play to the important role
of educational tourism in Building Morality and
cultivating people. People's Education, 2017 (23): 13-
15.
Yan Lin. (2021). The mission and responsibility of
educational publishing under the "double reduction"
policy. Editors Monthly, 2021(06):70-76.
A Game of Stakeholders in Evolutional Tourism
463
