
On the Performance of UAV-Assisted IRS-NOMA Networks
Fan Gao
1,†
, Shuangshuang Zhao
1,‡
, Yu Zhou
1,§
, Chao Zhou
1
, Gaoying Cui
1,**
, Zhen Zhang
1
and Minghe Mao
2,*
1
Marketing Service Center of State Grid Jiangsu Electric Power Co., Ltd, Nanjing, China
2
School of Computer and Information, Hohai University, Nanjing, China
zhngen@outlook.com,
*
maominghe@hhu.edu.cn
Keywords: IRS, Passive Relay, NOMA, OFDMA, User Rate.
Abstract: In order to further improve the spectral efficiency of the communication system, we introduce the non-
orthogonal multiple access (NOMA) technique into the UAV-IRS system. Specifically, a UAV-IRS
communication system model using the NOMA scheme is first proposed. Then a physical-optics based IRS
path loss model is used to derive the received signal-to-noise ratio and ergodic capacity formulas under the
two-user scenario. Finally, we compare the total user capacity of the proposed system under the OFDMA
scheme with the NOMA scheme. The numerical results show that the NOMA scheme improves the total user
capacity by almost two times compared to the OFDMA scheme, and the area of the IRS is found to have a
significant impact on the system performance.
1 INTRODUCTION
In the face of major natural disasters and emergencies,
effective emergency communication is of great
significance to improve rescue efficiency and
safeguard people's lives. When an accident or disaster
occurs, local fixed base stations usually cannot be
used normally, while UAV-based relays (unmanned
aerial vehicles) in next-generation communication
systems have better flexibility, especially for remote
areas or areas lacking base station facilities. UAV-
based air relay can be quickly built. Therefore, UAVs
make an important contribution to the orderly
response to emergencies and reduce their harm as
much as possible. In response to the problem of scarce
spectrum resources and the destruction of base
stations in emergency communication scenarios, it is
important to improve the spectrum efficiency of
UAVs.
Non-orthogonal multiple access (NOMA)
technology is considered as a key technology for 5G
and even next-generation wireless communication
systems because of its high spectral efficiency and
good fairness. In power domain NOMA systems,
users with good channel conditions are assigned
*
Correspondence
lower power allocation factors, while users with poor
channel conditions are assigned higher power
allocation factors. At the receiver side, SIC
(successive interference cancellation) technique is
used to eliminate the interference of part users and to
realize more users in the same time frequency domain
multiplexing, thus improving the spectral efficiency.
The introduction of power domain NOMA into
UAV relay systems allows the full utilization of
power domain resources, thus ensuring better
transmission of signals (downlink) from the ground
base station for ground users or better transmission of
signals (uplink) from the base station for ground
users.
The application of IRS in NOMA has been
discussed by scholars (Z. Ding, 2020) (M. Fu, 2019).
In (Z. Ding, 2020) explored the trade-off between
reliability and complexity of relaying and IRS. The
work in (M. Fu, 2019) jointly optimizes transmit
beamforming and IRS phase shift matrix to minimize
the transmission power of the base station. Related
studies under large-scale MIMO-NOMA systems
have been conducted in (L. Dai, 2019) (W. Hao,
2017) (B. Wang, 2017) (W. Yuan, 2017) (Y. Zhao,
2017). The work in (L. Dai, 2019) maximizes the total
Gao, F., Zhao, S., Zhou, Y., Zhou, C., Cui, G., Zhang, Z. and Mao, M.
On the Performance of UAV-Assisted IRS-NOMA Networks.
DOI: 10.5220/0012034800003612
In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 709-714
ISBN: 978-989-758-622-4; ISSN: 2975-9463
Copyright
c
2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
709

achievable user rate by jointly optimizing the
allocated power and the power splitting factor, while
guaranteeing the user base reception rate and power.
The energy efficiency of large-scale MIMO-NOMA
systems is maximized by optimizing the power
allocation in (W. Hao, 2017). In (B. Wang, 2017),
NOMA is used for the first time in beam-space
MIMO to maximize the total user achievable rate
through power allocation. NOMA is applied to HP
precoding structures under large-scale MIMO
systems in order to improve the system performance
by exploiting the characteristics of NOMA in (W.
Yuan, 2017). Total achievable user rate is maximized
by designing digital precoding in (Y. Zhao, 2017).
Studies on UAV-NOMA systems, classified by
channel characteristics, mainly include air-to-ground
(A2G, air to ground) channels, Nakagami-m fading
channels, path loss channels, and Rice channels. In
(M. F. Sohail, 2018), the author investigates the sum-
rate maximization problem in different urban
environments and also compares the effect of fixed
and dynamic UAV heights to reduce energy
consumption with the UAV-NOMA system
considering A2G channels. Under the same model,
the work in (M. F. Sohail, 2019) considers the multi-
user quality of service constraint and equates the
energy efficiency maximization problem to a
nonlinear fractional programming problem, where the
user grouping scheme in channel conditions is
considered. For UAV-NOMA systems considering
Nakagami-m fading channels, a UAV-centric offload
operation strategy and a user-centric emergency
communication strategy are proposed for dense
networks and scenarios where all users need to be
served simultaneously in order to improve the system
coverage probability in (T. Hou, 2019). In (T. Hou,
2019), the effect of LoS links and NLoS (non-line of
sight) links is considered, and a stochastic geometric
model is used to model the location of users and
UAVs, and a closed-form expression for the system
outage probability and traversal rate is derived. For
the LoS link and NLoS link scenarios, the work in (M.
Liu, 2020) first determines the user grouping scheme
based on the access priority, then uses a message
passing algorithm for sub-channel assignment, and
finally jointly optimizes the transmit power of the
UAV-NOMA system.
Most of the above works on the IRS-NOMA
system do not consider the path loss model, but only
focus on the small-scale fading model. The UAV
system is mainly affected by the line of sight (LoS)
link, so the conventional Rayleigh fading is not
suitable for representing its channel characteristics.
Importantly, the conjecture in (E. Basar, 2019) that
the received power would be proportional to 1/(d+r)
2
.
That conjecture might hold for an infinitely large IRS
or in the near-field, if the IRS is configured to act as
a mirror, but probably not in the far-field setup studied
herein. In particular, one cannot use multiple infinite-
sized IRS as in (E. Basar, 2019). So we use a pathloss
model based on physical optics techniques for an IRS
that is configured to reflect an incoming wave from a
far-field source towards a receiver in the far-field to
study the performance of our proposed system.
Although UAV-IRS and NOMA have been
studied in great detail, for all I know, system
combining the two together has not been studied yet.
UAV-IRS can provide additional flexibility to
communication systems, improve service coverage,
and avoid service blind spots. Meanwhile, IRS as a
passive relay can alleviate the technical problem of
limited energy due to UAV battery limitations. And
the introduction of power domain NOMA can further
ensure the quality of service for edge users, thus
improving the average system performance.
This paper mainly studies the system performance
of the UAV-assisted IRS-NOMA communication
system. We compare the results with the OFDMA
method and verify that the UAV-assisted IRS-NOMA
communication system has obvious advantages over
OFDMA in terms of spectral efficiency and
communication capacity. The main contributions of
this paper are as follows:
(1) An IRS-NOMA communication network
model based on UAV assistance is developed for the
case of multiple groups of users in a single cell of the
downlink. An UAV acts as an airborne passive relay
station equipped with an IRS and serves multiple
ground users, which are evenly divided into groups.
According to the traditional IRS-NOMA system
setup, we assume that the number of users in each
group is 2, i.e., each group contains only one near-end
user and one far-end user.
(2) When considering the path loss model, in order
to further explore the communication performance of
the UAV-assisted IRS-NOMA system, we consider
both large-scale fading and small-scale fading. The
IRS path loss model based on the physical optics
negates a past erroneous path loss model (Özdogan,
2020). In terms of small-scale fading, we adopt the
LoS fading channel setup commonly used in
traditional UAV wireless communication systems.
(3) To verify the performance of our proposed
system, we compare the system with NOMA scheme
ISAIC 2022 - International Symposium on Automation, Information and Computing
710

and the system with OFDMA scheme. The formulas
of the receiver SNR and throughput of the two
schemes are deduced respectively. The numerical
results show that under the same system settings, the
NOMA scheme has a greater improvement compared
to the OFDMA scheme.
The rest of this paper is organized as follows. In
Section 2, we introduce the system model. In Section
3, we use a pathloss model based on physical optics
to derive the SNR and the capacity of users. In Section
4, numerical results are provided to demonstrate the
performance of proposed system. Conclusions are
presented in Section 5.
2 SYSTEM MODEL
Consider a downlink UAV-NOMA system as shown
in Fig.1. The system consists of a ground base station
with a single antenna, fixed at a specified altitude H
BS
.
An UAV equipped IRS operates at a specified
location and the ground coverage of it is a circle of
radius R. Furthermore, the system has M single-
antenna terrestrial users. Assuming that M users are
divided into 𝑇 groups, each group has 2 users denoted
as 𝑢
, the set of group numbers is defined as
𝑡𝜖{1,2,…,𝑇} and the set of user serial numbers is
𝑘𝜖{1,2}. 𝑢
of all groups are uniformly distributed in
circles with radius 𝑟
, while 𝑢
of all groups are
uniformly distributed in Distributed within a circle of
outer radius 𝑟
and inner radius 𝑟
, where 𝑟
<𝑟
. In
addition, users in a group share the same time-
frequency domain resources by using the power
domain NOMA technology, and orthogonal multiple
access (OMA, orthogonal multiple access) is
maintained between each group, that is, inter-group
interference is ignored. Set up a three-dimensional
Cartesian coordinate system as shown in Fig.1, with
the base station as the coordinate origin,
perpendicular to the ground as the z-axis, and the line
between the base station and the projection of UAV
on the ground as the x-axis. Then the coordinates of
the transmitter are (0, 0, H
BS
), and the coordinates of
the UAV are (x
UAV
, 0, H
UAV
) (H
UAV
> H
BS
).
The base station transmits a signal 𝑥
to user k,
where 𝐸
[
|
𝑥
|
]
=1, with transmission power 𝑃
.
The sum of 𝑃
is restricted to 𝑃 at maximum. In the
NOMA, 𝑥
and 𝑥
are superposition coded as (Y.
Saito, 2013)
𝑥=
𝑃
𝑥
+
𝑃
𝑥
(1)
Figure 1: A system diagram for UAV-IRS under two-user
scenario
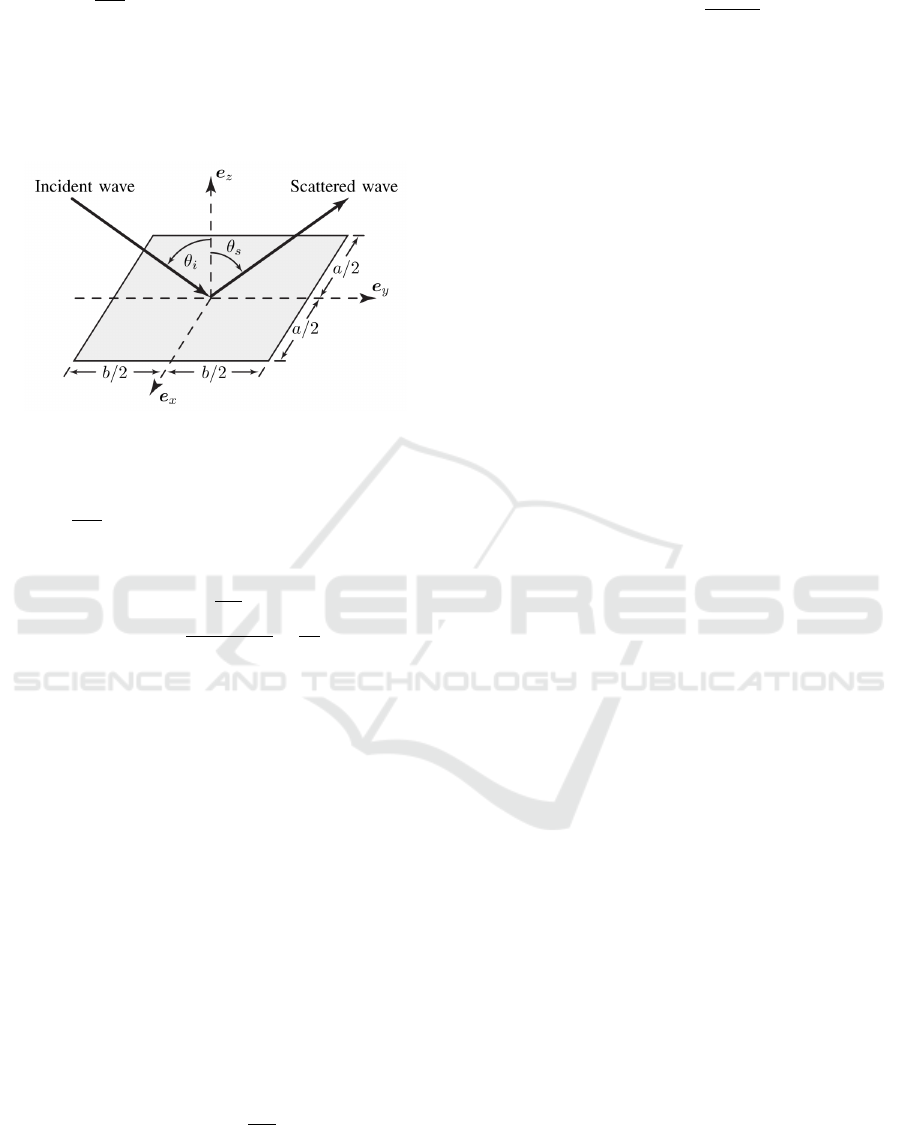
We consider the UAV to carry a rectangular,
perfectly conductive IRS plate of size 𝑎×𝑏 with
negligible thickness, lying in a horizontal plane
(spanned by 𝑒
,𝑒
). For the sake of argument, we
assume that the polarization of the source is such that
the electric field is parallel to 𝑒
and the 𝐻 field lies
in the plane spanned by 𝑒
and 𝑒
. Let 𝜃
∈
[
0,𝜋/2
]
denote the angle of incidence, that is, the angle
between the Poynting vector of the wave and 𝑒
. The
setup is shown in Fig.2. When including the reflected
path from the IRS, we get the received signal as:
𝐺=
𝐼
ℎ
Φℎ
𝑥+ 𝜔 (2)
We use a pathloss model based on physical optics
techniques for an IRS that is configured to reflect an
incoming wave from a far-field source towards a
receiver in the far-field which is illustrated in Fig.2.
The pathloss can be expressed as:
𝐼
=
(
)
(
)
cos
(
𝜃
)
(3)
where𝜃
∈ [0,π/2] denote the angle of incidence, a
and b is the width and the length of the IRS. Suppose
the IRS consists of 𝑁
×𝑁
=𝑁 elements, each
having the size a 𝑎/𝑁
×b/𝑁
. d and r are the
distance between the source and the IRS and the
distance between IRS and the user. ℎ
=
[e
,…,e
,…,e
]
and ℎ
=
[e
,…,e
,…,e
]
are the normalized LoS
channels between the source and IRS and the IRS and
receiver, respectively. 𝜔~𝑁(0,𝜎
) is additive noise,
and the surface phases of each surface element are
stacked in Φ=diag
(
e
,…,e
,…,e
)
, which
is a diagonal matrix.
An equivalent way to write the received signal is
On the Performance of UAV-Assisted IRS-NOMA Networks
711
𝐺=
𝐼
e
(
)
𝑥+𝜔 (4)
The IRS can select Φ to keep the received signal
power maximum. It can be easily seen from the
expression that the optimal choice of 𝜙
which
maximizes the instantaneous SNR is 𝜙
=𝜓
+
𝜓
. Notably, this requires the channel
Figure 2: An incident wave is reflected by a × b IRS.
phases are known to the RIS. When phase-align all
the terms in (4), received signal can be simplified to
𝐺=𝑁
𝐼
𝑥+𝜔 and the signal-to-noise ratio
(SNR) can be obtained is
𝑆𝑁𝑅=
=
(5)
In the NOMA scenario, the successive
interference cancellation (SIC) process is
implemented at the receiver. The optimal order for
decoding is in the order of the increasing channel gain
normalized by the noise and inter-cell interference
power. Based on this order, any user can correctly
decode the signals of other users whose decoding
order comes before that user for interference
cancellation. Thus, in the two-user case, the closer
user can remove the inter-user interference from the
farther user whose receive power is lower. The farther
user does not perform interference cancellation since
it comes first in the decoding order. Denote the closer
user as u
1
, the farther user as u
2
. Then we can obtain
the signal-interference-to-noise ratio (SINR) of the
u
1
:
𝑆𝐼𝑁𝑅
=
(6)
the signal-interference-to-noise ratio (SNR) of u
2
is
𝑆𝐼𝑁𝑅
=
(7)
Assuming that the overall system transmission
bandwidth is 1 Hz. The throughputs of two users are
represented as
𝑅
=𝑙𝑜𝑔
(
1+𝑆𝐼𝑁𝑅
)
(8)
𝑅
=𝑙𝑜𝑔
(
1+𝑆𝐼𝑁𝑅
)
(9)
In the OFDMA with orthogonal user multiplexing
scenario, where the bandwidth of 𝛼(0 < α < 1)Hz
is assigned to u
1
and the remaining bandwidth,1−
𝛼Hz, is assigned to u
2
, the throughputs of two users
are represented as
𝑅
=𝛼𝑙𝑜𝑔
(
1+𝑆𝐼𝑁𝑅
)
(10)
𝑅
=(1−𝛼)𝑙𝑜𝑔
(
1+𝑆𝐼𝑁𝑅
)
(11)
3 NUMERICAL RESULTS
In this section, computer simulation results are
presented to demonstrate the performance of UAV-
IRS under OFDMA scheme and NOMA scheme. In
Fig.3, the performance of UAV-IRS is studied by
focusing on the two-user case. Assuming that the
height of the base station H
BS
is 15m, and the UAV
which carries a square IRS with a side length of 1m is
fixed at (20,0,15). The gain of one-antenna
transmission and one-antenna reception are G
t
=15dBi
and G
r
=10dBi. Total transmission power is
P=60dBm. The bandwidth of both schemes is 1Hz. In
the OFDMA scheme, when equal bandwidth and
equal transmission power are allocated to each user,
the user rates are calculated according to (10) and (11)
as R
1
=1.4555 bps/Hz and R
2
=0.9446 bps/Hz,
respectively. On the other hand, in the NOMA
scheme, when the power allocation is inversely
proportional to the distance from the user to the IRS,
the user rates are calculated according to (8) and (9)
as R
1
=1.7660 bps/Hz and R
2
=1.2921 bps/Hz,
respectively. The corresponding gains of NOMA
comparing with OFDMA are 21% and 37% for u
1
and
u
2
, respectively.
ISAIC 2022 - International Symposium on Automation, Information and Computing
712
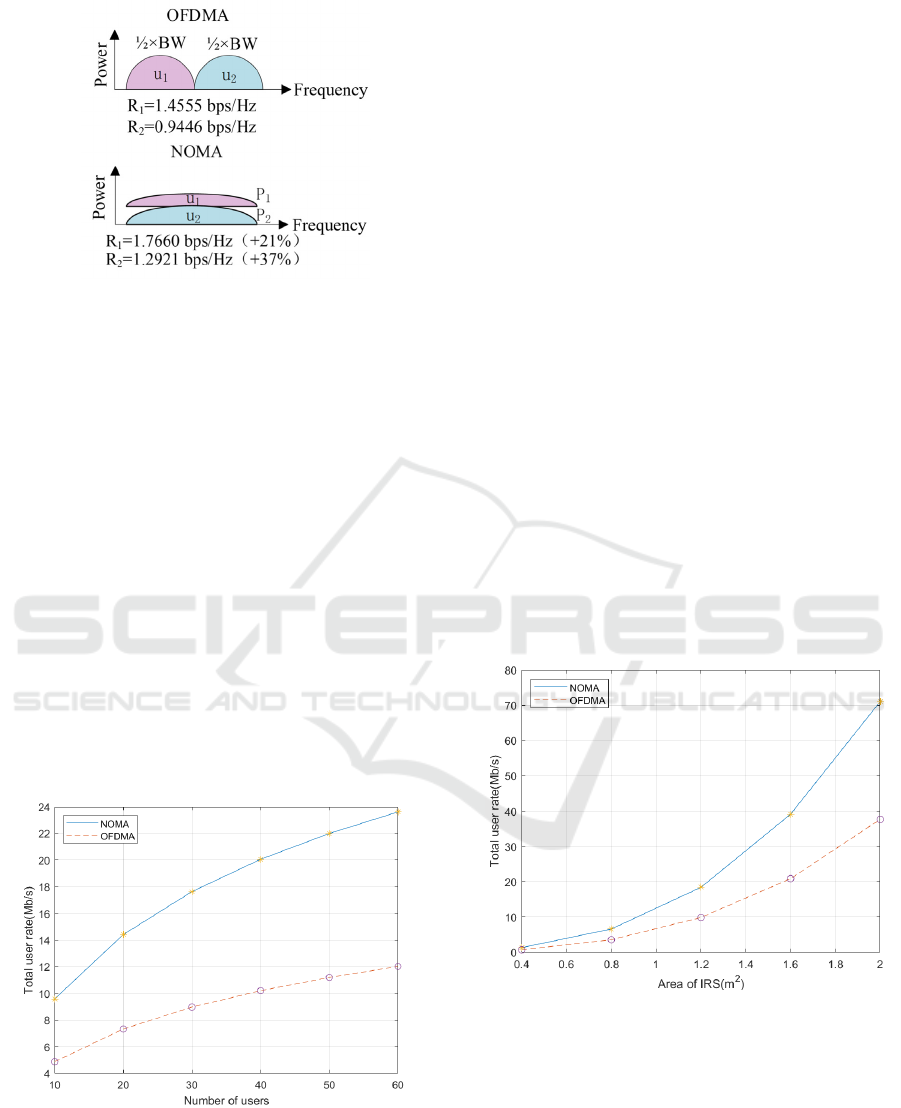
Figure 3: OFDMA vs. NOMA (two-user case).
Fig.4 showed that the total user rate of the
proposed UAV-IRS under multi-group of user
scenarios. Assuming the total bandwidth is 200MHz.
The cell radius of the users is set to r
1
=30m, r
2
=100m.
In the OFDMA scheme, all users share bandwidth
equally. In the NOMA scheme, all user groups (each
group includes two users) share bandwidth equally.
Other settings are the same as before. As can be seen
in Fig.4, when the number of users increases from 10
to 60, we find that there is almost a two-fold gain
when comparing the total user rate under the NOMA
scheme with the total user rate under the OFDMA
scheme. Further, Fig.4 shows that when the number
of users is small, it has a greater impact on the total
user rate than the big user number. For example, the
total user rate increases 49.4% when the number of
users increases from 10 to 20. However, the total user
rate only increases 6.8% when the number of users
increases from 50 to 60.
Figure 4: Comparison of the total user rate of two schemes
under different number of users.
Fig.5 shows the effect of different IRS areas on the
total user rate. It can be seen that when the IRS area
is very small, the total user rate is quite unsatisfactory.
The area of the IRS has a significant impact on the
total rate which can be explained by the pathloss
expression (3) as the second term which shows that
the received signal power is proportional to the square
of the IRS area. So, choosing a larger IRS is critical
to a better system performance. However, in practice,
the carrying capacity of UAV is limited. In addition,
as the IRS area increases, it will affect the flight
duration of the UAV. A trade-off must be made in the
practical application scenarios. The figure also shows
that the proposed NOMA scheme also has almost
two-fold increase compared with OFDMA scheme
under different IRS areas.
4 CONCLUSION
In this paper, we have proposed a UAV-assisted IRS-
NOMA scheme to improve the performance of the
cellular network. We have first constructed a practical
system working model under two-user scenario.
Then, we have used a pathloss model based on
physical optics techniques to derive the received
signal-to-noise ratio and throughput under two-user
scenario. Finally, numerical simulation has been
carried out to compare the total user rate under
OFDMA scheme and NOMA scheme.
Figure 5: Comparison of the total user rate of two schemes
under different IRS areas.
It has been found that using the NOMA scheme
can bring almost twice the performance improvement
under the same transmission power and total
bandwidth. Meanwhile, we have investigated the
impact of IRS area on the total user rate, where a
larger IRS area will bring rapid system performance
improvement, while a too-small IRS area will result
On the Performance of UAV-Assisted IRS-NOMA Networks
713

in awful system performance. In further research, we
will study the impact brought by mobile UAV
platform, and different channel models and non-ideal
IRS on the system performance.
There are several possible future works. The first
is to consider the impact of UAV’s position on the
system performance. The second is to jointly optimize
the power allocation and beamforming design to
minimize the power consumption. The third is to
explore the performance of IRS-NOMA with finite
resolution beamforming.
REFERENCES
Z. Ding, R. Schober and H. V. Poor, "On the Impact of
Phase Shifting Designs on IRS-NOMA," in IEEE
Wireless Communications Letters, vol. 9, no. 10, pp.
1596-1600, Oct. 2020.
M. Fu, Y. Zhou and Y. Shi, "Intelligent Reflecting Surface
for Downlink Non-Orthogonal Multiple Access
Networks," 2019 IEEE Globecom Workshops (GC
Wkshps), 2019, pp. 1-6.
L. Dai, B. Wang, M. Peng and S. Chen, "Hybrid Precoding-
Based Millimeter-Wave Massive MIMO-NOMA With
Simultaneous Wireless Information and Power
Transfer," in IEEE Journal on Selected Areas in
Communications, vol. 37, no. 1, pp. 131-141, Jan. 2019.
W. Hao, M. Zeng, Z. Chu and S. Yang, "Energy-Efficient
Power Allocation in Millimeter Wave Massive MIMO
With Non-Orthogonal Multiple Access," in IEEE
Wireless Communications Letters, vol. 6, no. 6, pp.
782-785, Dec. 2017.
B. Wang, L. Dai, Z. Wang, N. Ge and S. Zhou, "Spectrum
and Energy-Efficient Beamspace MIMO-NOMA for
Millimeter-Wave Communications Using Lens
Antenna Array," in IEEE Journal on Selected Areas in
Communications, vol. 35, no. 10, pp. 2370-2382, Oct.
2017.
W. Yuan, V. Kalokidou, S. M. D. Armour, A. Doufexi and
M. A. Beach, "Application of Non-Orthogonal
Multiplexing to mmWave Multi-User Systems," 2017
IEEE 85th Vehicular Technology Conference (VTC
Spring), 2017, pp. 1-6.
Y. Zhao, W. Xu and S. Jin, "An minorization-maximization
based hybrid precoding in NOMA-mMIMO," 2017 9th
International Conference on Wireless Communications
and Signal Processing (WCSP), 2017, pp. 1-6.
M. F. Sohail, C. Y. Leow and S. Won, "Non-Orthogonal
Multiple Access for Unmanned Aerial Vehicle Assisted
Communication," in IEEE Access, vol. 6, pp. 22716-
22727, 2018.
M. F. Sohail, C. Y. Leow and S. Won, "Energy-Efficient
Non-Orthogonal Multiple Access for UAV
Communication System," in IEEE Transactions on
Vehicular Technology, vol. 68, no. 11, pp. 10834-
10845, Nov. 2019.
T. Hou, Y. Liu, Z. Song, X. Sun and Y. Chen, "Exploiting
NOMA for UAV Communications in Large-Scale
Cellular Networks," in IEEE Transactions on
Communications, vol. 67, no. 10, pp. 6897-6911, Oct.
2019.
T. Hou, Y. Liu, Z. Song, X. Sun and Y. Chen, "Multiple
Antenna Aided NOMA in UAV Networks: A
Stochastic Geometry Approach," in IEEE Transactions
on Communications, vol. 67, no. 2, pp. 1031-1044, Feb.
2019.
M. Liu, G. Gui, N. Zhao, J. Sun, H. Gacanin and H. Sari,
"UAV-Aided Air-to-Ground Cooperative
Nonorthogonal Multiple Access," in IEEE Internet of
Things Journal, vol. 7, no. 4, pp. 2704-2715, April
2020.
Ö. Özdogan, E. Björnson and E. G. Larsson, "Intelligent
Reflecting Surfaces: Physics, Propagation, and Pathloss
Modeling," in IEEE Wireless Communications Letters,
vol. 9, no. 5, pp. 581-585, May 2020.
Y. Saito, Y. Kishiyama, A. Benjebbour, T. Nakamura, A. Li
and K. Higuchi, "Non-Orthogonal Multiple Access
(NOMA) for Cellular Future Radio Access," 2013
IEEE 77th Vehicular Technology Conference (VTC
Spring), 2013, pp. 1-5.
E. Basar, M. Di Renzo, J. De Rosny, M. Debbah, M.-S.
Alouini, and R. Zhang, “Wireless communications
through reconfigurable intelligent surfaces,” IEEE
Access, vol. 7, pp. 116753–116773, 2019.
ISAIC 2022 - International Symposium on Automation, Information and Computing
714
