A Comparative Study of Traditional Linear Models and Nonlinear

Neural Network Model on Asset Pricing

Wen Wang

School of Finance, Southwestern University of Finance and Economics, Chengdu, 611130, China

Keywords: Asset Pricing, CAPM Model, Fama-French Three-Factor Model, RESET Test, Neural Network.

Abstract: Models in traditional asset pricing theories, such as CAPM and the Fama-French three-factor model, explain

the linear relationship between market returns, company size, company type, and return on assets. But in a

more complex financial market, the linear relationship contained in the above model may not hold. Therefore,

the main focus of this paper is to analyze the nonlinearity between stock excess return and its influencing

factors. The existence of nonlinearity is confirmed via the RESET test proposed by Ramsey. Then, the

nonlinear neural network model is used to further study the nonlinear relationship. Based on the data of the

A-share market, it is verified that there is a nonlinear relationship between stock excess returns and their

influencing factors, and the nonlinear neural network model shows better prediction performance than

traditional linear models.

1 INTRODUCTION

Modern asset pricing theory mainly focuses on the

difference between expected returns of different

assets and the dynamics of the market risk premium.

Among the large number of theoretical models in this

field, the capital asset pricing model (CAPM)

undoubtedly occupies an important position. It is the

cornerstone of modern financial economics and the

pillar of financial market price theory. The model was

developed from the theory of modern portfolio

selection (Sharpe, 1964; Lintner, 1969; Fischer,

1972).

With the continuous development in the research

fields of asset pricing theory, academic circles

gradually discovered that, in addition to a single risk

factor, the return on assets is also affected by the

company's market value and book-to-market ratio.

Combining these new findings, Fama and French

(Eugene, 1996) proposed a three-factor model that

combines the risk factor, size factor, and value factor

as an improvement of CAPM.

However, most of the traditional asset pricing

models, such as the CAPM model and the Fama-

French three-factor model, adopt a linear form and

usually have a problem with poor prediction of stock

returns. Therefore, the academic community has

gradually begun to explore the nonlinear relationship

in asset pricing models. According to empirical

research, there are complex internal structures in

asset price time series such as non-normal

distribution with fat tails, volatility clustering

phenomenon, and seasonal effects (Edgar, 1996; Xu,

2001; Michael, 1976). Faced with these nonlinear

characteristics, it is natural that reducing strict

assumptions in traditional models and building

nonlinear models becomes a new research direction

in the field of asset pricing (Xing, 2019; James,

2002).

This paper conducts an empirical analysis of the

traditional CAPM model, the Fama-French three-

factor model, and the neural network model based on

the A-share market data. Since it is confirmed that the

Fama-French three-factor model is more suitable for

the Chinese market than the Fama-French five-factor

model (Zhao, 2016), the Fama-French five-factor

model is not selected in this paper.

The Ramsey RESET method (James, 1969; Ruey,

2005) is used in the process to test whether there is a

nonlinear relationship between stock excess returns

and relevant factors under the single-factor

assumption and three-factor assumption,

respectively. Subsequently, the predicted stock return

of each model is compared via out-of-sample R2 and

mean absolute error (MAE).

In this paper, the nonlinear neural network model

is introduced to price assets in order to analyze the

Wang, W.

A Comparative Study of Traditional Linear Models and Nonlinear Neural Network Model on Asset Pricing.

DOI: 10.5220/0012036400003620

In Proceedings of the 4th International Conference on Economic Management and Model Engineering (ICEMME 2022), pages 535-541

ISBN: 978-989-758-636-1

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

535

nonlinear relationship between traditional pricing

factors and stock returns in the Chinese market. As a

result, the nonlinear problem existing in the

traditional linear asset pricing model is verified, and

the effectiveness of the neural network model applied

to the field of asset pricing is proven. The conclusions

obtained in this paper help to provide some guidance

for the improvement of the asset pricing model for the

Chinese market in the future.

2 MODELS

This section will introduce the pricing model used in

this paper. Pricing models are divided into two

categories: linear pricing models and nonlinear

pricing models.

2.1 Traditional Linear Models

Traditional asset pricing models generally take a

linear form. In this paper, the most classic CAPM and

the Fama-French three-factor models are selected for

empirical research.

CAPM. The single-factor CAPM formula

(including the market risk premium factor) is shown

below:

𝑅



−𝑅



=𝛼



+𝛽





𝑅



−𝑅





+𝜀



Among the equation above, R



represents the

rate of return of stock i at time t; R



is the risk-free

interest rate at time t; α



and β



are parameters to be

estimated; R



is the rate of return of the market

index at time t; ε



is the regression residual.

Fama-French three-factor model. Compared

with CAPM, the Fama-French three-factor model

includes two additional factors: stock market value

and book-to-market value. The formula of the model

(including market risk premium factor, size premium

factor and value premium factor) is shown below:

𝑅



−𝑅



=𝛼



+𝛽







𝑅



−𝑅





+𝛽





𝑆𝑀𝐵



+𝛽





𝐻𝑀𝐿



+𝜀



In the equation above, R



is the rate of return of

stock i at time t; R



is the risk-free interest rate at

time t; α



, β





, β





and β





are parameters to

be estimated; R



is the rate of return of the market

index at time t; SMB



represents the size premium at

time t, which is the difference between the return of a

portfolio of stocks with small market value and a

portfolio of stocks with large market value; HML



represents the value premium at time t, which is the

difference between the return of a portfolio of value

stocks and a portfolio of growth stocks at time t; ε



represents regression residuals at time t.

2.2 Nonlinear Neural Network Model

In order to further explore the nonlinearity between

stock returns and their influencing factors, the

nonlinear neural network model is introduced in this

paper.

Principle of the model. A neural network is one

of the most powerful nonlinear models in all kinds of

machine learning methods. The principle of the model

is to imitate the structure and function of a biological

neural network. As for the traditional feedforward

neural network, it mainly consists of an input layer for

raw data input, several hidden layers for processing

the input data, and an output layer that outputs the

final prediction results. Similar to the axons of a

biological brain, different layers in a neural network

model represent a group of neurons, and each layer is

connected by "synapses" that transmit signals between

neurons in different layers.

Figure 1: A single hidden layer neural network structure.

ut la

Hidden la

Out

ut la

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

536

Figure 1 shows a single-hidden-layer neural

network structure. In this neural network structure,



, x



, x



and x



are the input data;θ

()

and θ

()

are the weight matrices mapped from the first layer to

the second layer and from the second layer to the third

layer, respectively; b

()

and b

()

are bias between

the first layer and the second layer, and between the

second layer and the third layer, respectively; g is the

nonlinear activation function; y is the final output

value. The overall structure of the model can be

expressed as equations below:



()

=g(𝜃

,

(



)

()

+𝜃

,

(



)

𝑥



)





𝑦=𝜃



(



)

𝑏

(



)

+𝜃



(



)



()





The form of the model. First, relevant data used

in asset pricing is expressed in vector form:



[

𝑥



⋯𝑥



]

𝑌



=[𝑦



…𝑦



]

In the equations above, X



is a dataset containing

m factors that impacts stock prices at time t; x



represents the ith factor at time t; Y



is the stock

excess return of n stocks at time t; y



represents the

excess return of stock i at time t.

Introducing the neural network into asset pricing,

a nonlinear model can be obtained as follows:

𝑌



=𝑓(X



;𝜃)

In this model, f is the nonlinear function that

maps the stock factor dataset X



to the excess return



, and θ is the parameter set to be estimated.

3 EMPIRICAL ANALYSIS

The monthly data of 163 stocks selected from the A-

share market from January 2000 to May 2022 is used

in the paper to carry out the empirical experiment. All

stock data is obtained from the CSMAR database.

Stocks carrying “ST” (special treatment) or “*ST”

tags (which have suffered losses for two consecutive

years or more) are excluded. The market index used

here is the CSI 300 index, which includes the 300 A-

share stocks traded on the Shanghai and Shenzhen

stock exchanges, and the risk-free interest rate is the

one-year short-term treasury bond rate. The stock

data from January 2000 to December 2020 is used as

the training set of the pricing model, and the stock

data from January 2021 to May 2022 is used as the

test set.

3.1 Performance Evaluation

In order to compare the predictive ability of different

models, this paper selects two quantitative indicators:

and mean absolute error (MAE).

Out-of-sample R

. The predictive ability of each

model is evaluated by the out-of-sample R





=1−

∑



𝑟

,

−𝑟̂

,





(,)

∑

𝑟

,



(

,

)

In the formula above, r

,

represents the actual

excess rate of return of stock i at time t+1, and r

,

represents the excess rate of return of stock i at time

t+1 predicted by pricing models. Considering that

there is too much noise in the historical average excess

return of a single stock, it is better to directly use 0 as

the benchmark (Gu, 2020). Therefore, the

denominator of the out-of-sample R

defined here is

without demeaning, which means the historical mean

is replaced by 0.

Mean absolute error. In addition to R

, the

predictive ability of each model is also evaluated by

mean absolute error (MAE):

𝑀𝐴𝐸 =

𝑛





𝑟

,

−𝑟̂

,







In the formula above, r

,

represents the actual

excess rate of return of stock i at time t+1, and r

,

represents the excess rate of return of stock i at time

t+1 predicted by pricing models.

3.2 Nonlinearity Test

In this paper, regression specification error test

(RESET) is selected to detect the possible nonlinear

relationship in the model.

Testing method. The RESET test is a commonly

used test method in econometrics. It is a specification

test for linear least-squares regression analysis

proposed by Ramsey (1969). The basic idea of the

RESET test is that if there is no nonlinearity, the

coefficient of the multinomial term of the regression

model should be 0. In other words, the null hypothesis

of the RESET test is that the coefficient of the higher-

order term is equal to 0. This can be tested by the F

test.

Test result. The monthly excess returns of the 163

stocks selected in this paper are tested by RESET

under the assumption of a single factor (i.e. market

risk premium factor) and three factors (i.e. market risk

premium factor, size premium factor, and value

premium factor) respectively. The P values obtained

by the F test are shown in Table 1 and Figure 2.

A Comparative Study of Traditional Linear Models and Nonlinear Neural Network Model on Asset Pricing

537

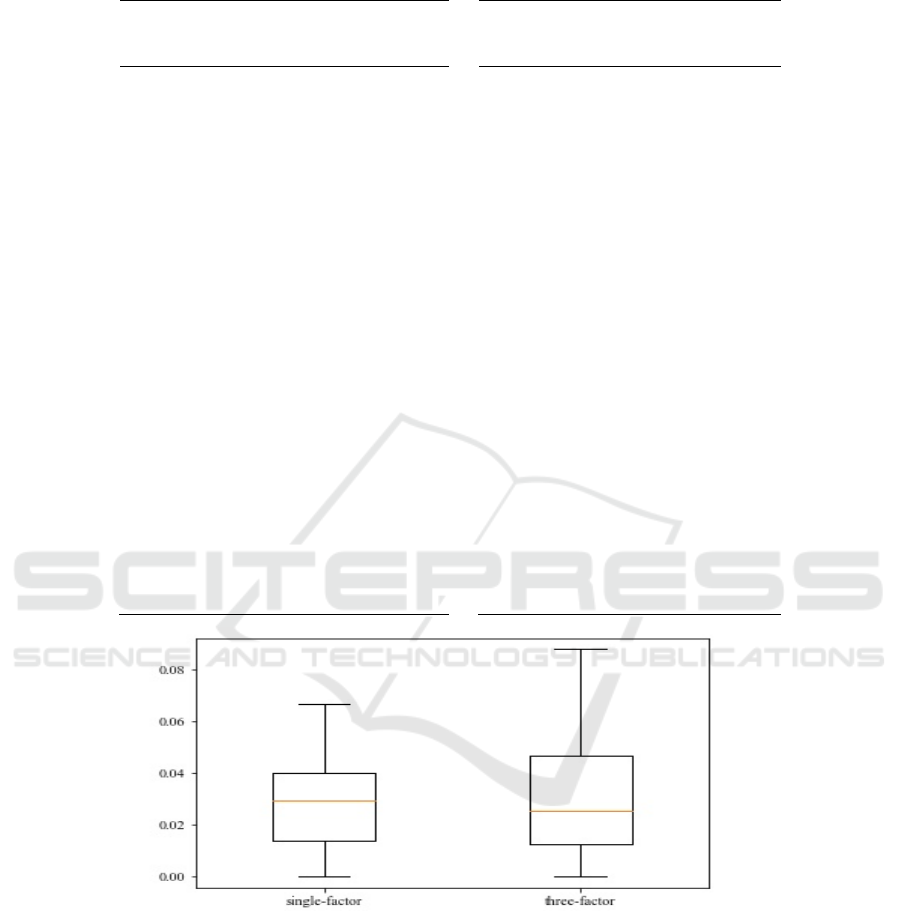
Table 1: Partial results of P value obtained by F test.

Stock

code

P value for

single-factor

P value for

three-factor

Stock

code

P value for

single-factor

P value for

three-factor

000012

0.0406 0.0170

000551

0.0118 0.0441

000021

0.0418 0.0368

000559

0.0664 0.0201

000026

0.0350 0.0681

000570

0.0062 0.0249

000039

0.0370 0.0292

000573

0.0434 0.0366

000055

0.0359 0.0493

000581

0.0140 0.0173

000060

0.0259 0.0110

000589

0.0350 0.0014

000078

0.0289 0.0466

000597

0.0072 0.0681

000089

0.0372 0.0135

000598

0.0197 0.0508

000402

0.0178 0.0333

000599

0.0377 0.0475

000404

0.0312 0.0242

000632

0.0639 0.1399

000417

0.0481 0.0342

000637

0.0129 0.0246

000419

0.0491 0.0161

000661

0.0159 0.0231

000422

0.0185 0.0023

000667

0.0090 0.0220

000425

0.0241 0.0148

000680

0.0378 0.0485

000507

0.0244 0.0242

000685

0.0274 0.0278

000521

0.0484 0.1164

000701

0.0083 0.0125

000528

0.0112 0.0483

000702

0.0080 0.0118

000543

0.0043 0.0171

000729

0.0178 0.0352

000548

0.0142 0.0034

000733

0.0242 0.0296

Figure 2: p value of the RESET test.

As shown in Table 1 and Figure 2, among the 163

selected stocks, P values of most stocks' excess

returns are less than 0.05. 92.64% of the stocks have

a P value less than 0.05 under the single factor

assumption, and 84.66% of the stocks have a P value

less than 0.05 under the three-factor hypothesis.

Hence, there are sufficient reasons to reject the null

hypothesis, that is, there are nonlinear terms in the

model under the single-factor and three-factor

assumptions. Consequently, it is reasonable to use

nonlinear neural network models to predict stock

excess returns.

3.3 Model Training

The stock data from January 2000 to December 2020

is used as the training set to estimate the parameters

of three different models, and the stock data from

January 2021 to December 2022 is used as the test set

to compare the performance of models via out-of-

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

538

sample R

OOS

and MAE.

Linear Regression for Traditional Models. The

linear regression is performed on the training set data

to calculate the parameters of the CAPM and Fama-

French three-factor models. Part of results of each

model are shown in table 2 and table 3 respectively.

As can be seen from table 2 and table 3, the

regression coefficients of the market risk premium

factor are generally around 1, while the coefficients

of the size premium factor and the value premium

factor are basically distributed between 1 and -1.

Table 2: Partial CAPM Model Regression Coefficients.

Stock code β Stock code β

000012

1.3623

000551

1.0514

000021

1.0567

000559

1.1099

000026

1.0829

000570

1.1503

000039

1.0150

000573

1.1043

000055

1.1454

000581

0.9272

000060

1.4895

000589

1.0393

000078

1.2271

000597

1.0332

000089

0.9121

000598

1.0690

000402

0.9913

000599

1.1078

000404

1.0987

000632

0.9774

000417

0.9409

000637

0.9588

000419

1.0821

000661

1.0209

000422

1.1367

000667

1.1438

000425

1.0501

000680

1.3344

000507

1.1369

000685

1.3469

000521

1.1357

000701

1.1495

000528

1.2415

000702

0.9878

000543

1.2621

000729

0.6887

000548

1.2354

000733

1.1190

Table 3: Partial FF three-factor model regression coefficients.

Stock

code

βM βSMB βHML Stock

code

βM βSMB βHML

000012

1.2984 0.8745 0.2684

000551

0.9667 1.0525 0.1440

000021

0.9835 0.6161 -0.4609

000559

1.0265 1.0905 0.2469

000026

0.9729 1.0106 -0.5234

000570

1.0791 0.8716 0.0944

000039

1.0365 -0.1216 0.2529

000573

1.0465 0.9281 0.5163

000055

1.0565 1.0752 0.0905

000581

0.8934 0.3855 -0.0135

000060

1.4956 0.0598 0.2589

000589

0.9865 0.8760 0.5254

000078

1.1373 0.9139 -0.2511

000597

0.9531 1.1435 0.4302

000089

0.8898 0.2253 -0.0658

000598

1.0308 0.6422 0.3988

000402

1.0414 -0.4816 0.1966

000599

1.0207 1.1217 0.2238

000404

1.0260 1.0489 0.4129

000632

0.8818 1.0587 -0.0961

000417

0.8932 0.7500 0.3928

000637

0.8985 0.8616 0.3242

000419

1.0099 0.7348 -0.1998

000661

0.9102 1.1682 -0.2256

000422

1.1040 0.6689 0.5791

000667

1.1074 0.7903 0.7325

A Comparative Study of Traditional Linear Models and Nonlinear Neural Network Model on Asset Pricing

539

000425

1.0329 0.4887 0.5753

000680

1.3322 0.1623 0.2709

000507

1.0981 0.5070 0.1139

000685

1.3244 0.3403 0.1592

000521

1.0679 0.9031 0.2354

000701

1.0545 1.0158 -0.1671

000528

1.2709 -0.2598 0.1607

000702

0.9178 1.0581 0.4926

000543

1.2454 0.4936 0.5963

000729

0.6727 0.1638 -0.0433

000548

1.1806 0.7695 0.2683

000733

1.0211 0.6783 -0.9043

Linear Regression for Traditional Models.

Considering the limited amount of data, the neural

network models used here have only up to 4 hidden

layers. Four neural network structures (NN1, NN2,

NN3 and NN4) are selected respectively according to

the geometric pyramid rule [13]. NN1 has a single

hidden layer with 32 neurons; NN2 has two hidden

layers with 32 and 16 neurons, respectively; NN3 has

three hidden layers with 32, 16, and 8 neurons,

respectively; NN4 has four hidden layers with 32, 16,

8, and 4 neurons respectively. Under the single-factor

assumption, the input layer of each neural network

model receives market risk premium data; under the

three-factor assumption, the input layer receives

market risk premium, size premium and value

premium data.

3.4 Model Comparison

The R

OOS

and MAE of CAPM and the neural

network model under the single-factor assumption is

shown in Table 3. It can be seen that the performance

of neural network models with all four different

structures is better than CAPM. The R

OOS

and MAE

of the Fama-French three-factor model and the neural

network under the three-factor assumption are shown

in Table 4. The neural network model also shows

better performance than the linear three-factor model

does.

Table 4: R

OOS

and MAE under the single-factor assumption.

Model CAPM NN1 NN2 NN3 NN4

OOS

0.1271 0.1307 0.1308 0.1300 0.1300

MAE 0.0799 0.0795 0.0795 0.0796 0.0795

Table 5: R

OOS

and MAE under the three-factor assumption.

Model FF NN1 NN2 NN3 NN4

OOS

0.2261 0.2287 0.2274 0.2278 0.2302

MAE 0.0741 0.0740 0.0737 0.0737 0.0736

4 CONCLUSION

Through empirical method, according to A-share

market data, the Ramsey RESET method is used in

this paper first to confirm that there is a nonlinear

relationship between the stock excess return and its

influencing factors. Then, from the results of both R

and MAE, we can see that all four nonlinear neural

network models with different structures show better

performance than traditional linear asset pricing

models. Hence, it is further verified that the non-

linear form may be a better option when it comes to

predicting asset returns.

However, the improvement of the neural network

model over traditional linear models is not very

significant. In addition, it is difficult to give an

intuitive explanation of the specific nonlinear

relationship between expected returns and their

influencing factors via a neural network model

because it is like a “black box”. Consequently, other

nonlinear models are needed to further explore the

nonlinear relationship between stock excess return

and relevant factors.

REFERENCES

Edgar, E., Peters. (1996). Chaos and Order in the Capital

Markets: A New View of Cycles, Prices, and Market

Volatility.

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

540

Eugene, F., Fama., Kenneth, R., French. (1996).

Multifactor Explanations of Asset Pricing Anomalies.

Journal of Finance, 51(1):55-84.

Fischer, Black. (1972). Capital Market Equilibrium with

Restricted Borrowing. The Journal of Business,

45(3):444-455.

James, Davidson., Timo, Teräsvirta. (2002). Long memory

and nonlinear time series. Journal of Econometrics,

110(2):105-112.

James, B., Ramsey. (1969). Tests for Specification Errors

in Classical Linear Least-Squares Regression Analysis.

Journal of the royal statistical society series b-

methodological, 31(2):350-371.

Lintner, J. . (1969). The valuation of risk assets and the

selection of risky investments in stock portfolios and

capital budgets *. Stochastic Optimization Models in

Finance, 51(2), 220-221.

Michael, S., Rozeff., William, R., Kinney. (1976). Capital

market seasonality: The case of stock returns. Journal

of Financial Economics, 3(4):379-402.

Ruey, S., Tsay. (2005). Analysis of Financial Time Series:

Tsay/Analysis of Financial Time Series.

Sharpe, W. F. . (1964). Capital asset prices: a theory of

market equilibrium under conditions of risk*. Journal

of Finance, 19(3), 425-442.

Shihao, Gu., Bryan, T., Kelly., Dacheng, Xiu. (2020).

Empirical Asset Pricing via Machine Learning. Review

of Financial Studies, 33(5):2223-2273.

Xu, L. . (2001). Empirical Research on the Stable

Properties of Stock Return in China Stock Market.

Journal of Financial Research(06), 36-43.

Xing, H. , & Liu, W. . (2019). Nonlinear asset pricing

model and the idiosyncratic volatility puzzle. Journal of

Systems Engineering.

Zhao, S. , Yan, H. , Kai, Z. , Finance, S. O. , & University,

N. . (2016). Does fama-french five factor model

outperform three factor model? evidence from china's

a-share market. Nankai Economic Studies.

A Comparative Study of Traditional Linear Models and Nonlinear Neural Network Model on Asset Pricing

541