Automatic Evaluation Algorithm for Intersection Hole Cylindrical

Feature in on Machine Measurement Operation

Andri Pratama

, Yogi Muldani Hendrawan

, Andini Eka Rahmani

, Nizar Miftah Ilyasa

Herman Budi Harja

, Muhammad Udin Harun Al Rasyid

and Idris Winarno

Department of Manufacturing Engineering Technology, Politeknik Manufaktur Bandung, Dago, Bandung, Indonesia

Department of Informatics and Computer Engineering, Politeknik Elektronika Negeri Surabaya, Sukolilo,

Surabaya, Indonesia

Keywords: CAIP, OMM, Feature Recognition, Intersection Cylindrical Feature.

Abstract: This paper discusses an algorithm that can automatically evaluate the intersection hole feature. It takes input

data probe, data reference, data measurement, and ISO 2768 tolerance database to run algorithms on software

which is programmed by the python language. The test model that has the counterbore and countersink

features is tested on an algorithm whose results will then be presented in the form of a standard QC sheet. The

results of OMM measurements will be compared with manual standard measurements to determine the

performance of the algorithm.

1 INTRODUCTION

The manufacturing industry is constantly trying to

meet market demands and satisfy customers. To

realize this, technological developments in the

manufacturing process should be more effective and

efficient. One of them, automation of manufacturing

processes in production process which is not produce

added value directly. This process is a process that

requires time, resources, and capacity but does not

increase product value directly, such as the process of

setting the machine, inspection, and delivery (Abdul

and Musazali, 2020). The inspection process has the

opportunity to make more efficient in manufacturing

process because the inspection process time is depend

on the number of functional dimensions in a product.

By On-Machine Measurement (OMM),

inspection process can be done in CNC machine. So

the workpiece not need to be removed from CNC

machine (Chen et al., 2016; Ding et al., 2020; Huang

et al., 2018; Liu et al., 2015; Mutilba et al., 2017). The

automation inspection process can be developed by

implemented Computer Aided Inspection Planning

(CAIP) on the On-Machine Measurement (OMM)

system (Chung, 1999). It is an integrated process that

https://orcid.org/0000-0003-4774-4966

https://orcid.org/0000-0002-4473-2364

involves designing, machining, and inspecting the

manufacturing process to measure products directly

at the machine. While CAIP is a product modelling

system that can describe the need for intelligent

geometry and dimension measurements. CAIP is

divided into four stages, face detection, feature

reconstruction, inspection planning, and inspection

code generated (Hendrawan et al, 2014). Thus, CAIP

and OMM are a combination that allows the OMM

method to automate and integrate the inspection

process. In conducting OMM inspections, which

requires feature properties information from the

extracted feature reconstruction phase (Hendrawan et

al, 2021) as input inspection code generated.

After the measurement which is using the OMM

method has been successfully generated (Hendrawan

et al., 2021), the next step is to compare the data from

the initial two-stage output on the CAIP and the

results of the OMM measurement. This activity is

called post CAIP which will give a GO or NO GO

decision on the condition of the hole that has been

made. This paper focuses on intersection hole

cylindrical feature such as the counterbore and

countersink features which are often found in

manufactured products or fasteners application,

especially.

Pratama, A., Hendrawan, Y., Rahmani, A., Ilyasa, N., Harja, H., Al Rasyid, M. and Winarno, I.

Automatic Evaluation Algorithm for Intersection Hole Cylindrical Feature in on Machine Measurement Operation.

DOI: 10.5220/0012037100003575

In Proceedings of the 5th International Conference on Applied Science and Technology on Engineering Science (iCAST-ES 2022), pages 1023-1029

ISBN: 978-989-758-619-4; ISSN: 2975-8246

1023

2 HOLE PROPERTIES

EVALUATION

This algorithm focuses on the double hole feature

including counterbore and countersink. The

dimension parameters of the size and position of the

two features that will be evaluated by this algorithm.

Therefore, information about the feature properties of

the hole is needed.

2.1 Counterbore Properties

Detailed counterbore feature properties information

will be shown in the image below.

Figure 1: Countersink properties. Source: (Hendrawan et al,

2021).

Basically, counterbore consists of two single hole

features that are on the same axis, namely the blind

hole and the through hole, each of which has diameter

and depth information as shown in Fig. 1. Di1, Di2,

Cpi, Li, di1, di2, Ci1, and Ci2 are top circular

diameter, bottom circular diameter, centre point, line

axis, top depth, bottom depth, top cylindrica, and

bottom cylindrical in i

feature, respectively.

To evaluate this counterbore feature requires the

condition that D

and di1 as the depth evaluated

from the inbus bolt head that becomes the

counterbore hole pair. CPi will only be represented

by CPx and CPy coordinates. The counterbore feature

information that needed for evaluation is D

, D

, d

CPx and CPy.

2.2 Countersink Properties

Detailed feature properties information of

countersink will be shown in the image below.

Figure 2: Counterbore properties. Source: (Hendrawan et

al, 2021).

Countersink consists of a tapered hole and

through hole that are on the same axis. The built

tapered feature consists of the upper diameter, bottom

diameter, and depth are represented by D

oi1

, D

oi2

, and

i1,

respectively with the provisions of D

oi1

> D

oi2

which can form an αi angle with the following

formula.

= tan

-1

(





)

(1)

di1 =





(2)

Where αi = 45º is set according to the standard.

CPi is represented as CPx dan CPy. The countersink

feature information that needed for evaluation is D

oi2

, CPx, and CPy.

3 MEASUREMENT METHODS

To evaluate based on the feature properties that have

been defined, a measurement cycle method is needed,

namely the diameter measurement cycle and the

depth measurement cycle.

3.1 Hole Measurement Cycle

In taking measurements by On Machine

Measurement on the hole cylindrical feature, a hole

measurement cycle is required which is stated as

follows.

iCAST-ES 2022 - International Conference on Applied Science and Technology on Engineering Science

1024

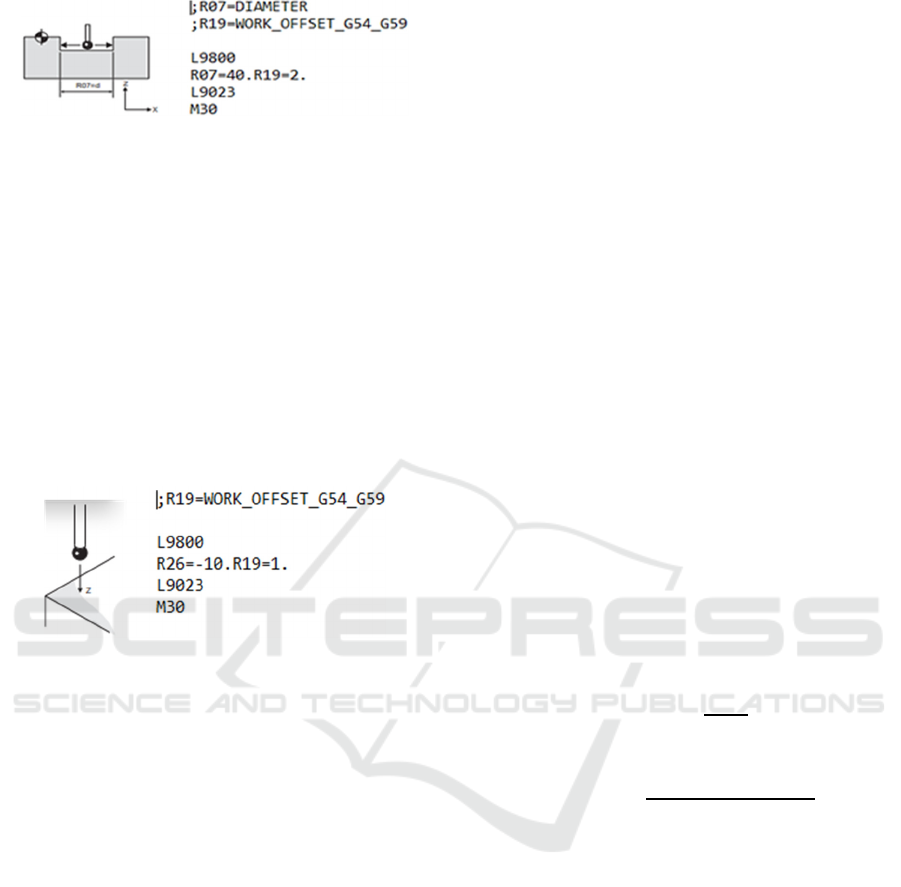
Figure 3: Measure hole illustration. Source: (Renishaw,

2014).

After the hole measurement cycle is executed by a

machine that has installed a probe interface and

PRIMO™ system from RENISHAW, measurement

results in the form of diameter and centre points of the

hole (X and Y) can be produced.

3.2 Depth Measurement Cycle

In addition to the hole measurement cycle, a depth

measurement cycle is needed to complete the

measurements on the hole cylindrical feature. The

depth measurement cycle is expressed as follows.

Figure 4: Measure depth illustration Source: (Renishaw,

2014).

Results in the form of depth in the hole can be

produced After the depth measurement cycle is

executed by the machine that has installed the probe

interface and primo™ system from RENISHAW.

4 AUTOMATIC HOLE

EVALUATION

To complement the previously proposed hole

evaluation module which is only for single-hole

features, a hole evaluation module was added to

evaluate the double hole feature which certainly

enhances the four stages already implemented.

4.1 Inspection Code Generator

With the definition of the cycle to be used as well as

the planning of the probe path that has been

generated. So an inspection code generator was

formed in accordance with existing standards.

Therefore, the measurement touching points

information is needed. To define touching points on

the counterbore, Eq. (3) is used as follows:

𝑡𝑝



𝑐𝑝





 Ø𝑝𝑟𝑜𝑏𝑒

(3)

a. Touching points for measuring diameter pilot hole

counterbore:

𝑡𝑝



𝑐𝑝





1.3 𝑑







(4)

b. Touching points for measuring counterbore depth:

In defining touching points for measuring depth.

It takes a shift in the centre point (X) expressed as

follows.

- If the center1_cbn value is positive

𝑚𝑜𝑣𝑒_𝑐𝑒𝑛𝑡𝑒𝑟 𝑐𝑝





  𝑟 𝑐𝑝





0.05

(5)

- If the center1_cbn value is negative

𝑚𝑜𝑣𝑒_𝑐𝑒𝑛𝑡𝑒𝑟 𝑐𝑝





𝑟 𝑐𝑝





0.05

(6)

After the central point shift value (X) is generated,

the next step is to execute the cycle for depth

measurement.

Meanwhile, the measurement touching points is

defined to measure countersink. The presence of

differences due to the profile in this type of hole is

oblique. Thus, it can be concluded that the touching

point for depth measurement cannot be carried out

and replaced to make the countersink Ø measurement

which is stated as follows.

ℎ𝑦𝑝𝑜𝑡𝑒𝑛𝑜𝑢𝑠𝑒 

















(7)

𝑡𝑝_𝑝𝑟𝑜𝑏𝑒  𝑐𝑝





 3

(8)

𝑛𝑒𝑤_ℎ𝑦𝑝𝑜 





_











(9)

𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛_𝑛𝑒𝑤  𝑡𝑝_𝑝𝑟𝑜𝑏𝑒  𝑛𝑒𝑤_ℎ𝑦𝑝𝑜

(10)

𝑡𝑝





 𝑑𝑒𝑣𝑖𝑎𝑡𝑖𝑜𝑛_𝑛𝑒𝑤  𝑡𝑝_𝑝𝑟𝑜𝑏𝑒

(11)

After the measurement for the Ø countersink is

carried out, the next step is to measure the Ø pilot hole

on the countersink by below equation.

𝑡𝑝



𝑐𝑝





1.3 𝑑







(12)

4.2 Hole Evaluation Module

By calculating the difference value between the

feature properties data which is created by the

previously algorithm to evaluate the single hole

feature, and feature properties information from the

double hole which is added with measurement result

data that becomes increased depending on their

respective features. For this reason, probe path data,

Automatic Evaluation Algorithm for Intersection Hole Cylindrical Feature in on Machine Measurement Operation

1025

feature properties data, measurement data that has

been added, and ISO 2768 tolerance data are needed.

Due to the limitations of the measurement method,

the depth of the countersink feature can be calculated

using Eq. (1). The difference in evaluation for each

parameter entering the tolerance area will be given a

GO decision while the difference outside the

tolerance area will be given a NO GO decision.

5 EXPERIMENT

To prove that the proposed algorithm can be applied,

the algorithm was tested at the Hyundai WIA F510M

Vertical Machining Centre with a SIEMENS 828D

controller as shown in Fig. 5 and a measurement tool

the 3D probe RENISHAW PRIMO to conduct

experiments.

Figure 5: VMC Hundyai WIA f510M.

The machines used have travel axes of X 1060 mm,

Y 635 mm, Z 635 mm, and table dimensions of 1200

mm x 500 mm, respectively. The 3D diameter size of

the Renishaw PRIMO probe selected is 6mm to take

measurements at the inspection stage of the code

generator. The measurement results will be directly

tested on proposed software that has been embedded

with an evaluation module programmed using the

Python language.

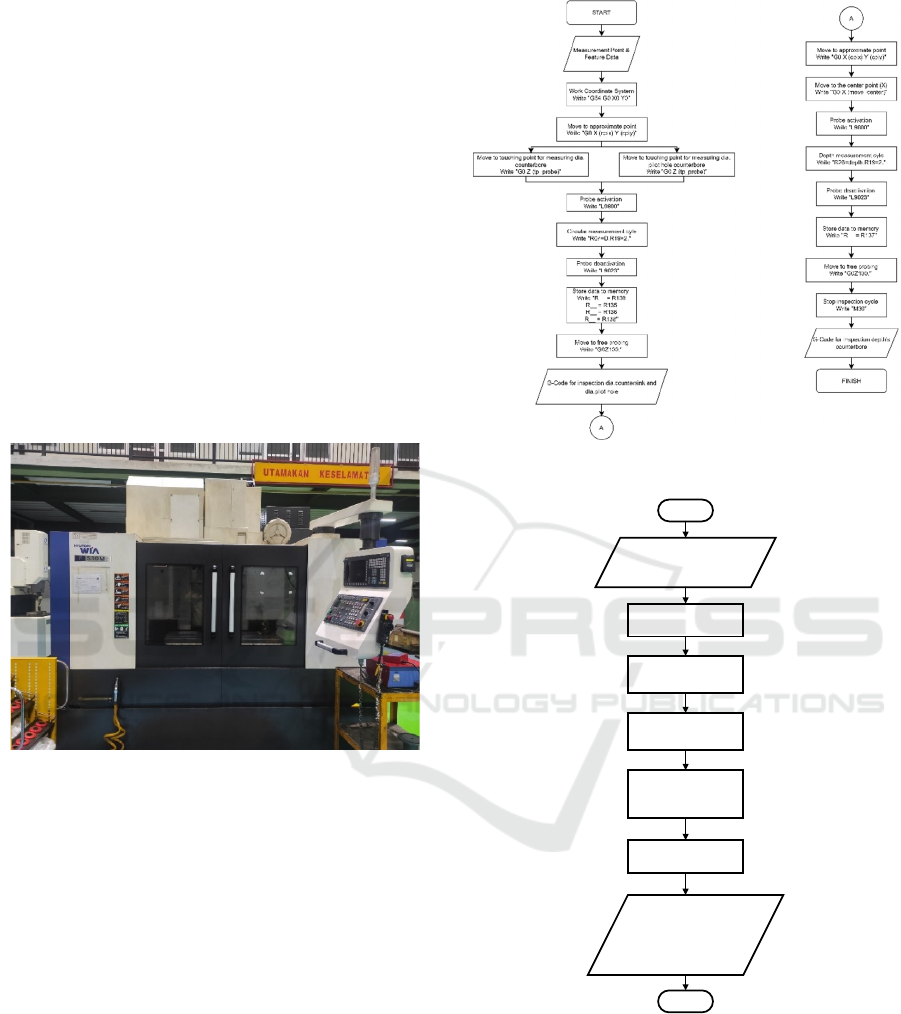
Figure 6: Inspection code algorithm.

Start

• Probe path file (.txt)

• Reference file (.txt)

• Measurement file (.txt)

• ISO 2768

Find x and y coordinates

from probe path file

Find feature parameteres

from reference file base on

x,y probe path coordinates

Find feature parameteres

from measurement file

(R parameter format)

Calculate the difference of

nominal parameters between

reference and measurement

file

Check the difference to the

tolerance zone

• Decision GO for the

parameters that enter

the tolerance zone

• Decision NO GO for

the parameters that out

of the tolerance zone

End

Figure 7: Hole evaluation algorithm.

5.1 Experimental Scenario

The G-Code generated at the inspection stage of the

generator code will be tested on a workpiece that

features an M12 counterbore with details of the upper

diameter of 20 mm, a lower diameter of 13.5 mm, and

a depth of 12.8 mm as well as an M10 countersink

hole with details of a lower diameter of 11 mm, a

iCAST-ES 2022 - International Conference on Applied Science and Technology on Engineering Science

1026

depth of 5.7 mm, and an angle of 45 degrees as shown

in Fig.8.

Figure 8: Product specimen.

The error results from the measurements will be

compared to the medium tolerance range listed in ISO

2768 automatically. The results of the evaluation will

be listed in a standard QC sheet format. To validate

the measurement results directly on the machine,

standard manual measurements were carried out

using a vernier calliper with a precision of 0.02 mm

because the evaluation was still based on moderate

tolerances.

5.2 Experimental Result

The evaluation results are listed as shown with the full

information listed in the table.

Figure 9: Holes Evaluator interface.

It was found that counterbores 1 and 2 with actual

sizes and positions respectively are the upper

diameters of 20.035 mm and 19.985 mm, the lower

diameters of 13.339 mm and 13.350 mm, the depths

of 12.811 mm and 12.821 mm, the X coordinates of

14.996 mm and -14.966 mm, and finally the Y

coordinates of 0.048 mm and 0.010 mm. For other

features, countersinks 1, 2, 3, and 4 respectively

obtained bottom diameters of 11,046 mm, 10.961

mm, 11.045 mm, and 11.032 mm, depths of 5,662

mm, 5,702 mm, 5,668 mm, and 5,672 mm, X

coordinates 34.994 mm, 34.968 mm, -34.991 mm,

and -34.994 mm, and finally coordinates Y -30.000

mm, 29.995 mm, 30.008 mm, and -29.986 mm. The

differences from the counterbore features are the

upper diameters of 0.035 and -0.014, the lower

diameters of -0.160 mm and -0.149 mm, the depths of

0.011 mm and 0.021 mm., the X coordinates -0.003

mm and 0.033 mm, and the Y coordinates 0.0487 mm

and 0.010 mm. The differences for the countersink

feature were obtained successively, namely the lower

diameters of 0.046 mm, -0.038 mm, 0.045 mm, and

0.032 mm, depths -0.038 mm, 0.002 mm, -0.032 mm,

and -0.028 mm, X coordinates -0.005 mm, -0.031

mm, 0.008 mm, and 0.005 mm, as well as coordinates

Y -0.0009 mm, -0.004 mm, 0.008 mm, and 0.013 mm.

All parameters evaluated for both the counterbore and

countersink features are categorized GO because they

fall within the tolerance range.

The second experiment is to validate the

measurement results on the machine by a vernier

calliper to evaluate all parameters evaluated in on-

machine measurement. The difference results for the

counterbore feature were obtained respectively,

namely the upper diameters of 0.04 mm and -0.016

mm, the lower diameters of -0.156 mm and -0.16 mm,

depths of -0.012 mm and -0.004 mm, X coordinates -

0.002 mm and 0.032 mm, and coordinates of Y -0.014

mm and -0.004 mm. For the countersink feature

obtained successively, namely the lower diameters of

0.008 mm, -0.044 mm, 0 mm, and 0.004 mm, depths

of 0.05 mm, 0.06 mm, 0.03 mm, and 0.02 mm, X

coordinates 0 mm, -0.026 mm, 0.02 mm, and 0.018,

and finally coordinate Y -0.06 mm, -0.014 mm, -

0.044 mm, and -0.004 mm. All parameters evaluated

by using the calliper are categorized GO because they

fall within the tolerance range as shown in table 1

and 2.

When viewed from the experiments of the hole

evaluation algorithm automatically and measuring it

manually, both show the same decision results,

namely GO for all the parameters evaluated. This

means that the proposed algorithm has proven to be

correct in providing decisions by comparing the

results of measurements manually using calipers.

Countersin

Counterbore

Automatic Evaluation Algorithm for Intersection Hole Cylindrical Feature in on Machine Measurement Operation

1027

6 CONCLUSIONS

The proposed algorithm already evaluates the

counterbore and countersink features. The proposed

algorithm is developed and implemented in software

programmed using the Python language. Experiments

are needed to test the performance of the algorithm.

The software created requires probe path data, feature

properties data as a reference, measurement data on

the machine, and ISO 2768 tolerance database as

input data. The parameters evaluated are the upper

diameter, lower diameter, depth, x coordinate, and y

coordinate of the counterbore feature as well as the

lower diameter, depth, X coordinate, and Y

coordinate of the countersink feature. The evaluation

results are displayed in a standard QC sheet format.

Based on the experiments that have been carried out,

the algorithm can already work properly.

Figure 10: Automatic hole evaluation result (mm).

ACKNOWLEDGEMENTS

This work was supported by the Ministry of Culture,

Education, Research, and Technology of the Republic

of Indonesia. We would like to thank them for the

support.

Figure 11: Manual hole evaluation result.

REFERENCES

Abdul Rasib, A.H., Musazali, M. (2020). Undestanding of

Non-Value Added Overtime in Manufacturing

Operations. In IOP Conference Series: Material Science

and Engineering. doi: 10.1088/1757-899X/994/1/01

2004

Chung, S.C. (1999). CAD/CAM Integration of on-the-

machine measuring and inspection system for free

formed surfaces. Proceedings of American Society for

Precision Engineering, vol.20, pp 267-270.

Hendrawan, Y.M., Yuwana, M.Y., and Raharno, S. (2014).

Development of computer aided inspection planning

(CAIP) application in on machine measurement

operation (OMM) operations for box primitive features:

Generating inspection codes. In Applied Mechanics and

Materials, vol 660, pp.889-893.

Chen, Y. L., Cai, Y., Shimizu, Y., Ito, S., Gao, W., & Ju, B.

F. (2016). On-machine measurement of microtool wear

and cutting edge chipping by using a diamond edge

artifact. Precision Engineering, 43, 462–467.

https://doi.org/10.1016/j.precisioneng.2015.09.011

Ding, D., Zhao, Z., Zhang, X., Fu, Y., & Xu, J. (2020).

Evaluation and compensation of laser-based on-

machine measurement for inclined and curved profiles.

Measurement, 151, 107236. https://doi.org/

10.1016/j.measurement.2019.107236

No Feature Std Tol Result Error Status

20.0 0.2 20.0354 0.0354 GO

13.5 0.2 13.3395 -0.1605 GO

12.8 0.2 12.8112 0.0112 GO

X 15.0 0.2 14.9967 -0.033 GO

Y 0.0 0.1 0.0106 0.04875 GO

20.0 0.2 19.9853 -0.0147 GO

13.5 0.2 13.3503 -0.1497 GO

12.8 0.2 12.8212 0.0212 GO

X -15.0 0.2 -14.96605 0.03395 GO

Y 0.0 0.1 0.0106 0.0106 GO

11.0 0.2 11.046 0.046 GO

5.7 0.1 5.662 -0.038 GO

X 35.0 0.3 34.9943 -0.0057 GO

Y -30.0 0.2 -30.00095 -0.00095 GO

11.0 0.2 10.9614 -0.0386 GO

5.7 0.1 5.702 0.002 GO

X 35.0 0.3 34.9681 0.0319 GO

Y 30.0 0.2 29.9955 -0.0045 GO

11.0 0.2 11.0453 0.0453 GO

5.7 0.1 5.668 -0.032 GO

X -35.0 0.3 -34.99135 0.00865 GO

Y 30.0 0.2 30.008 0.008 GO

11.0 0.2 11.0323 0.0323 GO

5.7 0.1 5.672 0.0319 GO

X -35.0 0.3 -34.99465 0.00535 GO

Y -30.0 0.2 -29.9867 0.0133 GO

Dl 11

De 5.7

Dim

Du 20

Dl 13.5

De 12.8

Du 20

Dl 13.5

CB1

CB2

CS1

CS2

CS3

De 12.8

Dl 11

De 5.7

Dl 11

CS4

De 5.7

Dl 11

De 5.7

No Feature Std Tol Result Error Status

20.0 0.2 20.004 0.004 GO

13.5 0.2 13.344 -0.156 GO

12.8 0.2 12.788 0.012 GO

X 15.0 0.2 14.998 -0.002 GO

Y 0.0 0.1 -0,014 -0.014 GO

20.0 0.2 19.984 -0.016 GO

13.5 0.2 13.34 -0.16 GO

12.8 0.2 12.796 -0.004 GO

X -15.0 0.2 -14.968 0.032 GO

Y 0.0 0.1 -0.004 -0.004 GO

11.0 0.2 11.008 0.008 GO

5.7 0.1 5.75 0.05 GO

X 35.0 0.3 35.0 0.0 GO

Y -30.0 0.2 -30.06 -0.06 GO

11.0 0.2 10.956 -0.044 GO

5.7 0.1 5.76 0.06 GO

X 35.0 0.3 34.974 -0.026 GO

Y 30.0 0.2 29.986 -0.014 GO

11.0 0.2 11.0 0.0 GO

5.7 0.1 5.73 0.03 GO

X -35.0 0.3 -34.98 0.02 GO

Y 30.0 0.2 29.956 -0.044 GO

11.0 0.2 11.004 0.004 GO

5.7 0.1 5.72 0.02 GO

X -35.0 0.3 -34.982 0.018 GO

Y -30.0 0.2 -29.998 0.002 GO

Dim

Du 20

Dl 13.5

De 12.8

Du 20

Dl 13.5

5 CS3

6 CS4

Dl 11

De 5.7

3 CS1

4 CS2

Dl 11

De 5.7

Dl 11

De 5.7

1CB1

2 CB2

De 12.8

iCAST-ES 2022 - International Conference on Applied Science and Technology on Engineering Science

1028

Huang, N., Yin, C., Liang, L., Hu, J., & Wu, S. (2018).

Error compensation for machining of large thin-walled

part with sculptured surface based on on-machine

measurement. International Journal of Advanced

Manufacturing Technology, 96(9–12), 4345–4352.

https://doi.org/10.1007/s00170-018-1897-x

Liu, H. B., Wang, Y. Q., Jia, Z. Y., & Guo, D. M. (2015).

Integration strategy of on-machine measurement

(OMM) and numerical control (NC) machining for the

large thin-walled parts with surface correlative

constraint. International Journal of Advanced

Manufacturing Technology, 80(9–12), 1721–1731.

https://doi.org/10.1007/s00170-015-7046-x

Hendrawan, Y.M., Muttaqin, R., Pratama, A., Budi Harja,

H., Udin, M., al Rasyid, H., & Winarno, I. (2021).

Intersection Cylindrical Feature Recognition

Algorithm for Counterbore and Countersink Geometry

Application.

Hendrawan, Y.M., Pratama, A., Budi Harja, H., Udin, M.,

al Rasyid, H., & Winarno, I. (2021). Inspection Code

Generator for Hole Cylindrical Feature Evaluation in

On-Machine Measurement Process for Computer

Aided Inspection Planning.

Mutilba, U., Gomez-Acedo, E., Kortaberria, G., Olarra, A.,

& Yagüe-Fabra, J. A. (2017). Traceability of on-

machine tool measurement: A review. In Sensors

(Switzerland) (Vol. 17, Issue 7). MDPI AG.

https://doi.org/10.3390/s17071605

Renishaw. (2014). “Easyprobe cycle for machining center,”

Programming Guide, no, H-2000-6294-00-B

Automatic Evaluation Algorithm for Intersection Hole Cylindrical Feature in on Machine Measurement Operation

1029