Evaluation Method of Agricultural Talent Education and Training

Effect Based on AHP-Entropy Weight Method

Qi Wang

, Guanghai Li

2,*

and Yang Liu

Shenyang Urban Construction Colloge, School of Management, Shenyang, 110167, China

Guangxi Normal University, School of Education, Guilin, 541004, China

Keywords: Agricultural Education, Educational Quality Evaluation, Analytic Hierarchy Process, Entropy Weight

Method.

Abstract: In recent years, agricultural higher education has mostly focused on the quality of education and the

efficiency of resource allocation, often ignoring the systematic study of the development level of

agricultural education, and lacking a comprehensive measurement of the effect of agricultural education on

personnel training. This paper constructs the evaluation system of the talent education and training effect in

agricultural colleges and universities. According to the construction of teaching and scientific research, it

applies the analytic hierarchy process-entropy weight method to give weight to the index, which reduces the

error caused by subjective factors. The method of entropy weight and data envelopment analysis is adopted

to evaluate the training quality and efficiency in colleges and universities. It enriches the research on the

evaluation of the final effect of education, makes up for the shortcomings of traditional methods, and makes

the evaluation results more objective and reasonable. From a practical point of view, it can not only

understand the actual situation of input and output of higher education, but also provide a reference for the

allocation of talent training resources or the improvement of governance efficiency in Colleges and

universities.

1 INTRODUCTION

With the increasingly prominent role of education

informatization and the increasing investment of the

state, the teaching environment of agricultural

education has been greatly improved. The level of

professional education has been effectively

improved. However, in the process of talent

education construction and application in the

agricultural field, due to the mismatch between some

factors such as personnel, technology and system

and the current development, a large number of

equipment, digital resources and funds have not

been able to play their maximum role. There is a

significant difference between the actual results of

informatization and the expected goals (Kaur, 2018).

Therefore, it is very necessary to analyze the

existing informatization training effect of

agricultural education and evaluate the

informatization governance effectiveness of colleges

and universities.

The effect of educational personnel training is

a long-term accumulation process with multiple

inputs and outputs, and the effective evaluation of

its governance effectiveness is more conducive to

the school to achieve good economic and social

benefits. However, at present, there are few

evaluations on the effectiveness of personnel

training in China and abroad. Relevant studies

have been conducted on the input-output of the

effectiveness of personnel training from the

perspective of performance (

Schlichtkrull, 2018).

DEA (Data Envelopment Analysis) method can

effectively deal with the problem of performance

evaluation of educational personnel training

effect. Thus, according to different evaluation

objects, the methods of different fields are

introduced, and a series of educational personnel

training effect performance evaluation models

with strong operability based on DEA theory is

constructed (Ali Derakhshan,2020).

The TOPSIS model mainly evaluates the

development level of the sample unit according to

the degree of proximity (distance) between the

evaluation unit and the positive (negative) ideal

Wang, Q., Li, G. and Liu, Y.

Evaluation Method of Agricultural Talent Education and Training Effect Based on AHP-Entropy Weight Method.

DOI: 10.5220/0012040100003620

In Proceedings of the 4th International Conference on Economic Management and Model Engineering (ICEMME 2022), pages 587-591

ISBN: 978-989-758-636-1

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

587

solution (Aikens, 2020). The core of this decision is

to calculate the closeness degree between each

evaluation scheme and the ideal scheme, which is

used to represent the development level of the

evaluation object, and to reflect the development

level of provincial higher education through the

closeness degree of each evaluation object. When

using the TOPSIS model, we should focus on the

determination of the index weight. When objectively

calculating the index weight, the following two

methods are favored: one is the principal component

analysis (PCA) method (Xu, 2020). The PCA

method is to integrate a number of indicators

through dimensionality reduction, and to retain the

original information as much as possible. Its

disadvantage is that PCA is aimed at cross-sectional

data and can not compare the original indicators,

which happens to be the main focus of this paper.

The other is the entropy weight method, which is

mainly based on the variability of indicators to

determine the objective weight. This method not

only eliminates human subjective factors, enhances

the discrimination significance and difference of

indicators, avoids the difficulty of analysis caused

by the small difference of selected indicators, but

also comprehensively reflects the information of

research objects (Conijn, 2018).

In the multi-base model experiment, this paper

establishes a multi-layer combination capacity

prediction model, and compares the prediction

results with other models in terms of indicators. The

results indicate that the algorithm in this paper has a

certain improvement in performance compared with

other models in terms of different indicators. From

MAE, MSE, the multi-level combination model of

RMSE performs the best, which illustrates that the

predicted value of the model is closer to the actual

value, and its residual distribution is also the

smallest, which proves that the research content of

this paper is the optimal choice for the evaluation

scheme. Besides, it also provides technical support

for the quality evaluation of agricultural personnel

training.

2 HIERARCHICAL INDEX OF

AGRICULTURAL EDUCATION

The purpose of agricultural talent education and

training effectiveness evaluation is not to get the

evaluation results, but to help colleges and

universities improve their governance effectiveness

and bring convenient services to every teacher,

student and staff. The formulation of the evaluation

index of higher education training efficiency can

evaluate the input-output results of higher education,

so that colleges and universities can understand the

current problems of low efficiency, and ultimately

solve the problems and improve the quality of

education (Wilson, 2021). The establishment of

evaluation index of the higher education

informatization can also provide evaluation data and

information for researchers in the direction of

education, and provide a reference for them to carry

out relevant research.

The quality of education summarizes the relevant

evaluation contents of educational effectiveness

according to colleges and universities, as displayed

in Table 1.

Table 1: Educational effect evaluation index.

Level 1

indicato

Level 2 indicator Level 3 indicator

Input

Infrastructure

Number of network

access points

Total amount of

management

information system

data

Digital source

Input quantity of

electronic journals

Dissertation input

quantit

Teaching and

research

construction

Teaching and

scientific research per

student

New teaching and

scientific research

Output

Personnel

training

Number of students

Competition awards

Teacher

development

MOOC Courses

Virtual simulation

experiment teaching

ect

Science research

patent

Core thesis

Subject

Social Services

Science and

Technolo

Awar

3 EDUCATIONAL QUALITY

ASSESSMENT ALGORITHM

The influence of different dimensions is removed, so

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

588

that the index value after treatment falls in the

interval [0,1]. In addition, in the case that a few

indicators are 0 after the indicators are processed. In

order to make the subsequent calculation

meaningful, it is necessary to translate the

dimensionless data to the right with a minimum unit

value of 0.0001 (Adejo, 2018).

The global spatial auto-correlation is generally

measured by the Moran 'sI, and its calculation

formula is:

()

1, 1

ij i

′

−



(1)

Where

is the spatial weight matrix,

the distance between region i and region j, and

is the deviation mean of region i.

If the comparison result between the

development level of higher education in two

adjacent provinces and the mean value is one big

and one small, the product of deviation is negative,

that is, when the province with high development

level of higher education is interlaced with the

province with low development level, the Moran 'sI

is negative. When the development level of

provincial higher education is randomly and

uniformly distributed, the Moran'sI is equal to 0. In

addition, the value of Moran'sI after variance

normalization will fall on the interval [-1,1]. The

more the higher education development level C

and

of adjacent provinces deviate from the mean

value C, the greater the value of Moran'sI (C. Kiu,

2018).

After the Moran 'sI has been calculated, a

significance test is performed with the standardized

normal statistic IZ, whose standardized form is:

()

Var i



(2)

4 ANALYSIS OF EXPERIMENT

4.1 Experimental Scheme

The fusion method first trains the base model, then

takes the output results of the base model as the

features of the new data set. Then, it adopts linear

model fitting to calculate the optimal weight

coefficients of different features, and applies the

weights to represent the relative importance of each

base model. In this paper, random forest, XGBoost

and AHP-entropy method are chosen as examples.

The paper takes the output value

123

,,yyy

of the

three basic models as the new features of the input,

and uses the linear model to fit, so as to obtain the

weight coefficient

123

λλλ

corresponding to the

three new features. Then, it calculates the final result

by the weighted fusion through Formula 3

(Riestra-Gonz, 2021).

11 2 2 3 3

Yy y y

λλλ

=+ +

(3)

4.2 Weight Determination

In the linear weighted fusion, it is a key step to

obtain the weight coefficient. The main weighting

methods adopted are subjective weighting methods,

such as expert investigation method, AHP, etc.,

which are set subjectively according to the

recognition degree of experts or relevant decision

makers in some fields for different attributes. There

are also objective weighting methods, such as

principal component analysis, entropy weight

method, etc. The weight of the attribute is given

according to the difference degree of the face value

under different attributes (Javier, 2021).

The AHP-entropy weight method is adopted in

the experiment. This method can effectively

compress the data dimension and reduce the

complexity of the original data while minimizing the

loss. After taking the optimal prediction results of

the base model random forest, XGBoost and the

algorithm in this paper as new features, three

weights corresponding to the base model are

obtained, which are arranged from high to low as

displayed in Table 2.

Table 2: Weight of base model.

Model Weight value

Random forest 0.328

XGBoost 0.268

AHP-entropy weight

method

0.404

Linear weighting formula:

123

0.328 0.268 0.404Yyy y=++

(4)

Where,

123

,,yyy

represent the respective

predicted values of the three models, respectively.

Evaluation Method of Agricultural Talent Education and Training Effect Based on AHP-Entropy Weight Method

589

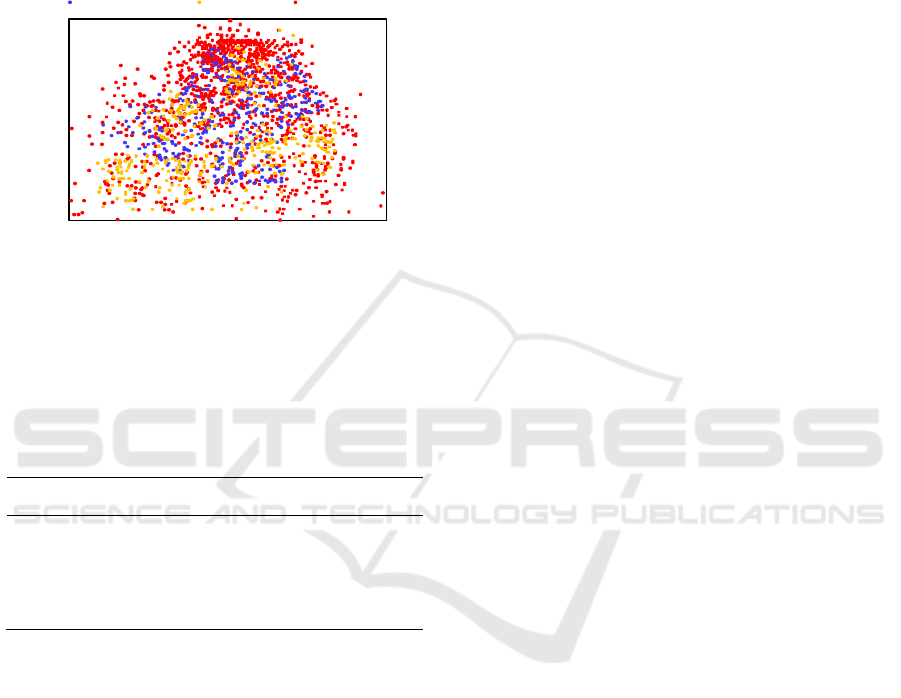
4.3 Analysis of Prediction Results

In this paper, the weights obtained by the principal

component analysis method and the optimal results

of the three base learners are linearly weighted and

fused according to Formula 3. The prediction effect

of the final test set is displayed in Figure 1.

8 9 10 11 12

Estimate

Matrix distribution

Random forest XGBoost Algorithm

Figure 1: Model test set fitting.

By calculating the evaluation index of the model,

the error results of the linear weighted fusion model

are obtained as indicated in Table 3.

Table 3: Evaluation index of the linear weighted fusion

model based on PCA.

Model MSE MAE RASE MAPE

Random

forest

1.43 1.82 2.63 4.47

XGBoost 2.35 2.14 2.68 6.32

Algorithm 8.25 7.38 7.89 8.46

Compared with other models, the proposed

algorithm performs best. The MSE (RMSE) of the

linear weighted fusion model based on PCA

decreases a little, but the MAPE (MAE) has a

certain degree of improvement, which is the smallest

linear weighted error after fusion. The predicted

value is closer to the actual value in comparison.

5 CONCLUSION

In this paper, the collected education data are

cleaned and integrated, and the key factors affecting

the effect of agricultural talent education are

explored by using the multi-layer linear model. The

weighted model of entropy weight is applied to

evaluate the development level of higher education.

Through the experimental analysis, it is proved that

the algorithm has the advantages of low data

requirements and small amount of calculation, which

is not only suitable for the comparison between

horizontal multi-units, but also suitable for the

vertical time series analysis, and further improves

the stability of the spatio-temporal pattern.

In this paper, the dynamic efficiency analysis is

carried out, and the effect evaluation of agricultural

talent education informatization is studied. However,

the output has a certain lag, and some colleges and

universities may not see the results soon after

investing in a lot of information resources. Thus, it is

biased to judge the governance effectiveness of

colleges and universities by the results of specific

time nodes. In the follow-up study, we should

collect the data over a longer period and establish

the DEA-Malmquist index method to measure the

dynamic efficiency of time series data.

REFERENCES

Ali Derakhshan. Tasks, Pragmatics and Multilingualism in

the Classroom: A Portrait of Adolescent Writing in

Multiple Languages [J]. Journal of Pragmatics, 2020,

168, 53-55.

Aikens Nikki, Atkins-Burnett Sally, Tarullo Louisa,

Malone Lizabeth, Kelly Annalee, Cannon Judith.

Preschool boys of color: Portraits of the population

served by Head Start [J]. Journal of Applied

Developmental Psychology. 70. 101167.

10.1016/j.appdev.2020.101167,2020.

Adejo O W, Connolly T. Predicting student academic

performance using multi-model heterogeneous

ensemble approach [J]. Journal of Applied Research in

Higher Education, 2018, 10(1): 61-75.

C. Kiu. Data Mining Analysis on Student’s Academic

Performance through Exploration of Student’s

Background and Social Activities[C].2018 Fourth

International Conference on Advances in Computing,

Communication & Automation (ICACCA), Subang

Jaya, Malaysia,2018:1-5, doi: 10.1109/ ICACCAF.

2018.8776809.

Conijn R, Van den Beemt A, Cuijpers P. Predicting

Student Performance in a Blended MOOC[J].Journal

of Computer Assisted Learning, 2018,34(5):615-628.

Javier B A, Sonia J, Romero S P. Early prediction of

undergraduate Student's academic performance in

completely online learning: A five-year study[J/OL].

Computers in Human Behavior, 2021,115

[2021-03-9].

Kaur H. A Literature Review from 2011 TO 2014 on

Student’s Academic Performance Prediction and

Analysis using Decision Tree Algorithm [J]. Journal

of Global Research in Computer Science, 2018, 9(5):

10-15.

Riestra-Gonz M, Paule-Ruiz M, Ortin F. Massive LMS

ICEMME 2022 - The International Conference on Economic Management and Model Engineering

590

log data analysis for the early prediction of

course-agnostic student performance[J/OL].Computers

& Education, 2021,163 [2021-03-9].

Schlichtkrull, Michael et al. (2018). “Modeling relational

data with graph convolutional networks”. In: European

Semantic Web Conference. Springer, pp. 593–607.

Wilson C, Rebeca C, Cristóbal R. Multi-source and

multimodal data fusion for predicting academic

performance in blended learning university courses-

Science Direct [J]. Computers & Electrical

Engineering, 2021,89.

Xu Z, Yuan H, Liu Q. Student Performance Prediction

Based on Blended Learning[J].IEEE Transactions on

Education, 2020,PP(99):1-8.

Evaluation Method of Agricultural Talent Education and Training Effect Based on AHP-Entropy Weight Method

591