Optimizing the Quality of Electric Lighting with the Use of
Minkowski’s Geometric Difference
Mashrabjon Mamatov
a
and Jalolxon Nuritdinov
b
Department of Geometry and Topology, National University of Uzbekistan, 4 Universitet street, Tashkent, Uzbekistan
Keywords: Geometric Difference of Minkowski, Lighting Set, Euclidean Plane, Methods, Theorem.
Abstract: In the paper, using the geometric difference of Minkowski, which are often used in the theory of differential
games, the geometric data of the set of a certain lighting instrument are obtained. Found a way to build the
set that needs to be installed in the lighting set to provide the lighting level corresponding to the requirement.
In this work, conditions are obtained for the sufficiency and necessity of given triangles on the Euclidean
plane, i.e. it is shown that if the place of illumination is a triangle of sufficiently large size and the illuminated
place of the lighting set is also a triangle, then the place of installation of the set will have a triangular shape.
Methods for finding the Minkowski difference of some groups of triangles by vectors corresponding to their
sides are also shown and proved. At the end of the article is a theorem on the Minkowski difference of
triangles. The theorem on the difference of Minkowski triangles is proved. The results obtained can be applied
in the implementation of the installation of lighting devices for residential buildings, offices and enterprises.
1 INTRODUCTION
The effect of light and light pollution on nature,
including humans, requires additional research. For
example, in part when solving safety problems on
highways, it is advisable to solve problems in an
integrated manner, while simultaneously increasing
the quality of lighting and the characteristics of the
road surface. The last factor is essential for
compliance with the requirements for standardizing
brightness (Bowers, 1998).
Many works have been devoted to optimizing the
qualities of electric lighting (Bommel', 2009). But
these works do not consider the geometric data of the
illuminated areas and the capabilities of the
illuminating tool.
In the article, using the geometric difference of
Minkowski (Bekker, Brink, 2004) - (Pontryagin,
1981), which are often used, the geometric data of the
set of a certain lighting instrument are obtained
(Mamatov, 2009) -( Tukhtasinov, 2009).
Definition 1. The sum of the two sets
1
P
and
2
P
given in the
n
-dimensional
n

space is defined as:
a
https://orcid.org/0000-0001-8455-7495
b
https://orcid.org/0000-0001-8288-832X
12 12112 2
{| ,,}.
n
PPP x xx xx Px P+∈=+∈∈
(1)
Equation (1) can also be expressed by the
operation of union of sets
11
12 12
().
xP
PP x P
∈
++

(2)
Definition 2. The Minkowski difference of two
sets is defined as follows:
{}
12 2 1
|;
n
QPP x xP P
∗
∈+⊂
(3)
If the set is
1
P
the area that is being sanctified,
2
P
is the possibility of the illuminating instrument, then
Q
is the set that must be set for the illuminating
instrument. The purpose of the work is using the
geometric Minkowski differences, to obtain geometric
data for the location of a certain lighting set.
2 METHODS
It is necessary and sufficient for the condition
12
rr≥
to exist for the Minkowski difference of closed circles
1
1
()
r
Bx
,
2
1
()
r
By
with radius
12
,rr
in the plane
2

(
Satimov, 1973)
Mamatov, M. and Nuritdinov, J.
Optimizing the Quality of Electric Lighting with the Use of Minkowskiâ
˘
A
´
Zs Geometric Difference.
DOI: 10.5220/0012046100003612
In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 751-756
ISBN: 978-989-758-622-4; ISSN: 2975-9463
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
751

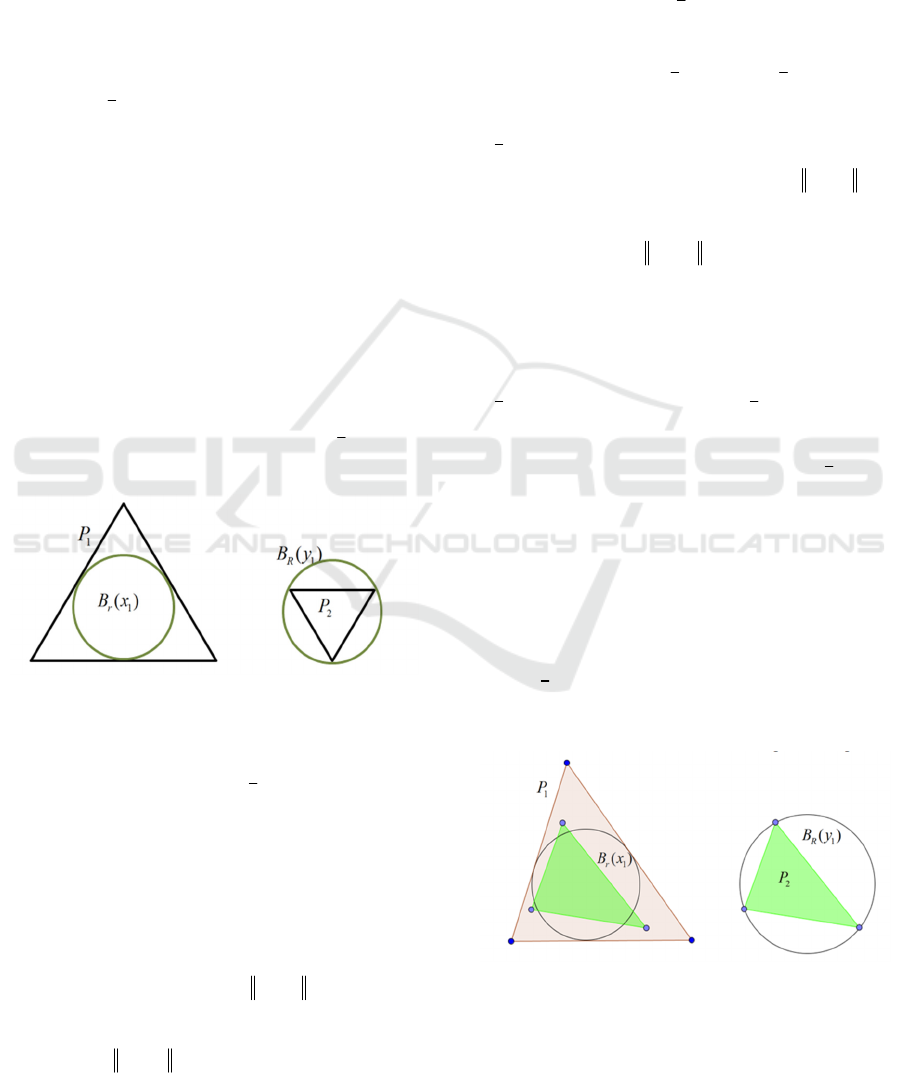
In the first case, this means that if, for example,
the length of the room is longer than the width, then
the lighting fixtures must be installed along the
segment, in the second case, along the circles, the
radius of which is
12
rr−
.
In (Pontryagin, 1981)-(Mamatov, 2009)
geometric differences are calculated when
,XY
it
has a rather complex structure, that is, place of
lighting (this
X
) and illuminated place of the lighting
set (this
Y
) then you can find the place of installation
of the set
XY
∗
. In this work, the results obtained
are more effective than previously known works. The
proposed methods for calculating the geometric
difference are new, they allow solving the problem
when
Y
it has a complex structure, i.e. it can be an
arbitrary set.
3 RESULTS AND DISCUSSIONS
Theorem 1. If sets
1
P
and
2
P
are triangles on the
plane
2

, and the radius of the incircle the triangle
1
P
is not less than the radius of the circumcircle of
the triangle
2
P
, then the difference
12
PP
∗
is not
empty.
Figure 1.
Theorem 2. If the sets
1
P
and
2
P
are triangles on
the plane, and the relation
12
PP
∗
is valid, then the
radius of the incircle of the triangle
1
P
is not smaller
than the radius of the incircle of the triangle
2
P
.
Theorem 3. If the Minkowski difference of any
triangle
2
P
from any triangle
1
P
in the plane
2

consists of more than one point, then the difference
will be a triangle similar to triangle
1
P
.
Let circle
{
1
11111
() : ,, ,
r
Bx xx x rxx P=−≤∈
}
1
r ∈
be a incircle of the triangle
1
P
, and circle
{
}
2
2
1121 2
() : , , ,
r
By yy y r yy r=−≤ ∈∈
be a
circumcircle of the triangle
2
P
. Then it is obvious that
(1), (2)
11
()
r
Bx P⊂
and
2
12
()
r
By P ⊃
(4)
According to the condition of theorem
12
rr≥
and by
the
12
11
() ()
rr
Bx B y
∗
≠∅
(5)
Since (4) and by the property in [6]
12
1112
() ()
rr
Bx B y PP
∗∗
⊂
(6)
Considering expression (4), (5), it follows that
12
PP
∗
≠∅
. The theorem has been proved.
Let circle
{
1
111
() : ,
r
Bx xx x r=−≤
}
111
,, xx Pr ∈∈
be a incircle of the triangle
1
P
, and
circle
{}
2
112122
() : , , ,
r
By yy y r yyPr=−≤ ∈∈
be a circumcircle of the triangle
2
P
. Then it is
obvious that
1
11
()
r
Bx P ⊂
and
2
12
()
r
By P ⊂
(7)
According to the condition of theorem
12
PP
∗
≠∅
. For any point
12
aPP
∗
∈
we can write
21
aP P+⊂
. Since (7)
2
121
()
r
aBy aP P +⊂+⊂
and
2
11
().
r
aPBy
∗
∈
This means that it is possible to place a circle
2
1
()
r
By
inside (6) a triangle
1
P
. Since circle
1
1
()
r
Bx
is a
incircle of the triangle
1
P
(circle with the largest
radius lying inside triangle
1
P
), it follows that
12
rr≥
. The theorem has been proved.
The opposite of this theorem is not always valid,
since
12
PP
∗
≠∅
does not mean that the radius of the
incircle of the triangle
1
P
is greater than or equal to
the radius of circumcircle of the triangle B (Fig. 2).
Figure 2.
Therefore, the given by above theorem only
sufficient condition. Following theorem is a
necessary condition.
ISAIC 2022 - International Symposium on Automation, Information and Computing
752

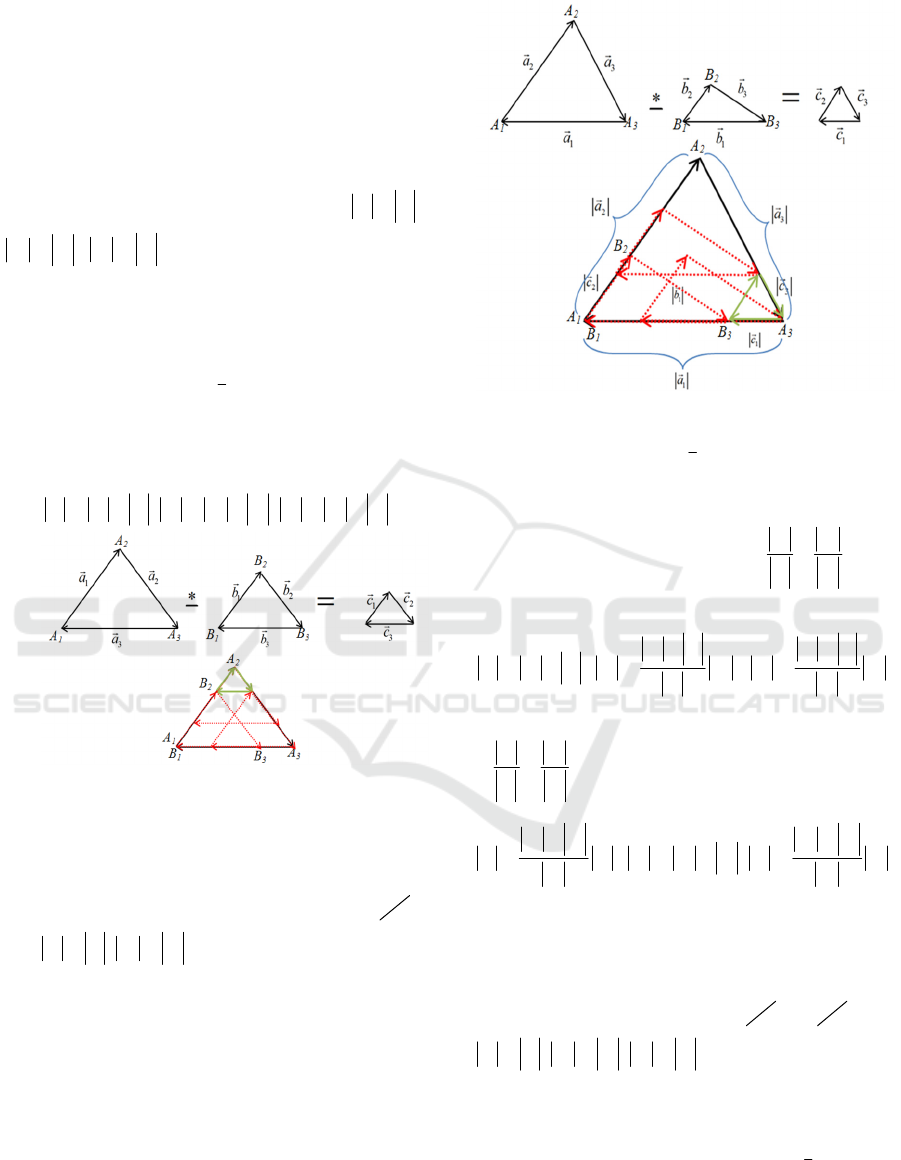
1. Finding the Minkowski difference of triangles
whose vectors on the corresponding sides are in the
same direction.
In this case, the result of the difference is that the
vectors on the sides are the same as the direction of
the vectors on the corresponding sides of the given
triangle, and their lengths are equal to the difference
in the lengths of these vectors. Let the conditions
112 2
,,aba b ↑↑ ↑↑


33
ab ↑↑


and
11
,ab≥


22
,ab≥


33
ab≥


are satisfied for the vectors
123
,,aa a
 
on the sides of triangle
2
P
and the
corresponding vectors
123
,,bbb

on the sides of
triangle
2
P
(Fig.3).
Then the difference
12
PP
∗
is also a triangle, and
for the corresponding vectors
123
,,сс с
 
on its sides,
the following relation holds:
112 23 3
1112 223 33
,,;
,,.
с a с a с a
с abс abс ab
↑↑ ↑↑ ↑↑
=− =− =−


   
(8)
Figure 3.
2. Finding the Minkowski difference of triangles
whose vectors on the two corresponding sides are in
the same direction.
Let the conditions
112 23
,,aba ba↑↑ ↑↑ ↑↑



3
b

and
112 2
,abab≥≥


are satisfied for the vectors
123
,,aa a
 
on the sides of triangle
1
P
and the
corresponding vectors
123
,,bbb

on the sides of
triangle
2
P
(Fig.4).
Figure 4.
Then the difference
12
PP
∗
is also a triangle, and
for the corresponding vectors
123
,,сс с
 
on its sides,
the following relation holds:
112 23 3
,,с a с a с a↑↑ ↑↑ ↑↑
 
. If
12
12
aa
bb
<


, then
the length of these vectors are
11 11
1112 23 3
11
,,;
ab ab
с abс a с a
aa
−−
=− = =



   

(9)
if
12
12
aa
bb
>




, then
22 22
112223 3
22
,, .
ab ab
с a с abс a
aa
−−
==−=





(10)
3. Finding the Minkowski difference of triangles
whose vectors on the only one corresponding sides
are in the same direction.
Let the conditions
112
,aba↑↑ ↑↑


23
,ba↑↑


3
b

and
112 23 3
,,ababab≥≥≥

 
are satisfied for the
vectors
123
,,aa a
 
on the sides of triangle
1
P
and the
corresponding vectors
123
,,bbb

on the sides of
triangle
2
P
. In this case the difference
12
PP
∗
may be
empty (9). For example, Minkowski difference of
triangles in fig.5 is not existence, because it is not
Optimizing the Quality of Electric Lighting with the Use of Minkowskiâ
˘
A
´
Zs Geometric Difference
753

possible to place a triangle
123
BBB
inside a triangle
123
AAA
.
Figure 5.
For this reason, we also include the condition
given in theorem 1. However, there are three possible
cases of triangles in this group.
In first case, the angles adjacent to the
1
b

side of
the triangle
2
P
greater than the angles adjacent to the
1
a

side of the triangle
1
P
as shown in fig. 6 that is,
11
AB∠<∠
and
33
AB∠<∠
are appropriate.
Figure 6.
Then the difference
12
PP
∗
is also a triangle, and
for the corresponding vectors
123
,,сс с
 
on its sides,
the relation
112 23 3
,,с a с a с a↑↑ ↑↑ ↑↑
 
is valid, that
is, it is a triangle similar to triangle
1
P
, as in the
second group. The lengths of the vectors
123
,,сс с
 
are
as follows:
11
11
11
1
1
1
112 2
33
,,
.
aa
bb
aa
a
b
a
hh hh
с a с a
hh
hh
с a
h
−−
==
−
=








(11)
Where
1
a
h

and
1
b
h

are the heights of side
1
a

of
triangle
1
P
and the heights of side
1
b

of triangle
2
P
, respectively. And they can be calculated as follows
(10):
1
123
1
123
2
()()(),
;
2
aa a a
a
a
h ppapapa
a
aaa
p
=−−−
++
=




1
123
1
123
2
()()(),
.
2
bb b b
b
b
h ppbpbpb
b
bbb
p
=−−−
++
=

 

 
In second case, the relation
11
AB∠<∠
,
33
AB∠>∠
is satisfied for the angles of triangles
1
P
and
2
P
, which are parallel to each other (Fig. 7).
Figure 7.
The difference (3)
12
PP
∗
is a triangle similar to
triangle
1
P
, and the lengths of the vectors on its sides
are (11):
2
2
2
2
2
2
2
2
2
33
11
33
22
33
33
,
,
.
a
a
a
a
a
a
a
a
a
hbprojb
с a
h
hbprojb
с a
h
h b proj b
с a
h
−−
=
−−
=
−−
=















(12)
Here
2
a
h

is the height of the triangle
1
P
on the
side
1
a

, and
2
3a
p
roj b


is the orthogonal projection of
the vector
3
b

on the vector
2
a

, which are calculated
as follows:
2
123
2
123
2
()( )(),
;
2
aa a a
a
a
h ppapapa
a
aaa
p
=−−−
++
=




ISAIC 2022 - International Symposium on Automation, Information and Computing
754

2
2
2
2
23 23
33
2
(,)
,
a
ab ab
bprojb
a
−
−=





In third case, the relation
11
AB∠>∠
,
33
AB∠>∠
is satisfied for the angles of triangles
1
P
and
2
P
,
which are parallel to each other (Fig. 8).
The difference
12
PP
∗
is a triangle similar to
triangle
1
P
, and the lengths of the vectors on its sides
are(12):
22 22
112223 3
22
,, .
ab ab
с a с abс a
aa
−−
==−=





4. Finding the difference Minkowski of triangles
whose vectors on the corresponding side are not in
the same direction.
Figure 8.
Let the conditions
1
a ↑↑

12
,ba↑↑


23
,ba↑↑


3
b

and
112 23 3
,,ababab≥≥≥

 
are satisfied for the
vectors
123
,,aa a
 
on the sides of triangle
1
P
and the
corresponding vectors
123
,,bbb

on the sides of
triangle
2
P
. In this case, as in the third group, the
difference
12
PP
∗
can be an empty set, so in this case,
we assume that the condition of theorem 1 holds. It is
not difficult to see that this difference also results in a
triangle like
1
P
(Fig. 9).
Figure 9.
The following equations are valid for the vectors
123
,,сс с
 
on the sides of this triangle:
()
()
()
()
22
22
22
21 21 33 33
1 1
22 2222
12 12 13 13
,,
1,
,,
ab ab ab ab
с a
a a aa a a aa

−−

=− −

−−


 
 

   
()
()
()
()
22
22
22
21 21 33 33
2 2
22 2222
12 12 13 13
,,
1,
,,
ab ab ab ab
с a
aa aa aa aa

−−

=− −

−−


 
 

     
()
()
()
()
22
22
22
21 21 33 33
3 3
22 2222
12 12 13 13
,,
1.
,,
ab ab ab ab
с a
aa aa aa aa

−−

=− −

−−


 
 

   
Thus,
2
P
the illuminated place of the lighting set
can be of arbitrary shape. We can find the installation
location of the kit
12
PP
∗
.
4 CONCLUSIONS
Thus, we have established that if the set of the 𝑃

-
triangle is the area that is being sanctified, the
𝑃

-
capabilities of the illuminating instrument are also a
triangle and
𝑄∅, then 𝑄will be a point or triangle
similar to the
𝑃

set that must be installed by the
illuminating instrument. In this work, we present our
results for calculating the Minkowski difference of
triangle-shaped sets. Despite the relatively simple
nature of the problem, its complete solution and
analysis of this solution allows us to solve more
general problems on this topic. In fact, when working
with triangles, it is clear that the shape of the triangle
is not important, but its size. The results obtained can
be applied in the implementation of the installation of
lighting devices for residential buildings, offices and
enterprises.
REFERENCES
Bowers, B., 1998. A History of Lighting Technology.
Published by Oxford University Press, Oxford .
Bommel', W., 2009. The spectrum of light sources and low
lighting levels: the basics. Light and Engineering. 6. pp
13–16.
Bekker, H., Brink, A., 2004. Reducing the time complexity
of Minkowski-sum based similarity calculations by
using geometric inequalities. (Conference Paper in
Lecture Notes in Computer Science)
Pontryagin, L. S., 1981. Linear differential games of
pursuit, Math. USSR-Sb., 40:3, 285-303
Satimov, N., On the pursuit problem in linear differential
games. Differ. Uravn., 9:11, 2000–2009
Optimizing the Quality of Electric Lighting with the Use of Minkowskiâ
˘
A
´
Zs Geometric Difference
755

Mamatov, M.Sh., 2009. Application of the finite difference
method to the problem of pursuit in the distributed-
parameter systems. Automation and Remote
Control, 70(8), pp. 1376–1384
Mamatov, M.Sh., 2009. On the theory of differential pursuit
games in distributed parameter systems. Automatic
Control and Computer Sciences., 43(1), 1-8
Mamatov, M.S., Sobirov, K.K., 2020. On the Theory of
Position Pursuit Differential Games. Journal of
Mathematica Sciences (United States), 245(3). 332–
340 pp.
Mamatov, M.S., Zunnunov, A.O., Esonov, E.E., 2020.
Quantitative analysis of the problem of lion and man in
the presence of a circular obstacle. Journal of
Automation and Information Sciences, 52(2). pp.42–
52.
Tukhtasinov, M., Mamatov, M.Sh., 2009. On transfer
problems in control systems. Differential
Equations, 45(3), pp. 439–444.
ISAIC 2022 - International Symposium on Automation, Information and Computing
756