Multi-Stage Path Planning Strategy for Intelligent Cleaning Robot

Xingxing Cheng

, Xianfeng Ding

, Chia E. Tungom

and Ji Yuan

Onewo Space-Tech Service Co., Ltd., Shenzhen, China

Keywords:

Garbage Clearance, TPP, Yolov5, MDDPG.

Abstract:

The clearance of public garbage is a challenging case in artiﬁcial intelligence implementation. The difﬁculty

is how to recognize the public garbage and make path planning. In comparison with Traditional Path Planning

(TPP) architecture, we utilized a method of Multi-stage Path Planning for garbage clearance to improve the

accuracy and speed of TPP architecture. Within this paper, the original public video frames are taken as input

and the garbage is separated into several classes by Yolov5. Its location is estimated by the location of the

camera. Taking the garbage class and location as input, the path planning is calculated by an improved Multi-

stage Deep Deterministic Policy Gradient (MDDPG). Our novel architecture was trained and tested using

videos from a real community place and achieved ideal effects.

1 INTRODUCTION

With the fast growth of the application of the artiﬁcial

intelligence technology in last decade, mobile robots

have become smarter. As known that, path planning

is an important topic in the mobile robots’ research

ﬁeld. The goal of path planning is both to perfect

keep away from obstacles and to fast plan the best

moving path to the target location. According to the

literature review, there are two main algorithms for

the path planning of mobile robots, namely the tra-

ditional and reinforcement-learning-based path plan-

ning algorithms.

As the traditional algorithm, the A* algorithm is

a correct path-planning algorithm based on a heuris-

tic function. The results show that the A* algorithm

has a good deceleration effect in processing time, and

its running speed is fast (Guruji et al., 2016; Shukla

et al., 2008; Kala et al., 2009; Weiteng et al., 2013).

Nevertheless, there still exist some problems during

the application, such as the length of the path, the risk

of colliding with obstacles, and trafﬁc isolation rules,

etc. Ant Colony Optimization (ACO) is deﬁned as a

kind of constructive meta-heuristic algorithm for suit-

able path planning (Mirjalili et al., 2020; Dorigo et al.,

1991; Brand et al., 2010; Liu et al., 2017).Notice that,

local optimization, slow convergence, and low search

https://orcid.org/0000-0003-3608-1984

https://orcid.org/0000-0002-2990-4391

https://orcid.org/0000-0003-3708-4044

https://orcid.org/0000-0002-4369-647X

efﬁciency are frequent problems caused by ACO.

The Artiﬁcial Potential Field (APF) method pro-

vides a simple and effective strategy for robot navi-

gation. However, there is a local minimum problem

by applying this method (Khatib, 1985; Sun et al.,

2019). Genetic algorithm has been widely used in

path planning of mobile robots and has achieved good

results (Zhang et al., 2016; Karami and Hasanzadeh,

2015). Notice that, the genetic algorithm has some

drawbacks in obstacle environment, i.e. path infea-

sibility. Traditional robot path planning and control

methods, they cannot deal with emergency circum-

stances, extract information from environmental per-

ception and analysis, and make decisions about ap-

propriate action.

Deep reinforcement learning (DRL) applied in the

path planning can be separated into two main sub-

type algorithms: value function algorithm (Liu et al.,

2018) and strategy gradient algorithm (Liu et al.,

2019). The most important four value function algo-

rithms for robot path planning are DQN, IDDDQN,

Dueling DQN, and D3QN. For instance, Tai et al.

proposed a DQN algorithm to implement robot path

planning in a virtual environment (Tai and Liu, 2016).

There are several drawbacks of overestimation and

poor stability of the algorithm. Sichkar et al. pro-

posed the IDDDQN algorithm to improve the net-

work’s convergence speed, and results are shown that,

in an unknown complex environment, this algorithm

can obtain an optimal path better (Sichkar, 2019). In

the paper from Wen et al., a full convolutional resid-

Cheng, X., Ding, X., Tungom, C. and Yuan, J.

Multi-stage Path Planning Strategy for Intelligent Cleaning Robot.

DOI: 10.5220/0012046400003612

In Proceedings of the 3rd International Symposium on Automation, Information and Computing (ISAIC 2022), pages 757-765

ISBN: 978-989-758-622-4; ISSN: 2975-9463

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

757

ual network and the dueling DQN algorithm are ap-

plied for obstacle detection and path planning, respec-

tively ( (Wen et al., 2020)). This algorithm can help

robots to recognize and keep away from static obsta-

cles in the complex environment. Wen et al. (Wen

et al., 2020) proposed a dual-depth q network obstacle

avoidance algorithm (D3QN), which can be trained

in the virtual environment, and directly applied in

the complex unknown environment (Xie et al., 2017).

The DRL algorithm based on the value function can

execute continuous action decisions unless the ac-

tion strategies are independent. Then, the strategy

gradient method is adopted for DRL. In robot path

planning, the strategy gradient algorithms mainly in-

clude TRPO, PPO, and DDPG. Lillicrap et al. pro-

posed a DDPG algorithm which apply the DQN esti-

mation function based on the DPG algorithm. It can

be utilized for continuous state and action space, and

straightforwardly improving the move stability (Lilli-

crap et al., 2015). Since TRPO algorithm have some

drawbacks, such as the strategy and environment are

too large and it can produce large errors easily. To

overcome aforedmentioned problems, Schulman et al.

proposed a neighborhood strategy optimization algo-

rithm based on the TRPO algorithm (Schulman et al.,

2017). The robot path planning algorithm which uti-

lized a random gradient replace the common policy

gradient to optimize the transformation of the objec-

tive function with sample data interacting with the en-

vironment, which has ﬁne information robustness and

efﬁciency.

According to previous research, DRL algorithms

outperform the traditional algorithm in solving the

mobile robot path planning problem. In the dis-

crete action strategy scenario, the value function-

based DRL algorithm can make continuous action de-

cisions. However, the stability and convergence speed

via online learning is an urgent issue which is worth

to be investigating. Since it is difﬁcult to solve a

sophistical multi-stage design problem with a single

algorithm. Multi-functional ﬂoor cleaning robot has

gained popularity in our daily life (Milinda and Mad-

husanka, 2017; Milinda and Madhusanka, ). More-

over, there are few types of researches on the plan-

ning and cleaning of the garbage sorting path plan-

ning. This paper is devoted to the research of the

multi-step path planning for a cleaning robot. The

main contributions of this paper can be summarized

as follows:

• 1. Proposed MDDPG algorithm to speed up

model convergence:

1.1 Adopt multi-strategy network, centralized

value network, value network receives data gen-

erated by multiple strategy networks at the same

time, and improves the efﬁciency of value net-

work estimation;

1.2 Divide the experience playback pool by pri-

ority to speed up the convergence of the model;

1.3 Design the reward function for the inter-

mediate starting point to improve the convergence

speed and degree of the reinforcement learning al-

gorithm;

• 2. The classiﬁcation of garbage is deﬁned, and

the garbage classiﬁcation model is trained based

on an improved YOLOv5;

• 3. We build a multi-stage garbage path planning

model to improve the generalization of garbage

path planning problems.

The rest of this paper is organized as follows. The

DDPG is given in Section 2. Our proposed method

is in Section 3. The experimental results and analysis

are present in Section 4, and conclusions and future

work can be found in Section 5.

2 DEEP DETERMINISTIC

POLICY GRADIENT(DDPG)

Traditional reinforcement learning algorithms use ta-

bles to record value functions, and once dealing prob-

lems in cases with high states or action space ex-

ploded, it will cause a dimensionality disaster. On the

other hand, deep reinforcement learning parameter-

izes the value function or policy function and makes

full usage of the representation ability of the neu-

ral network to ﬁt the value function or policy func-

tion. Therefore, scholars combine deep learning to

propose deep reinforcement learning. This improve-

ment enables deep reinforcement learning having a

good performance in cases with high-dimensional and

continuous-state spaces.

2.1 AC Network

The Actor-Critic framework(AC network) utilizes a

neural network to approximate the value function and

the policy function at the same time, its schematic di-

agram is shown in Figure 1. The AC network contains

two neural networks: actor-network and the critic net-

work. The actor-network is responsible for ﬁtting the

current policy function and outputting corresponding

actions according to the state of the input, while the

critic network is responsible for estimating the value

function, according to the state or state of the input.

The action pair outputs the corresponding state or ac-

tion value. Actor and critic neural networks respec-

tively parameterize the policy function and the value

ISAIC 2022 - International Symposium on Automation, Information and Computing

758

function, and the value function can choose the state

value function or the action value function, as shown

in Eq.1. The parameterization of the strategy function

is shown in Eq.2:

(s) = φˇ(s,w)Q

(s, a) = Qˇ(s, a, w) (1)

π(s, a) = P[a|s, θ] (2)

The ultimate training goal of the AC network is to

obtain an optimal policy, in other words, an actor-

network that can represent the optimal policy. The

training method of the network adopts gradient as-

cent, and the network parameters are updated accord-

ing to the objective function of the actor-network. The

objective function, parameter update, and gradient of

the objective function of the actor-network are shown

in Eq.3:

V (θ) =

∑

(s)d

(s)

θ = θ + BΠ

V (θ)

V (θ) = Π

logπ

(s, a)·

(3)

In Eq.3, the score function Π

logπ

(s, a) is

widely applied in the ﬁeld of machine learning and

is easy to calculate. Hence, actor-networks can be

trained as long as the action-value function can be

accurate estimated.

Figure 1: AC network schematic diagram.

In the actor-critic framework, the critic network

is responsible for estimating the value function to as-

sist the actor-network in training. During actor-critic

training, actor and critic networks are trained simul-

taneously, and the critic network is updated by calcu-

lating TD error:

l = R

t+1

+ ΨQ

t+1

, a

t+1

) − Q

, a

) (4)

dw = ℘

£l

(5)

2.2 DDPG

DDPG methods include behavior criticism, experi-

ence replaying, objective network, and deterministic

strategy gradient theorem. It proves the existence of

deterministic strategies µ(ω) : S→A , and generates

the exact actions of the agent based on the given state

and not based on the probability distribution of all ac-

tions. In this method, the performance target is de-

ﬁned as follows:

J(π

) =

(s)

(s, a)r(s, a)dads

= E

s∼ρ

,a∼π

[r(s, a)],

(6)

where ρ

(s) denotes the state distribution. The objec-

tive with deterministic policy is:

J(µ

) =

(s)r(s, µ

(s))ds

= E

s∼ρ

[r(s, µ

(s))],

(7)

The state-action value or state-action critic net-

work Q(s

, a

, θ) and the actor-network µ(s

, ω), in

which the θ and ω as a parameter of neural network)

approximates the state action value function and ac-

tion function in this method, respectively. Once the

network is updated, the training experience comes

from experience playback. It is commonly a buffer

that stores a tuple of four elements (s

, a

, r

, s

t+1

), and

provides a batch of updates for the network of actors

and ﬁlm critics. As the buffer is full, the updated ex-

perience will replace the oldest one, hence only a lim-

ited number of the latest experience will remain. In

addition, by providing a constant target in the training

process, the target network updates the critic network.

The target network is usually constructed as a copy

of the critic network. The target network, denoted

as Q

tar

, is applied as a replacement of

Q(s

t+1

, a

) in

Eq.8:

tar

(θ) = (r(s

, a

)+γQ

tar

t+1

, a

t+1

, θ

−

)−Q(s

, a

, θ))

(8)

where the θ

−

is the parameter of the previous itera-

tion. Experience replay and target network are vital

for training stable DDPG methods and creating the

deep neural network possible.

Multi-stage Path Planning Strategy for Intelligent Cleaning Robot

759

3 OUR PROPOSED METHOD

Our proposed method is shown in Fig.. It can be

seen that the YOLOv5-MDDPG schematic diagram

mainly included a garbage recognition and a path

planning module.

Figure 2: YOLOV5-MDDPG schematic diagram.

3.1 YOLOV5

YOLOv5 (Zhao et al., 2022) is one of the preva-

lent target detection models with high accuracy.

Within this framework, as a regression problem, ob-

ject detection trained end-to-end, it enables training

quickly and achieved competitive performance. For

YOLOv5, the main contribution is to port YOLO

from the dark web neural network framework(Chen

et al., 2019) to PyTorch. This allows 16-bit ﬂoating-

point calculations to be used insteading of 32-bit ones,

further, greatly reducing the reasoning time. YOLO

consist of three main parts. The body mesh pro-

duces image features of different resolutions, the neck

mixes different features and combines it, and the head

uses mixed features to forecast classes and boxes. Its

loss function includes a combination of GIoU, ob-

ject loss, and class loss. In particular, the framework

of YOLOv5 adopts a bottleneck based on a phase-

to-phase local network (CSPNet)(Alkhamaiseh et al.,

2021). CSPNet aims to reduce the number of gradient

computation iterations found in densenets-based net-

works(Tian et al., 2019). This reduces training time

and allows smaller models to have less impacts on

performance. Detection is considered as a regression

problem in the YOLO models. Each anchor box has

x and y coordinates, width, and height. It forecasts

how much each feature should modify. If it is ap-

proaching the anchor box, the box contains the target

object. This implementation uses k-means and a ge-

netic learning algorithm to ﬁrst learn the anchor boxes

from the distribution of boxes in the training dataset.

This is useful in this case because the appearance of

tear gas canisters is limited. By using an anchor frame

that better ﬁts the size of the tear gas canister, the

model learns faster to forecast the correct contain-

ment area of the tear gas canister. In addition to us-

ing CSPNet and learning anchor boxes, YOLOv5 uti-

lizes speciﬁc data augmentation techniques which are

useful for applications. The most notable data exten-

sion is the mosaic data extension, which was the ﬁrst

used in YOLOv4 (Bochkovskiy et al., 2020). This

enhancement technique combines four different im-

ages side by side at different scales into one image.

Like random throttling, this helps the network handle

congestion better. This also makes it easier to use, as

many tear gas canisters are blocked usually. More-

over, this data addition method merges objects of var-

ious classes into a single image. It is useful for real-

life images that may contain different types of tear

gas canisters. Lastly, by combining various images,

the image background becomes more manifold. This

could be considered a type of domain randomization,

and previous research has shown it to be very useful

in this application(Tobin et al., 2017).

3.2 MDDPG

3.2.1 MDP

After obtaining the state information such as the cate-

gory and location of garbage, it is used as the input of

the subsequent model. Established a cleaning robot

path planning model based on MDDPG, and describe

the cleaning robot path planning problem as a Markov

decision process (MDP), that is, a sequence decision

problem. At the same time, the basic MDP problems

such as state, action, and reward in the process of

cleaning robot path planning are deﬁned. The state

space of the MDDPG algorithm(S

) includes: lidar

data (SA), the current control command of the clean-

ing robot (SC), the control command of the mobile

robot at the last moment, the orientation of the target

point (SD) and the distance (SE); the current control

command of the cleaning robot refers to the angular

velocity (SF) and linear velocity (SP) of the cleaning

ISAIC 2022 - International Symposium on Automation, Information and Computing

760

robot, as shown in the Eq.9. The action space of the

MDDPG algorithm(a

) includes: the angular velocity

of the cleaning robot body coordinate system rotating

around the Z axis(SF

) and the linear velocity along

the X axis(SP

), as shown in the Eq.10.

= SA + SC + SD + SE + SF +SP (9)

= SF

+ SP

(10)

3.2.2 AC Network

The MDDPG algorithm utilizes a multi-actor-

network. Generate data by combined N actor-

networks, which improves the stability of the data,

reduces the uncertainty of data, and is conducive

to speeding up the convergence speed of the model

and improving its convergence depth. Each actor-

network is divided into the current network fa-

therly(responsible for the iterative update of the actor-

network parameters) and the critic network (respon-

sible for selecting the optimal next action based on

the experience of replaying the next state sampled

in the replay buffer), where the current network loss

function(H(ω)) is shown in the Eq.11:

H(ω) =

•

∑

i=1

∑

l=1

(y − Q(ϕ(s

), a

, ω))

(11)

where k,y are constants, N is the number of the actor-

network, Q is the target value, ϕ(s) is the function of

the state value, a is action, ω is the trainable parameter

after parameterization of the actor-network function.

3.2.3 Reward design

The reward function of the MDDPG algorithm is de-

signed as follows whether the cleaning robot reaches

the garbage, whether the distance between the clean-

ing robot and the target point changes, and whether it

collides and encounters obstacles.

The reward function designed considered whether

the cleaning robot reaches the garbage is shown in

Eq.(12) :

arr

(

arr

if d

≤ d

0 if d

> d

(12)

The reward function designed considered the dis-

tance between the cleaning robot and the target point

changes is shown in Eq.13 :

dis

(

dis

if d

− d

t−1

< 0

−g

dis

if d

− d

t−1

≤ 0

(13)

The reward function designed considered whether it

collides is shown in Eq.14 :

col

(

col

if d

≤ d

0 if d

> d

(14)

The reward function designed considered whether it

encounters obstacles is shown in Eq.15 and Eq.16:

J =

∑

i=1

logπ

(ε

)[G(ε

, r

)− G(π

, r

)] (15)

: G

min

< G(π

, r

) < G

max

(16)

The total reward function is shown in Eq. (17):

G = G

arr

+ G

dis

+ G

col

+ Γ

J (17)

3.2.4 Replay Buffer

DDPG utilizes a replay buffer to eliminate strong cor-

relations between input experiences. Here, experi-

ence refers to a quadruple (s

, a

, r

, s

t+1

). Meanwhile,

DDPG applies the target network method to stabilize

the training process. As a fundamental part of the

DDPG algorithm, the replay buffer greatly affects the

training speed and ﬁnally effect of the network.

We have improved the replay buffer of the MD-

DPG algorithm, and divided the replay buffer by pri-

ority. During the training process of the cleaning

robot, the training data obtained is put into four re-

play buffers with different priorities. Through prior

knowledge, unnecessary search time is reduced, and

the convergence speed of the model is improved.

(1) When the cleaning robot reaches the garbage

location (i.e. target point), it puts the acquired training

data into the replay buffer 1 with the highest priority;

(2) When the cleaning robot is in the exploration

stage, put the acquired training data into the replay

buffer 2 with the second highest priority;

(3) When the cleaning robot collides, put the ac-

quired training data into the replay buffer 3 with lower

priority;

(4) When the cleaning robot encounters an im-

passable obstacle (such as a ditch, a river, etc.), the

obtained training data is put into the replay buffer 4

with the lowest priority.

The training data includes status information, cur-

rent time and previous action instruction, and reward

value data at a moment. The state information in-

cludes Lidar data, and orientation and distance infor-

mation of the target point.

4 EXPERIMENTAL RESULTS

AND ANALYSES

In this paper. we proposed a multi-stage garbage

recognition and cleaning, and the results of public

garbage recognition and path planning are shown in

Fig.3. There are two parts in our method that included

improved YOLOv5 for garbage recognition and path

planning based on MDDPG.

Multi-stage Path Planning Strategy for Intelligent Cleaning Robot

761

Figure 3: Results of public garbage recognition and path planning.

4.1 Imporoved YOLOv5 for Garbage

Recognition

Our improved YOLOv5 model was trained by the

Onewo daily images dataset, and the training dataset

and the validation dataset are 52,224 and 13,056 re-

spectively. Fig.4 shows the recognition result of 600

rounds of training based on our improved YOLOv5

model. It can be seen from the ﬁgure that the model

can identify and classify the garbage accurately in dif-

ferent scenarios.

Figure 4: Part of garbage recognition by improved

YOLOv5. (a) Original image; (b) Detect image.

Table.1 shows the evaluation information about

the experimental data. As can be seen from the ta-

ble, the validation dataset is 13,056. For class all, the

Labels is 38,122, the Precision is 0.929, the Recall

is 0.913, the mAP@.5 is 0.922, the mAP@.5:.95 is

0.835; For class other, the Labels is 8,022, the Preci-

sion is 0.91, the Recall is 0.906, the mAP@.5 is 0.89,

the mAP@.5:.95 is 0.81; For class Bulky garbage,

the Labels is 8,843, the Precision is 0.947, the Re-

call is 0.946, the mAP@.5 is 0.933, the mAP@.5:.95

is 0.834; For class Decoration garbage, the Labels

is 8217, the Precision is 0.913, the Recall is 0.94,

the mAP@.5 is 0.966, the mAP@.5:.95 is 0.84; For

class Green garbage, the Labels is 4114, the Precision

is 0.898, the Recall is 0.837, the mAP@.5 is 0.881,

the mAP@.5:.95 is 0.803; For class Packed garbage,

the Labels is 8,926, the Precision is 0.975, the Re-

call is 0.938, the mAP@.5 is 0.942, the mAP@.5:.95

is 0.886. By data analysis the experimental re-

sults, it can be observed that the recognition accu-

racy of four class garbage is well, for mAP@.5, Bulky

garbage, Decoration garbage, and Packed garbage are

all greater than 0.9. Thereby, it has better actual

garbage recognition effect. However, in the train-

ing dataset, due to the small number of samples, the

mAP@.5 of Green garbage is less than 0.9, and it can

be optimized by increasing the number of samples.

In this section, as can be seen in ﬁgure 5, we an-

alyze the training iterations and the step size of the

model by comparing the traditional DDPG algorithm

and our proposed MDDPG algorithm.

In this ﬁgure, the abscissa represents the iterations

of training and the ordinate is the amount of each iter-

ation steps required from the cleaning robot position

to the trash position. The green dashed line repre-

sents the iterative trend results of the DDPG algorithm

and the red solid line is the proposed algorithm iter-

ative trend results. This ﬁgure obviously shows the

training effect and convergence speed between these

two algorithms. It can be seen that, around the 190th

round, the the proposed MDPDG algorithm’s number

of iteration steps starts to decrease, showing a con-

vergence trend gradually, while the DDPG algorithm

starts to show a convergence trend about the 470th

iteration. Meanwhile, the DDPG algorithm’s itera-

tion steps stay at the level of about 220 steps and do

not converge to the minimum steps number, while our

ISAIC 2022 - International Symposium on Automation, Information and Computing

762

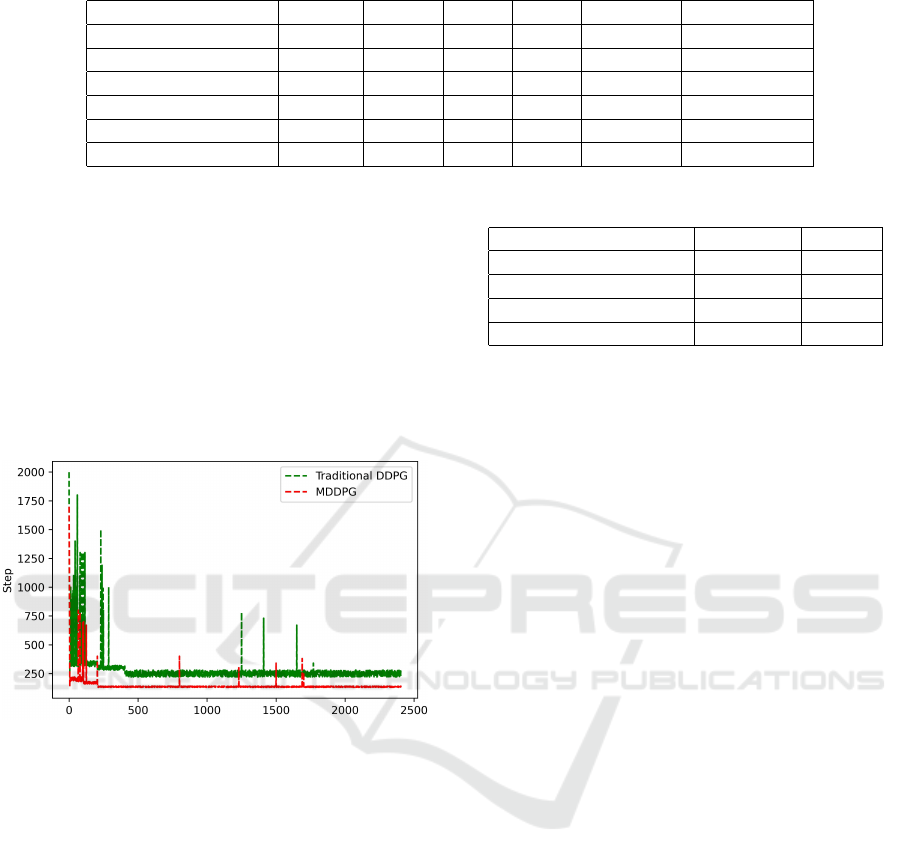
Table 1: The evaluation of our trained improved YOLOv5 model.

Class Images Labels P R mAP@.5 mAP@.5:.95

all 13056 38122 0.929 0.913 0.922 0.835

other 13056 8022 0.91 0.906 0.89 0.81

Bulky garbage 13056 8843 0.947 0.946 0.933 0.834

Decoration garbage 13056 8217 0.913 0.94 0.966 0.84

Green garbage 13056 4114 0.898 0.837 0.881 0.803

Packed garbage 13056 8926 0.975 0.938 0.942 0.886

proposed MDDPG algorithm converges at about 110

steps. Obviously, the path computed by the DDPG

algorithm has a larger number of steps. In the fol-

lowing training process, our proposed MPDDG al-

gorithm has a lower ﬂuctuation frequency and supe-

rior stability than the DDPG algorithm. Besides, as

can be seen from experimental results, our proposed

MDDPG algorithm has both fast iteration speed and

strong decision-making ability, and can quickly reach

the debris location with fewer steps.

Figure 5: The convergence trend comparison results of step

iteration.

Figure 6a shows the result of path planning after

2,500 training rounds by the traditional Q-learning

algorithm. Intuitively, due to the size limitation of

the Q table, there are many redundant corners in this

path and the algorithm training takes a long time.

Figure 6b shows the path planning result of 2,500

training rounds by the traditional DDPG algorithm.

Intuitively, the planned path is a curve. Since the

DDPG algorithm achieves a continuous action value

that bringing the robot’s action changes in real-time.

Since the beach robot needs as few actions as possible

during navigation, the path achieved by our proposed

method cannot meet the real navigation needs. Figure

6c shows the result of A* algorithm path planning. As

shown, the closer the planning path is to the obstacle,

the more corners the path has, which increases the risk

of the robot moving. Compare the aforementioned al-

gorithm with our proposed MDDPG algorithm (ﬁgure

6d). Our proposed MDDPG path planned is smoother,

Table 2: The comparison of experimental data.

Method Path Length/m Time/s

Q-learning algorithm 170.238 0.7556

A* algorithm 144.626 1.2365

DDPG algorithm 177.251 0.8011

MDDPG algorithm 165.342 0.5768

maintains a safe distance from obstacles, and is more

linear with the robot’s real navigation speciﬁcations.

In addition, based on the experimental data, differ-

ent performances of algorithms are compared in terms

of trip length, trip planning time, and a number of

turns. The comparison result is shown in table 2, the

length of planning path via algorithm in our research

is 165.342m, which takes 0.5768s. The Q-learning

algorithm plans path length is 170.238m and takes

0.7556s. The DDPG algorithm planned path length

is 177.251m, which takes 0.8011s. The length of the

route planned by algorithm A* is 144.626m, which

takes 1.2365s. By data analysis of the experimental

results, our proposed algorithm meets the actual nav-

igation speciﬁcations well, the method has a shorter

path planning ability and a good performance in im-

plementation.

5 CONCLUSIONS AND FUTURE

WORK

We present the multi-stage framework for public

garbage recognition and path planning that accurately

recognizes the classes of garbage and location, and

subsequently outputs a fast worksheet for path plan-

ning. The experimental results show that, for the

recognition task, and the best mPrecision is 0.929,

the best mRecall is 0.913, the best mAP@.5 is 0.922,

the best mAP@.5:.95 is 0.835. For path planning, the

best path length planned by this paper’s proposed al-

gorithm is 165.342m and the best taking is 0.5768s.

Multi-stage Path Planning Strategy for Intelligent Cleaning Robot

763

Figure 6: Different algorithm’s path planning results. (a) Q-learning algorithm path planning; (b)A* algorithm path planning;

REFERENCES

Alkhamaiseh, K. N., Grantner, J. L., Shebrain, S., and

Abdel-Oader, I. (2021). Towards automated perfor-

mance assessment for laparoscopic box trainer using

cross-stage partial network. In 2021 Digital Image

Computing: Techniques and Applications (DICTA),

pages 01–07. IEEE.

Bochkovskiy, A., Wang, C.-Y., and Liao, H.-Y. M. (2020).

Yolov4: Optimal speed and accuracy of object detec-

tion. arXiv preprint arXiv:2004.10934.

Brand, M., Masuda, M., Wehner, N., and Yu, X.-H. (2010).

Ant colony optimization algorithm for robot path

planning. In 2010 international conference on com-

puter design and applications, volume 3, pages V3–

436. IEEE.

Chen, R.-C. et al. (2019). Automatic license plate recog-

nition via sliding-window darknet-yolo deep learning.

Image and Vision Computing, 87:47–56.

Dorigo, M., Maniezzo, V., and Colorni, A. (1991). The ant

system: An autocatalytic optimizing process.

Guruji, A. K., Agarwal, H., and Parsediya, D. (2016). Time-

efﬁcient a* algorithm for robot path planning. Proce-

dia Technology, 23:144–149.

Kala, R., Shukla, A., Tiwari, R., Rungta, S., and Janghel,

R. R. (2009). Mobile robot navigation control in mov-

ing obstacle environment using genetic algorithm, ar-

tiﬁcial neural networks and a* algorithm. In 2009 WRI

World Congress on computer science and information

engineering, volume 4, pages 705–713. IEEE.

Karami, A. H. and Hasanzadeh, M. (2015). An adaptive ge-

netic algorithm for robot motion planning in 2d com-

plex environments. Computers & Electrical Engineer-

ing, 43:317–329.

Khatib, O. (1985). Real-time obstacle avoidance system for

manipulators and mobile robots. In Proceedings of the

1985 IEEE International Conference on Robotics and

Automation, St. Louis, MO, USA, pages 25–28.

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T.,

Tassa, Y., Silver, D., and Wierstra, D. (2015). Contin-

uous control with deep reinforcement learning. arXiv

preprint arXiv:1509.02971.

Liu, J., Gao, F., and Luo, X. (2019). Survey of deep rein-

forcement learning based on value function and policy

gradient. Chinese Journal of Computers, 42(6):1406–

1438.

Liu, J., Yang, J., Liu, H., Tian, X., and Gao, M. (2017).

An improved ant colony algorithm for robot path plan-

ning. Soft computing, 21(19):5829–5839.

Liu, Q., Zhai, J. W., Zhang, Z.-Z., Zhong, S., Zhou, Q.,

Zhang, P., and Xu, J. (2018). A survey on deep re-

inforcement learning. Chinese Journal of Computers,

41(1):1–27.

Milinda, H. and Madhusanka, B. Multi-functional ﬂoor

cleaning robot for domestic environment.

Milinda, H. and Madhusanka, B. (2017). Mud and dirt

separation method for ﬂoor cleaning robot. In 2017

Moratuwa Engineering Research Conference (MER-

Con), pages 316–320. IEEE.

ISAIC 2022 - International Symposium on Automation, Information and Computing

764

Mirjalili, S., Song Dong, J., and Lewis, A. (2020). Ant

colony optimizer: theory, literature review, and appli-

cation in auv path planning. Nature-inspired optimiz-

ers, pages 7–21.

Schulman, J., Wolski, F., Dhariwal, P., Radford, A., and

Klimov, O. (2017). Proximal policy optimization al-

gorithms. arXiv preprint arXiv:1707.06347.

Shukla, A., Tiwari, R., and Kala, R. (2008). Mobile robot

navigation control in moving obstacle environment

using a* algorithm. Intelligent Systems Engineering

Systems through Artiﬁcial Neural Networks, 18:113–

120.

Sichkar, V. N. (2019). Reinforcement learning algorithms in

global path planning for mobile robot. In 2019 Inter-

national Conference on Industrial Engineering, Ap-

plications and Manufacturing (ICIEAM), pages 1–5.

IEEE.

Sun, J., Liu, G., Tian, G., and Zhang, J. (2019). Smart

obstacle avoidance using a danger index for a dynamic

environment. Applied Sciences, 9(8):1589.

Tai, L. and Liu, M. (2016). A robot exploration strategy

based on q-learning network. In 2016 ieee interna-

tional conference on real-time computing and robotics

(rcar), pages 57–62. IEEE.

Tian, Y., Yang, G., Wang, Z., Wang, H., Li, E., and Liang,

Z. (2019). Apple detection during different growth

stages in orchards using the improved yolo-v3 model.

Computers and electronics in agriculture, 157:417–

426.

Tobin, J., Fong, R., Ray, A., Schneider, J., Zaremba, W., and

Abbeel, P. (2017). Domain randomization for transfer-

ring deep neural networks from simulation to the real

world. In 2017 IEEE/RSJ international conference on

intelligent robots and systems (IROS), pages 23–30.

IEEE.

Weiteng, Z., Baoming, H., Dewei, L., and Bin, Z. (2013).

Improved reversely a star path search algorithm based

on the comparison in valuation of shared neighbor

nodes. In 2013 Fourth International Conference on

Intelligent Control and Information Processing (ICI-

CIP), pages 161–164. IEEE.

Wen, S., Zhao, Y., Yuan, X., Wang, Z., Zhang, D., and Man-

fredi, L. (2020). Path planning for active slam based

on deep reinforcement learning under unknown en-

vironments. Intelligent Service Robotics, 13(2):263–

272.

Xie, L., Wang, S., Markham, A., and Trigoni, N. (2017).

Towards monocular vision based obstacle avoidance

through deep reinforcement learning. arXiv preprint

arXiv:1706.09829.

Zhang, X., Zhao, Y., Deng, N., and Guo, K. (2016). Dy-

namic path planning algorithm for a mobile robot

based on visible space and an improved genetic al-

gorithm. International Journal of Advanced Robotic

Systems, 13(3):91.

Zhao, Y., Shi, Y., and Wang, Z. (2022). The improved

yolov5 algorithm and its application in small target

detection. In International Conference on Intelligent

Robotics and Applications, pages 679–688. Springer.

Multi-stage Path Planning Strategy for Intelligent Cleaning Robot

765