
Research on Network Public Opinion Communication Model of
Fusion Emotion
Xiding Xing
a
and Hongmei Yang
*b
Shandong University of Science and Technology, Qing Dao, China
Keywords: Internet Public Opinion, Emotional Tendency, Communication Model, Anylogic simulation, Case analysis.
Abstract: To effectively simulate the network public opinion dissemination process and study the evolution law of
different public opinion groups under the influence of emotion intervention, we propose a group network
public opinion communication model SPQNR that integrates emotions. The model divides netizens into
three categories according to the sentiment value of netizens' main comments and introduces the positive
rate and negative rate of netizens to design the relationship between the mutual conversion parameters
between groups. Finally, this paper conducts case analysis through Anylogic simulation. The SPQNR model
can effectively simulate the evolution of public opinion of different groups.
1 INTRODUCTION
1
As of December 2021, the number of Chinese
netizens has reached 1.032 billion, and the Internet
penetration rate has reached 73.0%. The number of
online social platforms has increased accordingly.
Netizens use various social platforms to disseminate
information (Alvarez-Galvez 2016). Weibo is an
information dissemination platform with a large
number of users. In Weibo, many topics co-exist,
and the topic information is difficult to distinguish
between true and false. Netizens' comments on
events can be followed and commented on by Weibo
users, making the Weibo platform an essential
channel for disseminating negative information. The
malicious dissemination of negative public opinion
on the internet will distort the truth of the incident
and cause social conflicts. It has become an essential
factor in social instability.
Internet public opinion information is created by
netizens' subjects and spread by them. Although the
government, online media, and other objects
influence the dissemination of online public opinion,
the emotions of netizens play a crucial role in the
dissemination of online public opinion. Therefore, it
is of great practical significance to build a model of
a
https://orcid.org/0000-0002-1071-7297
b
https://orcid.org/0000-0001-6237-3302
*
Correspoonding Author
public opinion dissemination and implement
interventions based on the emotions of netizens to
control public opinion. The infectious disease model
is a top-down modeling approach, which evolved
from the DK model (
Daley 1964
). Many scholars
have found that the contagion model can simulate
the spread of public opinion information, and the
two transmission mechanisms are relatively similar,
so scholars have proposed improved models to more
accurately simulate the spread of online public
opinion among groups (Liu et al. 2020; Zhang et al.
2020; Yang et al. 2018; Huo et al. 2019; Liu et al.
2019). Wang Zhiying et al. studied the dissemination
interaction of solid and weak public opinion
information and the dissemination pattern of
emergencies under government intervention, which
provided a reference for the government to develop
emergency plans (
Wang et al. 2020
) (Li et al. 2017).
Di Lan et al. established a three-divisional opinion
online dissemination model under media
intervention (
Di et al. 2018
). They determined that the
media role had the most significant influence on
neutrals because neutrals were the majority among
netizens. MI-SEIR considered the impact of media
communication and interpersonal cusps on opinion
dissemination based on the SEIR model (
Kumar et al
2020
). Zhang et al. identified a significant effect of
government intervention on the intervention effect
of opinion leaders under media, opinion leaders, and
government intervention (Zhang et al. 2021). Zhang
184
Xing, X. and Yang, H.
Research on Network Public Opinion Communication Model of Fusion Emotion.
DOI: 10.5220/0012071800003624
In Proceedings of the 2nd International Conference on Public Management and Big Data Analysis (PMBDA 2022), pages 184-189
ISBN: 978-989-758-658-3
Copyright
c
2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
Lin and Du Cuicui et al. studied the effects of online
media and government intervention on the
interactive dissemination of public opinion
information from different perspectives (Zhang et al.
2022).
The above study analyzed the state
transformation of different groups in online opinion
dissemination under the participation of varying
intervention subjects. However, the main subjects in
online opinion dissemination are netizens. The
government, opinion leaders, and media are all
objects that affect the state transformation of
netizens. They are not studied with the attributes of
netizens themselves as the main subjects, so our
study takes netizens themselves as the main subjects
and uses their emotions as the entry point to study
the dissemination process of online opinion
information among different groups. Besides, the
parameters of inter-group state transformation are
relatively independent and cannot be related to the
main body of netizens.
In this study, we propose a model of public
opinion dissemination incorporating netizens'
emotions. We consider that communication subjects
carry personal subjective emotions in public opinion
dissemination, so we divide communication subjects
into positive, negative, and neutral emotion
communicators. At the same time, we consider the
cognitive differences of communication subjects, so
we assign a positive rate to positive emotion
communicators and a negative rate to negative
emotion communicators, so that the group state
transformation parameters form a correlation, which
can more effectively simulate the law of online
opinion dissemination.
2 SPQNR MODEL
2.1 The SPQNR Model of Integrating
Emotion
2.1.1 Model Assumptions
Hypothesis 1: When netizens browse negative public
opinion information on the Weibo platform, if they
become interested in public opinion events, netizens
will have personal emotional tendencies. It is
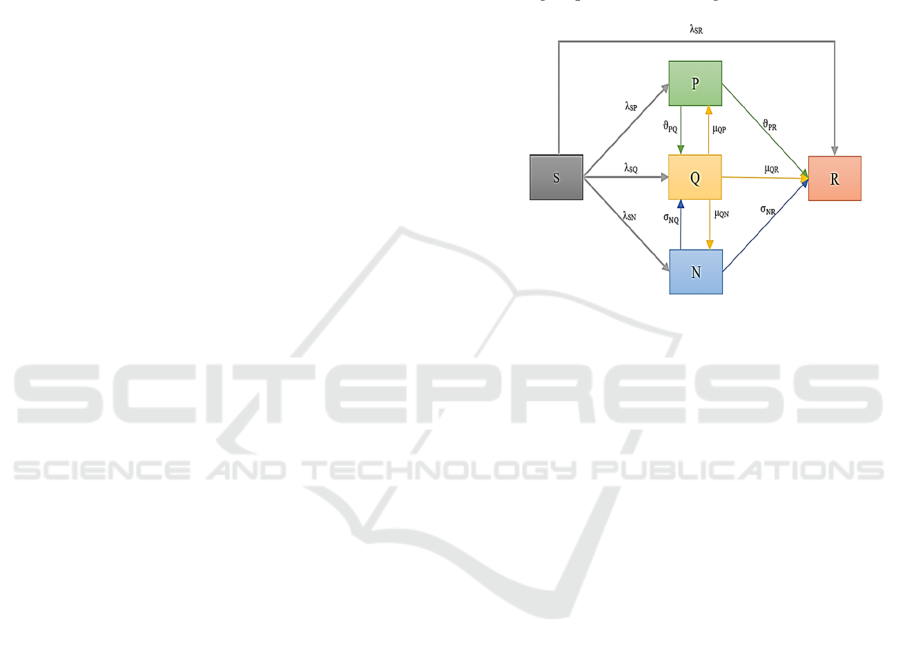
assumed that there are five types of netizen groups.
The unknown group 𝓢 refers to people who pay
attention to events and comments and are easily
affected; The positive emotional group 𝓟 refers to
the group who pays attention to the event and makes
positive comments; the neutral emotional group 𝓠
refers to the group who still publishes neutral
comments after paying attention to the event; the
negative emotional group 𝓝 refers to the group who
pays attention to the event and makes negative
comments; the removed group 𝓡 refers to people
who have lost interest in the event. 𝓢 can be
converted into 𝓟, 𝓠, 𝓝, 𝓡; 𝓟 can be converted into
𝓠, 𝓡; 𝓠 can be converted into 𝓟, 𝓝, 𝓡; 𝓝 can be
converted into 𝓠, 𝓡; the state transformation among
the five groups is shown in Figure 1.
Figure 1. The model of SPQNR
Hypothesis 2: We assume that
0,𝑎
、
𝑎,𝑏
、
𝑏,1
represent negative emotion interval, neutral
emotion interval and positive emotion interval,
where 𝑎∈
0,0.5
,𝑏∈
0.5,1
.
Hypothesis 3: We assume that people with
positive emotions have a specific "positive rate" and
will not easily transform into neutral people. The
"positive rate" is expressed as (b+1)/2, and it
belongs to (0.75,1).
Hypothesis 4: We assume that people with
negative emotional comments have a certain
"negative rate" themselves, and they will not easily
transform into neutral people. The "negative rate" is
expressed as 1- a/2 and belongs to (0.75,1).
2.1.2 Model Parameters
The model design process involves many
parameters. To form a relationship between the
parameters, we will simplify the parameters. α
represents the probability that 𝓢 may be transformed
into 𝓟 after browsing comments at a certain
moment, β represents the probability that 𝓢 may
transform into 𝓠 after viewing comments at a certain
moment, γ represents the probability that 𝓢 may
transform into 𝓝 after viewing comments at a
certain moment, and δ represents The probability
Research on Network Public Opinion Communication Model of Fusion Emotion
185

that 𝓢 is transformed into 𝓡 after viewing comments
at a certain moment.
In the SPQNR model, the conversion parameters
among 𝓟, 𝓠, 𝓝, and 𝓡 are set according to the
positive rate and negative rate among groups. 𝓠 has
a weak subjective judgment, so it is assumed that 𝓠
and 𝓢 have the same probability of conversion to
other groups. The applicable conversion rates are
shown in Table 1.
Table 1: The description of model parameters.
Conversio
n Rate
Representati
on
Explanation
𝝀
𝑺𝑷
𝜶 The conversion rate of 𝓢 to
𝓟
𝝀
𝑺
𝑸
𝜷 The conversion rate of 𝓢 to 𝓠
𝝀
𝑺𝑵
𝜸 The conversion rate of 𝓢 to
𝓝
𝝀
𝑺𝑹
𝜹 The conversion rate of 𝓢 to
𝓡
𝝑
𝑷𝑸
𝒃𝟏
𝟐
𝜷
The conversion rate of
𝓟
to 𝓠
𝝑
𝑷𝑹
𝟏
𝒃𝟏
𝟐
𝜹
The conversion rate of
𝓟
to
𝓡
𝝁
𝑸
𝑷
𝜶 The conversion rate of 𝓠 to
𝓟
𝝁
𝑸𝑵
𝜸 The conversion rate of 𝓠 to
𝓝
𝝁
𝑸
𝑹
𝜹 The conversion rate of 𝓠 to
𝓡
𝝈
𝑵𝑸
𝟏
𝒂/𝟐
𝜷
The conversion rate of
𝓝
to
𝓠
𝝈
𝑵𝑹
𝟐 𝒂/𝟐𝜹 The conversion rate of
𝓝
to
𝓡
2.2 Model Analysis
2.2.1 Dynamic Analysis Model
Netizens have five states at time t, which are
denoted by 𝒮
t
,𝒫
t
,𝒬
t
,𝒩
t
,and ℛ
t
,
respectively. According to the conversion
relationship and conversion rate among groups in the
SPQNR model, the system dynamics differential
equations are shown in formula (1).
⎩
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎧
𝑑𝒮
t
𝑑𝑡
𝐴𝛼𝒮𝒫𝛽𝒮𝑄𝛾𝒮𝑁𝛿𝒮
𝑑𝒫
t
𝑑𝑡
𝛼𝒮𝒫𝛼
𝑏1
2
∗𝛽𝒫𝒬
𝑏1
2
∗𝛿𝒫
𝑑𝒩
t
𝑑𝑡
𝛾𝒮𝒩
𝛾
1
𝑎
2
∗𝛽
𝒩𝒬
1
𝑎
2
∗𝛿𝒬
𝑑𝒬
t
𝑑𝑡
𝛽𝒮𝒬
𝑏1
2
∗𝛽𝛼𝒫𝒬
1
𝑎
2
∗𝛽𝛾𝒬𝒩𝛿𝒬
𝑑ℛ
t
𝑑𝑡
𝛿𝒮
𝑏1
2
∗𝛿𝒫𝛿𝒬
1
𝑎
2
∗𝛿𝒩
1
In order to facilitate the solution of the
equilibrium point, we simplify the formula (1), let
𝜏
𝛼
∗𝛽
, 𝜏
∗𝛿
, 𝜏
1
∗𝛽𝛾
, 𝜏
1
∗𝛿
, then the
above equations can be transformed into formula
(2).
⎩
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎧
𝑑𝒮
t
𝑑𝑡
𝐴𝛼𝒮𝒫𝛽𝒮𝑄𝛾𝒮𝑁𝛿𝒮
𝑑𝒫
t
𝑑𝑡
𝛼𝒮𝒫𝜏
𝒫𝒬 𝜏
𝒫
𝑑𝒬
t
𝑑𝑡
𝛽𝒮𝒬𝜏
𝒫𝒬 𝜏
𝒬𝒩 𝛿𝒬
𝑑𝒩
t
𝑑𝑡
𝛾𝒮𝒩𝜏
𝒩𝒬 𝜏
𝒩
𝑑ℛ
t
𝑑𝑡
𝛿𝒮𝜏
𝒫𝛿𝒬𝜏
𝒩
2
2.2.2 Basic Reproduction Number &
Equilibrium Point
The basic reproduction number R
0
is a critical
parameter in the infectious disease dynamics model,
representing the proportion of the number of people
a contagious person can infect without any
intervention. The basic reproduction number R
0
can
measure whether public opinion spreads on a large
scale on the network platform. When R
0
<1, network
public opinion will not spread on a large scale; when
R
0
>1, network public opinion is in a state of large-
scale transmission.
Let 𝑥
𝒫,𝑄,𝑁
, the model can be expressed
as 𝑑𝑥ℱ
𝑥
𝒱
𝑥
, where the expressions of
ℱ
𝑥
and 𝒱
𝑥
are respectively:
ℱ
𝑥
𝛼𝒮𝒫
𝛽𝒮𝒬
𝛾𝒮𝒩
0
,𝒱
𝑥
𝜏
𝒫𝜏
𝒫𝒬
𝜏
𝒫𝒬 𝛿𝒬 𝜏
𝒬𝒩
𝜏
𝒩𝒬 𝜏
𝒩
𝛼𝒮𝒫 𝛽𝒮𝑄 𝛾𝒮𝑁 𝛿𝒮 𝐴
3
Assuming that public opinion does not exist,
there is only 𝓢 in the process of Internet public
opinion dissemination, which is the equilibrium
point of no public opinion dissemination, The
Jacobian matrices of ℱ
𝑥
and 𝒱
𝑥
are expressed
as:
𝓕
𝜕ℱ
𝑥
𝜕𝑥
𝑥𝑋
𝛼𝒮 0 0
0𝛽𝒮0
0
0
0
0
𝛾𝒮
0
0
0
0
0
,𝒮
𝐴
𝛿
4
𝓥
𝜕𝒱
𝑥
𝜕𝑥
𝑥𝑋
𝜏
00
0𝛿0
0
𝛼𝒮
0
𝛽𝒮
𝜏
𝛾𝒮
0
0
0
𝛿
,𝒮
𝐴
𝛿
5
Thus, the spectral radius R
0
of the reproduction
matrix 𝓕𝓥
𝟏
is obtained as:
𝑅
𝜌
𝓕𝓥
𝟏
𝑚𝑎𝑥
,
,
6
When R
0
<1, the internet public opinion will not
spread, so there are
1,
1,
1.
To solve the equilibrium solution of the equation
system, we set the formula (2) to be 0, then,
𝑋
:
𝒮
,𝒫0,𝒬0,𝒩0
,
𝑋
:
𝒮
,𝒫
,𝒬0,𝒩0
,
𝑋
:
𝒮
,𝒫0,𝒬
,𝒩0
,
PMBDA 2022 - International Conference on Public Management and Big Data Analysis
186

𝑋
:
𝒮
,𝒫0,𝒬0,𝒩
.
So the Jacobian matrix at X
0
is expressed as:
ℐ
⎣
⎢
⎢
⎢
⎢
⎢
⎡
𝛿 𝛼
𝐴
𝛿
𝛽
𝐴
𝛿
0𝛼
𝐴
𝛿
𝜏
0
0
0
0
0
𝛽
𝐴
𝛿
𝛿
0
𝛾
𝐴
𝛿
0
0
𝛾
𝐴
𝛿
𝜏
⎦
⎥
⎥
⎥
⎥
⎥
⎤
7
We obtain the four eigenvalues as follows: 𝜃
𝛿,𝜃
𝛼
𝜏
,𝜃
𝛽
𝛿,𝜃
𝛾
𝜏
.
According to
1,
1,
1, we
judge that the four eigenvalues are all negative
numbers, so X
0
is the equilibrium point of no public
opinion propagation.
In addition, X
1
, X
2
, and X
3
are local propagation
equilibrium points. There are two values of 0 in each
set of solutions, representing only one kind of
emotional comment in the actual communication
situation. The final emotional comments of
statements opinion will end with positive emotions,
so in the equilibrium state, 𝓟 is not less than 𝓠 and
𝓝. Therefore, when R
0
>1, there can only be one
local communication equilibrium point X
1
when
network public opinion spreads.
3 SIMULATION ANALYSIS
3.1 Dataset Description
We select the "Yugou Middle School Beating
Incident" on Weibo in April 2022. We first used
crawler technology to crawl 6,000 valid comments
on the incident from April 1 to April 14 on the
Weibo platform. After data cleaning, we use the
natural language processing method to get each
comment's sentiment value. We set the comment
value in (0, 0.35] belongs to 𝓟, in (0.35, 0.65]
belongs to 𝓠, in (0.65, 1] belongs to 𝓝.
We use the Anylogic simulation platform to
simulate the SPQNR model dynamically and obtain
the optimal parameters after multiple calibration
experiments. The relevant parameter settings after
calibration are shown in Table 2.
3.1.1 Dynamic Analysis Model
Table 2: Optimal Parameter Settings.
Paramete
r
Value Explanation
A 0.0001 The crowd input rate of concerning events
𝜶
0.275
The conversion rate of 𝒮 to
𝒫
𝜷
0.111
The conversion rate of 𝒮 to 𝒬
𝜸
0.139
The conversion rate of 𝒮 to 𝒩
𝜹
0.248
The conversion rate of 𝒮 to ℛ
𝒃
0.65
The interval of positive score
𝒂
0.35
The interval of negative score
3.2 Effectiveness Analysis
We use the simulation software to build the SPQNR
model to obtain the population change over time, as
shown in Figure 2, where Real-P\Q\N respectively
represents the three groups of people 𝓟,𝑸,and 𝑵
under the real data, and Sim-P\Q\N respectively
represents the three groups of people 𝓟,𝑸,and 𝑵
under the simulation data.
Figure 2: Comparison between simulation data and real
data.
From figure 2, it can be concluded that at the
initial stage of the outbreak of public opinion, S was
transformed into three emotional groups, and the
number of each group increased sharply. Over time,
the three populations transform into each other or
removers. At t = 14, the three groups of people
tended to 0, and the public opinion disappeared,
which is consistent with the actual situation.
The real data of the three groups of people have a
high degree of fitting with the simulated data, which
can well simulate real public opinion events.
Therefore, the SPQNR model constructed in this
paper can effectively simulate the real situation when
public opinion events occur, and the model is suitable
for the simulation of negative public opinion events
in different situations.
3.3 Parameter Sensitivity Analysis
Since the between-group conversion parameter is
linked to the parameter for conversion of 𝓢 to other
groups, we performed a sensitivity analysis on the
four base conversion rates. To fix the emotional
Research on Network Public Opinion Communication Model of Fusion Emotion
187

range, we mainly analyze the impact of the changes
in the number of the three types of emotional
groups.
(1) The sensitivity analysis of α
We only change α, and the rest of the parameters
are set to 𝛽: 0.111,𝛾:0.139,𝛿:0.248,𝑎:0.35,
b:0.65.
(a)
(b)
(c)
Figure 3: The number of 𝓟,𝓠,𝓝 groups.
It can be concluded from figure 3 that as α
increases continuously, the number of 𝓟 constantly
increases, while the numbers of 𝓠 and 𝓝 decrease
continuously. In the time dimension, 𝓟 and 𝓝 drop
straight after the second day, while 𝓠 is a neutral
population in a state of gentle decline in mutual
transformation. The three groups of people remained
stable on the 10th day, the three groups gradually
turned into the remover 𝓡, and the public opinion
gradually eased.
(2) The sensitivity analysis of
𝛾
We only change 𝛾, and the rest of the parameters
are set to 𝛼:0.275,𝛽:0.111,𝛿: 0.248,𝑎:0.35,
b:0.65.
(a)
(b)
(c)
Figure 4: The number of 𝓟,𝓠,𝓝 groups.
It can be concluded from figure 4 that as γ
continues to increase, the number of 𝓟 and 𝓠
continues to decrease, and the number of 𝓝
continues to increase, and the increase and change
are apparent. In the time dimension, after the second
day, the numbers of the three groups of people
continued to decrease. Finally, the three groups of
people remained stable on the 11th day, and public
opinion gradually disappeared.
4 CONCLUSIONS
The traditional SIR model is widely used in the
study of public opinion dissemination. In practice,
PMBDA 2022 - International Conference on Public Management and Big Data Analysis
188

the main subjects in the process of online opinion
dissemination are netizens, and the government,
opinion leaders, or media are the objects that
influence the state transformation of netizens. These
studies need to consider the different emotions of
online communication subjects fully.
In this paper, the SPQNR model is constructed
by integrating netizens' emotions and simulated by
using theoretical data, which can effectively
simulate the evolution trend of online opinion
dissemination. Finally, combined with the actual
data of the "Yugou Middle School Beating Incident"
incident on Weibo, we prove that the SPQNR model
matches well with the real incident and has certain
universality.
REFERENCES
J. Alvarez-Galvez, Network models of minority opinion
spreading, Soc. Sci. Comput, Rev. 34 (2016) 567-581.
Daley D J, Kendall D G. Epidemics and rumours [J].
Nature, 1964, 204(4963): 1118- 1118.
Q. Liu, D. Jiang, T. Hayat, A. Alsaedi, B. Ahmad, A
stochastic SIRS epidemic model with logistic growth
and general nonlinear incidence rate, Phys. A Stat.
Mech. Its Appl. 551 (2020) 124152.
Zhang Y M, Du C C, Su Y Y. The Model and Simulation
of Internet Public Opinion Dissemination Under
Multi-agent Intervention [J]. Journal of Modern
Information, 2020,40(05):130-139.
R.Q. Yang, Y.X. Zhang, Research on IC-SEIR public
opinion propagation model based on complex
network, Meas. Control Technol. 37 (2018) 72–77.
H.F. Huo, P. Yang, H. Xiang, Dynamics for an SIRS
epidemic model with infection age and relapse on a
scale-free network, J. Frankl. Inst. 356 (2019) 7411–
7443.
L. Liu, X. Wei, N. Zhang, Global stability of a network-
based SIRS epidemic model with nonmonotone
incidence rate, Phys. A Stat. Mech. Appl. 515 (2019)
587–599.
Wang Z Y, Wang W K, Yue C L. Model and Simulation
of Interactive Dissemination of Multiple Public
Opinion Information under Government Intervention
[J]. Journal of System Simulation,2020,32(05):956-
966.
Wang Z Y, Li Y J. Propagation law and coping strategies
for public opinions in emergency with the
consideration of the government intervention[J].
Journal of Management Sciences In China, 2017,
20(02):43-52+62.
Di Lan, Gu Yudi. Internet Public Opinion Dissemination
Model with Triple Opinion Group under Media
Intervention[J]. Journal of System Simulation, 2018,
30(8): 2958-2965.
Kumar A, Swarnakar P, Jaiswal K, et al. SMIR model for
controlling the spread of information in social
networking sites[J]. Physica A: Statistical Mechanics
and its Applications, 2020, 540: 122978.
Zhang J et al. Research on Network Public Opinion
communication Tripartite Opinion Groups Under Mu
ti-Subiect Intervention [J]. Journal of Chongqing
University of Technology (Natural Science),
2021,35(12):292-305.
Zhang L, Chen L. Study on the interactive Dissemination
Model of Micro-Blog Public Opinion Topics Under
Multi-Agent intervention [J/OL]. Information
Science,1-17[2022-08-29].
Research on Network Public Opinion Communication Model of Fusion Emotion
189
