Optimization Method of Project Manager Based on Particle Swarm
Optimization Algorithm
Yunfen Zang
1,* a
and Xiuting Xu
2b
1
West Coast New Area Western Office Center, No.166 Shuangzhu Road, Huangdao, Qingdao, China
2
West Coast New Area Tieshan School, Huangdao, Qingdao 266400, China
Keywords: Project Management, Manager Configuration, Cost Optimization, Particle Swarm Algorithm.
Abstract: Managers are the guarantee of the project. They are good at execution, leadership and management. A good
team of managers can greatly improve the efficiency. However, a good team does not mean that a lot of
managers are included. On the contrary, too much managers and an unreasonable distribution would led to
many problems such as more project costs and overlapping management functions. In existing research, the
management structure and personnel allocation only stay in qualitative analysis. No quantitative indicators
have been formed, so that the suggestions given can only give optimization directions and it is difficult to
give quantitative goals. A novel project manager optimization method based on particle swarm optimization
is proposed. Firstly, a manager optimization model, a project exception handling time model and a cost
model respectively are established. And then, the number of managers and Job configuration are optimized
with the goal of ensuring timely handling of project exceptions and reducing management costs. Finally, a
project with four tasks are used as the research object, and the algorithm convergence speed, task cost and
number of managers are studied. The results show that the method can consider the working efficiency of
managers and management cost comprehensively. With this method, an optimal management combination
can be sought.
1 INTRODUCTION
1
Managers lead employees to practice project goals
and values, coordinate employee relations, and deal
with emergencies during the completion of project
tasks. They are the backbone of the healthy
operation of the entire project. Reasonable manager
configuration can help the project team run more
efficiently, reduce the operating cost of the project
and enhance the competitiveness of the enterprise.
However, the existing project managers allocation is
unreasonable, and there is no effective distribution
standard. These problems lead to the overlapping of
functions of some managers and low work
efficiency.
Ensuring the stable operation of the project while
reducing the cost is the purpose of the project
(Marnewick 2020). In order to respond to the
government's call, various factors should be
considered, such as high efficiency (Liu 2020,
a
https://orcid.org/0000-0002-1047-8177
b
https://orcid.org/0000-0003-0490-8975
Daisik 2020), low carbon, and flexibility (Gu 2021).
As the backbone of a project, managers are
concerned by researchers. In recent years, many
researches pay attention to managers. Firstly, to
ensure a reasonable project structure, project
management model is studied. For example, a
collaborative delivery method is proposed by Sina et
al (Moradi 2020) and a cooperative management
approach by project managers and systems engineers
is proposed by Sigal et al (Kordova 2019). Besides,
many researchers try to find the relationship between
the competence of the project manager and the
success of the project. In this aspect, emotional
intelligence (Montenegro 2021) and experience
(Salvador 2021) are studied. Also, it is necessary to
give certain restrictions to the project manager.
Thus, the influence of accountability arrangements is
studied (Mac 2020). Project managers’ influence
strategies is also studied (Crowston 2007). At
present, improving management mode, enhancing
team building and optimizing personnel allocation
are the main means to optimize project management.
As the project progresses, different businesses and
Zang, Y. and Xu, X.
Optimization Method of Project Manager Based on Particle Swarm Optimization Algorithm.
DOI: 10.5220/0012073100003624
In Proceedings of the 2nd International Conference on Public Management and Big Data Analysis (PMBDA 2022), pages 267-273
ISBN: 978-989-758-658-3
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
267

departments intersect with each other. This problem
leads to a complex management structure and
redundant department functions, thereby increasing
operating costs and reducing work efficiency.
Simplifying the decision-making process by
improving the management model and reducing the
length of the control chain can help improve work
efficiency and reduce operating costs (Aghamolla
2021). With the development of science and
technology, the Kanban management model based
on big data, the management construction paradigm
based on knowledge graph (Lundin 2022) and the
model optimization method with human capital
(Hamstra 2021) have been widely studied and
applied. These technologies have simplified the
management structure and achieved good results.
However, the original management model of the
project is often deeply rooted, and a large-scale
change of the management model can easily lead to
a decrease in the stability of the existing structure.
Enhancing team building if helpful to forming an
efficient operation team, promoting the realization of
block operation of the project, and realizing multi-
point parallel construction to promote the operation
of the project (Fang 2022). In the existing team
building research, the influence of methods such as
gender factor (Keith 2021), abusive management
(Varty 2020), and performance management
(Zimmermann 2021) are proposed, and reasonable
management suggestions are also given. However,
this kind of team building is very dependent on the
personal ability of the team leader, and the
replacement of the leader often leads to the
replacement of most of the personnel, thus the long-
term stability of the team is difficult to guarantee.
Improving the quality of members is an important
means to improve project efficiency and reduce
costs. At the same time, it is also the basic guarantee
for improving the management model. Reasonable
managers allocation helps motivate members and
effectively deal with project abnormalities. In recent
years, managers allocation has gradually been
valued by researchers. For example, Johanna
Anzengruber et al. examines whether managerial
capability fit between line managers, middle
managers and top-level managers enhances
effectiveness (Anzengruber 2021). Chen et al.
analyze the role of staffing in the infrastructure
industry. It is not difficult to see that staffing plays
an important role in project operation, at the same
time it directly determines the quality and efficiency
of project completion. However, in the existing
staffing research, the management structure and
staffing allocation only remain in the qualitative
analysis, and there are no quantitative and
quantitative indicators. As a result, the suggestions
given can only give the optimization direction and it
is difficult to give the quantitative target.
Aiming at the existing problems, an optimal
allocation method of project managers based on
particle swarm algorithm is proposed. First a number
of managers and allocation matrix is established.
And then, a cost and time management model is
built. A particle swarm optimization algorithm with
the goal of reducing costs and improving efficiency
was constructed, and the project managers allocation
suggestions were given. The performance of the
algorithm is analyzed by taking a project data as a
case.
2 OPTIMAL CONFIGURATION
METHOD OF PROJECT
MANAGERS
2.1 Particle Swarm Optimization
Algorithm
Reasonable optimization criteria and efficient
optimization methods are the basic requirements for
assigning project managers. The particle swarm
optimization algorithm was originally an
evolutionary computing technology based on swarm
intelligence, inspired by the predation behavior of
birds. Like most swarm intelligence optimization
algorithms, this algorithm usually initializes a set of
solutions (particles) in a random way. Then
continuously updates these solutions in an iterative
way, so that the entire population is adjusted to a
better fitness value as a whole. Finally, it is expected
that the optimal solution to the problem can be found
within a limited number of iteration steps. Suppose a
group of birds randomly search for food in an area
with only one piece of food. All birds in the group
do not know the location of the food, but they know
the distance between their current position and the
food. area to search. Its mathematical description is
as follows: a swarm of q particles flies at a certain
speed in a d-dimensional search space, where, each
particle contains three attributes, that is: current
position, historical best position and velocity when
searching. Assuming that the t-th generation of birds
is currently preying on the flock, the i-th particle in
the D-dimensional search space can be expressed as
Particle position:
12
(, ,..., )
ttt t
iii id
X
xx x=
Particle velocity:
12
( , ,..., )
ttt t
iii id
Vvv v=
PMBDA 2022 - International Conference on Public Management and Big Data Analysis
268

The current individual optimal of the particle:
12
( , ,..., )
ttt t
iii id
Ppp p=
The velocity update formula consists of three
parts: inertial motion, cognitive learning and social
learning. Relying on individual experience and
social learning experience, it guides the flight
trajectory of the next generation of particles. The
current individual optimum and the current group
optimum of each particle in the t-th generation are
determined by evaluating the fitness value of each
particle. Then update the velocity and position of
each particle. The specific algorithm is shown in
Equation 5 and Equation 6 (Song 2021).
1
11 2 2
()( )
tt tt t
id id id id gd id
VVcrpxcrpx ω
+
=+ −+ −
(1)
11ttt
id id id
x
xv
++
=+
(2)
Where, V
t+1
id
is the velocity of the i-th particle in
the d-th dimension during the t-th iteration, i=1, 2,
…, q is the i-th individual, q is the population size,
t=1, 2, …,t
max
is the number of iterations, d=1, 2, …,
D is the dimension of the optimization problem, w is
the inertia weight and its role is to control the
influence of the current speed on the back. A larger
value of w can make the global search ability of the
algorithm stronger. Particle swarms explore the
entire search space. Conducive to the detection of
new advantageous areas. c
1
,c
2
is the acceleration
factor and its function is to make the particle have
self and social cognition ability, usually a positive
constant. Contrary to the parameter w, the larger the
acceleration coefficient, the stronger the local
development ability of the algorithm, and the
particle swarm will be more inclined to the local
optimal position. The parameters c
1
and c
2
interact
with the w parameter to jointly control the global
exploration and local development of the search
space by the population. r
1
, r
2
is a random number
uniformly distributed on [0,1] to maintain the
diversity of the population, x
t+1
id
is the current
position of the i-th particle in the d-th dimension
during the t-th iteration, p
t+1
id
is the position of the i-th
particle in the t-th iteration process of the individual
extreme point of the d-th dimension and P
gd
is the
position of the best global extreme point searched by
the entire particle swarm in the d-th dimension so
far. In order to prevent particles from moving away
from the search space, the velocity v of each
dimension of the particle is usually limited to the
range [-v
max
, v
max
]. The choice of v
max
will affect the
global and local search ability of the algorithm. If its
value is too large, the particles will fly away from
the optimal solution, and if it is too small, it will fall
into the local optimal solution. Therefore, v
max
is
generally set as the variation range of each
dimension variable without fine selection and
adjustment (Feng 2021).
In the PSO algorithm, each generation of
particles flies in the direction of the optimal particle
according to the experience gt of the group and its
own experience pti, that is, the PSO algorithm
executes a kind of "conscious" mutation, and the
algorithm features is shown as follow.
1) The particles have memory. It can memorize
the optimal position (gt) experienced by the entire
particle swarm and pass it to other particles.
2) The algorithm has a simple structure and
requires fewer parameters to adjust.
3) It does not contain complex operations and is
based on particle motion. Complete the search.
4) The particle motion is modified by self-
cognition (cognitive learning part) and social
cognition (social learning part).
2.2 Managers Layout Optimization
Model Establishment
Managers are responsible for project task
assignment and abnormal status processing. The
management layout optimization model is
established to deal with members and task abnormal
status in a timely and effective manner. A typical
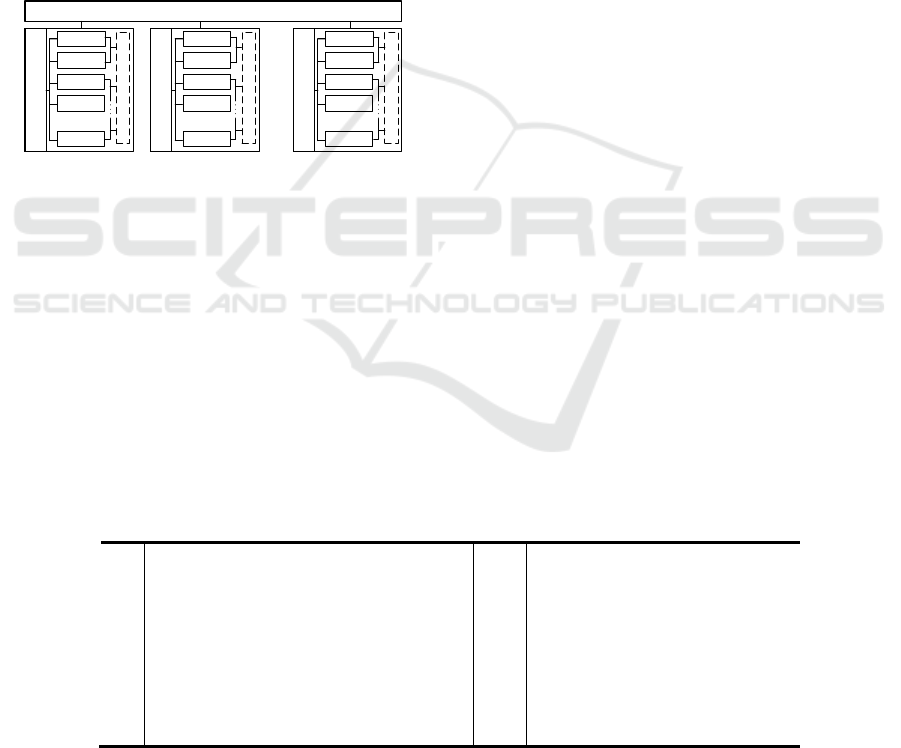
multitasking project structure is shown in Figure 1.
The project mainly includes B
1
, B
2
, … B
n
, a total of
n tasks, each task has O
1
, O
2
, ...O
n
sub-tasks, and a
manager allocate and optimize matrix M and X are
defined as Equation 3 and Equation 4.
12
[, ,, ](1 , )
nkk
M
mm m k nm O=∀≤≤≤…
(3)
1
2
12
11
11 1
12
22
22 2
12
(1 , )
k
n
m
om
m
om
m
kk
m
oi mn
nn n
O
xx x
O
xx x
X
Knx m
O
xx x
−
−
−



=∀≤≤≤




…
…
…
……… …
…
(4)
Where M is the vector of the number of
managers, m
1
, m
2
,…, m
n
are the main tasks
respectively, B
1
,B
2
,…B
n
are the number of managers
assigned, X is the manager position matrix, x
ij
is the
number of subtasks that the j-th manager of the i-th
business is responsible for.
The two major goals of optimizating the number
of managers and the location allocation scheme are
reducing the cost of management and improving
management efficiency. Suppose that there are t
exceptions occurring in the subtask during the daily
operation. The objective function of the manager's
arrangement optimization model can be expressed
by Equation 5.
Optimization Method of Project Manager Based on Particle Swarm Optimization Algorithm
269

1
1
min
min
i
s
um k
t
s
um k
M
m
CC

=


=




(5)
Where M
sum
is the sum of project managers, Ck is
the exception handling cost of the k-th subtask, and
C
sum
is the total cost of handling abnormal states.
In order to ensure the quality of completion of all
project tasks, constraints to set maximum individual
management thresholds for each project. The
number of tasks assigned should not exceed the
corresponding maximum processing threshold
(TOL) for the project.
1
2
11
22
()
...
n
j
j
kk
j
nn
xTOL
xTOL
j
m
xTOL

≤

≤

≤



≤

(6)
Project
…
Task B
1
Subtask1
Subtask2
Subtask3
Subtask4
O
1
Managers
…
Task B
2
Subtask1
Subtask2
Subtask3
Subtask4
O
2
Managers
…
Task B
n
Subtask1
Subtask2
Subtask3
Subtask4
O
n
Managers
…
Figure 1: Personnel structure and task allocation of a
project.
The optimization method of project managers
based on particle swarm optimization is shown in
Table 1. The steps include initialization parameter
space dimension d, population particle number N,
maximum number of iterations ger, position
parameter limit X
limit
and speed parameter limit V
limit
.
In the process of iterative, the particle velocity and
particle position are updated, the fitness function of
the particle is calculated, the current global optimal
solution and local optimal solution are updated
according to the fitness function. When the number
of iterations meets the requirements, the final global
optimal solution and local optimal solution are
output. A single optimal solution for the sensor
layout is finally obtained by analyzing the optimal
solution set.
3 CASE STUDY
3.1 Model Building and Optimization
Process
A project with four tasks in an enterprise is selected
as the research object. In the project, the number of
subtasks of each task is 10, 8, 8, 6. Then, the
common time for project managers to deal with
abnormal events is obtained. When establishing
discrete particle swarm optimization, the inertia
weight is taken as ω=0.4, the self-learning factor is
c
1
=0.7, the global learning factor is c
2
=0.3, the
maximum number of iterations is 600, and the
population size is N=8. When the case exceeds the
maximum position limit Xlimit, a correction
algorithm is used to determine and correct the
particle position. The managers of each task are
assigned to optimize under different numbers of
managers. The global optimal solution in the
optimization process is recorded. And, the iterative
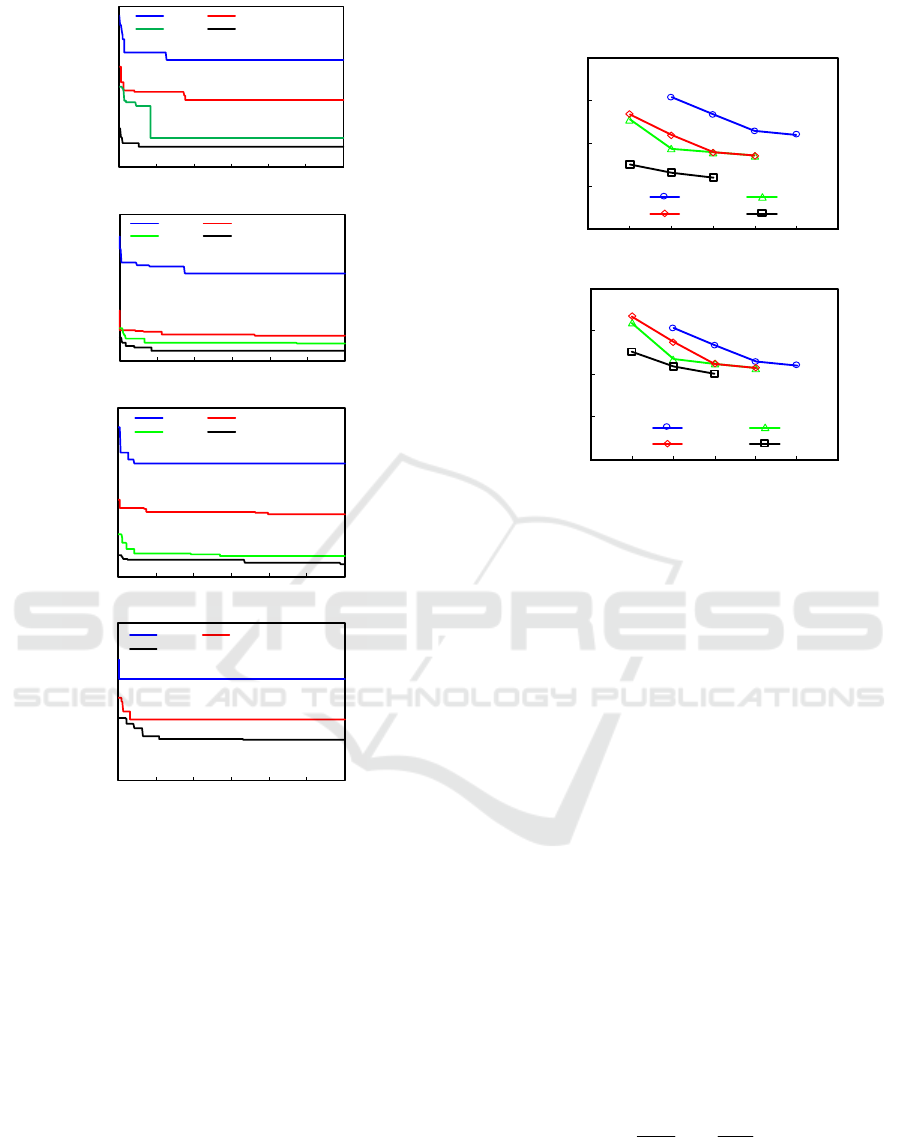
convergence process of the assignment optimization
of each task manager is obtained in Figure 2. It can
be seen from Figure 2 that the objective function
converges to the optimal solution interval when
iteratively reaches 200 times, and obtains the
optimal solution after iterating to about 400 times.
The results show that the particle swarm
optimization algorithm with the current optimization
parameters has efficient convergence.
Table 1: Managers optimization method based on particle swarm optimization algorithm.
1
2
3
4
5
5.1
Define d, N, ger, X
limit
, V
limit
;
Define
ω , c
1
, c
2
;
Initialize pbest, Gbest=[gbest
1
,...,gbest
N
];
Initialize P
1
j
, V
1
j
;
While i=1
Renew Gbest=[
g
best
1
,...,
g
best
N
];
5.2
5.3
5.4
5.5
5.6
6
If i>ger
break;
Else
comtimue
Renew V
t+1
j
;
Renew P
i+1
j=P
i
j+V
t+1
j
;
Renew i=i+1;
end while
end
12
1
min
min
s
um i
p
sum k
M
mm m
TT
=++
=

…+
PMBDA 2022 - International Conference on Public Management and Big Data Analysis
270

1000
1100
1200
1300
1400
1500
1600
1700
1800
0 100 200 300 400 500 600
Objective function
Number of iterations
m1=4 m1=5
m1=6 m1=7
(a)
800
900
1000
1100
1200
1300
1400
1500
1600
0 100 200 300 400 500 600
Objective function
Number of iterations
m2=3 m2=4
m2=5 m2=6
(b)
800
900
1000
1100
1200
1300
1400
1500
1600
0 100 200 300 400 500 600
Objective function
Number of iterations
m3=3 m3=4
m3=5 m3=6
(c)
500
550
600
650
700
750
800
850
900
0 100 200 300 400 500 600
Objective function
Number of iterations
m4=3 m4=4
m4=5
(d)
(a) Task1 (b) Task2 (c) Task3 (d) Task4
Figure 2: Iterative Convergence Process of Assignment
Optimization of Each Task Manager.
The allocation of managers for each task project
is optimized, and the optimal solution for the
allocation of task managers under different number
of managers is obtained. The relationship between
management cost and the number of managers is
shown in Figure 3. It can be seen from Figure 3 (a)
that under the same number of managers in the
project, task 1 has the highest management cost; task
4 has the lowest management cost, cause the small
number of subtasks. Figure 3 (b) shows the optimal
solution obtained by the method. This method makes
the average cost of sub-tasks of each task of the
project basically close and ensures that each sub-task
can be effectively managed. At the same time, the
method avoids the uneven distribution of resources.
Subtasks are over-managed or under-managed.
0
500
1000
1500
2000
2345678
Objective function
Number of managers
Task 1 Task 2
Task 3 Task 4
(a)
0
50
100
150
200
2345678
Objective function
/number of subtasks
Number of managers
Task 1 Task 2
Task 3 Task 4
(b)
(a) The total cost of each task management (b) Average
management cost of each subtask
Figure 3: Iterative Convergence Process of Assignment
Optimization of Each Task Manager.
3.2 Optimal Solution Discussion
The optimal solutions for each task under different
numbers of managers are cross-combined to
determine the number of task managers, and a total
of 192 combinations are obtained. The optimal
combination is selected from the total number of
different managers, and the total management cost
of the project under different managers is shown in
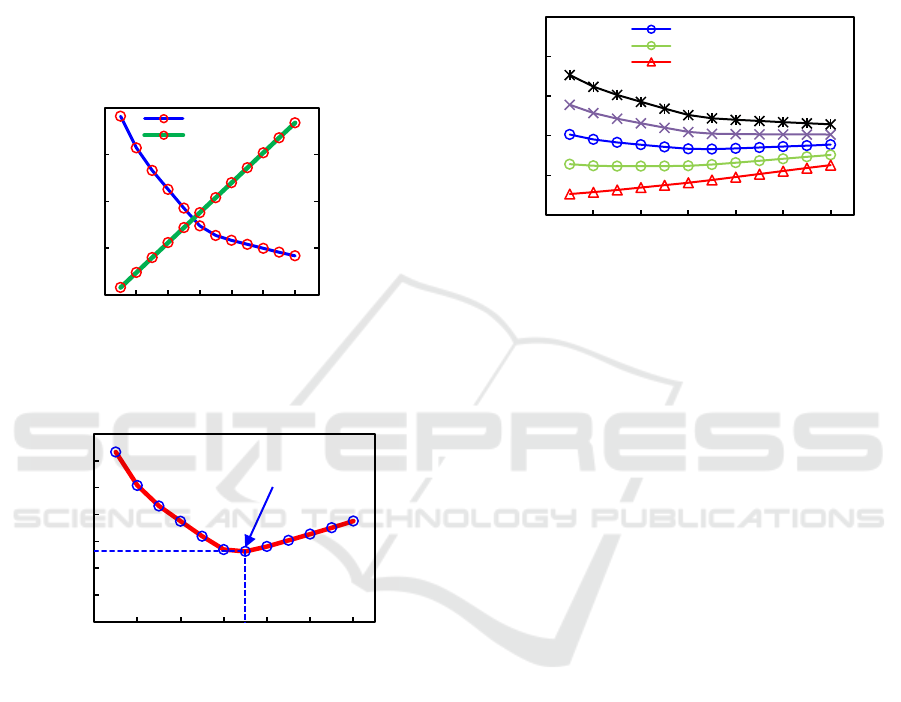
Figure 4. It can be seen from Figure 4 that when the
number of managers is greater than 19, the effect of
increasing managers on the total project cost is no
longer significant. When the optimization goal is set
to be no higher than 4000 total management costs,
the project requires 17 managers. The personnel cost,
which increases with the number of people, is
modeled as a linear growth. Rather than using the
number of people as a constraint, it is more efficient
to construct an integrated objective function. The
method of constructing the integrated objective
function is given by Equation 7.
12
**
p
er
man
i
man per
C
C
O
CC
ωω =+
(7)
where there O
i
is the value of integrated objective
function; ω
1
, ω
2
are weight factors (ω
1
+ω
2
=1), and
its value depends on the importance of the two costs
Optimization Method of Project Manager Based on Particle Swarm Optimization Algorithm
271

in decision-making; C
man
and C
per
are represent
management costs and personnel costs respectively;
C
*
man
and C
*
per
represent the dimensionless constants
of the corresponding indicators, respectively. The
integrated objective function for placing orders with
different weight factors is given in Figure 5. Under
the conditions of C
*
man
=1000, C
*
per
=18000, ω
1
=0.5, ω
2
=0.5, the objective function O
i
reaches the
minimum when the number of managers is 19. That
is, under the goal of balancing management costs
and personnel costs, the optimal number of
managers is 19.
Figure 4: The relationship between the total management
expenditure and the number of managers.
Figure 5: The integrated objective function for placing
orders with different weight factors.
At the same time, the distribution of the
objective function under different weight
assignments is also studied. The trend of oi under
different values of ω
1
and ω
2
is shown in Figure 6. It
can be seen that the trend and extreme value of the
objective function can change with the weight
factor. In the extreme case when the weight
distribution is ω
1
=0.1, ω
2
=0.9, the objective
function is monotonically increasing. The strategies
that minimize personnel costs are selected as the
optimal solutions. In the scheme discussed again, the
optimal solution is when the number of managers is
13. On the contrary, when the weight distribution is
ω
1
=0.9, ω
2
=0.1, the objective function is
monotonically increasing. The strategies that
minimize personnel costs are selected as the optimal
solutions. In the scheme discussed again, the optimal
solution is when the number of managers is 24.
Therefore, in some management-oriented and
personnel-oriented tasks, decision makers can
reasonably adjust the weights based on expert
experience.
Figure 6: Objective function distribution under different
weight assignments.
4 CONCLUSIONS
An optimization method for project managers based
on particle swarm optimization is proposed in this
paper. The manager optimization model, the project
exception handling time model and the cost model
are established respectively. The positions and
numbers of managers are optimized to ensure timely
handling of project exceptions while reducing
management costs. The project with 4 tasks is
studied as the research object, and the research
results show that the managers optimization model
based on particle swarm optimization has efficient
convergence. Experiments show that for a project
with the number of sub-tasks is 10, 8, 8, 6, and 4,
when the number of managers is greater than 19, the
effect of increasing the number of managers is no
longer significant. When the optimization goal is set
to be no higher than 4000 total management costs,
the project requires 17 managers. The objective
function equation is introduced to discuss 192
combination schemes. Through the proper selection
of dimensionless parameters and weighting factors,
the optimal solution of the model can be
quantitatively evaluated and obtained. The
distribution of weighting factors can realize the
multi-objective and unbalanced guiding needs of
decision makers.
Based on the method proposed in this paper,
several challenges and direction can be further
20000
25000
30000
35000
40000
3000
3500
4000
4500
5000
12 14 16 18 20 22 24
Personnel Cost
Management Costs
Number of managers
management…
personnel cost
2,4
2,5
2,6
2,7
2,8
2,9
3
3,1
12 14 16 18 20 22 24
Oi
Number of managers
O
p
timal solution
1
2
3
4
5
6
12 14 16 18 20 22 24
Oi
Number of managers
w1=0.5,w2=0.5
w1=0.3,w2=0.7
w1=0.1,w2=0.9
PMBDA 2022 - International Conference on Public Management and Big Data Analysis
272

studied. First, a quantitative algorithm for the ability
of managers is important, because the managers are
arranged more reasonably with this quantitative
algorithm. What’s more, the ability to deal with
emergencies of a management team also needs to be
evaluated.
REFERENCES
Aghamolla, C., Corona, C., & Ronghuo, Z. (2021). No
reliance on guidance: counter-signaling in
management forecasts.
Rand J. Econ. 52(1), 207-245.
Anzengruber, J., Bergner, S., Nold, H., & Bumblauskas,
D. (2021). Leadersh. Org. Dev. J. Leadership &
organization development journal, 42(2), 316-332.
Crowston, K., Qing, L., Kangning W., Eseryel, U. Y., &
Howison, J. (2007). Self-organization of teams for
free/libre open source software development. Inf.
Softw. Technol. 49(6), 564-575.
Feng, W., Heng, Z., & Aimin, Z. (2021). A particle swarm
optimization algorithm for mixed-variable
optimization problems. Swarm Evol. Comput. 60,
100808.
Gu, L. Y., Ryzhov, I. O., & Eftekhar, M., (2021) The facts
on the ground: Evaluating humanitarian fleet
management policies using simulation. Eur. J. Oper.
Res. 293(2), 681-702.
Hamstra, M. R. W., Schreurs, B., Jawahar, I. M.,
Laurijssen, L. M., & Hunermund, P. (2021). Manager
narcissism and employee silence: A socio-analytic
theory perspective. J. Occup. Organ. Psychol. 94(1),
29-54.
Hanqing, F., Chrisman, J. J., Daspit, J. J., & Madison, K.
(2022). Do Nonfamily Managers Enhance Family
Firm Performance. Small Bus. Econ. Group, 58(3),
1459-1474.
Keith, A. C., Warshawsky, N., Neff, D., Loerzel, V., &
Parchment, J. (2021). Factors that influence nurse
manager job satisfaction: An integrated literature
review. J. Nurs. Manag. 29(3), 373-384.
Kordova, S., Katz, E., & Frank, M. (2019). Managing
development projects-The partnership between project
managers and systems engineers. Syst. Eng. 22(3),
227-242.
Lundin, K., Silen, M., Stromberg, A., Engstrom, M., &
Skytt, B. (2022). Staff structural empowerment-
Observations of first-line managers and interviews
with managers and staff. J. Nurs. Manag. 30(2), 403-
412.
Mac, D. K., Rezania, D., & Baker, R. (2020). A grounded
theory examination of project managers'
accountability. Int. J. Proj. Manag. 38(1), 27-35.
Marnewick, A. L., & Marnewick, C. (2020). The Ability
of Project Managers to Implement Industry 4.0-
Related Projects. IEEE Access, 8, 314-324.
Ming, L., Bian, L., Maoran, Z., & Chengbin, C. (2020).
Stochastic Check-in Employee Scheduling Problem.
IEEE Access, 8, 80305-80317.
Montenegro, A., Dobrota, M., Todorovic, M., Slavinski,
T., & Obradovic, V. (2021). Impact of Construction
Project Managers' Emotional Intelligence on Project
Success. Sustainability, 13(19), 10804.
Moradi, S., Kahkonen, K., & Aaltonen, K. (2020). Project
Managers' Competencies in Collaborative
Construction Projects. Buildings, 10(3), 50.
Nam, D., & Park, M. (2020). Improving the Operational
Efficiency of Parcel Delivery Network with a Bi-Level
Decision Making Model. Sustainability, 12(9), 8042.
Salvador, F., Alba, C., Madiedo, J. P., Tenhiala, A., &
Bendoly, E. (2021). Project managers' breadth of
experience, project complexity, and project
performance. J. Oper. Manag. 67(6), 729-754.
Varty, C. T., Barclay, L. J., & Brady, D. L. (2020).
Beyond adherence to justice rules: How and when
manager gender contributes to diminished legitimacy
in the aftermath of unfair situations. J. Organ. Behav.
42(6), 767-784.
Zimmermann, F. (2021. OCT). Managing the Gender
Wage Gap-How Female Managers Influence the
Gender Wage Gap among Workers. Eur. Sociol. Rev.
38(3), 355-370.
Optimization Method of Project Manager Based on Particle Swarm Optimization Algorithm
273