Constrained ALS for Estimation of Human Upper Limb Synergies

Rabya Bahadur

1,2 a

and Saeed ur Rehman

Department of Electrical & Computer Engineering, COMSATS University Islamabad, Abbottabad Campus, Pakistan

Department of Electrical & Computer Engineering, SS CASE Institute of Information Technology, Multi Garden,

Keywords:

Non-Negative Matrix Factorization, Neuromuscular Synergies, Correlation, Regularization, Electromyogram.

Abstract:

Human body movement is a complex task that requires the control of multiple joints via a network of muscles.

The biological signals, particularly electromyography (EMG), are correlated by nature. The brain transmits

these signals through the neuromuscular transmission system of the body. The combination of muscular acti-

vation for each particular movement presents a set of weights known as synergies. The traditional alternating

least square (ALS) based non-negative matrix factorization (NMF) gets trapped in local minima for co-linear

data. Therefore, it is not a suitable method for extracting muscle synergies. This paper advocate using l2-norm

as an additional constraint for ALS-based NMF. The addition of l2-norm decorrelates the data, resulting in a

better estimation of synergistic weights. For our results, we acquired EMG signals from six healthy subjects.

Both plain and regularized NMF were used to extract the synergies. The synergies acquired via plain NMF

have a higher cross-correlation within and indicate the triggering of the same muscles irrespective of the tar-

geted isometric contraction. In contrast, the regularized NMF synergies targeted the correct muscular set for

a particular isometric contraction. Our results show that the synergies acquired via regularized NMF are also

more correlated with the physiologically inspired synergies.

1 INTRODUCTION

Human body movement is a complex task requir-

ing multiple joint control via a network of muscles.

The human hand movement is performed by a pair

of agonist/antagonist muscles in coordination with

assistance from adjacent muscles(Ayhan and Ayhan,

2020). The agonist muscle is a prime mover, while

the antagonist is a sleeping partner in that direction.

For the opposite direction of the same joint, the role

of the agonist and antagonist are switched. The par-

ticipation of muscles in any movement varies between

0 to 1 on a normalized scale. Where 0 refers to relax

state of a muscle while 1 refers to maximum contrac-

tion. The action of these muscles is controlled via

the neuromuscular translational system of the human

body. It is a hierarchical process; initiated by the mo-

tor neurons in the brain, ending up at synergistic level

activation (Bahadur and Rahman, 2018). Synergies

describe the level of muscle activation involved in a

particular movement. The concept of muscular syn-

ergies reduces the dimensionality of complex human

neuromuscular coordination systems.

https://orcid.org/0000-0002-1923-403X

Finding the muscle synergies can be challenging

as the only available data is a matrix of recorded

electromyographic (EMG) signals. Separating mus-

cle synergies from time-variant motor unit action po-

tentials using surface EMG is a blind source separa-

tion problem(Bahadur R. and Khan, 2021). There ex-

ist several algorithms in literature for the estimation

of muscle synergies, among which the most promi-

nent are principal component analysis (PCA), inde-

pendent component analysis (ICA), and non-negative

matrix factorization (NMF) (Rodrigues et al., 2022;

Rasool et al., 2016; Ma et al., 2021). PCA requires

the sources to be uncorrelated, while ICA requires in-

dependence of the sources (Naik and Nguyen, 2015;

Zhao et al., 2022). For biological systems, such as-

sumptions about the sources cannot be established;

therefore, the literature is more focused on NMF and

its variants (Roh J. and Bee, 2015; Naik and Nguyen,

2015; Lin C. and Farina, 2018; Bahadur R. and Khan,

2021). NMF is a non-convex optimization problem;

the implementation of the problem via an iterative

multiplicative update was a revival of this technique

(Lee and Seung, 2000). However, the convergence of

this algorithm is not guaranteed (Lin, 2007); there-

fore, several algorithms are adopted to implement

Bahadur, R. and Rehman, S.

Constrained ALS for Estimation of Human Upper Limb Synergies.

DOI: 10.5220/0011604400003414

In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 4: BIOSIGNALS, pages 29-35

ISBN: 978-989-758-631-6; ISSN: 2184-4305

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

NMF. One very famous approach is the alternating

least square (ALS) method. The solution is faster and

convergent; however, it gets trapped in local minima,

especially becoming very slow for co-linear data (Ci-

chocki and Zdunek, 2007).

Biological signals in general and EMG data, in

particular, are naturally co-linear; traditional ALS

lacks to provide an optimal solution. Therefore, this

paper advocates using constrained ALS-based NMF

for synergy estimation from EMG signals. The pa-

per is organized in the following manner, section 2

presents the mathematical details, while the experi-

mental setup is presented in section 3. The 4

module

describes synergies for elbow & shoulder based on the

physiological studies. The methodology is provided

in section 5. Results and discussion are presented in

section 6, followed by a conclusion at the end.

2 MATHEMATICAL MODEL

In the initial part of this section, we will introduce the

plain NMF, followed by the recommended regulariza-

tion function.

2.1 NMF and Traditional ALS

A standard NMF problem is deﬁned by eq(1).

Y = SΦ(t) + E, S, Φ(t) ≥ 0 (1)

Where Y ∈ R

[N×M]

is the root mean square (RMS)

of the recorded EMG signal for a length of

, N is

the total number of channels, and M is the total num-

ber of RMS values, S ∈ R

[N×P]

is the synergy matrix

and P is the estimated rank of matrix Y. Φ(t) ∈ R

[P×M]

is a matrix of P time variant signals (motor units) and

E ∈ R

[N×M]

is the additive noise. For error minimiza-

tion, consider calculating the Euclidean norm.

D(Y|SΦ(t)) = ||Y − SΦ(t)||

, S, Φ(t) ≥ 0 (2)

Since both the motor signals and synergies are un-

known, the overall problem is non-convex. ALS pro-

poses the use of an alternating procedure for estima-

tion of S and Φ(t), converting the non-convex prob-

lem into convex (eq. (3)).

(t) = arg min

φ(t)

||Y − S

k−1

Φ(t)||

, Φ(t) ≥ 0

(3a)

= arg min

||Y − SΦ

k−1

(t)||

, S ≥ 0 (3b)

and Φ

(t) are initialized randomly. S

and Φ

(t)

are the k

estimates while S

k−1

and Φ

k−1

(t) are the

estimates from the previous iteration. Gradient de-

scent is adopted to attain minimum error. For pNMF,

there is only one essential constraint: elements of all

decomposed matrices should be positive; there is no

additional constraint in the traditional ALS. The prob-

lem can quickly get caught in the local minimum; si-

multaneously, the algorithm can become much slower

to converge for co-linear data such as EMG signals

(Cichocki and Zdunek, 2007). Therefore, additional

penalty functions are required to address these issues.

2.2 Constrained ALS for Synergy

Estimation

Stochastic theory’s two famous optimization con-

straints are the l

− norm and the l

− norm. l

−

norm is used for sparse data while l

− norm (also

known as regularization) has the inherited property

of decorrelating the channels(Cichocki and Zdunek,

2007). Physiological signals, especially multiple

channel EMG from a speciﬁc limb, are correlated

with each other (Ma et al., 2021). Therefore, this pa-

per uses regularization as an additional penalty func-

tion to accelerate and obtain an optimal solution for

synergy extraction from EMG signals using the ALS-

based NMF algorithm. It is a kind of regression that

restricts the error towards zero; thus, the modiﬁed ver-

sion of eq.(3) would be:

(t) = arg min

φ(t)

||Y − S

k−1

Φ(t)||

+ α

||Φ

(t) − Φ

k−1

(t)||

, Φ(t), α

≥ 0

(4a)

= arg min

||Y − SΦ

k−1

(t)||

+ α

||S

− S

k−1

, S, α

≥ 0 (4b)

The regularization parameters α

and α

are non-

negative values that compel the variation in the de-

composed matrices towards zero. The values of these

parameters are based on error variance. The sys-

tem’s noise variance (σ

) is calculated from the initial

state where the muscles are at rest. The regulariza-

tion values are iteratively updated using the formula

= cα

k−1

;0 < c < 1,. The smaller values of the

regularization constraint result in the imposition of a

full rank matrix providing the possible optimal solu-

tion. For the given problem, the iterations stop when

an optimal value is achieved, i.e., α

≈ σ

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

3 EXPERIMENTAL SETUP

3.1 Consent & Declarations

Arms + Hands SRA Labs provided a database for car-

rying out this study. The experiment was conducted

with the consent of participants following the Decla-

ration of Helsinki under the approval of the North-

western University Institutional Review Board.

3.2 Participants

Six healthy subjects’ data is selected for this study.

The database comprised EMG signals using isomet-

ric contractions collected from two females and four

males aged 55 to 71. All subjects were right-hand

dominant with no neuromuscular impairment in the

upper limbs.

3.3 Setup

The participants were comfortably seated in a chair,

and the arm and hand movement was restricted using

a brace and strap mechanism; the setup is provided

in ﬁg. (1a). Isometric contractions were applied in a

3D space, and forces generated were recorded using

the multi-axis cartesian-based arm rehabilitation ma-

chine (MARCARM). The subject grasped the MAR-

CARM’s handle to exert isometric contraction infor-

mally in a 3D space. Setup details can be further ex-

plored in (Roh J. and Bee, 2015) paper.

Figure 1: (a) Experimental brace and strap setup followed

using MARCARM. (b) Target force contractions applied in

multiple directions matching the exemplary target in 3D.

3.4 EMG Acquisition

EMG signals are recorded using the Delsys Bagnoli

EMG acquisition unit at a sampling frequency of 1850

Hz. The signals are ﬁltered via a built-in zero-lag 20-

450 Hz bandpass ﬁlter. Eight channel surface EMG

data are recorded from both arms while performing

isometric force contractions in multiple directions,

presented in ﬁg. (1b). The targeted muscles of the up-

per arm are bicep brachii (BI), brachioradialis (BRD),

tricep longus (T I

long

), tricep lateral (TI

lat

), deltoid an-

terior (DA), deltoid medial (DM), and pectoralis ma-

jor (PM). The recording duration is 9 sec for each

contraction with a 2 sec initial baseline period. A suc-

cessful trial would mean maintaining the target force

at the sphere’s center for 0.8 sec. A total of 10 trials

were performed for each target sphere in a 3D space.

To avoid fatigue, a break of 1 min is given between

each trial.

4 SYNERGY & HUMAN

PHYSIOLOGY

Synergy is the interrelated actuation of several mus-

cles using a smaller number of activation patterns.

The human upper arm works by activating the shoul-

der and elbow joints. The two joints are controlled

by employing multiple muscles working as antago-

nistic pairs with assistive secondary muscles (Ayhan

and Ayhan, 2020). Each shoulder and elbow joint

requires two dedicated synergies activating the ﬂex-

ion and extension of each joint (Inouye and Cuevas,

2016). Thus, four synergies (i.e., 2

) are required to

analyze the movement of the upper arm. The four

synergies of the human upper limb based on the two

joints (elbow and shoulder) can be categorized as el-

bow ﬂexor-pronator/extensor-supinator and shoulder

abduction/adduction. Based on our study of the kine-

siology of elbow and shoulder complex (Yesilyaprak,

2020; Ayhan and Ayhan, 2020) ﬁg. (2) presents the

physiologically inspired synergistic weights present-

ing the involvement of the targeted eight muscles in

the movement of elbow and shoulder joints. The mus-

cles on x-axis are organized in such a manner that the

left most muscles start with the elbow activation while

the right most is pectoralis major of the shoulder.

Figure 2: Synergistic distribution involved in upper limb

movements according to human physiology. E

: El-

bow Flexion-Pronation; E

: Elbow Extension-Supination;

Add

: Shoulder Adduction; S

Abd

: Shoulder Abduction.

To understand the statistical behavior of the phys-

iologically inspired synergies, table (1) presents the

auto-correlation of the synergies. Elbow ﬂexion and

Constrained ALS for Estimation of Human Upper Limb Synergies

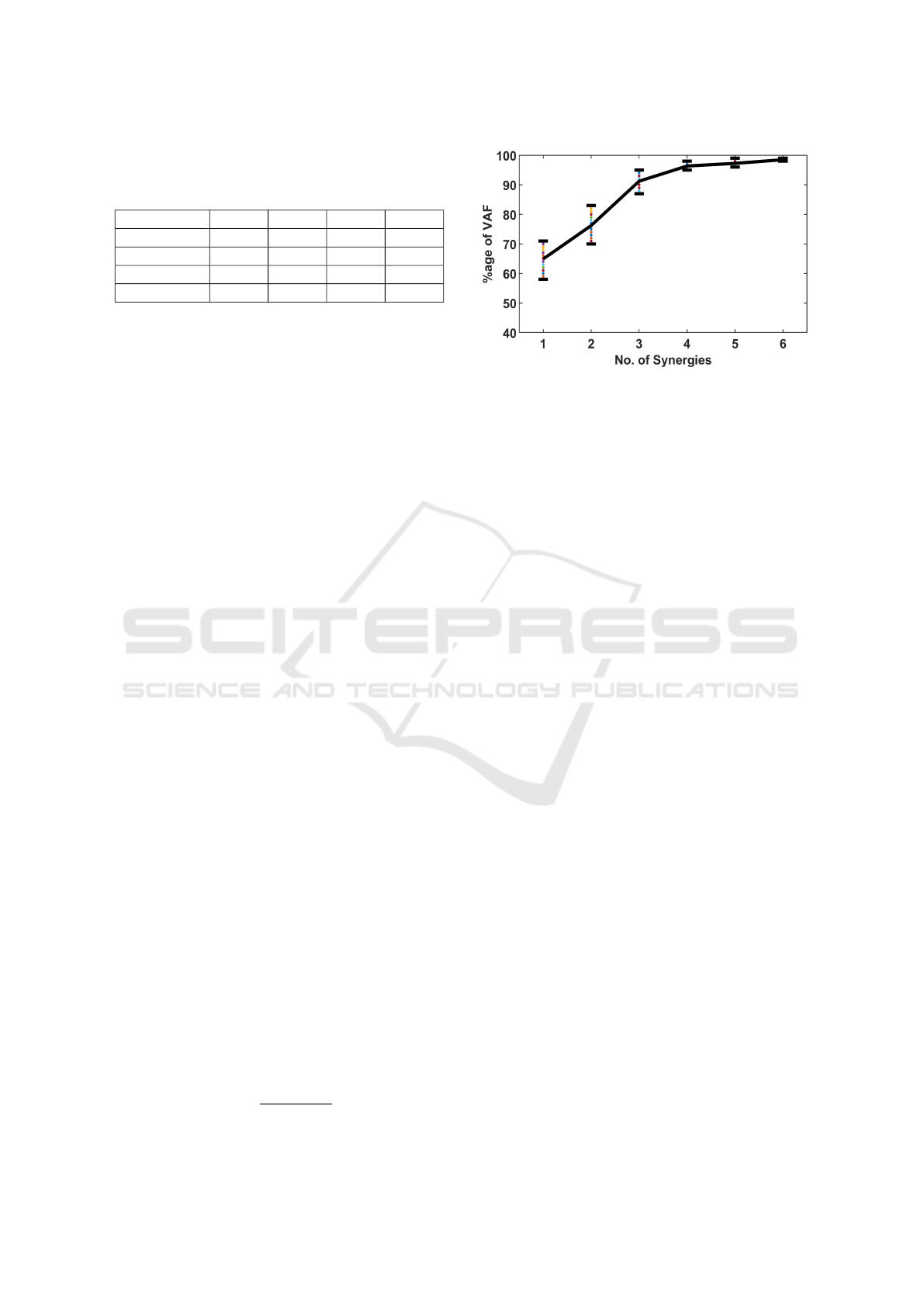
Table 1: Auto-correlation matrix of synergies based on hu-

man physiology. E

: Elbow Flexion; E

: Elbow Extension;

Add

: Shoulder Adduction; S

Abd

: Shoulder Abduction.

Movements E

Abd

Add

1 -0.629 -0.380 -0.220

-0.629 1 -0.111 -0.131

Abd

-0.380 -0.111 1 -0.350

Add

-0.220 -0.131 -0.350 1

extension result from the bicep-triceps muscles work-

ing as agonist/antagonist pair. Therefore, a minimum

correlation is observed between the two synergies.

The correlation among other cross synergies is neg-

ative or close to zero because the assistive muscles in

all movements are the same with variation in intensi-

ties, while prime movers are the exact opposite.

5 METHODOLOGY

5.1 Pre-processing

Matlab R2020a is used to analyze the data. The re-

spective mean value is subtracted from each surface

EMG signal for pre-processing, and the baseline was

removed. The active areas are selected based on sig-

nal segmentation and recorded timings. RMS of the

segmented surface EMG was calculated with a win-

dow length of 0.1 sec (T

= 180 samples) and an over-

lapping window, T

= 10 samples. EMG signals from

multiple trials for each subject were concatenated to

acquire the synergies.

5.2 Variance Accounted For Test

We infer from eq. (1 & 2) that the pseudo rank ‘P’

of the matrix Y is substantial for effectively decom-

posing the EMG signals into motor signals and in-

tended synergistic weights. To determine the mini-

mum number of synergies (P) using NMF, we use the

Variance Accounted For (VAF) test, eq. (5). The tra-

ditional and regularized NMF were used to perform

VAF; from ﬁg. (3) it can be observed that the knee-

curve is attained near 4 synergies with an average ac-

curacy of 96.5%. The ﬁndings of number of synergies

‘P’ is in accordance with the physiological study as

mentioned in section (4). Therefore, the dimension of

the synergy matrix S would be [8 × 4], where N = 8

presents the number of channels and P = 4 is the min-

imum number of synergies to effectively reconstruct

the database.

VAF =

1 −

var(Y −

var(Y)

× 100 (5)

Figure 3: VAF test to determine the number of minimum

synergies required. Each dotted color presents percentage

the VAF score for the reconstructed EMG signal from its

decomposed matrices using NMF.

5.3 Synergy Alignment

As per our ﬁndings, the knee curve is obtained around

four synergies with an accuracy of 96.5% using the

VAF test. Therefore, four synergies were acquired us-

ing plain NMF and regularized NMF. As synergistic

weights are the coefﬁcients associated with the tem-

poral motor signals; therefore, temporal motor signals

acquired via the NMF are used to align the muscle

synergies. For this purpose, a pivot signal is ran-

domly selected from an arbitrary subject. The correla-

tion between estimated motor signals across different

subjects is calculated. Maximum correlated value is

used in a nested procedure to align the four synergis-

tic weight patterns for the entire database.

6 RESULT & DISCUSSION

6.1 Synergy Estimation Via Traditional

ALS

This section provides a detailed discussion on the syn-

ergy estimation using the plain NMF, i.e., ALS with-

out additional constraints. The traditional ALS is an

iterative procedure; the estimations stop when a count

limit is reached. For this study, the count limit is set to

300. Synergistic muscle activation involves identify-

ing speciﬁc muscles engaged in a particular contrac-

tion. However, in ﬁg. (4), we do not observe such

unique muscle activation patterns; in fact, different

synergies indicates the activation of similar muscles.

For example, on average same pattern is observed in

synergy 1 and 2 (with a correlation coefﬁcient, r =

0.6), while synergy 2 and 3 are also closely correlated

(r = 0.647). Table (2) presents the auto-correlation

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

matrix for the four synergistic weights estimated via

plain NMF. It can also be inferred that the estimated

synergies lack the recognition of speciﬁc antagonistic

muscular pairs. Synergy 2 (ﬁg.(4)-top right) refers to

the activation of BI and TI muscles simultaneously,

which is not feasible in case of a healthy subject. The

behavior observed in the cross-correlation of syner-

gies using plain NMF is very opposite to that assessed

by actual human physiology. These observations refer

to the inaccurate or non-optimal synergy estimation of

traditional ALS.

Figure 4: Synergistic estimated via traditional ALS-

based NMF. E

: Elbow Flexion-Pronation; E

: Elbow

Extension-Supination; S

Add

: Shoulder Adduction; S

Abd

Shoulder Abduction.

Table 2: Correlation matrix of synergies estimated using

plain NMF. E

: Elbow Flexion-Pronation; E

: Elbow

Extension-Supination; S

Add

: Shoulder Adduction; S

Abd

Shoulder Abduction.

Movements E

Abd

Add

1 0.6 0.298 -0.414

0.6 1 0.647 -0.4336

Abd

0.298 0.647 1 0.136

Add

-0.414 -0.4336 0.136 1

6.2 Synergy Estimation via Regularized

ALS

Regularized NMF refers to the adaptation of the

ALS algorithm with additional Tikhonov constraint.

The mathematical details are already discussed in

section(2.2). The algorithm converges when regu-

larization parameter reaches its optimal value α

∗

≈

. Synergies extracted via regularized NMF are pre-

sented in ﬁg. (5), and the correlation table is presented

in table (3;). The ﬁrst synergy indicates activation of

bicep BI and BR, referring to elbow ﬂexion. In com-

parison, the second synergy identiﬁes elbow exten-

sion with the tricep (T I

lat

and T I

long

) as the most ac-

tive identiﬁed muscle, followed by PM and BR. Syn-

ergy 3 presents a low composite activation of BR, BI,

and shoulder muscles, referring to shoulder abduc-

tion. Finally, synergy 4 with dominant deltoid ante-

rior followed up by PM, T I

long

, and the BR as shoul-

der adduction. The behavior of synergies estimated

via the proposed algorithm and human-inspired phys-

iological synergies are closely related, p=0.753. The

cross-correlation among the synergies is negative in

the majority of cases (table(3)); a correlation of 0.38

is observed in the case of elbow ﬂexion and extension

due to the secondary muscles involved. Unlike plain

NMF, regularized NMF does not simultaneously pro-

vide multiple antagonistic pair activation in a single

synergy.

Figure 5: Synergistic estimated via regularized NMF.E

Elbow Flexion-Pronation; E

: Elbow Extension-

Supination; S

Add

: Shoulder Adduction; S

Abd

: Shoulder

Abduction.

For better evaluation of synergies estimated via

plain and regularized NMF, this paper investigates

the cross-correlation of estimated weights with phys-

iological synergies, presented in ﬁg.(6). Correla-

tion between estimated synergy and physiologically-

inspired synergy is called ‘auto’ if they belong from

the same order. Correlation between different or-

ders will be referred to as ‘cross’. In majority cases

regularized NMF provides maximum auto correlation

with physiologically-inspired synergy as compared

to plain NMF. Secondly, the synergies estimated via

plain NMF indicates a higher cross correlation; shoul-

der abduction synergy is comprised on the activation

of BR and BI as opposed to the actual deltoid muscles.

This synergy estimated via regularized NMF is also

having a consideraly low correlation (r = 0.6637),

yet it is able to detect the correct activation of deltoid

muscles. Also in case of elbow extension-supination

synergy a very low correlation factor (r = 0.1848 was

observed when comparing physiologically inspired

synergy to plain NMF. In this particular case, the syn-

ergy estimated via plain NMF shows an almost uni-

form activation of all muscles. In contrast, regular-

ized NMF targets the activation of tricep muscles in

assistance with PM (r = 0.8321).

It can be overall concluded that the synergy es-

timated via regularized NMF are rigorous and pro-

vides much similarity to the actual physiological data.

Therefore, this paper recommends using the proposed

regularized NMF compared to plain NMF.

Constrained ALS for Estimation of Human Upper Limb Synergies

Table 3: Correlation matrix of synergies estimated using

regularized NMF. E

: Elbow Flexion; E

: Elbow Exten-

sion; S

Add

: Shoulder Adduction; S

Abd

: Shoulder Abduc-

tion.

Movements E

Abd

Add

1 0.380 -0.353 0.388

0.380 1 -0.633 -0.136

Abd

-0.353 -0.633 1 0.079

Add

0.388 -0.136 0.079 1

Figure 6: A comparison of synergies estimated for healthy

subjects with Synergistic activation based on human phys-

iology. The red ‘*’ refers to cross correlation of regular-

ized NMF based synergistic weight with physiologically in-

spired synergies; the black dots present auto correlation for

similar order synergies. The purple ‘∆’ refers to the one

estimated via plain NMF and the blue ‘∆’ are the correla-

tion between similar order synergies E

: Elbow Flexion-

Pronation; E

: Elbow Extension-Supination; S

Add

: Shoul-

der Adduction; S

Abd

: Shoulder Abduction.

7 CONCLUSION

Human body movements are based on the synergis-

tic activation of muscles. This paper investigates the

number of synergies and the approriate muscular acti-

vation involved in isometric contraction of the human

upper arm. According to our ﬁndings four synergies

are sufﬁcient for upper limb movement identiﬁcation.

Plain ALS-based NMF algorithm is insufﬁcient for

synergy estimations as the method fails to provide op-

timal solution for co-linear data. Therefore, this paper

proposes using a constrained ALS-based NMF; the

regularization constraint decorrelates the EMG sig-

nals to attain the synergies behind the particular con-

tractions, thus, resolving the issue. Our statement is

supported by the results presented in section (6). In

the future, we look forward to analyzing the patholog-

ical disorder in the upper limbs of post-stroke subjects

using muscle synergies.

ACKNOWLEDGEMENTS

For carrying out this research work, we are very

thankful to Dr. Zev Rymer and his team at Shirley

Ryan Ability Lab, Chicago, USA, for providing us

with the entire database.

REFERENCES

Ayhan, E. and Ayhan, C. (2020). Kinesiology of the elbow

complex. In Comparative Kinesiology of the Human

Body. Elsevier Inc.

Bahadur, R. and Rahman, S. (2018). A robust and adaptive

algorithm for real-time muscle activity interval detec-

tion using emg signals. In 11th International Joint

Conference on Biomedical Engineering Systems and

Technologies. INSTICC.

Bahadur R., Rahman S., R. G. and Khan, M. (2021). Syn-

ergy estimation method for simultaneous activation of

multiple dofs using surface emg signals. Frontiers in

Neuroscience, 16:1–8.

Cichocki, A. and Zdunek, R. (2007). Regularized Alter-

nating Least Squares Algorithm for Non-negative Ma-

trix/Tensor Factorization, volume 4493. Springer,

Berlin.

Inouye, J. M. and Cuevas, F. J. V. (2016). Muscle synergies

heavily inﬂuence the neural control of arm endpoint

stiffness and energy consumption. PLOS: Computa-

tional Biology, pages 1–24.

Lee, D. and Seung, H. (2000). Algorithms for non-negative

matrix factorization. In Neural Information Process-

ing Systems, pages 556–562. NIPS.

Lin, C.-J. (2007). On the convergence of multiplicative up-

date algorithms for nonnegative matrix factorization.

IEEE Transactions on Neural Networks, 18(6):1589–

1596.

Lin C., Wang B., J. N. and Farina, D. (2018). Robust ex-

traction of basis functions for simultaneous and pro-

portional myoelectric control via sparse non-negative

matrix factorization. Journal of Neural Engineering,

15:26017(9pp).

Ma, Y., Shi, C., Xu, J., Ye, S., Zhou, H., and Zuo, G. (2021).

A novel muscle synergy extraction method used for

motor function evaluation of stroke patients: A pilot

study. Sensors, 21:11:3833.

Naik, G. R. and Nguyen, H. T. (2015). Non negative matrix

factorisation for the identiﬁcation of emg ﬁnger move-

ments: Evaluation using matrix analysis. IEEE Jour-

nal of Biomedical and Health Informatics, 19:478–

485.

Rasool, G., Iqbal, K., Bouaynaya, N., and White, G. (2016).

Real-time task discrimination for myoelectric con-

trol employing task-speciﬁc muscle synergies. IEEE

Transactions on Neural Systems and Rehabilitation

Engineering, 24:98–108.

Rodrigues, C., Correia, M., Abrantes, J., Rodrigues, M.

A. B., and Nadal, J. (2022). Muscle synergies es-

timation with pca from lower limb semg at differ-

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

ent stretch-shortening cycles. In IFMBE Proceedings.

SPRINGER.

Roh J., R. W. and Bee, R. F. (2015). Evidence for altered up-

per extremity muscle synergies in chronic stroke sur-

vivors with mild and moderate impairment. Frontiers

in Human Neuroscience, 9:6:1–14.

Yesilyaprak, S. S. (2020). Kinesiology of the shoulder com-

plex, volume 4493. Elsevier, Rio de Janeir0.

Zhao, K., Wen, H., Zhang, Z., Atzori, M., Muller, H., Xie,

Z., and Scano, A. (2022). Evaluation of methods for

the extraction of spatial muscle synergies. NUST Jour-

nal of Engineering Sciences, 16.

Constrained ALS for Estimation of Human Upper Limb Synergies