Flexible Extrinsic Structured Light Calibration Using Circles

Robert Fischer

, Michael H

odlmoser

and Margrit Gelautz

1 a

Visual Computing and Human-Centered Technology, TU Wien, Vienna, Austria

emotion3D GmbH, Vienna, Austria

ﬁ

Keywords:

Device Calibration, Structured Light Calibration, Stereo Camera.

Abstract:

We introduce a novel structured light extrinsic calibration framework that emphasizes calibration ﬂexibility

while maintaining satisfactory accuracy. The proposed method facilitates extrinsic calibration by projecting

circles into non-planar and dynamically changing scenes over multiple distances without relying on the struc-

tured light’s intrinsics. Our approach relies on extracting depth information using stereo-cameras. The imple-

mentation reconstructs light-rays by detecting the center of circles and reconstructing their 3D-positions using

triangulation. We evaluate our method by using synthetically rendered images under relevant lighting- and

scene conditions, including detection drop-out, circle-center detection error, impact of distances and impact

of different scenes. Our implementation achieves a rotational accuracy of below 1 degree and a translational

accuracy of approximately 1 cm. Based on our experimental results we expect our approach to be applicable

for use cases in which more ﬂexible extrinsic structured light calibration techniques are required, such as au-

tomotive headlight calibration.

1 INTRODUCTION

The process of registering the position and orientation

of a camera or projector relative to another camera

is called extrinsic calibration. It is a common task

in computer vision, whose main application ﬁelds

cover robotics, automotive scenarios, and virtual real-

ity. Our work focuses on the calibration of a projector

in relation to a stereo-camera, also known as a dual-

camera structured light system (Chen et al., 2018)

(An et al., 2016) (Zhang and Yau, 2008). In gen-

eral, our approach is applicable to different use cases

and scenarios, such as surveillance, stage-productions

or other sensor-supported smart lighting applications

(Sonam and Harshit, 2019) (Gillette and McNamara,

2020). In particular, we apply our method to the cal-

ibration of headlights of cars, allowing the develop-

ment of programmable automotive headlights (Tam-

buro et al., 2014). Such a system illuminates spe-

ciﬁc regions of interest, which could be extracted us-

ing different sensors (e.g. camera, LIDAR sensor,

etc.). In order to transform such regions of interest

(e.g. road signs, pedestrians, etc.) from the sensor co-

ordinate system into the projector coordinate system,

an extrinsic calibration of the projector relative to the

sensor has to be available.

https://orcid.org/0000-0002-9476-0865

In general, current state-of-the-art approaches for

projector extrinsic calibration are limited in terms of

ﬂexibility. In particular, they usually assume a pla-

nar projection target at a relatively close distance to

the projector (Garrido-Jurado et al., 2016) (Huang

et al., 2018) (Chen et al., 2016). This limits the ap-

plicability of extrinsically calibrating a projector in

non-controlled environments, particularly where non-

planar projection surfaces are predominant, or envi-

ronments in which the calibration must be performed

over a large range of distances. Hence, the design of

our structured light calibration approach is motivated

by the following challenges:

• Support of non-planar calibration targets: In cer-

tain situations it is necessary to calibrate a struc-

tured light system in a non-controlled environ-

ment, where the availability of a regular planar

calibration target cannot be assumed.

• Support of dynamically changing scenes: Sim-

ilarly, non-controlled environments may change

during calibration.

• Independent of structured light intrinsics: In gen-

eral, in order to estimate the extrinsics of a struc-

tured light, homography-based approaches rely on

the intrinsics of the structured light (Zhang, 2000).

Our approach does not require the intrinsics of the

structured light device to be known.

Fischer, R., Hödlmoser, M. and Gelautz, M.

Flexible Extr insic Structured Light Calibration Using Circles.

DOI: 10.5220/0011614500003417

In Proceedings of the 18th Inter national Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 4: VISAPP, pages

47-55

ISBN: 978-989-758-634-7; ISSN: 2184-4321

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

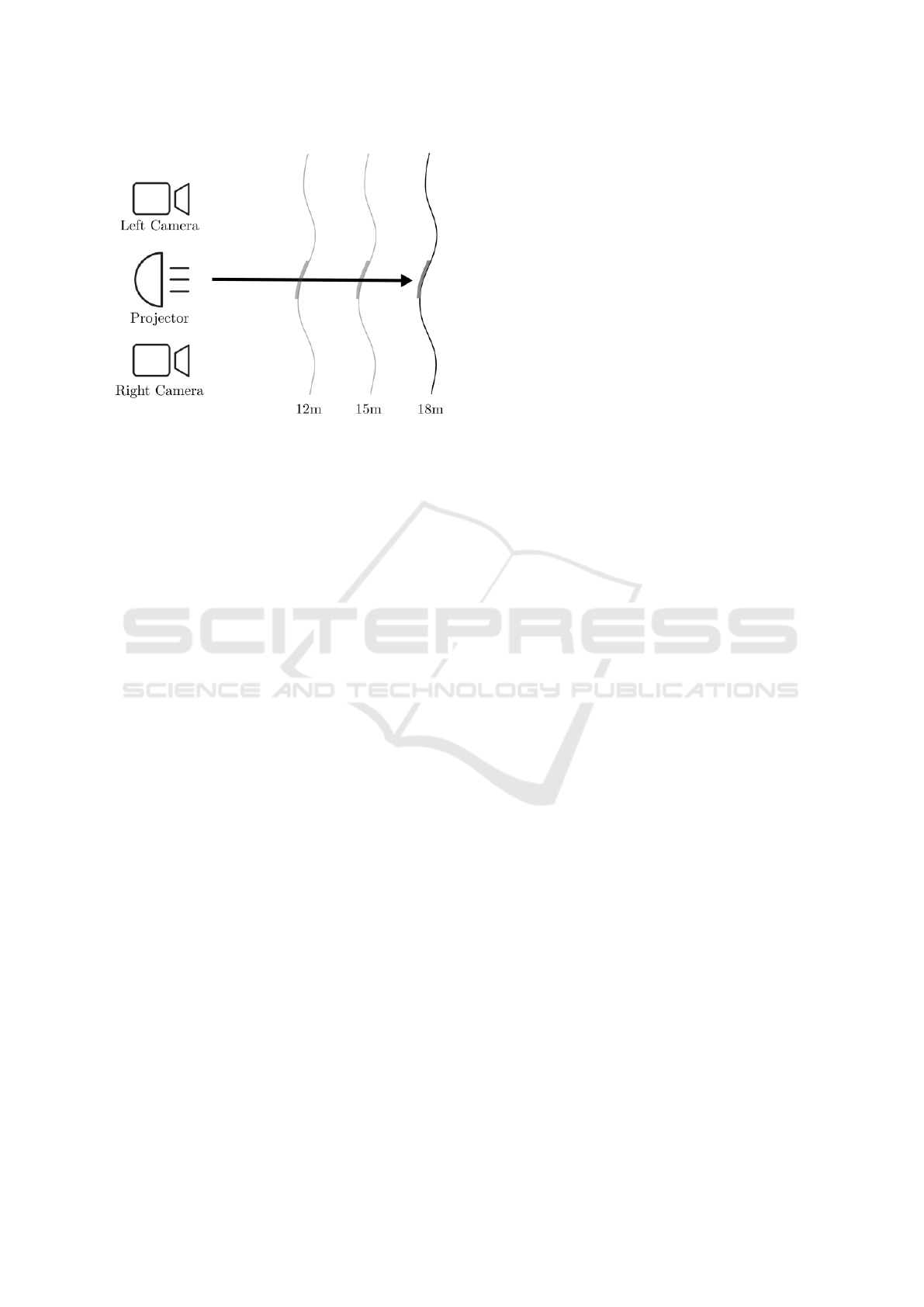
Figure 1: Schematic overview of the calibration setup for

a single ray. Note that our approach supports non-planar

target projection surfaces, as long as the circle detector can

detect the centers of the circles reliably.

Our method projects circles sequentially onto var-

ious non-planar projection surfaces within a scene,

which are located at different relative distances from

the camera center. The circles are detected in both

the left and the right images of the stereo camera and

the 3D positions of the circles are triangulated. By

identifying multiple such circles and their centers in

3D, projection rays going through the centers can be

deﬁned and the extrinsics between the stereo camera

and the projector can be calculated using the inter-

section of all these rays. Our approach works with a

wide range of different projection surfaces. The only

prerequisite is that circles can be detected. Hence,

the calibration can be done automatically, which al-

lows re-calibration during operation (e.g. because of

misalignment over time due to vibrations, etc.). In

contrast to the extrinsics, the intrinsics of a struc-

tured light system are static and usually require less

frequent re-calibration. Figure 1 shows a schematic

overview of the projector and camera setup we use for

our approach. It consists of two time-synchronized

cameras with known camera parameters (both intrin-

sic and extrinsic parameters) and a projector capa-

ble of projecting a monochrome circle pattern into

the scene. Our method provides a calibration accu-

racy sufﬁcient for intelligent lighting systems (Tam-

buro et al., 2014) or applications with similar pre-

cision, such as smart lighting installations (Sonam

and Harshit, 2019) and stage-productions (Gillette

and McNamara, 2020). More precisely, we aim for

a translational error in the range of 1 cm (or less) and

a rotational error of not more than 1 degree. Contrary

to alternative solutions, our method projects a simple

circular calibration pattern into a variety of possible

scenes, allowing calibration over a wide range of dis-

tances and also with different projector types.

2 RELATED WORK

Most previous methods for calibration of a stereo-

camera structured light system involve the projection

of more complex patterns (often fringe patterns) into

the scene, while also expecting a controlled environ-

ment (Zhang and Yau, 2008) (Chen et al., 2016).

(Chen et al., 2018) propose to simplify structured

light calibration by reducing the amount of projected

images. (Garrido-Jurado et al., 2016) generalize to

simultaneously reconstruct and calibrate structured

light systems. Some methods focus on calibration

with a single camera (Huang et al., 2018) (Shah-

paski et al., 2017). Other structured light extrinsic

calibration approaches are based on the homographic

extrinsic calibration approach proposed by (Zhang,

2000). One problem associated with projecting rel-

atively complicated patterns into the scene is that cal-

ibration becomes challenging over larger distances or

in non-controlled environments (An et al., 2016), as

in these cases the higher frequency details (such as

lines and gradients) are challenging to detect.

Multi-Camera Structured Light Systems: In order

to estimate the calibration of a structured light sys-

tem, (Chen et al., 2018) propose to project fringe im-

ages into the scene and apply a variant iterative clos-

est point algorithm. Earlier work of (Chen et al.,

2016) also applies circles for calibration, they use

(Zhang, 2000) for the intrinsic calibration of the pro-

jector. (Zhang and Yau, 2008) propose to use ab-

solute phase-assisted three-dimensional data for reg-

istration of a dual-camera structured light system.

Their approach also requires the projection of rather

complicated fringe images into the scene. Similarly,

(Garrido-Jurado et al., 2016) also project a relatively

complicated image pattern into the scene.

Single-Camera Structured Light Systems: There

are also various works on single camera structured

light system calibration. Notably, (Huang et al., 2018)

propose a single-shot-per-pose approach which han-

dles imperfect planar targets, again, assuming a pla-

nar target and also projecting a more complicated pat-

tern into the scene. (Shahpaski et al., 2017) perform

a radiometric and a geometric calibration simultane-

ously, again relying on projecting a relatively com-

plex calibration pattern into the scene, while also as-

suming a planar projection target. (An et al., 2016)

propose a method for long-range structured light sys-

tem calibration. However, their approach projects a

relatively complex calibration pattern into the scene

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

Figure 2: Sample pattern used for calibration, from which

one circle per calibration step is projected. Circles I and II

are used to estimate the projector’s rotation.

and assumes a planar projection target. Thus, their

approach is not applicable to the distances and scenes

our approach is able to operate in.

3 METHOD

In the following subsections, we discuss the struc-

tured light calibration method in more detail. In Sub-

section 3.1 we provide the requirements regarding the

hardware set-up of our proposed method. In Subsec-

tion 3.2 we explain the algorithm of our method both

in form of a textual description and pseudo-code.

3.1 Hardware Set-Up

Our calibration technique estimates both the rotation

and translation of a projector relative to the coordinate

system deﬁned by the stereo camera. Our method is

comprised of two main hardware components: (1) A

stereo camera with two time-synchronized cameras

and known camera parameters (both intrinsics and ex-

trinsics) and (2) a projector. Instead of using stereo

cameras, other camera systems (e.g.: RGB-D) can

also be used, as long as a depth estimation for selected

pixels of the projected pattern can be computed. The

projector must be capable of projecting individual cir-

cles into the scene (Figure 2). In order to perform

the extrinsic calibration of the projector, the circles of

the calibration pattern must be detectable using visual

cues. Refer to Section 4 for a more detailed evaluation

of the associated constraints of our approach.

3.2 Algorithm

In the following, we describe the algorithm for esti-

mating the projector’s extrinsics. Algorithm 1 shows

the corresponding pseudo-code.

Step 1: The projector sequentially projects the circles

from the calibration pattern into the scene (Figure 2).

The circles are relatively easy to project using digital

light processing (DLP) (Packer et al., 2001). Even

a sequence of simple circular stencils in front of the

light source could be sufﬁcient. Refer to Figure 1 for

a schematic overview of the setup.

Step 2: Then, the stereo camera captures a frame of

the projected circle in the scene. Ideally, the projec-

tion of the circle is fully visible in both cameras, as

this simpliﬁes the circle center detection of step 3.

Figure 3 shows a typical example of a captured stereo

image. In practice, there will typically be some occlu-

sions present (e.g.: occlusion with the ﬂoor), which

may hinder the reliable detection of the calibration

circles. Surfaces with high reﬂectivity (mirrors) or

very diffuse projection surfaces might make reliable

circle detection more challenging as well.

Step 3: Our algorithm detects the circles in both

stereo camera views using the expected calibration

pattern template and assigns a correspondence be-

tween the template and the detected pattern. To ease

correspondence detection and avoid mismatching cir-

cle projections, we project a single circle at a time.

For simpler scenes, the circles can be detected us-

ing Hough transformations, while for more compli-

cated scenes a Convolutional Neural Network (Red-

mon et al., 2016) might be more appropriate. To avoid

the necessity of ﬁnding correspondences for multi-

ple detected circles, we project exactly one circle per

frame into the scene.

Step 4: Triangulation of the center positions of the

detected circles from the stereo images results in a

3D position representing the circle’s center position

relative to the stereo camera. For RGB-D camera se-

tups, this triangulation step can be skipped, as the Z

component of the point is already known.

Step 5: Repeat steps 1 - 4 for several relative dis-

tances. We measure the relative distance from the

projector’s lens to the projection target in a straight

line. Principally, the more of these relative distances

per calibration circle are captured, the more accurate

the estimation of the extrinsics will be. In the next

step, we use the extracted 3D points to construct rays,

hence at least two points per calibration circle (Fig-

ure 2) are required to construct a ray. In general,

the combination of different calibration distances in-

creases the accuracy of the extrinsic calibration re-

sults. The decrease in accuracy with fewer calibration

distances can be attributed mainly to the inherent in-

accuracy of the 3D triangulation of the circle center

points of the projected calibration pattern. In Sec-

tion 4.6 we evaluate the impact of different distance

conﬁgurations and in Section 4.7 we evaluate the im-

pact of different target projection surfaces.

Flexible Extrinsic Structured Light Calibration Using Circles

Figure 3: Stereo images (left and right camera) from the car parking scene. Depicts how non-planarity affects the projection

of circles into the scene. Resulting calibration evaluated in Section 4.7.

Figure 4: Visualization of the ray intersections using the tri-

angulated 3D points. The projector is placed with increas-

ing distance to the projection surface. The green points have

a distance of roughly 5m, the blue points 8m and the cyan

points 13m relative to the projector. Figure 2 shows the vis-

ible parts of the corresponding calibration pattern applied

for this calibration.

Step 6: For all corresponding points of different dis-

tances to the projection surface of the calibration pat-

tern template, rays are constructed. In practice, the

points will most likely not be located on a single ray

(mainly due to the previously mentioned inaccuracy

when detecting the circles). Hence, we ﬁt a line that

minimizes the least-square Euclidean distances to the

3D points (Megiddo and Tamir, 1983). Refer to Fig-

ure 4 for a visualization of the ray intersections.

Step 7: Calculate intersections of the previously con-

structed rays, resulting in the 3D position of the pro-

jector relative to the stereo camera. In practice, those

rays will most likely not intersect in a single point,

therefore we take the point which has the closest ac-

cumulated distance to all rays (Megiddo and Tamir,

1983).

Step 8: The calibration pattern (Figure 2) has been

constructed in such a way that we can extract the for-

ward direction and the up direction of the projector.

The circle in the center indicates the forward direction

of the projector. Similarly, we placed a circle which

represents the up direction of the projector directly

above the center. Refer to Figure 5 for an illustra-

tion. We calculate the cross-product of the forward

and up vector to obtain the orthogonal side vector.

Combining the directional vectors (up, forward and

side) forms the basis of the rotation matrix (Smith,

Figure 5: Illustration of rotation estimation. Cone repre-

sents projector. (A) Red arrow represents forward direction

estimated using circle I in the middle of the calibration pat-

tern. (B) Blue arrow represents up direction estimated using

top-middle circle II. (C) Green arrow represents calculated

up-vector obtained by projecting vector A on vector B.

1983). In order to increase the robustness and accu-

racy of the rotation estimation, the same calculations

for the remaining rays may be performed.

4 EXPERIMENTS

In this section, we present several experiments and

evaluate our method under a variety of different

modalities by using a 3D simulator. Refer to Sec-

tion 4.2 for more details on the generation of the sim-

ulated data. We place a projector in front of a wall

or other more complicated calibration objects. For

calibration, we place a stereo-camera near the projec-

tor. Our approach assumes the intrinsics and extrin-

sics of the stereo-camera to be known. Figure 1 shows

a schematic overview of the calibration setup. We

do not assume speciﬁc cameras, sensors or structured

light projectors. Instead, we perform all our calibra-

tion experiments from the assumption that a certain

set of projected circles can be reconstructed with a set

circle-center detection accuracy in different modali-

ties. In essence, our evaluation method answers the

following question: If it is possible to detect X% of

circle-centers with Y% positional accuracy, can our

method be expected to produce an extrinsic calibra-

tion within Z% error? An advantage of this evalua-

tion methodology is that it gives insights into the cal-

ibration procedure, while not being limited to certain

hardware setups.

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

Algorithm 1: Flexible extrinsic structured light calibration algorithm.

1: Points3D = {}

2: do

3: for CircleID in CircleGrid do

4: ProjectCircleIntoScene(CircleID) ▷ Step 1

5: Left, Right = CaptureStereoFrames() ▷ Step 2

6: LeftCircle = FindCircle(Left) ▷ Step 3

7: RightCircle = FindCircle(Right) ▷ Step 3

8: Skip if LeftCircle or RightCircle not found ▷ Step 3

9: L = GetCircleCenter(LeftCircle) ▷ Step 4

10: R = GetCircleCenter(RightCircle) ▷ Step 4

11: Point3D = Triangulate(L, R, Intrinsics, Extrinsics) ▷ Step 4

12: Add Point3D to Points3D[CircleID]

13: end for

14: while insufficient relative Distances? ▷ Step 5

15: Rays = []

16: for CircleID in CircleGrid do ▷ Step 7

17: CorrespondingPoints = Points3D[CircleID] ▷ Step 6

18: Ray = FitRay(CorrespondingPoints) ▷ Step 6

19: Add Ray to Rays

20: end for

21: FinalPosition = NearestPointToRays(Rays) ▷ Step 7

22: RayForward = CalculateForwardRay(Rays) ▷ Step 8

23: RayUp = CalculateUpRay(Rays) ▷ Step 8

24: FinalRotation = CalculateRotation(RayForward, RayUp) ▷ Step 8

25: Return FinalPosition, FinalRotation

The baseline setup consists of a calibration pat-

tern with nine circles arranged as shown in Figure 2.

For the baseline approach, we assume that all circles

which are visible are recognized by the camera sys-

tem. As this assumption may not always hold, we ad-

ditionally consider a random drop-out. Similarly, we

assume that the 3D point triangulation is accurate, but

we also perform several experiments where we simu-

late a 3D reconstruction error by introducing synthetic

noise to the 2D circle-center detections. We perform

the calibration using 2m, 5m, 8m, 12m, 17m, 23m and

26m distances, while also evaluating the impact of us-

ing subsets of these distances as well. For the baseline

calibration, we project the circle pattern onto a wall,

but we also perform experiments with other calibra-

tion targets. In order to increase reproducibility and

limit the impact of stochastic inﬂuences, we repeat

each experiment 100 times and report the mean error

metrics.

4.1 Evaluation Metrics

Current state-of-the-art structured light calibration

methods typically use reprojection errors for eval-

uation (Garrido-Jurado et al., 2016) (Huang et al.,

2018). Our method only focuses on estimating the

extrinsics of a structured light projector, while for

calculating the reprojection error the intrinsics are

also required. Hence, we cannot use the reprojec-

tion error for evaluation. Instead, we evaluate the per-

formance using the translational error and the rota-

tional error. The translational error is the Euclidean

distance between the ground truth position p

of the

projector and the estimated position p

est

of the pro-

jector. For the rotational error, we use the angular

difference between two rotations (Huynh, 2009). We

deﬁne the ground truth rotation as R

, the estimated

rotation as R

est

, tr(R) as the trace of a rotation matrix

R and deﬁne err(R

, R

est

) as described in Equation 1

(Huynh, 2009) (Huynh, 2009). We deﬁne a rotational

error of below 1 degree and a translational error of

approximately 1 cm as acceptable for the usefulness

of our method. In our test set-up, a rotational error

of 1 degree corresponds to a Euclidean projection er-

ror of approximately 3 pixels. A translational error

of 1 cm corresponds to a Euclidean projection error

of below 1 pixel for all points within a distance from

approx. 2m to Inﬁnity. In general, the speciﬁc criteria

for error thresholds are highly dependent on the actual

use case.

err(R

, R

est

) = arccos(

tr(R

est

) − 1

) (1)

Flexible Extrinsic Structured Light Calibration Using Circles

Figure 6: Baseline evaluation setup showing the projection

of the calibration pattern for the baseline experiment.

4.2 Simulator

We use a 3D simulator to evaluate our calibration

method. This approach allows us to differentiate

and isolate various parameters that might inﬂuence

the calibration performance. The simulator is imple-

mented in Unity3D (Uni, ) and uses state-of-the-art

physically based rendering for synthesizing the 2D

images (Pharr et al., 2016). Figure 3 shows a stereo

image from our simulation environment. In partic-

ular, it shows how the non-planarity of the surfaces

affects the projection of the circles into the scene.

Performing similar evaluations using real hardware

would be challenging, especially when trying to sep-

arate and reproduce different potential inﬂuences in-

dependently. Potential error sources we examine in-

clude variations in 2D circle-center detection error,

projection drop-out, projection distance and 3D en-

vironment.

4.3 Baseline Experiment

For the baseline experiment, we performed the struc-

tured light extrinsic calibration in front of a white wall

without applying additional synthetic noise to any of

the inputs. Figure 6 depicts a projection of a circle

on a white wall for this experiment. We included all

available distances (2m, 5m, 8m, 12m, 17m, 23m,

26m) for the extrinsic estimation. The results for

the baseline experiment are a translational error of

0.36 cm and a 0.35 degrees of rotational error. In our

test set-up, this corresponds to a projection error of

slightly above 1 px for a target 50 meters in front of

the projector.

4.4 Impact of 2D Circle-Center

Detection Error

In practice, we expect some inaccuracies in the cir-

cle center detection to occur. In existing literature,

the impact of different calibration estimation param-

eters and their correlation with the estimation accu-

racy of stereo camera calibration is well studied. (Liu

et al., 2006) analyze geometric camera parameters for

stereo camera setups. (Guo et al., 2006) research

structural parameter optimization for stereo vision.

(Xu et al., 2013) investigate error analysis of calibra-

tion parameters of stereo vision systems. In this ex-

periment we try to quantify how the accuracy of the

2D circle center detection approach impacts the ac-

curacy of our calibration method. Such errors may

happen due to different factors, such as different con-

ditions related to surface reﬂectivity, surface texture

or lighting conditions. Hence, in order to simulate

these factors, we apply a normally distributed noise

to the 2D position of the detected circle center po-

sitions with increasing standard deviation on the x-,

y- and xy- axes. The normal distribution is set to a

mean of 0 and a standard deviation corresponding to

the assumed pixel error for the circle-centers. False

detection of circles can be interpreted as a case of 2D

circle-center detection error with potentially large de-

viation. In Figure 7, we see that increasing the circle

detection error has a relatively strong impact on the

overall calibration accuracy. We observe that apply-

ing the synthetic noise on the y-axis alone has a rel-

atively minor impact on the rotational error. In con-

trast, applying an error along the x-axis has a stronger

impact. Regarding the translational error, we observe

steeper curves in all cases. We observe again that the

y-axis has a lower impact on the translational error

than the x-axis. We believe that this phenomenon is

due to the fact that the structured light is placed to the

side of the camera setup along the x-axis, hence the y-

axis is similar for both the cameras and the structured

light. In summary, a standard deviation of 1 pixel

for the circle centers still yields calibration outputs of

approximately 1 cm translational error and 1 degree

of rotational error. Based on assumptions outlined in

Subsection 4.1, we deem such accuracy as acceptable.

4.5 Impact of Synthetic Detection

Drop-Out

In practice, we cannot expect that all circles of the

calibration pattern will be always visible. Often-

times, there will be surfaces that do not reﬂect the

pattern well (e.g.: mirrors, highly diffuse surfaces,

etc). Hence, we simulate these phenomena by in-

troducing a uniformly distributed random dropout of

the triangulated 3D points. Our experiments in Sec-

tion 4.7 capture a drop-out expected to be present in

real-world scenarios. In this experiment, we increase

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

Figure 7: Impact of circle center detection error. The detected circle centers are varied by a normally distributed error with a

standard deviation denoted on the x-axis. y-axis denotes the rotational error (left) and translational error (right).

the dropout from 0% to 80% with an increment of

10%. In Table 1, we see that up until a dropout of

30% the calibration remains near 1 cm in translational

error and 0.5 degrees rotational error, which we deem

as acceptable calibration accuracy. With higher drop-

out, the error increases steadily, until at 70% the rota-

tional error spikes to 10 degrees, suggesting that the

reconstructed rays are inaccurate or missing. Inves-

tigation of the calibration data reveals that the algo-

rithm is only able to reconstruct a single ray. In order

to construct a ray, at least two 3D points are required,

but for the simulated drop-out of 70% and more, only

one potential ray had enough points associated with

it.

4.6 Impact of Distances

Our approach for estimating the relative orientation

and translation of a projector with respect to a stereo

camera relies on triangulating points from differ-

ent distances in order to perform ray intersection.

This experiment evaluates how much the range of

distances of the triangulated 3D points impacts the

calibration accuracy. We perform several calibrations

with different subsets of selected distances and com-

pare them with the baseline approach (2m, 5m, 8m,

Table 1: Calibration accuracy due to random drop-out, with

column Drop-Out indicating the drop-out percentage.

Drop-Out

Translational

Error

Rotational

Error

[cm] [deg]

Baseline (0 %) 0.36 0.35

10 % 0.99 0.44

20 % 1.22 0.47

30 % 1.60 0.50

40 % 2.18 0.53

50 % 2.20 0.68

60 % 3.62 0.79

70 % 5.52 10.00

80 % 18.01 10.00

12m, 17m, 23m, 26m). Table 2 shows that using cir-

cles from near distances leads to a better calibration

accuracy (IDs 1 - 4) than using only circles from far-

ther distances (IDs 5 - 9). We obtain the best results

by using the distances 2m and 5m (ID 2), namely a

translational error of 0.14 cm and a rotational error

of 0.42 degrees. We suspect this is caused by the 3D

triangulation becoming more sensitive to detection in-

accuracies the farther away the point is located, rela-

tive to the stereo cameras. The impact of 3D trian-

gulation error is discussed in greater detail in binocu-

Flexible Extrinsic Structured Light Calibration Using Circles

Table 2: Calibration accuracy across different distances rel-

ative to the structured light projector and the target calibra-

tion object. Row with ID 1 contains the baseline results.

ID Distances

Trans.

Error

Rot.

Error

[cm] [deg]

1 2m, 5m, 8m, 12m 0.36 0.35

17m, 23m, 26m

2 2m, 5m 0.14 0.42

3 2m, 26m 0.16 0.40

4 2m, 5m, 8m 0.23 0.39

5 23m, 26m 39.24 0.53

6 17m, 23m, 26m 7.31 0.37

7 8m, 12m 2.43 0.42

8 17m, 23m 9.13 0.40

9 12m, 17m 4.44 0.35

23m, 26m

lar stereo camera reconstruction literature (Guo et al.,

2006) (Xu et al., 2013). In Table 2, we see that the

proposed structured light extrinsic calibration method

estimates with satisfactory accuracy from 2m to 26m

(ID 1, 3) with a translational error of 0.36 cm and

0.35 degrees. Similar results are obtained from dis-

tances up to 8m, with up to 0.23 cm translational- and

0.42 degrees rotational error, respectively. In sum-

mary, we ﬁnd that our approach is applicable for a

wide range of distances, especially when we compare

it to current state-of-the-art approaches (Chen et al.,

2018) (Huang et al., 2018).

4.7 Impact of Different Scenes

In this experiment, we analyze the impact of differ-

ent target scenes. Our method is intended to be used

in non-controlled environments. Hence, we perform

the calibration using our simulator described in Sec-

tion 4.2. We created multiple scenes: A scene con-

taining a white wall, a scene containing several geo-

metric shapes (cylinders with different surfaces) and a

scene consisting of a simulation of parked cars. Refer

to Figure 8 for images of the geometric shapes scene

and the car parking scene. The geometric shape scene

consists of multiple procedurally placed cylinders of

varying scale, position and rotation. We also vary the

surface of the cylinders using different albedo-color

and reﬂectivity values. The car parking scene consists

of ﬁve 3D-models of a car placed side-by-side. Us-

ing the synthetically rendered images, we perform an

extrinsic structured light calibration and summarize

our ﬁndings in Table 3. It shows that the rotational

error is relatively stable across different scenes, sug-

gesting that our method generalizes well for different

scenes. For all selected scenes, the translational error

Table 3: Calibration accuracy across different scenes.

Scene

Trans.

Error

Rot.

Error

[cm] [deg]

Baseline (White Wall) 0.36 0.35

Geometric Shapes 1.57 0.38

Parked Cars 1.57 0.37

and rotational error satisfy our accuracy constraints

of approximately 1 cm translational error and 1 de-

gree rotational error. Hence, our calibration method

yields satisfactory results for synthetically rendered

scenes, which may generalize to real-world applica-

tions as well.

5 CONCLUSION AND FUTURE

WORK

We have demonstrated the feasibility of a ﬂexible

extrinsic structured light calibration approach. Our

calibration setup consists of two time-synchronized

cameras with known camera parameters (both intrin-

sics and extrinsics) and a projector capable of pro-

jecting a monochrome circle pattern into the scene.

Our method sequentially projects a known circle pat-

tern from different relative distances into the scene

and then triangulates the 3D positions of the detected

circles. After deﬁning rays through the triangulated

3D points, the extrinsics of the projector are deter-

mined by calculating the intersection of these rays.

Our extensive evaluation shows that our approach

works with different projection surfaces and is rel-

atively stable towards different potentially negative

inﬂuences related to drop-out, circle detection, cali-

bration distances, etc.. Our implementation achieves

a rotational accuracy of below 1 degree and transla-

tional accuracy of approximately 1 cm. Our method

provides a calibration accuracy sufﬁcient for intelli-

gent vehicle lighting systems (Tamburo et al., 2014)

or applications with requirements for similar preci-

sion, such as smart lighting installations (Sonam and

Harshit, 2019) and stage-productions (Gillette and

McNamara, 2020). Contrary to alternative solutions,

our method does not rely on ﬁnding a homography be-

tween the projected calibration pattern, thus allowing

the ﬂexible extrinsic calibration of a structured light

projector on calibration surfaces that do not need to

be planar.

In the future, our approach could be generalized

to additionally estimate the intrinsics of a structured

light projector, as well as intrinsically and extrinsi-

cally calibrating the stereo-cameras themselves.

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

Figure 8: Simulated Geometric Shapes (left) and Parked Cars (right) test scenes.

ACKNOWLEDGEMENTS

This work was partly supported by the SmartPro-

tect project (no. 879642), which is funded through

the Austrian Research Promotion Agency (FFG) on

behalf of the Austrian Ministry of Climate Action

(BMK) via its Mobility of the Future funding pro-

gram.

The method described in this publication is

registered under the patent “Device and method

for calibrating a light projector” (AT523670A1 /

WO2021191121A1)

REFERENCES

Unity3D. https://unity.com/. Accessed: 2022-04-17.

An, Y., Bell, T., Li, B., Xu, J., and Zhang, S. (2016). Method

for large-range structured light system calibration. Ap-

plied optics, 55 33:9563–9572.

Chen, C., Gao, N., and Zhang, Z. (2018). Simple calibra-

tion method for dual-camera structured light system.

Journal of the European Optical Society-Rapid Publi-

cations, 14:1–11.

Chen, R., Xu, J., Chen, H., Su, J., Zhang, Z., and Chen,

K. (2016). Accurate calibration method for camera

and projector in fringe patterns measurement system.

Applied Optics, 55(16):4293–4300.

Garrido-Jurado, S., Mu

noz-Salinas, R., Madrid-Cuevas, F.,

and Mar

ın-Jim

enez, M. (2016). Simultaneous re-

construction and calibration for multi-view structured

light scanning. Journal of Visual Communication and

Image Representation, 39.

Gillette, J. M. and McNamara, M. J. (2020). Designing With

Light - An Introduction to Stage Lighting. Routledge.

Guo, Y., Yao, Y., and Di, X. (2006). Research on structural

parameter optimization of binocular vision measuring

system for parallel mechanism. In Proc. IEEE In-

ternational Conference on Mechatronics and Automa-

tion, pages 1131–1135.

Huang, B., Ozdemir, S., Tang, Y., Liao, C., and Ling, H.

(2018). A single-shot-per-pose camera-projector cal-

ibration system for imperfect planar targets. In IEEE

International Symposium on Mixed and Augmented

Reality Adjunct, pages 15–20.

Huynh, D. (2009). Metrics for 3d rotations: Comparison

and analysis. Journal of Mathematical Imaging and

Vision, 35:155–164.

Liu, J., Zhang, Y., and Li, Z. (2006). Selection of cameras

setup geometry parameters in binocular stereovision.

In Proc. IEEE Conference on Robotics, Automation

and Mechatronics, pages 1–6.

Megiddo, N. and Tamir, A. (1983). Finding least-distances

lines. Siam Journal on Algebraic and Discrete Meth-

ods, 4.

Packer, O., Diller, L. C., Verweij, J., Lee, B. B., Poko-

rny, J., Williams, D. R., Dacey, D. M., and Brainard,

D. H. (2001). Characterization and use of a digital

light projector for vision research. Vision Research,

41(4):427–439.

Pharr, M., Wenzel, J., and Humphreys, G. (2016). Physi-

cally Based Rendering: From Theory to Implementa-

tion. Morgan Kaufmann Publishers Inc., 3rd edition.

Redmon, J., Divvala, S., Girshick, R., and Farhadi, A.

(2016). You only look once: Uniﬁed, real-time ob-

ject detection. In Proc. IEEE conference on computer

vision and pattern recognition, pages 779–788.

Shahpaski, M., Sapaico, L. R., Chevassus, G., and

usstrunk, S. (2017). Simultaneous geometric and ra-

diometric calibration of a projector-camera pair. In

Proc. IEEE Conference on Computer Vision and Pat-

tern Recognition, pages 3596–3604.

Smith, A. R. (1983). The viewing transformation. Com-

puter Graphics Project, Computer Division, Lucas-

ﬁlm, Ltd. Technical Memo, (84).

Sonam, T. and Harshit, S. M. (2019). Smart lightning and

security system. In Proc. IEEE International Confer-

ence on Internet of Things: Smart Innovation and Us-

ages, pages 1–6.

Tamburo, R. J., Nurvitadhi, E., Chugh, A., Chen, M., Rowe,

A. G., Kanade, T., and Narasimhan, S. G. (2014). Pro-

grammable automotive headlights. In Proc. European

Conference on Computer Vision, pages 750–765.

Xu, Y., Zhao, Y., Wu, F., and Yang, K. (2013). Er-

ror analysis of calibration parameters estimation for

binocular stereo vision system. In Proc. IEEE Inter-

national Conference on Imaging Systems and Tech-

niques, pages 317–320.

Zhang, D. and Yau, S.-T. (2008). Absolute phase-assisted

three-dimensional data registration for a dual-camera

structured light system. Applied Optics, 47 17:3134–

42.

Zhang, Z. (2000). A ﬂexible new technique for camera cal-

ibration. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 22:1330–1334.

Flexible Extrinsic Structured Light Calibration Using Circles