Automatic Prediction of 3D Checkpoints for Technical Gesture Learning

in Virtual Environments

Noura Joudieh

1 a

, Djadja Jean Delest Djadja

2 b

, Ludovic Hamon

2 c

and S

ebastien George

2 d

Faculty of Sciences, Lebanese University, Hadat, Lebanon

LIUM, Le Mans University, Le Mans, France

Keywords:

Virtual Learning Environment, Gesture Learning- Evaluation Set up, 3D Checkpoints, Random Forest.

Abstract:

Nowadays, Virtual Learning Environments (VLE) dedicated to learning gestures are more and more used in

sports, surgery, and in every domain where accurate and complex technical skills are required. Indeed, one

can learn from the observation and imitation of a recorded task, performed by the teacher, through a 3D

virtual avatar. In addition, the student’s performance can be automatically compared to that of the teacher by

considering kinematic, dynamic, or geometric properties. The motions of the body parts or the manipulated

objects can be considered as a whole, or temporally and spatially decomposed into a set of ordered steps, to

make the learning process easier. In this context, CheckPoints (CPs) i.e. simple 3D shapes acting as “visible

landmarks”, with which a body part or an object must go through, can help in the deﬁnition of those steps.

However, manually setting CPs can be a tedious task especially when they are numerous. In this paper, we

propose a machine learning-based system that predicts the number and the 3D position of CPs, given some

demonstrations of the task to learn in the VLE. The underlying pipeline used two models: (a) the “window

model” predicts the temporal parts of the demonstrated motion that may hold a CP and (b) the “position model”

predicts the 3D position of the CP for each predicted part from (a). The pipeline is applied to three learning

activities: (i) glass manipulation (ii), geometric shapes drawing and (iii), a dilution process in biology. For

each activity, the F1-score is equal to or higher than 70% for the “window model”, while the Normalized Root

Mean Squared Error (NRMSE) is below 0.07 for the “position model”.

1 INTRODUCTION

Virtual Learning Environments (VLE) hold signiﬁ-

cant educational value as they can provide safe and

engaging learning situations (Adolf et al., 2019). The

effectiveness of learning mainly relies on the design

of appropriate sensory-multimodal feedback, bring-

ing pedagogical information to the learners in re-

sponse to their natural interactions (Liu et al., 2020).

Nowadays, those natural interactions are supported by

the democratization of motion capture interfaces and

therefore, VLE dedicated to the learning of motions

and technical gestures can be built. In sports, medical

domains, and all other domains requiring the mastery

of non-trivial gestures of the body parts and manip-

ulated objects, VLE offers simple and efﬁcient ped-

https://orcid.org/0000-0003-3142-2962

https://orcid.org/0000-0001-7923-0690

https://orcid.org/0000-0002-3036-0854

https://orcid.org/0000-0003-0812-0712

agogical means (Park et al., 2017; H

ulsmann et al.,

2018; Jeanne et al., 2017). One can, for example,

demonstrate the task to learn in the Virtual Environ-

ment (VE), according to an observation and imitation

strategy thanks to the visualization of 3D captured

motions (Le Naour et al., 2019; Djadja. et al., 2020).

As the perception abilities of the users (i.e. learn-

ers and teachers) can be challenged in the context of

quick or complex gestures, VLE can be enhanced by

some evaluation and assistance abilities with the au-

tomatic computation of geometric, kinematic, and dy-

namic features (Larboulette and Gibet, 2015; Fazeli

et al., 2018). From the recording process to the evalu-

ation and restitution part, the performed gestures can

be considered as a whole or decomposed in steps to

make easier the learning (Le Naour et al., 2019). In

this last case, we proposed a method that allows any

teacher to build an evaluation process, by making a

demonstration and using 3D Checkpoints (CPs) rep-

resenting those steps (Djadja. et al., 2020). CPs are

3D geometrical shapes (i.e. 3D rectangle or sphere),

Joudieh, N., Jean Delest Djadja, D., Hamon, L. and George, S.

Automatic Prediction of 3D Checkpoints for Technical Gesture Learning in Virtual Environments.

DOI: 10.5220/0011618100003417

In Proceedings of the 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 1: GRAPP, pages

39-51

ISBN: 978-989-758-634-7; ISSN: 2184-4321

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

placed by the teacher in VE, with which a body part or

a manipulated object must go through. The use of CPs

can be very valuable as: (i) the motions can be auto-

matically segmented from unwanted or noisy motions

performed before or after the task and (ii), each step

can be independently replayed and analyzed. How-

ever, it can be a tough job to create CPs and place

them in VLE depending on the complexity and the

accuracy of the task to learn.

Contribution: The core contribution of this work

relies on a method to automatically decompose the

gesture-based task to learn in VR, in temporal and

spatial steps, from demonstrations of the teacher. This

method was implemented through a system, using

Machine Learning (ML) tools, to predict the num-

ber of required CPs as well as their conﬁguration.

To achieve this goal, an architecture with two ML-

based models was designed. Given some motion ﬁles

of the same task to learn, the ﬁrst model uses a ran-

dom forest to predict the time windows, in the ﬁles,

where a collision may occur with a CP. A second ran-

dom forest gives, for each window, the 3D position

of the CP in the VLE. This architecture was tested

on three different learning activities: a glass manip-

ulation, a shape drawing task, and a dilution task in

biology with very good results in terms of prediction.

This method can be applied to any manual learning

task in VR, on any object or body part whose mo-

tions must be learned. However, its predictive perfor-

mances must still be studied in other contexts. One

will note that: (a) contributing to the machine learn-

ing theory ﬁeld is out of the scope of this paper and (b)

this paper does not focus on the interest of decompos-

ing a gesture-based task to make easier its teaching

and learning in VR, as it was studied in our previous

works (Djadja. et al., 2020; Le Naour et al., 2019).

The remainder of this paper is organized as fol-

lows. Section 2 gives an overview of related work fo-

cusing on VLE dedicated to the learning of technical

gestures, from the point of view of the evaluation pro-

cess and its building. Section 3 delves deeper into the

methodology by presenting the learning activities, the

system architecture, and the two ML models. Section

4 focuses on the data-generating process, the applica-

tion of the pipeline for each of the three activities, and

the results. Section 5 discusses the results and current

ﬁndings and section 6 concludes the paper and gives

directions for future work.

2 RELATED WORK

Thanks to the democratization of Virtual Reality (VR)

and motion capture technologies, several domains can

beneﬁt from VLE to assist users in learning and evalu-

ating their motions (de Morais and Wickstr

om, 2011;

Chiang et al., 2018; Sror et al., 2019). For exam-

ple, (Swee et al., 2017) proposed a VR application

for post-stroke rehabilitation. A Microsoft Kinect and

Leap Motion sensor were used to strengthen hand

muscles, improve ﬁnger motor dysfunctions, post-

stroke balance skills, and walking through: (1) a pick

and place activity and (2), a balance & movement

rehabilitation training. Users are mainly evaluated

through time measurement over trials in addition to

task completion. In a simulation for learning carpen-

try, learners’ performances were evaluated through

a comparison between the curves of their skills and

those of the experts (Jose et al., 2016). The sys-

tem recorded the user’s activity (e.g. position of the

working tool, downward pressure, number of broken

blades) and calculated metrics (e.g. straightness of the

cut, its speed, downwards force, cut mark deviation,

angular inclination, the time needed). For learning

manual assembly, (Pilati et al., 2020; Rold

an et al.,

2019) proposed a training system that can assist op-

erators involved in such gesture-based procedures in

real-time. Experts executed consecutive sequences

of actions for the assembly of objects in various sit-

uations. Then the systems memorized all these se-

quences to verify that the learners’ movements were

correctly executed through various methods such as

the use of ”Control Volumes (CVs)” i.e. a pre-deﬁned

geometrical shape to check if the body joints ”enters

into”/”exits from” it.

The gesture or motion evaluation is a contextual

dependent task that is still hard to deﬁne i.e. de-

pending on the ﬁnal purpose of the performed mo-

tion, the pedagogical strategy, the observations needs,

etc. (Djadja. et al., 2020). In addition, the evalua-

tion can be done by observing whether the object or

body part respects an ordered (or not) set of action

sequences. For instance, (L

ecuyer et al., 2020) pro-

posed an editor allowing the visual representation of

action sequences in terms of VR scenarios. The action

sequences were extracted from the expert demonstra-

tion using #FIVE (Bouville et al., 2015) and #SEVEN

(Claude et al., 2014) (cited by (L

ecuyer et al., 2020))

models. #FIVE is an object-relation model to rep-

resent interactions based on four main concepts: ob-

jects, types, relations, and object patterns. Objects are

enriched with types to make them interactive and the

relations use those types to perform the interaction.

#SEVEN uses a Petri net to represent the sequenced

scenario: the places indicate the states of the scenario

and the transitions are triggered by changes in the en-

vironment. The expert was able to edit the sequence

on demand to have a more complex one for instance.

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

The work of (L

ecuyer et al., 2020) was used for the

learning of the preparation procedures of a room be-

fore surgery. Unfortunately, the underlying motions

of the user leading to the object manipulations are not

evaluated, resulting in a loss of information for pro-

fessional gesture learning.

When the movement is considered as a time series

made of position and orientation of body joints or ma-

nipulated objects, several approaches could be used

such as the observation and imitation of 3D avatars.

For example, (Kora et al., 2015) developed a golf

learning support environment where the learner can

mimic and practice golf swing. They used Microsoft

Kinect to record, save and replay learner’s body data,

displayed with the expert one, simultaneously super-

imposed in real-time. Although widely used, this

method suffers from the problem of temporal and

spatial synchronization of both motions. (Le Naour

et al., 2019) performed a deep review of the beneﬁts

of 3D model observation for motion learning. They

compared different visualization techniques using the

learner’s virtual avatar and that of the teacher (e.g. su-

perimposed or not; both concurrently played or not,

played during the task or after). The task was the

throwing of a rugby ball and they highlighted the ben-

eﬁts of a superimposed approach. In addition, a new

metric to measure the spatial regularity of the motion,

based on the Dynamic Time Warping (DTW) algo-

rithm was produced. Using 3D virtual avatars for mo-

tion learning is strongly related to the perception abil-

ities of users that can be challenged with complex, ac-

curate, and/or quick gestures. Therefore, some stud-

ies such as those of (Morel, 2017), deeply investigated

the use of an automatic evaluation based on DTW

techniques. They also automatically displayed spatial

and temporal errors with visual colors on the joints

to assist students in learning a tennis serve and karate

motions (Morel et al., 2017). However other metrics

can be considered to evaluate gestures.

Motions can be evaluated using kinematic, dy-

namic, and/or geometric metrics. (Larboulette and

Gibet, 2015) made an overview of those descriptors

representing the expressiveness of motions, accord-

ing to the three previously cited kinds considered as

“low-level” descriptors. They also identiﬁed “high-

level” ones, computed from ”low-level” metrics, and

classiﬁed them into four categories (i.e. body, space,

shape, effort). They represent “kinematic, spatial or

physical quantities that can give rise to an interpre-

tation by movement experts”. (Kico and Liarokapis,

2020) proposed a mobile Augmented Reality (AR)

application for assisting the process of learning folk

dance. 37 passive markers were used to capture body

motions to: (i) analyze for each joint, the angle be-

tween quaternions in two successive frames that are

saved in a vector, (ii) create, from this vector, an-

other vector that contains a score for each joint, by

comparing the learner’s and teacher’s motions using

DTW and (iii), get the total score as the mean value

of all values calculated, for the joints, by using the

previous vector. Contextual metrics had also been

used in the context of gait analysis of patients (Jarchi

et al., 2018). For instance, step length, stance du-

ration, lateral foot position, walk ratio, swing dura-

tion, etc., helped doctors to differentiate the precise

gait characteristics of normal healthy subjects, from

those of people with pathologies causing gait disor-

ders. There is a variety of metrics that can help users

in evaluating their movements. Among them, kine-

matic and geometric metrics (e.g. velocity, acceler-

ation, bounding box/space) are easily calculable and

convertible into high-level descriptors to get the ap-

propriate multimodal feedback in VLE (Larboulette

and Gibet, 2015). However, by often spatially and

temporally analyzing the motion as a whole, the user

can miss some steps of a complex motion to learn.

There is a diversity of evaluation metrics, and once

they have been chosen, their thresholds/acceptance

intervals must be deﬁned which can be a hard task.

For example, in a virtual training system for physi-

cal therapy, (Wei et al., 2015) used Bayesian Deci-

sion Theory to deﬁne a threshold for a metric named

”the accuracy of the users”. However, this method

is not fully automated, indeed, the experts must con-

struct a database made of users’ motions with their

performance score computed from the expert evalu-

ation and the DTW score. To avoid these kinds of

issues, several works used Machine Learning (ML)

for motion evaluation in a learning context (see the

second to last paragraph of this section). Moreover,

VLEs dedicated to the learning of motions have other

shortcomings such as: (a) not considering the gestures

as a time series made of geometrical data composed

of clear and observable temporal and spatial steps and

(b), the lack of editing and adaptation abilities regard-

ing the task to learn. Indeed, in a VLE, the teacher

usually cannot: (i) create their own demonstration be-

ing the comparison and guidance point of the task (b),

choose objects/artefacts that must be observed, and

(c), deﬁne their steps and metrics for the evaluation.

To counterbalance these issues, we introduced a

framework called MEVEL that can import any built

VLEs, made with Unity Engine, with the aim of in-

corporating a set of ordered CheckPoints (CPs) as

3D visible geometrical shapes (i.e. 3D rectangle or

sphere) (Djadja. et al., 2020). Within the VLE, the

teacher can place, rotate and size three kinds of CPs

(Djadja. et al., 2020): Starting CheckPoint (SCP),

Automatic Prediction of 3D Checkpoints for Technical Gesture Learning in Virtual Environments

Intermediate CheckPoints (ICP), and Ending Check-

Points (ECP). The SCP and ECP were used to state

the beginning and end of the motion, whereas the ICP

were numbered CPs representing each sub-step of the

gesture-based task to learn. Beforehand, the teacher

chose an Object of Interest (OI) i.e. the virtual object

or the part of the user body from which the motion

must be studied and go through the CPs. The teacher

made a demonstration of the task that can be replayed,

step by step at will, and used to make some compar-

isons. A complex task being composed of several

steps and each step requiring an ICP, it can be hard

for the teacher to create those CPs and place them in

the VLE, even with a natural interaction as the one

proposed by (Dimmel and Bock, 2017). A ﬁrst idea is

to use ML to automate the creation of ICPs given the

features of the gestures to learn in accordance with the

observation needs.

Furthermore, in the context of learning gestures,

ML has been used with efﬁciency for different pur-

poses. (Brock and Ohgi, 2017) designed a system

for the automatic recognition of ﬂight-style errors in

ski jumping. They positioned inertial sensors to mea-

sure the motion of all necessary limbs. A set of mo-

tions was annotated by an expert, and transformed

into a set of features (e.g. mean, variance, skewness

of data points on the same dimension, acceleration,

and angular velocities). A Support-Vector Machine

(SVM) was trained with the labeled motion captures.

The average accuracy of the error recognition, rating

between 60 and 75%, indicated the applicability of

the system. Moving to the medical ﬁeld, (Winkler-

Schwartz et al., 2019) used ML to classify the surgical

expertise of participants when performing a resection

of a neurosurgical tumor. The raw data extracted from

each trial were transformed into 270 metrics (e.g. ve-

locity, acceleration, and jerk of the instrument, the

rate of change in volume of the tumor). Finally, they

tested four different algorithms for which a set of fea-

tures was selected for each by an iterative process. An

accuracy of 90% was achieved using six performance

features by k-Nearest Neighbor (K-NN). (D’Amato

et al., 2020) collected motion capture data from vio-

lin exercises to train a Random Forest (RF). The level

of skills of violin players (i.e. novice or expert) were

classiﬁed. A 10s time window parsed the data and

is converted to a set of features including the mean,

the signal-pair correlation, and the signal magnitude

area for both the time and frequency domain. Us-

ing two different scenarios, RF attained an average

of 77%, 71%, and 63% for respectively the accuracy,

precision, and recall. In a learning situation on how

to troubleshoot a surgical robot, (Moore et al., 2020)

employed an SVM to predict which group (i.e. low

learning or high learning) each participant belongs to,

based on the linear and angular velocities of the Head-

Mounted Display (HMD) and controllers. They ex-

plored the Principal Component Analysis (PCA) and

the convex matrix factorizations for the feature rep-

resentations. Their results showed that the velocities

of the HMD and controllers yielded a high mean ac-

curacy for both the training (85.7%) and testing data

(93.1%).

The aforementioned examples of studies give con-

crete hopes in terms of automatic evaluation of the

learner’s progression, skills, or level. However, to

our knowledge, none of them used ML with mo-

tion capture data to predict the steps of a gesture to

learn, represented by a set of 3D virtual checkpoints.

Consequently, this work focuses on a methodological

proposal to automatically predict, from task demon-

strations, the number of required ICPs as well as

their probable positions in the VLE, using a machine

learning-based architecture. Note that, only ICPs are

considered here, the SCP and ECP being manually

placed, to automatically segment in time and space

the motion (Djadja. et al., 2020). Indeed, in multi-

ple cases, SCP and ECP usually correspond to well-

identiﬁed and simple actions leading to collision or

event detection (e.g. taking/releasing a speciﬁc tool

or object).

3 METHODOLOGY

In this section, the overall methodology is described

and consists in building an architecture aiming at two

goals given some motions of the task to learn: (i)

predicting all the steps of the task by guessing the

number of required ICPs and (ii), estimating, for each

ICP, the 3D position in the VLE. After describing the

three learning activities considered in this study, and

the structure of the raw captured data, we present, for

each goal, the considered input and output data from

which the problem is formalized from the ML per-

spective. The choice of the appropriate ML algorithm

and its main parameters are given from the results of

a cross-validation process.

3.1 Learning Activities

Following the novelty of the problem and the method

to solve it, two simple learning activities are tested

to give some insights into the method’s validity.

Afterward, we applied it to two steps of a real

practical case in biology. Figure 1 presents all the

pictures of the considered activities.

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

(a) Glass manipulation task (b) Dilution task - step 1 (c) Dilution task - step 2

(d) 3-sided polygon task (e) 4-sided polygon task (f) 5-sided polygon task

Figure 1: Examples of the considered tasks in VLE.

- Glass Manipulation: The goal is to hold the glass

containing a ball, drop the ball in the container, turn

the glass, and put it in the deposit area (ﬁgure 1a).

This activity is made of one ICP and used as a “toy

problem” in the context of manipulating an object.

- Geometrical Shape Drawing: The learner must

draw, with one hand the exact shape of 3-sided,

4-sided, and 5-sided polygons demonstrated by the

teacher (ﬁgure 1d, e, f). This task was chosen to

increase the number of ICPs (i.e. as many as the

number of sides) and illustrate steps not detectable

by trivial collisions between 3D objects.

- Dilution: Dilution is the action of adding a liquid

to decrease the concentration of a solution. This task

requires several phases following a strict protocol

in case of dangerous solutions. Among them, we

will focus on two phases. Phase 1: (a) taking the

test tube containing the solution (b), homogenizing

it (c), sterilizing its opening after opening it, and

(d), putting it in its place after closing it. Phase

2: (a) taking the test tube containing the liquid

(b), sterilizing its opening after opening it, and (c),

putting it in its place after closing it. Phases 1 and 2

respectively require 2 and 1 ICP(s) (ﬁgure 1b, c).

3.2 System Architecture

For predicting the number and the conﬁguration of

ICPs, the proposed architecture requires taking the

motion ﬁles of a task demonstration as an input and

outputs 4 targets: the number of required ICPs, and

their 3D positions i.e. Px, Py, Pz. For this ﬁrst study,

the orientation and dimension of the ICP are not yet

considered (see the last paragraph of section 5 for this

non-trivial problem). The problem can be separated

into two modules for each step. The ﬁrst step is to

predict all time windows in the motion ﬁle that may

hold an ICP, while the second step is to estimate the

3D position of the ICP given all the data contained in

each time window (ﬁgure 2).

Apply Window Model

Apply Position Model

Local Motion File of OI Predicted window with ICP

Predicted Windows with ICP

Predicted Number of ICP

3D Position of ICP(s)

Figure 2: Pipeline for the system architecture.

3.3 Raw Data Structure and Time

Window

A recorded demonstration of a task by the teacher

consists of saving in a ﬁle: (a) the 3D positions of

Automatic Prediction of 3D Checkpoints for Technical Gesture Learning in Virtual Environments

the Object of Interest (OI) taken in reference to the

local coordinate system placed at the SCP (Djadja.

et al., 2020) and (b), the collision of the OI with the

CPs, manually placed beforehand by the teacher in

the VLE. A motion ﬁle has the structure seen in Ta-

ble 1. The ”CPType” speciﬁes the type of checkpoint

(”SCP”, ”ICP”, ”ECP” or ”None” if there is no col-

lision) that the OI may collide with, at each recorded

time ”t”. The data used to build the training and test

sets are made of data points between the SCP and the

ECP, these two kinds of CP(s) are considered as given

in any case. The term ”frame” represents ”one data

point” made of the 3D position Px, Py, Pz of the OI,

and the value of the ”CPType” ﬁeld. A ”time win-

dow” is used to parse motion and get a subset of ”w”

consecutive frames in time, ”w” being its size.

Table 1: Data structure of a motion ﬁle.

Px Py Pz Time CPType

3.4 Time Window Prediction Module

For the ﬁrst step, given the motion ﬁles of an OI, we

try to predict which parts of the motion can hold an

ICP. The time window parses the motion ﬁle every

”w” frames (Figure 3) and we check, for each ”win-

dow”, if it can hold an ICP, or not, thanks to an ML-

based model. ”holding/containing an ICP” means that

the OI collides with an ICP at any of the data points

belonging to the time window.

Figure 3: Example of dividing data into time windows with

size 3.

3.4.1 Input/Output Data and Problem

Formalization

Each window is converted to a row of features made

of the mean of kinematic metrics (Larboulette and

Gibet, 2015): velocity (vel), acceleration (acc), cur-

vature (curve), and jerk (table 2). These inputs of the

ML model were selected for their wide use in motion

analysis (Vabalas et al., 2020; Kacem et al., 2018;

Kapur et al., 2005) (also see section 2 paragraphs 4

and 7). The binary label ”Has ICP” is the output of

the model that states whether a window contains an

ICP (value 1) or not (value 0). A training ﬁle with

rows of feature vectors coming from all motion ﬁles

is constructed after the application of Savitzky Golay

ﬁlter

to remove the noise due to an unstable frame

rate (Savitzky and Golay, 1964; Schafer, 2011). The

inputs are normalized by the mean. Therefore, this

is a usual supervised classiﬁcation problem with 4

inputs and a binary output.

Table 2: Structure of training dataset for the window model.

Mean Vel Mean Acc Mean Curv Mean Jerk Has ICP

3.4.2 ML Algorithm Choice and

Cross-Validation

The input data are used to train and test a Random

Forest Classiﬁer (RFC) (Breiman, 2001) with 200

trees, where the inputs are the ﬁrst 4 features men-

tioned in the previous section and the output is the bi-

nary ”Has ICP” feature. The RFC was chosen as fol-

lows. Among the existing classiﬁcation ML models,

the appropriate one for our case must have suitability

with motion data, good performances with both large

and especially small datasets. Indeed, the availabil-

ity of a large number of motion ﬁles from a learning

activity is not guaranteed as these data are provided

by the teachers through their demonstrations (see the

fourth paragraph of section 5 for more details).

A comparison of seven different supervised ML

classiﬁcation algorithms namely: Decision Tree, Ran-

dom Forest (RF), Na

ıve Bayes (NB), SVM, Neu-

ral Networks (Perceptron), JRip, and Decision Table

done by (Akinsola, 2017) concluded that RF, SVM,

and Na

ıve Bayes can offer high accuracy and preci-

sion regardless of the number of attributes, and the

number of records in the dataset. They applied these

algorithms on the same dataset while changing its

number of attributes and number of instances, thus

testing with a large dataset and a small one. Based

on this comparison, we limited the choice of the algo-

rithm to either RFC, SVM, or NB.

To further select one ﬁnal machine learning

model, ﬁve-fold cross-validation was performed on

each using all the motion ﬁles of the training set col-

lected for each activity. The performance of each with

every fold is evaluated using the F1 metric. The de-

fault hyperparameters were used for each model.

RFC was chosen as it ranked ﬁrst with the highest

F1 score for the three learning activities (table 3). In

the process, several numbers of trees were tested but

all were not presented as: (i) signiﬁcant results but

not satisfying ones were obtained from 100 trees (ii),

200 gave satisfying ones, and (iii) a signiﬁcant dif-

ference was not observed above 200 trees. Multiple

values (10, 15, 25,...60, 90) for the size of the win-

A polyorder of 2 and a window size 25 were used as

usual parameters in this context

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

Table 3: Model selection for the time window prediction.

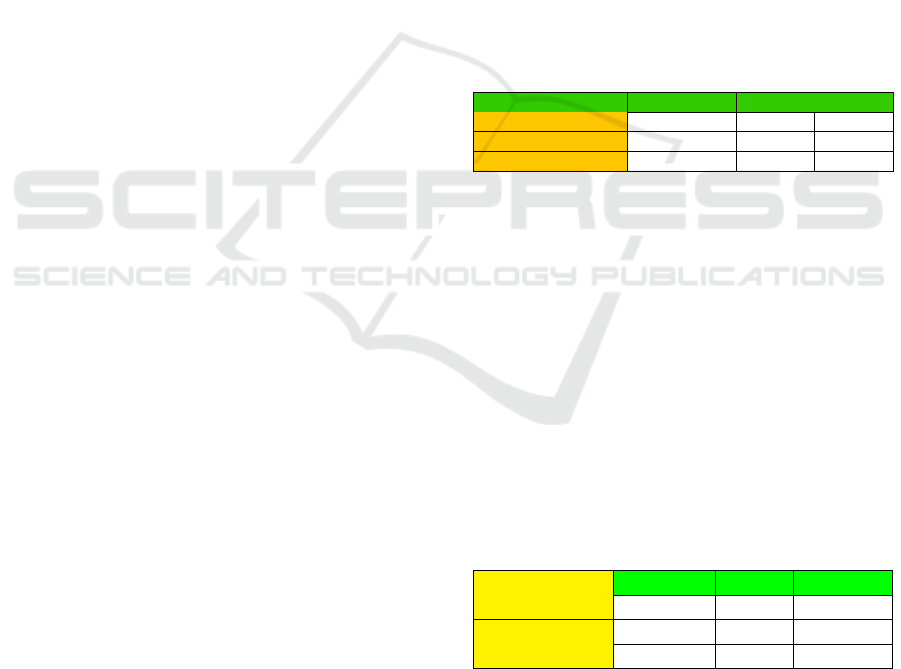
Learning Activity Window Size ML Model F1

Glass Manipulation 60

RFC 0.707

SVM 0.66

ıve Bayes 0.62

Shapes Drawing 30

RFC 0.63

SVM 0.6

ıve Bayes 0.32

Dilution 60

RFC 0.67

SVM 0.51

ıve Bayes 0.41

dow were also tested for each learning activity, the

size was chosen relative to what achieves a balance

between the accuracy of the model and the size of the

motion ﬁles.

3.5 3 D Positions Estimation Module

The ﬁrst part of the work predicts, for a given motion

ﬁle, the possible time windows that may hold an ICP.

The second step aims to estimate the ICP 3D position

for each predicted time window.

3.5.1 Input/Output Data and Problem

Formalization

The ﬁrst step can generate false positives that must be

avoided. Therefore, to generate the training samples

for this second step, we take the time windows con-

taining the ICPs directly from the dataset, following

the parsing method described in the ﬁrst paragraph of

section 3.4. Each window is converted to a row of

kinematic features (i.e. velocity/acceleration mean)

and geometrical ones (i.e. the maximum/minimum

of each component of the position acting as bound-

ing volume around the ICP position) considering their

good performances in the literature (Vabalas et al.,

2020; Kacem et al., 2018; Kapur et al., 2005) (also

see section 2, paragraphs 4 and 7). The data contained

in the generated training ﬁle were normalized by the

mean before training. The problem becomes a regres-

sion problem of 8 input features and 3 output features

(3D Position of the ICP) (Table 4).

Table 4: Features of the training dataset for the position

model.

Mean Vel Mean Acc Max px Max py

Max pz Min px Min py Min pz

ICP px ICP py ICP pz

3.5.2 ML Algorithm Choice and

Cross-Validation

The best model must perform well with small datasets

and be suitable for this kind of data. A Random For-

est Regressor (RFR) is the ﬁrst candidate, as it works

well for motion analysis (Baoxing and Bo, 2018). To

approve its suitability with our training data, we per-

formed a cross-validation to compare RFR with Sup-

port Vector Regressor (SVR) that was also reported

to be a strong regression model (Izonin et al., 2021;

Giarmatzis et al., 2020; Thomas et al., 2017). The de-

fault hyper-parameters were also used for each model.

Note that RFR supports multiple outputs, while SVR

does not. Therefore, a Multi-Output Regressor (Bor-

chani et al., 2015) was used with SVR as a kernel. The

two candidate models were evaluated using the Root

Mean Squared Error (RMSE). RFR with 200 trees at-

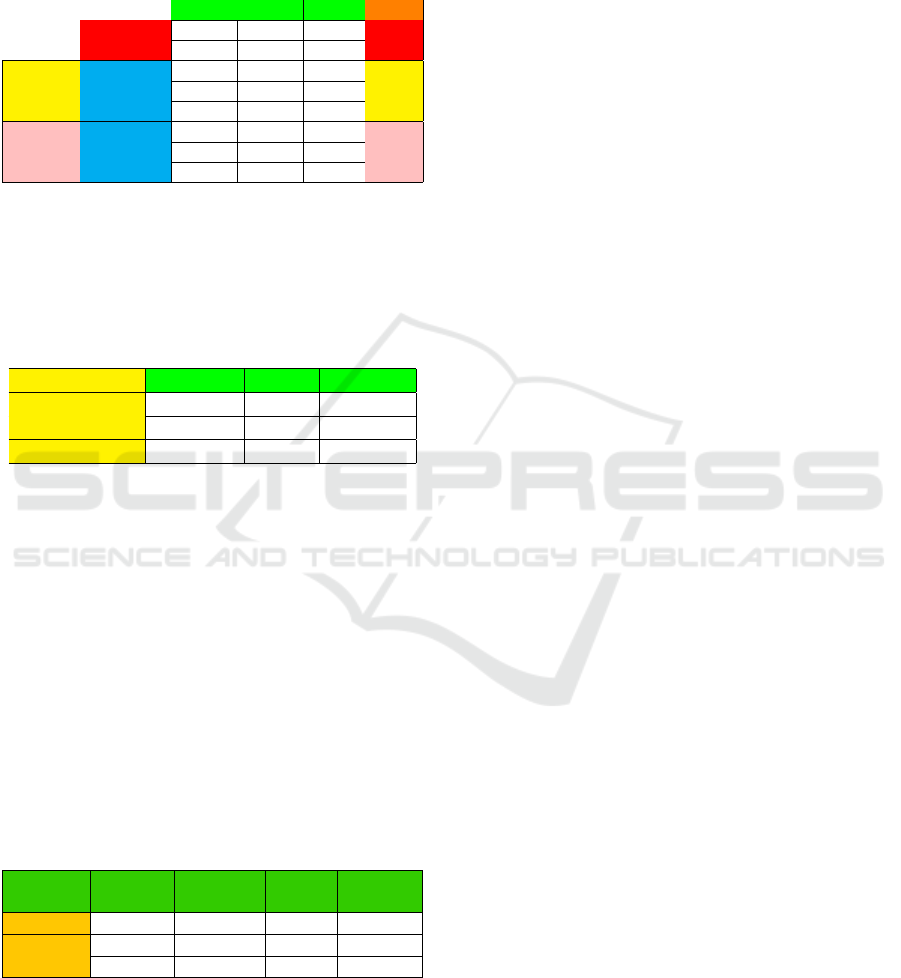
Table 5: Model selection for the position prediction.

Learning Activity Window Size ML Model RMSE

Glass Manipulation 60

RFR 0.06

SVR 0.1

Shapes Drawing 30

RFR 0.07

SVR 0.09

Dilution 60

RFR 0.008

SVR 0.06

tained lower RMSE than SVR for the three learning

activities, thus it was chosen to be the core of the po-

sition model (Table 5). Other numbers of trees were

tested but they did not give better results above 200 or

satisfying results under 200. As for the window size,

the ﬁnal decision was achieved in a similar fashion to

the time window model.

4 IMPLEMENTATION AND

RESULTS

The proposed architecture is applied to the three

learning activities. In this section, details about the

dataset generated for each activity are given, as well

as the application method and the results obtained

once the models are trained and tested.

4.1 Training and Test Sets

The data collected is a set of demonstrations for

each activity. To generate enough variability, several

different conﬁgurations are deﬁned for each task to

learn. A conﬁguration represents the positions of the

3D objects of the VLE and the placement of CPs. For

each conﬁguration, we make several demonstrations.

For each learning activity, the OI, the ICPs, and the

number of conﬁgurations and demonstrations are de-

scribed

Click here for the collected data, video of the three

activities, predicted ICPs and conﬁguration examples

Automatic Prediction of 3D Checkpoints for Technical Gesture Learning in Virtual Environments

- Glass Manipulation: OI was the glass. One ICP

was used close to the container. 10 conﬁgurations

were set and an average of 10 demonstrations were

generated for each conﬁguration, to end up with 106

demonstrations.

- Shapes Drawing: The OI is the right hand. The

number of ICPs varied among 1, 2, and 3 ICPs to

draw 3, 4, and 5-sided polygons respectively. 115

demonstrations were done per conﬁguration to end

up with 345 motion ﬁles.

- Dilution: Two conﬁgurations were set (one conﬁgu-

ration for each phase described in section 3.1) and 100

demonstrations were done for each conﬁguration. For

the ﬁrst conﬁguration, the OI is the ﬁrst test tube hav-

ing the solution. Two ICPs are used: one close to the

homogenizing device and one close to the heating de-

vice for sterilizing. For the second conﬁguration, the

OI is the test tube holding the diluted solution. One

ICP is used close to the heating device for sterilizing.

A total of 200 motion ﬁles were recorded.

The dataset was divided into a training set (80% of the

data) and a test set (20% of the data).

4.2 Implementation and Evaluation

Strategy

All the architecture was coded using python language

with the scikit-learn library. Given a chosen window

size “w”, for each learning activity, we trained one

window model and one position model. The training

process and test one were run with the same window

size. The scripts were run on an Intel(R) Core(TM)

i7-7500U laptop with 8GB RAM. The VLE was made

using Unity 2019.4.19f1 and the headset used is the

HTC Vive Pro. Multiple window sizes were tested

and only the results for three speciﬁc values, i.e. 20,

30, and 60, are presented. These values were chosen

to show the main tendencies, while knowing that no

better results were obtained above those values, when

applicable, given the maximum number of frames of

all motion ﬁles in each learning scenario (see the sec-

ond paragraph of section 5 for a discussion on the au-

tomation in getting the best window size).

For the training and test phases of the window

model, the ﬁles were parsed according to the parsing

method described in the ﬁrst paragraph of section 3.4.

On each time window, the feature vector, described

in the same section, was computed and normalized

by the mean before giving it to the window model.

To measure the performance of the window model for

each activity, F1-score was used as this model repre-

sents a solution to a classiﬁcation problem.

For training and testing the position model, we

took all the time windows holding an ICP in the ﬁles

(cf. section 3.5.1), computed the feature vector, and

normalized them. The NRMSE evaluates the accu-

racy of the position model as a regression problem. It

represents the Normalized Root Mean Squared Error

(Naser and Alavi, 2020), which can be used to com-

pare the results from datasets with different ranges of

values, as we have three different activities.

4.3 Training

The results of the training process are brieﬂy summa-

rized for each learning activity through the considered

evaluation metrics described in section 4.2. The train-

ing process takes around 1 minute for each learning

activity and table 6 depicts very good results, in terms

of model convergence, both for the window model

F1-score, and the position model NRMSE.

Table 6: Results of the training process for position and

window models.

Learning Activity Window Size NRMSE F1 Score

Glass Manipulation 60 0.04 99%

Shapes Drawing 30 0.02 99%

Dilution 60 0.02 99%

4.4 Validation

The results of the evaluation process obtained from

the application of the models on the test data are pre-

sented and analyzed.

4.4.1 Time Window Model

For the glass manipulation activity, there were 21

ICPs in total for all the test ﬁles (one ICP for each

ﬁle). Applying the window model for a window size

equal to 20, 30, and 60 gave the results of table 7, with

a best score for value 60.

Table 7: Accuracy metrics of the window model applied on

the glass manipulation activity with different window sizes.

Window Size Precision Recall F1 Score

20 59% 67% 61%

30 43% 48% 44%

60 71% 76% 72%

In the shape drawing activity, the results are pre-

sented for each conﬁguration separately (i.e. with 1,2

and 3 ICP(s)) and considering all the demonstrations

(around 60 test ﬁles) no matter what the conﬁgura-

tions are. After applying the window model for val-

ues 20 and 30, a window size equal to 30 has the best

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

results (72% for f1-score). 60 is not applicable for

this activity because it is larger than the size of some

motion ﬁles. The results are shown in table 8.

Table 8: Accuracy metrics of the window model applied on

the shape drawing activity with different window sizes.

1 ICP 2 ICP 3 ICP Total

Test Files 21 18 20 59

ICP 21 36 60 117

window Precision 62% 89% 91% 81%

size Recall 71% 64% 63% 66%

20 F1-Score 65% 72% 71% 69%

window Precision 71% 62% 91% 75%

size Recall 86% 64% 77% 76%

30 F1-Score 76% 60% 81% 72%

For the dilution activity, the window model is ap-

plied with three different window sizes on 40 test

ﬁles. The results show that 60 is the best window size

for this activity (see table 9).

Table 9: Accuracy metrics of the window model applied on

the dilution activity with different window sizes.

Window Size Precision Recall F1 Score

20 42% 31% 35%

30 54% 47% 48%

60 73% 70% 69%

4.4.2 Position Model

For the glass manipulation activity, a window size

equal to 60 is chosen for the position model. From the

21 test ﬁles, the 21 time windows having an ICP were

selected and given to the position model to predict,

for each time window, the 3D position of ICP. Simi-

larly, for the shape drawing activity, the same test ﬁles

of the window model are used for the position model

with the selected window size 30 to get 117 time win-

dows. As for the dilution activity, a window size equal

to 60 is chosen for the position model leading to the

extraction of 60 time windows. Applying the position

model, gave the results provided in table 10.

Table 10: Accuracy metrics of the position model.

Learning

Activity

Window

Size

Test

Windows

RMSE NRMSE

Glass 60 21 0.02 0.07

Shapes 30 117 0.06 0.05

Dilution 60 60 0.006 0.03

4.5 Application in VLE

To have a concrete idea of the prediction quality in

VLE, ﬁgures (4a), (4b) and (4c) show an example of

a conﬁguration for the glass manipulation task with

ICPs manually placed, predicted by our models and

both superimposed respectively. In the same way, ﬁg-

ures (4d), (4e) and (4f) show an example for the ge-

ometrical shape drawing task while ﬁgures (4g), (4h)

and (4i) are dedicated to an example for the dilution

task. The predicted ICPs are green and the other blue

CPs are SCP/ECP or manually placed ICPs for the

comparison with the predicted ones. The ICPs orien-

tation and size were manually reproduced in ﬁgure 4

(see the last paragraph of the next section for more

explanation).

5 DISCUSSION

We obtained an F1-score equal to or higher than 70%

for the window model regardless of the learning ac-

tivity and an NRMSE equal to or under 0.07 in any

case. Those values are more than acceptable. The

proposed method seems to work with efﬁciency in

terms of model convergence and testing in the con-

text of the proposed tasks. However, those promising

results must be tempered considering their dependen-

cies to the window size that must be tuned according

to the motion ﬁle size.

The automation of the choice of window size

could be performed through a cross-validation pro-

cess. Such a strategy is not trivial as, for the same

task, the motion ﬁles can have very different numbers

of frames. A heuristic could be stated considering the

minimum, the maximum, the average, etc., number

of frames. Beforehand, a complementary idea con-

sists in rebuilding each ﬁle with the same number of

frames, through an interpolation process rebuilding

each frame, taking the risk to lose the natural and re-

alistic aspect of the motion.

Regarding the training phase, the data used to train

the position model came from the motion ﬁles com-

bined with the parsing method described in the begin-

ning of section 3.4, as the window model can return

false positives and miss some ICP(s) (i.e. false neg-

atives). The window model is supposed to give time

windows where the ICP can be, without giving the ex-

act position (or frame index) in this set of data points.

Considering this last point, one can think that the po-

sition model must be trained with data representing

all the possible positions of the ICP in this set. For

instance, if the window size is 3, then the ICP can be

in 3 possible windows, i.e. positioned at the last data

point for the ﬁrst window, at the center for the second

one, and at the ﬁrst data point for the third one (see

Figure 5). In case of unsatisfactory results of the posi-

tion model, this strategy could be considered and can

Automatic Prediction of 3D Checkpoints for Technical Gesture Learning in Virtual Environments

(a) Glass manipulation task - ICPs man-

ually placed

(b) Glass manipulation task - ICPs pre-

dicted

ually placed & predicted

(d) Geometrical shape drawing task -

ICPs manually placed

(e) Geometrical shape drawing task -

ICPs predicted

(f) Geometrical shape drawing task -

ICPs manually placed & predicted

(g) Dilution task - ICPs manually

placed

(h) Dilution task - ICPs predicted (i) Dilution task - ICPs manually placed

& predicted

Figure 4: Some examples of CPs and their ICPs predictions.

Figure 5: Example of considering all the possible positions

of the time window around two ICPs with a window size

equal to 3.

contribute, at the same time, to increasing the sam-

ple number, partially tackling the problem of having

enough samples from a few demonstrations.

Indeed, our proposal can be usable by a teacher

depending on the minimum number of required

demonstrations. We cannot ask them to perform 200

demonstrations for example. Obviously, this is a hard

question depending on many factors (i.e. domain,

task to learn, ergonomics, usability of the VLE, etc.).

However, we can have some insights for the three con-

sidered activities i.e. by studying the evolution of the

window and position model performances with the in-

crease of the percentage of data used for training (as

seen in ﬁgures 6 and 7). The motion ﬁles collected

for each activity are divided into [training, test] sets,

with [70, 36], [270, 78], and [150,50] for the glass,

drawing shapes, and dilution tasks respectively. As

the graphs show, 70% of training data gives satisfying

metric scores for the three activities. Table 11 shows

for each activity how the ”70%” of motion ﬁles are di-

vided among ﬁles having 1, 2 or 3 ICP(s). From this,

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

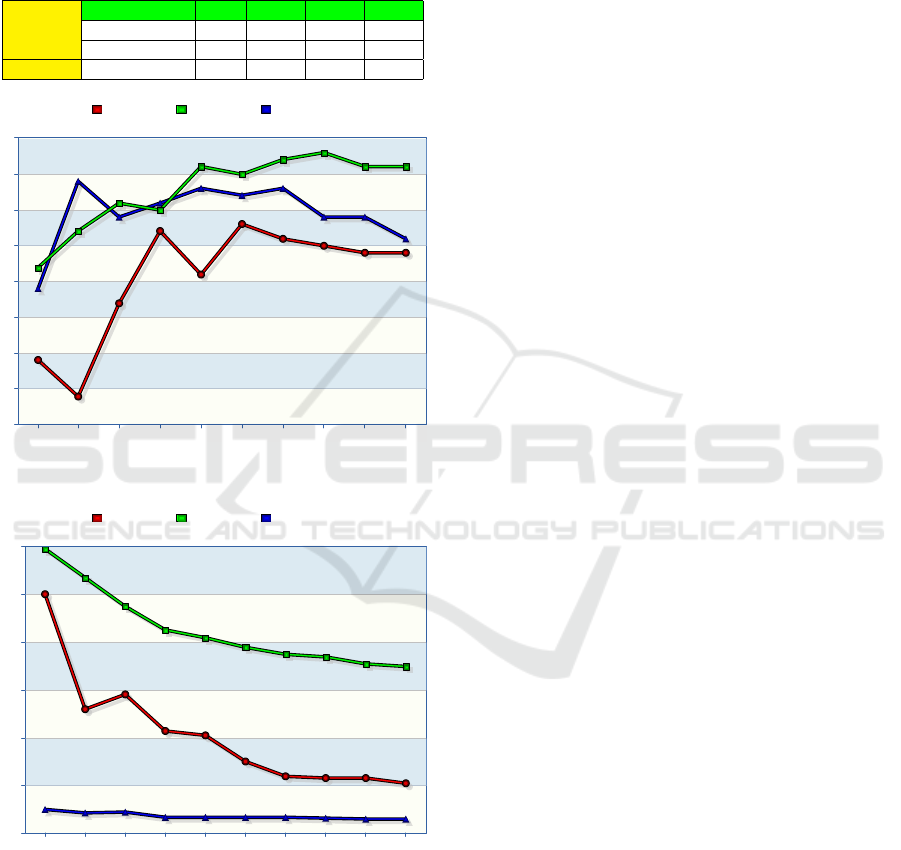
it seems that the minimum number of training motion

ﬁles required for each number of ICP ranges between

50 and 65. However, this point must be further inves-

tigated before making any conclusions.

Table 11: Minimum number of motion ﬁles needed for

training the models.

Activity Training Files 70% 1 ICP 2 ICP 3 ICP

Glass 70 49 49 - -

Shapes 270 189 63 63 63

Dilution 150 105 53 52 -

Glass Task Shapes Task Dilution Task

64 64

71 71

59 59

10% 20% 30% 40% 50% 60% 70% 80% 90% 100%

Figure 6: F1 score evolution with the percentage of training

data.

Glass Task Shapes Task Dilution Task

0.02

0.04

0.06

0.08

0.1

0.12

0.01

0.008

0.009

0.007 0.007 0.007 0.007

0.006

0.006 0.006

0.119

0.107

0.095

0.085

0.082

0.078

0.075

0.074

0.071

0.07

0.1

0.052

0.058

0.043

0.041

0.03

0.024

0.023 0.023

0.021

10% 20% 30% 40% 50% 60% 70% 80% 90% 100%

Figure 7: RMSE evolution with the percentage of training

data.

Regarding the ICP orientation, a naive approach

consists in extending the position model with new

outputs or building a similar model for only predict-

ing the orientation. This strategy will give unsatis-

factory results as most of the pre-implemented ML

algorithms work with an estimation of the error be-

tween the prediction and the ground truth. From this

estimated error, a discrepancy is computed to evolve

weights or parameters of the hypothesis function that

the ML tries to build. The ML algorithms in the

scikit-learn library use a linear distance to get the er-

ror and the discrepancy. This is correct for the po-

sition, not for the orientation. Indeed, the distance

between two orientations must be computed by using

the geodesic distance if the orientation is formalized

through a triplet of angles for example. That implies

the re-implementation of the ML algorithms.

6 CONCLUSION AND FUTURE

WORK

Our contribution relies on a methodological proposal

to automatically predict, from the demonstrations

of a gesture-based task to learn, the number and 3d

position of the required 3D Intermediate Checkpoints

(ICP). ICPs represent a set of simple and ordered

3D shapes (e.g. sphere, rectangle) from which the

observed motion of an object or a body part must

go through. This concept is used to decompose

the gesture-based task in several spatial and tem-

poral steps to make it easier to learn. By using

an ML-based architecture, the importance of this

contribution dwells in facilitating the building of the

evaluation process by the teacher knowing that some

tasks are complex. For example, a complex/long task

might be divided into 8 sub-tasks where each sub-task

must have its own set of checkpoints (one SCP, one

or more ICP(s), and one ECP). If 4 sub-tasks need 2

steps (i.e. 1 ICP) and the other 4 need 3 steps (i.e. 2

ICPs), the teachers will have to create for this single

task up to 12 ICP(s). There is therefore a major

challenge in automating this task.

The proposed methodology was implemented on 3

different learning activities (i.e. glass manipulation,

shape drawing, biology dilution), obtaining an F1-

score equal to or higher than 70%, regardless of the

learning activity, for the window model guessing the

number of ICPs. The results of the position model

predicting the position of the ICPs in the VLE gave

an NRMSE equal to or under 0.07 in all cases. As for

future considerations, the following points are listed:

- Automating the choice of the window size parsing

the motion ﬁles for extracting and computing the

dataset. Indeed the size of the time window can

strongly inﬂuence the results and depends on the

number of frames that can signiﬁcantly vary from

one motion to another one for the same task. We will

work on a method to uniformize the frame number by

rebuilding each motion ﬁle through an interpolation

process, according to one or more heuristic to set

Automatic Prediction of 3D Checkpoints for Technical Gesture Learning in Virtual Environments

this number while keeping the natural and realistic

aspect of the task. From those uniformed motions,

we will perform a cross-validation process to get the

appropriate window size given a speciﬁc activity.

- Predicting more properties of the ICP conﬁguration

as it is not only deﬁned by its 3D position but

also by its orientation and 3D dimensions in VLE.

The orientation prediction requires recoding the

ML-algorithm parts using the Euclidean distance,

with a more appropriate distance computation such

as the geodesic one.

- Considering other tasks and activities to learn.

Finally, an interesting point is related to the false

positives given by the window model i.e. some ICPs

that do not exist in the dataset. As the creation and

placement of the ICPs is only the consequence of the

teacher’s decision, can these false positives (or part of

it), be in fact consistent ICPs that are useful to decom-

pose the task? The same question can be asked for the

false negatives, some of them indicating, perhaps, the

presence of useless ICPs in the dataset in terms of task

decomposition. These problems will be addressed in

future work.

REFERENCES

Adolf, J., K

an, P., Outram, B., Kaufmann, H., Dole

zal, J.,

and Lhotsk

a, L. (2019). Juggling in vr: Advantages of

immersive virtual reality in juggling learning. VRST

’19: 25th ACM Symposium on Virtual Reality Soft-

ware and Technology.

Akinsola, J. E. T. (2017). Supervised machine learning

algorithms: Classiﬁcation and comparison. Interna-

tional Journal of Computer Trends and Technology

(IJCTT), 48:128–138.

Baoxing, B. and Bo, L. (2018). Upper body motion recogni-

tion based on key frame and random forest regression.

Multimedia Tools and Applications, 79:5197–5212.

Borchani, H., Varando, G., Bielza, C., and Larranaga, P.

(2015). A survey on multi-output regression. Wiley

Interdisciplinary Reviews: Data Mining and Knowl-

edge Discovery, 5:216–233.

Bouville, R., Gouranton, V., Boggini, T., Nouviale, F., and

Arnaldi, B. (2015). # ﬁve: High-level components for

developing collaborative and interactive virtual envi-

ronments. In 2015 IEEE 8th Workshop on Software

Engineering and Architectures for Realtime Interac-

tive Systems (SEARIS), pages 33–40. IEEE.

Breiman, L. (2001). Random forests. Machine Learning,

45:5–32.

Brock, H. and Ohgi, Y. (2017). Assessing motion style er-

rors in ski jumping using inertial sensor devices. IEEE

Sensors Journal, 17(12):3794–3804.

Chiang, P.-Y., Chang, H.-Y., and Chang, Y.-J. (2018). Pot-

terygo: A virtual pottery making training system.

IEEE Comput. Graph. Appl., 38(2):74–88.

Claude, G., Gouranton, V., Berthelot, R. B., and Arnaldi, B.

(2014). Short paper:# seven, a sensor effector based

scenarios model for driving collaborative virtual envi-

ronment. In ICAT-EGVE, International Conference on

Artiﬁcial Reality and Telexistence, Eurographics Sym-

posium on Virtual Environments, pages 1–4.

D’Amato, V., Volta, E., Oneto, L., Volpe, G., Camurri, A.,

and Anguita, D. (2020). Understanding violin players’

skill level based on motion capture: a data-driven per-

spective. Cognitive Computation, 12(6):1356–1369.

de Morais, W. O. and Wickstr

om, N. (2011). A serious

computer game to assist tai chi training for the elderly.

In 2011 IEEE 1st International Conference on Serious

Games and Applications for Health (SeGAH), pages

1–8.

Dimmel, J. and Bock, C. (2017). Handwaver: A gesture-

based virtual mathematical making environment. In

Proceedings of the 13th International Conference on

Technology in Mathematics Teaching.

Djadja., D., Hamon., L., and George., S. (2020). De-

sign of a motion-based evaluation process in any unity

3d simulation for human learning. In Proceedings

of the 15th International Joint Conference on Com-

puter Vision, Imaging and Computer Graphics The-

ory and Applications - GRAPP, pages 137–148. IN-

STICC, SciTePress.

Fazeli, H. R., Venkatesh, S. K., and Peng, Q. (2018). A vir-

tual environment for hand motion analysis. Procedia

CIRP, 78:127–132. 6th CIRP Global Web Conference

– Envisaging the future manufacturing, design, tech-

nologies and systems in innovation era (CIRPe 2018).

Giarmatzis, G., Zacharaki, E. I., and Moustakas, K. (2020).

Real-time prediction of joint forces by motion capture

and machine learning. Sensors.

ulsmann, F., G

opfert, J. P., Hammer, B., Kopp, S., and

Botsch, M. (2018). Classiﬁcation of motor errors to

provide real-time feedback for sports coaching in vir-

tual reality — a case study in squats and tai chi pushes.

Computers & Graphics, 76:47–59.

Izonin, I., Tkachenko, R., Gregus, M., Khrystyna, Z., and

Lotoshynska, N. (2021). Input doubling method based

on svr with rbf kernel in clinical practice: Focus on

small data. Procedia Computer Science, 184:606–

613.

Jarchi, D., Pope, J., Lee, T. K., Tamjidi, L., Mirzaei, A., and

Sanei, S. (2018). A review on accelerometry-based

gait analysis and emerging clinical applications. IEEE

reviews in biomedical engineering, 11:177–194.

Jeanne, F., Thouvenin, I., and Lenglet, A. (2017). A study

on improving performance in gesture training through

visual guidance based on learners’ errors. In Proceed-

ings of the 23rd ACM Symposium on Virtual Reality

Software and Technology, VRST ’17, New York, NY,

USA. Association for Computing Machinery.

Jose, J., Unnikrishnan, R., Marshall, D., and Bhavani, R. R.

(2016). Haptics enhanced multi-tool virtual interfaces

for training carpentry skills. In 2016 International

Conference on Robotics and Automation for Humani-

tarian Applications (RAHA), pages 1–6. IEEE.

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

Kacem, A., Hammal, Z., Daoudi, M., and Cohn, J. (2018).

Detecting depression severity by interpretable repre-

sentations of motion dynamics. In 13th IEEE Inter-

national Conference on Automatic Face and Gesture

Recognition, FG 2018, pages 739–745.

Kapur, A., Kapur, A., Virji-Babul, N., Tzanetakis, G., and

Driessen, P. (2005). Gesture-based affective comput-

ing on motion capture data. In International Confer-

ence on Affective Computing and Intelligent Interac-

tion, ACII, volume 3784, pages 1–7.

Kico, I. and Liarokapis, F. (2020). Investigating the learn-

ing process of folk dances using mobile augmented

reality. Applied Sciences, 10(2):599.

Kora, T., Soga, M., and Taki, H. (2015). Golf learning envi-

ronment enabling overlaid display of expert’s model

motion and learner’s motion using kinect. Proce-

dia Computer Science, 60:1559–1565. Knowledge-

Based and Intelligent Information & Engineering Sys-

tems 19th Annual Conference, KES-2015, Singapore,

September 2015 Proceedings.

Larboulette, C. and Gibet, S. (2015). A review of com-

putable expressive descriptors of human motion. In

Proceedings of the 2nd International Workshop on

Movement and Computing, MOCO ’15, page 21–28.

Association for Computing Machinery.

Le Naour, T., Hamon, L., and Bresciani, J.-P. (2019). Super-

imposing 3d virtual self + expert modeling for motor

learning: Application to the throw in american foot-

ball. Frontiers in ICT, 6:16.

ecuyer, F., Gouranton, V., Reuzeau, A., Gaugne, R., and

Arnaldi, B. (2020). Action sequencing in VR, a no-

code approach. LNCS Transactions on Computational

Science, pages 57–76.

Liu, J., Zheng, Y., Wang, K., Bian, Y., Gai, W., and Gao, D.

(2020). A real-time interactive tai chi learning system

based on vr and motion capture technology. Procedia

Computer Science, 174:712–719. 2019 International

Conference on Identiﬁcation, Information and Knowl-

edge in the Internet of Things.

Moore, A. G., McMahan, R. P., Dong, H., and Ruozzi, N.

(2020). Extracting velocity-based user-tracking fea-

tures to predict learning gains in a virtual reality train-

ing application. In 2020 IEEE International Sym-

posium on Mixed and Augmented Reality (ISMAR),

pages 694–703.

Morel, M. (2017). Multidimensional time-series averag-

ing: Application to automatic and generic evaluation

of sport gestures. Theses, Universit

e Pierre et Marie

Curie - Paris VI.

Morel, M., Achard, C., Kulpa, R., and Dubuisson, S.

(2017). Automatic evaluation of sports motion: A

generic computation of spatial and temporal errors.

Image and Vision Computing, 64:67–78.

Naser, M. and Alavi, A. (2020). Insights into performance

ﬁtness and error metrics for machine learning. Re-

search Gate.

Park, D.-S., Lee, D.-G., Lee, K., and Lee, G. (2017). Ef-

fects of virtual reality training using xbox kinect on

motor function in stroke survivors: A preliminary

study. Journal of Stroke and Cerebrovascular Dis-

eases, 26(10):2313–2319.

Pilati, F., Faccio, M., Gamberi, M., and Regattieri, A.

(2020). Learning manual assembly through real-time

motion capture for operator training with augmented

reality. Procedia Manufacturing, 45:189–195. Learn-

ing Factories across the value chain – from innovation

to service – The 10th Conference on Learning Facto-

ries 2020.

Rold

an, J. J., Crespo, E., Mart

ın-Barrio, A., Pe

na-Tapia,

E., and Barrientos, A. (2019). A training system for

industry 4.0 operators in complex assemblies based

on virtual reality and process mining. Robotics and

computer-integrated manufacturing, 59:305–316.

Savitzky, A. and Golay, M. (1964). Smoothing and differen-

tiation of data by simpliﬁed least squares procedures.

Analytical Chemistry, 36:1627–1639.

Schafer, R. W. (2011). What is a savitzky-golay ﬁlter?

IEEE Signal Processing Magazine, 28:111 – 117.

Sror, L., Vered, M., Treger, I., Levy-Tzedek, S., Levin,

M. F., and Berman, S. (2019). A virtual reality-based

training system for error-augmented treatment in pa-

tients with stroke. In 2019 International Conference

on Virtual Rehabilitation (ICVR), pages 1–2.

Swee, S. K., You, L. Z., Hang, B. W. W., and Kiang, D. K. T.

(2017). Development of rehabilitation system using

virtual reality. In 2017 International Conference on

Robotics, Automation and Sciences (ICORAS), pages

1–6.

Thomas, S., G.N., P., and Kirat, P. (2017). Prediction of

peak ground acceleration using e-svr, v-svr and ls-

svr algorithm. Geomatics Natural Hazards and Risk,

8:177–193.

Vabalas, A., Gowen, E., Poliakoff, E., and Casson, A. J.

(2020). Applying machine learning to kinematic and

eye movement features of a movement imitation task

to predict autism diagnosis. Scientiﬁc Reports.

Wei, W., Lu, Y., Printz, C. D., and Dey, S. (2015). Motion

data alignment and real-time guidance in cloud-based

virtual training system. In Proceedings of the Con-

ference on Wireless Health, WH ’15, New York, NY,

USA. Association for Computing Machinery.

Winkler-Schwartz, A., Yilmaz, R., Mirchi, N., Bissonnette,

V., Ledwos, N., Siyar, S., Azarnoush, H., Karlik, B.,

and Del Maestro, R. (2019). Machine Learning Identi-

ﬁcation of Surgical and Operative Factors Associated

With Surgical Expertise in Virtual Reality Simulation.

JAMA Network Open, 2(8):e198363–e198363.

Automatic Prediction of 3D Checkpoints for Technical Gesture Learning in Virtual Environments