
Explainable Feature Learning with Variational Autoencoders for
Holographic Image Analysis
Stefan R
¨
ohrl
1∗ a
, Lukas Bernhard
1∗ b
, Manuel Lengl
1 c
, Christian Klenk
2 d
, Dominik Heim
2 e
,
Martin Knopp
1,2 f
, Simon Schumann
1 g
, Oliver Hayden
2 h
and Klaus Diepold
2 i
1
Chair of Data Processing, Technical University of Munich, Germany
2
Heinz-Nixdorf Chair of Biomedical Electronics, Technical University of Munich, Germany
Keywords:
Quantitative Phase Imaging, Blood Cell Analysis, Machine Learning, Variational Autoencoder, Digital
Holographic Microscopy, Microfluidics, Flow Cytometry.
Abstract:
Digital holographic microscopy (DHM) has a high potential to be a new platform technology for medical
diagnostics on a cellular level. The resulting quantitative phase images of label-free cells, however, are widely
unfamiliar to the bio-medical community and lack in their degree of detail compared to conventionally stained
microscope images. Currently, this problem is addressed using machine learning with opaque end-to-end
models or inadequate handcrafted morphological features of the cells. In this work we present a modified
version of the variational Autoencoder (VAE) to provide a more transparent and interpretable access to the
quantitative phase representation of cells, their distribution and their classification. We can show a satisfying
performance in the presented hematological use cases compared to classical VAEs or morphological features.
1 INTRODUCTION
Quantitative Phase Imaging (QPI) in combination
with microfluidics proves to be an extremely flexible
method for the analysis of cellular samples (Nguyen
et al., 2022). The resulting optical tool allows re-
searchers to investigate kinetic and morphological
anomalies of cells free of labeling costs while pre-
serving a high amount of detail. The sample presen-
tation via a microfluidics cartridge leverages the ap-
proach to high throughput comparable to modern flow
cytometry devices and therefore a profound statistical
validity. Hence, it is not surprising that the method
offers great potential in the research, diagnosis and
treatment of various diseases. Recent publications
a
https://orcid.org/0000-0001-6277-3816
b
https://orcid.org/0000-0002-5694-0902
c
https://orcid.org/0000-0001-8763-6201
d
https://orcid.org/0000-0002-4664-8107
e
https://orcid.org/0000-0001-8463-1544
f
https://orcid.org/0000-0002-1136-2950
g
https://orcid.org/0000-0002-7074-473X
h
https://orcid.org/0000-0002-2678-8663
i
https://orcid.org/0000-0003-0439-7511
*
These authors contributed equally to this work
C
This research was funded by BMBF ZN 01 | S17049.
in the medical fields of oncology (Lam et al., 2019;
Nguyen et al., 2017) and hematology (Paidi et al.,
2021; Ugele et al., 2018) are only a small subset of its
capabilities. Furthermore, advances in machine learn-
ing have also been applied to this discipline, enabling
automated processing, segmentation, and differentia-
tion for a wide variety of problems (Jo et al., 2019).
Besides their usage for improving the phase recon-
struction technique itself (Allier et al., 2022; Paine
and Fienup, 2018), big convolutional neural networks
(CNNs) surpassed many classical approaches for in-
stance segmentation and object classification. These
black boxes show great performances for the retrieval
and analysis of blood as well as tissue cells (Midtvedt
et al., 2021; Kutscher et al., 2021).
Besides all their advantages, holography and a
microfluidics system for sample presentation entails
some new challenges. Performing a classical blood
smear, as the gold standard for hematological anal-
ysis, ensures a defined orientation of the cells and a
precise alignment in the focal plane of a microscope
(Barcia, 2007). A microfluidics cartridge holds some
uncertainties here. In addition, there is the absence of
the usual color information and the lack to selectively
label individual cell components. Of course, it is still
possible to catch sight of a misaligned red blood cell,
but the differentiation of white blood cell (WBC) dif-
Röhrl, S., Bernhard, L., Lengl, M., Klenk, C., Heim, D., Knopp, M., Schumann, S., Hayden, O. and Diepold, K.
Explainable Feature Learning with Variational Autoencoders for Holographic Image Analysis.
DOI: 10.5220/0011632800003414
In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 2: BIOIMAGING, pages 69-77
ISBN: 978-989-758-631-6; ISSN: 2184-4305
Copyright
c
2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
69

ferentiation becomes impossible for the human eye.
Here, we want to enable human researches to re-
take control of the quality assurance in their cell se-
lection pipeline. Also, the classification itself should
become more transparent as when using huge state
of the art CNNs. We present a fused approach of a
lightweight variational Autoencoder in combination
with a small classifier, as this technique allows an as-
sessment of the underlying data and the decision mak-
ing process on a human like level of abstraction. Un-
intuitive low-level features are often incapable of de-
scribing the desired behavior of an analysis pipeline.
The Autoencoder approach provides an easy visual
interface and the ability to present an enormous data
set in a compact way. We demonstrate this behavior
in different experiments involving whole blood sam-
ples, purified white blood cells as well as defocused
and misaligned cells.
2 MICROSCOPY AND DATA SET
2.1 Digital Holographic Microscopy
A digital holographic microscope is capable of ob-
taining high-quality phase images of samples by using
the principle of interference between an object beam
and a reference beam. This makes it very interest-
ing for bio-medical applications (Jo et al., 2019) as
holography solves the problem of low contrast asso-
ciated with typical bright-field microscopy caused by
the transparent nature of most biological cells. This
problem is usually overcome by staining or molecu-
lar labeling of cells, which requires time-consuming
preparation and analysis (Barcia, 2007; Sahoo, 2012;
Klenk et al., 2019). Phase images, on the other hand,
reveal much more detailed cell structures compared to
intensity images.
We use a customized differential holographic mi-
croscope by Ovizio Imaging Systems as shown in Fig-
ure 1. It enables label-free cell imaging of untreated
blood cells in suspension. Our approach is closely re-
lated to off-axis diffraction phase microscopy (Dubois
and Yourassowsky, 2015), but allows us to use a low-
coherence light source and does not rely on a refer-
ence beam. Precise focusing of cells is performed
with a 50×500 µm PMMA (polymethyl methacry-
late) microfluidics channel. We are using four sheath
flows to center blood cells in the channel and avoid
contact with the channel walls. More detailed infor-
mation about the used holographic microscope can
be found in (Dubois and Yourassowsky, 2008) and
(Ugele et al., 2018).
Figure 1: The PMMA chip uses hydrodynamic focusing to
align the sample stream in the focal plane of the digital holo-
graphic microscope.
20 µm
0
1
2
3
(a) Raw Phase Image.
20 µm
0
1
2
3
(b) Background Subtraction.
20 µm
0
1
2
3
(c) Segmentation.
20 µm
0
1
2
3
(d) Filtering.
Figure 2: Several pre-processing steps are required to obtain
clean image patches of individual cells.
2.2 Pre-Processing
The microscope setup provides quantitative phase im-
ages with a size of 512×384 pixels containing multi-
ple cells. We apply several pre-processing steps to
obtain isolated image patches, which contain the in-
dividual cells. Figure 2a shows an example of an un-
processed phase image of white blood cells in the mi-
crofluidics channel.
2.2.1 Background Subtraction
To remove background noise and artifacts of the
microfluidics channel, background subtraction is re-
quired. The background is estimated using the me-
dian of 1,000 images, which gives much better results
compared to using the mean. Due to the fixed ori-
entation of the lens, camera, light, and microfluidics
channel, the background is assumed to be static over
the whole recording. As a result of background sub-
traction Figure 2b clearly shows a minimized expres-
sion of noise and artifacts compared to the raw image.
BIOIMAGING 2023 - 10th International Conference on Bioimaging
70

2.2.2 Segmentation
To find the important regions of the image that con-
tain cells, we apply a binary thresholding to the phase
images. Here, a phase shift threshold of 0.3 rad
provides good results for filtering out small debris.
From the resulting binary images, we extract the con-
tours of each region of interest using the OpenCV
findContours implementation of the algorithm pro-
posed by (Suzuki and Abe, 1985). As Figure 2c
shows, not only valid cells are identified by this rather
simple method of object detection.
2.2.3 Filtering
Debris and smaller cell fragments are likely to con-
tain enough optical mass to be sensed by the thres-
holding procedure. Therefore, a first simple size fil-
ter is applied, so only contours covering more than
30 pixels are stored with the corresponding 48×48
pixel image area around their center. An exemplary
result containing six valid cells can be seen in Fig-
ure 2d. Whereas this task could also be solved by the
proposed approach, this filtering step restricts the va-
riety of events and simplifies the convergence of the
used machine learning models, allowing us to employ
smaller neural networks.
2.3 Data Sets
All samples used in this work are provided by three
healthy donors
1
while keeping the measurement pro-
tocols as consistent as possible. Since our microscopy
approach illustrated in Section 2.1 works label-free
and therefore does not require any sample prepara-
tion, the whole blood (2.3.2) and defocused (2.3.3)
data set were measured within 15 minutes after blood
collection. To minimize spatial coincidences of cells
a 1:100 diluted blood sample is used for the robust
microfluidics flow focusing. To distill single fractions
of the five common types of white blood cells as a
ground truth, we isolate the cells for the leukocyte
(2.3.1) data sets. Therefore, these samples have an
additional preparation time of maximum three hours.
The measurement itself only takes less than two min-
utes for every sample resulting in more than 10,000
uncorrelated frames each. These frames are pre-
processed as outlined in Section 2.2 yielding the de-
sired phase image patches of single cells.
1
All human samples were collected with informed con-
sent and procedures approved by application 620/21 S-KK
of the ethic committee of the Technical University of Mu-
nich.
2.3.1 Leukocytes
Responsible for the immune defense, white blood
cells represent the most interesting group for the di-
agnosis of diseases and the general state of human
health. While making up only 1.5% of the total cell
count, these cells are in focus of every modern hema-
tology analysis device. These so-called leukocytes
can be divided in five major groups. For healthy indi-
viduals, Neutrophils (62%) make up the biggest pro-
portion, followed by Lymphocytes (30%), Monocytes
(5.3%), Eosinophils (2.3%) and Basophils (0.4%)
(Alberts, 2017; Young et al., 2013). We apply the
isolation protocol according to (Ugele, 2019; Klenk
et al., 2019): Starting from a whole blood sample
2
,
the leukocytes are separated from the red blood cells
using selective hypotonic water lysis as proposed by
(Vuorte et al., 2001). Remaining fragments are fil-
tered out using an Erythrocyte Depletion Kit. Five
different Immunomagnetic Isolation Kits from Mil-
tenyi Biotec are then employed to obtain the individ-
ual fractions of WBCs. With this process we gathered
single cell images of 77,672 Lymphocytes, 58,760
Monocytes, 41,881 Eosinophils and 269,228 Neu-
trophils. Note that a 100% purity of those fractions
can not be ensured.
10 µm
−3
0
3
6
9
12
(a) Monocyte.
10 µm
−3
0
3
6
9
12
(b) Lymphocyte.
10 µm
−3
0
3
6
9
12
(c) Neutrophil.
10 µm
−3
0
3
6
9
12
(d) Eosinophil.
Figure 3: The quantitative phase shift is color mapped in a
Giemsa stain (Barcia, 2007) fashion.
2.3.2 Whole Blood
Whole blood samples are of high value for many di-
agnostics as they do not require any sample prepara-
tion besides anticoagulants, which are already present
in a blood tube, and are therefore very close to in
vivo conditions. Omitting time consuming purifica-
tion or staining steps facilitate insights to volatile ef-
fects in the sample. Mainly consisting of red blood
2
EDTA is used to prevent coagulation.
Explainable Feature Learning with Variational Autoencoders for Holographic Image Analysis
71
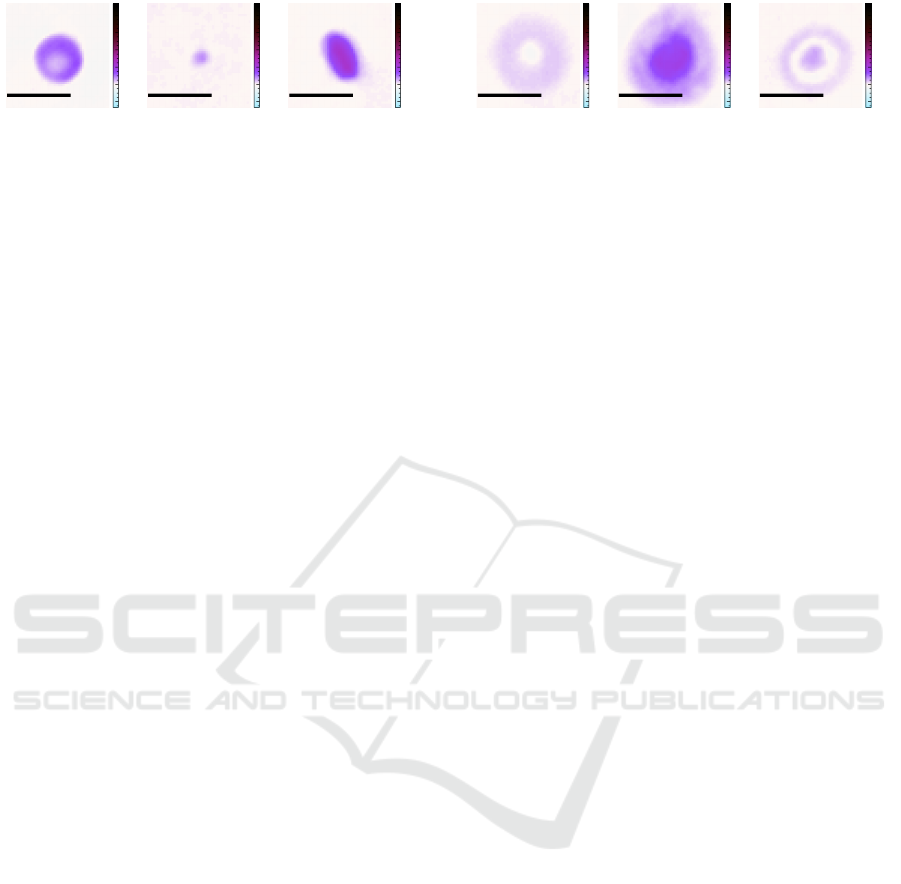
10 µm
−3
0
3
6
9
12
(a) RBC.
10 µm
−3
0
3
6
9
12
(b) Thrombocyte.
10 µm
−3
0
3
6
9
12
(c) Tilted RBC.
Figure 4: The whole blood samples contain besides white
blood cells mainly (a) red blood cells and (b) platelets. For
red blood cells the orientation (c) is crucial.
cells (erythrocytes), white blood cells (leukocytes)
and platelets (thrombocytes) are only a minority in
the human blood (Sender et al., 2016). Typical ex-
amples for red blood cells and platelets can be seen
in Figure 4. For comparability with the white blood
cells, we apply the same artificial Giemsa stain. The
viscoelastic focusing in the channel cannot guarantee
the alignment of the erythrocytes to the focal plane.
E.g. a tilted red blood cell as displayed in Figure 4c
cannot be used for malaria detection (Ugele, 2019).
The only preparation step for all whole blood sam-
ples is a dilution of 1:100 to facilitate the segmenta-
tion of individual cells. With the current laboratory
prototype and manual dilution step, results are ob-
tained within 15 min after blood draw. (Advanced
workflow integration could reduce the time-to-result
even further.) The whole blood data set contains a
total 126,480 images of single cells.
2.3.3 Defocused Cells
To simulate the behavior of unskilled measurement
personal, a technical defect or challenges of the opti-
cal setup (Cao et al., 2022), we created different cap-
tures from whole blood with a obviously misaligned
focus. We use the microscope stage to place the mi-
crofluidics channel and thereby the sample stream
at different offsets above as well as below the focal
plane of the objective. The misplacement ranges from
-10µm to +10µm with respect to the ideal focus. Fig-
ure 5 shows these clearly defocused images which are
again colored according to the previously introduced
scheme. As it may happen that individual cells get out
of focus even in a well calibrated setup, these images
serve as training set to detect this effect. These cells
are no longer usable for serious image analysis since
refocusing is impossible with our optical setup. With
this setting, we captured 7,269 examples of defocused
cells.
3 METHODOLOGY
Dimensionality reduction is an important area of un-
supervised learning. For high-dimensional data such
10 µm
−3
0
3
6
9
12
(a) -10 µm.
10 µm
−3
0
3
6
9
12
(b) −5 µm.
10 µm
−3
0
3
6
9
12
(c) +5 µm
Figure 5: This data set contains cell images which where
captured with different focal offsets with respect to the ideal
focal plane.
as images, it is often necessary to reduce dimensional-
ity as a pre-processing step. This provides deeper in-
sight into the structure of the data and often improves
the performance of classification or regression mod-
els. One of the most popular dimensionality reduction
techniques is principal component analysis (PCA),
which can provide deep insights into the most impor-
tant features of a data set (Jolliffe and Cadima, 2016).
The use of PCA implies an underlying linear sys-
tem, which cannot always be guaranteed. In contrast,
the Autoencoder approach used in this work repre-
sents an alternative, which, as a neural network, is not
bound to these assumptions (Schmidhuber, 2015). As
a deep-learning technique it utilizes non-linearly acti-
vated neurons which are organized in layers to encode
data samples into a compressed latent space (simi-
lar to principal components) and decode this compact
representation to recover the original data. The be-
havior and learned codes of an Autoencoder can be
affected by the number of codes (size of the latent
space) and hidden layers in use. It is important to note
that compared to PCA, which maximizes the variance
of the codes, the interpretation of the learned codes is
highly dependent on the trained data set.
3.1 Variational Autoencoder
Variational Autoencoders. (VAEs) introduce an ad-
ditional constraint to the latent space (Kingma and
Welling, 2013). The encoding should not only rep-
resent the original data as well as possible, but should
also follow a certain distribution (usually a Gaussian
distribution). This makes the latent space continu-
ous and allows sampling, which means we can gen-
erate artificial data by changing the value of the en-
codings. This generative behavior provides a deeper
insight into the learned feature representation, espe-
cially when sliding over an encoding (see Figure 7),
one can see the effect and its intensity of that feature
on the data at the output layer (Larsen et al., 2016).
The encoder is trained to encode the input data set X
into a distribution Q(z|X) represented by a mean vec-
tor µ
z
and a standard deviation vector σ
z
. This allows
sampling from that distribution to obtain an encod-
ing vector z which is fed into the decoder network to
BIOIMAGING 2023 - 10th International Conference on Bioimaging
72
create a reconstruction
ˆ
X = P(X|z). Hereby, the en-
coder is forced to create codes following a prior dis-
tribution P(z) by including the Kullback-Leibler Di-
vergence D
KL
of the learned distribution Q(z|X) and
the desired prior distribution P(z) in the loss function
of the VAE (Perez-Cruz, 2008). Hence, the loss
L (X,
ˆ
X, z) = MSE(X,
ˆ
X) + D
KL
[Q(z|X)||P(z)] (1)
optimizes the reconstruction error under the con-
straint of a Gaussian distribution.
As we work directly on image data, the use of
convolutional layers instead of dense layers is ob-
vious, since these proved to be state of the art in all
sorts of image classification and object detection tasks
over the last decade (Ciregan et al., 2012; Krizhevsky
et al., 2012). This leads to an improved representation
of spatial information in the VAE.
A well-known problem of VAEs are entangled
codes, which means that the codes are correlated and
a learned characteristic of the data is represented in
more than one encoding, leading to a reduced inter-
pretability of the latent space. Employing β-VAEs
addresses this problem (Burgess et al., 2018) by driv-
ing the network to disentangle its encodings using an
updated loss function
L
β
(X,
ˆ
X, z) = MSE(X,
ˆ
X) + β D
KL
[Q(z|X)||P(z)].
(2)
Choosing β > 1 emphasizes the Kullback-Leibler Di-
vergence which forces z to be even more multivari-
ate Gaussian and consequently µ
z
→ 0 and σ
z
→ 1.
This reduces the correlation between the encodings z
i
leading to three important properties (Higgins et al.,
2017):
• z approximates a basis for the latent space Z
• The network is encouraged to use as few dimen-
sions of z as possible
• The latent space is smoothed out, improving the
generative behavior and allowing clearer interpre-
tations of the information stored in the encodings.
3.2 Classifying Variational Autoencoder
The aforementioned approaches do not incorporate
prior knowledge about the data samples and can learn
in an unsupervised way. Therefore, the trained en-
coder provides not necessarily clear and distinct clus-
ters in an interpretable manner. Conditional Varia-
tional Autoencoders allow to add another condition
c to the encoder Q(z|X, c) and decoder P(X|z, c) of
the VAE. This changes the latent space from a normal
distribution P(z) to a conditional distribution P(z|c),
yielding to some kind of class awareness of the en-
coder. Several publications showed the advantages of
this architecture as a generative model (Mishra et al.,
2018; Yan et al., 2016; Maaløe et al., 2016; Kingma
et al., 2014). Nevertheless, this turns into chicken-egg
problem for new samples, as a class label must be as-
signed to the unknown data point in order to be en-
coded correctly.
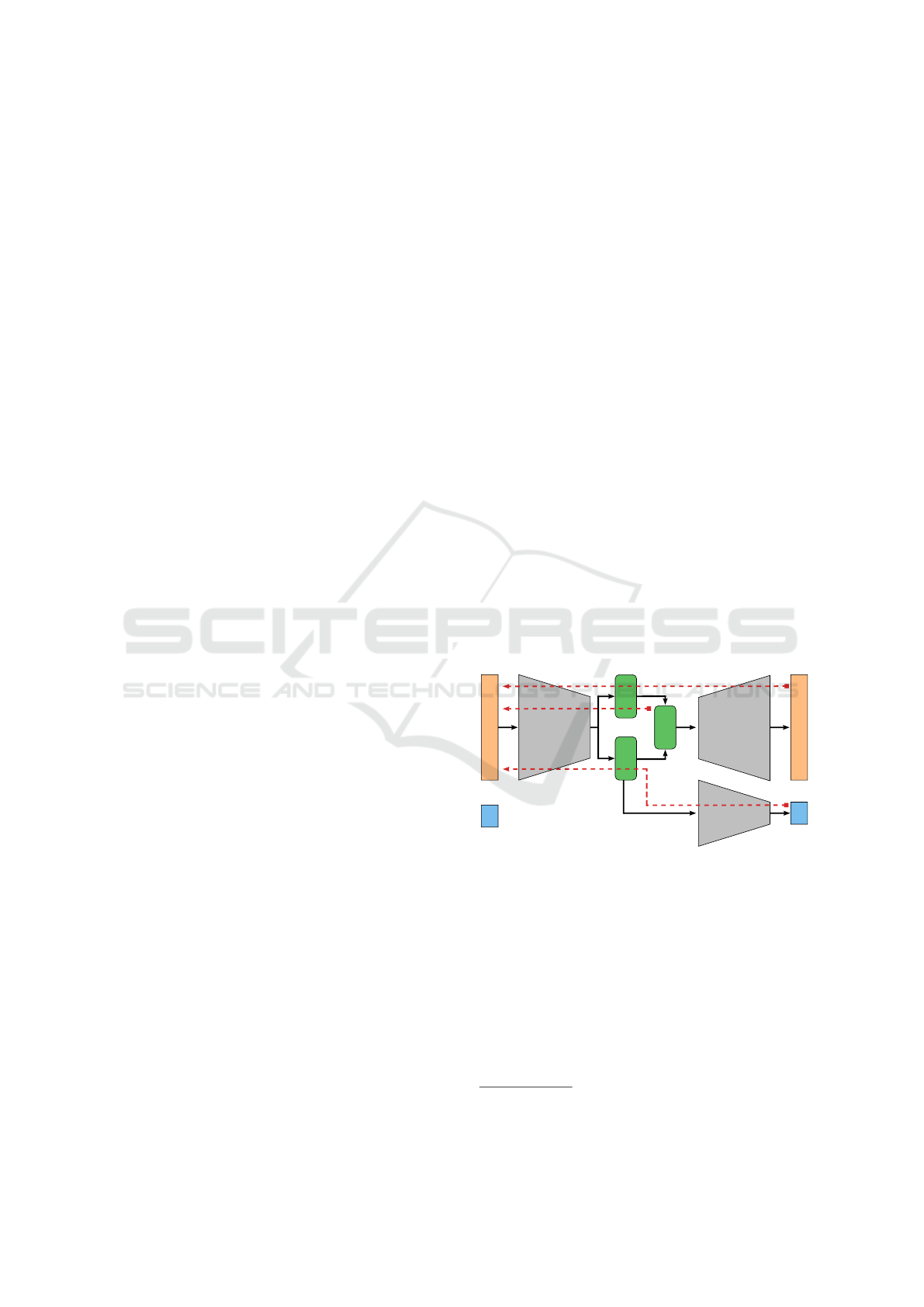
To overcome this problem we came up with a
new architecture to provide the VAE additional infor-
mation about labels during training while preserving
the encoding and generative nature of the VAE. The
classifying VAE (claVAE) is equipped with an ad-
ditional fully connected classifier network
3
which is
connected to the µ
z
from the latent space as shown
in Figure 6. This provides the encoder and the latent
space with information about the ground truth labels
of the data, so that the encoder can optimally place the
data in the latent space by grouping samples of one
class together (path a) while maintaining a continu-
ous space from which we can sample (path b). The
decoder is responsible for reconstructing the original
image from the latent space (path c). Combining the
back-propagated errors along the three paths yields a
loss function
L
claVAE
(X,
ˆ
X, z, y, ˆy) = L
β
(X,
ˆ
X, z) + θL
BCE
(Y,
ˆ
Y),
(3)
where θ controls the influence of the Binary Cross-
Entropy loss L
BCE
between the ground truth label Y
and the prediction
ˆ
Y.
µ
z
σ
z
E
D
C
X
ˆ
X
Y
ˆ
Y
z
a
b
c
Figure 6: The claVAE architecture combines the classifica-
tion error (a) the Kullback-Leibler Divergence (b) and the
reconstruction error (c).
3.3 Experimental Setup
For the training of the individual models, the de-
scribed data sets are divided into 60% training set (of
which 20% for validation) and 40% test set for the
evaluations shown later. Depending on the combi-
nation of data sets, the samples are balanced using
random undersampling according to their class label.
3
Inspired by https://www.datacamp.com/tutorial/
autoencoder-classifier-python accessed Jan 16, 2020
Explainable Feature Learning with Variational Autoencoders for Holographic Image Analysis
73

The neural network architecture is kept constant be-
tween all models: The encoder (E) consists of four
convolutional layers with max pooling, two dropout
layers with a dropout rate of 0.25 and two dense layers
connected to z. The decoder (D) is implemented with
three dense layers to increase the dimensionality of
the bottleneck z and adapt it to five subsequent trans-
pose convolutional layers. The claVAE is addition-
ally equipped with a small dense classifier network
(C) consisting of three hidden layers attached to z and
a softmax layer as output. The parameters β = 0.1 and
θ = 1 to weight the components of the loss function
are chosen via a grid search and visual inspection of
the latent space. We could chose to encode more in-
formation by increasing the dimensions of the latent
space, striving for a better classification accuracy. Ac-
cordingly, Figure 7 shows different kinds of character-
istics stored in each additional dimension of z ∈ R
3
.
Though we keep the latent space two-dimensional to
preserve its easy visualization and clarity.
z
0
z
1
−4 −2 0 2 4
z
2
Figure 7: A three-dimensional latent space can encode more
details of the input data. Here, one component of the latent
vector z
i
is varied, while the others z
j
and z
k
are kept at zero.
4 RESULTS
4.1 Overview
A typical workflow in a new project starts with getting
an overview. Therefore, we train the claVAE with all
data and labels introduced in Section 2.3. The result-
ing latent space in Figure 8 resembles a map for all
components of the presented blood samples, which
can be easily interpreted by the human observer. Re-
gion a) contains all defocused cells or cell aggregates.
These cells cannot easily be processed further in a
meaningful way and can be considered as outliers for
the scenarios presented in this work. Since they come
in a wide variety in shape and size, it is not surprising
that they occupy a large share in latent space. Reg-
ular shaped white blood cells and well-aligned red
blood cells can be found in the smaller areas b) and
d), respectively. The claVAE places red blood cells,
which might be unusable for further analysis as they
−4 −3 −2 −1 0 1 2 3 4
z
0
−4
−3
−2
−1
0
1
2
3
4
z
1
a) b) c)
d)
e)
Figure 8: The spatial representation of the cells in the latent
space of the claVAE can be partitioned in five groups: a)
defocused and doublets cells; b) WBCs; c) tilted RBCs; d)
RBCs; e) Platelets.
are tilted vertically, in sector c). It is visible how
the approach also tries to map the concept of orien-
tation. The last division e) contains only the smaller
cells like platelets or fragments. This arrangement is
quite stable over repeated iterations of training with
random initialization and randomly sub-sampled data
sets. The individual placement of the groups may vary
or the latent space might be rotated, but it can always
be used as an intuitive map to filter the cells of inter-
est for subsequent and more detailed analysis. We see
this way of pre-filtering cells as a distinct advantage
over selection by morphological metrics, as it is more
similar to the established gating workflow. Further-
more, it allows a discussion of this processing step
on a higher level, which is more in line with human
nature to make decisions, especially in this interdisci-
plinary context.
4.2 Focus Detection
To make sure that no defocused cells get into the data
set, it is possible to sensitize claVAE to this appli-
cation case. We take well-focus WBCs b) and defo-
cused cells a) using the filters from before and pro-
vide the according labels from our training sets. Fig-
ure 9 shows the resulting distributions of the test set
in the latent space. We can see the well focused cells
mapped to the left whereas the defocused cells dom-
inate the right half plane. Aggregates of two or more
cells tend to be rather blurred, due to their size and the
limited optical depth of the microscope, and are there-
fore mapped more to the right. This can be seen by
BIOIMAGING 2023 - 10th International Conference on Bioimaging
74

−4 −3 −2 −1 0 1 2 3 4
z
0
−4
−3
−2
−1
0
1
2
3
4
z
1
Defocused
Focused
Figure 9: The density estimation of the test samples is eas-
ily separable due to the practical arrangement of the latent
space.
the smaller right-bound population originating from
the focused data set. The trained classifier reaches
an accuracy around 96% when deciding if a cell is
well-focused or not. However, with this conveniently
arranged latent space, it would also be possible to use
simple logistic regression or a threshold as a decision
unit. Without the additional loss on the classification
error, the training results from a β-VAE show a more
unstable behavior and consequently support the use of
the claVAE instead of a conventional variational Au-
toencoder.
4.3 Whole Blood Components
Considering only whole blood samples and purified
white blood cells for training, we aim to achieve more
detailed insights in the discrimination of RBCs and
WBCs. Both classes show a rather easy separability
in the latent space of this specialized claVAE. Drawn
in Figure 10 the RBCs populate the top part and the
WBCs are rather at the bottom.
Under the assumption that whole blood is prac-
tically RBCs, we neglected the other blood compo-
nents in our labeling. Looking at the apostate group of
RBCs, we hoped the claVAE would also find WBCs
hiding under an incorrect ground truth label. Unfor-
tunately, the lower orange population consists of dou-
blet RBCs which where misplaced due to their bigger
appearance. The prolonged sample preparation time
and the special treatment of the purified WBCs might
have changed their appearance compared to the ones
in the untreated whole blood samples. However, the
classification task in this space turns out to be rather
simple again, as the populations are basically linearly
separable. The employed classifier can differentiate
both classes with an accuracy of around 97% based
−4 −3 −2 −1 0 1 2 3 4
z
0
−4
−3
−2
−1
0
1
2
3
4
z
1
WBC
RBC
Figure 10: WBCs and RBCs mostly populate different re-
gions of the latent space and are suitably distinguishable.
on their encoded representation.
4.4 Four-Part Differential
Getting more and more into the details of hematol-
ogy we now select only the available four single frac-
tions of WBCs as a training set. The rendering of
the latent space in the background of Figure 11 first
suggests the distribution according to the size ratios
of the individual groups. As expected, the arrange-
ments of Neutrophils and Eosinophils overlap more
clearly, while the distributions for Lymphocytes and
Monocytes are better differentiated. Considering the
classification performance already while training, the
four groups get pulled in different directions with re-
spect to the origin of the latent space. Using only the
β-VAE the mapping looks even worse. In general,
the overlapping regions lead to problems in classifi-
−4 −3 −2 −1 0 1 2 3 4
z
0
−4
−3
−2
−1
0
1
2
3
4
z
1
Lym
Mon
Eos
Neu
Figure 11: The four leukocyte sub-populations are drawn
apart in the latent space of the claVAE but still overlap in
many areas.
Explainable Feature Learning with Variational Autoencoders for Holographic Image Analysis
75

cation. With this latent representation, the classifier
network only reaches an accuracy of 74% performing
the four-part differential. Having a closer look at the
confusion matrix in Figure 12, it is evident that Neu-
trophils and Eosinophils get mixed up. Also Lympho-
cytes get partly confused with Eosinophils. Note that
a possible origin of this classification error might be
the initial impurity of the ground truth labels them-
selves. The classification performance could be im-
Lym Mon Eos Neu
Predicted label
Lym
Mon
Eos
Neu
True label
11695 603 2146 13
1390 12436 597 46
326 1118 9443 3487
1006 1829 2307 9249
2000
4000
6000
8000
10000
12000
Figure 12: The confusion matrix for the four-part differ-
ential reveals the respective classification mistakes between
the cell types.
proved by allowing more dimensions for the latent
space, since two dimensions seem to be insufficient to
preserve the precise details of the rater similar leuko-
cytes. Though, we choose not to do this as a high-
dimensional space would loose its intuitiveness and
would need a more complex interface for humans to
access it.
5 CONCLUSION
In summary, we can say that the developed approach
is well suited to obtain a compact overview of a large
data set. Researchers can use it to perform robust and
illustrative quality assurance as well as data cleaning,
as it is more intuitive and visual than nitpicking rules
of morphological features. In most of the demon-
strated use cases the claVAE generates clear and sep-
arable embeddings in its latent space, which can be
easily selected or classified. Its continuity and trans-
parency gives the method the potential to be more ro-
bust against outliers and unknown data compared with
large and opaque black-box approaches. In our inter-
disciplinary research, claVAE provides us with a basis
for “eye-level” exchange, even with people from out-
side the domain.
Yet, the method will never be totally accurate
since it would be necessary to sample the latent space
at an infinitesimal level to prove its continuity. Even
if the latent space appears linearly separable and easy
to overlook, the employed encoder still uses a con-
volutional neural network, which cannot be fully ex-
plained and may hide some incontinuities. As we
chose the latent space two-dimensional, we fostered
its accessibility for human observers, but also lim-
ited the encoding power of the claVAE. This prevents
us from resolving the subtle differences in the white
blood cells needed for a classical five-part differential
with sufficient accuracy.
Nevertheless, we plan to employ this non-linear
method for dimensionality reduction in a zoomable
user interface. Eventually, even novice users can get
an intuitive overview and perform gating in visual and
comprehensible manner. With further improvements
of DHM in the field of label-free cell imaging, it is
to be expected that phase imaging flow cytometry and
will be able to reach the high accuracy required for
automated hematology analysis.
ACKNOWLEDGMENTS
The authors would like to especially honor the contri-
butions of L. Bernhard for the software implementa-
tion and experiments as well as D. Heim and C. Klenk
for the sample preparation and measurements.
REFERENCES
Alberts, B. (2017). Molecular biology of the cell. WW
Norton & Company.
Allier, C., Herv
´
e, L., Paviolo, C., Mandula, O., Cioni,
O., Pierr
´
e, W., Andriani, F., Padmanabhan, K., and
Morales, S. (2022). CNN-Based Cell Analysis: From
Image to Quantitative Representation. Frontiers in
Physics, 9:848.
Barcia, J. J. (2007). The Giemsa stain: Its History and Ap-
plications. International Journal of Surgical Pathol-
ogy, 15(3):292–296.
Burgess, C. P., Higgins, I., Pal, A., Matthey, L., Watters,
N., Desjardins, G., and Lerchner, A. (2018). Un-
derstanding Disentangling in β-VAE. arXiv preprint
arXiv:1804.03599.
Cao, R., Kellman, M., Ren, D., Eckert, R., and Waller, L.
(2022). Self-calibrated 3D differential phase contrast
microscopy with optimized illumination. Biomedical
Optics Express, 13(3):1671–1684.
Ciregan, D., Meier, U., and Schmidhuber, J. (2012). Multi-
column deep neural networks for image classification.
In 2012 IEEE Conference on Computer Vision and
Pattern Recognition, pages 3642–3649. IEEE.
Dubois, F. and Yourassowsky, C. (2008). Digital holo-
graphic microscope for 3D imaging and process using
it.
BIOIMAGING 2023 - 10th International Conference on Bioimaging
76

Dubois, F. and Yourassowsky, C. (2015). Off-axis interfer-
ometer.
Higgins, I., Matthey, L., Pal, A., Burgess, C., Glorot, X.,
Botvinick, M., Mohamed, S., and Lerchner, A. (2017).
beta-VAE: Learning Basic Visual Concepts with a
Constrained Variational Framework. In International
Conference on Learning Representations.
Jo, Y., Cho, H., Lee, S. Y., Choi, G., Kim, G., Min, H. S.,
and Park, Y. K. (2019). Quantitative Phase Imaging
and Artificial Intelligence: A Review. IEEE Journal
of Selected Topics in Quantum Electronics, 25(1):1–
14.
Jolliffe, I. T. and Cadima, J. (2016). Principal compo-
nent analysis: a review and recent developments.
Philosophical Transactions of the Royal Society A:
Mathematical, Physical and Engineering Sciences,
374(2065):20150202.
Kingma, D. P., Mohamed, S., Jimenez Rezende, D., and
Welling, M. (2014). Semi-supervised learning with
deep generative models. Advances in neural informa-
tion processing systems, 27.
Kingma, D. P. and Welling, M. (2013). Auto-encoding vari-
ational bayes. arXiv preprint arXiv:1312.6114.
Klenk, C., Heim, D., Ugele, M., and Hayden, O. (2019).
Impact of sample preparation on holographic imaging
of leukocytes. Optical Engineering, 59(10):102403.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-
agenet classification with deep convolutional neural
networks. In Advances in neural information process-
ing systems, pages 1097–1105.
Kutscher, T., Eder, K., Marzi, A., Barroso, A., Schneken-
burger, J., and Kemper, B. (2021). Cell Detection
and Segmentation in Quantitative Digital Holographic
Phase Contrast Images Utilizing a Mask Region-based
Convolutional Neural Network. In OSA Optical Sen-
sors and Sensing Congress 2021 (AIS, FTS, HISE,
SENSORS, ES), page JTu5A.23. Optica Publishing
Group.
Lam, V. K., Nguyen, T., Phan, T., Chung, B.-M., Nehmetal-
lah, G., and Raub, C. B. (2019). Machine learning
with optical phase signatures for phenotypic profiling
of cell lines. Cytometry Part A, 95(7):757–768.
Larsen, A. B. L., Sønderby, S. K., Larochelle, H., and
Winther, O. (2016). Autoencoding beyond pixels us-
ing a learned similarity metric. In Proceedings of The
33rd International Conference on Machine Learning,
volume 48 of Proceedings of Machine Learning Re-
search, pages 1558–1566. PMLR.
Maaløe, L., Sønderby, C. K., Sønderby, S. K., and Winther,
O. (2016). Auxiliary deep generative models. In In-
ternational Conference on Machine Learning, pages
1445–1453. PMLR.
Midtvedt, B., Helgadottir, S., Argun, A., Pineda, J.,
Midtvedt, D., and Volpe, G. (2021). Quantitative dig-
ital microscopy with deep learning. Applied Physics
Reviews, 8(1):011310.
Mishra, A., Krishna Reddy, S., Mittal, A., and Murthy,
H. A. (2018). A generative model for zero shot learn-
ing using conditional variational autoencoders. In
Proceedings of the IEEE Conference on Computer Vi-
sion and Pattern Recognition Workshops, pages 2188–
2196.
Nguyen, T. H., Sridharan, S., Macias, V., Kajdacsy-Balla,
A., Melamed, J., Do, M. N., and Popescu, G. (2017).
Automatic Gleason grading of prostate cancer us-
ing quantitative phase imaging and machine learning.
Journal of Biomedical Optics, 22(3):036015.
Nguyen, T. L., Pradeep, S., Judson-Torres, R. L., Reed, J.,
Teitell, M. A., and Zangle, T. A. (2022). Quantita-
tive phase imaging: Recent advances and expanding
potential in biomedicine. American Chemical Society
Nano, 16(8):11516–11544.
Paidi, S. K., Raj, P., Bordett, R., Zhang, C., Karandikar,
S. H., Pandey, R., and Barman, I. (2021). Raman and
quantitative phase imaging allow morpho-molecular
recognition of malignancy and stages of B-cell acute
lymphoblastic leukemia. Biosensors and Bioelectron-
ics, 190:113403.
Paine, S. W. and Fienup, J. R. (2018). Machine learning
for improved image-based wavefront sensing. Optics
Letters, 43(6):1235–1238.
Perez-Cruz, F. (2008). Kullback-Leibler divergence esti-
mation of continuous distributions. In 2008 IEEE In-
ternational Symposium on Information Theory, pages
1666–1670.
Sahoo, H. (2012). Fluorescent labeling techniques in
biomolecules: A flashback. Royal Society of Chem-
istry Advances, 2(18):7017–7029.
Schmidhuber, J. (2015). Deep learning in neural networks:
An overview. Neural Networks, 61:85–117.
Sender, R., Fuchs, S., and Milo, R. (2016). Revised esti-
mates for the number of human and bacteria cells in
the body. PLoS biology, 14(8):e1002533.
Suzuki, S. and Abe, K. (1985). Topological structural anal-
ysis of digitized binary images by border following.
Computer Vision, Graphics and Image Processing,
30(1):32–46.
Ugele, M. (2019). High-throughput hematology analy-
sis with digital holographic microscopy. PhD thesis,
Friedrich-Alexander-Universit
¨
at Erlangen-N
¨
urnberg
(FAU).
Ugele, M., Weniger, M., Stanzel, M., Bassler, M., Krause,
S. W., Friedrich, O., Hayden, O., and Richter, L.
(2018). Label-Free High-Throughput Leukemia De-
tection by Holographic Microscopy. Advanced Sci-
ence, 5(12).
Vuorte, J., Jansson, S.-E., and Repo, H. (2001). Evaluation
of red blood cell lysing solutions in the study of neu-
trophil oxidative burst by the DCFH assay. Cytometry,
43(4):290–296.
Yan, X., Yang, J., Sohn, K., and Lee, H. (2016). At-
tribute2image: Conditional image generation from vi-
sual attributes. In European Conference on Computer
Vision, pages 776–791. Springer.
Young, B., Woodford, P., and O’Dowd, G. (2013).
Wheater’s functional histology E-Book: a text and
colour atlas. Elsevier Health Sciences.
Explainable Feature Learning with Variational Autoencoders for Holographic Image Analysis
77
