Efﬁcient Hashing of Multiple Spaced Seeds with Application

Eleonora Mian, Enrico Petrucci, Cinzia Pizzi and Matteo Comin

Department of Information Engineering, University of Padova, Padova, 35131, Italy

Keywords:

k-Mers, Gapped q-Gram, Multiple Spaced Seeds, Efﬁcient Hashing.

Abstract:

Alignment-Free analysis of sequences has enabled high-throughput processing of sequencing data in many

bioinformatics pipelines. Hashing k-mers is a common function across many alignment-free applications and

it is widely used for indexing, querying and rapid similarity search. Recently, spaced seeds, a special type

of pattern that accounts for errors or mutations, are routinely used instead of k-mers. Spaced seeds allow to

improve the sensitivity, with respect to k-mers, in many applications, however the hashing of spaced seeds

increases substantially the computational time. Moreover, if multiple spaced seeds are used the accuracy can

further increases at the cost of running time. In this paper we address the problem of efﬁcient multiple spaced

seed hashing. The proposed algorithms exploit the similarity of adjacent spaced seed hash values in an input

sequence in order to efﬁciently compute the next hashes. We report the results on several tests which show that

our methods signiﬁcantly outperform the previously proposed algorithms, with a speedup that can reach 20x.

We also apply these efﬁcient spaced seeds hashing algorithms to an application in the ﬁeld of metagenomic,

the classiﬁcation of reads performed by Clark-S (Ounit and Lonardi, 2016), and we shown that a signiﬁcant

speedup can be obtained, thus resolving the slowdown introduced by the use of multiple spaced seeds. Code

available at: https://github.com/CominLab/MISSH.

1 INTRODUCTION

Alignment-free methods are at the basis of

many state-of-the-art tools in sequence analysis

(A.Zielezinski et al., 2017). In fact, the scale of

data produced by current sequencing technologies

is such that alignment-based approaches struggle to

cope with the high throughput processing needed by

current applications based on sequence analysis of

massive datasets.

Most alignment-free approaches are based on se-

quences decomposition into consecutive k-mers and

on their indexing through efﬁcient data structures

(Marc¸ais et al., 2019). An example of a popular ap-

plication for such indexes is similarity search for se-

quence classiﬁcation, where the query sequence is

also decomposed into k-mers and rapidly searched for

matches on the data structure to determine the closest

similarity with the indexed sequences. Kraken (Wood

and Salzberg, 2014) and CLARK (Ounit et al., 2015)

are two popular examples of k-mers based classiﬁers

for reads in metagenomics samples.

With respect to alignment-based techniques, k-

mer based approaches are orders of magnitude faster.

However, speed improvements come at the cost of

a loss of sensitivity, due to the exact matches re-

quired in all k positions of the patterns. To allevi-

ate this problem variants of the exact k -mer matches

paradigm have been proposed. Notable examples of

such generalizations are, for example, considering

longest matches with mismatches rather than ﬁxed

length exact matches (Leimeister and Morgenstern,

2014; Apostolico et al., 2016) or allowing for not con-

secutive matches within k-mers.

The latter approach was ﬁrst proposed in the con-

text of homology search with the tool PatternHunter

(Ma et al., 2002). In that paper, Ma and colleagues

introduced the concept of spaced seed, i.e. pat-

terns of ﬁxed length that allow for wildcards in pre-

determined positions, greatly improving the chance of

ﬁnding relevant similarities. Besides further improve-

ments in homology search, e.g. (Kucherov et al.,

2006; No

e and Martin, 2014), spaced seeds have since

enabled the design of many successful algorithms in

several different context in bioinformatics. A non-

exhaustive list of examples includes: protein clas-

siﬁcation (Onodera and Shibuya, 2013); read map-

ping (Rumble et al., 2009); phylogenetic tree re-

construction (Leimeister et al., 2014; R

ohling et al.,

2020); metagenomics reads clustering and classiﬁca-

Mian, E., Petrucci, E., Pizzi, C. and Comin, M.

Efﬁcient Hashing of Multiple Spaced Seeds with Application.

DOI: 10.5220/0011632900003414

In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 3: BIOINFORMATICS, pages 155-162

ISBN: 978-989-758-631-6; ISSN: 2184-4305

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

155

tion (B

rinda et al., 2015; Girotto et al., 2017b; Ounit

and Lonardi, 2016; Wood et al., 2019); and the predic-

tion of protein-protein interaction (Li and Ilie, 2017).

Although alignment-free techniques based on

spaced seeds are faster than alignment-based ap-

proaches, they suffer from a notable slowdown in run-

ning time with respect to equivalent k-mers based so-

lutions. Indeed, k -mers indexing can beneﬁt from the

fact that consecutive k-mers share a large portion of

the sequence and this can be exploited for faster hash-

ing (Mohamadi et al., 2016). On the contrary, the

projection of two consecutive segments of a sequence

with respect to a given spaced seeds might have very

little in common, due to the positioning of the wild-

cards (Girotto et al., 2018b).

This phenomenon is ampliﬁed when multiple

spaced seeds are used. For example, it was reported

in Clark-S (Ounit and Lonardi, 2016) that using three

spaced seeds lead to a 17x slowdown. However, using

multiple spaced seed can further improve the results

of using a single spaced seed (Dencker et al., 2019).

These considerations motivate the compelling

need for the development of fast approaches for ef-

ﬁcient hashing of (multiple) spaced seeds. The ﬁrst

attempt to speeding up this process was done in (Har-

ris, 2007), where hard coding was used to speed-

up non-linear packing. More recently, several ap-

proaches have been developed based on block in-

dexing (Girotto et al., 2018a), and on spaced seeds

self correlation (Girotto et al., 2017a; Girotto et al.,

2018b; Petrucci et al., 2020) to reuse part of the hash

values that had already been computed for hashing the

previous segments of the sequence.

In this paper we present a series of algorithms

called ISSH Multi, a generalization of the ISSH

method (Petrucci et al., 2020), speciﬁcally designed

for multiple spaced seeds. Experimental comparison

showed that by processing multiple spaced seeds at

once, it is possible to further improve the speed of

spaced seed hashing. Moreover, we applied these ef-

ﬁcient spaced seeds hashing algorithms to the metage-

nomic classiﬁcation of reads performed by Clark-S

(Ounit and Lonardi, 2016), and we showed that a sig-

niﬁcant speedup can be obtained in practice on a real

application.

2 METHODS: HASHING OF

MULTIPLE SPACED SEEDS

2.1 Spaced Seeds Hashing: Background

In this section we deﬁne what spaced seeds are and

describe the way they can be used to perform the

hashing of a DNA sequence, as well as highlighting

what makes the hashing of sequences based on k-mers

more computationally efﬁcient.

A spaced seed Q is a string over the alphabet

{0, 1} of length k = s(Q) and weight w = |Q|. This

string contains w matching positions (corresponding

to the character ‘1’), and k − w non-matching posi-

tions, or “don’t care”, (corresponding to the character

‘0’): the spaced seed’s weight is therefore equal to the

number of 1s contained in the seed itself. A spaced

seed Q can be represented as a set of non negative in-

tegers corresponding to the matching positions (1s) in

the seed.

These spaced seeds can be used as a mask that,

when super-imposed on a DNA sequence with an

AND operation, only lets through the characters that

corresponds to a matching position ‘1’. The sub-

strings obtained will be called Q-grams, and they are

deﬁned as x[i+Q] = {x

i+k

, k ∈ Q}, where i is the posi-

tion in the sequence where the spaced seed is aligned.

Example 2.1. Given the spaced seed Q = 10111011,

deﬁned as Q = {0, 2, 3, 4, 6, 7}, with length k = 8

and weight w = 6. Let us consider the string x =

AT GGCAGTCA, the Q-gram x[1 + Q] = T GCATC

can be deﬁned as follows:

x A T G G C A G T C A

Q 1 0 1 1 1 0 1 1

x[1+Q] T G C A T C

As mentioned before, the use of spaced seeds

signiﬁcantly improves the sensitivity of similarity

searches regarding DNA sequences, but, when used

in conjunction with hashing, it does so at the detri-

ment of the computation speed. The reason for this

is that the hash of a generic k -mer can be computed

from the hash of its predecessor, something that is not

immediately possible when computing the hash of a

Q-gram obtained from a spaced seed.

In this paper, for ease of discussion, we will

consider as hashing function the simple encoding

of a string, that is a special case of the Rabin-

Karp rolling hash. Let’s consider a coding func-

tion from the DNA alphabet A = {A,C, G, T } to a

binary codeword, encode : A → {0, 1}

log

|A|

, where

encode(A) = 00, encode(C) = 01, encode(G) = 10,

and encode(T ) = 11. Given a string of n consecu-

tive characters, ﬁrst the encoding function is applied

to each character. Then a shift based on the position

the character occupies in the original string will be

performed. Formally:

h(x[i + Q]) =

k∈Q

(encode(x

i+k

) ≪ m(k) ∗ log

|A|) (1)

where m(k) = |{i ∈ Q, such that i < k}| is the number

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

156

of matching positions that appear to the left of k. Each

character is encoded, as seen above, with 2 bits, and

the number of shifts required to set the k-th character

in the correct position is m(k) ∗log

|A|.

Example 2.2. Given the sequence x, we compute

the hashing value of the ﬁrst Q-gram obtained using

spaced seed Q = 10111011. x

is the Q-gram obtained

from the ﬁrst projection:

x = A T G G C A G T C A

1 0 1 1 1 0 1 1

= A G G C G T = x[0 + Q]

The hashing value of x

is therefore:

h(x

) = h(AGGCGT )

= 111001101000

To compute the hash of a contiguous k-mer it is

possible to use the hash of its predecessor. In fact,

given the hashing value at position i, the hashing for

position i + 1 can be obtained with two operations, a

shift and the insertion of the encoding of the new sym-

bol, since the two hashes share k − 1 symbols. How-

ever, if we consider the case of a spaced seed Q, we

can clearly see that this observation does not hold. In

fact, in the above example, two consecutive Q-grams,

like x[0 + Q] = AGGCGT and x[1 + Q] = T GCATC,

do not necessarily have much in common.

Computing efﬁciently the hash of the a DNA se-

quence based on a spaced seed is more complicated

than with k-mers. When we overlap the spaced seed

on the DNA sequence, we need, ﬁrst of all, to ex-

tract the corresponding Q-gram, and only then we can

compute the hash of this substring. Then, the spaced

seed is moved one position to the right, and the pro-

cess is repeated for each Q-gram that can thus be ex-

tracted from the DNA sequence.

= A G G C G T

= T G C A T C

h(x

) = 11 10 0110 1000

h(x

) = 01 11 00 0110 11

It is evident that recovering certain positions from

the previous hash to reuse them in the second one

is not as straightforward as with k-mers, because the

spaced seed, depending on how the matching posi-

tions where overlapping on the DNA sequence, will

have ﬁltered different nucleotides.

2.2 Previous Work

The problem of spaced seeds hashing is to ﬁnd in-

creasingly more efﬁcient ways to exploit the similar-

ity between different Q-grams, in order to minimize

the number of encoding and shift operations that need

to be applied to compute the hashing of a DNA se-

quence based on spaced seeds. Here, we review the

most common approaches proposed in the literature:

Fast spaced Seed Hashing (Girotto et al., 2018b),

Fast Indexing for spaced Seed Hashing (Girotto et al.,

2018a) and Iterative Spaced Seed Hashing (Petrucci

et al., 2020).

The ﬁrst approach is Fast spaced Seed Hashing

(FSH) (Girotto et al., 2018b), which exploits the sim-

ilarity of adjacent hash values of the same DNA se-

quence to compute each hash more efﬁciently. To do

so, it recovers some information from previous com-

putations: speciﬁcally, it reuses parts of a hash value

already computed by extracting them through a mask

and then combining the result with the encoding of

the remaining positions.

In Fast Indexing for Spaced seed Hashing (FISH),

described in (Girotto et al., 2018a), a completely dif-

ferent approach, based on block-indexing, was pro-

posed. A unit block is a block of consecutive ‘1’s, in

which the spaced seed is decomposed. These blocks

are interpreted by the algorithm as k-mers of different

lengths, which can be hashed quickly. Since FISH re-

duces the problem of spaced seed hashing to the hash-

ing its k-mer components, this approach can obtain a

substantial improvement in computation time with re-

spect to FSH.

The Iterative Spaced Seed Hashing (ISSH) algo-

rithm described in (Petrucci et al., 2020), ﬁnally, is an

evolution of FSH. What distinguishes the two is that

ISSH recovers information from more than one pre-

vious hash: it uses a greedy approach to iteratively

search for hashes that allow to maximize the num-

ber of positions recovered (each time only taking into

consideration the characters remaining to be encoded)

and does not stop until either all positions are recov-

ered, or no more positions can possibly be recovered

from the hashes already computed.

Example 2.3. Given spaced seed Q = 11101010101,

we look for the positions where both Q and its shift

Q − 1 or Q − 2 present a matching position ‘1’. Those

positions in the hashing of the Q-gram extracted by

the seed Q will be recovered and reused to compute

the hashing of the Q-gram corresponding to the

spaced seed Q − 1 (or Q − 2).

Efﬁcient Hashing of Multiple Spaced Seeds with Application

157

FSH only considers the ﬁrst possible attachment

point:

Pos. ‘1’ 0 1 2 3 4 5 6

Q 1 1 1 0 1 0 1 0 1 0 1

Q − 1 1 1 1 0 1 0 1 0 1 0 1

Pos. ‘1’ 0 1 2 3 4 5 6

Q 1 1 1 0 1 0 1 0 1 0 1

Q − 2 1 1 1 0 1 0 1 0 1 0 1

ISSH can also choose a different shift, as seen

when recovering positions from Q − 2:

Pos. ‘1’ 0 1 2 3 4 5 6

Q 1 1 1 0 1 0 1 0 1 0 1

Q − 1 1 1 1 0 1 0 1 0 1 0 1

Pos. ‘1’ 0 1 2 3 4 5 6

Q 1 1 1 0 1 0 1 0 1 0 1

Q − 2 1 1 1 0 1 0 1 0 1 0 1

In FSH and ISSH masks are used to extract from

a previous hash the relevant positions to be recovered,

and these masks can be computed by a preprocessing

that only takes the spaced seeds in input, and is inde-

pendent from the actual DNA sequence to be hashed.

2.3 Efﬁcient Multiple Spaced Seed

Hashing

In the following we describe our contribution to the

speedup of the computation of the hashing of DNA

sequences using multiple spaced seeds. We expand

on the method described in ISSH (Petrucci et al.,

2020) to further improve its efﬁciency by consider-

ing a group of spaced seeds at the same time, and we

analyze and compare three different approaches to do

so.

2.3.1 ISSH Multi

The ﬁrst method we describe is called ISSH Multi.

This approach considers multiple spaced seeds at the

same time, but the hashing of the DNA sequence is

computed almost completely independently for each

spaced seed. This means that, for each hashing, infor-

mation is only recovered from hash values that were

calculated on the same spaced seed. In practice, this

implies that the preprocessing necessary for this ap-

proach is the same that was used in ISSH.

However, unlike ISSH, the hashing matrix is ﬁlled

in by columns: for each possible overlap with the

DNA sequence, the hash values are computed for each

ISSH Multi

Current hash

Encoding computed

only once

Previously computed hashes, more than one is used in order to

recover all the position but the last one.

In each row only previous hashes from the same row are reused

ISSH Multi Column

Current hash

Previously computed hashes, more than one is used in

order to recover all the positions

ISSH Multi Row

Previously computed hashes, more than one

is used in order to recover all the positions

Current hash

Figure 1: A schematic representation of the ISSH Multi

computations. The rows of the matrix represent the differ-

ent spaced seeds, whereas the columns the position of the

sequence where to compute the hash.

spaced seed one after the other. This provides a com-

putational advantage in the encoding of the last char-

acter of each Q-gram, which is always being seen for

the ﬁrst time and which always belongs to all hash-

ing values, because by deﬁnition a spaced seed’s last

character is ‘1’. This encoding can therefore be com-

puted only once through the encoding function, and

inserted into the hash values of the current overlap for

all spaced seeds considered, thus saving a number of

encoding operations equal to # of spaced seeds−1 for

each position. For space limitation we do not report

the algorithm as it is a special case of the next algo-

rithm ISSH Multi Column. A schematic description

of the method ISSH Multi is shown in Figure 1.

2.3.2 ISSH Multi Column

The second approach we explored is ISSH Multi Col-

umn, which, once again, considers multiple spaced

seeds in input at the same time, and, like ISSH Multi,

it ﬁlls in the hashing matrix by columns.

The difference with the former is that ISSH Multi

Column introduces a new degree of freedom, by al-

lowing the choice of the hashing to recover position

from to include hashes computed using a different

spaced seed from the current one considered (that is, it

searches the best hash also from different rows/spaced

seeds of the hashing matrix). A schematic description

of ISSH Multi Column can be found in Figure 1.

This means that, to compute the generic hash

h(i, j), where i is the index of the spaced seed (i.e.

row in the hashing matrix) and j is the index of the

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

158

Algorithm 1: ISSH Multi Column (x, spacedSeeds,

ssLength, ssWeight).

Input: x ← DNA sequence

spacedSeeds ← group of spaced seeds

ssLength ← length of the spaced seeds

ssWeight ← weight of the spaced seeds

Output: Hash ← matrix containing all the computed

hashes.

1: for j := 0, |x| − ssLength do

2: for all i ∈ spacedSeeds do

3: Hash[i][ j] := 0

4: while missing positions can be recovered

from available hashes do

5: (n, m, l) := such that condition (2)

holds and Hash[n][m] with shift l allows to re-

cover the highest number of missing positions.

6: Hash[i][ j] := Hash[i][ j] OR

(Hash[n][m] ≫ 2 ∗ l AND mask(i, n, m, l))

7: end while

8: if there are still missing positions then

9: add missing encodings to Hash(i, j)

10: end if

11: end for

12: end for

13: return matrix Hash

Q-gram to be hashed (i.e. column in the hashing ma-

trix), we can search for the one that allows to recover

most positions among all previously computed hashes

h(n, m). Note, that the best previous hash h(n, m), it

does not depend on the sequence to be hashed, but

only on the structure of the spaced seed, and thus

the best values of (n, m) and the shift l can be eas-

ily pre-computed. In order to extract the symbols

from h(n, m) to be reused in the new hash h(i, j) we

deﬁne a mask, mask(i, n, m, l), that ﬁlters these po-

sitions. However, the hash h(n, m) must be already

computed. The following condition sums up all the

constraints that a hash h(n, m) needs to satisfy in or-

der to be used for recovering positions for the current

hash h(i, j):

(m < j OR (m = j AND n < i)) AND m ≥ 0 (2)

The big advantage of this method is that the num-

ber of encoding operations to be done during the tran-

sient is much lower: even the hashing of the ﬁrst

Q-gram of the second spaced seed already has the

chance of recovering positions from the very ﬁrst

hash, which wasn’t possible before. Ultimately, the

encoding function is only used once for each charac-

ter in the sequence even during the transient, allowing

for a signiﬁcant improvement in computation times

compared to ISSH Multi.

2.3.3 ISSH Multi Row

The third and last method – ISSH Multi Row – fol-

lows the same scheme of the previous one, but it ﬁlls

in the hashing matrix by rows, making it possible

to also recover positions from hashes that have been

computed with different spaced seeds, and that corre-

spond to a Q-gram on the right of the current one.

Equivalently to what we described before, to com-

pute the generic hash h(i, j) we can search for a hash

h(n, m) from which to recover information where n <

i (that is, all preceding rows) or n = i and m < j (that

is, same row but preceding columns – all hashes that

have been computed with the same spaced seed but of

Q-grams extracted from preceding overlaps). There-

fore in order to use h(n, m) to compute h(i, j) the fol-

lowing condition must hold:

[n < i OR (n = i AND m < j)]

AND (0 ≤ m ≤ |sequence| − s(Q))

(3)

A schematic description of the method ISSH

Multi Row is shown in Figure 1. The introduction

of subsequent hashes in addition to preceding ones,

(meaning that they correspond to Q-grams generated

from overlaps of the spaced seeds located further on

the right of the current position) also implies a sig-

niﬁcant modiﬁcation of the transient phase. Specif-

ically, there are two transients, one at the beginning

and one at the end of the DNA sequence, because

the hashes “on the right” computed in the preprocess-

ing will eventually not be available, just as the hashes

“on the left” were not initially available. For these

reasons, we expect this method to perform better on

longer sequences.

3 RESULTS

Here we present the results of our experiments that

compare the newly presented Multi Spaced Seed al-

gorithms against the previously available approaches

in literature, namely FISH (Girotto et al., 2018a)

(block-based), FSH (Girotto et al., 2018b) and ISSH

(Petrucci et al., 2020) (overlap-based). All the tests

were performed consistently with the experiments

presented in previous studies. In order to evaluate

our methods under different circumstances we con-

sidered several group of spaced seeds with differ-

ent weights and lengths and computed using different

methods (maximizing the hit probability (Ounit and

Lonardi, 2016); minimizing the overlap complexity

and maximizing the sensitivity (Hahn et al., 2016)).

The spaced seeds used can be found in the appendix of

(Petrucci et al., 2020). The DNA sequences of which

Efﬁcient Hashing of Multiple Spaced Seeds with Application

159

the hashing is computed consist in several dataset of

metagenomic reads, each with a different read count

and a different read length. All the experiments have

been performed on a laptop equipped with an Intel i9-

9980HK CPU at 2.4 GHz and 16 GB of RAM. For the

consistency of the results and comparisons presented

we run on the same machine the programs made avail-

able by the previous papers (Girotto et al., 2018b;

Girotto et al., 2018a; Petrucci et al., 2020).

The results are expressed in terms of the speedup,

that is the ratio of the time that is spent to compute the

hash using the reference method (that calculates each

hash position starting from the read in input using for-

mula (1)) over the time needed by the method that is

currently being evaluated.

3.1 Performance Evaluation

In Figure 2 is shown the speedup for the different

methods when considering the ﬁrst group of 9 spaced

seeds with length 31 and weight 22. The datasets,

displayed on the x-axis, are ordered by increasing av-

erage read length.

Figure 2: Speedup of the hashing computation when con-

sidering spaced seeds W22L31.

From this graph we can see how the three new

methods presented in this paper provide a greater

speedup with respect to the previously proposed

methods. In particular we found out that, for this

group of spaced seeds, even the ISSH method reit-

erated for each of the seed obtains a higher speedup

with respect to the FISH approach.

Among all the newly proposed methods ISSH

Multi Column obtains overall the highest speedup, but

it is slightly surpassed by ISSH Multi Row for the

datasets with the longest reads. For each of the tested

methods an increase in the speedup can be noticed

when the average read length increases: this is due

to the contribution of the transient time that is more

predominant the shorter the read.

This holds especially true for ISSH Multi and

ISSH Multi Row: the ﬁrst method only improves after

the transient and uses the same transient as ISSH; the

second method is additionally penalized when dealing

with short reads because it requires two transients. On

this test, these new methods can reach speedups above

17x whereas all previous methods are lower than 10x.

If we consider another group of spaced seeds, hav-

ing length 45 and weight 32 (data not shown), we can

obtain even higher speedups. Overall, on this test the

average speedup of FSH-Multi is 1.9x, FISH-Multi

7.2x, ISSH Multi Row 14.9x and ISSH Multi Column

18.1x.

Figure 3: Average speedup for all spaced seeds groups of

the hashing computation.

In Figure 3 we show the average speedup for each

group of seeds. We can see that the previous consid-

erations still hold: having groups of spaced seeds that

are longer and have a higher weight leads to higher av-

erage speedups irrespective of the method used. Even

considering the average speedup, the method rank-

ing is the same: the ISSH Multi Column approach

is the one which offers the highest speedup for each

group of spaced seeds, with ISSH Multi Row being a

close second. From Figure 2 it is possible to see how

ISSH Multi Row starts to perform better when longer

sequences are considered, even obtaining a speedup

slightly higher than ISSH Multi Column.

Our tests show how performing the hashing con-

sidering multiple spaced seeds at a time can decrease

the computation time signiﬁcantly, which can be no-

ticed for each method. Using multiple spaced seeds,

the average speedup for FSH improves from 1.5x

to 1.56x, for FISH improves from 3.4x to 6.3x and

for ISSH improves from 6.8x to 13.38x, obtained by

ISSH Multi Column.

In Figure 4 we present the analysis on how

the speedup changes when changing the number of

spaced seeds considered in a group. We conducted

this test by considering the group of spaced seeds

W22L31, speciﬁcally computing the hashing using

subsets incrementally bigger up to using all the 9

spaced seeds. We can see in Figure the improvement

of using a “multi” version of the algorithm – with re-

spect to using the single seed version – when increas-

ing the number of spaced seed considered. It is inter-

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

160

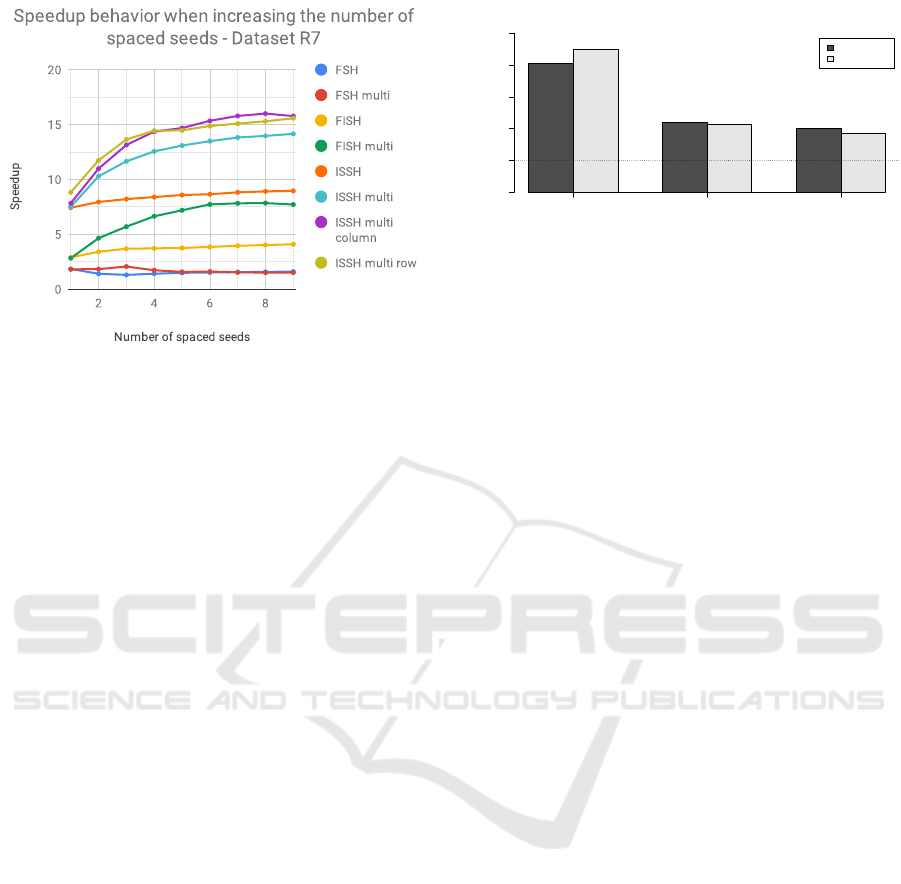
Figure 4: Speedup on dataset R7 when considering a differ-

ent number of spaced seeds.

esting to note that the highest speedup improvement

is noticeable when considering a number of spaced

seeds between 2 and 6. Obtaining comparably higher

speedups even for smaller groups of spaced seeds that

contain only 2-6 of them is an interesting result: the

proposed methods can offer signiﬁcant improvements

in terms of speed even in the case of having to use less

spaced seeds for memory limitations, like with Clark-

S that uses only 3 spaced seeds (Ounit and Lonardi,

2016).

3.2 Multiple Spaced Seeds Application:

Metagenomic Classiﬁcation of

Clark-S

In this section we test the ability of our hashing al-

gorithms to speed up the metagenomic classiﬁcation

of reads performed by Clark-S (Ounit and Lonardi,

2016). Clark-S is the spaced seed version of Clark

and it signiﬁcantly improves the sensitivity w.r.t. to

the original k-mers version. However, this gain comes

at the cost of the computational time, in fact Clark-S

is much slower than Clark. There are two main rea-

sons for this slowdown, one is the fact that Clark-S is

based on spaced seeds, the second is that it is uses not

just one, but three spaced seeds simultaneously. Thus,

the metagenomic classiﬁcation of reads performed by

Clark-S is the perfect application to test our new hash-

ing algorithms.

We modiﬁed the source code of Clark-S in order

to include ISSH Multi Column, and test the speedup

with respect to the original implementation of Clark-

S. We used as test a set of short reads from the Hu-

mane Microbiome Project, SRR1804065, and a set of

long reads, named Rlong, obtained by merging the

datasets R7, R8 and R9.

Qw14 Qw18 Qw22

SRR1804065

Rlong

Speedup with Variably−Weighted Seeds

Spaced Seeds Set

speedup

0 1 2 3 4 5

4.046

4.478

2.206

2.141

2.018

1.859

Figure 5: Speedup brought by ISSH Multi Column to Clark-

S with different spaced seeds of variable weight.

In Figure 5 are reported the speedups for a set

of spaced seeds with length 32, while varying the

weight. It can be observed that, the new implemen-

tation of Clark-S is much faster than the original one,

in fact the speedup ranges between 1.85x to 4.47x. It

is worth noting that these speedups are lower than the

ones we have seen in the previous experiments. In

fact, the classiﬁcation of reads performed by Clark-S

is based on the hashing values of spaced seeds, but it

also requires other speciﬁc processing and data struc-

tures. Nevertheless, we showed that efﬁcient hashing

algorithms can be applied to Clark-S, with a signiﬁ-

cant speedup with respect to the original implementa-

tion, and thus resolving the slowdown introduced by

the use of spaced seeds.

4 CONCLUSIONS

In this paper we present an set of new algorithms for

problem of multiple spaced seed hashing, to address

the computational slowdown that has been shown in

literature with respect to the use of k-mers.

By considering multiple spaced seeds at the same

time the methods we presented managed to exploit the

hash values already computed at preceding steps to

minimize both the number of encoding operations to

be carried out and the number of previously computed

hashes from which positions are recovered.

We reported the results on several tests, which

show that our methods offer a valuable speedup even

when considering a small number of spaced seeds,

and signiﬁcantly outperform in all tests the previously

proposed algorithms, with a speedup that can reach

20x. ISSH Multi Column appears to be the fastest

algorithm, but the results reported suggest that, for

longer reads, ISSH Multi Row could offer even better

performance.

We also apply these efﬁcient hashing algorithms

to an application in the ﬁeld of metagenomic, the

classiﬁcation of reads performed by Clark-S (Ounit

Efﬁcient Hashing of Multiple Spaced Seeds with Application

161

and Lonardi, 2016), and we shown that a signiﬁcant

speedup can be obtained, thus resolving the slowdown

introduced by the use of spaced seeds.

The approaches that we presented rely on a greedy

preprocessing, similarly to the one adopted by ISSH.

Possible future extensions could focus on improving

this preprocessing: instead of using a greedy pol-

icy for selecting the group of previously computed

hashes from which to extract the positions to reuse,

it could be beneﬁcial to investigate global optimiza-

tion schemes in order to make the computation even

faster.

REFERENCES

Apostolico, A., Guerra, C., Landau, G. M., and Pizzi,

C. (2016). Sequence similarity measures based on

bounded hamming distance. Theoretical Computer

Science, 638:76 – 90.

A.Zielezinski, Vinga, S., Almeida, J., and et al. (2017).

Alignment-free sequence comparison: beneﬁts, appli-

cations, and tools. Genome Biol, 18:186.

rinda, K., Sykulski, M., and Kucherov, G. (2015). Spaced

seeds improve k-mer-based metagenomic classiﬁca-

tion. Bioinformatics, 31(22):3584.

Dencker, T., Leimeister, C.-A., Gerth, M., Bleidorn, C.,

Snir, S., and Morgenstern, B. (2019). ‘Multi-SpaM’:

a maximum-likelihood approach to phylogeny recon-

struction using multiple spaced-word matches and

quartet trees. NAR Genomics and Bioinformatics,

2(1). lqz013.

Girotto, S., Comin, M., and Pizzi, C. (2017a). Fast spaced

seed hashing. In Proceedings of the 17th Workshop

on Algorithms in Bioinformatics (WABI), volume 88

of Leibniz International Proceedings in Informatics,

pages 7:1–7:14.

Girotto, S., Comin, M., and Pizzi, C. (2017b). Metage-

nomic reads binning with spaced seeds. Theoretical

Computer Science, 698:88–99.

Girotto, S., Comin, M., and Pizzi, C. (2018a). Efﬁcient

computation of spaced seed hashing with block index-

ing. BMC Bioinformatics, 19(15):441.

Girotto, S., Comin, M., and Pizzi, C. (2018b). Fsh: fast

spaced seed hashing exploiting adjacent hashes. Al-

gorithms for Molecular Biology, 13(1):8.

Hahn, L., Leimeister, C.-A., Ounit, R., Lonardi, S.,

and Morgenstern, B. (2016). Rasbhari: Optimiz-

ing spaced seeds for database searching, read map-

ping and alignment-free sequence comparison. PLOS

Computational Biology, 12(10):1–18.

Harris, R. S. (2007). Improved Pairwise Alignment of Ge-

nomic Dna. PhD thesis, University Park, PA, USA.

Kucherov, G., No

e, L., and Roytberg, M. A. (2006). A uni-

fying framework for seed sensitivity and its applica-

tion to subset seeds. Journal of Bioinformatics and

Computational Biology, 4(2):553–569.

Leimeister, C. and Morgenstern, B. (2014). Kmacs: the

k-mismatch average common substring approach to

alignment-free sequence comparison. Bioinformat-

ics., 30(14):2000–8.

Leimeister, C.-A., Boden, M., Horwege, S., Lindner, S., and

Morgenstern, B. (2014). Fast alignment-free sequence

comparison using spaced-word frequencies. Bioinfor-

matics, 30(14):1991.

Li, Y. and Ilie, L. (2017). Sprint: ultrafast protein–protein

interaction prediction of the entire human interac-

tome. BMC Bioinformatics, 18(485).

Ma, B., Tromp, J., and Li, M. (2002). Patternhunter: faster

and more sensitive homology search. Bioinformatics,

18(3):440.

Marc¸ais, G., Solomon, B., Patro, R., and Kingsford, C.

(2019). Sketching and sublinear data structures in ge-

nomics. Annual Review of Biomedical Data Science,

2(1):93–118.

Mohamadi, H., Chu, J., Vandervalk, B. P., and Birol, I.

(2016). ntHash: recursive nucleotide hashing. Bioin-

formatics, page btw397.

e, L. and Martin, D. E. K. (2014). A coverage criterion

for spaced seeds and its applications to support vector

machine string kernels and k-mer distances. Journal

of Computational Biology, 21(12):947–963.

Onodera, T. and Shibuya, T. (2013). The gapped spectrum

kernel for support vector machines. In Proceedings

of the 9th Conference on Machine Learning and Data

Mining in Pattern Recognition, MLDM’13, pages 1–

15. Springer-Verlag.

Ounit, R. and Lonardi, S. (2016). Higher classiﬁcation

sensitivity of short metagenomic reads with clark-s.

Bioinformatics, 32(24):3823.

Ounit, R., Wanamaker, S., Close, T. J., and Lonardi, S.

(2015). Clark: fast and accurate classiﬁcation of

metagenomic and genomic sequences using discrim-

inative k-mers. BMC Genomics, 16(1):1–13.

Petrucci, E., No

e, L., Pizzi, C., and Comin, M. (2020). It-

erative spaced seed hashing: Closing the gap between

spaced seed hashing and k-mer hashing. Journal of

Computational Biology, 27(2):223–233.

Rumble, S. M., Lacroute, P., Dalca, A. V., Fiume, M.,

Sidow, A., and Brudno, M. (2009). Shrimp: Accurate

mapping of short color-space reads. PLOS Computa-

tional Biology, 5(5):1–11.

ohling, S., Linne, A., Schellhorn, J., Hosseini, M.,

Dencker, T., and Morgenstern, B. (2020). The num-

ber of k-mer matches between two dna sequences as

a function of k and applications to estimate phyloge-

netic distances. PLoS One, 15.

Wood, D., Lu, J., and Langmead, B. (2019). Improved

metagenomic analysis with kraken 2. Genome Biol,

20(257).

Wood, D. E. and Salzberg, S. L. (2014). Kraken: ultra-

fast metagenomic sequence classiﬁcation using exact

alignments. Genome Biology, 15:R46.

BIOINFORMATICS 2023 - 14th International Conference on Bioinformatics Models, Methods and Algorithms

162