Optimal Static Bidding Strategy for Running Jobs with Hard Deadline

Constraints on Spot Instances

Kai-Siang Wang, Cheng-Han Hsieh and Jerry Chou

National Tsing Hua University, Hsinchu, Taiwan, Republic of China

Keywords:

Cloud Computing, Bidding Strategy, EC2, Spot Instance, Deadline Constraint.

Abstract:

Spot-instances(SI) is an auction-based pricing scheme used by cloud providers. It allows users to place bids for

spare computing instances and rent them at a substantially lower price compared to the ﬁxed on-demand price.

This inexpensive computational power is at the cost of availability, because a spot instance can be revoked

whenever the spot market price exceeds the bid. Therefore, SI has become an attractive option for applications

without requiring real-time availability constraints, such as the batch jobs in different application domains,

including big data analytics, scientiﬁc computing, and deep learning. For batch jobs, service interruptions and

execution delays can be tolerated as long as their service quality is gauged by an execution deadline. Hence,

this paper aims to develop a static bidding strategy for minimizing the monetary cost of a batch job with hard

deadline constraints. We formulate the problem as a Markov chain process and use Dynamic Programming

to ﬁnd the optimal bid in polynomial time. Experiments conducted on real workloads from Amazon Spot

Instance historical prices show that our proposed strategy successfully outperformed two state-of-art dynamic

bidding strategies (Amazing, DBA), and several deadline agnostic static bidding strategies with lower cost.

1 INTRODUCTION

Clouds have become an attractive computing platform

for many applications. It is a computing paradigm

to deliver ready-to-use, on-the-ﬂy conﬁgurable re-

sources as services on Internet, and to charge these

services on a pay-as-you-use pricing model. The elas-

ticity and on-demand characteristics of cloud com-

puting further ensure higher resource utilization and

lower computing cost to users. One of the most fa-

mous cloud services is Amazon’s EC2 (EC2, 2009).

EC2 provides raw computing resources in the form of

Virtual Machines(VM). To meet computing require-

ments of a wide variety of applications, different pric-

ing options are offered, including On-Demand (OD),

Reserved and Spot Instances (SI). On-Demand pro-

vides dedicated access to a set of machines for a ﬁxed

cost per hour with no long term commitments. On the

other hand, Reserved offers a signiﬁcant discount on

hourly charge over On-demand, but users must make

a one-time, upfront payment to lease the VMs for long

periods of time (1 or 3 year terms).

In contrast to On-Demand and Reserved instances

which are charged with ﬁx price rates, Spot Instances

allow customers to bid on spare computing capacity

with no upfront commitment and at a variable hourly

rates called the spot price (or market price). The spot

price is determined by the cloud providers based on

the demand of VMs within their infrastructure. If

the bid price submitted by a user is higher than the

spot price (which is called in-bid), then the user re-

ceives his requested instances and only pay at the

cost of spot price. Hence, many studies (Yi et al.,

2012a; Mazzucco and Dumas, 2011) have shown that

spot instances can greatly reduce the execution cost.

But, this inexpensive computational power is at the

cost of availability, because a spot instance can be

revoked whenever the spot market price exceeds the

bid (which is called out-bid). Furthermore, when a

out-bid event occurs, not only the VM becomes un-

available for the given hour, its jobs also need to be

recovered from a previous checkpoint. As a result, a

lower bid price can reduce the monetary cost, but also

potentially increase the job execution time.

While SI may not meet the computing require-

ments of any application, it is an attractive option for

batch jobs. A batch job is often described by a com-

putation time and a deadline, The computation time

can be spread within the time-window speciﬁed by

the deadline, so that the service interruptions and exe-

cution delays caused on the revocable resource can be

tolerated. (Andrzejak et al., 2010a) is one of the earli-

Wang, K., Hsieh, C. and Chou, J.

Optimal Static Bidding Strategy for Running Jobs with Hard Deadline Constraints on Spot Instances.

DOI: 10.5220/0011645400003488

In Proceedings of the 13th International Conference on Cloud Computing and Services Science (CLOSER 2023), pages 123-130

ISBN: 978-989-758-650-7; ISSN: 2184-5042

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

123

est work to show the potential cost saving from using

SI, and analyze the complicated correlation between

bid price, job execution time and monetary cost on

SI. Since then, many research efforts have been made

aiming to ﬁnd the bidding strategies for minimizing

monetary cost under different problem settings, in-

cluding the constraints of job execution, the check-

point scheme for fault recovery, the transition model

of spot price, etc.

Amazing (Tang et al., 2012) and DBA(dynamic

bidding algorithm) (Song et al., 2012) are the two

start-of-art dynamic approaches that claims to achieve

optimal bids for job with deadline constraints. Amaz-

ing uses a dual-option bidding strategy, which either

bids on the max price or zero dollars for the next

instance hour according to the current running state

and spot price. It formulates this problem as a Con-

strained Markov Decision Process (CMDP), and ﬁnds

an optimal randomized bidding strategy through lin-

ear programming. However, Amazing only guarantees

the expected execution time to be less or equal to the

deadline, so it is an approach for job with soft dead-

line constraints. On the other hand, DBA guarantee

jobs to be ﬁnished before their deadlines by switching

to On-Demand instances when necessary. Like most

dynamic approaches, it assumes the bid price can be

adjusted without interrupting the VM instances. But

in the real EC2 environment, spot instance request can

only be associated with one bid price. Thus, in order

to change bid price, users have to cancel the exist-

ing SI request, and then re-create a new request with

the new bid. As a result, in practice, users still prefer

to use static bidding strategies which use a ﬁxed bid

price throughout the job execution.

To accommodate to the real cloud provider en-

vironment and cloud users behavior, this work pro-

posed a static bidding strategy for jobs with hard

deadline constraint and using hourly checkpoint re-

covery. This is one of the most commonly seen use

scenarios for spot instance. But, to our knowledge,

its optimal bids have not been discussed in the previ-

ous literature. We formulate the problem as a ﬁnite-

time stochastic dynamic program, and prove the opti-

mal bid can be determined in polynomial time. We

also show our formulation can be extended to in-

clude the execution time overhead from checkpoint

and restart process. The performance of our algo-

rithm is extensively evaluated using a real data-set of

Amazon EC2 spot price history obtained from (EC2,

). By comparing with the state-of-art dynamic bid-

ding strategies (Amazing, DBA), and several deadline

agnostic static bidding strategies, we demonstrate that

our optimal static strategy can achieve the lowest cost

with better computation efﬁciency and applicability

in practice.

The remainder of this paper is organized as fol-

lows: Section 2 introduces the characteristics of spot

instances and our problem formulation. Our bidding

algorithm is describe in Section 3 and extensively

evaluated in Section 4. Finally, related work and con-

clusions are given in Section 5 and Section 6, respec-

tively.

2 SPOT INSTANCES & PROBLEM

FORMULATION

2.1 Spot Instance Characteristics

Amazon introduces spot instances as a bidding op-

tion for excess EC2 resources. Currently there are 64

types of Spot Instances available in market, and they

differ by computing power, memory/disk space, OS

and geographical location, etc (Stokely et al., 2009a).

Amazon sets the spot price, which ﬂuctuates depend-

ing on the supply and demand of Spot Instance capac-

ity. While the Spot Price may change anytime, in gen-

eral the spot price will change once per hour, which

is named as instance hour (or time interval) in this

work, and in many cases less frequently. As observed,

the spot price is often less than 1/3 of the on-demand

price. But occasionally, the spot price can also ex-

hibit some spikes higher than the on-demand instance

price. Nevertheless, in general, spot instances still

provide a huge cost saving opportunity to users (Yi

et al., 2012b).

To use Spot Instances, users place a spot instance

request, specifying the instance type, the AWS re-

gion, the number of instances, and the maximum price

they are willing to pay per hour which is known as

the bid price. There are two main ways of request-

ing an instance also referred as bidding strategies: the

dynamic bidding strategy consists of placing a bid at

each time epoch while the static bidding strategy de-

cides only one bid until completion of the job. Cur-

rently, EC2 doesn’t allow users to change the bid price

of a Spot Instance request once it is submitted. To

change the bid price, users have to cancel the orig-

inal request, stop the running instances and create a

new request with the updated bid price. Thus, as

shown in ﬁgure. 1, dynamic strategy requires to set

a bid for each time epoch while static bidding strat-

egy bids with the same price for the course of the ex-

ecution. When a user’s bid is higher than the current

spot price, the requested resource is granted and the

user is charged by the current spot price, not the bid

price. In contrary, when a user’s bid is less than the

current price, the requested instance is stopped imme-

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

124

Figure 1: Dynamic and Static bidding strategies on Spot

Instances. The green intervals indicates the effective job

computation time. b is the static unique bid price; and for

dynamic strategy, b

represent the bid price for each time

instant.

Figure 2: Spot instance Model: the in-bid intervals are the

time epochs in which the resource is granted. The red in-

tervals require an on-demand instance to complete the job.

The completion time of the job includes the sum of all in-

tervals and is bounded by the given deadline D. The sum of

in-bid and on-demand intervals must be higher or equal to

the estimated execution time E.

diately

, and the instance usage of that partial hour is

not charged. In this work, we call the former case as

in-bid interval, and the later case as out-bid inter-

val. To recover the job progress after out-bid inter-

vals, users must make checkpoint (i.e. VM snapshot)

at the end of an in-bid interval, and restart from the

next in-bid interval using the snapshot VM image to

resume the job. As shown in ﬁgure. 1, both check-

point and restart require additional time which often

depends on the resource usage of an instance (Jang-

jaimon and Tzeng, 2015). Thus these overhead are

also considered in our problem formulation and ex-

periments.

2.2 Spot Price Model

There is very limited information available from

Amazon as to how they determine the spot price.

Amazon does not reveal bids by users or the amount

of demand. But the historical spot prices are made

available and accessible via the Amazon Console

API (Amazon, 2004). Hence, there is a general

agreement in the recent literature (Song et al., 2012;

Chohan et al., 2010; Tang et al., 2012) that the spot

price should be modeled as a stochastic process using

Markov Chain, where its current spot price depends

Currently Amazon offers a 2min notice prior to stop-

page.

only on the previous spot price. In this work, we use

S(t) to denote the spot price at an instance hour t, and

adapt the same price model deﬁned in (Song et al.,

2012). Let S(t) be a stochastic process following the

Markov model below at time t:

S(t) =

(

S(t − 1), with probability p

S, with probability (1 − p)

(1)

where S is a random variable generated from a

general distribution function f (s). We also use F(s)

to denote the cumulative distribution function of spot

price, such that F(s) = Pr(S < s). In practice, there

are only limited number of spot prices (|S| = n), and

f (s) can be an empirical distribution function derived

from observed spot price traces. Thus given a current

spot price, the price will remain the same for the next

instance hour with probability p, and change to a new

price determined by the random variable S with prob-

ability (1 − p).

We note that the above synchronous discrete-time

model is an an approximation of an actual continuous-

time spot bidding system, and the spot price could be

modeled by other Markov Chain deﬁnitions (Javadi

et al., 2011). But we justify the above model by show-

ing it captures the essential variation behavior of spot

price and provides a tractable mathematical model for

ﬁnding the optimal bids. In the experiments, we also

use the real trace of historical spot price to evaluate

our algorithms and models, and show F(s) can be de-

ﬁned as an empirical distribution function according

to the historical spot prices.

2.3 Problem Formulation

Here we formally describe our problem formulation.

Table 1 summarizes all the variables we use through-

out the paper. As shown in Figure. 2, the input of

our problem is a job described by an execution time

E and a deadline D, and the goal of our algorithms is

to ﬁnd an optimal bid price b

∗

, such that the mone-

tary cost for completing the job on spot instances is

minimized.

To form the optimization function, we ﬁrst intro-

duce the following variables to describe the running

status of a job associated with a given bid price b and

time interval t. As described in the previous subsec-

tion, the cloud provider generates a spot price S(t)

at each time interval t according to Eq. 1. If the spot

price S(t) is less or equal to the bid price b, user’s spot

instance request is granted, and the requested VM in-

stances are charged by the spot price S. Otherwise,

the user does not get any VM. Hence, we use I(t) to

Optimal Static Bidding Strategy for Running Jobs with Hard Deadline Constraints on Spot Instances

125

Table 1: Variables and descriptions.

variable description

input E job execution time

D job deadline

output b

∗

optimal bid

S spot prices. (|S| = n)

p transition probability of spot price

problem f (s) spot price distribution. F(s) = Pr(S < s)

setting S

price of on-demand instances

γ restart time overhead

κ checkpoint time overhead

B(t) bid price at time t

I(t) in-bid status at time t

status K(t) checkpoint time spent at time t

R(t) restart time spent at time t

e(t) remaining execution time

at the beginning of time t

progress at the current time interval

c(b,s

t−1

) with given bid price b and

previous spot price s

t−1

indicate whether t is an in-bid interval or out-bid in-

terval. The cost of an in-bid interval is S(t), and the

cost of a out-bid interval is 0.

I(t) =

(

1, if S(t) ≦ b(t is an in-bid interval)

0, otherwise(t is a out-bid interval)

(2)

In this paper, we consider a hourly checkpoint

strategy is used, and assume the time for checkpoint-

ing and restarting are constant values κ and γ, respec-

tively. We leave it as a future work to discuss the

possibility of adapting our model to other checkpoint

strategies, such as rising edge. Under hourly check-

point strategy, there is a checkpoint overhead at every

in-bid interval. But the restart overhead only occurs

when a out-bid interval followed by an in-bid inter-

val. Hence, at each in-bid interval t, we use variables

K(t) and R(t) to denote the overhead time spent on

checkpoint and restart as follows.

K(t) =

(

κ, if I(t) == 1

0, otherwise

(3)

R(t) =

(

γ, if I(t − 1) == 0 && I(t) == 1

0, otherwise

(4)

Accordingly, the remaining execution time at in-

terval t can be denoted by e(t) as below. The value is

taken by the ceiling function because spot instances

are purchased in the unit of hourly interval.

e(t) = ⌈E −

t−1

∑

i=0

(I(i) − K(i) − R(i))⌉ (5)

Therefore, let (e,s

t−1

,t) denote the state where e

is the amount of computation left at the start of in-

terval t, and s

t−1

is the observed spot price from the

previous interval t − 1. The monetary cost for com-

pleting the reminding execution time e starting from

job state (e,s

t−1

,t) under a given static bid b is de-

noted as C

(e,s

t−1

,t).

Furthermore, to guarantee job completion before

deadline, on-demand instance must be used when the

reminding execution time is equal to the time left.

Otherwise, any out-bid interval occurs in the future

will certainly cause job exceeds deadline. For in-

stance, if deadline is D = 8, and the reminding execu-

tion time is 3, then spot instances must be used from

t = 5. Therefore, we enforce a boundary condition,

such that

(e,s

t−1

,T ) = S

· ⌈e⌉, if ⌈e⌉ ≧ T,∀s

t−1

(6)

where S

is the on-demand price.

In sum, our problem can be formulated as below:

Input: (E, D), a job description.

init

, the spot price observed initially.

< p, f (s),S

,κ,γ >, problem set-

tings.

Output: b, the optimal bid

Objective: C

(E,s

init

,0) is minimized.

Subject to: Eq. 1 ∼ Eq. 6.

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

126

3 BIDDING STRATEGY

Our goal is to compute C

(E,s

init

,0) with a given bid

price b. First of all, at any state < e,s

t−1

,t >, as-

sume we already know the cost of all possible future

states, C

′

t−1

′

) where e

′

≤ e,s

′

t−1

∈ S, and t

′

≥ t.

Thus the monetary cost of a state < e,s

t−1

,t > can be

formulated as below based on the random variable of

current spot price s

at time interval t:

(e,s

t−1

,t) = E

(e,s

,t + 1) · (1 − I(s

≦ b))

+(s

(e − c(b, s

t−1

),s

,t + 1)) · I(s

≦ b)]

(7)

The ﬁrst term represents the cost when the current

spot price is larger than the bid price, and the second

term represents the cost when it is not. In ﬁrst term,

the current interval is out-bid, so the cost is simply

equal to the cost from t + 1 with the same remain-

ing computation time e. Whereas in the second term,

the current interval is in-bid, so the cost is the sum

of cost incurred at current time t and the accumulated

cost from time t + 1 with the remaining computation

(e − c(b,s

t−1

), where c(b,s

t−1

) is the progress of job

execution in the in-bid interval. In this work, we use

hourly checkpoint, and the restart is only required if

the previous interval is a out-bid interval. Thus, the

actual progress of an interval is depending on the pre-

vious spot price and bid price as below:

c(b,s

t−1

) =

(

1 − κ, if s

t−1

≤ b

1 − κ − γ, otherwise

(8)

Next, we replace the value of s

in Eq 7 with the

random variable S according to the spot price deﬁned

in Eq 1. After re-writing the equation, we get

(e,s

t−1

,t) = p{s

t−1

I(s

t−1

≦ b)

(e − c(b, s

t−1

),s

t−1

,t + 1)I(s

t−1

≦ b)

(e,s

t−1

,t + 1)(1 − I(s

t−1

≦ b))}

+ (1 − p){E

[SI(S ≦ b)]

+ E

(e − c(b, s

t−1

),S,t + 1)I(S ≦ b)]

+ E

(e,S,t + 1)(1 − I(S ≦ b))]}

(9)

As shown in the above equation, the value of s

t−1

remains the same throughout the recursion, and b is a

given ﬁxed value. Therefore, we further simplify the

equation and discuss its solution in two separate cases

based on the relation between s

t−1

and b as follows.

For the case of s

t−1

≦ b: The term with (1 −

I(s

t−1

≦ b)) can be eliminated from Eq. 9, and

c(b,s

t−1

) is equal to (1−κ). Therefore, the ﬁnal form

of our recursion equation becomes

(e,s

t−1

,t) =

p(s

t−1

(e − (1 − κ),s

t−1

,t + 1))

+ (1 − p){E

[SI(S ≦ b)]

+ E

(e − (1 − κ),S,t + 1)I(S ≦ b)]

+ E

(e,S,t + 1)(1 − I(S ≦ b))]}

(10)

For the case of s

t−1

> b: The term with (I(s

t−1

≦

b)) can be eliminated from Eq. 9, and c(b,s

t−1

) is

equal to (1 − κ − γ). Therefore, the ﬁnal form of our

recursion equation becomes

(e,s

t−1

,t) = pC

(e,s

t−1

,t + 1))

+ (1 − p){E

[SI(S ≦ b)]

+ E

(e − (1 − κ − γ),S,t + 1)I(S ≦ b)]

+ E

(e,S,t + 1)(1 − I(S ≦ b))]}

(11)

Clearly, in both cases, C

(e,s

t−1

,t) can be derived

from its own equation with decreasing values of e and

increasing values of t. Therefore, with the known

boundary condition stated in Eq. 6, we can compute

(e,s

t−1

,t) recursively using a DP algorithm intro-

duced in the next subsection.

4 EVALUATIONS

4.1 Setup

In order to evaluate the performance of our model,

we collected historical prices form Amazon EC2

API (Amazon, 2004) for the period of January ∼

June 2015. For the following experiment, we con-

sider the prices of the instance type us-west-1a.linux-

m1.small. We derived the price transition matrix from

the real traces, then mapped it to the random variable

S described in the problem deﬁnition in sect. 2.2. The

variation of the price interval spans from 1 to 1$.

By default, we set the checkpoint time to 5min and

the required time to restart an instance to 10min. We

compare our strategy labeled as static to a number

of existing strategies: Dynamic represents the dy-

namic optimal bidding strategy (Song et al., 2012)

and the Amazing (Tang et al., 2012) strategy which

proposed an optimal cost reduction for average com-

pletion time. Amazing basically does not propose to

solve the problem with a constrained deadline. There-

fore, it often forces to use on-demand instance when

leftover time is equal to the deadline. For a fair com-

parison, we introduced two different values (b = 0)

and (b = 0.5) which represents the percentage of ex-

tra time margin when deciding the bidding price with

Optimal Static Bidding Strategy for Running Jobs with Hard Deadline Constraints on Spot Instances

127

Amazing. For example, when b = 0 the actual ex-

ecution time is used and the likelihood of switch-

ing to on-demand instance is high. In the contrary,

when the bid price is estimated with b = 0.5, less

on-demand instances will be required. We also in-

clude naive scheduling algorithms such as bidding at

the maximum price, the mean price among al the bid-

ding prices, a randomly selected bidding price and us-

ing on-demand instances only, labeled respectively as

Max, Mean, Random and On-demand. The base-

line experiment consists of running jobs that requires

100hrs to complete. We vary the deadline D from 100

to 200 by a step of 10. The reason for doing so, is to

measure different levels of looseness of the deadline

and to capture behavior of the strategies at each point.

4.2 Monetary Cost Analysis

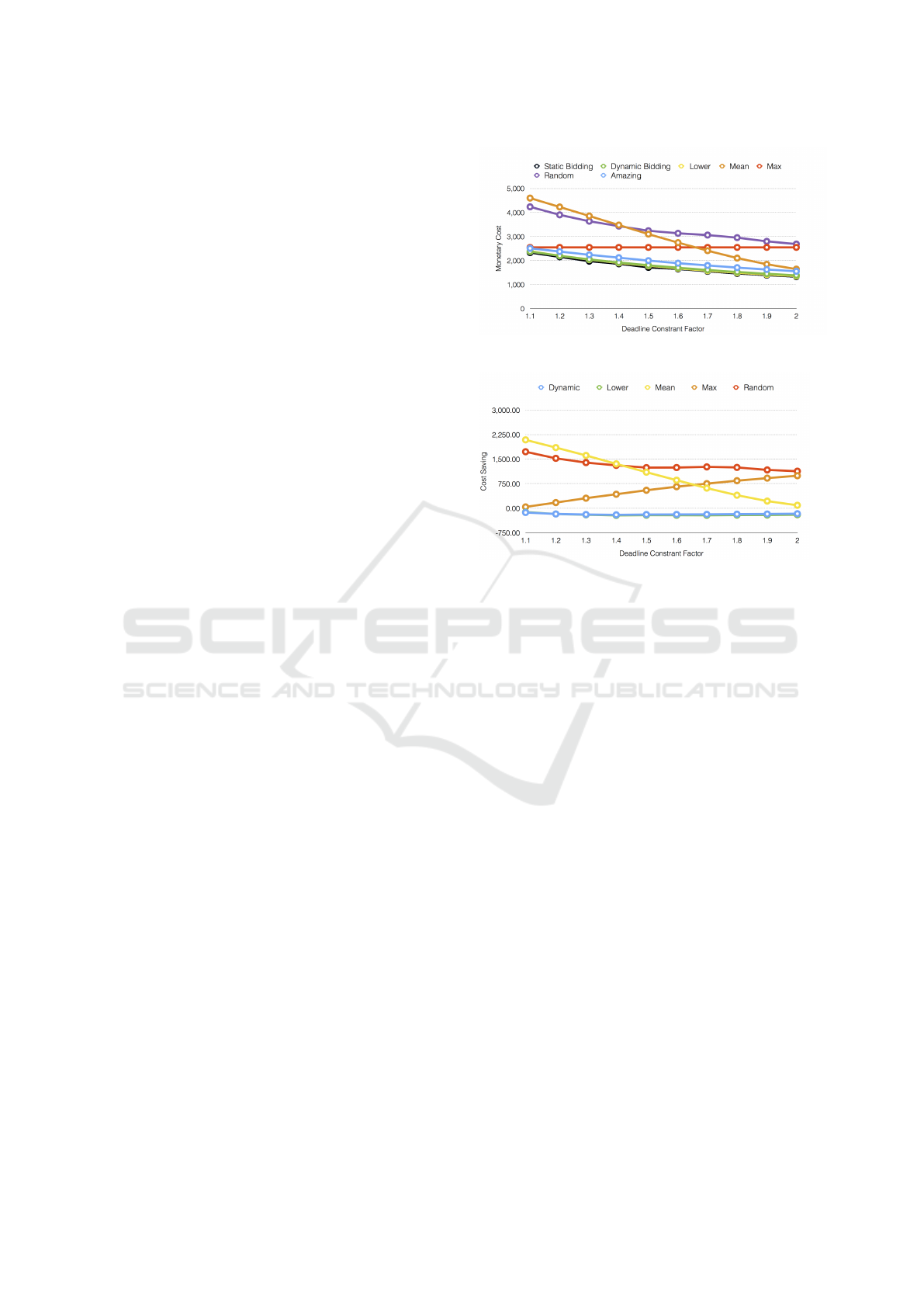
In Fig. 3, we present the average cost of 1000 runs for

all compared algorithm. Static outperforms Dynamic

by a small 2% of cost reduction. In all experiments,

Static performs the best or equal to Dynamic. The

reason lies on the restart overhead carried out in dy-

namic bidding strategy. In fact, Dynamic can make

better decisions on which interval to bid or give up,

however, it requires a restart each time a new bid is

introduced. Bidding, at on-demand price is unaware

of the deadline ﬂexibility and therefore the cost re-

mains high when deadline is loosened. In contrast,

by adopting the Mean price bidding strategy, the cost

is proportionally decreased as the deadline is loos-

ened. Amazing strategy performs better than Max,

Min and Random. However, Amazing still costs

higher than Static and Dynamic. Random price bid-

ding strategy results in a high cost when deadline is

loosened. That’s because the Random price bidding

strategy is oblivious to the execution time and the

deadline. In order to minimize the cost our strategy

takes into consideration both the execution time the

deadline and the captures the price ﬂuctuations. That

is also the case of Dynamic with a minor difference

that a new bidding price is introduced at each time

epoch, which leads to restart conditions.

Next, we evaluate the cost saving by the com-

pared algorithms. In Fig. 4, we present the cost sav-

ing as compared to the optimal Static bidding strat-

egy. Based on our observations, the cost saving as

compared to Max and Mean price bidding strategies

are inversely proportional. This is expected because

as deadline is tight, Mean quickly turns to use more

on-demand instances and cost high. At the same time

Max will use the ﬁrst T market prices. However, as

the deadline is loosened, Mean and Static both re-

duce the cost by avoiding high price intervals. There-

Figure 3: Monetary cost.

Figure 4: The amount of cost Saving from the optimal static

bidding strategy.

fore, the cost saving of static over Mean reduces as

deadline is loosened. In contrary, Max, invariably to

the deadline factor, will still use the ﬁrst T intervals.

As such, the cost saving increased because Static is

aware of the deadline factor and minimizes the cost

accordingly.

As expected using on-demand instance results in

higher cost than all other bidding strategies in Spot

instance except for tight deadline like when the ratio

E/D is 1. In this case, using spot instance will in-

troduce additional cost for restarts and checkpoints.

The Max bid strategy fails to capture the market price

ﬂuctuations . The rational in bidding on the Maxi-

mum bidding price is that the user still pays the mar-

ket price, instead of the bid price. As such, users can

achieve high availability while paying less than the

Max. However, the main reason bidding at the max-

imum price is not suitable strategy for workload with

ﬂexible deadline is that user still pays for higher price

rather than postponing for potential cheaper price.

There is inherently a dual-option bid when bidding

on spot instances as described by ShaoJie Tang et

al. (Tang et al., 2012) which consists for each time

epoch to decide to bid or not depending on the job ur-

gency and the current price. However, bidding at the

maximum price withdraws from this principle. The

conclusion we draw from these naive algorithms is

that a bidding strategy is needed.

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

128

Amazing strategy has a higher cost than our strat-

egy because Amazing cannot guarantee the deadline.

Therefore in most of the cases with tighter deadlines,

Amazing will switch quickly to on-demand instance.

Depends on the buffer setting of Amazing. It could

perform the best, but also could be worst. Neverthe-

less, Amazing has much larger variance than other

compared strategies because it bids on the highest

spot price. It shows Amazing is a more risky bid-

ding strategy and will rely more often on on-demand

instances to complete the job.

Static has similar or even lower cost than Amaz-

ing and Dynamic. It shows that dynamically chang-

ing the price is not necessary, and could cause addi-

tional computation and running overhead as explained

in section 2.1.

5 RELATED WORK

Cloud economies has drawn a tremendous attention

over the past decade (Regev and Nisan, 1998; Stokely

et al., 2009b; Chaisiri et al., 2011; Genaud and Gossa,

2011; Chard et al., 2015; Oh et al., 2022). Part of

this is attributable to the dynamic nature of cloud and

the vast pool of underutilized resources in data cen-

ters (Stokely et al., 2009a). In auction-based cloud

economies such as Spot Instances (SI), availability

and cost saving are difﬁcult tradeoff to make (Andrze-

jak et al., 2010b; Chaisiri et al., 2011; Genaud and

Gossa, 2011) since it involves understanding the mar-

ket ﬂuctuations and the resource model including the

availability. Nevertheless, spot instances still provide

cheaper resources (Lu et al., 2013). It is therefore im-

portant to design a bidding strategy to beneﬁt from

this resource model.

6 CONCLUSION

In this paper, we proposed a Static Bidding strategy to

efﬁciently decide the bid price for executing deadline-

constraint jobs on Spot Instances. The inputs of our

problem are the estimated job execution time and the

deadline to complete the job. With these information,

we use the historical market data to map the price ﬂuc-

tuation in to random variable based on the Markov

chain decision process. Furthermore, to guarantee the

completion of the job within the constrained deadline,

on-demand instances are used when the deadline is

close. We have modeled and included these consider-

ations in the optimal solution. We then pointed out the

recursive behavior of solution. Next, we prove that by

a means of a Dynamic Programming algorithm, the

optimal bidding price can be derived with the check-

point and restart overhead. Our evaluations conducted

with real historical traces from Amazon Spot markets

show that Static Bidding strategy can signiﬁcantly re-

duce the execution cost on Spot Instance, guarantee

the deadline requirement and effectively cope with the

checkpoint/restart overheads. As compared to the dy-

namic bidding strategy, our method is more practical

and suitable to the current spot markets. Moreover,

we can achieve similar or even better result than the

existing strategies.

REFERENCES

Amazon (2004). Amazon console.

Andrzejak, A., Kondo, D., and Anderson, D. (2010a). Ex-

ploiting non-dedicated resources for cloud computing.

In Network Operations and Management Symposium

(NOMS), 2010 IEEE, pages 341–348.

Andrzejak, A., Kondo, D., and Yi, S. (2010b). Decision

model for cloud computing under sla constraints. In

MASCOTS, pages 257–266.

Chaisiri, S., Kaewpuang, R., Lee, B.-S., and Niyato, D.

(2011). Cost minimization for provisioning virtual

servers in amazon elastic compute cloud. In MAS-

COTS, pages 85–95.

Chard, R., Chard, K., Bubendorfer, K., Lacinski, L., Mad-

duri, R., and Foster, I. (2015). Cost-aware cloud pro-

visioning. In IEEE International Conference on e-

Science, pages 136–144.

Chohan, N., Castillo, C., Spreitzer, M., Steinder, M.,

Tantawi, A., and Krintz, C. (2010). See spot run: Us-

ing spot instances for mapreduce workﬂows. In Hot-

Cloud, pages 7–7.

EC2, A. (2009). Amazon ec2.

Genaud, S. and Gossa, J. (2011). Cost-wait trade-offs in

client-side resource provisioning with elastic clouds.

In Cloud Computing (CLOUD), 2011 IEEE Interna-

tional Conference on, pages 1–8.

Jangjaimon, I. and Tzeng, N.-F. (2015). Effective cost re-

duction for elastic clouds under spot instance pricing

through adaptive checkpointing. IEEE Transactions

on Computers, 64(2):396–409.

Javadi, B., Thulasiramy, R., and Buyya, R. (2011). Sta-

tistical modeling of spot instance prices in public

cloud environments. In Utility and Cloud Computing

(UCC), 2011 Fourth IEEE International Conference

on, pages 219–228.

Lu, S., Li, X., Wang, L., Kasim, H., Palit, H., Hung,

T., Legara, E., and Lee, G. (2013). A dynamic hy-

brid resource provisioning approach for running large-

scale computational applications on cloud spot and

on-demand instances. In ICPADS, pages 657–662.

Mazzucco, M. and Dumas, M. (2011). Achieving perfor-

mance and availability guarantees with spot instances.

In HPCC, pages 296–303.

Optimal Static Bidding Strategy for Running Jobs with Hard Deadline Constraints on Spot Instances

129

Oh, K., Zhang, M., Chandra, A., and Weissman, J.

(2022). Network cost-aware geo-distributed data ana-

lytics system. IEEE Transactions on Parallel and Dis-

tributed Systems, 33(6):1407–1420.

Regev, O. and Nisan, N. (1998). The popcorn mar-

ket—an online market for computational re-

sources. In Proceedings of the First Interna-

tional Conference on Information and Computation

Economies, ICE ’98, pages 148–157.

Song, Y., Zafer, M., and Lee, K.-W. (2012). Optimal bid-

ding in spot instance market. In INFOCOM, pages

190–198.

Stokely, M., Winget, J., Keyes, E., Grimes, C., and Yolken,

B. (2009a). Using a market economy to provision

compute resources across planet-wide clusters. In

IPDPS, pages 1–8.

Stokely, M., Winget, J., Keyes, E., Grimes, C., and Yolken,

B. (2009b). Using a market economy to provision

compute resources across planet-wide clusters. In

IPDPS, pages 1–8.

Tang, S., Yuan, J., and Li, X. Y. (2012). Towards opti-

mal bidding strategy for amazon ec2 cloud spot in-

stance. In 2012 IEEE Fifth International Conference

on Cloud Computing, pages 91–98.

Yi, S., Andrzejak, A., and Kondo, D. (2012a). Monetary

cost-aware checkpointing and migration on amazon

cloud spot instances. IEEE Transactions on Services

Computing, 5(4):512–524.

Yi, S., Andrzejak, A., and Kondo, D. (2012b). Mone-

tary cost-aware checkpointing and migration on ama-

zon cloud spot instances. Services Computing, IEEE

Transactions on, 5(4):512–524.

CLOSER 2023 - 13th International Conference on Cloud Computing and Services Science

130