Measurements of Cross-Border Quantum Key Distribution Link

Filip Lauterbach

1 a

, Libor Michalek

1 b

, Piotr Rydlichowski

2 c

, Patrik Burdiak

1 d

Jaroslav Zdralek

1 e

and Miroslav Voznak

1 f

Faculty of Electrical Engineering and Computer Science,

VSB – Technical University of Ostrava, 17. listopadu 2172/15, 708 00 Ostrava, Czech Republic

Institute of Bioorganic Chemistry, Polish Academy of Sciences Poznan Supercomputing and Networking Center, Poznan,

Wielkopolska, Poland

Keywords:

SKR, Secret Key Rate, QBER, Attenuation, QKD, Correlation, Statistical Analysis.

Abstract:

The paper presents measurements of a Quantum Key Distribution system operating on a cross-border QKD

link between Ostrava (CZ) and Cieszyn (PL). The system is part of the Horizon OpenQKD project. The study

attempted to determine the maximum attenuation where the QKD system was still functional and also any

correlation between the crucial parameters of the quantum bit error rate (QBER), secret key rate (SKR) and link

attenuation (dB). Providing a statistical analysis of the measured data, the paper expands our understanding of

the behaviour of the QKD link as it approaches its technological limits.

1 INTRODUCTION

Data security for public internet and corporate net-

works is a logical and integral component of com-

munications infrastructure. Digital security is con-

sequential to every individual, for example in us-

ing internet banking services, social networks and

cloud services, or to companies and institutions pro-

tecting their sensitive data. Quantum key distribu-

tion (QKD) technology and post-quantum cryptogra-

phy (PQC) provide solutions which address security

problems in the emerging era of quantum comput-

ers. The main problem with symmetric cryptosystems

is securing key exchange over unsecured channels.

Public key cryptosystems, for example RSA (Rivest,

Shamir, Adleman) (Gardner, 1977) and DH (Difﬁe–

Hellman) (Li, 2010), provide the means to exchange

secret keys. Security in these public key cryptosys-

tems is based on the assumption that their complex

mathematical problems cannot be solved in real time.

Using Shor’s algorithm, however, quantum comput-

ers will be able to break these cryptosystems. Cryp-

tosystems, though, are still able to extend the size of

the secret key in the future, for example with RSA-

3072, and be ITS (Information-Theoretically Secure)

https://orcid.org/0000-0002-0176-1288

https://orcid.org/0000-0002-1117-5477

https://orcid.org/0000-0002-5050-742X

https://orcid.org/0000-0002-9739-9278

https://orcid.org/0000-0002-6886-2577

https://orcid.org/0000-0001-5135-7980

(Lauterbach et al., 2022). Quantum key distribution

(QKD) is a network communications technology that

provides information-theoretically secure (ITS) cryp-

tographic keys. Its primary purpose is to distribute

keys between distant locations. QKD also provides

other operations, such as generating and managing

these keys (Dianati and All

eaume, 2007). The work-

ing principle of QKD is based on quantum physics;

for example, the BB84, B92 and COW protocols use

elements of quantum physics (Mehic et al., 2015),

(Mehic et al., 2017), (Gisin et al., 2004). Every node

in a QKD network is connected by QKD links, which

consist of two channels – a quantum channel and a

public channel (Mehic et al., 2020). The secret key

rate (SKR) and quantum bit error rate (QBER) are

the two quantities generally presented to characterise

the performance of a QKD scheme. It is important

to keep the QBER as low as possible and the SKR as

high as possible to maintain the best achievable trans-

mission quality.

The main aim of post-quantum cryptography is to

secure against both quantum and classic computing

technology. In 2016, the National Institute of Stan-

dards (NIST) released information claiming that by

2030, quantum computers will be able to break the

2000-bit RSA algorithm in just a few hours. This is

a serious, major threat to the cryptosystems currently

standardized by NIST. (Moody et al., 2016). NIST

selected the following algorithms in the 2022, Round

4 Submissions – BIKE, Classic McEliece, HQC and

SIKE.

418

Lauterbach, F., Michalek, L., Rydlichowski, P., Burdiak, P., Zdralek, J. and Voznak, M.

Measurements of Cross-Border Quantum Key Distribution Link.

DOI: 10.5220/0011647200003405

In Proceedings of the 9th International Conference on Information Systems Security and Privacy (ICISSP 2023), pages 418-423

ISBN: 978-989-758-624-8; ISSN: 2184-4356

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

2 STATE OF THE ART

Mingjian He et al. studied the application of noise-

less attenuation and noiseless ampliﬁcation in multi-

mode continuous variable quantum key distribution

over satellite-to-ground channels. In their experi-

ments, the authors applied noiseless attenuation and

noiseless ampliﬁcation at the receiver and transmit-

ter (He et al., 2020).

Alia et al. demonstrated a four-node, trusted-

node-free metro network which used dynamic

discrete-variable quantum key distribution DV-QKD

technology (Alia et al., 2022). The authors used IDQ

Clavis2 with six links and measured SKR and QBER

in both real-time and when the parameters were up-

dated (every two minutes). The ﬁrst link had the

lowest power budget (attenuation of 5.19 dB) and

achieved a QBER of 1.31% and SKR of 1762.06 bps.

The sixth link had the highest power budget (attenu-

ation of 9.61 dB) and attained a QBER of 3.65% and

SKR of 360.08 bps.

In 2012, Zhang et al. developed and presented a

QKD system on FPGA, achieving a 17 kbps sifted key

rate, with the lowest QBER being 1% and the maxi-

mum almost 4% (Zhang et al., 2012).

In 2011, researchers experimented with the Tokyo

QKD network. This network uses a Cerberis system

and the BB84 protocol. The achieved QKD link was

45 km long, with a channel loss of 14.5 dB, an average

QBER of 2.7% and and average SKR of 268.9 kbps.

In 2008, researchers from the University of Wa-

terloo in Canada developed quantum key distribution

over two free-space optical links. The link was 1575

metres (435 + 1325 metres) long and attained an SKR

of 565 bps, QBER of 4.92%, and SKR generation of

85 bps (Sasaki et al., 2011).

3 DESCRIPTION OF THE

OPTICAL LINK

The experiments in the current study were per-

formed with IDQ Cerberis3 hardware situated at

VSB–Technical University of Ostrava. Two QKD

IDQ Cerberis3 nodes are connected by a quantum

channel and a service channel (public channel) and

offer wire-speed encryption of trafﬁc up to 10 Gbps.

QKD encryptors are positioned between the DU and

5G Core Network at the 5G Campus Network in Os-

trava. These devices contain IDQ Centauris encryp-

tors operated under the OpenQKD and NATO Quan-

tum5 projects.

The optical link is 10 kilometres long and has been

upgraded to 18 dB and uses a dense WDM multi-

plexing system. This system functions in the 1550

nm band. The link operates passively, with attenu-

ation below 16 dB; maximum optical attenuation is

18 dB (cer, 2022). The testbed is composed of high-

performance computers connected to the beginning

and end of the QKD link. QKD nodes monitor the

state of the quantum link and measure the link param-

eters (QBER, SKR, key buffer, etc.). The quantum

channel was established as a unidirectional via a dark

single mode optical ﬁber. Since we did not have a free

SM optical ﬁber, it was necessary to rebuild the exist-

ing DWDM from a pair to a single-ﬁber system, for

which splitters were used, see Fig. 1.

Figure 1: DWM rebuilt for the QKD link.

Thanks to this change, one SM ﬁber has been re-

leased for the quantum channel. The logical connec-

tion between QKD nodes and encryptors is depicted

in Fig. 2.

Figure 2: The logical connection between the QKD nodes

and encryptors.

Cerberis3, which is the newest generation Quan-

tum Key Distribution system from ID Quantique, pro-

vides a fast and secure solution which combines high-

speed layer 2 encryption with QKD. The system is

cost-effective since it evolves with the network. The

Cerberis3 system has the following key parameters

(cer, 2022):

• Key generation rate: 1.25 GHz pulse repetition

rate

• High-speed hardware-based key processing to

Measurements of Cross-Border Quantum Key Distribution Link

419

distil secret keys

• Key security parameter: ε

QKD

= 4.10

−9

• Dynamic range: 12 dB (up to 16/18 dB on re-

quest); our system has been upgraded to 18 dB

• Maximum quantum channel length (0.23

dB/km): 50 km (up to 70 or 80 km on request)

• Secret key rate: 1.4 kb/s (12 dB)

4 RESULTS

The experiments in the current study have shown

that the system is able to achieve 20 dB attenuation

despite having been upgraded to achieve a maximum

attenuation of 18 dB. The experiments attempted to

verify the hypothesis that with increasing attenuation,

the QBER increases and the SKR decreases. This

hypothesis was conﬁrmed by the experimental results

graphed in the correlation diagrams below (Figs. 3

and 4).

Experimental Procedure:

• Add optical attenuation elements of 15, 16, 17,

18, 19 and 20 dB to the QKD link in the quantum

channel (service channel).

• Wait 15 to 30 minutes for the quantum channel to

achieve steady state.

• Start measuring the QBER and SKR parameters

on the quantum channel.

A statistically signiﬁcant correlation was observed

between the QBER values and the SKR. The ob-

served correlation (Pearson coefﬁcient = –0.2842677,

p-value = 0.0004041) is statistically signiﬁcant at the

0.05 materiality level (i.e., the p-value is less than α).

Table 1: Table of Shapiro–Wilk test for normality.

Attenuation (dB)

Shapiro–Wilk test (QBER/SKR)

α = 0.05

Normality

15 0.1155/0.03403 X

16 0.06783/0.07514 X

17 0.05455/0.2834 X

18 0.431/0.8939 X

19 0.4385/7.787e-07 ×

20 0.09408 /0.1773 X

The assumption of normality was rejected only

for the SKR (parameters measured at 19 dB attenu-

ation) based on the descriptive statistical analysis re-

sults from Table 1 and the Shapiro–Wilk test. Tables

2 and 3 indicate the statistical characteristics of the

QBER and SKR.

Table 2: Table of statistical characteristics of the QBER.

QBER without outliers

Attenuation (dB) 15 16 17 18 19 20

Measures of position

Minimum 0.01354771 0.01468608 0.008509465 0.01154514 0.008805045 0.0098548

Lower quartile 0.01454422 0.01940843 0.01774629 0.01825826 0.01631018 0.01722791

Median 0.02145256 0.01570058 0.023395 0.0223911 0.01938833 0.02191777

Mean 0.01576297 0.02167488 0.02156005 0.02164785 0.02013117 0.02149707

Upper quartile 0.01661779 0.02315336 0.02698076 0.02515219 0.02396917 0.02515678

Maximum 0.01761039 0.02881422 0.02921345 0.03014283 0.0346447 0.03649546

Measures of variability

Sd 0.001227924 0.003503342 0.006008694 0.004586078 0.005858772 0.006077548

Var (%) 1.507797e-06 1.22734e-05 3.61044e-05 2.103211e-05 3.432521e-05 3.693659e-05

Table 3: Table of statistical characteristics of the SKR.

SKR without outliers

Attenuation (dB) 15 16 17 18 19 20

Measures of position

Min 893.7377 680.4253 313.9602 140.0565 65.30242

Lower quartile 1022.563 860.2464 455.5616 386.9134 252.7231

Median 1054.274 962.5391 557.1544 513.2131 352.2911

Mean 1040.95 933.5389 543.4928 487.5706 334.6116

Upper quartile 1087.441 1008.488 632.2455 591.8002 406.8988

Max 1117.546 1131.726 767.7501 737.2001 585.566

Measures of variability

Sd 61.4457 103.0566 118.2302 144.0575 127.5171

Var (%) 3775.574 10620.67 13978.37 20752.57 16260.62

• QBER: the quantum bit error rate is the ratio of

errors to the SKR and contains information about

the existence of an eavesdropper. The QBER

speciﬁes the quality of the quantum signal and

is calculated from the equation (Mlejnek et al.,

2018):

QBER =

·p

ram

LCXT

ISI

β·p

·p

ram

LCXT

ISI

(1)

where the ISI error detection probability p

ISI

caused by chromatic dispersion according to

ISI

= 2 · f

(ISI)

err

· µ · t

· t

· η. (2)

• Secret key rate: describes the rate at which bits

are transferred from one location to another.

• Measures of position: indicate a typical distribu-

tion of the variable values.

• Minimum: x

min

= x

, i.e., 0% of values are less

than minimum.

• Quartile: when the division is in four parts,

the values of the variate corresponding to 25%

(lower), 50% (median) and 75% (upper) of the to-

tal distribution are called quartiles.

• Mean: the sum of the values divided by their

number.

• Maximum: x

max

= x

, i.e., 100% of values are

less than maximum.

• Measures of variability: indicate a variability

(variance) of the values around their typical po-

sition.

• Standard deviation (sd): calculated from the

square root of the variance.

• Coefﬁcient of variation (var): represents the rel-

ative measure of variability of the variable x, often

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

420

expressed as a percentage. The coefﬁcient of vari-

ation is the ratio of the sample standard deviation

to the sample mean. (Lauterbach et al., 2022)

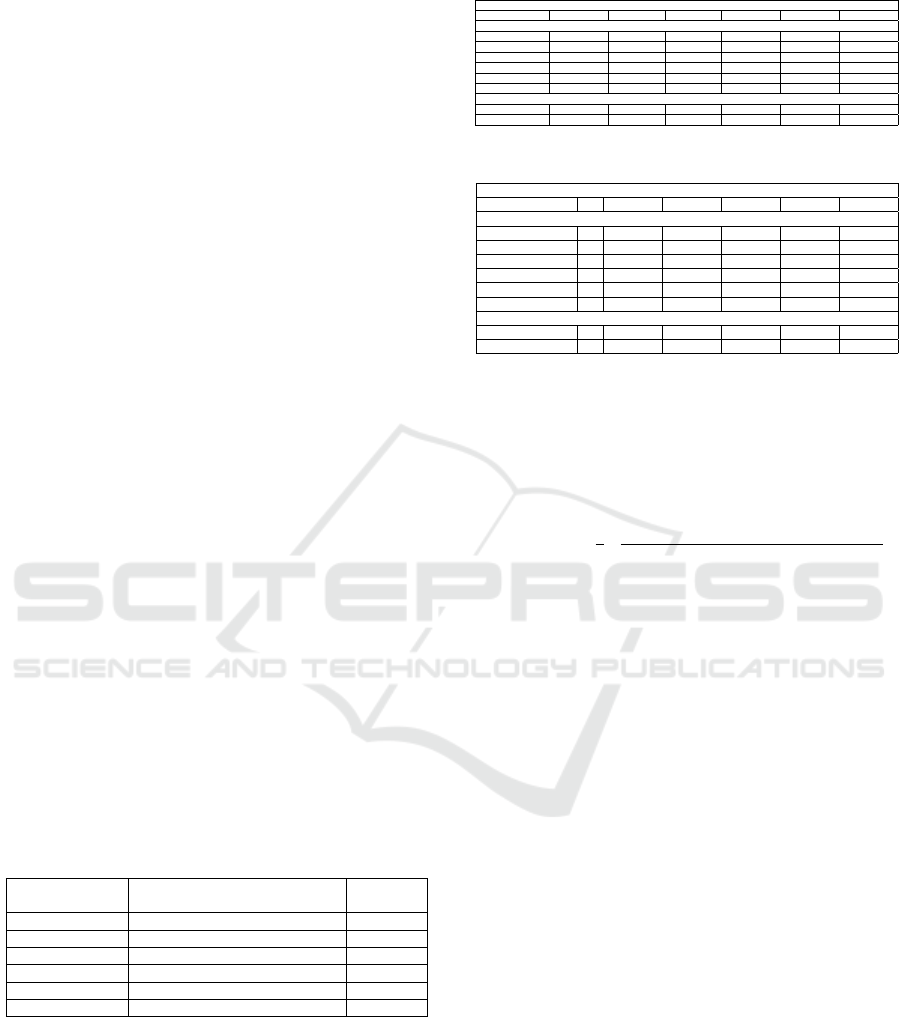
The plot in Figure 3 suggests a correlation between

attenuation and the QBER exists; the plot in Figure 4

suggests a correlation between the SKR and QBER.

Theoretically, as attenuation increases, the resulting

QBER should produce a decrease in the SKR; this

hypothesis is veriﬁed by the results, which indicate

a statistically signiﬁcant correlation between the SKR

and QBER values. All outlier values were identiﬁed

according to the 1.5IQR rule:

< x

0.25

− 1.5 · IQR) ∨ (x

> x

0.25

+ 1.5 · IQR),

where IQR refers to the inter-quartile range.

Figure 3: Scatterplot of QBER vs attenuation.

The estimated regression line equation for QBER

vs attenuation is

QBER = 16.66 + 41.21 · Attenuation.

Figure 4: Scatterplot of QBER vs SKR.

Figure 5: Scatterplot of the regression line of QBER vs

SKR.

Figure 5 plots the regression line of QBER vs

SKR. The estimated regression line equation for

QBER vs SKR is

QBER = 1368 − 24373 · Bitrate(SKR).

Figure 6: Histogram of QBER values without outliers.

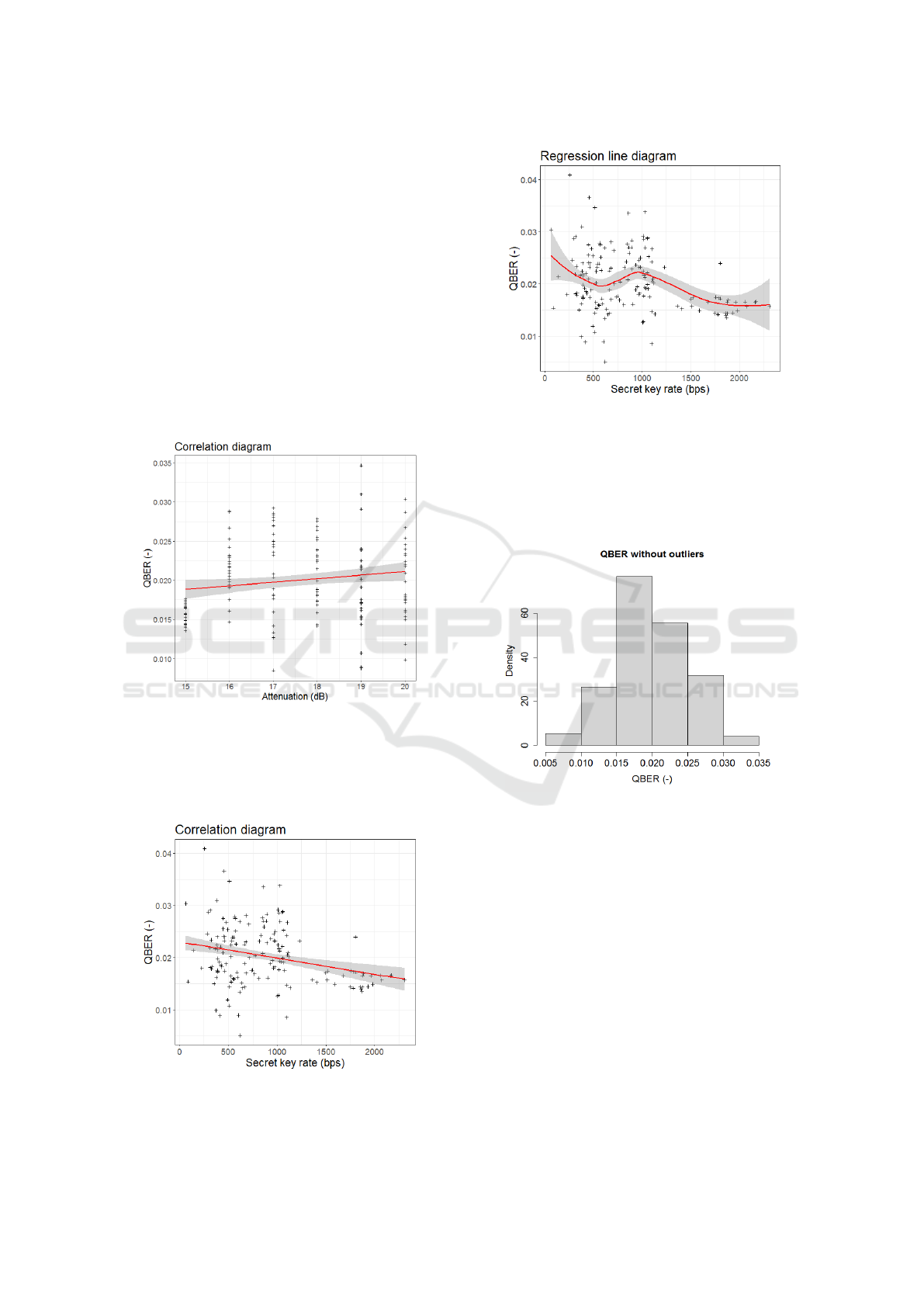
The histogram of the QBER values in Figure 6 and

the Q-Q plots in Figures 7 and 8 indicate that the data

may follow normal distribution.

5 CONCLUSION

The measurements were observed and recorded over

ﬁve days. Optical attenuation elements of 15, 16, 17,

18, 19 and 20 dB were added to the QKD link in the

quantum channel (service channel).

The system measured the quantum bit error rate

(QBER) and secret key rate (SKR). These parame-

ters were logged to a CSV ﬁle; a subsequent statisti-

cal analysis processed the measurements with the R-

studio tool in R language.

Measurements of Cross-Border Quantum Key Distribution Link

421

Figure 7: Q-Q Plot of the QBER.

Figure 8: Q-Q Plot of the SKR.

A statistical analysis of QBER inrelation to at-

tenuation and QBER in relation to SKR suggested

correlations between each of these parameter pairs.

Regression curves were calculated for these relation-

ships and showed statistically signiﬁcant correlations

between QBER and SKR and QBER and attenuation.

These results were expected. The results for normal-

ity, the histogram and Q-Q plots indicate that the mea-

sured values can be regarded as population samples

from a normal distribution.

The experiments were conducted to demonstrate

the hypothesis that as attenuation increases, the

QBER increases and the SKR decreases. The hy-

pothesis was veriﬁed by the results in correlation dia-

grams (Figs. 3, 4 and 5). Future work will include

a test for the limits in capability of the IDQ QKD

system. The system was upgraded for a maximum

attenuation of 18 dB, but the experiments in the cur-

rent study showed that it has an attenuation limit of

approximately 20 dB. The experiment was performed

on a real QKD link and thus provides a valuable con-

tribution to understanding its behaviour.

ACKNOWLEDGEMENTS

The research leading to the published results was sup-

ported under the NATO SPS G894 project “Quantum

Cybersecurity in 5G Networks (QUANTUM5)” and

partly under the H2020 project “OPENQKD Grant

Agreement No. 857156”.

REFERENCES

(2022). Idq,https://www.idquantique.com/quantum-safe-

security/products/cerberis3-qkd-system/.

Alia, O., Tessinari, R. S., Hugues-Salas, E., Kanellos, G. T.,

Nejabati, R., and Simeonidou, D. (2022). Dynamic

dv-qkd networking in trusted-node-free software-

deﬁned optical networks. Journal of Lightwave Tech-

nology, 40(17):5816–5824.

Dianati, M. and All

eaume, R. (2007). Architecture of the

secoqc quantum key distribution network. In 2007

First International Conference on Quantum, Nano,

and Micro Technologies (ICQNM’07), pages 13–13.

IEEE.

Gardner, M. (1977). A new kind of cipher that would

take millions of years to break. Scientiﬁc American,

237(8):120–124.

Gisin, N., Ribordy, G., Zbinden, H., Stucki, D., Brunner,

N., and Scarani, V. (2004). Towards practical and

fast quantum cryptography. arXiv preprint quant-

ph/0411022.

He, M., Malaney, R., and Bumett, B. A. (2020). Multi-

mode cv-qkd with noiseless attenuation and ampliﬁ-

cation. In 2020 IEEE Globecom Workshops (GC Wk-

shps, pages 1–7.

Lauterbach, F., Burdiak, P., Rozhon, J., Dervisevic, E.,

Slivova, M., Plakalovic, M., Mehic, M., and Voz-

nak, M. (2022). Quantum channel characteristics from

the point of view of stability. In 2022 XXVIII Inter-

national Conference on Information, Communication

and Automation Technologies (ICAT), pages 1–6.

Li, N. (2010). Research on difﬁe-hellman key exchange

protocol. In 2010 2nd International Conference on

Computer Engineering and Technology, volume 4,

pages V4–634. IEEE.

Mehic, M., Maurhart, O., Rass, S., and Voznak, M. (2017).

Implementation of quantum key distribution network

simulation module in the network simulator ns-3.

Quantum Information Processing, 16(10).

Mehic, M., Niemiec, M., Rass, S., Ma, J., Peev, M.,

Aguado, A., Martin, V., Schauer, S., Poppe, A.,

Pacher, C., and Voznak, M. (2020). Quantum key dis-

tribution: A networking perspective. ACM Comput.

Surv., 53(5).

Mehic, M., Niemiec, M., and Voznak, M. (2015). Calcu-

lation of the key length for quantum key distribution.

Elektronika ir Elektrotechnika, 21(6):81–85.

Mlejnek, M., Kaliteevskiy, N., and Nolan, D. (2018). Mod-

eling high quantum bit rate qkd systems over optical

ﬁber.

ICISSP 2023 - 9th International Conference on Information Systems Security and Privacy

422

Moody, D., Chen, L., and Jordan, S. e. a. (2016). Nist report

on post-quantum cryptography. http://dx.doi.org/10.

6028/NIST.IR.8105.

Sasaki, M., Fujiwara, M., Ishizuka, H., Klaus, W., Wakui,

K., Takeoka, M., and S. Miki, e. a. (2011). Field test

of quantum key distribution in the tokyo qkd network.

Opt. Express, 19(11):10387–10409.

Zhang, H.-F., Wang, J., Cui, K., Luo, C.-L., Lin, S.-Z.,

Zhou, L., Liang, H., Chen, T.-Y., Chen, K., and Pan,

J.-W. (2012). A real-time qkd system based on fpga.

Journal of Lightwave Technology, 30(20):3226–3234.

Measurements of Cross-Border Quantum Key Distribution Link

423