Model Order in Sugiyama Layouts

oren Domr

, Max Riepe

and Reinhard von Hanxleden

Department of Computer Science, Kiel University, Kiel, Germany

Keywords:

Sugiyama Layout, Layered Drawings, User Intentions, Model Order.

Abstract:

Graph drawing algorithms traditionally consider a graph to consist of unordered sets of nodes and edges, which

may disregard information already provided by the developer. In practice, as recently argued by (Domr

os and

von Hanxleden, 2022), a graph often consists of ordered sets, which have an intended model order of nodes and

edges. We present how this model order can be enforced or used as a tie-breaker, while optimizing common

aesthetic criteria. This allows the developer to control the layout of layered graphs via the model order. On the

example of SCCharts, we show that the order of nodes and edges does indeed correlate with the way people

think about a model, and how that order can be used to emphasize the semantics of a sensibly designed model.

Moreover, we suggest model order strategies to be used for control-ﬂow and data-ﬂow diagrams based on

expert developer feedback on SCCharts and Lingua Franca.

1 INTRODUCTION

In previous work, (Domr

os and von Hanxleden, 2022)

argued to use model order—the order of the input

model—to inﬂuence the layout since common algo-

rithms usually only optimize for geometric criteria

such as backward edges, edge length, edge straight-

ness, or edge crossings.

As introductory example, Figure 1a and 1b show

two different drawings of the same small graph G,

which in the common mathematical unordered set no-

tation consists of nodes N = {n1, n2, n3} and edges

E = {(n1, n2), (n2,n3), (n3, n2)}. Throughout this

paper, we assume nodes to be ordered according to

their numbering, e. g., that n1 is “before” n2.

In Figure 1a the number of backward edges is the

same as in Figure 1b. Figure 1a is the result of a ran-

dom decision, which places n3 as a dangling node—

a node that goes against the main layout direction,

which we assume without loss of generality to be left-

to-right. Thus, we consider Figure 1a to be Obviously

Non-Optimal (ONO) violating the Nothing is Obvi-

ously Non-Optimal (NONO) principle (Kieffer et al.,

2016). Using model order, the desired Obvious Yet

Easily Superior (OYES) solution in Figure 1b empha-

sizes the control-ﬂow and prevents the dangling node,

as now n3 is to the right of n2.

https://orcid.org/0000-0002-8011-8484

https://orcid.org/0000-0001-6779-2207

https://orcid.org/0000-0001-5691-1215

As the main layout direction is left-to-right, the

layer-based Sugiyama algorithm forms vertical lay-

ers. In Figure 1c, n2 and n4 are in the same vertical

layer; in Figure 1d, n3 and n4 share the same layer.

The node n4 can be put in the same layer as n2 or n3

without increasing the edge length or size of the draw-

ing. The ordering suggests that n4 should be “after”

n3, which is not clearly represented by the layout in

Figure 1c in which the order of n3 and n4 is ambigu-

ous since n3 is above n4 but n4 is left of n3. Thus, we

consider Figure 1c to be ONO. Figure 1d solves this

problem by moving n4 to the same layer as n3.

Figures 1e and 1f also show the same graph. Here,

the vertical ordering inside a layer differs. Figure 1e is

ONO since it does not respect the order of n2, n3, and

n4 and orders them differently, although there is no

aesthetic criterion such as edge crossings that would

justify it. The OYES solution in Figure 1f places the

nodes by their ordering in the input model.

ONO drawings are a practical obstacle to the adap-

tion of automatic layout and with it modeling prag-

matics (Fuhrmann and von Hanxleden, 2010), which

embraces the best of textual and graphical modeling.

In the past, Figure 1a and 1e have been the standard

layout for SCCharts (von Hanxleden et al., 2014), a

control-ﬂow based state-chart dialect, as a result of

a speciﬁc random seed. Since the order was scram-

bled by previous phases before crossing minimiza-

tion started and was randomized during crossing min-

imization, the developer had very limited control over

Domrös, S., Riepe, M. and von Hanxleden, R.

Model Order in Sugiyama Layouts.

DOI: 10.5220/0011656700003417

In Proceedings of the 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 3: IVAPP, pages 77-88

ISBN: 978-989-758-634-7; ISSN: 2184-4321

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

(a) ONO cycle breaking

n1 n2 n3

(b) OYES cycle breaking

n2 n3

(d) OYES layer assignment

(e) ONO crossing

minimization

(f) OYES crossing

minimization

Figure 1: All drawings are optimal in terms of number of

backward edges for cycle breaking, edge length for layer

assignment, and edge crossings for crossing minimization.

However, (a), (c), (e) violate the model order.

the layout. To nevertheless inﬂuence the layout, de-

velopers renamed or reordered the states and intro-

duced constraints to force nodes in the ﬁrst or last

layer, which did not always work if multiple edges

were involved. The same applies for the data-ﬂow

based polyglot coordination language Lingua Franca

(Lohstroh et al., 2021). Lingua Franca allows speci-

fying deterministic actors called reactors mainly con-

sisting of actions and reactions, which are event trig-

gered and execute their body consisting of code in the

desired target language.

1.1 Contribution & Outline

Section 2 brieﬂy reviews the Sugiyama algorithm.

This paper extends the model order approach for

Sugiyama layouts proposed by (Domr

os and von

Hanxleden, 2022) by adding strategies for cycle

breaking, layer assignment, and crossing minimiza-

tion to the already existing strategies for tie-breaking

model order crossing minimization. The main contri-

butions covered in the next sections are as follows:

• We propose two strategies for cycle breaking, a

tie-breaking and an enforcing model order cycle

breaking strategy (Section 3);

• We present a node promotion strategy for model

order layer assignment (Section 4);

• We present a new tie-breaking strategy and en-

forced model order strategies for crossing mini-

mization (Section 5).

Cycle Breaking

Layer Assignment

Crossing Minimization

Node Placement

Edge Routing

Intermediate Processor Slots

Topological

Geometrical

Figure 2: Structure of the layered algorithm.

Section 6 evaluates the enforced cycle breaking and

crossing minimization strategies and discuses poten-

tial use cases based on developer feedback for SC-

Charts and Lingua Franca in Section 6. Section 7

presents further related work and Section 8 concludes

this paper.

2 THE LAYERED ALGORITHM

The Sugiyama algorithm, or layered algorithm, han-

dles the inherent complexity of assigning coordinates

to nodes and routes to edges by dividing the layout

problem of directed graphs into ﬁve phases: The topo-

logical phases cycle breaking, layer assignment, and

crossing minimization compute the relative position-

ing between the nodes and edges. The geometrical

phases node placement and edge routing set x and

y-coordinates of nodes and edge routes. In its im-

plementation in the Eclipse Layout Kernel (ELK) the

algorithm is further divided, as seen in Figure 2, by

adding intermediate processors between the phases

that handle pre- and post-processing (Schulze et al.,

2014).

A directed ordered graph G = (V, E) consists of an

ordered set of nodes V = ⟨n

, . . ., n

⟩ and an ordered

set of p

outgoing edges for each node n

with E =

⟨⟨e

1,1

, . . ., e

1,p

⟩, . . ., ⟨e

k,1

, . . .e

k,p

⟩⟩. As explained by

(Domr

os and von Hanxleden, 2022), the edges im-

plicitly deﬁne the ordered set of ports, which are the

anchor points on the edges on the nodes and which

deﬁne the ordering between the edges. However, for

simplicity we here only use the edge order, which

we use as an equivalent to the order of the outgoing

ports, since incoming ports can be ordered by their

incoming connections. A layered ordered graph G =

(V, E, L) additionally has a layering L = ⟨L

, . . ., L

⟩

of m layers of r

nodes with L

= ⟨n

i,1

, . . ., n

i,r

⟩,

which assigns a node to exactly one layer. In-layer

edges, i. e. edges between nodes of the same layer,

are forbidden.

The layered algorithm assigns nodes to vertical

layers, as seen in the graph in Figure 1c, which

has four layers L = ⟨⟨n1⟩, ⟨n2, n4⟩,⟨n3⟩, ⟨n5⟩⟩. Such

IVAPP 2023 - 14th International Conference on Information Visualization Theory and Applications

a layered graph is proper, if edges only occur be-

tween neighboring layers. To create a proper layer-

ing, dummy nodes are added to break edges that span

multiple layers, e. g., by adding a dummy node to ⟨n3⟩

to break the edge from n4 to n5 into two. We deﬁne

dummy : V → {true, false} as the dummy node predi-

cate that returns true if a node is a dummy node. Fur-

thermore, we call nodes that do occur in the model

real nodes; dummy nodes that are placeholders for

edge labels are called label dummy nodes.

Furthermore, let s : E → V with e = (u, v) ∈ E and

s(e) = u be the source function and t : E → V with

e = (u, v) ∈ E and t(e) = v be the target function. Let

o : V ∪ E → N ∪ ⊥ be the order function that outputs

the model order value for edges and nodes, and re-

turns ⊥ for any dummy node or node without a model

order. Let indegree : V → N and outdegree : V → N

be the functions that return the number of incoming

and outgoing connections respectively.

There already exist several heuristics that opti-

mize aesthetic criteria for the different phases. We

argue that model order should be considered in the

ﬁrst three topological phases, since they establish the

relative position between nodes and edges. Since all

phases should work independently of each other, we

cannot guarantee that nodes are ordered before each

phase. Therefore, the nodes and edges should be

sorted before using model order strategies, which is

the main concept of model order crossing minimiza-

tion by (Domr

os and von Hanxleden, 2022).

Cycle breaking makes the input graph acyclic by

reversing edges. The problem of minimizing the num-

ber of edges that need reversing is called feedback

arc set problem (Eades et al., 1993) and is NP-hard.

Therefore, heuristics are used to reverse edges, which

sometimes rely on randomization to make decisions

if no unique optimal alternative exists.

Layer assignment creates a (proper) layered

graph from a given acyclic digraph by assigning

nodes to layers. Beginning from the sources (or

sinks), nodes are assigned to layers. These can be

optimized for aesthetic criteria such as edge length

(Gansner et al., 1993) or total layer width (Nikolov

and Tarassov, 2006). If the graph is built with a node

model order that emphasizes the layers, model order

layer assignment can form semantic grouping, as de-

tailed in Section 4.

Crossing minimization minimizes edge cross-

ings by changing the order of nodes and ports in the

same vertical layer. Crossing minimization may uti-

lize model order either as a tie-breaker, as discussed

by (Domr

os and von Hanxleden, 2022), or to con-

strain nodes and edges, as proposed in Section 5.

n1n2n3

(a)

(b)

n1 n2 n3

(c)

Figure 3: (a) The greedy cycle breaker tries to optimize the

number of backward edges and uses random decisions if no

unique solution exists. (b) The greedy model order cycle

breaker tries to optimize the number of backward edges and

uses model order if multiple optimal solutions exist. (c)

The model order cycle breaker reverses edges to nodes with

a lower model order.

3 CYCLE BREAKING

There are two basic concepts of model order during

cycle breaking. Figure 3 showcases how model or-

der can be ignored, be used as a tie-breaker, or be

enforced.

In Figure 3a the greedy cycle breaker optimizes

the number of backward edges. However, reversing

the edge from n1 to n2 instead of n2 to n1 results in

the same number of backward edges but violates the

model order.

Figure 3b solves this by using model order as a tie-

breaker. As a result n1 is placed in the layer before n2

and not the other way around.

In Figure 3c we assume that the backward edge

aesthetic criterion is disregarded in favor of order.

Such assumptions depend on the speciﬁc graphical

language in use, as seen in Section 6.2 and 6.4.

3.1 Model Order as Tie-Breaker

Many cycle breaking algorithms, such as depth-ﬁrst

(Gansner et al., 1993) or breadth-ﬁrst, already implic-

itly use model order. A depth-ﬁrst cycle breaker be-

gins with the sources. Next, all nodes on the sources

are visited recursively, and edges that point to already

visited nodes are reversed. If model order is not taken

into account, there might be multiple solutions based

on the traversal order of the graph. Even though it

is not explicitly stated by Gansner et al., it is as-

sumed that the next nodes are visited based on the

edge model order or the node model order.

The same applies for other layout algorithms such

as the greedy cycle breaker presented by (Eades et al.,

1993) and (Di Battista et al., 1999), seen in Algo-

rithm 1, in which removeFirst is a function that re-

moves and returns the ﬁrst element of a list, up-

dateNeighbors removes the edges to a node for a

given graph and node, and ﬁndMaxOutﬂow returns the

nodes with the highest out-in-degree difference. In

addition to the traversal order, this algorithm makes

random decisions in line 19 if the nodes have the same

Model Order in Sugiyama Layouts

Algorithm 1: greedy[ModelOrder]CB.

Input: An digraph G = (V, E)

Output: An acyclic digraph

1 G

′

:= G,sources :=

0, sinks :=

2 for ( n ∈ V )

3 if ( indegree(n) = 0 )

4 sources ∪= n

5 if ( outdegree(n) = 0 )

6 sinks ∪= n

7 unprocessed := |V |

8 while ( unprocessed > 0 )

9 while ( |sinks| > 0 )

10 sink := removeFirst(sinks)

11 updateNeighbors(G

′

, sink)

12 unprocessed − −

13 while ( |sources| > 0 )

14 source := removeFirst(sources)

15 updateNeighbors(G

′

, source)

16 unprocessed − −

17 if ( unprocessed > 0 )

18 maxNodes := ﬁndMaxOutﬂow(G

′

)

19 n = choose[ModelOrder]Node(maxNodes)

20 // Reverse incoming edges

21 for ( e = (v, n) )

22 E := (E\e) ∪ (n,v)

23 unprocessed − −

24 return G

outﬂow. Here chooseNode randomly chooses a node

for which all incoming edges are reversed. Applied

to real graphs, this can create ONO-cases such as Fig-

ure 1a. Here, a backward dangling node is produced

since the algorithm randomly decides to reverse the

edge from n2 to n3 and not the one from n3 to n2 as

it is suggested by the model order.

We propose that in the greedy model order cy-

cle breaker, chooseModelOrderNode returns the node

with the minimal model order o(n) instead.

In such a way every cycle breaker can use model

order as a tie-breaker while traversing ordered sets or

making random decisions.

3.2 Model Order as Constraint

If model order is enforced by reversing all edges to

a node with a lower model order, the graph becomes

acyclic. Moreover, any edge reversal that results in

an acyclic graph can be enforced, e. g., by travers-

ing the resulting tree-like structure breadth-ﬁrst and

ordering the nodes such that their model order corre-

sponds the breadth-ﬁrst visiting order. This gives the

modeler full control over the cycle breaking step.

A model order cycle breaker that additionally al-

lows constraining nodes to the ﬁrst or last layer, which

is common for e. g. SCCharts, can be seen in Algo-

rithm 2, where c : V → {−1, 0, 1} is deﬁned as fol-

lows:

c(n) =











−1, n shall be in the ﬁrst layer

1, n shall be in the last layer

0, otherwise

Algorithm 2: modelOrderCB.

Input: A digraph G = (V, E)

Output: An acyclic digraph

1 for ( e ∈ E )

2 if ( c(s(e)) > c(t(e)) ∨ (c(s(e)) = c(t(e))∧ o(s(e)) > o(t(e))) )

3 E := (E\e) ∪ (t(e),s(e))

4 return G

The algorithm groups the nodes into nodes with

ﬁrst-layer constraint, nodes without constraints, and

nodes with last-layer constraint and orders the nodes

within these groups. The order of constraints and the

order inside the constraint groups create a total order

for all nodes, which identiﬁes the edges to reverse.

The runtime of this algorithm is in O (|E|), making

it the fastest possible cycle breaking algorithm.

In Section 6.1 we evaluate the model order cycle

breaker against the depth-ﬁrst, the breadth-ﬁrst, and

the greedy cycle breaker.

4 LAYER ASSIGNMENT

The effect of model order layer assignment can be

seen in Figure 1d compared to Figure 1c.

Model order layer assignment needs cycle break-

ing done by the model order cycle breaker and a

breadth-ﬁrst node model order. The strategy assigns

nodes to layers such that no node has a node with a

smaller model order in a higher layer and no node

with a bigger model order in a smaller layer. The

breath-ﬁrst ordering of nodes is necessary to compare

different control-ﬂow branches. This may create ad-

ditional layers, as seen in Figure 4a and 4b.

SCCharts have one initial state (see state without a

name) and ﬁnal states, hierarchy, and parallel regions

of execution, which are not shown here. Priorities on

the edges (see 1. on the edge from the initial state to

s1) express the evaluation order of their guards, which

are omitted here, and derive from the order of the out-

going transitions of a state in the textual model, hence

they represent the edge model order. The node order

in the textual model has no semantics and could be

arbitrary. However, control-ﬂow branches are a com-

mon sight. Developers think one case of their pro-

gram, e. g., branch b1, from start to ﬁnish before im-

plementing a new one. The developer does, therefore,

only intend that nodes in b1 are before nodes in b2

and does not intend the layering shown in Figure 4b.

Thus, for SCCharts the nodes in b1 and b2 are not

comparable by model order during layer assignment.

Model order layer assignment works by doing a

trivial layer assignment beginning with the sources,

which again implicitly utilizes the model order of the

nodes or edges to traverse the nodes. As a second

IVAPP 2023 - 14th International Conference on Information Visualization Theory and Applications

Example01

(a)

Example01

(b)

Figure 4: Drawing of an obfuscated SCCharts model. (a)

Branches b1 and b2 are only used to infer on ordering be-

tween the nodes in them but not used to infer an alignment.

(b) Interpreting the model order as a depth-ﬁrst ordering

creates an additional layer.

step in the I2 intermediate processing slot, nodes are

moved based on the model order of nodes in the next

and the current layer, as seen in Algorithm 3.

Algorithm 3: modelOrderNodePromotion.

Input: A layered graph G = (V, E)

Output: A layered ordered graph

1 somethingChanged := false

2 do

3 for ( n | !dummy(n)∧ outdegree(n) > 0 )

4 if ( o(n) = ⊥ )

5 continue

6 currentLayer := L

L(n)

7 if ( |currentLayer| = 1 ∧ L(n) = 0 )

8 continue

9 for ( v ∈ currentLayer )

10 if ( o(n) < o(v) )

11 continue

12 nextLayer := L

L(n)+1

13 allowsPromotion := false

14 dummyLayer := true

15 for ( v ∈ nextLayer )

16 if ( !dummy(v) )

17 allowsPromotion |= o(v) < o(n)

18 dummyLayer := false

19 else if ( !allowsPromotion∧ dummyLayer )

20 if (

(n, v) ∈ E ∧ L(longEdgeTarget(n))− L(n) ≤ 2 )

21 dummyLayer := false

22 if ( allowsPromotion∨ dummyLayer )

23 promoteNode(G, n)

24 somethingChanged := true

25 while somethingChanged;

26 return G

Here promoteNode moves a node to the next layer

while also recursively promoting connected nodes

that would otherwise end up in the same layer and

would create in-layer edges.

A real node is promoted if (1) it has a model or-

der (line 4-5), (2) it is not the only node in the ﬁrst

layer (line 7-8), (3) it has the highest model order in

its layer (line 9-11), and (4) the next layer either has at

least one real node with a lower model order (line 16-

18) or (5) the next layer contains only dummy nodes

while the current node has enough space to its con-

nected real node such that it can safely be moved in

the next layer (line 19-21).

Constraint (1) is necessary since there might be

nodes that are not dummy nodes that are created by

the synthesis, which translates the model into a graph

layout problem, as it is the case for Lingua Franca

(von Hanxleden et al., 2022).

Constraint (2) makes sure that the source node

does not promote the whole graph over and over.

Constraint (3) makes sure that only the node with

the highest model order can be promoted.

Constraints (4) and (5) describe the two differ-

ent criteria for the next layer, the layer the current

node might be moved to. Either a real node with a

lower model order is in the next layer, as seen in Fig-

ure 4a for s5 and s3, or the next layer has only dummy

or dummy label nodes, as seen in Figure 5a, which

shows an Systems Theoretic Process Analysis (STPA)

control structure that is used to analyze hazardous

scenarios. Here Engine System can be moved since

Vehicle, its long edge target, which is the real node

it is connected to, is far enough away to move the

node and the label dummy without also moving Ve-

hicle. Note that Safety System could be in the layer

directly after Operator Safety, Safety System aligns

itself with Telemetry based on the model order.

Each layering can be recreated by model order by

ordering the nodes breadth-ﬁrst based on their posi-

tion in their intended layer, as seen in Figure 5b.

5 CROSSING MINIMIZATION

Crossing minimization determines the vertical order

of nodes and ports inside a layer. This is done by

sweeping back and forth through the layers and re-

ordering all nodes and ports in a layer based on the

previous layer. The outcome of a layer sweep depends

on the starting conﬁguration. Multiple runs and ran-

dom starting conﬁgurations bounded by the thorough-

ness prevent local minima. As shown by (Domr

os and

von Hanxleden, 2022), it may need a high thorough-

ness to get the desired result if several starting conﬁg-

urations exist.

5.1 Pre-Ordering Nodes and Edges

Domr

os and von Hanxleden introduced model order

as a tie-breaker during crossing-minimization by be-

ginning the ﬁrst crossing minimization runs with a

proper layered graph pre-ordered by model order in

the I2 intermediate processing slot. Moreover, they

consider order violations in addition to edge crossings

during crossing minimization.

Model Order in Sugiyama Layouts

Operator Backend

Operator Safety

Telemetry

Safety System

Drive Box

Auto Box

Lidar

Camera

BMU

IMU

Engine System

Steering System

Steering sensors

Engine Sensors

Vehicle

driving task

emergency

free space,

objects

lane info,

objects

charge level

yaw rate,

acceleration

yaw rate,

acceleration

torque,

angle

speed,

power

drive axle

powered wheels,

torque

restoring force

(a) ONO decision during layer assignment. The number of layers is minimal, however, the relationship between the different

states, which is partly expressed by model order, is lost.

Operator Backend

Operator Safety

Telemetry

Safety System

Drive Box

Auto Box

Lidar

Camera

BMU

IMU

Engine System

Steering System

Steering sensors

Engine Sensors

Vehicle

driving task

emergency

free space,

objects

lane info,

objects

charge level charge level

yaw rate,

acceleration

yaw rate,

acceleration

torque,

angle

speed,

power

drive axle

powered wheels,

torque

restoring force

7 8 9 10 11

13 14

(b) OYES decision during layer assignment. The actuators and sensors Lidar, Camera, BMU, IMU, Engine System, Steering

System, Steering Sensors, and Engine Sensors are in the same layer.

Figure 5: STPA control structure with downward layout direction of an autonomous vehicle

. The node model order is marked

in red to the right of each node.

(a)

(b)

(c)

Figure 6: (a) Tie-breaking crossing minimization that pre-

orders nodes and edges (no crossings). (b) The node order is

enforced after pre-ordering (one crossing). (c) No crossing

minimization, only model order (three crossings).

This algorithm conﬁguration produces results

such as Figure 6a. Since the ordered solution is

checked ﬁrst and order violations can be weighted

against crossings, a solution is chosen from the cross-

ing minimization runs that has minimal edge cross-

ings with minimal ordering violations as a secondary

criterion.

(Domr

os and von Hanxleden, 2022) introduced

two different ordering strategies. These strategies

serve as an initial order or as a tie-breaker during

crossing-minimization. Subsequent runs might be

randomized and are only taken if they are better than

the ordered solution.

The preferEdges approach prefers the edge model

order and only refers to the node model order if no

clear solution could be found, as it is the case for dan-

gling nodes such as n3 in Figure 1a or Figure 3b.

The nodesAndEdges approach considers nodes

and edge order by ordering nodes and edges by their

respective order and using the edge order of the con-

nected source ports in the previous layer as a fallback

if dummy nodes and real nodes are compared.

Additionally, we propose the preferNodes ap-

www.smartload-project.de

IVAPP 2023 - 14th International Conference on Information Visualization Theory and Applications

(a)

(b)

(c)

Figure 7: Different pre-ordering strategies for crossing min-

imization (I2 slot) visualized by omitting crossing mini-

mization. (a) Edge order orders nodes and edges. Node

order is used as a secondary criterion. (b) Edge order orders

the edges and the dummy nodes. Node order orders the real

nodes. (c) Edge order orders dummy nodes. Node order

orders real nodes and edges.

proach that orders real nodes by model order, dummy

nodes—as before—by their connected source ports,

which are already ordered by node model order, and

edges by their long edge target node’s model order.

The different strategies can be seen in Figure 7. Fig-

ure 7a and Figure 7c do not change during crossing

minimization, since they are already optimal in terms

of edge crossings. Crossing minimization reduces the

crossing in Figure 7b resulting in the ordering de-

picted in Figure 7a.

As already described in Section 3.2, the model or-

der can also be interpreted as a constraint resulting in

the following strategies.

5.2 Constraining Node Model Order

If we constrain the real nodes in each layer, many

node positions for dummy nodes, which deﬁne the

relative routes of edges, are still feasible without com-

promising the node model order. Crossing minimiza-

tion is edge-centric and often disregards the node or-

der in favor of the edge order if the initial solution is

not crossing minimal. Therefore, a special crossing

minimization strategy is necessary.

A crossing minimization strategy, such as the

barycenter heuristic (Sugiyama et al., 1981) or the

median heuristic (Di Battista et al., 1999), can take

the model order into account if it does layer sweeps

and applies a strategy to order a bipartite graph—here

the barycenter heuristic—such that it does not change

an ordering if it is already optimal. The model order

and the barycenter values form a partial and a total or-

der on the nodes. Therefore, transitive orderings have

to be taken into account and a sorting algorithm that is

order preserving such as insertion sort has to be used.

As seen in Figure 6b, constraining the nodes cre-

ates additional crossings compared to Figure 6a but

always maintains the node model order. Note that this

approach might not ﬁnd the optimal solution (edge 5

on top) in terms of edge crossings, since it is still lim-

ited by the used starting conﬁgurations.

Constraining only edges, as presented in this sec-

tion for the nodes, constraints all parts of the graph

except source nodes. Therefore, this strategy is dis-

cussed as part of the no crossing minimization ap-

proach.

5.3 No Crossing Minimization

For many models, crossing minimization might not

be necessary if nodes and edges are already pre-

ordered. Enforcing model order by pre-ordering

nodes and edges with the preferEdges, nodesAnd-

Edges, or preferNodes approach without doing cross-

ing minimization at all is a viable solution.

If the edge order is enforced, it deﬁnes the order

of the nodes and ports if a graph has only one source

and no dangling source nodes are created. This is the

case for SCCharts where each region must have ex-

actly one initial state and all states must be reachable.

If multiple sources are present, the node model order

is used as a secondary criterion. This is enough to

create any edge or node order inside a layer if the

order of nodes and edges has no semantics. Since

the pre-crossing minimization sorting strategy pref-

erEdges fulﬁlls these criteria, edge order can create a

layout by sorting nodes and edges with this strategy

and not doing crossing minimization at all, as seen

in Figure 7a. This makes it compatible with the en-

forced cycle breaking and layer assignment breadth-

ﬁrst node order constraint.

If the node order should be enforced, the prefer-

Nodes pre-crossing minimization sorting strategy is

used while also omitting crossing minimization. This

results in a layout such as Figure 7c. Since this or-

dering depends on the long edge target nodes, it may

be conﬂicting with a breadth-ﬁrst node order. Since

it is, therefore, not compatible with cycle breaking’s

and layer assignment’s constructive breadth-ﬁrst or-

dering constraint, it cannot be used to create any given

layout, as seen in Figure 4a. If one would order the

states breadth-ﬁrst ⟨init, s1,s2, s5, s3, s6, s4⟩ to create

the layering ⟨⟨init⟩, ⟨s1, s2, s5⟩, ⟨s3,s6, s4⟩⟩, the edge

ordering would be different and create crossings if en-

forced, e. g., between the edge from s5 to s6 and the

initial state to s3.

The nodesAndEdges strategy should only be used

for a no crossing minimization approach if node and

edge order are not conﬂicting. Otherwise, edge cross-

ings are created as the one in Figure 7b.

For complicated models, we advise using cross-

ing minimization since moving edges and nodes in

the textual model—while an automatic solution is

available—can control their placement but doing this

manually on a regular basis is tiresome.

Model Order in Sugiyama Layouts

6 DISCUSSION

Before discussing what strategies can be used effec-

tively in which scenario, we summarize the model or-

der strategies for Sugiyama layouts with their respec-

tive slot in the algorithm:

Phase 1: Cycle breaking.

Greedy Model Order Cycle Breaking. Optimize

for backward edges but use model order as a

tie-breaker.

Model Order Cycle Breaking. Edges are reversed

by model order such that edges always point to

a node with a higher model order.

Phase 2 and intermediate slot I2: Layer assign-

ment and post-processing.

Model Order Layerer. Promote nodes by model or-

der after a simple long edge layering beginning

from the sources.

Intermediate slot I2: Crossing minimization pre-

processing.

PreferEdges. Order nodes and edges before crossing

minimization primarily based on the edge order.

(Domr

os and von Hanxleden, 2022)

NodesAndEdges. Order nodes by node order and

edges by edge order before crossing minimiza-

tion. (Domr

os and von Hanxleden, 2022)

PreferNodes. Orders nodes and edges before cross-

ing minimization primarily based on the node or-

der.

Phase 3: Crossing minimization.

Weighting. Include weights for node and edge order

additionally to edge crossings that rate the cross-

ing minimization runs. (Domr

os and von Hanxle-

den, 2022)

Enforce Node Order. Instead of pure barycenter-

based crossing minimization, the node order pri-

marily determines the ordering.

No Crossing Minimization. Pre-ordering nodes and

edges is sufﬁcient; the crossing minimization step

does nothing.

In the following we discuss these strategies de-

pending on their usage for SCCharts and Lingua

Franca. A study on cycle breaking for SCCharts,

quantitative analysis, and feedback of expert SCCha-

rts and Lingua Franca developers serves as a basis for

this. The feedback was collected in multiple itera-

tions during weekly developer meetings, while ver-

ifying the extracted information on existing models.

We recommend a similar process when considering

model order for other languages to identify desired or-

der and ordering conventions in the textual and graph-

ical model.

6.1 Model Order Cycle Breaking in

SCCharts

We analyzed 265 SCChart models using the greedy

(see Algorithm 1), the breadth-ﬁrst, the depth-ﬁrst,

and the model order cycle breaker (see Algorithm 2)

and the nodesAndEdges crossing-minimization pre-

ordering. The textual models were created without

model order inﬂuencing the drawing. Instead, the

greedy cycle breaker optimized backward edges, the

layering optimized for minimum edge length, and the

crossing minimization optimized the number of edge

crossings.

Only 47 of these SCChart graphs resulted in

unique solutions for all algorithms. Eight selected

graphs were rated by 27 participants based on their

ﬁrst impression, crowdedness, ability to follow edges,

state grouping based on perceived semantics deduced

from state names, and ﬁnal impression on a Likert

scale. On average the model order cycle breaking

returned the best results before the depth-ﬁrst, the

breadth-ﬁrst, and the greedy cycle breaker. Partici-

pants rated the clear edge routes and state grouping

as their primary incentive for their decisions. Other

factors mentioned are that the initial state should be

in the ﬁrst layer and the ﬁnal state be in the last, sym-

metry, edge crossings, no dangling nodes, and under-

standable and readable node labels, which is partly

based on the compactness of the graph.

The greedy algorithm performed worst, mainly

because state grouping is only randomly created with

this approach and because dangling nodes seem to

disturb the ﬂow of the diagram (see n3 in Figure 1a).

The breadth-ﬁrst approach created compact draw-

ings with fewer layers but more edge crossings.

Sometimes, however, it is rated above average if the

breadth-ﬁrst order creates thematic state groups as

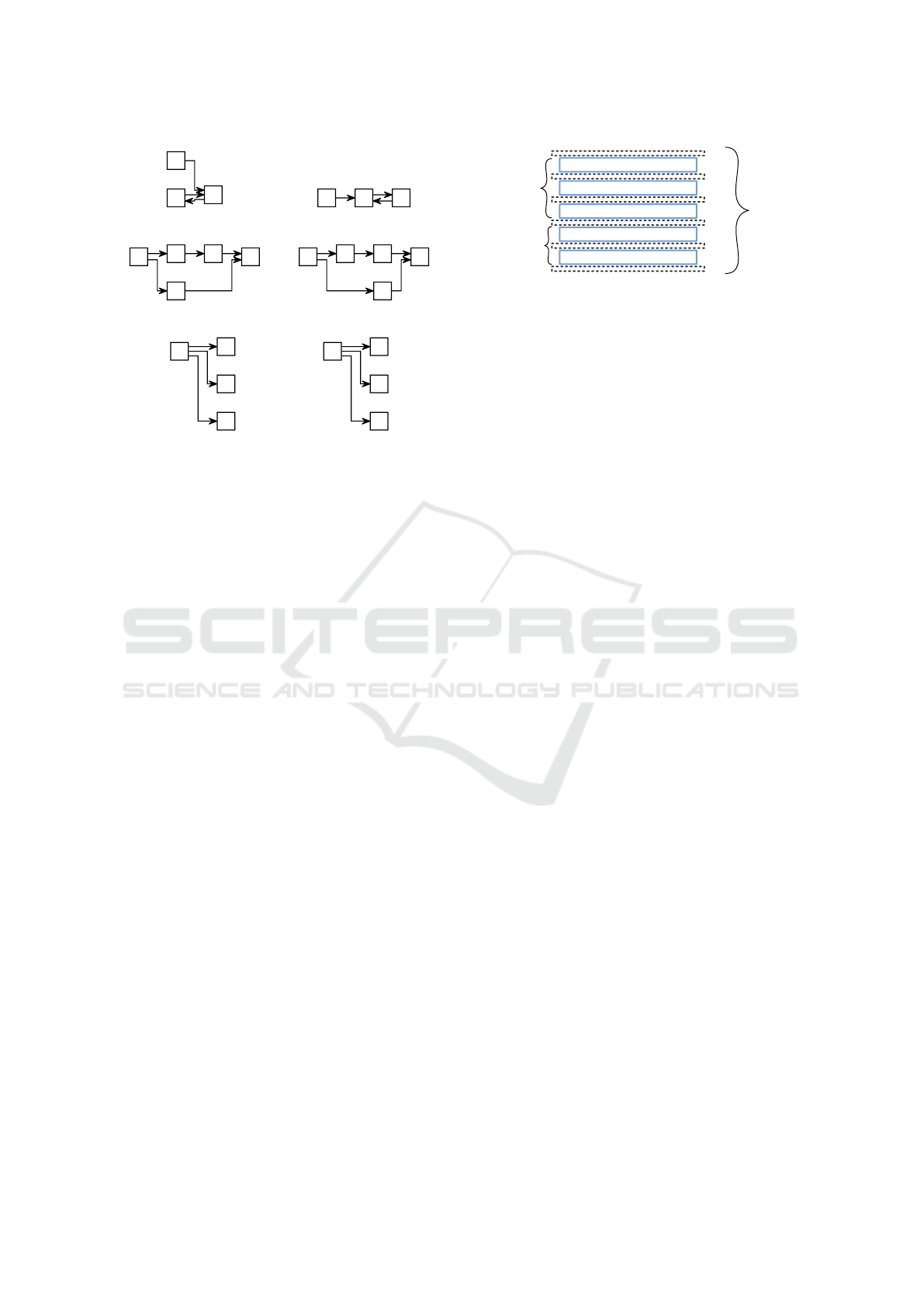
seen in Figure 8. Here, the second layer holds all sta-

tionary states (stretched, stopped, and contracted) and

the third all intermediate states (stretching and con-

tracting). Although many edge crossings are created,

half of the participants preferred this solution. The

second half heavily disliked the drawing because of

the introduced edge crossings. This effect occurred

for all participants regardless of their prior knowledge

in computer science or graph drawing.

To summarize: The node model order between

connected nodes should be utilized during cycle

breaking since the analyzed models show that the de-

veloper desires the same ordering in the diagram. Us-

ing this, control-ﬂow loops introduce the backward

edge just at the end of the loop, where it seman-

tically ﬁts best. Further analysis revealed that the

few exceptions are copy-pasted models and models

IVAPP 2023 - 14th International Conference on Information Visualization Theory and Applications

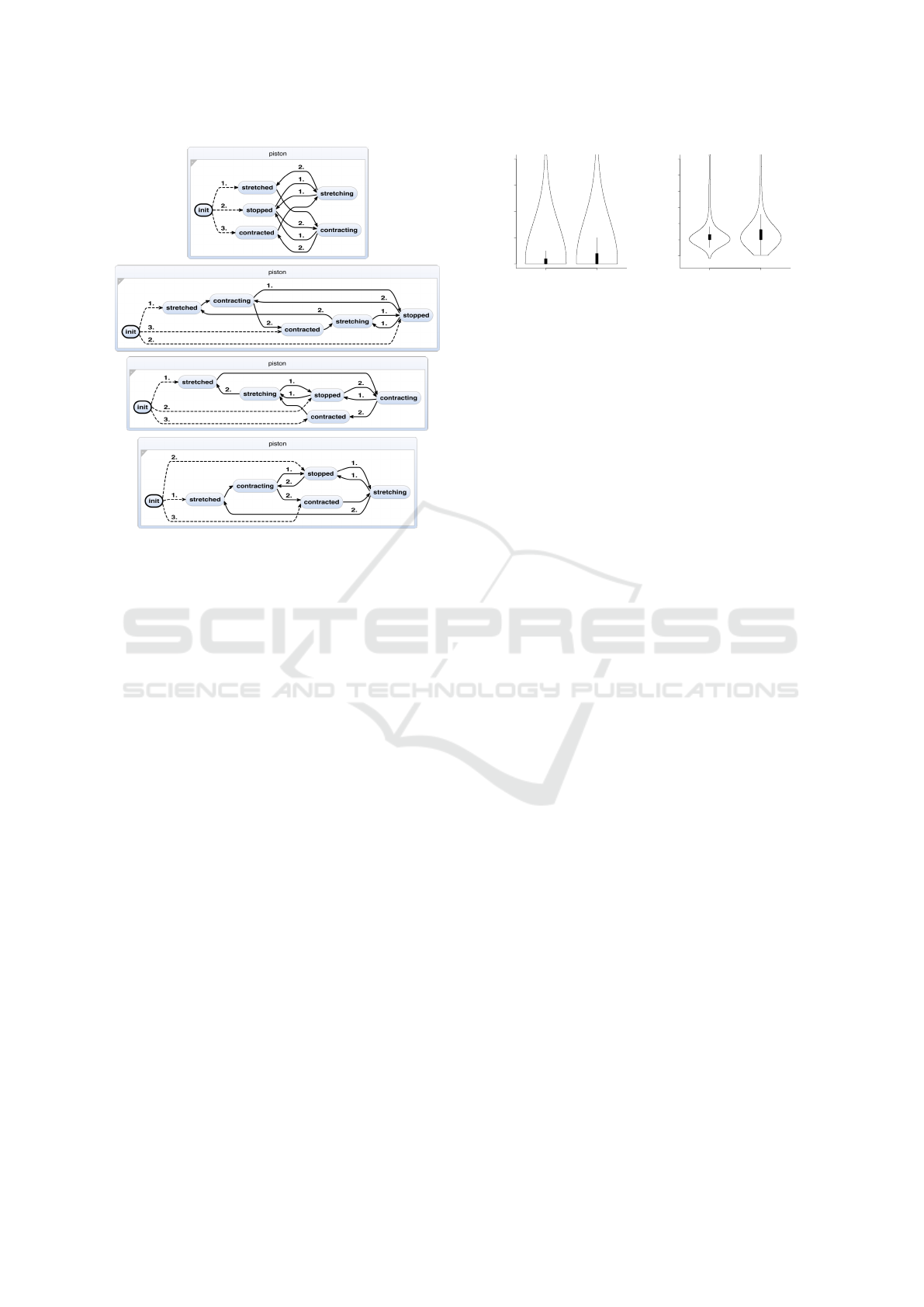
Figure 8: Different cycle breaking strategies compared.

From top to bottom: breadth-ﬁrst cycle breaker, greedy

cycle breaker, model order cycle breaker, depth-ﬁrst cycle

breaker.

with changed ordering with the hope to inﬂuence the

layout. This can be generalized to control-ﬂow lan-

guages that model connections explicitly. Therefore,

we propose to use the model order cycle breaker for

such languages. Furthermore, we see that, as already

explained in Section 4, a breadth-ﬁrst node model

order is uncommon in SCCharts models and hence

probably also in other languages that model control-

ﬂow. However, it can be used to create any desired

layering if necessary.

6.2 Model Order Crossing

Minimization in SCCharts

As mentioned earlier, edges in SCCharts are num-

bered by their priorities. The placement inside the

diagram has no semantics, therefore, their drawing or-

der can be freely chosen. Expert developer feedback

revealed that although a correct ordering is helpful, it

should be overridden if the drawing can be simpliﬁed

by reducing the edge crossings. The order of nodes it-

self is less relevant and should be disregarded in favor

of edge order.

The layered algorithm should, therefore, apply the

preferEdges crossing minimization pre-processing

and weight node and edge order violation as, e. g., one

tenth as important as edge crossings (Domr

os and von

Hanxleden, 2022). For complete control over the lay-

0 5 10 15 20

E − wE N − wN

● ●

Crossing Difference

(a) Edge crossing difference

−20 20 60 100

E − wE N − wN

● ●

Edge Length Difference

(b) Edge length difference

Figure 9: The preferEdge/preferNodes (E/N) approach

without crossing minimization compared to the crossing

minimization approach (wE/wN) with node and edge order

violation weights during crossing minimization. The edge

crossing difference is cut off at 20 crossings to increase the

readability.

out the model order layer assignment and preferEdges

without crossing minimization should be used, since

it can recreate any layout given a breadth-ﬁrst node

model order.

The same conclusions can be drawn for other

control-ﬂow languages for which the drawing order

of edges or ports and nodes has no semantics.

6.3 Model Order Without Crossing

Minimization

We evaluated 357 SCCharts with at least 3 states and

more than 3 edges between them created by students

during lectures and projects between 2014 and 2022.

The results can be seen in Figure 9.

When using preferNodes without crossing mini-

mization, 151 models are different compared to the

solution that uses pre-ordering and crossing mini-

mization with a node and port order violation weight

of 0.1. When using preferEdges, only 127 are dif-

ferent. We see very few models that create many ad-

ditional edge crossings. Edge crossings tend to get

induced primarily when models are particularly com-

plicated, relied on copy and paste during creation, or

model order had no effect on the layout during their

creation. For the preferEdges approach, 75% of all

models create at most one additional crossing. For

preferNodes, 75% of all models create up to two ad-

ditional crossings. For both approaches the median

is 0, which emphasizes that most models are already

layouted optimally by just following the model order.

Since model order did not affect the creation on these

models, we expect that this number will only increase

in the future, which will be evaluated in future work.

The edge length only gets signiﬁcantly worse for

the same big, not carefully designed models men-

tioned earlier. For other graphs it increases on average

only slightly.

Model Order in Sugiyama Layouts

1 . ..

2 main reactor {

3 logical action a:char

;

4 physical action b:char

;

6 reaction (startup) → a {=. . . =}

7 reaction (a) → b {=.. . =}

8 reaction (b) → a {=.. . =}

10 }

(a) Textual Lingua Franca

model visualizing the com-

mon ordering of actions and

reactions.

reactionOrder

(b) Enforcing the

model order is only

sensible if the tex-

tual model intends

its ordering.

reactionOrder

1 2 3

cle breaker.

1 . ..

2 main reactor {

3 a = new Accelerometer();

4 dx = new Display(row = 0);

5 dy = new Display(row = 1);

7 timer t(0, 250 msec);

8 .. .

(d) Textual accelero-

meter display Lingua . . .

8 .. .

9 state count:int(0);

11 reaction(t) → a.trigger {=. . . =}

12 reaction(a.x, a.z) →

13 dx.message {=. . . =}

14 reaction(a.y) →

15 dy.message {=. . . =}

16 }

(e) . . . Franca model, au-

thored by Edward A. Lee.

AccelerometerDisplay

a : Accelerometer

trigger

dx : Display

message

dy : Display

message

(0, 250 msec)

(f) A Lingua Franca model of an accelerometer display, au-

thored by Edward A. Lee.

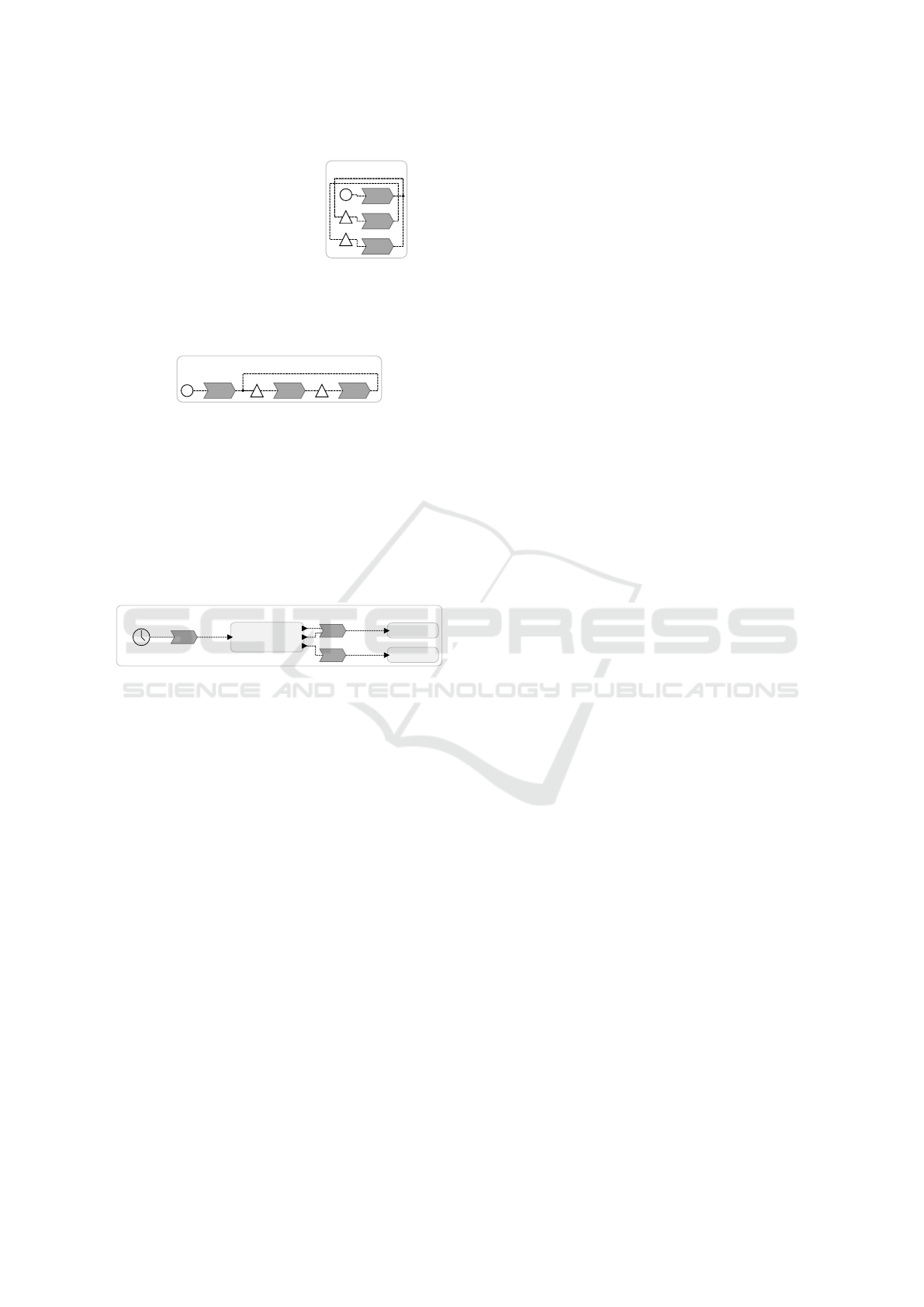
Figure 10: Textual and graphical Lingua Franca models.

The startup node is drawn as a cycle, a timer as a clock,

an action as a triangle, reactions as an arrow shape with a

number, and reactors as rounded rectangles.

These results emphasize that node and edge model

order is in most cases intended by the SCCharts devel-

oper and should, therefore, be respected in the draw-

ing, as also reported by (Domr

os and von Hanxleden,

2022).

6.4 Model Order in Lingua Franca

Lingua Franca models are data-ﬂow based, as seen in

Figure 10. Even though the textual order of reactors,

reactions, actions, and timers, is interchangeable, they

are usually grouped by category, e. g., ﬁrst all action

then all reactions, as seen in Figure 10a, 10d and 10e.

Not every node has a model order. In Figure 10a,

the round startup node is not explicitly modeled. It is

created when the textual model is synthesized into a

view model, which creates the graph. Here, the dia-

gram synthesis takes care of giving the startup node

the correct order inside the list of view model nodes.

For the startup node this question is easy, since it is

the entry point of execution and should, therefore, be

the ﬁrst node. For other nodes this is not trivial and

has to be done with care, especially if model order is

used as a constraint. Therefore, it is a valid option to

not give these nodes a model order. If this is the case,

cycle breaking may ignore them, which works as long

as no cycles are created by them, and crossing mini-

mization sorts them by their incoming connections.

6.4.1 Cycle Breaking in Lingua Franca

Since nodes are ordered by convention only in-

side their respective category, the model order cy-

cle breaker performs badly, as seen in Figure 10b.

Declaring the actions (line 3 and 4) before the reac-

tions (line 6-8) results in backward edges from the re-

actions to the actions. The greedy model order cycle

breaker should be used instead to get a drawing with

minimal backward edges that creates a deterministic

solution, as seen in Figure 10c. Minimizing the back-

ward edges is especially important for Lingua Franca,

since they have to be routed around the nodes since

outgoing edges are always on the right of a node and

incoming edges always on the left side. As seen in

Figure 10b, backward edges create, therefore, dummy

nodes routing the output backward and the input for-

ward, which increases the clutter, makes edges harder

to follow, and may increase the size of the drawing.

The model order cycle breaker can still be used

if the textual convention is disregarded to be able to

use model order to constrain the drawing. This is also

the only use case for model order layer assignment

for Lingua Franca. Additionally, the diagram can be

conﬁgured assigning model order only to reactions,

to reactions and reactors, or to everything, since each

might be the intended behavior.

6.4.2 Crossing Minimization in Lingua Franca

In contrast to other data-ﬂow languages, Lingua

Franca deems the order of connected edges as unim-

portant, as reported by expert developers, since the

edges can be identiﬁed by port labels and not relate to

real hardware. Hence, changing the port order from x

y z to x z y in Figure 10f is viable to reduce the number

of crossings.

Enforcing the node order inside a layer improves

orientation in complex models such as Figure 11.

Here, the order of the Ghosts pinky, blinky, inky, and

clyde is maintained.

Doing no crossing minimization often proved to

be ineffective, since edges are not explicit and many

dummy nodes are created to route backward edges.

IVAPP 2023 - 14th International Conference on Information Visualization Theory and Applications

PacMan

controller : GameController

ghost_sprites

pacman_sprite

tick

wall_list

gate

block_list

score

game_over

player : Player

wall_list

gate_list

icon

sprite

icon_name

pinky : Ghost

wall_list

gate_list

icon

tick

sprite

icon_name

blinky : Ghost

wall_list

gate_list

icon

tick

sprite

icon_name

inky : Ghost

wall_list

gate_list

icon

tick

sprite

icon_name

clyde : Ghost

wall_list

gate_list

icon

tick

sprite

icon_name

display : Display

moving_sprites

static_sprites

game_over

score

icon_name

tick

icon

Figure 11: The PacMan Lingua Franca model, which contains the ghosts pinky, blinky, inky, clyde in that order.

Model order could be inferred for dummy nodes such

that an implicit ordering could be calculated with

other means than the connection to a previous layer,

which is evaluated as part of future work on model

order. Currently, it is solved by greedily switching

edges and nodes in a one-pass algorithm instead of

doing crossing minimization.

7 FURTHER RELATED WORK

(Gansner et al., 1993) state that even cyclic graphs

have an edge direction based on their graph input that

represents their natural direction. They do, however,

only conclude that depth-ﬁrst cycle breaking is prefer-

able to other approaches and do not use the model

order—which they implicitly already do for travers-

ing nodes and edges—for cycle breaking.

(Nikolov and Tarassov, 2006) propose two node

promotion algorithms that are applied after a longest-

path-layering, which is also the starting point for the

model order layerer. Instead of considering the order-

ing, the algorithms minimizes the layer width while

also considering dummy nodes. Their algorithms op-

timize the edge length and edge density but utilize

node promotion similar to our approach.

Several solutions exist to constrain node and edge

order via absolute or relative constraints (B

ohringer

and Paulisch, 1990; Waddle, 2001; Mennens et al.,

2019). Even though enforced model order can repli-

cate any layout by breadth-ﬁrst order, it is not an al-

ternative to using constraints but rather one additional

instrument to constrain nodes and edges. Since lay-

out constraints need a reference layout and, therefore,

two layout runs, the ﬁrst layout run can use model or-

der and the second one can evaluate the constraints

and move nodes. This tends to create the desired lay-

out with fewer constraints if the model order is sen-

sible, since the model order produces a stable initial

layout, which is most likely already desired. Since

model order layer assignment requires an often not

existing breadth-ﬁrst model order, constraints can be

used instead to force nodes in the correct layers.

8 CONCLUSION AND OUTLOOK

We presented a full overview on model order strate-

gies for Sugiyama layouts. Moreover, we suggest

strategies that are applicable to control-ﬂow graphs

and data-ﬂow graphs based on developer feedback,

studies, and quantitative analysis.

Future work on this topic goes in several direc-

tions.

Model order currently assumes that the given lin-

ear textual ordering can be applied to all elements.

Since this is not the case for Lingua Franca, the given

model order strategies should also be able to handle

different model order groups that represent different

kinds of semantic elements.

During cycle breaking and layer assignment, all

nodes are expected to have a model order or to be

dummy nodes. In practice this might not always be

the case, as shown on the example of Lingua Franca.

Model Order in Sugiyama Layouts

As part of future work, the algorithm should infer the

model order of these nodes.

Lingua Franca proposes another additional use

case in form of hyperedges, which are currently

treated as normal edges. Future work should investi-

gate what special treatment might be required to apply

model order to more general graphs.

Lingua Franca does not explicitly model edges but

rather ports. Future work should investigate whether

the port and edge order, which are handled equiv-

alently in SCCharts, need to be distinguished for

Lingua-Franca-like languages by having on explicit

order for input ports.

(Purchase, 1997) found that user performance

increased from drawings from medium symmetric

drawings to fully symmetric drawings. Since the na-

ture of model order and the grouping it creates relates

to the way symmetry allows us to quickly access a

model, part of future work should focus on whether

model order is also more effective if everything or

nearly everything is ordered.

Since the model order tends to produce more sta-

ble layouts than randomized solutions, its relation to

the mental map should be investigated, as it is deemed

as one of the most important aspects of graph draw-

ing (Purchase et al., 2006). In particular, it should be

investigated whether the mental map, which is repre-

sented by the textual and graphical model, is empha-

sized using model order in an interactive scenario.

REFERENCES

ohringer, K.-F. and Paulisch, F. N. (1990). Using con-

straints to achieve stability in automatic graph layout

algorithms. In Proceedings of the SIGCHI Conference

on Human Factors in Computing Systems, pages 43–

51, New York. ACM.

Di Battista, G., Eades, P., Tamassia, R., and Tollis, I. G.

(1999). Graph Drawing: Algorithms for the Visual-

ization of Graphs. Prentice Hall.

Domr

os, S. and von Hanxleden, R. (2022). Preserving or-

der during crossing minimization in sugiyama layouts.

In Proceedings of the 14th International Conference

on Information Visualization Theory and Applications

(IVAPP’22), part of the 17th International Joint Con-

ference on Computer Vision, Imaging and Computer

Graphics Theory and Applications (VISIGRAPP’22),

pages 156–163. INSTICC, SciTePress.

Eades, P., Lin, X., and Smyth, W. F. (1993). A fast and

effective heuristic for the feedback arc set problem.

Information Processing Letters, 47(6):319–323.

Fuhrmann, H. and von Hanxleden, R. (2010). On the prag-

matics of model-based design. In Proceedings of the

15th Monterey Workshop 2008 on the Foundations

of Computer Software. Future Trends and Techniques

for Development, Revised Selected Papers, volume

6028 of LNCS, pages 116–140, Budapest, Hungary.

Springer.

Gansner, E. R., Koutsoﬁos, E., North, S. C., and Vo, K.-

P. (1993). A technique for drawing directed graphs.

Software Engineering, 19(3):214–230.

Kieffer, S., Dwyer, T., Marriott, K., and Wybrow, M.

(2016). HOLA: human-like orthogonal network lay-

out. IEEE Trans. Vis. Comput. Graph., 22(1):349–

358.

Lohstroh, M., Menard, C., Bateni, S., and Lee, E. A. (2021).

Toward a Lingua Franca for Deterministic Concurrent

Systems. ACM Transactions on Embedded Computing

Systems (TECS), 20(4):Article 36.

Mennens, R. J., Scheepens, R., and Westenberg, M. A.

(2019). A stable graph layout algorithm for processes.

In Computer Graphics Forum, volume 38, pages 725–

737. Wiley Online Library.

Nikolov, N. S. and Tarassov, A. (2006). Graph layering by

promotion of nodes. Discrete Applied Mathematics,

154(5):848–860.

Purchase, H. C. (1997). Which aesthetic has the greatest

effect on human understanding? In Proceedings of the

5th International Symposium on Graph Drawing (GD

’97), volume 1353 of LNCS, pages 248–261. Springer.

Purchase, H. C., Hoggan, E. E., and G

org, C. (2006). How

important is the “mental map”? – an empirical in-

vestigation of a dynamic graph layout algorithm. In

Proceedings of the 14th International Symposium on

Graph Drawing (GD ’06), volume 4372 of LNCS,

pages 184–195. Springer.

Schulze, C. D., Sp

onemann, M., and von Hanxleden, R.

(2014). Drawing layered graphs with port constraints.

Journal of Visual Languages and Computing, Special

Issue on Diagram Aesthetics and Layout, 25(2):89–

106.

Sugiyama, K., Tagawa, S., and Toda, M. (1981). Methods

for visual understanding of hierarchical system struc-

tures. IEEE Transactions on Systems, Man and Cy-

bernetics, 11(2):109–125.

von Hanxleden, R., Duderstadt, B., Motika, C., Smyth, S.,

Mendler, M., Aguado, J., Mercer, S., and O’Brien,

O. (2014). SCCharts: Sequentially Constructive

Statecharts for safety-critical applications. In Proc.

ACM SIGPLAN Conference on Programming Lan-

guage Design and Implementation (PLDI ’14), pages

372–383, Edinburgh, UK. ACM.

von Hanxleden, R., Lee, E. A., Fuhrmann, H., Schulz-

Rosengarten, A., Domr

os, S., Lohstroh, M., Bateni,

S., and Menard, C. (2022). Pragmatics twelve years

later: a report on lingua franca. In International Sym-

posium on Leveraging Applications of Formal Meth-

ods, pages 60–89. Springer.

Waddle, V. (2001). Graph layout for displaying data struc-

tures. In Proceedings of the 8th International Sympo-

sium on Graph Drawing (GD ’00), volume 1984 of

LNCS, pages 98–103. Springer.

IVAPP 2023 - 14th International Conference on Information Visualization Theory and Applications