Multiclass Texture Synthesis Using Generative Adversarial Networks

Maro

s Koll

, Lukas Hudec

and Wanda Benesova

Faculty of Informatics and Information Technologies, Slovak University of Technology, Ilkovicova 2, Bratislava, Slovakia

Keywords:

Texture, Synthesis, Multiclass, GAN, Controllability.

Abstract:

Generative adversarial networks as a tool for generating content are currently one of the most popular methods

for content synthesis. Despite its popularity, multiple solutions suffer from the drawback of a shortage of

generality. It means that trained models can usually synthesize only one speciﬁc kind of output. The usual

synthesis approach for generating N different texture species requires training N models with changing training

data. However, few solutions explore the synthesis of multiple types of textures. In our work, we present

an alternative approach for multiclass texture synthesis. We focus on the synthesis of realistic natural non-

stationary textures. Our solution divides textures into classes based on the objects they represent and allows

users to control the class of synthesized textures and their appearance. Thanks to the controllable selections

from latent space, we also explore possibilities of creating transitions between classes of trained textures for

potential better usage in applications where texture synthesis is required.

1 INTRODUCTION

The texture deﬁnition highly depends on the appli-

cation area, in which we use this term (Haindl M.,

2013). Nevertheless, textures generally describe ob-

ject’s surface properties like appearance, structure,

consistency, or feeling from touch. Textures are an

essential component of computer vision because they

are used in tasks like classiﬁcation, detection, or seg-

mentation in medicine or the technology industry.

Textures are also essential for the graphics and the

entertainment industry since almost every animated

movie, video game, or other product depends on its

visual appearance.

We can classify textures based on their primary

characteristic into groups like smooth, rough, glossy,

matte, et cetera. There are also more general char-

acteristics like stationarity and homogeneity (Zhou

et al., 2018; Portilla and Simoncelli, 2000) that pro-

ﬁle textures. It is possible to say that both of these

features describe an aspect of texture complexity. Sta-

tionarity represents the regularity of structure. Homo-

geneity represents how many elementary textures are

included in the evaluated texture. The more complex

the texture structure is, the more difﬁcult it is to syn-

thesize.

https://orcid.org/0000-0002-1535-6830

https://orcid.org/0000-0002-1659-0362

https://orcid.org/0000-0001-6929-9694

Texture synthesis is a process of creating artiﬁcial

textures that can be used to augment datasets needed

for computer vision tasks. It can also replace texture

photographing or painting with a more comfortable

and less time-consuming content creation method.

There are multiple texture synthesis approaches; how-

ever, current research orients on Generative adversar-

ial networks (GANs) and diffusion networks. GANs

proved their advantages in the quality of outputs and

speed of generating. On the other hand, their disad-

vantages are long and challenging training accompa-

nied by problems like vanishing gradients or mode

collapse. Another drawback is that usual solutions

are trained to synthesize one texture class, and mul-

tiple learned models are required to synthesize multi-

ple texture classes (Zhou et al., 2018; Jetchev et al.,

2016). That results in higher disk storage require-

ments for storing the network models and the inability

of creating transitions between individual textures.

Our paper introduces the following contributions:

• We propose two approaches focused on control-

lable multiclass texture synthesis that uses a latent

space as a control mechanism. Our solution is

tuned to synthesize non-stationary textures from

the natural environment.

• Latent space used for texture control is computed

by pre-trained feature extractor before training the

synthesis solution. This gives the advantage to

modify the feature extractor based on class adja-

Kollár, M., Hudec, L. and Benesova, W.

Multiclass Texture Synthesis Using Generative Adversarial Networks.

DOI: 10.5220/0011657500003417

In Proceedings of the 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 1: GRAPP, pages

87-97

ISBN: 978-989-758-634-7; ISSN: 2184-4321

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

cency requirements to enhance the latent space in-

dependently from the generating process.

• We show that in the ﬁeld of texture synthesis, the

latent space can be used to create transitions be-

tween different classes of textures and also control

the appearance of a speciﬁed texture class.

2 RELATED WORK

Texture synthesis has been an active ﬁeld of research

for multiple decades. Many approaches were intro-

duced and categorized into groups during these years

based on their main feature.

Non-parametric sampling is considered a tradi-

tional approach and, for a long time, was one of the

most popular synthesis methods. This approach uses

copying parts of sample textures to create a new one.

Parts of sample textures are chosen based on their

neighbourhood similarity with an area of an already

synthesized part of the texture. There are two main

types of non-parametric sampling based on the size of

individual parts copied to synthesized texture. Pixel-

based synthesis (Efros and Leung, 1999; Wei and

Levoy, 2000; Shin et al., 2006; Ashikhmin, 2000) that

creates texture pixel by pixel and patch-based syn-

thesis (Praun et al., 2000; Liang et al., 2001; Kwa-

tra et al., 2003) that copies whole patches. These

approaches are intuitive and relatively easy to imple-

ment. On the other hand, their synthesis is quite slow,

and there is a possibility that synthesized textures will

contain visually duplicate parts.

In contrast to the non-parametric sampling, a para-

metric synthesis (Portilla and Simoncelli, 2000) uses

parameters to describe texture statistics. The synthe-

sized image is created by gradually changing random

noise (Gatys et al., 2015b). Two textures should have

identical statistics to be considered similar (Martin

and Pomerantz, 1978).

In recent years textures have been synthesized

mainly by using neural networks. Gatys et al. (Gatys

et al., 2015b) created a parametric approach that used

convolutional neural network VGG-19 (Simonyan

and Zisserman, 2014) to extract Gram matrices at

multiple layers as texture statistics. The new texture

is synthesized from random noise. Noise is passed

through the network and edited by gradient descent to

minimalize the difference between Gram matrices of

example texture and new texture.

Variational autoencoders (Kingma and Welling,

2014; Chandra et al., 2017; Pesteie et al., 2019) are

another approach that uses neural networks to synthe-

size textures. Variational autoencoders are similar to

autoencoders, but their function is to create similar

output, not identical. They consist of an encoder part

that maps input data to a low-dimensional representa-

tion and a decoder part that reconstructs this represen-

tation to output. A drawback of this synthesis solution

is the quality of output that could be blurry.

Diffusion networks (Ho et al., 2020; Croitoru

et al., 2022; Dhariwal and Nichol, 2021) are gener-

ative models inspired by nonequilibrium thermody-

namics. They are based on two stages. A forward

stage deﬁned as a Markovian chain slowly destroys

data by adding random noise to transform data into

pure noise. A backward stage learns to recover the

data by reversing the addition of noise. The new

data is created by passing random noise to the learned

model that synthesizes the ﬁnal image by gradually

predicting and removing noise. Diffusion networks

produce high-quality images and are currently consid-

ered a state-of-the-art approach. Even though there is

a disadvantage in long inference time due to the iter-

ative approach.

Although the quality of diffusion network, gener-

ative adversarial networks introduced by Goodfellow

et al. (Goodfellow et al., 2014) are still popular ap-

proaches for image synthesis. Generative adversarial

networks contain two neural networks, a discrimina-

tor and a generator. These networks train themselves

by min-max two-player game. That results in im-

proved output quality of generated output. The gener-

ator’s goal is to use random noise to create output that

the discriminator would not reveal as fake. The goal

of the discriminator is to determine which inputs are

real and which are fake correctly. Since the original

GAN solution introduction by Goodfellow et al., mul-

tiple GAN modiﬁcations have been created. Proposed

modiﬁcations changed the architecture of generator

or discriminator (Radford et al., 2016), used different

adversarial loss functions (Arjovsky et al., 2017; Gul-

rajani et al., 2017), stabilized training (Karras et al.,

2017), improve variation of outputs (Salimans et al.,

2016) or create a new approach of training (Zhu et al.,

2017).

Several GAN solutions have also focused on mul-

ticlass texture synthesis. Li et al. (Li et al., 2017)

introduced solution DTS that uses one hot encoding

vector as a control mechanism for the synthesis of

multiple types of textures. The architecture of their

proposed generator consists of two streams: one for

synthesizing the ﬁnal output and the second for pro-

cessing input information that controls the class of

synthesized texture. Their solution also showed that

it is possible to create interpolations between learned

textures that lead to new types of textures.

Another multiclass synthesis solution is PSGAN

introduced by Bergmann et al. (Bergmann et al.,

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

2017). Their solution can learn multiple types of peri-

odic and non-periodic textures from a dataset or high-

deﬁnition images. A disadvantage of this solution

is that the texture control mechanism (global dimen-

sions of the input) is sampled as a random vector, so

it does not allow control of which texture will be syn-

thesized. The solution also does not provide complete

coverage of the dataset.

Following these disadvantages, Alanov et al.

(Alanov et al., 2020) proposed a solution that updates

the creation of global input dimensions by using an

encoder. The encoder is trained alongside the gener-

ator to learn textures’ latent representation. Learned

representation is then used as a control mechanism.

They also ensure full dataset coverage by penalization

for incorrect reproductions of a given texture.

3 METHOD

The main goal of our work is to create a robust con-

trollable method for multiclass texture synthesis with

a focus on non-stationary textures and maintaining

the quality of generated textures. The controllability

should ensure a change of texture type and its look.

Proposed versions of the architecture of our solution

are shown in ﬁgure 1.

3.1 Generator

The core of our approach, the generator, uses the idea

of a two-stream network from the work of Li et al.

(Li et al., 2017). This architecture helps to force the

network to synthesize a required texture class. The

primary stream handles the synthesis process, and

the secondary stream processes information on which

texture class should be generated. Activations of sec-

ondary streams are merged as a 32-channel feature

map to activations of the primary stream after ev-

ery processed spatial upsample. This ensures that

the primary stream has additional information about

a class of synthesized textures at every resolution. An

upsample function upsamples the resolution in both

primary and secondary streams with scale factor 2.

The exception is the ﬁrst upsample of vector done by

transposed convolution. After upsample, activations

are processed by convolutional layers with instance

normalization and leaky relu activation functions.

Because of the exertion of multiclass non-

stationary texture synthesis, the solution suffered

from visual artifacts and had difﬁculty learning all

types of presented textures, even though there were

only six. To deal with this problem, we implemented

the generator as a progressively growing GAN (Kar-

ras et al., 2017). This approach helped to stabilize

learning thanks to the ability of the network ﬁrst to

learn the color palette of synthesized textures and then

increase resolution and learn details of textures. The

current implementation of our solution generates out-

puts of 128 × 128 pixels. However, thanks to the pro-

gressive, growing GAN implementation, more layers

can be easily added to increase the resolution of the

ﬁnal output. We also changed batch normalization to

instance normalization and added hyperbolic tangent

as the ﬁnal layer to improve the quality of outputs.

Hyperbolic tangent limits values of output pixels be-

tween -1 and 1 to prevent very high or low values. The

generated output is then used to train the discrimina-

tor without clipping to [0, 1] to force the generator to

learn the correct interval of pixel values.

3.2 Generator Inputs

The difference between alternatives of our solution is

based on changes in inputs for the generator and the

process of obtaining them. As a consequence of two

generator streams, the generator requires two inputs.

In our ﬁrst solution alternative, input for the sec-

ondary stream is realized as a one-hot encoding vec-

tor. This vector is inspired by the solution of Li et

al. (Li et al., 2017) and encoded as a position of a

single high bit, which clearly describes which texture

should be synthesized. The primary input is inspired

by the solution of Bergmann et al. (Bergmann et al.,

2017). In contrast with their solution, our input is not

constructed as a matrix of vectors but only as one vec-

tor. The input vector is concatenated from three parts:

random, texture, and selection, whose lengths were

set experimentally based on the quality and diversity

of outputs.

• The random part is sampled from the uniform dis-

tribution on the interval [0,1]. This part provides

variability between generated outputs.

• The selection part is a copy of the input for the

secondary stream. One-hot encoding vector is in-

cluded in primary input to contribute information

about the selected texture even at the ﬁrst layers

of the generator.

• The texture part is created from an example im-

age of the required texture class. An example

image transformed to a grey scale is used as in-

put for our pre-trained classiﬁcation network. We

selected the classiﬁcation network and principal

components analysis approach for initial experi-

ments because of relatively straightforward net-

work training and the possibility of identifying a

well-trained classiﬁcation network based on clas-

siﬁcation metrics. We took input activations of

Multiclass Texture Synthesis Using Generative Adversarial Networks

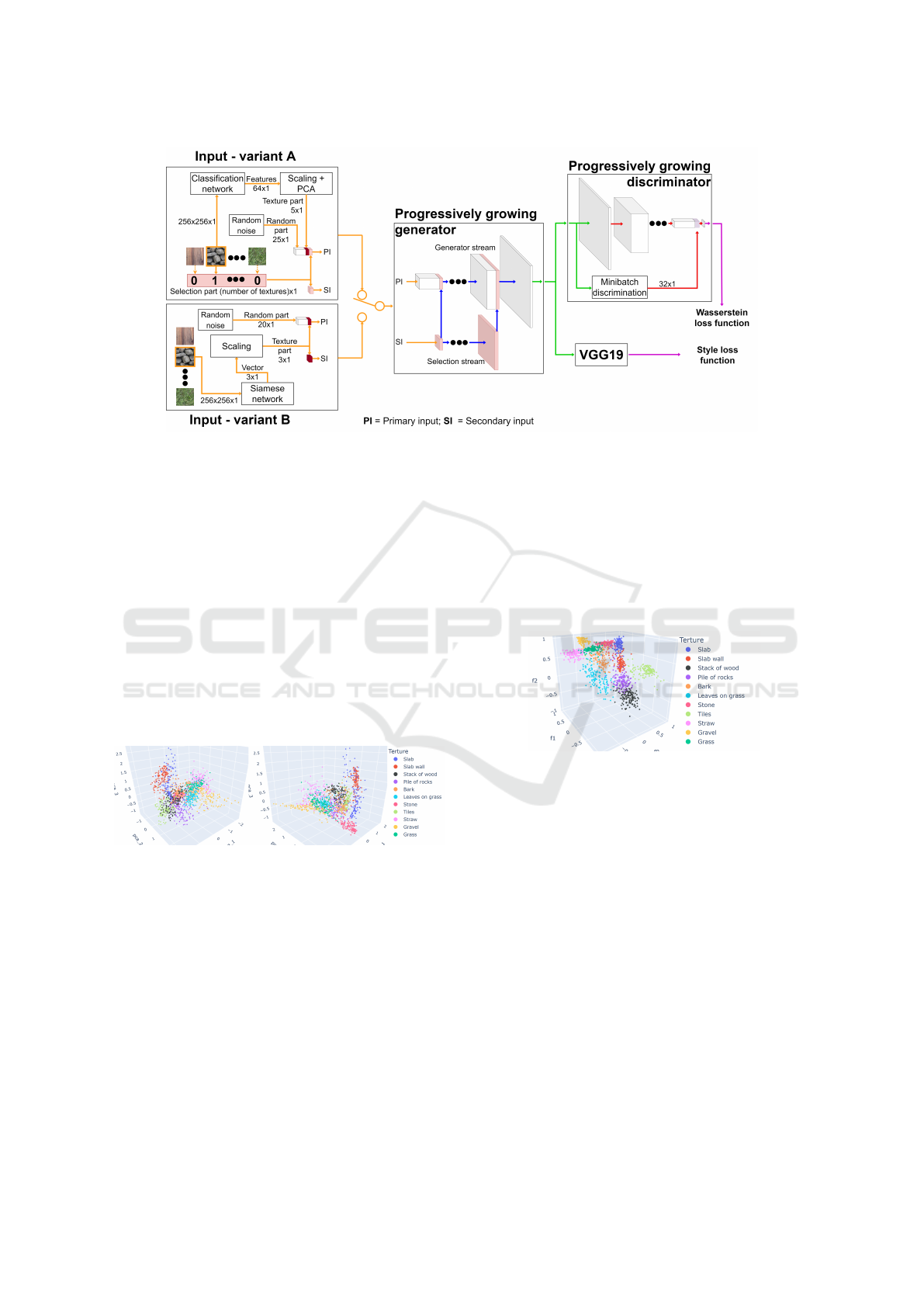
Figure 1: Visualization of the architecture of our solution. The left side of the ﬁgure shows variants of input for a generator.

Variant A uses classiﬁcation network as feature extractor with PCA for texture part of input. Variant B uses siamese network

for texture part of input. The generator consists of two streams for image synthesis and keeping the information about the

selected texture class. The discriminator is enriched with information from Minibatch discrimination. We use a combination

of Wasserstein loss with Style loss computed by a pre-trained VGG19 network as a loss function.

the last fully connected layer as a feature vector

and applied principal component analysis on this

vector to obtain a representation vector of length

ﬁve numbers. This part of the input assists the

selection part with information about the selected

texture and also brings variability to the input. To

conﬁrm that this vector carries information about

the selected texture type, we visualized part of the

vector in 3D space. As we can see in ﬁgure 2, ev-

ery cluster of texture type could be approximately

separated.

Figure 2: A visualization of the clusters of 3 out of 5 values

from the texture part created by the classiﬁcation network

and PCA. The visualisation shows that individual clusters

in the latent space are approximately separable.

In our second solution alternative, we replaced the

classiﬁcation network and PCA with a Siamese net-

work and left out the selector part of the input. That

leads to using the texture part as the only control-

ling mechanism in a primary and secondary input.

Siamese network as the texture part extractor was se-

lected for its ability to learn similarities that leads to a

better embedding of textures in the latent space. Fig-

ure 3 shows clusters that refer to trained texture types

in latent space created by our trained Siamese net-

work. The selection part was left out based on testing

the ﬁrst alternative. Tests showed that manual control

of generator inputs for changing texture type or cre-

ating transitions between different textures is hard to

use. That also leads to minimizing the length of the

texture part from 5 to 3 values.

Figure 3: A visualization of the clusters from the texture

part created by the Siamese network. The individual clus-

ters are better separable than in the version that uses classi-

ﬁcation network and PCA.

The decision to use the pre-trained feature extrac-

tors was made because of the advantage of review-

ing if the feature extractor is well-trained or needs

to be trained more. In the case of the siamese net-

work, we can affect the distribution to decrease dis-

tances between clusters of different texture classes or

rearrange the cluster neighbors. For this purpose, dur-

ing the training of the siamese network, we can deﬁne

shorter distances between feature vectors for concrete

pairs of textures that we want to be closer to in the

latent space. This will allow us to create transitions

between pairs of textures that we want. We can deﬁne

the higher distance between feature vectors for other

pairs of textures we don’t want to be closer to.

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

3.3 Discriminator

The initial discriminator used in our solution was in-

spired by the DCGAN solution (Radford et al., 2016).

We changed it by adding a sequence of batch nor-

malization, leaky relu activation function, and convo-

lutional layer with kernel size 5, stride 1, and zero

padding behind the last convolutional layer. Be-

cause of the implementation of the progressive, grow-

ing generator, the discriminator also had to be im-

plemented as progressively growing. That caused a

change of the parameters of the ﬁrst convolutional

layer to kernel size 3, padding, and stride set to 1.

A number of the following sequences of convolu-

tional, normalization, and activation layers from the

DCGAN solution are based on the current step of

progressive growth. We also added a fade-in mech-

anism to handle adding new layers during progressive

growth. Feature maps from the last convolutional se-

quence are ﬂattened to a 1D feature vector. To deal

with the mode collapse problem, we concatenated the

ﬁnal 1D vector of the discriminator with the 1D vec-

tor from minibatch discrimination (Salimans et al.,

2016). This helps the network to identify a batch

of generated images. Minibatch discrimination com-

pares all images in a batch and creates a vector that

references how similar images are. In case of high

similarity, we can assume that images are synthesized

and suffer from mode collapse. Based on executed

tests, we noticed that minibatch discrimination helps

mainly in the ﬁrst two steps of progressive growth,

which correspond to images of size 8 ×8 and 16×16.

The ﬁnal change was to switch the sigmoid layer to a

linear layer.

3.4 Loss Functions

Instead of the original loss function used in Good-

fellow’s proposed GAN solution, we used Wasser-

stein loss (Arjovsky et al., 2017) with weight clip-

ping to increase output quality and stability of train-

ing. That changed our discriminator to critic, which

does not determine real or fake textures but tells the

distance between the distribution of generated outputs

and training data. We combined Wasserstein loss with

style loss (Gatys et al., 2015a) during the training

process to speed up the training process and bring a

closer visual appearance of synthesized and real tex-

tures. The texture loss is calculated from feature vec-

tors of the ﬁrst ﬁve convolutional layers of the pre-

trained classiﬁcation network VGG19. Feature vec-

tors of synthesized and real textures were compared

using Gram matrices. Style loss L

style

is added to

Wasserstein loss W for generator loss L

and could

be controlled by the weight factor β. Based on exper-

imenting with the value of β, we found that the ideal

value in our setup is 1. In the case of a higher style

weight factor, the network learns style relatively fast,

but outputs suffer from strong mode collapse and low

quality. Formulas to calculate loss functions for the

generator and the discriminator are shown in equa-

tions 1 and 2 with L

as discriminator loss.

= −W

synth

+ β ∗ L

style

(1)

= W

real

−W

synth

(2)

3.5 Dataset

The dataset used for training our solution consists of

eleven different classes of textures. Examples of all

texture types are shown in ﬁgure 4.

Figure 4: Example of a patch from every 11 texture classes

used in the training dataset. Top: slab, slab wall, a stack of

wood, a pile of rocks, bark, leaves on grass.

Bottom: stone, tiles, straw, gravel, and grass.

We gathered our data by capturing close-up pho-

tos with textures of natural environment objects and

adding two publicly available textures from the In-

ternet to balance the number of photos in individual

classes. Every texture class contains 67 main images.

In our solution, textures are perceived by the objects

they represent. It means that, for example, barks from

different types of trees (like a cherry tree, a linden

tree, etc.) might be visually different, but we still see

them as one class of texture. Our intention behind this

is to increase the internal variation of classes. It also

brings an opportunity to create a solution that could

beneﬁt from the simpler controllability of the texture

class and the possibility of changing the appearance

of texture by different subtypes.

Images in the dataset are used to create smaller

cutouts of various sizes to augment the dataset. Be-

cause of differences in the scale of base texture struc-

tures in the images, we scaled various sizes of cutouts

to generalize the model to the variability of input im-

ages. Cutouts positions are selected randomly to get

numerous different cutouts of training data. Cutouts

for training are then down-scaled to the size of data in

mini-batch, which is always smaller than the size of

created cutouts.

Multiclass Texture Synthesis Using Generative Adversarial Networks

While creating the dataset, our primary goal was

to select non-stationary homogeneous textures. Be-

cause of this condition, we mainly selected natural

textures that are separable from their surroundings

and do not have any regular pattern. However, in a

few cases, we violated our intention to gain informa-

tion about the behavior of our solution in exceptional

cases. These cases are represented by adding the tex-

ture of tiles that is stationary and the texture of leaves

on grass that is heterogeneous. We also added two

similar textures, slab and slab wall, to determine how

well our solution would generate multiple similar tex-

tures.

3.6 Training

Various techniques that affect the alternation of

classes could be used during the training in multiclass

synthesis. We decided to use a simple cyclic alterna-

tion that ensures the change of texture class after ev-

ery batch. We implemented this alternation as a mod-

ulo operation of a count of batches and a total number

of texture classes where the result corresponds to the

currently synthesized/learned texture.

It is usual practice to violate the symmetry of

learning and train the discriminator more often than

the generator. The typical learning ratio between the

discriminator and the generator is 5:1 (the generator is

updated every ﬁfth update of the discriminator). This

helps the discriminator to be trained more than the

generator and to provide better feedback for the train-

ing of the generator. We also implemented this tech-

nique as the modulo of the count of batches and learn-

ing ratio. Because of that, it is necessary to ensure that

the generator is trained on every texture class. That

could be achieved by setting the learning ratio and the

total number of textures to be co-prime. Because of

the typical learning ratio (5:1), the easiest way to pre-

serve all conditions is to choose the number of texture

classes indivisible by ﬁve.

Whereas our solution is progressively growing,

we also needed to ensure a mechanism to control

when to add new network layers to be trained. This

issue is resolved using predetermined values assigned

to each step of progressive growth, indicating how

many epochs each step will be trained. This method,

despite its simplicity, allows control over the length

of training steps because later steps of the progres-

sive growth need more extended training than the ﬁrst

steps with low output resolution.

Yet ﬁnal training was trained for 2250 epochs un-

evenly divided into 5 steps from 8 × 8 to 128 × 128

pixels (100, 300, 450, 600, 800 epochs). The reso-

lution of every step is double the previous resolution.

Every epoch consisted of 275 batches of 64 images.

The training takes about six and a half days on a sin-

gle NVIDIA GeForce RTX 3090 GPU. As optimizers,

we used RMSprop with a learning rate set to 5 ×10

−5

for the generator and 9 × 10

−5

for the discriminator.

4 EVALUATION

To compare alternatives of our solution, we per-

formed a quantitative comparison based on Frechet

Inception Distance (FID) (Heusel et al., 2017) that

captures the similarity of real and synthesized image

collections. FID uses an Inception network to get dis-

tributions of activations of real and synthesized data.

Statistics (mean µ and variance Σ) of distributions are

used for calculating the distance between them. A

lower FID indicates more similar distributions, thus

better quality of synthesized images than those with

higher FID. FID could be calculated by equation 3.

FID(r, g) = ||µ

− µ

+ Tr(Σ

+ Σ

− 2(Σ

)

(3)

The quantitative comparison results (table 1) show

that for similar training steps, the alternative that uses

the classiﬁcation network for obtaining the texture

part of the input and uses the selection part achieves

better results than the alternative with the siamese net-

work. The table also shows that the quality of outputs

could still be improved by more extended training of

individual steps of progressive growth.

Considering the problem of non-stationary texture

synthesis, empirical evaluation by the human eye is

one of the most quality and accurate ways of eval-

uation that works even on a low number of gener-

ated outputs. This type of evaluation is a qualitative

technique based on human observation and feelings of

how accurate the texture is or how easily it could be

identiﬁed as fake. Thanks to this evaluation, we could

estimate the quality of our solution from the begin-

ning of implementation and lead the architecture to

better results.

Examples of synthesized textures by our solution

that use the classiﬁcation network are shown in ﬁgure

5. The ﬁgure also shows textures from our dataset

synthesized by the solution of Li et al. (Li et al.,

2017). Since their solution uses one image as a sin-

gle texture class, for every class of our dataset, we

selected 5 images preprocessed the same way as tex-

tures for our solution (random crop and resize). For

training of the solution, we used implementation and

parameters predeﬁned on the GitHub project

with a

github.com/Yijunmaverick/MultiTextureSynthesis

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

Table 1: Quantitative comparison (FID) of alternatives of our solution.

Epochs for steps of progressive growth

1 2 3 4 5 Total FID

Siamese 100 200 250 375 450 1375 77.53

Classiﬁcation + PCA 100 200 250 375 450 1375 62.71

Classiﬁcation + PCA 100 300 450 600 800 2250 39.58

Figure 5: Examples of synthesized textures by our solution with input from classiﬁcation network + PCA and solution by Li

et al. (Li et al., 2017). Left section from top: slab, slab wall, stack of wood, pile of rocks. Middle section from top: bark,

leaves on grass, stone, tiles. Right section from top: straw, gravel, grass.

change of the number of iterations to 455 000. As

we can see, both solutions synthesize simple non-

stationary textures like bark, stone or gravel well. On

the results of Li et al., we can see artefacts on textures

with stalks like grass or straw. However, these arte-

facts can possibly be removed by longer training. In

results of their solution, there is also a decreased qual-

ity of textures that require speciﬁc features like gaps

between individual slabs in slab walls or logs in pile

of wood. It is challenging to compare these two so-

lutions because both solutions have strong and weak

aspects of texture quality. In that case we can com-

pare these approaches by usability and controllability

of generated texture.

For our model that uses the classiﬁcation network,

we created a survey focusing on the possibility of par-

ticipants distinguishing if a texture is created by syn-

thesis or the camera. This model was selected based

on better performance calculated by FID value. For

testing purposes, we used ninety cherry-picked im-

ages from every synthesized texture class and ninety

images per class from real data. Cherry-picking was

done because in the artistic or prototyping process,

the user can also decide if the texture looks as he

wants and use it or synthesize a new texture and de-

cide again. Cherry-picked textures were about 10%

of all synthesized textures. However, this number

does not represent the number of usable textures be-

cause we wanted the user survey to contain balanced

classes. Because of this matter, 10% represents just

a ratio of relatively usable textures from the weak-

est class, which were the classes of piles of rocks

and tiles. The textures were shown to participants for

three seconds without the name label of showed tex-

Multiclass Texture Synthesis Using Generative Adversarial Networks

ture. These restrictions were used to rule out their

overthinking about texture quality based on possible

long-time analysis or their expectation of known class

appearances. 104 persons participated in the survey;

however, only answers from 93 participants were used

for ﬁnal statistics. We ﬁltered out all participants who

answered less than half of the survey. We also ﬁltered

out participants that identiﬁed correctly less than 45%

of real textures because if they could not identify real

textures correctly, their answers could have undesir-

ably inﬂuenced the outcome of the evaluation. The

histogram of correctly identiﬁed sources of textures

is shown in ﬁgure 6. Distributions of correctly iden-

tiﬁed sources of textures are shown in ﬁgure 7. By

Kolmogorov–Smirnov test, distributions were identi-

ﬁed as normal. Based on Student T-test, we found

out that the difference between distributions is statis-

tically signiﬁcant; thus, our solution could synthesize

textures that can fool a person. Per texture percent-

age accuracy of determining the origin of the texture

is shown in table 2.

Figure 6: Histograms of correctly identiﬁed real and syn-

thesized textures by participants of evaluation.

Figure 7: Distributions of correctly identiﬁed real and syn-

thesized textures by participants of evaluation.

5 CONTROLLABILITY

In the ﬁrst solution alternative (classiﬁcation network,

PCA, and selector part), the intention behind two dif-

ferent pieces of information on selected texture was

to:

• Specify precisely what texture type should be syn-

thesized (selection part).

Table 2: Percentage accuracy of determining the origin of

the texture based on texture class.

Class Real Synthesized

Slab 69.90 43.27

Slab wall 66.99 46.39

Stack of wood 80.49 65.79

Pile of rocks 87.91 70.48

Bark 62.92 35.51

Leaves on grass 76.47 58.70

Stone 59.00 61.70

Tiles 80.00 76.29

Straw 90.48 58.82

Gravel 71.08 49.53

Grass 79.17 51.06

• Change the appearance of generated texture (tex-

ture part), like the colour or pattern of the concrete

texture type.

Experiments of control mechanisms refuted the abil-

ity of the selection part to deﬁne texture class in every

case. The texture part must also be located in the la-

tent space area corresponding to the selected class for

the expected output class. In some cases of mismatch

between the selector and texture parts of the input,

the selected texture class could be created with lower

quality. In general, output could resemble the differ-

ent texture types or be unidentiﬁed as concrete tex-

ture class. On the other hand, experiments conﬁrmed

the expected behaviour of changing texture parts to

achieve different appearances. Examples of smooth

changes of texture appearance created by changing

the texture part of input are shown in ﬁgure 8. Be-

cause of multiple values that need to be set up during

the synthesis and the necessity of compatibility be-

tween the texture and selector part of the input, man-

ual control of all values is quite complex and hard to

use. Thus also, the creation of transitions between

different texture classes is complex. We also exper-

imented with omitting one of the texture-controlling

parts of the input. That led to a signiﬁcant problem

with overall quality or the inability to generate some

texture types.

To eliminate the disadvantages of the ﬁrst alter-

native, we simpliﬁed the controlling mechanism of

the solution by removing the selection part and mini-

mizing the dimensions of latent space. Thanks to the

usage of the Siamese network as a feature extractor

and its ability to learn similarities between textures

(Hudec and Benesova, 2018), the solution synthe-

sized all trained texture classes even though we used

only the texture part of the input without the selector

part. The controllability of this alternative is based

only on changing values of the texture part. By that,

we can control the change of texture class and appear-

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

Figure 8: Visualization of transitions between different subtypes of texture. From top: stone, grass, gravel, bark.

ance of texture and create transitions between neigh-

bouring texture classes in the feature space. However,

as shown by the comparison of FID, the alternative

that uses the siamese network has lower quality. This

problem can be solved by more extended training. Ex-

amples of transitions are shown in ﬁgure 9.

Experiments also showed that the appearance (not

just variability) of the synthesized texture class could

also be changed unintentionally by changing the ran-

dom part of the input. This happens if the interval of

the random part is set to [0,1]. By reduction of the

interval, the texture will keep its appearance even if

the random part is changed.

6 DISCUSSION

Compared to the solution of Li et al. (Li et al., 2017),

whose approach takes every image as an individual

texture, our approach perceives textures based on the

objects they represent. This increases the inner vari-

ability of used classes and allows the user to select the

exact texture type by class and adjust its appearance

by changing the input from latent space.

Latent space as a controllable mechanism was also

used in the work of Alanov et al. (Alanov et al.,

2020). However, latent space in our approach is ob-

tained from the pre-trained network rather than a net-

work that is trained during the training of the genera-

tive model. Thanks to that, we can see how the texture

classes will be distributed in latent space and consider

whether this layout is suitable for our synthesis inten-

tions or needs to be trained more or affected somehow.

Based on our survey results, we identiﬁed that the

most unrealistic-looking textures are: Tiles and Pile

of rocks. We assume that characteristics of these tex-

ture types or features of images used in the training

set could explain the low quality compared to other

synthesized texture types.

In the case of tiles, the texture does not belong to

a speciﬁc group of non-stationary homogeneous tex-

tures like most of the dataset. As human-created non-

natural objects, tiles are strictly stationary because of

their standard layout on roofs. Because of training

mainly on non-stationary textures, our solution cannot

periodically reconstruct repeating textures. The solu-

tion’s full potential must be conﬁrmed on a dataset

with more stationary textures.

The problem with the texture of the pile of rocks

could be caused by internal variation of images in the

training set for this class. It means that the dataset

contains a mix of images with different sizes and

colours of rocks. During training with a subset of

the dataset, where the class of rocks contained only

one subtype, the model synthesized satisfying results

that can be seen in ﬁgure 10. However, the texture of

bark or stone also contains high internal variability,

and we do not observe any problem with output qual-

ity. Another explanation behind the low quality of this

texture could be that texture that represents multiple

objects, like rocks, are more challenging than single-

object textures. This could also be a case of low qual-

ity behind the Stack of wood that represents the layout

of individual logs.

On the other hand, except for all other non-

stationary homogeneous textures, the texture of leaves

on grass, which is a heterogeneous texture, also

achieved a satisfactory look. However, we can notice

that leaves lack details like veins or midrib.

Possible improvements in our approach could be

based on experiments using the siamese neural net-

work. Because of the different subtypes of texture

classes used during training, it can be beneﬁcial to

train the siamese network based on the strong sim-

ilarity (between different classes) and weak similar-

Multiclass Texture Synthesis Using Generative Adversarial Networks

Figure 9: Visualization of transitions between different types of textures. From top: gravel-slab, grass-stone, bark-slab wall,

leaves on grass-grass, tiles-pile of rocks.

Figure 10: Example of synthesized piles of rocks from a

model trained on a dataset where the class of piles of rocks

contained only one type of rock.

ity (between different subclasses of the same texture

class). This can help create sub-areas in latent space

based on the appearance of textures (for example,

sub-area for individual barks, grass, etc.).

An interesting idea is also to increase the dimen-

sional space of the texture part and force the siamese

network to distribute the output so that it is possible

to transit between every pair of textures. However,

this can again lead to complex manual control of the

solution. Another improvement could be focused on

the tiling of textures or improvement based on adding

bump or normal maps to synthesis. That would lead to

synthesizing usable high-resolution textures for possi-

ble use in rendering or artistic prototyping.

7 CONCLUSION

This paper presents an alternative multiclass tex-

ture synthesis model based on generative adversar-

ial networks. Our approach is tuned to synthesize

non-stationary textures problematically synthesized

by traditional approaches. Parts of existing solutions

inspire our solution and GAN mechanics to obtain

user controllability, preservation of information about

selected texture along the entire length of the genera-

tor, training stability, and reduction of mode collapse.

In our work, we perceive texture class based on the

object it represents, which creates possible subtypes

of individual classes. As a generator’s input, we use

information about the selected class from the latent

space obtained by the pre-trained network. This helps

us control the synthesized class and its subtype ap-

pearance.

We evaluated the results of our approach through

the qualitative survey. This evaluation proved that

textures synthesized by our solution could fool hu-

mans in determining the texture’s origin. We also an-

alyzed possible reasons for the low quality of individ-

ual classes that can lead to future improvements.

ACKNOWLEDGMENT

This work was partially supported by STU Program

to support Young Researchers and excellent teams of

young researchers, and Cooperation (Financial sup-

port) with Siemens Healthineers Slovakia.

REFERENCES

Alanov, A., Kochurov, M., Volkhonskiy, D., Yashkov, D.,

Burnaev, E., and Vetrov, D. (2020). User-controllable

multi-texture synthesis with generative adversarial

networks. pages 214–221.

Arjovsky, M., Chintala, S., and Bottou, L. (2017). Wasser-

stein gan.

Ashikhmin, M. (2000). Synthesizing natural textures. Sym-

posium on Interactive 3D Graphics.

GRAPP 2023 - 18th International Conference on Computer Graphics Theory and Applications

Bergmann, U., Jetchev, N., and Vollgraf, R. (2017). Learn-

ing texture manifolds with the periodic spatial GAN.

34th International Conference on Machine Learning,

ICML 2017, 1:722–730.

Chandra, R., Grover, S., Lee, K., Meshry, M., and Taha, A.

(2017). Texture synthesis with recurrent variational

auto-encoder.

Croitoru, F.-A., Hondru, V., Ionescu, R. T., and Shah, M.

(2022). Diffusion models in vision: A survey. ArXiv,

abs/2209.04747.

Dhariwal, P. and Nichol, A. (2021). Diffusion models beat

gans on image synthesis. In Ranzato, M., Beygelz-

imer, A., Dauphin, Y., Liang, P., and Vaughan, J. W.,

editors, Advances in Neural Information Processing

Systems, volume 34, pages 8780–8794. Curran Asso-

ciates, Inc.

Efros, A. A. and Leung, T. K. (1999). Texture synthesis

by non-parametric sampling. In Proceedings of the

Seventh IEEE International Conference on Computer

Vision, volume 2, pages 1033–1038 vol.2.

Gatys, L., Ecker, A., and Bethge, M. (2015a). A neural

algorithm of artistic style. arXiv.

Gatys, L. A., Ecker, A. S., and Bethge, M. (2015b). Tex-

ture synthesis and the controlled generation of natural

stimuli using convolutional neural networks. CoRR,

abs/1505.07376.

Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative adversarial nets. Ad-

vances in Neural Information Processing Systems,

3(January):2672–2680.

Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V., and

Courville, A. (2017). Improved training of wasser-

stein GANs. Advances in Neural Information Process-

ing Systems, 2017-Decem:5768–5778.

Haindl M., F. J. (2013). Visual Texture, chapter Motivation.

Advances in Computer Vision and Pattern Recogni-

tion. Springer.

Heusel, M., Ramsauer, H., Unterthiner, T., Nessler, B., and

Hochreiter, S. (2017). Gans trained by a two time-

scale update rule converge to a local nash equilibrium.

In Proceedings of the 31st International Conference

on Neural Information Processing Systems, NIPS’17,

page 6629–6640, Red Hook, NY, USA. Curran Asso-

ciates Inc.

Ho, J., Jain, A., and Abbeel, P. (2020). Denois-

ing diffusion probabilistic models. arXiv preprint

arxiv:2006.11239.

Hudec, L. and Benesova, W. (2018). Texture similarity eval-

uation via siamese convolutional neural network. In

2018 25th International Conference on Systems, Sig-

nals and Image Processing (IWSSIP), pages 1–5.

Jetchev, N., Bergmann, U. M., and Vollgraf, R. (2016). Tex-

ture synthesis with spatial generative adversarial net-

works. ArXiv, abs/1611.08207.

Karras, T., Aila, T., Laine, S., and Lehtinen, J. (2017). Pro-

gressive growing of gans for improved quality, stabil-

ity, and variation.

Kingma, D. P. and Welling, M. (2014). Auto-encoding vari-

ational bayes.

Kwatra, V., Sch

odl, A., Essa, I., Turk, G., and Bobick, A.

(2003). Graphcut textures: Image and video synthe-

sis using graph cuts. ACM Transactions on Graphics,

22(3):277–286.

Li, Y., Fang, C., Yang, J., Wang, Z., Lu, X., and Yang,

M. H. (2017). Diversiﬁed texture synthesis with feed-

forward networks. Proceedings - 30th IEEE Con-

ference on Computer Vision and Pattern Recognition,

CVPR 2017, 2017-Janua:266–274.

Liang, L., Liu, C., Xu, Y.-Q., Guo, B., and Shum, H.-Y.

(2001). Real-time texture synthesis by patch-based

sampling. ACM Trans. Graph., 20:127–150.

Martin, R. and Pomerantz, J. (1978). Visual discrimination

of texture. Perception & Psychophysics, 24:420–428.

Pesteie, M., Abolmaesumi, P., and Rohling, R. N.

(2019). Adaptive Augmentation of Medical Data

Using Independently Conditional Variational Auto-

Encoders. IEEE Transactions on Medical Imaging,

38(12):2807–2820.

Portilla, J. and Simoncelli, E. (2000). A parametric texture

model based on joint statistics of complex wavelet co-

efﬁcients. International Journal of Computer Vision,

40.

Praun, E., Finkelstein, A., and Hoppe, H. (2000). Lapped

textures. In Proceedings of ACM SIGGRAPH 2000,

pages 465–470.

Radford, A., Metz, L., and Chintala, S. (2016). Unsuper-

vised representation learning with deep convolutional

generative adversarial networks.

Salimans, T., Goodfellow, I., Zaremba, W., Cheung, V.,

Radford, A., and Chen, X. (2016). Improved tech-

niques for training GANs. Advances in Neural Infor-

mation Processing Systems, pages 2234–2242.

Shin, S., Nishita, T., and Shin, S. Y. (2006). On pixel-based

texture synthesis by non-parametric sampling. Com-

puters and Graphics (Pergamon), 30(5):767–778.

Simonyan, K. and Zisserman, A. (2014). Very deep con-

volutional networks for large-scale image recognition.

arXiv 1409.1556.

Wei, L.-Y. and Levoy, M. (2000). Fast texture synthesis

using tree-structured vector quantization. Computer

Graphics (Proceedings of SIGGRAPH’00), 34.

Zhou, Y., Zhu, Z., Bai, X., Lischinski, D., Cohen-Or, D.,

and Huang, H. (2018). Non-stationary texture synthe-

sis by adversarial expansion. ACM Transactions on

Graphics, 37(4).

Zhu, J.-Y., Park, T., Isola, P., and Efros, A. (2017). Unpaired

image-to-image translation using cycle-consistent ad-

versarial networks. pages 2242–2251.

Multiclass Texture Synthesis Using Generative Adversarial Networks