Leveraging Unsupervised and Self-Supervised Learning for Video

Anomaly Detection

Devashish Lohani

1,2 a

, Carlos Crispim-Junior

1 b

, Quentin Barth

elemy

2 c

, Sarah Bertrand

Lionel Robinault

1,2 d

and Laure Tougne Rodet

1 e

Univ Lyon, Univ Lyon 2, CNRS, INSA Lyon, UCBL, LIRIS, UMR5205, F-69676 Bron, France

Foxstream, F-69120 Vaulx-en-Velin, France

Keywords:

Unusual Event Detection, Anomaly Detection, Unsupervised Learning, Self-Supervised Learning, Autoen-

coder.

Abstract:

Video anomaly detection consists of detecting abnormal events in videos. Since abnormal events are rare,

anomaly detection methods are mainly not fully supervised. One such popular family of methods learn nor-

mality by training an autoencoder (AE) on normal data and detect anomalies as they deviate from this nor-

mality. But the powerful reconstruction capacity of AE makes it still difﬁcult to separate anomalies from

normality. To address this issue, some works enhance the AE with an external memory bank or attention

modules but still these methods suffer in detecting diverse spatial and temporal anomalies. In this work, we

propose a method that leverages unsupervised and self-supervised learning on a single AE. The AE is trained

in an end-to-end manner and jointly learns to discriminate anomalies using three chosen tasks: (i) unsuper-

vised video clip reconstruction; (ii) unsupervised future frame prediction; (iii) self-supervised playback rate

prediction. Furthermore, to correctly emphasize the detected anomalous regions in the video, we introduce

a new error measure, called the blur pooled error. Our experiments reveal that the chosen tasks enrich the

representational capability of the autoencoder to detect anomalous events in videos. Results demonstrate our

approach outperforms the state-of-the-art methods on three public video anomaly datasets.

1 INTRODUCTION

Since past few years, the task of video anomaly detec-

tion (VAD) has attained a major attention in the com-

puter vision research (Li et al., 2013; Lu et al., 2013;

Kiran et al., 2018; Ramachandra et al., 2022). Indeed,

this task is interesting as well as challenging since it

requires in depth comprehension of space-time fea-

tures in order to distinguish anomalous events from

normal events in the video. The anomalous events

are the ones which do not conform with the largely

present normal events, i.e., they are rare. Due to this,

we do not know in advance what kinds of abnormal

events may appear in the video as they depend on the

context. For example, for a site where only pedes-

trians are authorized, all the vehicles are anomalies

https://orcid.org/0000-0003-2666-7586

https://orcid.org/0000-0002-5577-5335

https://orcid.org/0000-0002-7059-6028

https://orcid.org/0000-0003-0933-2485

https://orcid.org/0000-0001-9208-6275

but for another site where pedestrians and bicycles

are allowed, vehicles except bicycles are anomalies.

Similarly, on one site all abrupt movements like run-

ning, chasing, brawling, etc. are abnormal while for

another site running is considered normal. All these

points require the development of approaches which

can generalize on different contexts without labelled

data.

One of the most highly successful approaches to

tackle this problem is to use a deep convolutional au-

toencoder (AE) with proxy tasks such as frame recon-

struction or frame prediction (Hasan et al., 2016; Luo

et al., 2017; Zhao et al., 2017; Chang et al., 2020;

Ramachandra et al., 2022). Furthermore, AE based

approaches often have the least assumptions on data.

The basic idea of using an AE is to learn normal-

ity from training data in order to detect anomalous

events while testing. But many works have shown that

the strong reconstruction capacity of the autoencoder

makes it still difﬁcult to distinguish anomalous events

from normal events (Gong et al., 2019; Astrid et al.,

2021a; Lv et al., 2021a; Szymanowicz et al., 2022).

132

Lohani, D., Crispim-Junior, C., Barthélemy, Q., Bertrand, S., Robinault, L. and Rodet, L.

Leveraging Unsupervised and Self-Supervised Learning for Video Anomaly Detection.

DOI: 10.5220/0011663600003417

In Proceedings of the 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 5: VISAPP, pages

132-143

ISBN: 978-989-758-634-7; ISSN: 2184-4321

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

Many works have addressed this problem by attaching

different functionalities to the AE like memory mod-

ules (Gong et al., 2019; Park et al., 2020; Liu et al.,

2021b), attention modules (Lv et al., 2021a), pseudo

anomalies (Astrid et al., 2021a; Astrid et al., 2021b),

optical ﬂow (Liu et al., 2018; Liu et al., 2021b; Cho

et al., 2022), clustering (Chang et al., 2020), etc. But

all these works still struggle to detect diverse spa-

tial and temporal anomalies, especially in challeng-

ing datasets with multiple scenes such as the Shang-

haiTech dataset (Luo et al., 2017). External super-

vision can also be added to all the above approaches,

e.g., using a pre-trained network for ﬁrst detecting ob-

jects of interest and later employing an unsupervised

pipeline (with or without AE) to detect anomalies (Yu

et al., 2020; Georgescu et al., 2021a; Georgescu et al.,

2021b; Liu et al., 2021b). The main problem with

these approaches is that they assume all abnormal ob-

ject classes are known, i.e., they will fail to detect an

anomaly if it belongs to an object class unknown to

the object detector. Furthermore, their capability to

detect anomalies directly depend on the object detec-

tor and external dataset used to train it.

In this work, we proceed with the AE based ap-

proaches, proposing a method that leverages unsu-

pervised and self-supervised learning on a single AE.

To this end, we devise multiple tasks to enhance the

normal spatio-temporal understanding of the AE by

training it only on the normal data. Each task has

its speciﬁc objective: (i) video clip reconstruction

(VCR) to learn spatio-temporal characteristics of the

normal videos; (ii) future frame prediction (FFP) to

learn how normal spatio-temporal patterns propagate

along the videos; (iii) playback rate prediction (PRP)

to strengthen the playback speed perception of the en-

coder.

PRP task is popular in self-supervised representa-

tion learning and is used for downstream supervised

tasks like action recognition and video retrieval (Be-

naim et al., 2020; Wang et al., 2020a; Yao et al.,

2020). We carefully adapt this task for VAD with

the motivation to detect anomalies caused by abrupt

motion. To our knowledge, it is the ﬁrst time PRP

has been used for VAD and our experiments demon-

strate its effectiveness. Our method is end-to-end

trainable and is jointly trained on the three tasks.

While testing, the anomaly is detected as the com-

bined anomaly score of the three tasks is higher for

anomalous frames.

Most of the current methods use mean squared er-

ror (MSE) or peak signal to noise ratio (PSNR) for

the error measure between input and reconstructed

frames (Zhao et al., 2017; Gong et al., 2019; Park

et al., 2020; Astrid et al., 2021a; Astrid et al., 2021b;

Lv et al., 2021a). These measures integrate errors on

the whole image and are prone to noise (Sinha and

Russell, 2011; Gudi et al., 2022). Recently, the proxi-

mally sensitive error (PSE) remove incoherent noise

to better localize and thus detect anomalies (Gudi

et al., 2022). We take it further a step and introduce

a new measure, called the blur pooled error (BPE).

It is locally sensitive and keeps only relevant pixels

for error calculation. Most VAD works apply a min-

max rescaling to anomaly scores per video (Liu et al.,

2018; Gong et al., 2019; Park et al., 2020; Astrid

et al., 2021a; Astrid et al., 2021b). It is sensitive to

extreme values and to address this issue, we propose

a robust rescaling of scores.

Our main contributions are as follows:

• A method that leverages unsupervised and self-

supervised learning on a single AE, end-to-end

trained with chosen tasks: (i) video clip recon-

struction; (ii) future frame prediction; (iii) play-

back rate prediction.

• We introduce the blur pooled error (BPE), a lo-

cally sensitive measure that helps to correctly

detect the anomalous parts in the downsampled

video.

• We introduce a robust rescaling of anomaly score,

which is less sensitive to extreme values

• We conduct extensive experiments on three public

datasets, showing superior results to state-of-the-

art.

For research reproducibility, code is available here:

https://github.com/devashishlohani/luss-ae

vad.

The article is organized as follows: Section 2

highlights related works, Section 3 describes details

of our method, Sections 4 and 5 present experiments

and results for different works, and Section 6 con-

cludes this paper.

2 RELATED WORKS

VAD approaches are often not fully supervised due

to lack of anomaly examples. There are two com-

mon VAD settings: unsupervised learning where only

the normal training data is used (Li et al., 2013; Lu

et al., 2013; Luo et al., 2017), and weakly supervised

learning where the video-level annotations are used

(Feng et al., 2021; Lv et al., 2021b; Tian et al., 2021).

We focus on the unsupervised learning as it is a more

practical setting which can be deployed in the site

without any requirement of annotations. Due to avail-

ability of only single class (normal) data during train-

ing, the classical two-class supervised classiﬁer can-

not be used to detect anomalies. Thus, the VAD task

Leveraging Unsupervised and Self-Supervised Learning for Video Anomaly Detection

133

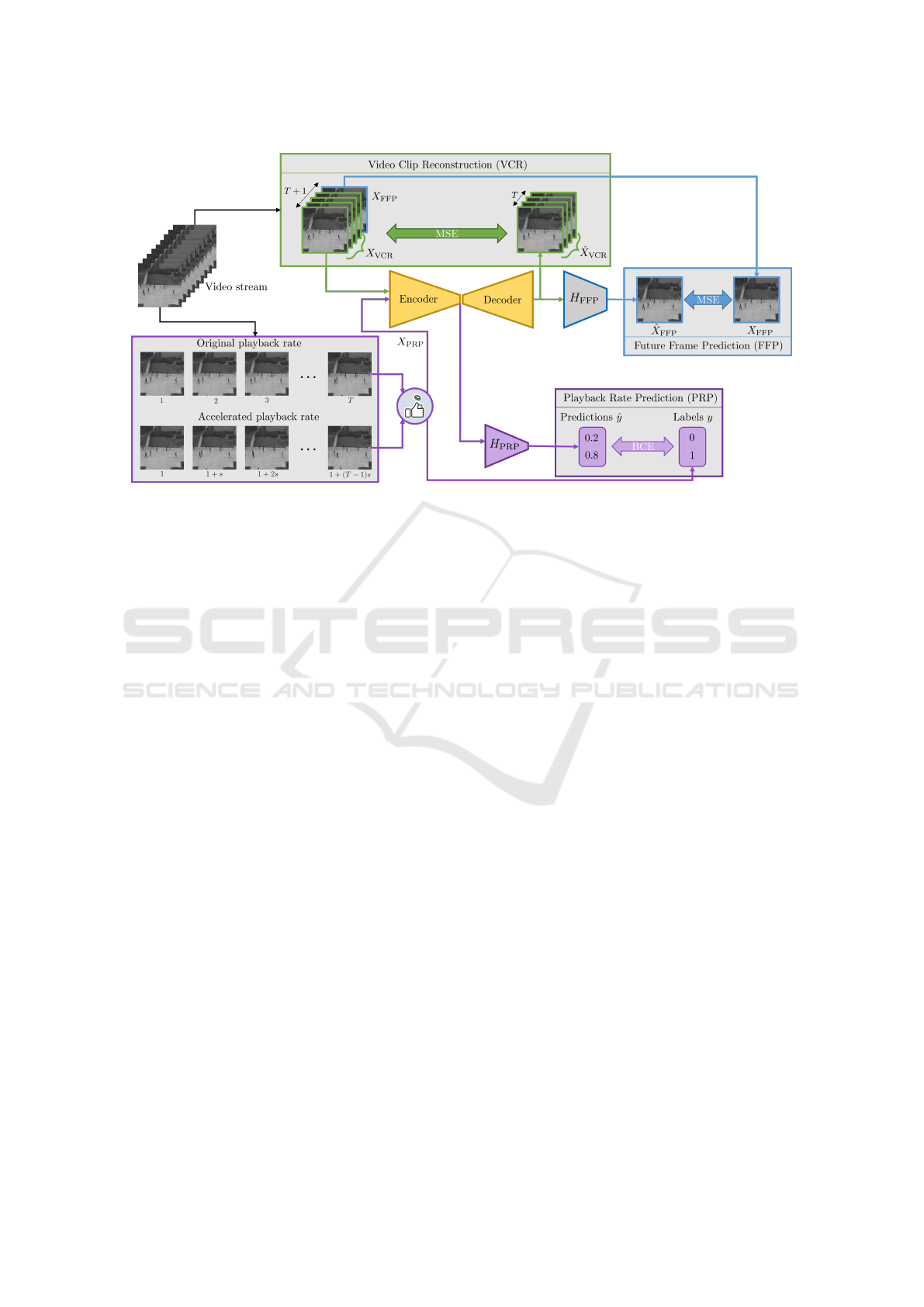
Figure 1: Overall schema of the proposed LUSS-AE method. A window of T consecutive frames is passed into the autoen-

coder, which reconstructs this window, followed by H

FFP

head which predicts the future (T + 1)

frame. Another window of

T frames with original or accelerated playback rate is passed through the encoder and H

PRP

head to predict the playback rate

in the self-supervised way.

is indirectly addressed using proxy tasks like video

clip / frame reconstruction (Hasan et al., 2016; Gong

et al., 2019; Liu et al., 2021b), frame prediction (Liu

et al., 2018; Park et al., 2022), self-supervised tasks

(Yu et al., 2020; Georgescu et al., 2021a), etc. The

principal learning component is often an autoencoder

(Hasan et al., 2016; Luo et al., 2017; Ramachandra

et al., 2022), or an adversarial network (Liu et al.,

2018; Ye et al., 2019).

In the last few years, we have seen a massive ap-

plication of AEs for VAD (Kiran et al., 2018; Ra-

machandra et al., 2022). They are used in future frame

prediction (Liu et al., 2018; Park et al., 2022) or video

clip / frame reconstruction task (Hasan et al., 2016;

Zhao et al., 2017). These approaches use the powerful

representational capacity of the AE to learn normal

features while training and detect anomalies as they

deviate from these features. The problem is that the

AE even reconstruct the abnormal frames well, mak-

ing it difﬁcult to separate them from normal frames

(Gong et al., 2019; Astrid et al., 2021a; Szymanowicz

et al., 2022). Many methods address this issue: (Gong

et al., 2019) and (Park et al., 2020) use memory mod-

ules to memorize normal patterns, (Lv et al., 2021a)

uses attention prototypes to encode normal dynam-

ics, (Astrid et al., 2021a; Astrid et al., 2021b) uses

pseudo anomalies to enrich encoder, etc. Still all these

works fail to detect diverse spatio-temporal anomalies

as they AE do not capture all the important and perti-

nent normal features.

Some works add an external supervision to the

VAD pipeline, often using a pre-trained object detec-

tor or feature extractor. The object detector detects all

objects of interest in the video, which are later fed to

a VAD pipeline. Also known as object-centric meth-

ods (Ionescu et al., 2019; Georgescu et al., 2021a;

Liu et al., 2021b), they assume that all possible object

classes are known a priori, and that datasets used to

train object detectors contain all these objects, which

is strong limitation for generalization. Furthermore,

omission or false detection of objects can also lead

to failure of VAD. Similarly, works that use a pre-

trained feature extractor (Wang et al., 2020b) have

same problems and are also biased towards external

dataset where features were learned.

Nowadays, self-supervised learning is used in

many applications (Liu et al., 2021a). It uses self-

supervisory signals from the data itself and does not

require external annotations. It is often used as a pre-

training step to enrich a learning module, which is

later used for downstream tasks like video classiﬁ-

cation, detection, etc. (Yao et al., 2020). Concern-

ing VAD, a recent work uses several self-supervised

tasks to jointly train a 3DCNN to detect anomalies

(Georgescu et al., 2021a). It has promising results

but relies on an external supervision via a pre-trained

YOLOv3 detector.

In this work, we propose a approach without any

external supervision, using unsupervised and self-

supervised learning to jointly train an AE for VAD.

We use three tasks, two common unsupervised VAD

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

134

tasks: video clip reconstruction (VCR), future frame

prediction (FFP) and a new task called the playback

rate prediction (PRP). The PRP task, often used in

self-supervised learning, deals with understanding the

playback rate of a video (Benaim et al., 2020; Wang

et al., 2020a; Yao et al., 2020). We carefully ac-

commodate this task for VAD, with the objective to

detect abrupt motion based anomalies by reinforcing

the speed understanding of the encoder. Overall, our

method is end-to-end trainable and can be applied on

any AE.

3 METHOD

In this section, we present our proposed LUSS-AE

(Leveraging Unsupervised and Self-Supervised Au-

toEncoder) method, illustrated in Figure 1. The main

idea is to learn normal spatio-temporal features in or-

der to detect anomalies. To this end, we propose

to train a 3D convolutional autoencoder (3DCAE)

on normal videos using carefully designed tasks in a

unsupervised or self-supervised manner. The video

clip reconstruction task learns spatio-temporal char-

acteristics of normal videos. The future frame pre-

diction task is designed to learn the propagation of

spatio-temporal patterns in the normal videos. Fi-

nally, the playback rate prediction task strengthens the

speed understanding of the encoder. The autoencoder

is jointly trained on all these tasks. During testing,

each of these branches provides a score to distinguish

anomalous frames from non-anomalous ones.

3.1 Learning Normality Using Multiple

Tasks

In this subsection, we explain how the proposed tasks

help in learning normal characteristics during train-

ing. We describe each task with its role, followed by

details on how all these tasks are trained in a joint and

end-to-end manner.

Before deﬁning the tasks, we deﬁne the video clip.

Given a video with n frames

{

, I

, . . . , I

}

, a video

clip V of length l and temporal gap s between frames

is deﬁned as:

l,s



, I

1+s

, . . . , I

1+(l−1)s



{

1+ts

}

0≤t<l

, (1)

where for simplicity, we assume clip starts from 1

frame.

3.1.1 Video Clip Reconstruction (VCR)

Reconstructing a video clip is one of the most pop-

ular tasks for unsupervised VAD (Zhao et al., 2017;

Gong et al., 2019; Astrid et al., 2021a; Astrid et al.,

2021b; Liu et al., 2021b). It aims to reconstruct an

input video clip using an AE type network. The AE is

trained only on normal video clips with the learning

objective of minimizing the MSE between the input

and reconstructed clips. The main hypothesis is that

the abnormal clips will be badly reconstructed during

testing.

Using Eq. (1), a non-strided video clip of length

T + 1 frames can be deﬁned as:

T +1,1

{

, I

, . . . , I

, I

T +1

}

. (2)

The ﬁrst T frames of this clip is used for the VCR task

and we denote it as X

VCR

, i.e., X

VCR

{

, I

, . . . , I

}

This video clip goes through the autoencoder fol-

lowed by an activation function to produce a re-

constructed clip as

VCR

= tanh(Dec(Enc(X

VCR

))),

where Enc and Dec stand for encoder and decoder

networks respectively. The loss function can then be

deﬁned as:

VCR

T ×C × H ×W



VCR

− X

VCR



, (3)

where C, H and W denotes channels, height and width

of each frame and ∥ · ∥

denotes the Frobenius norm.

3.1.2 Future Frame Prediction (FFP)

Predicting a future frame is also a well-spread task

for unsupervised VAD (Liu et al., 2018; Park et al.,

2020; Liu et al., 2021b; Lv et al., 2021a). It aims to

predict an unseen future frame, given an input video

clip. This requires comprehension of how normal

spatio-temporal patterns propagate along the video

clip. Similar to VCR task, the objective is to mini-

mize the MSE between the predicted and actual future

frame. Since the AE is trained only on normal videos,

it should predict the anomalous frames incorrectly.

This task uses the same input of VCR task, i.e.,

VCR

. After passing through the AE, the video clip

VCR

goes through the prediction head H

FFP

to predict

the future frame as

FFP

= H

FFP

(Dec(Enc(X

VCR

))).

This frame is compared with the actual future frame,

i.e., frame T + 1 of V

T +1,1

(see Eq. (2)) denoted as

FFP

, where X

FFP

= I

T +1

. The loss function is then

deﬁned as:

FFP

C × H ×W



FFP

− X

FFP



. (4)

3.1.3 Self-Supervised Playback Rate Prediction

(PRP)

The PRP task in self-supervised representation learn-

ing is used as a pretext task to learn transferable se-

mantic spatio-temporal features for downstream tasks

Leveraging Unsupervised and Self-Supervised Learning for Video Anomaly Detection

135

like action recognition (Benaim et al., 2020; Wang

et al., 2020a; Yao et al., 2020). In other words, ﬁrst

PRP task is performed and later the learned model is

adapted to downstream tasks. Contrary to them, we

perform the PRP task on a single AE with two other

tasks, all done simultaneously in a joint and end to

end manner.

The original PRP task generates speed labels for

video clip sampled at different rates and aims at pre-

dicting them (Benaim et al., 2020; Wang et al., 2020a;

Yao et al., 2020). Since we know that the training

videos in VAD are normal, we adapt this task to gen-

erate two speed-rate labels: original playback rate

(implying normal behaviour) and accelerated play-

back rate with 2x to 5x speed (implying abnormal be-

haviour). The motive is to enforce the encoder with

motion comprehension of normal videos. During test-

ing, we hypothesize that the encoder would detect

anomalies caused by irregular and abrupt motion.

Concretely, given a video clip, this task aims to

predict its playback rate. The clip with default play-

back rate of the video is termed as the original play-

back rate clip and the clip formed by skipping 1 (2x),

2 (3x), 3 (4x) or 4 (5x) frames is designated as an ac-

celerated playback rate clip. The input X

PRP

is a video

clip of length T , chosen between an original play-

back rate (class c = 1) and an accelerated playback

rate (class c = 2) with equal chance (50% probability

each):

PRP

(

T,1

when c = 1

T,s∈

{

2,3,4,5

}

when c = 2

, (5)

where the accelerated playback rate clip, when c = 2,

is a temporally strided video clip with temporal gap s

randomly chosen between 2 and 5. The loss function

for this classiﬁcation task is the binary cross-entropy

(BCE), deﬁned as:

PRP

= −

∑

c=1,2

y[c] log( ˆy[c]) , (6)

where ˆy = softmax(H

PRP

(Enc(X

PRP

))) ∈ R

, H

PRP

the playback rate prediction head and y is the one-hot

encoding of the ground-truth classes for X

PRP

3.1.4 Training Objective

A single autoencoder is trained with the above men-

tioned tasks in a joint and end-to-end manner. The

overall training loss is deﬁned as the weighted sum of

individual loss functions:

L = λ

VCR

+ λ

FFP

+ λ

PRP

, (7)

where λ

, λ

and λ

are the weights in (0, 1] that

regulate the importance of each task. The sum of

these weights is not necessarily 1, even though we

could regularize them such that the sum is always one.

Since it just the matter of regularization, the overall

impact of weights remains the same.

3.2 Detecting Anomaly

In this subsection, we describe how the video anoma-

lies are detected during testing. Given a test video

clip, each of the three tasks provides an anomaly score

and if the weighted sum of these scores is above a

threshold, it is ﬂagged as an anomaly, as illustrated in

Figure 2. We ﬁrst deﬁne below some image or video

error measures and then how these measures help to

calculate the ﬁnal anomaly score.

3.2.1 Image Error Measures

To quantitatively assess how well a future frame is

predicted or how well a video clip is reconstructed,

we need to compare them with the appropriate ground

truth using some error measures. The most widely

used measure in the domain of VAD is MSE (Zhao

et al., 2017; Liu et al., 2018; Gong et al., 2019; Lv

et al., 2021a). Given two images J,

J ∈ R

H×W×C

, the

MSE is calculated as:

MSE(J,

J) =

C × H ×W



J − J



. (8)

Since last few years, many VAD works use the peak

signal to noise ratio (PSNR) measure (Ye et al., 2019;

Astrid et al., 2021a; Astrid et al., 2021b; Park et al.,

2022). But PSNR also depends on MSE as can be

seen in its mathematical formulation. Both MSE and

PSNR integrate errors on the whole image and there-

fore are prone to random and incoherent noise (Sinha

and Russell, 2011; Gudi et al., 2022). To overcome

this, a new measure called the proximally sensitive

error (PSE) is proposed by (Gudi et al., 2022). It is

deﬁned as:

PSE(J,

J) =

C × H ×W



(

J − J) ∗ G

(σ,k)



, (9)

where ∗ is the convolution operator and G

(σ,k)

is a 2D

Gaussian kernel with size k and standard deviation σ,

given by:

(σ,k)

[i, j] =

2πσ

−

+ j

2σ

, (10)

where i and j are the pixel coordinates centered in the

kernel. Note, the kernel size has a direct relation with

standard deviation as k = 6σ − 1. Thanks to the Gaus-

sian convolution, PSE smooths incoherent noise and

is locally sensitive. However, an anomaly generating

an important error in some pixels can disappear in the

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

136

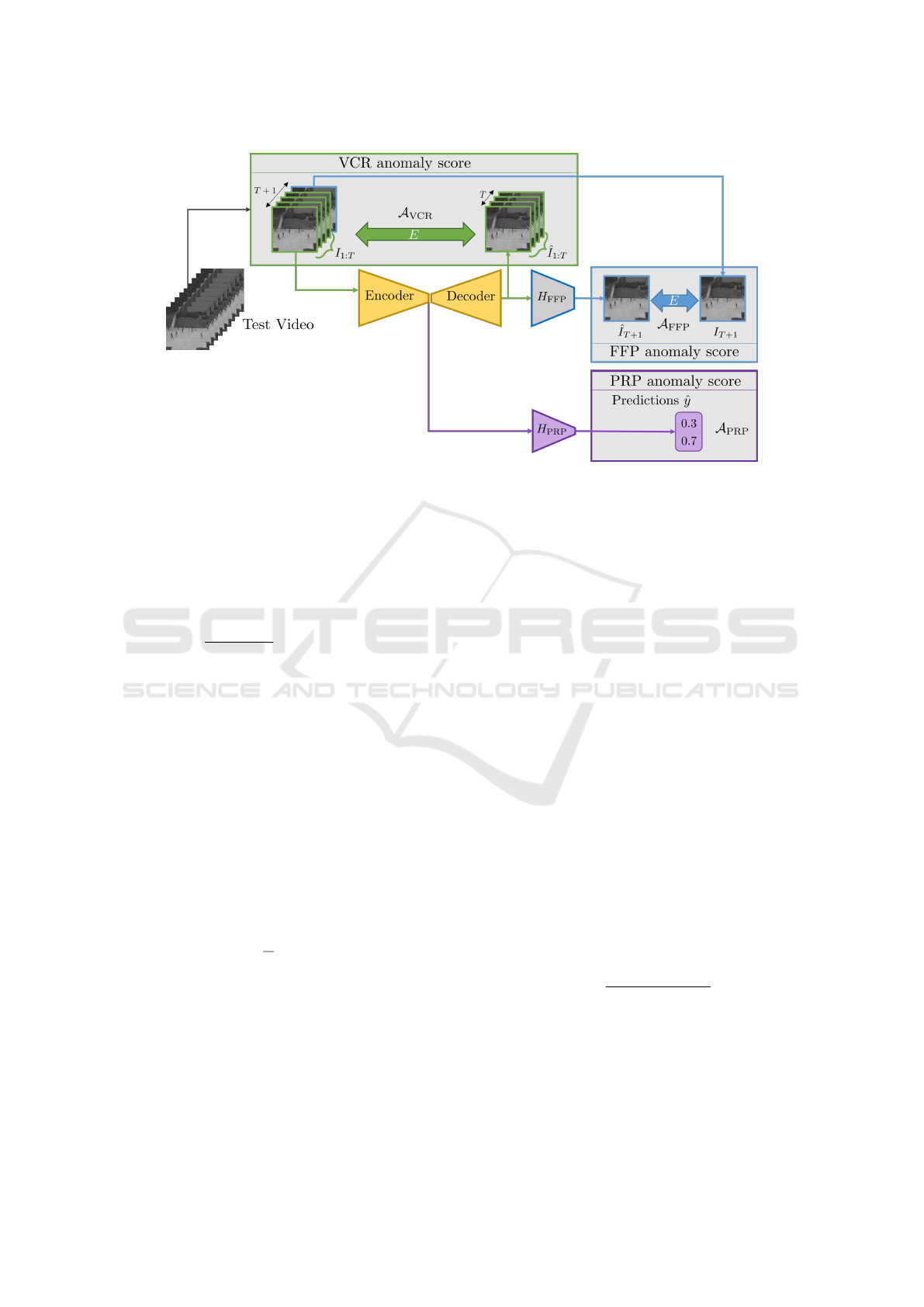
Figure 2: Overall schema of the proposed LUSS-AE method during testing. A window of T + 1 consecutive frames is drawn

sequentially from the test video. The ﬁrst T frames from this window is the input to the system and the output for each task

is computed on it. The anomaly score is determined for each task, i.e., A

VCR

, A

FFP

and A

PRP

, and the ﬁnal anomaly score is

their weighted sum.

noise of all other pixels of the high-dimensional im-

age.

In this article, we take this idea one step further

and introduce the blur pooled error (BPE), deﬁned as:

BPE(J,

J) =

C × H ×W



((

J − J) ∗ B

)



, (11)

where B

is a generic 2D low-pass ﬁlter with kernel

size k, and S

signiﬁes a subsampling with stride b

(Zhang, 2019). Using a low-pass ﬁlter smooths inco-

herent noise, like PSE, then subsampling keeps only

the most pertinent values from the input, increasing

sensitivity to anomalies. All these measures can eas-

ily be extended to video clip by applying them to each

frame.

3.2.2 Anomaly Score and Rescaling

During testing, a non-strided video clip of T + 1

frames is used. The anomaly score for frame T + 1

is composed of three parts, one for each task.

(i) The VCR anomaly score is deﬁned as:

VCR

∑

t=1

, I

) , (12)

where I

are the t

frame and its reconstruction,

and E can be one of MSE, PSE or BPE.

(ii) The FFP anomaly score is deﬁned as:

FFP

= E(

T +1

, I

T +1

) . (13)

(iii) The PRP anomaly score is deﬁned as the proba-

bility of accelerated class (c = 2):

PRP

= ˆy[2] , (14)

where ˆy is the output of PRP branch as deﬁned in

Eq. (6).

The ﬁnal anomaly score is deﬁned as:

A = α

VCR

+ α

FFP

+ α

PRP

, (15)

where α

, α

are the weights in [0, 1] for the three

scores. Even though these weights have similar func-

tioning like λ weights of training, they do not have a

direct relationship with them. This is because the A

and L values are different. While A

VCR

and A

FFP

can

also use PSE and BPE, their counterpart in L use only

MSE. Besides, A

PRP

is the softmax value, while L

PRP

is a binary cross-entropy value.

Most VAD works apply a min-max rescaling to

scores per video (Liu et al., 2018; Gong et al., 2019;

Park et al., 2020; Astrid et al., 2021a; Astrid et al.,

2021b). This scaling bounds values to interval [0, 1]

where the minimum and maximum values are forced

to be 0 and 1 respectively. Due to this, it is prone to

outliers with extreme values. To address this issue, we

propose a robust rescaling per video. For a test video

with n frames, the rescaled anomaly score for frame t

is deﬁned as:

− med (

{

}

)

iqr

1−99

(

{

}

)

, (16)

where med(·) and iqr

1−99

(·) are respectively the me-

dian and the interquantile range (between 1

and 99

percentiles) of scores

{

}

i=1

. Finally, like previous

methods, the higher scores correspond to anomalies.

Leveraging Unsupervised and Self-Supervised Learning for Video Anomaly Detection

137

4 EXPERIMENTS

4.1 Datasets

We perform experiments on three publicly available

benchmark datasets: UCSD Ped2 (Li et al., 2013),

CUHK Avenue (Lu et al., 2013), and ShanghaiTech

(Luo et al., 2017). Each dataset has a standard train-

ing / test division, where the training set consists of

only normal videos while testing set has videos with

one or more anomalous events.

UCSD Ped2. This dataset consists of 16 training and

12 test videos with 12 anomalous events, where nor-

mal videos include walking pedestrians and anoma-

lies include bikes, carts, or skateboards (Li et al.,

2013).

CUHK Avenue. It contains 16 training and 21 test

videos with 47 anomalous events, where anomalies

include objects such as bikes or human actions such

as unusual walking directions, running, or throwing

stuff (Lu et al., 2013).

ShanghaiTech. It contains 330 training and 107 test

videos with total of 130 anomalous events. Unlike

the previous two datasets, this dataset is multi-view

with 13 different views. Anomalous events include

running, stealing, riding bicycle, jumping and ﬁght-

ing (Luo et al., 2017).

4.2 Evaluation Metric

We evaluate with the highly used frame-level area

under the receiver operating characteristic (AUROC)

metric (Kiran et al., 2018). The ROC curve is ob-

tained by varying the threshold on the frame level

anomaly score, to separate anomaly from normality

class across the whole test set. A higher value in-

dication better performance. Some works compute

a “AUROC per video” and report the average, also

called macro-averaged AUC (Georgescu et al., 2021a;

Georgescu et al., 2021b; Ristea et al., 2022). In this

metric, the succession of thresholds to estimate the

ROC curve is not common to all test videos. Since

thresholds are adapted to each video, ROC curve is in

risk to be over-ﬁtted, providing overly optimistic per-

formances. Consequently, AUROC should always be

a “AUROC on all videos” (micro-averaged AUROC)

computed on the whole test set with thresholds com-

mon to all test videos (Fawcett, 2006; Lohani et al.,

2021).

4.3 Implementation Details

We resize each video frame to 256 × 256 and rescale

pixels to the range [−1, 1]. To be comparable with

other methods, we use the widely popular 3D con-

volutional AE architecture (Gong et al., 2019; Astrid

et al., 2021a; Astrid et al., 2021b), consisting of

strided 3D convolutions for encoding and strided 3D

deconvolutions for decoding. It takes a video clip of

16 frames in grayscale, i.e., T=16, C=1, H=256 and

W =256 respectively. The prediction head H

FFP

is at-

tached at the end of the AE and consists of a single 2D

convolution, followed by a tanh activation. The play-

back rate prediction head H

PRP

is attached at the end

of the encoder and consists of a series of 3D pooling,

2D convolution and pooling and fully connected lay-

ers to produce an output of size 2, one for each class.

The input clip for PRP task is chosen between origi-

nal playback rate and accelerated playback rate with

equal chance (50% probability for each). For each

batch of accelerated playback rate, the value of s is

chosen randomly from (2,3,4,5) with equal chance for

the four values. The balance weights in the training

objective function are set to λ

=0.6, λ

=0.4 and λ

respectively and they were found using grid search on

the overall loss. The whole model is trained end-to-

end using the Adam optimizer (Kingma and Ba, 2015)

with a learning rate of 10

−4

and a batch size of 16.

While testing, we use different measures like

MSE, PSE and BPE for the anomaly score. For PSE

and BPE, we use σ=1, b=2 while keeping the same

kernel size of k=5. For blur kernel, we use a Gaussian

ﬁlter. After grid search, we set the optimal weights

for anomaly score (α

, α

) as (0.1, 0.8, 1), (0.1, 1,

0.1) and (0.2, 0.2, 0.9) for Ped2, Avenue and Shang-

haiTech dataset respectively.

5 RESULTS

5.1 Video Anomaly Detection

5.1.1 Quantitative Comparison with State of the

Art

Table 1 shows the results of our LUSS-AE method

compared with existing state of the art methods. As

explained in Section 2, we do not compare with meth-

ods having external supervision. The work of MNAD

(Park et al., 2020) is re-implemented by (Menon and

Stephen, 2021), and MPN (Lv et al., 2021a) is re-

implemented by us using their provided source code.

In both cases, the claimed results were not repro-

ducible, and they are marked with * in the table.

We can observe that our method outperforms all

the other methods across all the datasets. The per-

formance gain in Ped2 and Avenue datasets is less

signiﬁcant as in the Shanghai dataset. In fact, it has

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

138

Table 1: Quantitative comparison with the existing state of the art methods: AUROC (in %) for VAD is computed on Ped2,

Avenue and Shanghai test sets. Numbers in bold indicate the best performance, and

∗

indicate non-reproducible results.

Method Ped2 Avenue Shanghai

AnoPCN (Ye et al., 2019) 96.80 86.20 73.60

MemAE (Gong et al., 2019) 94.10 83.30 71.20

UNet-inte (Tang et al., 2020) 96.30 85.10 73.00

Cluster AE (Chang et al., 2020) 96.50 86.00 73.30

MNAD (Park et al., 2020)

∗

97.00 88.50 70.50

MNAD (Menon and Stephen, 2021) 96.33 87.91 67.81

STEAL Net (Astrid et al., 2021b) 98.40 87.10 73.70

LNTRA (Astrid et al., 2021a) 96.50 84.91 75.97

MPN (Lv et al., 2021a)

∗

96.90 89.50 73.80

MPN [ours] 96.13 83.90 73.00

ITAE (Cho et al., 2022) 97.30 85.80 74.70

VQU-Net (Szymanowicz et al., 2022) 89.20 88.30 -

FastAno (Park et al., 2022) 96.30 85.30 72.20

LUSS-AE [ours] 98.52 89.04 81.21

been suggested to not use the Ped2 dataset as it is al-

most saturated (Acsintoae et al., 2022). The Shanghai

dataset is considered one of the most difﬁcult dataset

and our high performance gain of 5.24% demon-

strates the viability of our method. Furthermore, the

fact that our method works on all the datasets, irre-

spective of the type of anomalies, shows the gener-

alizing ability of our method. Even though, we use

the same architecture for autoencoder like many other

methods (Gong et al., 2019; Astrid et al., 2021a;

Astrid et al., 2021b), still our proposed method out-

performs them without using any sort of external

memory or supervision. All these points demon-

strate the strength and effectiveness of our LUSS-AE

method.

5.1.2 Qualitative Results

In this part, we discuss the strengths and weaknesses

of our method via illustrative examples.

Figure 3 demonstrates an illustrative example of

our method tested on a video with two anomalous

events, both containing movement of bikes. Here, the

people move with relatively normal speed while bikes

move with fast speed. Also, the number of people

are relatively less in this example and bike does oc-

cupy a big area, which means its displacement causes

a big spatio-temporal change. We can observe that

as soon as the bike enters the scene, we have a high

jump in A

PRP

and it remains high until the bike exits

the scene. It jumps up again in next scene and have

highest value when two bikes move in the scene. Re-

garding A

VCR

and A

FFP

, the scores remain high when

bikes are in the scene. Overall, our method detects

both anomalous events in this example.

Figure 4 demonstrates the working of LUSS-AE

on a test video of Shanghai dataset containing three

different anomalous events: person turning in wrong

direction and person jumping, brawling/chasing ac-

tion, and stone picking. In the ﬁrst anomalous event,

VCR

and A

FFP

have higher values than A

PRP

in the

beginning. The anomaly here consists of person turn-

ing in wrong direction which is well captured by the

VCR and FFP task. Later, when the person jumped,

PRP

suddenly increases, indicating its sensitivity to

abrupt motion. During the second anomalous event,

we observe that A

PRP

has higher values than A

VCR

and A

FFP

, thus contributing primarily to detect the

anomaly. The A

PRP

starts to increase just before the

start of this event because the person in red starts to

suddenly approach the other person. We then observe

a ﬁrst peak of A

PRP

as one person pushes other to the

ground. We later observe a big second peak of A

PRP

and this relates to fast movement chasing. However,

the third event is very rare (picking up stones) and

does not contain large spatio-temporal movement in

the scene and thus our method fails to detect it. In

fact, the score in later frames is slightly higher than

the third event because there are three people in close

proximity, trying to change directions, which is con-

sidered anomalous for Shanghai dataset. Overall, the

VCR and FFP tasks work better in anomalies without

abrupt motions and PRP task addresses the anomalies

with sudden motions. There is still a room to improve

the spatio-temporal comprehension of AE for VAD,

possibly with a data augmentation technique as the

datasets lack more examples of scenarios.

5.2 Ablation Studies

In this subsection, we study the importance and inﬂu-

ence of different parts of our proposed method.

Leveraging Unsupervised and Self-Supervised Learning for Video Anomaly Detection

139

Figure 3: LUSS-AE working illustration on video 11 0176 of Shanghai test set. Anomaly scores (A

VCR

, A

FFP

, A

PRP

, A) are

plotted per video frame; red regions depict anomalous events and some illustrative frames are shown above the plot, where

the yellow and red bounding boxes exhibit objects of interest and anomalies respectively.

Figure 4: LUSS-AE working illustration on video 05 0023 of Shanghai test set. Anomaly scores (A

VCR

, A

FFP

, A

PRP

, A) are

plotted per video frame; red regions depict anomalous events and some illustrative frames are shown above the plot, where

the yellow and red bounding boxes exhibit objects of interest and anomalies respectively.

5.2.1 Are all Tasks Useful for VAD?

In this ablation study, we analyze the impact of dif-

ferent tasks on the autoencoder for detecting anoma-

lies. Table 2 shows combinations of different tasks

and their respective AUROC performances on Avenue

and Shanghai datasets. Concretely, for each of these

combinations, we train and test AE using the chosen

tasks, and use the introduced BPE wherever applica-

ble.

We can observe that when AE is trained only with

the VCR task, the VAD performance is the least,

i.e., 82.72% and 73.11%. We consider this as the

baseline since this a standard task in VAD (Kiran

et al., 2018) and we combine it with other tasks to

assess their impact. Using VCR and FFP task to-

gether boosts the performance with a gain of 5.23%

and 3.24% over the baseline, indicating the impor-

tance of learning spatio-temporal propagation through

the FFP task. Similarly, when PRP task is trained

together with the VCR task, we observe an increase

of 4.71% and 6.09% on baseline, validating that in-

deed PRP task enriches the comprehension of normal

spatio-temporal features for anomaly detection. Fi-

nally, when all the tasked are used together, we ob-

serve a substantial yield in performance with 6.32%

and 8.10% over baseline, demonstrating the effective-

ness of our proposed approach to train AE by leverag-

ing unsupervised and self-supervised tasks for VAD.

Table 2: Inﬂuence of different tasks (VCR, FFP and FRP)

used during training and testing of AE on Avenue and

Shanghai datasets, in terms of AUROC (%).

Tasks AUROC (%)

VCR FFP PRP Avenue Shanghai

✓ 82.72 73.11

✓ ✓ 87.95 76.35

✓ ✓ 87.43 79.20

✓ ✓ ✓ 89.04 81.21

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

140

5.2.2 Is the Autoencoder Enriched by FFP and

PRP?

In this paper, we have a 3D convolutional AE well-

used in many previous works (Gong et al., 2019;

Astrid et al., 2021a; Astrid et al., 2021b). All these

works used AE with the VCR task. In this study, we

ﬁrst reproduced their work by training and testing AE

with the VCR task. Then we trained AE with the pro-

posed tasks, i.e., VCR, FFP and PRP, and tested using

only the VCR task. This way, we can assess the im-

pact of these tasks on AE’s comprehension of normal-

ity during training in order to detect anomalies during

testing.

Table 3 shows the impact of these tasks on AE. We

can clearly remark that our proposed training tasks

enriched the normality understanding of the autoen-

coder for VAD, with a gain of 3.76% and 2.26% in

performance on Avenue and Shanghai datasets.

Table 3: Inﬂuence of tasks (VCR, FFP and FRP) used dur-

ing training of AE on Avenue and Shanghai datasets, when

tested only with VCR, in terms of AUROC (%).

Training tasks

Testing with VCR

Avenue Shanghai

VCR 82.72 73.11

VCR + FFP + PRP 86.48 75.37

5.2.3 Are Error Measures Equivalent?

The goal of this ablation study is to see the effect of

different error measures, i.e., MSE, PSE and BPE, on

the VAD task. Since these measures apply to VCR

and FFP tasks, PRP task will not be considered here.

Figure 5 shows an illustrative example using the

FFP task to better understand these measures. We

can observe that AE did not correctly predict this

frame, where dropping bag is an anomaly. The er-

ror frame for MSE highlights this anomalous region

of image but it also captures the background noise of

the frame. The PSE error frame has a more visible

region of anomaly and it smooths some background

noise. Finally, the BPE error frame has a principal

focus on anomalous region and has least amount of

background noise. Furthermore, the BPE frame is

smaller than other maps as we remove irrelevant pix-

els via subsampling.

Table 4 shows the quantitative impact of these er-

ror measures. To be precise, we train our method with

the three tasks and test it with the respective tasks

and measures shown in the table. We can observe

that the PSE improves the performance in both tasks

with 1.01% and 1.23% respectively, signifying the

importance of proximity error and noise reduction.

BPE provides a signiﬁcant boost in results with 1.53%

and 1.62% performance improvement over MSE in

the two tasks. This validates that our proposed BPE

should be used for the VAD task whenever frames or

clips are compared.

Table 4: Inﬂuence of error measure (MSE, PSE and BPE)

on each task (VCR and FFP) during testing of AE on Av-

enue dataset, in terms of AUROC (%).

Error measure

Testing tasks

VCR FFP

MSE 84.95 85.38

PSE 85.96 86.61

BPE 86.48 87.00

5.2.4 Are Anomaly Score Rescalings

Equivalent?

We introduced the robust scaling in our work. In

Table 5, we provide the effect of rescaling scheme

on Avenue and Shanghai dataset. Ped2 and Avenue

dataset, being relatively simple and have smaller than

the Shanghai dataset, does not have many extreme

value outliers. We can observe in the table that due to

this, we do not have a big increase in performance in

Avenue dataset with robust scaling. However, we ob-

serve an impressive 2.06% increase in performance in

Shanghai dataset. This shows the viability of Robust

scaling, especially in the difﬁcult dataset like Shang-

hai. Overall, the robust scaling should be used regard-

less of the dataset.

Table 5: Inﬂuence of anomaly score rescaling (Min-Max

and Robust) on Avenue and Shanghai datasets, in terms of

AUROC (%).

Rescaling Avenue Shanghai

Min-Max 89.01 79.15

Robust 89.04 81.21

5.3 Computational Complexity

We use Nvidia GeForce RTX 3090 with 24 GB of

memory for all our experiments. Since our method

uses the 3DCAE proposed by (Gong et al., 2019) to

build LUSS-AE, we must compare with their autoen-

coder. Table 6 shows the computational complexity

comparison of our method with their autoencoder. We

can observe that our method uses only a bit more of

computational power both in terms of number of pa-

rameters and FLOPs (MAC). However, Section 5.1.1

of our paper shows that LUSS-AE largely outperform

their method in all the three datasets.

Leveraging Unsupervised and Self-Supervised Learning for Video Anomaly Detection

141

Figure 5: Illustration of different error measures on a test frame of the Avenue dataset. From left to right: actual frame (ground

truth), predicted frame, error frame for MSE, for PSE and for BPE.

Table 6: Computational complexity comparison of our

method with the baseline autoencoder (Gong et al., 2019).

Method #Params FLOPs

3DCAE (Gong et al., 2019) 5.98M 16.23G

LUSS-AE [ours] 6.12M 16.30G

6 CONCLUSIONS

In this work, we tackled the problem of detecting

video anomalies without annotations. To address this

problem, we proposed a novel regime that leverages

unsupervised and self-supervised learning on a single

autoencoder. Our method is end-to-end trained on the

normal data and jointly learns to discriminate anoma-

lies from normality using three chosen tasks: (i) unsu-

pervised video clip reconstruction; (ii) unsupervised

future frame prediction; (iii) self-supervised playback

rate prediction. To our knowledge, it was the ﬁrst time

when PRP task was adapted for video anomaly detec-

tion. Our ablation study demonstrated the importance

of this task for unsupervised video anomaly detection.

To correctly focus on anomalous regions in the video,

we also proposed a new error measure, called the blur

pooled error (BPE) and a robust rescaling of anomaly

scores.

Our experiments demonstrate that the chosen

tasks enriched the spatio-temporal comprehension of

the autoencoder to better understand the normality for

detecting anomalies. Furthermore, a signiﬁcant boost

in performance with respect to MSE showed the im-

portance of the BPE as it removes the background

noise by keeping only the pertinent pixels. Finally, the

overall results prove the relevance of our LUSS-AE

method since it outperformed all recent approaches in

three challenging datasets.

In future works, we would like to explore train-

ing our method with BPE and further strengthening it

with data augmentation techniques.

REFERENCES

Acsintoae, A., Florescu, A., Georgescu, M.-I., Mare, T.,

Sumedrea, P., Ionescu, R. T., Khan, F. S., and Shah,

M. (2022). UBnormal: New benchmark for super-

vised open-set video anomaly detection. In CVPR,

pages 20143–20153.

Astrid, M., Zaheer, M. Z., Lee, J.-Y., and Lee, S.-I. (2021a).

Learning not to reconstruct anomalies. In BMVC.

Astrid, M., Zaheer, M. Z., and Lee, S.-I. (2021b). Synthetic

temporal anomaly guided end-to-end video anomaly

detection. In ICCV, pages 207–214.

Benaim, S., Ephrat, A., Lang, O., Mosseri, I., Freeman,

W. T., Rubinstein, M., Irani, M., and Dekel, T. (2020).

SpeedNet: Learning the speediness in videos. In

CVPR, pages 9922–9931.

Chang, Y., Tu, Z., Xie, W., and Yuan, J. (2020). Clustering

driven deep autoencoder for video anomaly detection.

In ECCV, pages 329–345.

Cho, M., Kim, T., Kim, W. J., Cho, S., and Lee, S. (2022).

Unsupervised video anomaly detection via normaliz-

ing ﬂows with implicit latent features. Pattern Recog-

nit, 129:108703.

Fawcett, T. (2006). An introduction to ROC analysis. Pat-

tern Recognit Lett, 27:861–874.

Feng, J.-C., Hong, F.-T., and Zheng, W.-S. (2021). MIST:

Multiple instance self-training framework for video

anomaly detection. In CVPR, pages 14009–14018.

Georgescu, M.-I., Barbalau, A., Ionescu, R. T., Khan, F. S.,

Popescu, M., and Shah, M. (2021a). Anomaly detec-

tion in video via self-supervised and multi-task learn-

ing. In CVPR, pages 12742–12752.

Georgescu, M.-I., Ionescu, R., Khan, F. S., Popescu, M.,

and Shah, M. (2021b). A background-agnostic frame-

work with adversarial training for abnormal event de-

tection in video. IEEE Trans Pattern Anal Mach Intell.

Gong, D., Liu, L., Le, V., Saha, B., Mansour,

M. R., Venkatesh, S., and van den Hengel, A.

(2019). Memorizing normality to detect anomaly:

Memory-augmented deep autoencoder for unsuper-

vised anomaly detection. In ICCV, pages 1705–1714.

Gudi, A., B

uttner, F., and van Gemert, J. (2022). Proxi-

mally sensitive error for anomaly detection and fea-

ture learning. arXiv preprint arXiv:2206.00506.

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

142

Hasan, M., Choi, J., Neumann, J., Roy-Chowdhury, A. K.,

and Davis, L. S. (2016). Learning temporal regularity

in video sequences. In CVPR, pages 733–742.

Ionescu, R. T., Khan, F. S., Georgescu, M.-I., and Shao,

L. (2019). Object-centric auto-encoders and dummy

anomalies for abnormal event detection in video. In

CVPR, pages 7842–7851.

Kingma, D. P. and Ba, J. (2015). Adam: A method for

stochastic optimization. In ICLR.

Kiran, B. R., Thomas, D. M., and Parakkal, R. (2018).

An overview of deep learning based methods for un-

supervised and semi-supervised anomaly detection in

videos. J Imaging, 4:36.

Li, W., Mahadevan, V., and Vasconcelos, N. (2013).

Anomaly detection and localization in crowded

scenes. IEEE Trans Pattern Anal Mach Intell, 36:18–

32.

Liu, W., Luo, W., Lian, D., and Gao, S. (2018). Future

frame prediction for anomaly detection–a new base-

line. In CVPR, pages 6536–6545.

Liu, X., Zhang, F., Hou, Z., Mian, L., Wang, Z., Zhang, J.,

and Tang, J. (2021a). Self-supervised learning: Gen-

erative or contrastive. IEEE Trans Knowl Data Eng.

Liu, Z., Nie, Y., Long, C., Zhang, Q., and Li, G.

(2021b). A hybrid video anomaly detection frame-

work via memory-augmented ﬂow reconstruction and

ﬂow-guided frame prediction. In ICCV, pages 13588–

13597.

Lohani, D., Crispim-Junior, C., Barth

elemy, Q., Bertrand,

S., Robinault, L., and Tougne, L. (2021). Spatio-

temporal convolutional autoencoders for perimeter in-

trusion detection. In RRPR, pages 47–65.

Lu, C., Shi, J., and Jia, J. (2013). Abnormal event detection

at 150 fps in Matlab. In ICCV, pages 2720–2727.

Luo, W., Liu, W., and Gao, S. (2017). A revisit of

sparse coding based anomaly detection in stacked

RNN framework. In ICCV, pages 341–349.

Lv, H., Chen, C., Cui, Z., Xu, C., Li, Y., and Yang, J.

(2021a). Learning normal dynamics in videos with

meta prototype network. In CVPR, pages 15425–

15434.

Lv, H., Zhou, C., Cui, Z., Xu, C., Li, Y., and Yang, J.

(2021b). Localizing anomalies from weakly-labeled

videos. IEEE Trans Image Process, 30:4505–4515.

Menon, V. and Stephen, K. (2021). Re learning memory

guided normality for anomaly detection. In ML Re-

producibility Challenge 2020.

Park, C., Cho, M., Lee, M., and Lee, S. (2022). Fas-

tAno: Fast anomaly detection via spatio-temporal

patch transformation. In WACV, pages 2249–2259.

Park, H., Noh, J., and Ham, B. (2020). Learning memory-

guided normality for anomaly detection. In CVPR,

pages 14372–14381.

Ramachandra, B., Jones, M. J., and Vatsavai, R. R. (2022).

A survey of single-scene video anomaly detection.

IEEE Trans Pattern Anal Mach Intell, 44:2293–2312.

Ristea, N.-C., Madan, N., Ionescu, R. T., Nasrollahi,

K., Khan, F. S., Moeslund, T. B., and Shah, M.

(2022). Self-supervised predictive convolutional at-

tentive block for anomaly detection. In CVPR, pages

13576–13586.

Sinha, P. and Russell, R. (2011). A perceptually based

comparison of image similarity metrics. Perception,

40:1269–1281.

Szymanowicz, S., Charles, J., and Cipolla, R. (2022). Dis-

crete neural representations for explainable anomaly

detection. In WACV, pages 148–156.

Tang, Y., Zhao, L., Zhang, S., Gong, C., Li, G., and Yang, J.

(2020). Integrating prediction and reconstruction for

anomaly detection. Pattern Recognit Lett, 129:123–

130.

Tian, Y., Pang, G., Chen, Y., Singh, R., Verjans, J. W.,

and Carneiro, G. (2021). Weakly-supervised video

anomaly detection with robust temporal feature mag-

nitude learning. In ICCV, pages 4975–4986.

Wang, J., Jiao, J., and Liu, Y.-H. (2020a). Self-supervised

video representation learning by pace prediction. In

ECCV, pages 504–521.

Wang, Z., Zou, Y., and Zhang, Z. (2020b). Cluster attention

contrast for video anomaly detection. In ACM Int Conf

Multimed, pages 2463–2471.

Yao, Y., Liu, C., Luo, D., Zhou, Y., and Ye, Q. (2020). Video

playback rate perception for self-supervised spatio-

temporal representation learning. In CVPR, pages

6548–6557.

Ye, M., Peng, X., Gan, W., Wu, W., and Qiao, Y. (2019).

AnoPCN: Video anomaly detection via deep predic-

tive coding network. In ACM Int Conf Multimed,

pages 1805–1813.

Yu, G., Wang, S., Cai, Z., Zhu, E., Xu, C., Yin, J., and Kloft,

M. (2020). Cloze test helps: Effective video anomaly

detection via learning to complete video events. In

ACM Int Conf Multimed, pages 583–591.

Zhang, R. (2019). Making convolutional networks shift-

invariant again. In ICML, pages 7324–7334.

Zhao, Y., Deng, B., Shen, C., Liu, Y., Lu, H., and Hua,

X.-S. (2017). Spatio-temporal autoencoder for video

anomaly detection. In ACM Int Conf Multimed, pages

1933–1941.

Leveraging Unsupervised and Self-Supervised Learning for Video Anomaly Detection

143