Diverse Level Generation for Tile-Based Video Game using Generative

Adversarial Networks from Few Samples

Soichiro Takata, Yuichi Sei

, Yasuyuki Tahara

and Akihiko Ohsuga

Department of Informatics, The University of Electro-Communications, Chofu, Tokyo, Japan

Keywords:

Procedural Content Generation, Generative Adversarial Networks, Deep Learning.

Abstract:

The procedural generation of levels in video games has been studied mainly to reduce the burden on producers.

In recent years, methods based on deep learning have been attracting attention. In level generations with deep

learning, GAN-based methods have achieved some success in tile-based video games, but the preparation of

the dataset has been an issue. In this study, we investigate a method to acquire a model that can generate

various levels by learning a GAN from only a small amount of data. It was conﬁrmed that a greater variety

and lower playability of levels can be generated than with conventional methods by quantitative evaluation of

the levels generated by the proposed methods. In addition, the model learned by the proposed method can

generate levels that reﬂect the objectives more strongly than the conventional method by using CMA-ES to

search for latent variables.

1 INTRODUCTION

Research on automatic game content creation tech-

nology, known as Procedural Content Generation

(PCG), has been active since the birth of video games.

Among video game content, levels are directly related

to the diﬃculty and fun of a game, but the cost of

manually generating many levels is high. Therefore,

many studies on automatic level generation are being

conducted with the motivation of reducing the bur-

den on game creators. In recent years, PCG has also

been used to develop an environment for evaluating

and learning game AI (Justesen et al., 2018).

With the development of deep generative models,

deep learning has been increasingly used in PCG (Liu

et al., 2020). In tile-based video games, level genera-

tion using GANs, one of the deep generative models,

has been successful. However, the cost of preparing

data sets for training GANs is an issue, and it is gen-

erally diﬃcult to train generators that generate diverse

levels from a few samples. In video game level gen-

eration models, the ability to generate diverse levels

is important to create diﬀerent game experiences or to

create levels that are consistent with a concept from

a variety of levels. A variety of levels is also neces-

https://orcid.org/0000-0002-2552-6717

https://orcid.org/0000-0002-1939-4455

https://orcid.org/0000-0001-6717-7028

sary to evaluate and improve the generalization per-

formance of AI. Generators with neural networks can

generate a large amount of data in parallel, so if a va-

riety of levels can be generated, the desired level can

be selected from among many candidates.

In this study, we investigate a learning method

for GANs that can generate a variety of levels from

only a small amount of training set. Learning a gen-

erator that can generate diverse levels makes it pos-

sible to not only select good levels from generated

levels but also use more eﬀectively the level gener-

ation method that reﬂects the objective by optimiz-

ing latent variables as inputs to the GAN (Volz et al.,

2018). In this paper, we proposed a data augmentation

method that adds levels that satisfy the constraints

among the levels generated by GAN as training data

and regularization terms in GAN training that facili-

tate the exploration of diverse levels. We prepare sev-

eral evaluation indicators for quantitative evaluation

and the experimental results showed that the model

trained by the proposed method was able to generate

more diverse levels than the model trained by the con-

ventional method. Although the playability was re-

duced, it was quantitatively conﬁrmed that the model

trained by the proposed method was able to gener-

ate more diverse levels than the one by conventional

methods. We also conﬁrmed that models trained by

the proposed method can generate playable and more

objective-reﬂected levels than conventional methods

326

Takata, S., Sei, Y., Tahara, Y. and Ohsuga, A.

Diverse Level Generation for Tile-Based Video Game using Generative Adversarial Networks from Few Samples.

DOI: 10.5220/0011666200003393

In Proceedings of the 15th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2023) - Volume 3, pages 326-333

ISBN: 978-989-758-623-1; ISSN: 2184-433X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

by exploring the latent space.

This paper is organized as follows. Section 2 pro-

vides research backgrounds on PCG with deep learn-

ing. Section 3 describes the proposed method, fol-

lowed by experiments and results in Section 4. Fi-

nally, we conclude the paper and discuss future work.

2 BACKGROUND

2.1 Procedural Content Generation

(PCG)

The procedural generation of video game content,

called Procedural Content Generation, has been stud-

ied for many years, and a variety of game content

has been generated by algorithms. Within the ﬁeld of

PCG, game level generation is the most popular, and

many studies have targeted 2D tile-based games such

as Super Mario Bros. side-scrolling action games

and exploration-based action games called roguelike

games. (Nelson, 2016). In recent years, deep learn-

ing has achieved remarkable results in content gener-

ation, such as images and text. Thus, its usefulness

in the ﬁeld of PCG is expected to increase, and re-

search on the use of deep generative models and deep

reinforcement learning for game content generation

is gaining momentum (Liu et al., 2020; Gissl

en et al.,

2021; Bontrager and Togelius, 2021; Khalifa et al.,

2020).

2.2 Generative Adversarial

Networks(GAN)

Adversarial Generative Network (GAN), one of the

generative models based on deep learning, has been

actively studied mainly as a generative model for

images since it was proposed by Goodfellow et al.

(Goodfellow et al., 2014) in 2014 and has achieved

remarkable results in image generation. In a basic

GAN, in addition to the generator, a neural network

that generates data, a discriminator, a network that

discriminates between data generated by the gener-

ator and real data, is trained alternately to make the

distribution of data generated by the generator closer

to the distribution of real data. This is done by al-

ternately training the discriminator, which is a net-

work that discriminates between the data generated

by the generator and the real data. Speciﬁcally, the

generator G is learned through a minimax game using

the value function V(D, G) formulated in the form of

the equation (1).

min

max

V(D,G) = E

x∼p

data

[log D(x)]

+ E

z∼p

[log D(G(z))]

(1)

2.3 Procedural Content Generation

using Generative Adversarial

Networks

In recent years, research on level generation using

GANs has been successful. Volz et al. (Volz et al.,

2018) used DCGAN (Radford et al., 2015) to gen-

erate levels for Super Mario Bros. and proposed a

method to generate levels that satisfy speciﬁed ob-

jectives by optimizing latent variables in the GAN

using Covariance Matrix Adaption Evolution Strat-

egy (CMA-ES) (Hansen et al., 2003), a black box

optimization method based on evolutionary compu-

tation. The proposed method generates a level that

satisﬁes the speciﬁed objective by optimizing latent

variables of the GAN. Torrado et al. (Rodriguez Tor-

rado et al., 2020) performed level generation in the

Zelda environment of the GVGAI Framework (Perez-

Liebana et al., 2018) using a model based on Self-

Attention in SAGAN (Zhang et al., 2018) for the gen-

erator and discriminator. By combining the informa-

tion on the number of tiles on each level with the

Self-Attention Map and performing conditional gen-

eration, it was shown that level generation with higher

playability and a lower percentage of duplicated lev-

els were achieved than with conventional DCGAN

generation. A method for learning GANs from a

small number of data by adding data generated by

the generator as training data during the GAN train-

ing process is also proposed, and it is reported that

47% of the 15,000 levels generated were playable and

60.3% were duplicates. In addition, GAN-based level

generation methods have been studied for various tile-

based video games (Awiszus et al., 2020; Hald et al.,

2020; Park et al., 2019; Steckel and Schrum, 2021;

Kumaran et al., 2020).

3 METHOD

In this study, we aim to generate a variety of levels

in tile-based video games using GANs from only a

small number of training data. We propose a method

that focuses on a loss function during model training

and a better augmentation of training data with GAN-

generated data.

Diverse Level Generation for Tile-Based Video Game using Generative Adversarial Networks from Few Samples

327

3.1 Data Augmentation with Generated

Levels

This study diversiﬁes the training data by adding the

levels generated to the dataset during the GAN train-

ing process, as in the bootstrap method of Torrado et

al, so that the generator can generate a variety of data.

In this study, we propose two methods of data aug-

mentation.

3.1.1 Conventional Bootstrap Method

In a previous work (Rodriguez Torrado et al., 2020),

the bootstrap method was proposed to improve the

diversity of the training set by periodically adding

playable levels to the training set during model train-

ing. In this method, the generated playable levels are

mapped into a two-dimensional space using PCA, and

then clustered using the Elbow and k-means methods,

and the level closest to the center of gravity of each is

selected and added to the training set.

3.1.2 Method 1: Bootstrap with Filtering

An overview of this method is shown in Figure 1.

Conventional bootstrap method was a method to in-

Figure 1: An overview of proposed method 1.

crease the number of training data by adding playable

data to the dataset during the training of the GAN.

This method does not compare the data to be added

to the dataset with the data in the dataset, which may

result in the levels in the dataset being similar to each

other. To avoid the problem of biased data in the

dataset, this method compares all levels in the dataset

with the levels to be added when adding levels, and

adds only those with a large hamming distance (the

number of tiles of diﬀerent types placed at the same

location when two levels are compared). This would

add more novelty to the level and deal with the issue

of bias in the dataset. It is possible that a better crite-

rion could be used to reduce the bias of the data, but

that is a subject for future work. In this study, we used

a simple hamming distance criterion that is applicable

to all types of 2D tile-based games.

3.1.3 Method 2: Separeted Augmenration and

Training

An overview of this method is shown in Figure 2.

Figure 2: An overview of proposed method 2.

In the method with bootstrap, even with the pro-

cess of Method 1, if the distribution of data in the

dataset is biased, a cycle could occur in which the

data to be generated will also be biased. Therefore,

we propose a method to create and train a less bi-

ased dataset by separating the training part of the

GAN from the augmentation of the training data. In

this method, the GAN used for data augmentation is

learned from the original data, and the playable levels

generated by the GAN are used to train a new GAN

model. This method is inspired by previous work

(Park et al., 2019).

In this method, two types of models are prepared.

An augmentation model, which performs data aug-

mentation, and a performance model, which learns

with the augmented data. The augmentation model

is trained by augmenting data using training set for

the augmentation model according to Method 1, and

the levels bootstrapped by the augmentation model

is also added to training set for the performance

model. When the size of training set of the perfor-

mance model is large enough, the performance model

is trained from the training set. As the augmenta-

tion model is trained, training set for the augmenta-

tion model may become biased, but the weights of the

learned model and the initialization of training set for

the augmentation model are periodically performed to

ensure that the bias does not worsen. This will re-

sult in a less biased training set for the performance

model, which can be used to train GANs from a wide

variety of levels.

3.2 Diversity Loss

In order to generate various levels in the GAN train-

ing process, a regularization term that maximizes the

L1 distance between generated data in a minibatch

is added to the loss function during training. In the

implementation, it averages the L1 distance between

the two samples in the minibatch and adds the term

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

328

weighted by the coeﬃcient λ

div

to the generator’s loss

function.

We propose to train GAN by gradient descent ac-

cording to following equation (3), (4), which is the

Hinge Adversarial Loss (Lim and Ye, 2017) plus a

regularization term L

div

. L

and L

are loss functions

by minibatch of the discriminator D and generator G

respectively. x is sampled from training set, z is sam-

pled from standard normal distributions and m is the

size of the minibatch.

This regularization term is expected to facilitate

the exploration of levels diﬀerent from the levels in

training set in the GAN learning process.

div

= −λ

div

m − 1

m−1

i=0

|G(z

(i)

) −G(z

(i+1)

)| (2)

i=0

[ − min(0,−1 + D(x

(i)

))

− min(0, −1 − D(G(z

(i)

)))]

(3)

= [

i=0

[−D(G(z

(i)

))] + L

div

] (4)

4 EXPERIMENTS AND RESULTS

We evaluated and discussed quantitatively and visu-

ally the ability of the proposed method to learn GANs

from a small amount of data and to generate levels

and their diversity for a tile-based video game. We

also optimized latent variables using CMA-ES for the

model obtained by the proposed method, and veriﬁed

the degree to which it is able to generate levels in ac-

cordance with the objectives.

4.1 Experimental Settings

4.1.1 The Zelda Environment from GVGAI

Framework

In this study, the Zelda environment of the GVGAI

Framework was used as the environment for level

generation. In this environment, the player moves on

a grid-like level with a height of 12 and a width of 16,

and completes the game by obtaining keys and reach-

ing the goal square. Enemies may be present on the

level and must be defeated by avoiding or attacking

them. The level consists of a total of eight types of

squares, including wall squares, ﬂoor squares, enemy

squares etc.. The following constraints must be satis-

ﬁed for a level to be playable.

Figure 3: Original levels used for training GAN.

• There is only one player, one key, and one goal

tile.

• The key and goal tiles are reachable from the

player tile.

• The level is surrounded by wall tiles.

Five manually created levels which shown as Figure

3 were used as the training data for the GAN.

4.1.2 Model Architecture

The levels are represented as a 3D tensor of size

(8,12,16) and total of 8 diﬀerent tiles allocated in

the channel direction. When converting the genera-

tor output tensor to a level, the tile corresponding to

the channel with the highest value is selected for each

position. In generator and discriminator, three con-

volution layer and two self-attention layer, which has

been shown to be eﬀective in previous works (Chen

and Lyu, 2022; Rodriguez Torrado et al., 2020), were

used. The detailed model structure is shown in Table

4 and Table 5 in the appendix.

4.1.3 Experimental Parameters

The settings for each parameter during GAN train-

ing are shown in Table 6 in the appendix. Note that

the bootstrap method is implemented by starting the

training with an initial dataset of 5 × 7 = 35 since the

minibatch size is 32 and adding data satisfying the

constraints to the dataset every 10 epochs. In Method

1 and 2, only levels with a hamming distance of less

than 90% to each level in the training set were added.

In Method 2, the data was augmented with augmen-

tation models until 1000 levels were generated. The

weights of the model were initialized every time 50

levels were generated, and the dataset was initialized

every time 100 levels were generated.

4.2 Evaluation of Playability and

Diversity

4.2.1 Evaluation Metrics

In order to quantitatively evaluate the levels generated

by the learned model, the following metrics are used.

Playability. Whether the generated levels satisfy the

constraints, i.e., whether they are playable. In

implementation, heuristics were used to check

whether all constraints were satisﬁed.

Diverse Level Generation for Tile-Based Video Game using Generative Adversarial Networks from Few Samples

329

Average Hamming Distance(AHD). Average ham-

ming distance for all pairs of generated levels.

Duplication Rate(DR). Percentage of generated lev-

els that are not unique.

Special Tile Matches(STM). For all pairs of gener-

ated levels, the percentage of pairs for which the

position of the only existing tile in Zelda, such as

key, door, or player, matches.

Playability evaluation is necessary because the

level generation model should generate playable lev-

els. In addition, several indices were used to quan-

titatively measure the diversity of the generated lev-

els. We considered that the greater the percentage of

unique levels a generator can generate and the greater

the hamming distance between generated levels, the

more diverse the levels it can generate, so we used in-

dices such as duplication rate and average hamming

distance for quantitative evaluation. Furthermore, in

Zelda, there are only one each of the squares for the

key, goal, and player, and we considered these objects

to be important in the game. To evaluate whether we

were able to create diﬀerent levels as a game experi-

ence, we used the percentage of agreement in the po-

sitions of these objects as an evaluation index. Playa-

bility and duplication rate was calculated from 10000

levels, while average hamming distance and special

tile matches were calculated from 1000 levels.

4.2.2 Results and Discussion

The results of the evaluation for each of the learned

models are shown in Table 1 and 2. Examples of

the levels generated by each method are shown in

Figures 4,5,8 and 9. As a comparison method, we

use the conventional method using only bootstrap in

(Rodriguez Torrado et al., 2020) and the GAN train-

ing method without data augmentation and diversity

Loss.

Comparing the proposed and conventional meth-

ods, the proposed methods outperform the conven-

tional bootstrap method and the simple GAN method

in terms of diversity indices such as average hamming

distance, duplication rate, Special tile matches, and

variance of each tile number, indicating that the pro-

posed method is able to generate various levels. In

the conventional bootstrap method, the model used in

this experiment generated only levels that were close

to speciﬁc levels in the early stages of training, so the

dataset was biased as bootstrap continued to add only

similar levels as training data, resulting in small dif-

ferences between levels and a high duplication rate.

A simple GAN could only generate levels that were

nearly identical to the training dataset.

Comparing the proposed data augmentation meth-

ods, Method 1 and Method 2, the hamming distance

between the generated data increased for Method 1,

while the average number of tiles in the generated lev-

els was signiﬁcantly diﬀerent from the original data.

This may be due to the fact that the distribution of

the level in the dataset gradually became more bi-

ased as generated levels was added to the dataset. In

Method 2, the bias of the tile distribution and the value

of special tile matches are smaller because the data

was augmented so that level bias within the dataset

is less likely to occur. On the other hand, playability

is reduced. Most of the cases where a level cannot

be generated correctly are those where the constraints

on the number of keys, doors, and player tiles are not

satisﬁed. The baseline method and the simple GAN

method, where the position of these tiles is almost de-

terministic, show high playability, while the proposed

method, where the positions of these tiles are diversi-

ﬁed, shows low playability. As for the low playability,

it could be improved by devising a model structure

like CESAGAN, but since it is possible to generate a

large number of levels in parallel, playable levels can

be selected from among the many levels generated. It

is also possible to generate playable levels with suf-

ﬁcient probability by searching for latent variables as

described in the next subsection.

4.3 The Eﬀectiveness of Evolutionary

Latent Space Search

Since the proposed method has acquired a genera-

tor capable of various outputs, it can eﬀectively uti-

lize the method of generating levels following the ob-

jective by searching latent variables. In a previous

work (Volz et al., 2018), it was shown that level gen-

eration reﬂecting the creator’s objective is possible

by optimizing the input latent variables according to

the objective function using CMA-ES. CMA-ES is a

black-box optimization algorithm based on evolution-

ary computation and performs continuous optimiza-

tion by evolutionary computation using a multi-point

search with a Gaussian distribution. By optimizing

the latent vectors of the generator’s inputs with CMA-

ES, latent variables that generate levels in line with

the objective function can be discovered.

In this part, we optimize latent variables for the

following two objective functions F

and F

to exam-

ine the extent to which latent variables reﬂecting the

objective functions can be generated. Note that P is

a variable that takes 1 if the level is playable and 0

otherwise.

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

330

Table 1: Playability and diversity statistics of each method. These values are averages of 5 runs.

Playability(%)↑ AHD↑ DR(%)↓ STM(%)↓

Ours (Method 1) 80.1 44.6 0.0 50.5

Ours (Method 2) 23.8 37.2 0.0 18.4

Conventional Bootstrap 87.6 13.3 10.7 53.2

Simple GAN 84.2 14.1 97.8 65.2

Original Levels 100.0 34.8 0.0 0.0

Table 2: Average and standard deviation of the number of tiles in each level. These values are averages of 5 runs.

Wall Floor Enemy

avg. std. avg. std. avg. std.

Ours (Method 1) 89.2 10.1 94.7 10.1 5.1 1.9

Ours (Method 2) 76.5 6.5 108.1 6.7 4.4 2.3

Conventional Bootstrap 68.0 3.9 117.3 3.6 3.7 1.3

Simple GAN 66.7 3.0 119.1 2.9 3.3 0.4

Original Levels 71.4 8.2 114.4 8.1 3.2 0.39

= 100P − #walls − 5 × #enemies (5)

= 100P + #walls + 5 × #enemies (6)

was designed to maximize the number of walls

and enemies while achieving a playable level, and F

was designed to minimize the number of walls and

enemies while achieving a playable level.

For the implementation, we used pycma

, a CMA-

ES library in python, and initialized the number of

initial population to 14 and the standard deviation to

0.5 for the optimization of 150 iterations. Examples

of the results of optimization using the objective func-

tion of F

, F

with z sampled from the Gaussian dis-

tribution as the initial value for the model obtained by

the proposed method using data augmentation method

2 are shown in Figure 6,7.

In both cases of optimization with F

and F

, the

number of enemies and wall tiles can be varied as de-

sired, indicating that the level can be generated in ac-

cordance with the objective to some extent. By com-

paring the playability of the proposed method and

the conventional method after optimizing each from

50 diﬀerent initial values and their average objec-

tive function values, we veriﬁed whether the proposed

method is able to generate playable levels and how

well the proposed method is able to edit them to meet

the objectives compared to the conventional method.

From Table 3, both the proposed and conventional

methods are able to obtain playable levels by optimiz-

ing latent variables. Comparing the average hamming

distances of the generated levels, it can be seen that

the model with the proposed method is able to gener-

ate more levels with various variations. In addition,

comparing the objective function values, the model

https://github.com/CMA-ES/pycma

by the proposed method is as good at generating lev-

els with few enemies and walls and outperforms the

model using the existing method in generating lev-

els with many enemies and walls. From this result, it

can be said that the proposed method is more capable

of generating levels that meet the objective due to its

more diverse outputs.

5 CONCLUSION

In this study, we conﬁrmed that various levels can be

generated by GAN in the Zelda environment of the

GVGAI Framework by expanding training data using

generated data and regularizing during model train-

ing. We have found that we can generate numeri-

cally more diverse levels than GANs using conven-

tional bootstrapping methods. Although playability

is reduced, the latent variables can be optimized by

CMA-ES to generate playable levels in seconds. Not

only that, but the diversity of levels generated by the

proposed method has increased, making it possible to

generate levels that better reﬂect the intent of the ob-

jective function.

Although the proposed method was able to gen-

erate a variety of levels for Zelda, a relatively small

game with less complex constraints, it is possible to

generate a variety of levels for a game of this size by

randomly placing walls and enemy tiles without using

a GAN. Since the proposed method can be applied to

other tile-based games, we will conduct experiments

on games with larger or more complex levels to verify

their eﬀectiveness.

Diverse Level Generation for Tile-Based Video Game using Generative Adversarial Networks from Few Samples

331

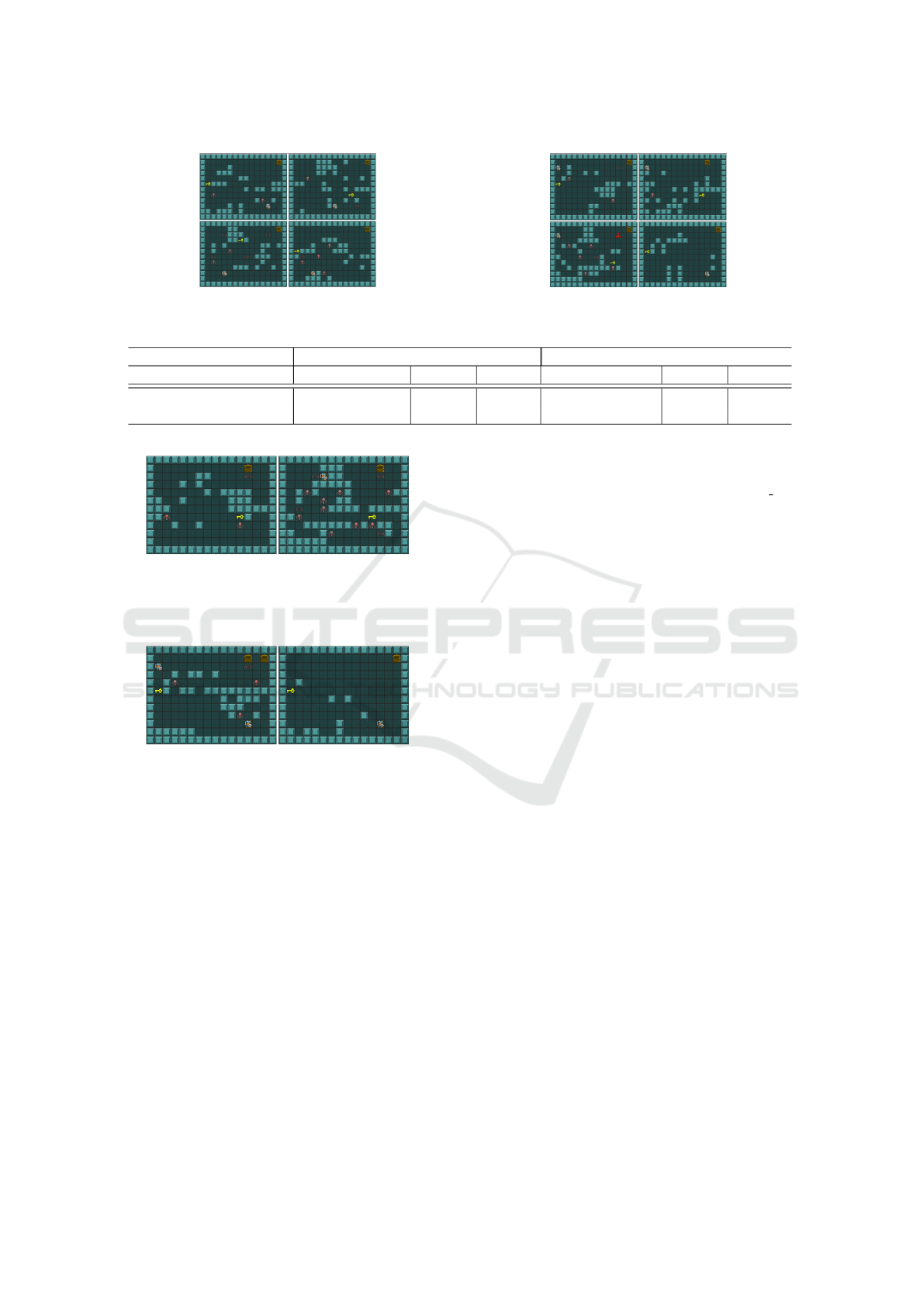
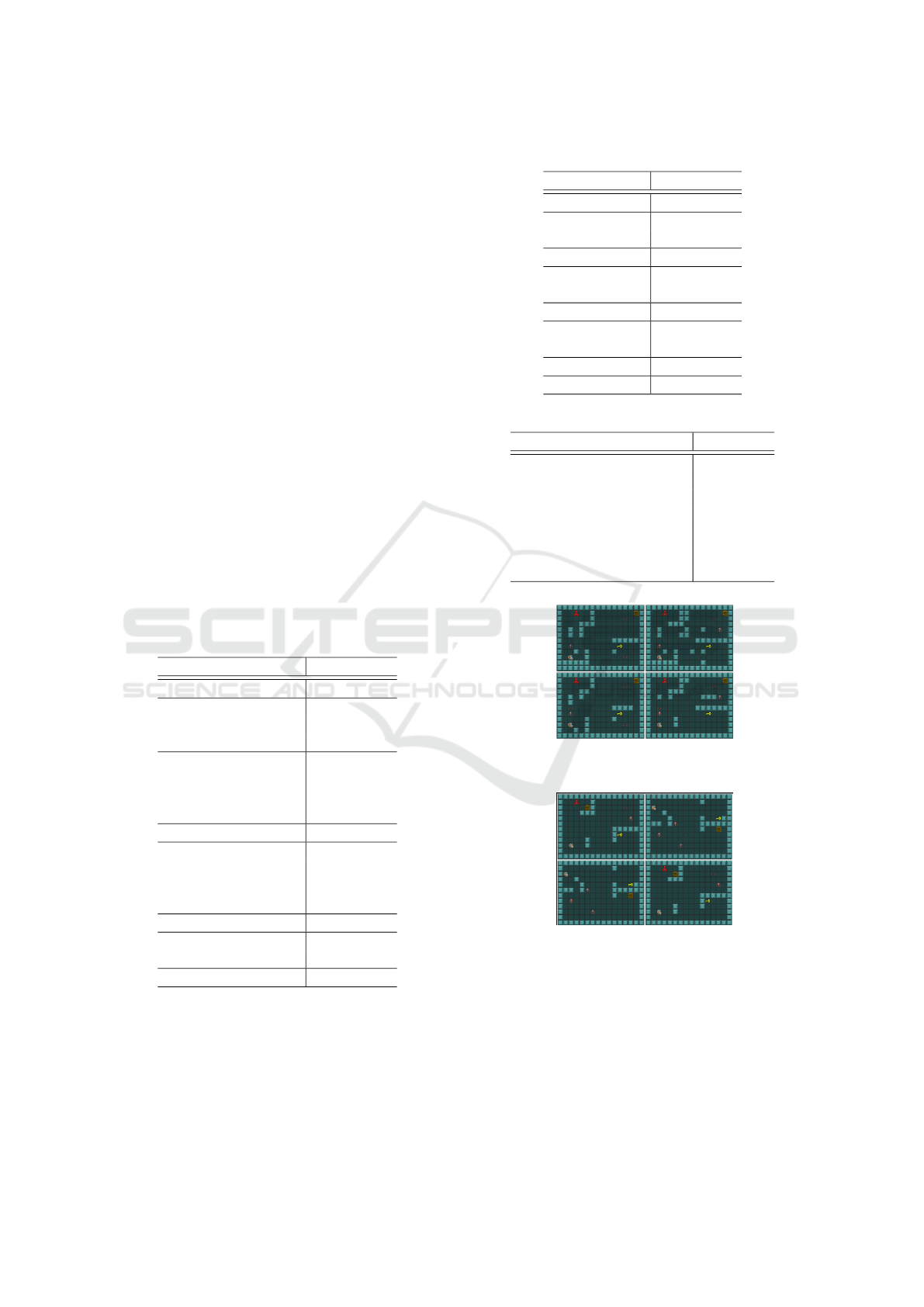
Figure 4: Examples of generated levels by proposed method 1. Figure 5: Examples of generated levels by proposed method 2.

Table 3: Playability and average values of objective function for levels generated from latent variables optimized by CMA-ES.

Playability(%)↑ Value ↓ AHD ↑ Playability (%)↑ Value ↓ AHD ↑

Ours (Method 2) 100.0 -144.2 40.8 100.0 59.6 14.6

Conventional Bootstrap 100.0 -119.2 15.8 100.0 59.8 4.4

Figure 6: Results of optimization with F

for the model

trained by the proposed method (Method 2). Levels on the

left are generated from the initial values, and levels on the

right are generated from the optimal values.

Figure 7: Results of optimization with F

for the model

trained by the proposed method (Method 2). Levels on the

left are generated from the initial values, and levels on the

right are generated from the optimal values.

ACKNOWLEDGEMENT

This work was supported by JSPS KAKENHI Grant

Numbers JP21H03496, JP22K12157.

REFERENCES

Awiszus, M., Schubert, F., and Rosenhahn, B. (2020). Toad-

gan: Coherent style level generation from a single ex-

ample.

Bontrager, P. and Togelius, J. (2021). Learning to Generate

Levels From Nothing. arXiv:2002.05259 [cs]. arXiv:

2002.05259.

Chen, Z. and Lyu, D. (2022). Procedural genera-

tion of virtual pavilions via a deep convolutional

generative adversarial network. Computer Anima-

tion and Virtual Worlds, 33(3-4):e2063. eprint:

https://onlinelibrary.wiley.com/doi/pdf/10.1002/cav.2

063.

Gissl

en, L., Eakins, A., Gordillo, C., Bergdahl, J.,

and Tollmar, K. (2021). Adversarial reinforcement

learning for procedural content generation. CoRR,

abs/2103.04847.

Goodfellow, I. J., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative adversarial networks.

Hald, A., Hansen, J. S., Kristensen, J. T., and Burelli,

P. (2020). Procedural content generation of puzzle

games using conditional generative adversarial net-

works. International Conference on the Foundations

of Digital Games.

Hansen, N., M

uller, S., and Koumoutsakos, P. (2003).

Reducing the time complexity of the derandomized

evolution strategy with covariance matrix adaptation

(cma-es). Evolutionary computation, 11:1–18.

Justesen, N., Torrado, R. R., Bontrager, P., Khalifa, A., To-

gelius, J., and Risi, S. (2018). Procedural level genera-

tion improves generality of deep reinforcement learn-

ing. CoRR, abs/1806.10729.

Khalifa, A., Bontrager, P., Earle, S., and Togelius, J. (2020).

PCGRL: Procedural Content Generation via Rein-

forcement Learning. arXiv:2001.09212 [cs, stat].

arXiv: 2001.09212.

Kumaran, V., Mott, B. W., and Lester, J. C. (2020). Gen-

erating game levels for multiple distinct games with a

common latent space. In AIIDE.

Lim, J. H. and Ye, J. C. (2017). Geometric gan.

Liu, J., Snodgrass, S., Khalifa, A., Risi, S., Yannakakis,

G. N., and Togelius, J. (2020). Deep learning for pro-

cedural content generation. CoRR, abs/2010.04548.

Nelson, N. S. T. J. (2016). Procedural Content Generation

in Games. SpringerLink.

Park, K., Mott, B., Min, W., Boyer, K., Wiebe, E., and

Lester, J. (2019). Generating educational game lev-

ICAART 2023 - 15th International Conference on Agents and Artiﬁcial Intelligence

332

els with multistep deep convolutional generative ad-

versarial networks. pages 1–8.

Perez-Liebana, D., Liu, J., Khalifa, A., Gaina, R. D., To-

gelius, J., and Lucas, S. M. (2018). General video

game ai: a multi-track framework for evaluating

agents, games and content generation algorithms.

Radford, A., Metz, L., and Chintala, S. (2015). Unsuper-

vised representation learning with deep convolutional

generative adversarial networks.

Rodriguez Torrado, R., Khalifa, A., Cerny Green, M., Juste-

sen, N., Risi, S., and Togelius, J. (2020). Bootstrap-

ping conditional gans for video game level generation.

In 2020 IEEE Conference on Games (CoG), pages 41–

48.

Steckel, K. and Schrum, J. (2021). Illuminating the space of

beatable lode runner levels produced by various gen-

erative adversarial networks. CoRR, abs/2101.07868.

Volz, V., Schrum, J., Liu, J., Lucas, S. M., Smith, A. M., and

Risi, S. (2018). Evolving mario levels in the latent

space of a deep convolutional generative adversarial

network. CoRR, abs/1805.00728.

Zhang, H., Goodfellow, I., Metaxas, D., and Odena, A.

(2018). Self-attention generative adversarial net-

works.

APPENDIX

Table 4: Model structure of generator.

Layer Shape

Input (32,)

Deconvolution (512,3,4)

Batch Normalization (512,3,4)

ReLU (512,3,4)

Upsample (512,6,8)

Convolution (256,6,8)

Batch Normalization (256,6,8)

ReLU (256,6,8)

Self-Attention (256,6,8)

Upsample (256,12,16)

Convolution (128,12,16)

Batch Normalization (128,12,16)

ReLU (128,12,16)

Self-Attention (128,12,16)

Convolution (8,12,16)

Softmax (8,12,16)

Output (8,12,16)

Table 5: Model structure of discriminator.

Layer Shape

Input (8,12,16)

Convolution (128,12,16)

Leaky ReLU (128,12,16)

Self-Attention (128,12,16)

Convolution (256,6,8)

Leaky ReLU (256,6,8)

Self-Attention (256,6,8)

Convolution (512,3,4)

Leaky ReLU (512,3,4)

Convolution (1,)

Output (1,)

Table 6: Experimental parameters.

values

Latent size 32

Minibatch size 32

Optimization RMSProp

Learning rate (G) 5.0 × 10

−5

Learning rate (D) 5.0 × 10

−5

div

50.0

Training iterations 10000

Figure 8: Examples of generated levels by a conventional

bootstrap GAN method.

Figure 9: Examples of generated levels by a simple GAN

method.

Diverse Level Generation for Tile-Based Video Game using Generative Adversarial Networks from Few Samples

333