Development, Implementation and Validation of a Stochastic

Prediction Model of UICC Stages for Missing Values in Large Data

Sets in a Hospital Cancer Registry

Sebastian Appelbaum

, Daniel Krüerke

2,3

, Stephan Baumgartner

, Marianne Schenker

and

Thomas Ostermann

Department of Psychology and Psychotherapy, Faculty of Health, Witten/Herdecke University, Witten, Germany

Society for Cancer Research, Hiscia Institute, Arlesheim, Switzerland

Clinic Arlesheim, Research Department, Arlesheim, Switzerland

{daniel.krueerke, Marianne.schwenker}@klinik-arlesheim.ch

Keywords: Clinical Registry, Cancer Staging, Missing Values, Prediction Models, Integrative Oncology.

Abstract: Cancer is still a fatal disease in many cases, despite intensive research into prevention, treatment and follow-

up. In this context, an important parameter is the stage of the cancer. The TNM/UICC classification is an

important method to describe a cancer. It dates back to the surgeon Pierre Denoix and is an important

prognostic factor for patient survival. Unfortunately, despite its importance, the TNM/UICC classification is

often poorly documented in cancer registries. The aim of this work is to investigate the possibility of

predicting UICC stages using statistical learning methods based on cancer registry data. Data from the Cancer

Registry Clinic Arlesheim (CRCA) were used for this analysis. It contains a total of 5,305 records of which

1,539 cases were eligible for data analysis. For prediction classification and regression trees, random forests,

gradient tree boosting and logistic regression are used as statistical methods for the problem at hand. As

performance measures Mean misclassification error (mmce), area under the receiver operating curve (AUC)

and Cohen’s kappa are applied. Misclassification rates were in the range of 28.0% to 30.4%. AUCs ranged

between 0.73 and 0.80 and Cohen kappa showed values between 0.39 and 0.44 which only show a moderate

predictive performance. However, with only 1,539 records, the data set considered here was significantly

lower than those of larger cancer registries, so that the results found here should be interpreted with caution.

1 INTRODUCTION

Cancer is still a fatal disease in many cases, despite

intensive research into prevention, treatment and

follow-up. With a deeper understanding of the

pathogenesis of cancer in the 19th century, first ideas

were developed to produce reliable statistics on

cancer-related mortality or morbidity rates Wagner,

1991). Around 1900, the first nationwide survey on

cancer was launched (Meyer 1911). Another 30 years

later, a first population-based cancer registry was

established in Germany, allowing to follow the

treatment process including survival time and

survival rate of cancer patients, which was one of the

starting points of cancer epidemiology (Alam 2011).

In cancer epidemiology, survival rates play an

important role: they provide information on the

percentage of people with the same cancer and cancer

stage who survived a certain period of time after

diagnosis (usually five years) following a specific

therapy. This information can be used to predict

treatment success. In particular, cancer registry data

can be used to identify patients with prolonged survival,

which is one of the main goals in clinical oncology.

In this context, an important parameter is the stage

of the cancer. The TNM classification is an important

method to describe a cancer. It dates back to the

surgeon Pierre Denoix (1944) and is an important

prognostic factor for patient survival (Takes et al.,

2010). It is based, as the title of the original paper

suggests, on the three pillars:

T = Tumor, extent and behavior of the primary

tumor.

N = Nodus (Latin nodus lymphoideus = lymph

node) absence or presence of regional lymph node

metastases

Appelbaum, S., Krüerke, D., Baumgartner, S., Schenker, M. and Ostermann, T.

Development, Implementation and Validation of a Stochastic Prediction Model of UICC Stages for Missing Values in Large Data Sets in a Hospital Cancer Registry.

DOI: 10.5220/0011667700003414

In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 5: HEALTHINF, pages 117-123

ISBN: 978-989-758-631-6; ISSN: 2184-4305

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

117

M = Metastases, absence or presence of distant

metastases

According to the definition of the International

Union against Cancer (Union internationale contre le

cancer (UICC)), founded in 1933, stages of cancer

can be grouped into five stages (UICC 0 to 4)

according to the TNM classification. These are:

- Stage 0: Tumors with no spread to connective

tissue, no lymph node involvement, and no

metastases.

- Stage I: Small and medium-sized tumors (T1,

T2) without lymph node involvement and metastases

- Stage II: Medium to large tumors (T3, T4)

without lymph node involvement and metastases

- Stage III: Tumors of any size with metastases in

1-4 lymph nodes in the surrounding area without

distant metastases

- Stage IV: tumors of any size with metastases in

1-4 lymph nodes in the surrounding area with distant

metastases.

Unfortunately, despite its importance, the

TNM/UICC classification is often poorly

documented in cancer registries (Søgaard et al., 2012).

For example, in one of the oldest national cancer

registries, the Danish Cancer Registry (DCR), a

proportion of 25% missing TNM information is

reported in patients with prostate cancer aged 0-39

years. In the same registry, the missing TNM

information of colon and rectal cancer was examined

with respect to age, comorbidities, and year.

For colon cancer, the percentage of missing TNM

information increased, from 28.7% in 2004 to a value

of 35.2% in 2009 (Ostenfels et al., 2012). Missing

TNM values are also observed in other cancer

registries, such as the Mallorca Cancer Registry

(Ramos et al. 2015).

The aim of this work is to investigate the

possibility of predicting the TNM classification into

the five UICC stages using statistical learning

methods based on cancer registriy data.

2 MATERIAL AND METHODS

The aim of this work is to investigate the possibility

of predicting the TNM classification into UICC

stages using statistical learning methods based on

cancer registry data.

2.1 Data Acquisition

Data from the Cancer Registry Clinic Arlesheim

(CRCA) were used for the analysis. The CRCA was

established in the 1960s. It has contained data from a

follow-up database since 1961, additional data from

the documentation of the international oncology

database QuaDoSta since 2010 (Schad, 2016), and

data from its own hospital information system (HIS)

since 2016. They contribute with different magnitude

to the documentation of the clinical course of

different cancer entities in the CRCA (Ostermann et

al. 2022).

The complexity of the data structure is already

evident from the different components from which

the CRCA obtains its data, which makes it likely that

the UICC stages will be missed, especially in the area

of the older follow-up database.

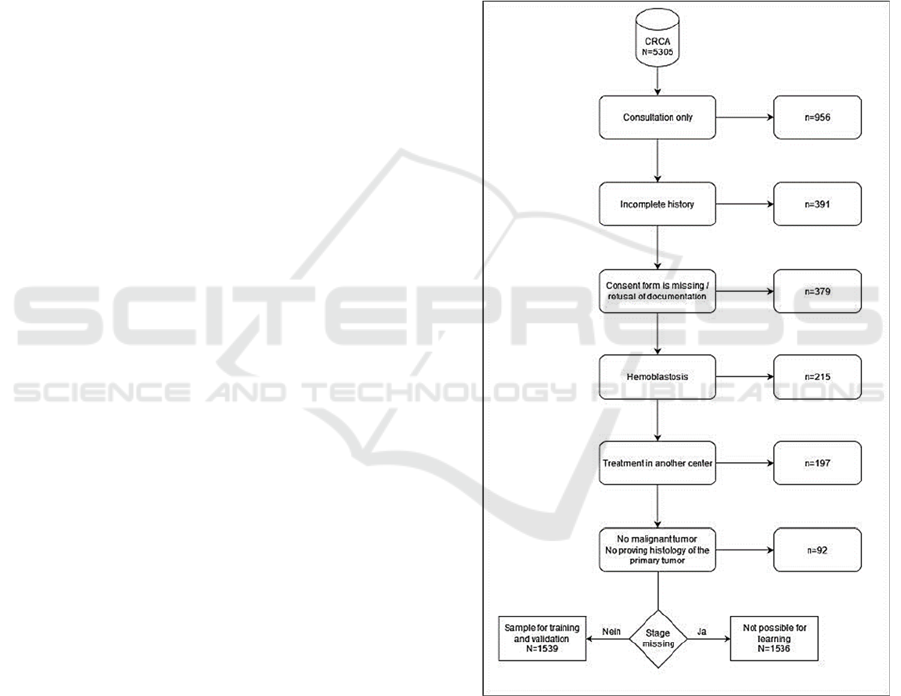
Figure 1: Flow chart for the inclusion/exclusion of data.

The CRCA contains a total of 5,305 records. In

n=956 cases (18.2%), only one consultation

appointment was available. An incomplete history led

to data exclusion in n=391 cases (7.4%). In n=379

records (7.1%), there was no informed consent from

the patient for further use of the data or

documentation was refused. In n=215 cases (4.1%),

the data concerned hematoblasts not amenable to

HEALTHINF 2023 - 16th International Conference on Health Informatics

118

TNM classification. In another 197 cases (3.7%),

treatments were performed at another clinical centre,

and in 92 cases (1.7%), there was no proving

histology of the primary tumour.

Therefore, a total of n = 3075 cases in principle

were suitable for evaluation. However, this sample

consisted of a total of only n=1539 cases (50.0%)

with tumor staging, which was used as a sample for

training and validation. For n=1536 cases without

tumor staging, supervised learning would have been

possible, but due to lack of cross-validation,

verification of learning outcomes would not have

been possible. Accordingly, the following analysis

was performed on N = 1539 cases (Fig.1).

2.2 Classification Methods

Especially in cases where no further data are available

or patient records are no longer accessible for

completion, appropriate statistical methods can be

important tools to complete the clinical

documentation in such cases for scientific evaluation.

However, the predictive power of such methods is

also linked to the existing data quality of the available

data in the registry. So far, there are only a few

corresponding studies in the literature on this topic.

Therefore, the choice of methods is not

predetermined by existing approaches or models.

From other studies, classification and regression

trees, random forests and gradient tree boosting and

logistic regression analysis are known as established

as reliable supervised learning methods (Hancock et

al., 2005, Freeman et al., 2016; Boughorbel et al.,

2016). Therefore, they are used as statistical methods

for the problem at hand.

Figure 2: Development of a CART-model (from:

https://dphi.tech/blog/introduction-to-decision-tree-

algorithm/).

Classification and Regression Trees

Classification and regression trees (CART) are

partitioning methods using recursive splits. A tree

consists of two elements: a tree decision structure and

a prediction structure. By using a series of recursive

binary splits for every possible predictor,

homogeneous subsets of the sample are created

(Buskirk, 2018) and a tree topology with nodes, leafes

and branches is created (Figure 1). To prevent

overfitting and overdimensionality of the grown

classification tree, the tree is pruned back in a next

step using the Gini index for categorical outcomes

and the sum of squared errors for continuous

variables.

Random Forests

Random forests as the name says, are collections of

decision trees whose results are aggregated into one

final result. According to (Breiman, 2001), the

algorithm for random forests is as follows:

For b=1 to B:

- Draw a bootstrap sample Z^* of sample size N

from the training data.

- Grow a random forest tree T on the bootstrap

sample by repeating the following steps until

the final node reaches a minimum size:

o Randomly choose m variables from the

p variables.

o Choose the best pair (splitting variable,

splitting point) from the m variables.

o Split the node into two daughter nodes.

o Output the ensemble of trees

For classification, the model prediction of the

random forest is given by the class selected by most

trees (Fig.3).

Figure 3: Process of the random forest algorithm

(from: https://www.tibco.com/de/reference-center/what-is-

a-random-forest) 1539 cases.

Gradient Tree Boosting

Besides the Random Forest method, Gradient tree

boosting (GBT) ensemble method. Again a learning

method is applied several times to the training data.

In contrast to Random forests the individual models

are not considered and adjusted separately, but rather

in an iterative procedure with each model trying to

predict the error left over by the previous model to an

Development, Implementation and Validation of a Stochastic Prediction Model of UICC Stages for Missing Values in Large Data Sets in a

Hospital Cancer Registry

119

additive overall model. In each step a regression tree

is fitted such that terminal regions emerge. The

algorithm therefore is as follows:

1. Initialize a simple prediction model

2. Train a new model that learns from the mistakes

of the old one

3. Combine the weak models to a stronger model

4. Repeat step 2 and 3 until selected termination

condition occurs.

Residuals here correspond to negative gradients

of the error function, which gives the naming of the

procedure (Mayr et al., 2014). Figure 4 illustrates the

algorithm graphically.

Figure 4: Illustration of the gradient tree boosting

algorithm (https://medium.com/swlh/gradient-boosting-

trees-for-classification-a-beginners-guide-596b594a14ea).

2.3 Dependent and Independent

Variables

In all three models, UICC classification was defined

as the dependent variable. However, due to sample

size for each stage, a dichotomous variable was

created:

0 = Stage 0 - II

1 = Stage III - IV

The following parameters served as independent

variables

- Age at diagnosis

- Chemotherapy history (y/n)

- First diagnosis of distant metastases

- Systemic therapy: 1st entry chemotherapy (y/n)

- Radiation therapy in the medical history (y/n)

- Radiotherapy (y/n)

- Chemotherapy (y/n)

- Surgery (y/n)

- 1 year survival (y/n)

- 2 year survival (y/n)

- 5 year survival (y/n)

2.4 Validation and Performance

Measures

In cases of small sample sizes performance measures

can be determined using cross-validation. In this

procedure, data are randomly divided into K

approximately equal subsamples. One part at a time

is used for validation and the remaining K-1 parts are

used for training. This is done k=1,...,K times

resulting in K performance measures which are

combined into one measure.

The following performance measures are applied:

Mean Misclassification Error

The Mean misclassification error (mmce) is the

misclassification rate, which can be calculated as

follows:

𝑚𝑚𝑐𝑒 





∑

𝐼𝑐̂





𝑥







with

𝐼𝑐̂





𝑥





1,𝑖𝑓 𝑐̂





𝑥



𝑐𝑥

0,𝑖𝑓 𝑐̂





𝑥



𝑐𝑥

That is, the errors are summed and divided by the

number of predictions n.

Receiver Operating Characteristic Curve

The Receiver Operating Characteristic curve (ROC

curve) is created by plotting the false positive rate

against the true positive rate. In doing so, the

threshold for class assignment is systematically

varied across all values. The area under the ROC

curve (AUC) is the respective performance measure

and ranges from 0.5 to 1. An AUC of > 0.8 is

considered to be good, and an AUC > 0.9 is

considered to be very good (Šimundić, A, 2009).

Cohen's Kappa Coefficient of Agreement

Cohen's kappa coefficient of agreement is given by

𝜅1

1  𝑝





1  𝑝





where p

is the observed frequency of agreement

and p

is the expected frequency of agreement at

independence. Cohen’s kappa normally ranges from

0 to 1. A value of 1 means perfect agreement. A value

of 0 corresponds to agreement that is consistent with

pure chance. In seldom cases negative values occur,

which indicate a match that is even smaller than a

random match. Landis and Koch (1977) judge values

of > 0.6 as sufficient for agreement.

2.5 Software

Classification and statistical analysis is performed

using the statistical software R (R version 3.6.1). For

classification the R package mlr2 is used.

HEALTHINF 2023 - 16th International Conference on Health Informatics

120

3 RESULTS

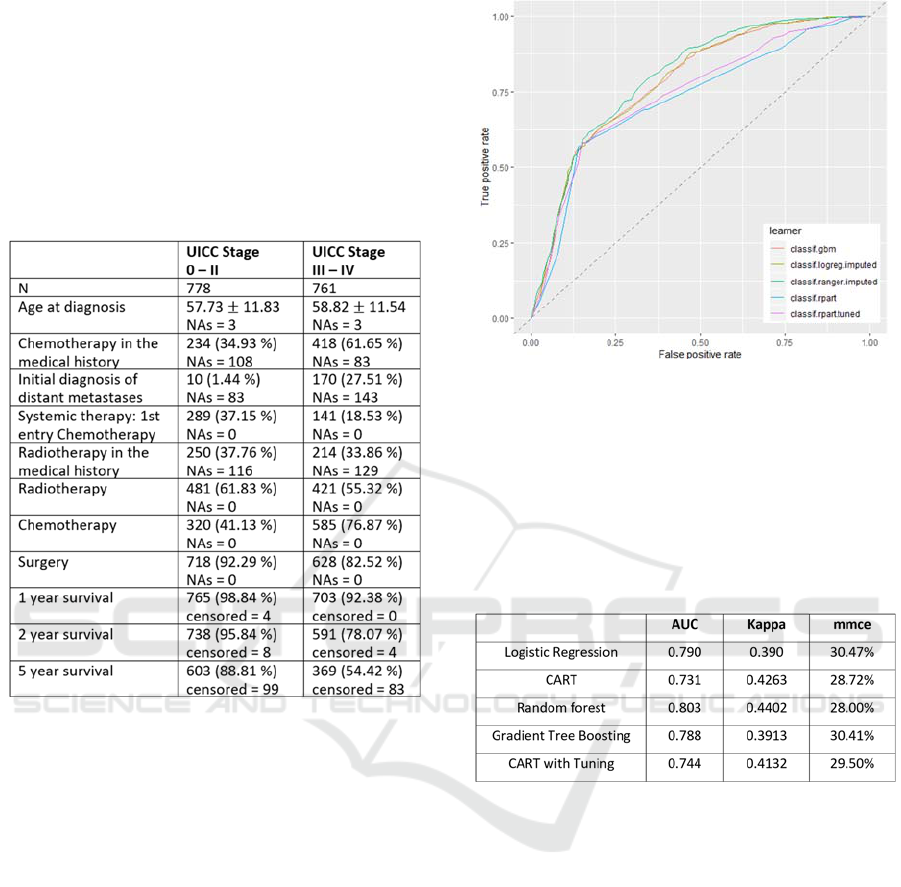
Table 1 shows the distribution of predictor data

among the respective UICC stagings.

Table 1: Distribution of the predictor data among the

respective UICC stagings. For metric variables mean ± SD

and for binary variables absolute frequency and relative

frequency in %) are shown. NAs denotes the number of

missing values.

Especially in the variables "Chemotherapy in the

medical history", "First diagnosis of distant

metastases" and "Systemic therapy" clear differences

between the two groups are recognizable. The extent

to which these differences lead to sufficiently good

classification results will be investigated in the

following analyses.

Figure 2 shows the joint display of the ROC

curves of the different classification methods. Even a

mere eye-validation of the curves shows a rather

moderate classification performance

Table 2 presents the summary of the performance

measures of goodness of the different methods.

Comparing the related methods with each other, it

is noticeable that the mean classification rate of all

methods is between 28.0% (random forest) and

30.41% (gradient boosting), which can be considered

rather insufficient for a classification algorithm.

Also, the AUCs have values between 0.731 and

0.803, which also does not meet the standards for a

valid procedure, for which an AUC > 0.8 is defined

as good and an AUC > 0.9 as very good (cf.

Šimundić, 2009).

Figure 5: ROC curves of the different classification

methods (classif.logreg.imputed: Logistic regression;

classif.rpart: CART; classif.ranger.imputed: random forest;

classif.gbm: gradient tree boosting; classif.rpart.tuned:

CART with tuning).

Table 2: Performance measures of goodness of the different

methods. (classif.logreg.imputed: Logistic regression;

classif.rpart: CART; classif.ranger.imputed: random forest;

classif.gbm: gradient tree boosting; classif.rpart.tuned:

CART with tuning).

The kappa values for the agreement between

classification result and actual UICC are also in a

comparable range with values between 0.39 and 0.43,

which, however, is also not sufficient according to the

classification of Landis and Koch (1977).

4 CONCLUSIONS

Missing data is a common problem in

epidemiological research (Shah et al., 2014),

especially in population-based cancer registries

(Seneviratne et al. 2014)). Both classical statistical

prediction models, such as logistic regression or

classification trees, and newer machine learning

methods, such as random forests or gradient boosting

methods, are used to impute missing data in many

areas of epidemiology (Eisemann et al. 2011). Both

the completeness of primary data and the accuracy of

Development, Implementation and Validation of a Stochastic Prediction Model of UICC Stages for Missing Values in Large Data Sets in a

Hospital Cancer Registry

121

staging coding need to be improved for cancer

registries to fulfill their growing role in cancer

control, according to a Europe-wide review of cancer

registries (Minicozzi et al., 2017).

Extensive analyses have not yet been conducted

in the area of cancer staging prediction. In their

simulation study, Eisemann's group reported initial

imputation of UICC stages with concordance rates of

approximately 80% (Eisemann et al. 2011). In this

work, we therefore investigated the extent to which

the above-mentioned methods for predicting missing

data in tumor stages yielded similar results. In this

context, logistic regression, as a well-known method,

served as a benchmark for comparison with the other

four methods.

The results of this work are below the orders of

magnitude of Eisemann's group. Even though no

multiple imputation was performed in the present

approach, the misclassification rates were in the range

of 28.0% to 30.4%. Similar to Eisemann's work, the

results of the classical methods (logistic regression,

classification tree) were not inferior to those of

machine learning (random forests, gradient boosting)

both in their concordance (0.39; 0.43) and in their

prognostic quality (AUC 0.79; 0.73) (concordance:

0.44; 0.39 AUC: 0.80; 0.79).

Nevertheless, the kappa values between 0.39 for

logistic regression and 0.44 for random forests

according to the classification of Koch and Landis

(1977) are in the rather moderate range. Moreover,

the UICC stagings were additionally combined into a

binary variable, which again reduces the significance.

Also, with only 1539 records, the data set

considered here was significantly lower than those of

larger cancer registries, so that the results found here

should be interpreted with caution. In addition, a

multiple imputation strategy (Burgette et al., 2010)

was not used here, although it is unclear whether this

would have led to a significant improvement in the

classification results in the present case.

While in contrast to Eisemann et al., 2011) the

methods used did not exhibit convergence problems,

the heterogeneity in the primary data was a clear

challenge for data management. Although in this

particular case this may be explained by the historical

genesis of the cancer registry, other work also

highlights the issue of primary data heterogeneity as

a source of statistical error (Carmora-Bayonas et al.,

2018). Here, it would be important to optimize the

harmonization of data across data sources through

standards for data collection, recording, and

presentation to facilitate the analysis of large data sets

(Le Sueur et al., 2020).

Although the results of this paper are somehow

disappointing, future work in this field should

nevertheless continue and particularly pay attention

to new technologies and strategies in the field of

artificial neural networks and machine learning to

develop sound prognostic classification models based

on available registry data to support an individualized

approach to cancer treatment.

ACKNOWLEDGEMENT

We would like to explicitly appreciate the friendly

support and constant helpfulness with all questions

concerning the QDS system by the FIH team (Antje

Merkle, Danilo Pranga and Friedemann Schad).

REFERENCES

Alam, A.S. (2011). Cancer Registry and Its Different

Aspects. Journal of Enam Medical College 1(2): 76-80.

Bhagat, N. K., Mishra, A. K., Singh, R. K., Sawmliana, C.,

& Singh, P. K. (2022). Application of logistic

regression, CART and random forest techniques in

prediction of blast-induced slope failure during

reconstruction of railway rock-cut slopes. Engineering

Failure Analysis, 137, 106230.

Boughorbel, S., Al-Ali, R., & Elkum, N. (2016). Model

comparison for breast cancer prognosis based on

clinical data. PLoS One, 11(1), e0146413.

Breiman, L. (2001). Random forests. Machine learning,

45(1), 5-32.

Burgette, L. F., & Reiter, J. P. (2010). Multiple imputation

for missing data via sequential regression trees.

American journal of epidemiology, 172(9), 1070-1076.

Buskirk, T. D. (2018). Surveying the forests and sampling

the trees: An overview of classification and regression

trees and random forests with applications in survey

research. Survey Practice, 11(1), 1-13.

Carmona-Bayonas, A., Jimenez-Fonseca, P., Fernández-

Somoano, A., Álvarez-Manceñido, F., Castañón, E.,

Custodio, A., ... & Valiente, L. P. (2018). Top ten errors

of statistical analysis in observational studies for cancer

research. Clinical and Translational Oncology, 20(8),

954-965.

Chen, M. M., & Chen, M. C. (2020). Modeling road

accident severity with comparisons of logistic

regression, decision tree and random forest.

Information, 11(5), 270.

Denoix, P. F. (1944). Tumor, node and metastasis (TNM).

Bull Inst Nat Hyg (Paris), 1(6), 1-69.

Edmonds, J. (1971). Matroids and the greedy algorithm.

Mathematical programming, 1(1), 127-136.

Eisemann, N., Waldmann, A., & Katalinic, A. (2011).

Imputation of missing values of tumour stage in

HEALTHINF 2023 - 16th International Conference on Health Informatics

122

population-based cancer registration. BMC medical

research methodology, 11(1), 129.

Freeman, E. A., Moisen, G. G., Coulston, J. W., & Wilson,

B. T. (2016). Random forests and stochastic gradient

boosting for predicting tree canopy cover: comparing

tuning processes and model performance. Canadian

Journal of Forest Research, 46(3), 323-339.

Friedman, J. H. (2002). Stochastic gradient boosting.

Computational statistics & data analysis, 38(4), 367-

378.

Hancock, T., Put, R., Coomans, D., Vander Heyden, Y., &

Everingham, Y. (2005). A performance comparison of

modern statistical techniques for molecular descriptor

selection and retention prediction in chromatographic

QSRR studies. Chemometrics and Intelligent

Laboratory Systems, 76(2), 185-196.

Hastie, T., Tibshirani, R., & Friedman, J. H. (2017). The

Elements of Statistical Learning: Data Mining,

Inference, and Prediction: Springer.

Landis, J. R., & Koch, G. G. (1977). The measurement of

observer agreement for categorical data. Biometrics,

159-174.

Le Sueur, H., Bruce, I. N., & Geifman, N. (2020). The

challenges in data integration–heterogeneity and

complexity in clinical trials and patient registries of

Systemic Lupus Erythematosus. BMC Medical

Research Methodology, 20(1), 1-5.

Mayr, A., Binder, H., Gefeller, O., & Schmid, M. (2014).

The evolution of boosting algorithms. Methods of

information in medicine, 53(06), 419-427.

Meyer, G (1911). Bericht über die zehnjährige Wirksamkeit

des Deutschen Zentralkomitees für Krebsforschung.

Zeitschrift für Krebsforschung 1911; 10: 8–33.

Minicozzi, P., Innos, K., Sánchez, M. J., Trama, A., Walsh,

P. M., Marcos-Gragera, R., ... & White, C. (2017).

Quality analysis of population-based information on

cancer stage at diagnosis across Europe, with

presentation of stage-specific cancer survival estimates:

A EUROCARE-5 study. European Journal of Cancer,

84, 335-353.

Ostenfeld, E. B., Frøslev, T., Friis, S., Gandrup, P., Madsen,

M. R., & Søgaard, M. (2012). Completeness of colon

and rectal cancer staging in the Danish Cancer Registry,

2004–2009. Clinical epidemiology, 4 Suppl 2(Suppl 2),

33-38. doi:10.2147/clep.s32362

Ostermann, T., Appelbaum, S., Baumgartner, S., Rist, L.,

& Krüerke, D. (2022). Using Merged Cancer Registry

Data for Survival Analysis in Patients Treated with

Integrative Oncology: Conceptual Framework and First

Results of a Feasibility Study. In HEALTHINF (pp.

463-468).

Ramos, M., Franch, P., Zaforteza, M., Artero, J., & Durán,

M. (2015). Completeness of T, N, M and stage grouping

for all cancers in the Mallorca Cancer Registry. BMC

Cancer, 15(1), 847. doi:10.1186/s12885-015-1849-x

Schad, F., Matthes,B., Pissarek, J. et al. (2016).

QuaDoSta: Qualitätssicherung, Dokumentation

und Statistik, eine open source Lösung am

Beispiel onkologischer Dokumentation; http://www.

fih-berlin.de/tumorbasisdokumentation.html [Stand:

07Also, the AUCs have values between 0.731 and

0.803, which also does not meet the standards for a

valid procedure, for which an AUC > 0.8 is defined as

good and an AUC > 0.9 as very good (cf. Šimundić,

2009).04.2016]

Seneviratne, S., Campbell, I., Scott, N., Shirley, R., Peni,

T., & Lawrenson, R. (2014). Accuracy and

completeness of the New Zealand Cancer Registry for

staging of invasive breast cancer. Cancer epidemiology,

38(5), 638-644.

Shah, A. D., Bartlett, J. W., Carpenter, J., Nicholas, O., &

Hemingway, H. (2014). Comparison of random forest

and parametric imputation models for imputing missing

data using MICE: a CALIBER study. American journal

of epidemiology, 179(6), 764-774.

Šimundić, A. M. (2009). Measures of diagnostic accuracy:

basic definitions. Ejifcc, 19(4), 203.

Søgaard, M., & Olsen, M. (2012). Quality of cancer registry

data: completeness of TNM staging and potential

implications. Clinical epidemiology, 4 Suppl 2, 1-3.

doi:10.2147/clep.s33873

Takes, R. P., Rinaldo, A., Silver, C. E., Piccirillo, J. F.,

Haigentz Jr, M., Suárez, C., . . . Ferlito, A. (2010).

Future of the TNM classification and staging system in

head and neck cancer. Head & Neck, 32(12), 1693-

1711. doi:10.1002/hed.21361

Wagner, G. (1991): History of cancer registration. In:

Jensen OM, Parkin DM, MacLennan R et al, (eds).

Cancer registration: principles and methods. IARC

scientific publication 95. Lyon: International Agency

for Research on Cancer: 3-6.

Development, Implementation and Validation of a Stochastic Prediction Model of UICC Stages for Missing Values in Large Data Sets in a

Hospital Cancer Registry

123