The Green Tourist Trip Design Problem with Time Windows: A Model

Application on a Urban Scale

Annarita De Maio

1 a

, Roberto Musmanno

2 b

and Aurora Skrame

2 c

Department of Economy, Statistics and Finance ”G. Anania”, University of Calabria, Italy

Department of Mechanical, Energy and Management Engineering, University of Calabria, Italy

Keywords:

Tourist Trip Planning, Multimodality, Green Orienteering Problem, Multiobjective.

Abstract:

We model a variant of the Tourist Trip Design Problem with time windows. The novelty of the proposed

model is that we also take care of the needs of vulnerable users and of the sustainability of the tour in terms of

reduction of the level of CO

emissions generated by the vehicles associated with the different transportation

modes that can be selected to plan the tour. The mathematical formulation of the proposed model consists

of three objective functions, with the attempt to generate a green tour which maximizes the number of point

of interests (POIs) to visit and, at the same time, the total scores of the visited POIs. The correctness of

the proposed model has been tested on a real case, at a urban level. The preliminary results allow to better

understand the impact of the sustainability constraints on the tour and to address the direction for further

research developments.

1 INTRODUCTION

The tourism is an important economic sector which

has always been affected by a growing development,

due to its positive impact on improving and sustain-

ing the economy of different countries ((Umurzakov

et al., 2022) and (Massidda and Mattana, 2013)). The

World Travel and Tourism Council stated that in 2021

the travel and tourism’s contribution to global GDP

(Gross Domestic Producut) increased by US$1 tril-

lion (+21.7% rise), after around a 54% of decline dur-

ing the pandemic, conﬁrming that tourism is one of

the largest industries that provides a strong impact

on the global economic development. The availabil-

ity of new technologies, like the mobile ICTs, arti-

ﬁcial intelligence and sensitive analysis techniques,

the massive use of big data and the spread of so-

cial networks has had a signiﬁcant impact on the

tourism. The paradigm of Tourism 2.0 changes the

digital tourist services from a product-driven envi-

ronment to a social and customer-driven one: e-

business development allows tourists to directly in-

teract with tourism service providers and with other

customers to exchange opinions and review visited

https://orcid.org/0000-0002-4650-3362

https://orcid.org/0000-0002-8852-6933

https://orcid.org/0000-0003-1728-4989

places. As a consequence, in the last years, it is pos-

sible to register the birth of different Tourist Recom-

mender Systems ((Ardito et al., 2019) and (De Maio

et al., 2020)), that simplify the life cycle of the

tourist experience, ﬁltering relevant information for

the users and providing a decision support based on

explicit preferences (Kontogianni et al., 2018). Fi-

nally, the debate arising from the Sustainable De-

velopment Goals (SDGs) of the Agenda 2030 in-

volves also the role of tourism in the near future (see

the World Tourism Organisation website https://www.

unwto.org/tourism-in-2030-agenda). In particular,

the concept of sustainability in tourism is transver-

sal to different development goals: tourism can con-

tribute to use and sale of local products in tourist

destinations (zero hunger goal), sustainable tourism

can creates jobs (decent work and economic growth

goal), tourism can push the investments for smarter

and greener cities (sustainable cities and communi-

ties and reducing inequality goals), and so on (see

(Fakfare and Wattanacharoensil, 2022) and (Alonso-

noz et al., 2022)). Under this respect, the research

interest in the numerical optimization ﬁeld is devoted

to support the tourist decisions in building appeal-

ing and sustainable tours. The problem of helping

tourists in the deﬁnition of a customized tour is de-

ﬁned Tourist Trip Design Problem (TTDP) (Gunawan

et al., 2016). In this problem a tourist usually wants

De Maio, A., Musmanno, R. and Skrame, A.

The Green Tourist Trip Design Problem with Time Windows: A Model Application on a Urban Scale.

DOI: 10.5220/0011669500003396

In Proceedings of the 12th International Conference on Operations Research and Enterprise Systems (ICORES 2023), pages 62-70

ISBN: 978-989-758-627-9; ISSN: 2184-4372

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

to visit a city, rich of attractions, in a limited amount

of time. The scope is to build a personalized tour,

according to the tourist’s preferences, selecting a se-

quence of POIs to visit. Each POI is characterized

by a score related to its attractiveness, a cost and a

time window for the visit. The tourist usually can

also impose limits about the total budget available

for the visits. Moreover, the tourist is able to move

from a POI to another using a variety of transporta-

tion modes, each of them with different costs (also

in terms of CO

emissions) and travel times. The

scope of this paper is to introduce a variant of the

Green Tourist Trip Design Problem (GTTDP), (Di-

vsalar et al., 2022), in which the sustainability of the

tour is considered. Under this respect, there are dif-

ferent aspects to be taken into account: the poten-

tial attractiveness of the tour, the number of POIs

to visit, the time windows of the POIs, the cost and

the time duration of the tour, and the quantity of

released during the movements between POIs.

From another perspective, smart and inclusive cities

should take care to the needs of the so-called vulner-

able road users (VRUs). Traditionally, pedestrians,

bicyclists, and motorcyclists are considered VRUs, as

well as people with disability, elder people and chil-

dren (Methorst, 2002). Under this respect, the re-

search interest is more concentrated to reduce crashes

involving VRUs (Oxley et al., 2010), to build per-

sonalized trips for people with mobility impairments

(Darko et al., 2022) or to deﬁne information systems

and mobile services sharing real-time information and

integrating a tour design for VRUs (Scholliers et al.,

2017). As argued by (Darko et al., 2022), it is nec-

essary in the next future to propose fully accessible

and personalized tours in a broader multimodal mo-

bility context for VRUs, as well as to include useful

functionalities into the smart services for the differ-

ent users’ needs. In order to consider all these as-

pects, a multimodal multiobjective GTTDP with time

windows is presented. The rest of the paper is orga-

nized as follows: Section 2 reports the literature re-

view in the ﬁeld and the main contributions of this

work. Section 3 describes the mathematical formula-

tion, whereas Section 4 introduces the case study set-

tings and the computational results. Finally, Section 5

reports the conclusions and the future developments.

2 LITERATURE REVIEW

The TTDP is a speciﬁc problem deﬁned in the tourism

sector, but it can be led back to the more general

class of the Vehicle Routing Problems (VRP) with

proﬁts (Archetti et al., 2014), in which two differ-

ent decisions have to be taken: 1) the best customers

to be served (not deﬁned a-priori like it happens in

the classical VRP) and 2) the routes to be used. If

only one route is built, the problem becomes a vari-

ant of the Travelling Salesman Problem (TSP), de-

scribed in the scientiﬁc literature by using in some

cases alternative denominations. The most diffused

denomination is the Orienteering Problem (OP), in-

troduced by (Golden et al., 1987) and deriving from

the well known orienteering sport, in which each par-

ticipant has to maximize the total collected prizes as-

sociated with the visited points, returning to the start-

ing point within a certain time. Alternative deﬁnitions

and variants of the same problem are: the Maximum

Collection Problem (Butt and Cavalier, 1994), the Se-

lective Travelling Salesperson Problem (Laporte and

Martello, 1990) and the Bank Robber Problem (Awer-

buch et al., 1998). Note that, when multiple ve-

hicles are involved, the most investigated variant is

the so-called Team Orienteering Problem (TOP). An

overview of the OPs that is worth mentioning is re-

ported in the survey of (Gunawan et al., 2016), in

which several variants are classiﬁed and described:

classical OP, TOP (Pessoa et al., 2009), TOP with

time windows (Labadie et al., 2012), time dependent

TOP (Verbeeck et al., 2014), stochastic OP (Ilhan

et al., 2008) and the generalized OP (Geem et al.,

2005). The authors, in their conclusions, also iden-

tiﬁed the tourism trip design as one of the major prac-

tical applications of this problem. The TTDP is il-

lustrated in the surveys of (Gavalas et al., 2014) and

(Ruiz-Meza and Montoya-Torres, 2022). The au-

thors underlined that the TTDP can be mainly classi-

ﬁed in single-objective and multiobjective problems.

In the single-objective case, the scope is the maxi-

mization of the beneﬁts associated with visiting the

POIs. Under this respect, several variants are in-

vestigated: presence of time windows denoting the

opening and closing times of each POI (Abbaspour

and Samadzadegan, 2009); the score of POIs de-

riving from personal preferences or sensitive analy-

sis (Zheng and Liao, 2019); hotel selection option

(Zheng et al., 2020) and, time and budget constraints.

In the multiobjective case, different objective func-

tions are considered in the TTDP formulations: min-

imizing transportation and visiting costs, minimizing

waiting times at POIs, maximizing attractiveness of

the tour, minimizing travel time between POIs and

maximizing the diversity of the selected POIs (see

(Castillo et al., 2008), (Lim et al., 2017) and (Huang

et al., 2019)). Finally, the authors introduced some

future perspective in the tourist trip design, indicat-

ing the green variant as one of the most promising re-

search areas in the next future. Green and sustainable

The Green Tourist Trip Design Problem with Time Windows: A Model Application on a Urban Scale

tourism can be declined in different forms: for exam-

ple, taking into account emission during movements

between POIs, suggesting alternative mobility options

to the users, protecting natural areas or potentiating

the development of nature tourism and ecotourism.

This discussion underlines the timeliness of this work,

and a GTTDP with time windows is introduced in the

following sections. From the best of our knowledge,

the GTTDP was previously investigated only by (Di-

vsalar et al., 2022). The authors introduced a mul-

tiobjective and multimodal GTTDP where a mixed-

integer linear model is formulated, considering three

objective functions: maximizing the total score of the

trip, minimizing the total cost and the total CO

emis-

sion produced by the trip. Under this respect, var-

ious transportation modes are considered as possible

choice for the tourists in order to move between POIs.

Constraints related to travel time are also considered.

In this work, an extension of the model in (Divsalar

et al., 2022) is proposed, with different novelties:

• three different objective functions are considered:

minimizing the total CO

emissions and maximiz-

ing both the number of visited POIs and the total

scores associated with visited POIs;

• the tour is designed considering additional con-

straints: budget constraint on the total cost (mov-

ing and visiting costs) and time windows con-

straints related to the opening and closing time

of the POIs and to the preferences of the tourist

for the starting and ending times of the tour; the

average visit time at each visited POI is also con-

sidered when building the tour;

• a larger variety of transportation modes is taken

into account (car, public transport, bike, feet and

push scooter);

• additional constraints are incorporated in the

model, in order to customize the tour consider-

ing only the transportation modes chosen by the

tourists, or considering their preferences related to

the own physical possibilities (for example, fami-

lies with children would not like moving by using

bicycles or elder people would like avoiding long

walking paths);

• the model is tested on a real-setting case study in

a urban context (city of Florence).

The detailed description of the mathematical formu-

lation is introduced in the following section.

3 MATHEMATICAL

FORMULATION

In order to formalize the model under investigation

we adopt the following notation. Let N

be the set

of n potential POIs to visit, starting from and ending

to a ﬁxed point denoted by node 0 and duplicated as

node n + 1. N = N

∪ {0, n + 1}, whereas A is the

arc set of the complete directed graph induced by N.

K is the set of possible transportation modes to real-

ize the visit (car, bus/metro, bike, on foot). For each

POI i ∈ N

the following parameters are assumed to

be known: a score p

, a cost f

, i.e., the price of the

entrance ticket, a time visit v

, e

and l

, that is, re-

spectively, the opening and closing times. Other pa-

rameters are: e

and l

, respectively, the earliest and

latest times at which the visit can be planned (the time

interval [l

− e

] corresponds to the time window at

node 0); T is the maximum travel time determined

by all movements between nodes, whereas T

is the

maximum travel time determined by all movements

between nodes considering the transportation mode k

(clearly, T

≤ T , ∀ k ∈ K); B is the cost budget avail-

able for the visit; c

i jk

, t

i jk

and s

i jk

are, respectively,

the cost, the time and the level of CO

emission as-

sociated with arc (i, j) ∈ A when travelled by using

transportation mode k; M is an arbitrarily large con-

stant. The decision variables are the following: z

i ∈ N

, are binary, each of them equal to one if the

POI i is visited, 0 otherwise; x

i jk

, (i, j) ∈ A, k ∈ K,

are binary, each of them equal to one if (i, j) is trav-

elled by using transportation mode k, 0 otherwise; u

i ∈ N, are continuous, each of them is the arrival time

at node i and, if i is a POI, corresponds to the starting

time of the visit at POI i. The three-objective problem

is formulated as follows:

Maximize

∑

i∈N

(1)

Maximize

∑

i∈N

(2)

Minimize

∑

(i, j)∈A

∑

k∈K

i jk

(3)

subject to

∑

i∈N\{0}

∑

k∈K

0ik

∑

i∈N\{n+1}

∑

k∈K

i,n+1,k

= 1 (4)

∑

i∈N\{ j}

∑

k∈K

i jk

∑

i∈N\{ j}

∑

k∈K

jik

= z

, ∀ j ∈ N

(5)

∑

k∈K

i jk

≤ 1, ∀ (i, j) ∈ A (6)

∑

(i, j)∈A

∑

k∈K

i jk

≤ T (7)

ICORES 2023 - 12th International Conference on Operations Research and Enterprise Systems

∑

(i, j)∈A

i jk

≤ T

∀ k ∈ K (8)

∑

(i, j)∈A

∑

k∈K

i jk

∑

i∈N

≤ B (9)

+ v

∑

k∈K

i jk

≤ u

+ M(1 −

∑

k∈K

i jk

∀ i ∈ N, j ∈ N \ {i} (10)

+ v

≤ l

, ∀ i ∈ N

(11)

≤ u

, ∀ i ∈ N

(12)

≥ e

(13)

n+1

≤ l

(14)

i jk

∈ {0, 1}, ∀ (i, j) ∈ A, k ∈ K (15)

∈ {0, 1}, ∀ i ∈ N

(16)

≥ 0, ∀ i ∈ N (17)

The objective function (1) is the number of POIs to

visit, whereas the objective function (2) represents the

corresponding total score of the visit. Both (1) and

(2) should be maximized. The third objective func-

tion (3), to be minimized, corresponds to the total

level of CO

emission associated with the visit. Con-

straint (4) states that the visit starts from node 0 and

ends to node n + 1. Constraints (5) ensure the con-

nectivity of the tour visiting the selected POIs. They

also provide the logic condition that an arc incident

in any node j can be travelled by any transportation

mode only if POI j is selected for the visit. Con-

straints (6) establishes that each arc (i, j) can be trav-

elled by using one transportation mode at most. Con-

straints (7) ensure that the total travel time of the tour

does not exceed the value of T (the constraint is as-

sumed because the visitor does not like to waste a lot

of time on travel). Constraints (8) impose a maximum

time budget to be spent for any transportation mode.

These constraints allow to limit (or completely forbid)

the use of a particular transportation mode, in accor-

dance with the speciﬁc needs of the tourist which can

be a VRU. Constraints (9) guarantees that the total

cost paid for travelling and visiting the POIs remains

under the budget limit B available. Constraints (10)

are subtour elimination constraints. They state that

if an arc (i, j) is visited (i.e., travelled by one trans-

portation mode), then the arrival time at node i plus

the duration of the visit at node i and the travel time

from node i to node j cannot be greater than the ar-

rival time at node j. Of course, if the arc (i, j) is not

visited, then, thanks to the arbitrarily large constant

M, the corresponding constraint is not active. Con-

straints (11) and (12) are time windows constraints at

each visited POI. Constraints (11) impose that if POI

i is visited, than the starting time of the visit at node

i plus the time visit should be within the closing time

of POI i and, thanks to constraints (12), the starting

time of the visit should be after the opening time of

POI i. Constraints (13) and (14) ensure that the visit

starts and ends within the time window [l

−e

] estab-

lished for the visit. Constraints (15) and (16) impose

that some decision variables are binary, whereas con-

straints (17) deﬁne the non-negative conditions on the

remaining ones. In the following section, some com-

putational experiments related to the real case study

are presented.

4 CASE STUDY SETTING AND

COMPUTATIONAL RESULTS

The mathematical model illustrated in Section 3 has

been applied to the city of Florence in Italy. A set

of 20 POIs is considered, whose features, in terms of

geographical coordinates, price, average duration of

the visit, time windows and score, are reported in Ta-

ble 1. Note that all data are extracted by using the

support of available databases: for the positions, the

travel times and distances between POIs (not reported

in details for the sake of brevity), a Python routine

linked with Google Maps has been used; the score

of each POI has been extracted from the database of

MIBACT (Italian Ministry of Cultural Heritage and

Activities and Tourism, https://storico.beniculturali.it/

mibac/export/MiBAC/index.html#&panel1-1). The

spatial distribution of the selected POIs is represented

in Figure 1.

Figure 1: Locations of some POIs chosen in the city of Flo-

rence.

Five different transportation modes are consid-

The Green Tourist Trip Design Problem with Time Windows: A Model Application on a Urban Scale

Table 1: Features of the 20 POIs chosen in the city of Florence.

ID POI Latitude Longitude Cost Time window Visiting time Score

i f

, (C) [e

, l

] v

, (minutes) p

1 Piazza Duomo 43.772904 11.257733 20 [09:30; 17:30] 150 10

2 Piazza della Signoria 43.769306 11.255592 22 [08:15; 18:30] 150 10

3 Ponte Vecchio 43.768459 11.253549 0 [00:00; 24:00] 30 10

4 Galleria degli Ufﬁzi 43.768665 11.25568 20 [08:15; 18:50] 150 10

5 Palazzo Strozzi 43.771527 11.251981 16 [09:30; 17:30] 60 9

6 Museo Galileo 43.767776 11.256297 10 [09:30; 18:00] 60 9

7 Dante’s House 43.771016 11.257115 8 [10:00; 18:00] 60 8

8 Basilica of Holy Spirit 43.766924 11.247824 0 [08:30; 18:00] 90 9

9 Synagogue and Jewish Museum 43.773316 11.265698 10 [10:00; 17:30] 120 10

10 English Cemetery 43.77685 11.268549 3 [14:00; 18:00] 60 7

11 Marini’s Museum 43.771968 11.249687 6 [10:00; 19:00] 120 7

12 Piazza della S. Annunziata 43.776338 11.260921 4 [07:30; 19:00] 60 8

13 Horne Museum 43.767522 11.259347 6 [10:00; 18:00] 30 7

14 Clet’s Workshop 43.764474 11.260829 0 [13:30; 19:30] 60 7

15 Basilica di Santa Croce 43.768737 11.26203 9 [09:30; 17:30] 90 10

16 Parco delle Cascine 43.782497 11.219324 5 [11:00; 19:00] 150 9

17 Complesso di Palazzo Pitti 43.765343 11.249898 22 [08:10; 19:10] 150 10

18 Enzo Pazzagli Art Park 43.768647 11.324149 6 [11:00; 21:00] 150 8

19 Piazzale Michelangelo 43.762464 11.264762 0 [00:00; 00:00] 30 10

20 Gardens and Villa of Castello 43.819098 11.229186 8 [08:30; 18:30] 150 10

ered: car, walking, traditional bike (not electric ver-

sion), public transportation (tram and bus) and push

scooter. The amount of produced CO

per transporta-

tion mode is extracted from the CO

Connect website

(www.co2nnect.org): 0.183 kg/km for car, 0 kg/km

for walking and bike, 0.065 kg/km for public trans-

portation and 0.126 kg/km for push scooter. Finally,

the kilometric cost per transportation mode is equal

to C 0.25 for car, C 0.00 for walking, C 0.20 for

bike, C 0.35 for public transportation and C 0.50 for

push scooter. Note that the costs for bike and push

scooter are referred to the most common services of

bike sharing and push scooter sharing. It is assumed

that the tourist has indicated the maximum duration

of the daily itinerary (in our test case 10.5 hours,

with a feasible time window set to [9:00;19:30]), the

maximum budget (C 40), the maximum time to be

spent for travelling between POIs (60 minutes) and

the departure/arrival point of the tour, represented by

Santa Maria Novella railway station. To determine a

Pareto optimal solution of problem (1)–(17), the lexi-

cographic method is applied, see (Collette and Siarry,

2003). The objective functions (1)−(3) are ranked in

order of importance, from best to worst. Then, a se-

quence of at most three single-objective optimization

problems is solved by considering a single objective

function at a time, starting with the most important

one and proceeding according to the order of impor-

tance given to the objectives. However, the optimal

value found for each objective is added as a constraint

for subsequent optimizations. More speciﬁcally, we

always keep the objective function (1) of highest pri-

ority. In this way, at the ﬁrst step, the lexicographic

optimization leads to the solution of problem (1),

(4)−(17). This guarantees that the tour always con-

tains the highest number f

∗

of selected POIs. At the

second step, we solve the problem (2), (4)−(17) with

the additional constraint

∑

i∈N

≥ f

∗

. Let f

∗

be the

optimal value of the objective function (2). At this

step, in our case, we always obtain a unique optimal

solution (otherwise, we should have to optimize this

objective). This solution, in correspondence of which

we compute the value of the objective function (3),

is taken as the desired solution of the original prob-

lem. A further Pareto optimal solution is obtained

by reversing the order of importance of the second

and third objectives. This gives the tourist a choice

between two alternatives and enables the evaluation

of the advantages of one over the other. The im-

plementation of any optimization problem has been

carried out by using GAMS 24.7.4 (GAMS Develop-

ment Corporation) as the algebraic modelling system,

with CPLEX 12.6 (IBM Corporation) as the solver.

The code has been executed on a PC Intel Core i7

(2.3 GHz) with 16 GB of RAM. In order to evaluate

the effectiveness of the described approach, in terms

of CO

emissions, of potential savings and of VRUs

preferences, a kind of what-if analysis has been con-

ducted, considering four cases (called in the following

as scenarios), on the basis of different settings of the

user preferences. These are described as follows:

• Scenario 1. The preferences of an eclectic tourist

are considered: all transportation modes are fully

usable. As a consequence, the budget limit for

each transportation mode is equal to the maximum

ICORES 2023 - 12th International Conference on Operations Research and Enterprise Systems

time budget, that is, T

= T = 60 minutes for each

k ∈ K.

• Scenario 2. The case of a VRU as a tourist is con-

sidered. The user is unwilling to walk or ride a

bike for more than 20 minutes. As a consequence,

the budget limit for each transportation mode is

equal to the maximum time budget, except for

walking and bike modes, that is, T

= T

T = 50 minutes and T

= T

= 20 minutes.

• Scenario 3. Again the case of a VRU is consid-

ered, with more extreme requirements. The user

is unwilling to walk for more than 10 minutes and

could use only e-bikes. As a consequence, the

budget limit for each transportation mode is equal

to the maximum time budget, except for walking

mode, that is, T

= T

= T = 50 minutes

and T

= 10 minutes. Note that, the e-bike has

similar CO

emission level of the push scooter, so

i j3

= s

i j5

, ∀ (i, j) ∈ A.

• Scenario 4. A baseline for the evaluation of

possible CO

emission savings is built, imposing

that the tour can allow only private transportation

modes: car (fully available) and walking (avail-

able only for movements within trafﬁc limited

zones). In this way, the greener transportation

modes cannot be activated.

Note that all the tests are solved optimally, so the cor-

responding optimality GAP is omitted. The results

obtained by applying for each scenario the lexico-

graphic method described above are reported in the

sequel. For Scenarios 1, 2 and 3, the optimal solu-

tion of problem (1), (4)−(17) is determined, with a

value of the objective function (1) equal to f

∗

= 9.

As a consequence,

∑

i∈N

≥ 9 is the new additional

constraint for the subsequent tests. For Scenario 4,

the optimal solution of problem (1), (4)−(17) leads

to f

∗

= 7. As previously described, two further tests

are executed for each scenario: the ﬁrst one considers

(2) as the objective function (referred with label Test

X.A), whereas the second one takes (3) as the objec-

tive function (with label Test X.B). ”X” indicates the

referred scenario. The results are reported in Table

2 organized as follows: column Test reports the cor-

responding setting under investigation, column POIs

refers to f

∗

; CO

reports the CO

emission level of

the tour; Score represents the total score of the se-

lected POIs and Time reports the execution time (in

seconds) of the test run.

In Table 3, the details about the travel times and

the transportation modes activated for each tour are

reported. The four tours associated with Tests 1.B,

2.B, 3.B and 4.B (the settings are related to the mini-

Table 2: Results of the what-if analysis obtained consider-

ing four different scenarios.

Test POIs ( f

∗

) CO

Score CPU Time

(kg) (seconds)

Test 1.A 9 0.052 79 6193.00

Test 1.B 9 0.000 77 0.33

Test 2.A 9 0.874 79 429

Test 2.B 9 0.0699 78 525

Test 3.A 9 2.012 79 88.91

Test 3.B 9 0.993 78 89.13

Test 4.A 7 2.934 56 34

Test 4.B 7 2.934 56 95

mization of the emissions) are also depicted, see Fig-

ures 2, 3, 4 and 5.

Table 3: Results of the what-if analysis obtained consider-

ing four different scenarios for the transportation modes.

Test Transportation Minutes

mode

Test 1.A walking 22.88

bike 35.67

car 1.43

Test 1.B walking 27.20

bike 31.50

Test 2.A car 8.50

walking 8.13

bike 19.61

public transportation 20.97

push scooter 1.62

Test 2.B walking 14.70

bike 19.95

public transportation 8.88

push scooter 2.32

Test 3.A car 17.42

walking 8.13

bike 27.13

public transportation 5.52

Test 3.B car 1.43

walking 9.00

bike 11.41

public transportation 19.36

Test 4.A car 48.24

Test 4.B car 48.24

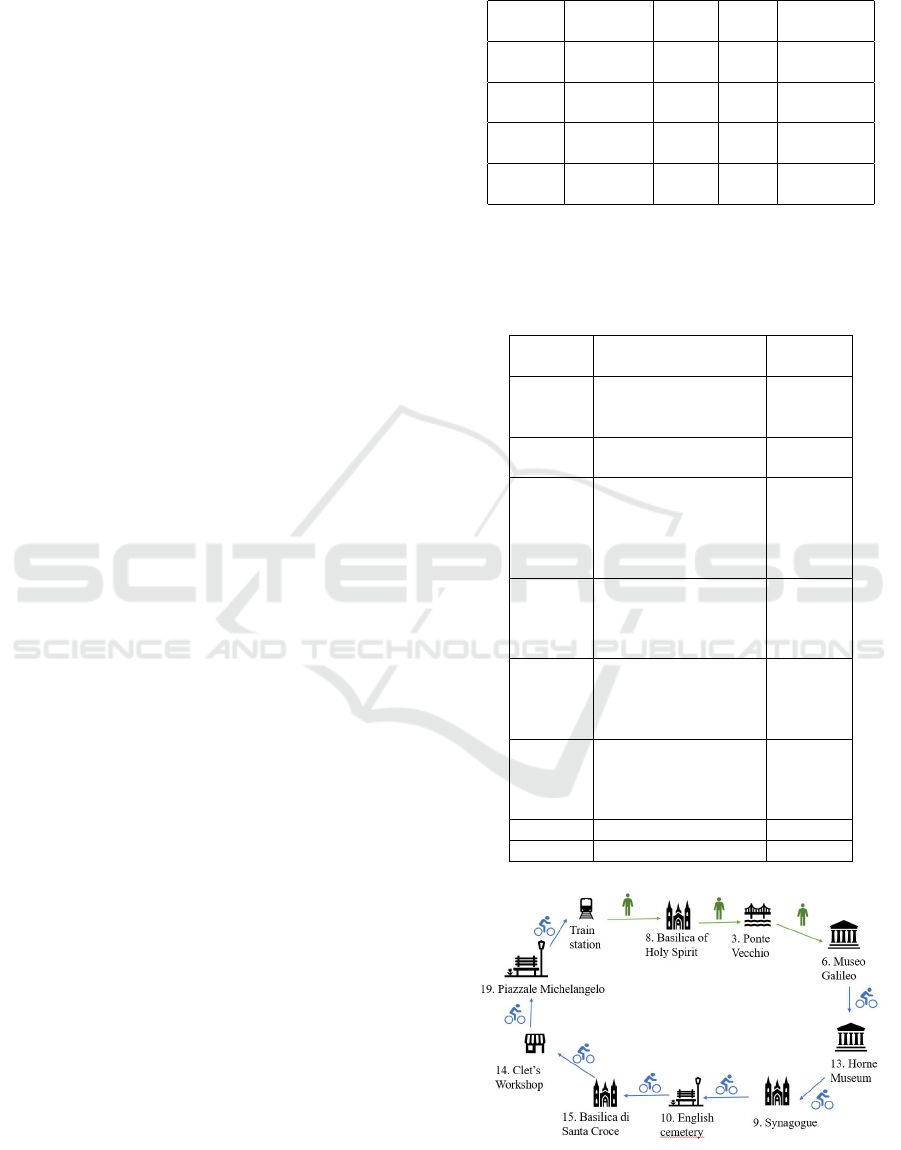
Figure 2: Green tourist tour generated for Test 1.B.

The Green Tourist Trip Design Problem with Time Windows: A Model Application on a Urban Scale

Figure 3: Green tourist tour generated for Test 2.B.

Figure 4: Green tourist tour generated for Test 3.B.

Figure 5: Green tourist tour generated for Test 4.B.

It is worth noting that the lexicographic method

can be considered as a suitable approach to generate

high quality solutions for different types of tourists.

First of all, the choice of assigning the highest pri-

ority to the objective function corresponding to the

maximization of the number of visited POIs respects

the needs of the tourist that generally likes to exploit

all the available time for the visit. Although all the

solutions obtained are Pareto optimal, some of them

seems to be more interesting for the GTTDP. Note

that, in Tests 1.B, 2.B and 3.B the reduction of the

emissions is higher than the loss in the tour scor-

ing. Indeed, comparing Tests 1.A and 1.B, a loss

of 2.53% in the tour scoring leads to a reduction of

5.24% of the CO

emissions. Similarly, for Scenarios

2 and 3 the reduction of the CO

emissions is more

than 100%, with a tour scoring loss of 1.27%. The

comparison of Scenarios 1, 2 and 3 with the solution

obtained in Scenario 4 (the baseline in terms of CO

emissions), highlights additional aspects: the reduc-

tion of the CO

emissions is about 100% for Scenar-

ios 1 and 2 with respect to the solution based on the

use of the private car as a transportation mode, and

about 45% for Scenario 3. Under this respect, our

model empirically shows a good balance between sus-

tainability and the speciﬁc requirements of a tourist

when acts as a VRU. Finally, note that in Scenario

4 also the tour scoring decreases, compared with the

lowest value (77 for Test 1.B): there is a gap equal to

28% between the two solutions. This is due to the typ-

ical conﬁguration of the city centre: Florence is char-

acterized by several limited trafﬁc zones, where the

POIs are relatively close to each other. For this rea-

sons, the green transportation modes encourage the

construction of more attractive tours. This aspect is

typical of many ancient tourist cities. Moreover, con-

sidering the results reported in Table 3, zero-emission

transportation modes are activated quite often. This

issue sometimes implies quite longer travel times with

respect to other solutions. Finally, the described so-

lutions underline the ﬂexibility of the proposed ap-

proach: for each scenario a high quality tour is gener-

ated, consuming all the time budget available for the

tourists and satisfying their needs in terms of trans-

portation modes.

5 CONCLUSIONS

In this work a multimodal and multiobjective GTTDP

is presented for generating a personalized tour com-

pliant with the preferences and the requirements of

different kind of tourists. At this stage the proposed

optimization model represents only a ﬁrst step of the

development of a more sophisticated decision support

tool in a tourism management context. The paradigm

of the Tourism 2.0 has deﬁnitely introduced the digi-

talization of tourist services, and several sophisticated

ICT platforms has been designed to support several

options to smarter tourists. The goal of the described

approach is to determine a low level of CO

emis-

sion tour containing a large number of POIs with high

scores. Different transportation modes have been con-

sidered as choices for the tourist to move between

POIs for a daily tour. This tour can be planned to fa-

cilitate the tourist category of VRUs, which imposes

transportation restrictions. The future steps can in-

ICORES 2023 - 12th International Conference on Operations Research and Enterprise Systems

volve a more in-depth sensitive analysis on the param-

eters chosen in the model, and the possibility to ex-

tend the experiments to other different urban contexts

(larger size cities with more transportation modes).

In this case, the possibility of implementing heuris-

tic algorithms cannot be excluded a priori. Under the

mathematical perspective, other variants of the opti-

mization model can be investigated by considering

multitrip, time-dependent travel times and the vari-

ability of the visit duration (dependent of the crowd-

ing level of the visited POIs). Under the managerial

perspective, further studies can be devoted to evalu-

ate the scalability of the proposed model in a regional

context, in which a tourist likes moving between POIs

in different cities using long-distance transportation

modes (bus, train, private car) and where discour-

aging the use of private cars has a stronger impact

on the CO

emission levels. Finally, speciﬁc studies

can be addressed to the tourist trip design for VRUs

with particular disabilities (for example, people in

wheelchairs or with low vision) who need to access to

POIs, and to transportation modes with speciﬁc fea-

tures.

REFERENCES

Abbaspour, R. and Samadzadegan, F. (2009). Itinerary

planning in multimodal urban transportation network.

J Appl Sci, 9(10):1898–1906.

Alonso-Mu

noz, S., Torrej

on-Ramos, M., Medina-Salgado,

M., and Gonz

alez-S

anchez, R. (2022). Sustainabil-

ity as a building block for tourism – future research:

tourism agenda 2030. Tourism Review.

Archetti, C., Speranza, M., and Vigo, D. (2014). Vehicle

routing problems with proﬁts. Vehicle Routing: Prob-

lems, Methods and Applications. SIAM, pages 273–

296.

Ardito, L., Cerchione, R., Del Vecchio, P., and Raguseo, E.

(2019). Big data in smart tourism: challenges, issues

and opportunities. Curr. Issues Tour., 22.

Awerbuch, B., Azar, Y., Blum, A., and Vempala, S. (1998).

New approximation guarantees for minimum-weight

k-trees and prize-collecting salesmen. SIAM Journal

on Computing, 28:254–262.

Butt, S. and Cavalier, T. (1994). A heuristic for the multi-

ple tour maximum collection problem,. Computers &

Operations Research, 21:101–111.

Castillo, L., Armengol, E., Onaind

ıa, E., Sebastia, L.,

Gonzalez-Boticario, J., Rodr

ıguez, A., Fernandez, S.,

Arias, J., and Borrajo, D. (2008). Samap: an user-

oriented adaptive system for planning tourist visits.

Expert Syst Appl, 34(2):1318–1322.

Collette, Y. and Siarry, P. (2003). Multiobjective Optimiza-

tion. Principles and Case Studies.

Darko, J., Folsom, L., Pugh, N., Park, H., Shirzad, K.,

Owens, J., and Miller, A. (2022). Adaptive personal-

ized routing for vulnerable road users. IET Intelligent

Transport Systems, WILEY., 16.

De Maio, A., Fersini, E., Messina, E., Santoro, F., and Anto-

nio Violi, A. (2020). Exploiting social data for tourism

management: the smartcal project. Quality and Quan-

tity.

Divsalar, G., Ali Divsalar, A., Jabbarzadeh, A., and Sahebi,

H. (2022). An optimization approach for green tourist

trip design. Soft Computing, 26:303–4332.

Fakfare, P. and Wattanacharoensil, W. (2022). Low-

carbon tourism: determining domestic tourist percep-

tion from thailand: Tourism agenda 2030. Tourism

Review.

Gavalas, D., Konstantopoulos, C., Mastakas, K., and

Pantziou, G. (2014). A survey on algorithmic ap-

proaches for solving tourist trip design problems. J

Heuristics., 20(3):291–328.

Geem, Z. W., Tseng, C. L., and Park, Y. (2005). Harmony

search for generalized ori- enteering problem: best

touring in china. In L. Wang, K. Chen and Y.S.Ong

(Eds.), Advances in natural computation. Lecture

Notes in Computer Science, Springer., 3612:741–750.

Golden, B., Levy, L., and Vohra, R. (1987). The orienteer-

ing problem. Naval Research Logistics, 34:307–318.

Gunawan, A., Lau, H., and Vansteenwegen, P. (2016). Ori-

enteering problem: A survey of recent variants, solu-

tion approaches and applications. European Journal

of Operational Research, 255:315–332.

Huang, T., Gong, Y., Zhang, Y., Zhan, Z., and Zhang, J.

(2019). Automatic planning of multiple itineraries: a

niching genetic evolution approach. IEEE Trans Intell

Transp Syst, 21(10):4225–4240.

Ilhan, T., Iravani, S. M. R., and Daskin, M. (2008). The ori-

enteering problem with stochastic proﬁts. IIE Trans-

actions, 40(4):406–421.

Kontogianni, A., Kabassi, K., Virvou, M., and Alepis, E.

(2018). Smart tourism through social network user

modeling: a literature review. 2018 9th International

Conference on Information, Intelligence, Systems and

Applications (IISA). IEEE.

Labadie, N., Mansini, R., Melechovsky, J., and

Wolﬂer Calvo, R. (2012). The team orienteer-

ing problem with time windows: an lp-based granular

variable neighborhood search. European Journal of

Operational Research, 220(1):15–17.

Laporte, G. and Martello, S. (1990). The selective travel-

ling salesman problem. Discrete Applied Mathemat-

ics, 26:193–207.

Lim, K., Chan, J., Leckie, C., and Karunasekera, S. (2017).

Personalized trip recommendation for tourists based

on user interests, points of interest visit durations and

visit recency. Knowl Inf Syst, 54(2):375–406.

Massidda, C. and Mattana, P. (2013). A svecm analysis

of the relationship between international tourism ar-

rivals, gdp and trade in italy. Journal of Travel Re-

search, 52(1).

Methorst, R. (2002). Vulnerable road users: new ap-

proaches needed. In: 15th ICTCT Workshop, Trans-

port Research Centre, Rotterdam.

The Green Tourist Trip Design Problem with Time Windows: A Model Application on a Urban Scale

Oxley, J., Langford, J., and Charlton, J. (2010). The safe

mobility of older drivers: a challenge for urban road

designers. Journal of Transport Geography. Special

issue: The mobility of older people., 18(5):642–648.

Pessoa, A., Poggi, M., and Uchoa, E. (2009). A ro-

bust branch-cut-and-price algo- rithm for the hetero-

geneous ﬂeet vehicle routing problem. Networks,

54(4):167–177.

Ruiz-Meza, J. and Montoya-Torres, J. (2022). A systematic

literature review for the tourist trip design problem:

Extensions, solution techniques and future research

lines. Operations Research Perspectives, 9:100228.

Scholliers, J., van Sambeek, M., and Moerman, K. (2017).

Integration of vulnerable road users in cooperative its

systems. Eur. Transp. Res. Rev., 9(15).

Umurzakov, U., Tosheva, S., and Salahodjaev, R. (2022).

Tourism and sustainable economic development: Evi-

dence from belt and road countries. J Knowl Econ.

Verbeeck, C., S

orensen, K., Aghezzaf, E. H., and Vansteen-

wegen, P. (2014). A fast solution method for the time-

dependent orienteering problem. European Journal of

Operational Research, 236(2):419–432.

Zheng, W., Ji, H., Lin, C., Wang, W., and Yu, B. (2020). Us-

ing a heuristic approach to design personalized urban

tourism itineraries with hotel selection. Tour Manag,

76(422):103956.

Zheng, W. and Liao, Z. (2019). Using a heuristic approach

to design personalized tour routes for heterogeneous

tourist groups. Tour Manag, 72(555):313–325.

ICORES 2023 - 12th International Conference on Operations Research and Enterprise Systems