Point to Segment Distance DTW for Online Handwriting Signals

Matching

Elmokhtar Mohamed Moussa

1,2

, Thibault Lelore

1 a

and Harold Mouch

ere

2 b

MyScript SAS, Nantes, France

Nantes Universit

e, Ecole Centrale Nantes, CNRS, LS2N, UMR 6004, F-44000 Nantes, France

Keywords:

Handwriting Matching, DTW Metric, Sampling Invariance.

Abstract:

In this paper, we propose DTW

seg

, a modiﬁed DTW algorithm based on a point-to-segment distance instead

of the euclidean point-to-point distance. Applying DTW

seg

to online handwriting matching proves to be ad-

vantageous compared to other algorithms as it is less sensitive to differences between signals sampling rates

occurring due to acquisition frequencies or handwriting speed. It eliminates the need for a commonly prac-

ticed resampling that omits an important dynamic part of the ductus. Experiments on IRONOFF french words

dataset and FLOWCHARTS dataset show DTW

seg

to be least impacted by sampling rate alterations. We also

propose a new benchmark of state-of-the-art methods on ofﬂine handwriting to online conversion based on

our new proposed metric.

1 INTRODUCTION

Pen and paper have been used for hundreds of years

by humans to record their activities, ideas, cre-

ations. . . The digitization and processing of docu-

ments have changed their usage: historians can access

ancient material easily, and companies created Elec-

tronic Document Management Systems to improve

their process. These images of documents are called

ofﬂine documents. In recent years, with the emer-

gence of digital tablets and touch screens, new us-

ages appear and new types of documents are created

with handwritten digital content: online documents.

Online documents and ofﬂine documents share the

same downstream processing task: document classiﬁ-

cation, document segmentation, handwriting recogni-

tion, and writer identiﬁcation, etc. but often with dif-

ferent approaches due to the different nature of their

respective input source. On the one hand, ofﬂine con-

tent is stored as matrices of pixels and on the other

hand, online documents are recorded as the pen tra-

jectory on a surface tablet represented as a time series

of x and y coordinates, in addition to other motion

measures (pen pressure, velocity, etc.).

This work focuses on the comparison of hand-

written samples of the online domain. It is useful

for many applications including handwriting trajec-

https://orcid.org/0000-0002-7083-2422

https://orcid.org/0000-0001-6220-7216

tory reconstruction from IMU-enhanced pen (Wehbi

et al., 2022) where synchronization between the pen

and recording tablet surface is challenging due to the

difference in sampling rates and acquisition start and

end. Other applications include signature veriﬁca-

tion (Sharma and Sundaram, 2018), template match-

ing for content clustering, keyword (or shape) spot-

ting (Szoke et al., 2005), and due to recent advances

in research topics such as online handwriting synthe-

sis (Graves, 2014), ofﬂine handwriting to online con-

version (Kato and Yasuhara, 2000), the need for perti-

nent online handwriting quality evaluation metrics of

the generated online handwriting is becoming more

acute. Matching of two online signals is commonly

done using linear interpolation alignment which de-

teriorates important temporal and spatial dynamics.

DTW (Sakoe and Chiba, 1978) algorithm provide an

elastic alignment capable of matching signals of dif-

ferent lengths. However, in our handwriting-speciﬁc

case, it can portray a very negative matching for hand-

writing with similar directions and spatial arrange-

ments as in Figure 1. We propose a new cost function

based on the segment-to-point distance to compute

DTW. It has the advantage to minimize the impact of

the sampling rate. Our modiﬁed DTW is presented in

Section 3. In Section 4, we experiment and compare

our metric to classic DTW on different datasets and

state-of-the-art ofﬂine handwriting to online conver-

sion approaches.

850

Mohamed Moussa, E., Lelore, T. and Mouchère, H.

Point to Segment Distance DTW for Online Handwriting Signals Matching.

DOI: 10.5220/0011672600003411

In Proceedings of the 12th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2023), pages 850-855

ISBN: 978-989-758-626-2; ISSN: 2184-4313

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

(a) Query and reference online signals. Notice the sampling

rate variation between the two.

(b) On the left linear alignment RMSE = 0.53 which require

a spatial resampling of both signal and on the right DTW

alignment total 1.65, without resampling.

cost of 0.25, without resampling.

Figure 1: Comparison between classic online handwrit-

ing alignment methods and the proposed DTW segment

method.DTW

seg

alignment is observed to best match the

query to the reference signal.

2 RELATED WORKS

DTW has been used in a wide range of document

analysis applications. Here we focus on recent hand-

writing analysis subtopics: online handwriting syn-

thesis and ofﬂine to online conversion. Other no-

table, applications such as isolated character recog-

nition (Bahlmann et al., 2002) can also be cited.

2.1 Online Handwriting Synthesis

This aims to generate the handwriting of a given text

with neural networks (Graves, 2014). The generation

is usually conditioned on a given writer and outputs

convincing handwriting regarding the writing style,

making online handwritten documents easily editable

(Aksan et al., 2018). Matching the neural network

predictions to ground truth online signals is essen-

tial to train such deep learning approaches. The MSE

loss is ubiquitous in state-of-the-art methods, imply-

ing that the neural network has also to learn the exact

correct sampling rate of the resampled ground truth

signal, creating small misleading artifacts in many

cases. Deﬁning a loss function with more meaning-

ful feedback on the general ductus rather than sam-

pling rate artifact can help further improve the gen-

erative models. Following that line, (Ji and Chen,

2020) employed a CNN-LSTM discriminator com-

bined with Graves Generator (Graves, 2014) in an ad-

versarial training framework to obtain more realistic

handwriting.

2.2 Ofﬂine Conversion to Online

Handwriting

Given a static ofﬂine handwritten document, the goal

here is to recover the temporal information of the pen

trajectory and thus an online document. This could

be used mainly for two reasons: use the existing on-

line tool as a recognizer; or allow the user to edit his

content as a vectorized image (instead of a ﬂat im-

age). The retrieved trajectory should be as faithful as

possible to the writer’s ofﬂine document. Such sys-

tems (Chan, 2020) are often evaluated using word er-

ror rate when intended for ofﬂine recognition. WER

presents a useful insight into the semantic coherence

of online reconstruction. However it presents a ma-

jor drawback, depending on the complexity of the

recognition systems, the correct word can be recog-

nized even if online reconstruction is unfaithful e.g.

slanting and rotation don’t usually affect recogniz-

ers. Root Mean Square Error (RMSE) and Dynamic

Time Warping algorithm (DTW) (Sakoe and Chiba,

1978) are commonly proposed as evaluation metrics

Point to Segment Distance DTW for Online Handwriting Signals Matching

851

(Hassa

ıne et al., 2013; Phan et al., 2015; Dinh et al.,

2016; Archibald et al., 2021; Mohamed Moussa et al.,

2021; Diaz et al., 2022) of the reconstructed online

signal w.r.t. to the ground-truth online signal. RMSE

(cf. equation 1) is a one-to-one mapping that mea-

sures the distance between two temporal signals x

and ˆx

of lengths N and M respectively. If N = M

and the signals are well aligned (same frequency and

in phase) RMSE is a straightforward measure of the

distance between them. Nevertheless, in many cases

where the signals are not perfectly aligned (stretched

or compressed at different time windows, out of phase

etc.) the pairing becomes far less obvious.

RMSE =

∑

t=1

− ˆx

)

(1)

3 PROPOSED METRIC

We ﬁrst present the classical DTW and then our pro-

posed DTW-seg.

3.1 DTW

DTW algorithm computes the optimal alignment be-

tween two signals of different lengths. It allows for

elastic one-to-many matching. A cumulative cost

N×M

matrix is constructed using a L2 distance func-

tion f (x

, ˆx

) = ∥x

− ˆx

∥

. DTW algorithm ﬁnd a

warping path w = {w

= (i, j) ∈ N

N×M

}

p=1

mini-

mizing equation 2 and satisfying the following con-

straints:

• boundaries: w

= (1, 1) ∧ w

= (N, M)

• monotonicity: let w

= (i, j) and w

p+1

= (i

′

, j

′

)

then i ≤ i

′

∧ j ≤ j

′

• continuity: i

′

≤ i + 1 ∧ j

′

≤ j + 1

This optimization is solved by recursively updating

the cumulative cost matrix with equation 3.

DTW (x, ˆx) = min

w∈W

(

∑

p=1

f (w

)

f (w

) = f (x

, ˆx

)

(2)

i j

= f (x

, ˆx

) + min







i, j−1

i−1, j−1

i−1, j

(3)

DTW distance is deﬁned as the cumulative cost of w

equal to C

normalized by the warping path length.

Figure 3 shows an example of DTW algorithm output.

In this work, we focus on deﬁning a sampling rate

invariant cost function f .

(a) Accumulated cost matrix and the associated warping path

in red.

(b) Warped time series. The query letter x stroke order is per-

muted compared to the reference and its strokes don’t cross.

Figure 2: DTW algorithm output for two online words.

3.2 DTW-seg

Let x

a point and [ˆx

, ˆx

j+1

] a segment between two

consecutive elements, we deﬁne a point to segment

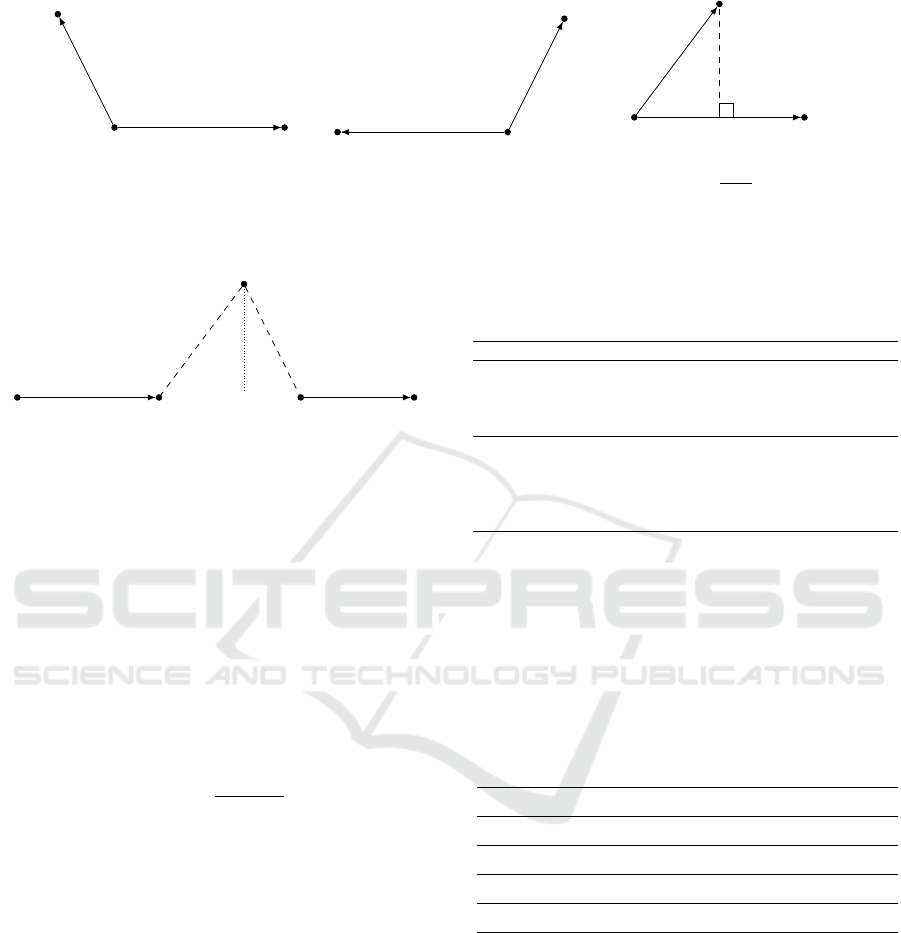
cost function, as illustrated in Figure 3, by:

⃗a =

−−−→

ˆx

j+1

⃗

b =

−→

ˆx

, ⃗c =

−−−→

ˆx

j+1

g(x

,[ ˆx

, ˆx

j+1

]) =











⃗a ·

⃗

b < 0, f (x

, ˆx

)

←−

a ·⃗c < 0, f (x

, ˆx

j+1

)

else,



pro j

⃗a

⃗



(4)

Replacing f by g as a cost function in equations 2

and 3 we deﬁne DTW

seg

which minimizes the align-

ment cost changes w.r.t. variation in the sampling rate.

The special case that needs to be mentioned, as illus-

trated by ﬁgure 4, is that of a point distance to a seg-

ment between a stroke end and the next stroke start. In

this case, the segment is considered invalid and thus

omitted.

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

852

ˆx

j+1

−→

(a)

−→

a ·

−→

b < 0.

ˆx

j+1

←−

−→

(b)

←−

a ·

−→

c < 0.

ˆx

j+1

−→

pro j

−→

a ·

−→

∥

≤ 1

Figure 3: Point to segment distance.

ˆx

j+1

ˆx

j+2

ˆx

j+3

stroke 1 stroke 2

Invalid

Figure 4: Query point x

lays between two reference stroke

extremities ˆx

j+1

and ˆx

j+2

. However, this segment is ig-

nored and x

can either be aligned with valid stroke seg-

ments [ ˆx

, ˆx

j+1

] or [ ˆx

j+2

, ˆx

j+3

4 EXPERIMENTS

To demonstrate the sensitivity to resampling of

RMSE, DTW and our DTW

seg

metric, we experiment

with different spatial resampling strategies:

• Equidistant linear resampling with distance d;

• Simple moving average (SMA) with previous 2

points:

′

+ x

t−1

We used the validation set of IRONOFF (Viard-

Gaudin et al., 1999) containing 19, 888 words and

the FLOWCHARTS (Awal et al., 2011) validation set

with 172 ﬂowcharts. Table 1 shows that DTW

seg

relatively small after oversampling or moving average

transformations compared with classic DTW. The

aforementioned transformations degrade the spatial

information of the signals the least compared to sub-

sampling yet the reported DTW and RMSE are high.

DTW is observed to be the highest when subsampling

IRONOFF with d = 10 in comparison, DTW

seg

is one

and a half folds smaller. For FLOWCHARTS when

subsampling with d = 15, DTW

seg

is 3 folds smaller

than DTW .

In addition, we use our metric to benchmark state-

of-the-art ofﬂine handwriting to online conversion ap-

proaches, namely, (Chan, 2020), (Diaz et al., 2022)

Table 1: Evaluation of different resampling strategies with

DTW and DTW

seg

. Linear spatial interpolation resampling

with distance d ∈ {2,5, 10,15} and SMA: simple moving

average.

Dataset resampling RMSE ↓ DTW ↓ DTW

seg

↓

IRONOFF

d=2 1.19 1.38 0.32

d=5 2.43 1.64 0.76

d=10 4.35 2.87 1.90

SMA 3.01 1.89 0.78

FCs

d=2 29.03 8.04 0.25

d=5 42.43 7.81 0.60

d=10 58.46 7.66 1.29

d=15 72.43 7.73 2.04

SMA 64.99 6.03 1.82

and (Archibald et al., 2021). Using their public of-

ﬁcial implementations. We also include an internal

rule-based method based on a smoothness criterion.

Table 2 shows the results of their evaluations on the

validation set of IRONOFF dataset. Synthetic of-

ﬂine images, with a stroke width randomly chosen

between one and three pixels, are rendered from the

ground truth online. We observe that the three met-

Table 2: Stroke extraction SoTA evaluation on IRONOFF.

Approach DTW ↓ DTW

seg

↓ RMSE ↓

Internal [Private] 5.00 4.40 11.94

(Chan, 2020) 5.64 5.06 12.89

(Archibald et al., 2021) 8.10 7.45 15.77

(Diaz et al., 2022) 22.71 21.81 33.14

rics rank the different approaches in the same man-

ner. All of the previously mentioned approaches pre-

dict oversampled online signals therefore they have a

bigger DTW alignment cost compared to DTW

seg

. In

fact, (Chan, 2020) approach is ranked second, closely

trailing behind our Internal approach. It is to be noted

that (Archibald et al., 2021) is based on a data-driven

CNN-LSTM trained only on English IAM (Marti and

Bunke, 2002) dataset. A ﬁnetuning on the training

set of IRONOFF could have helped the network to

adapt to unseen french words, yielding better results.

No meta-parameters tuning for (Diaz et al., 2022) ap-

Point to Segment Distance DTW for Online Handwriting Signals Matching

853

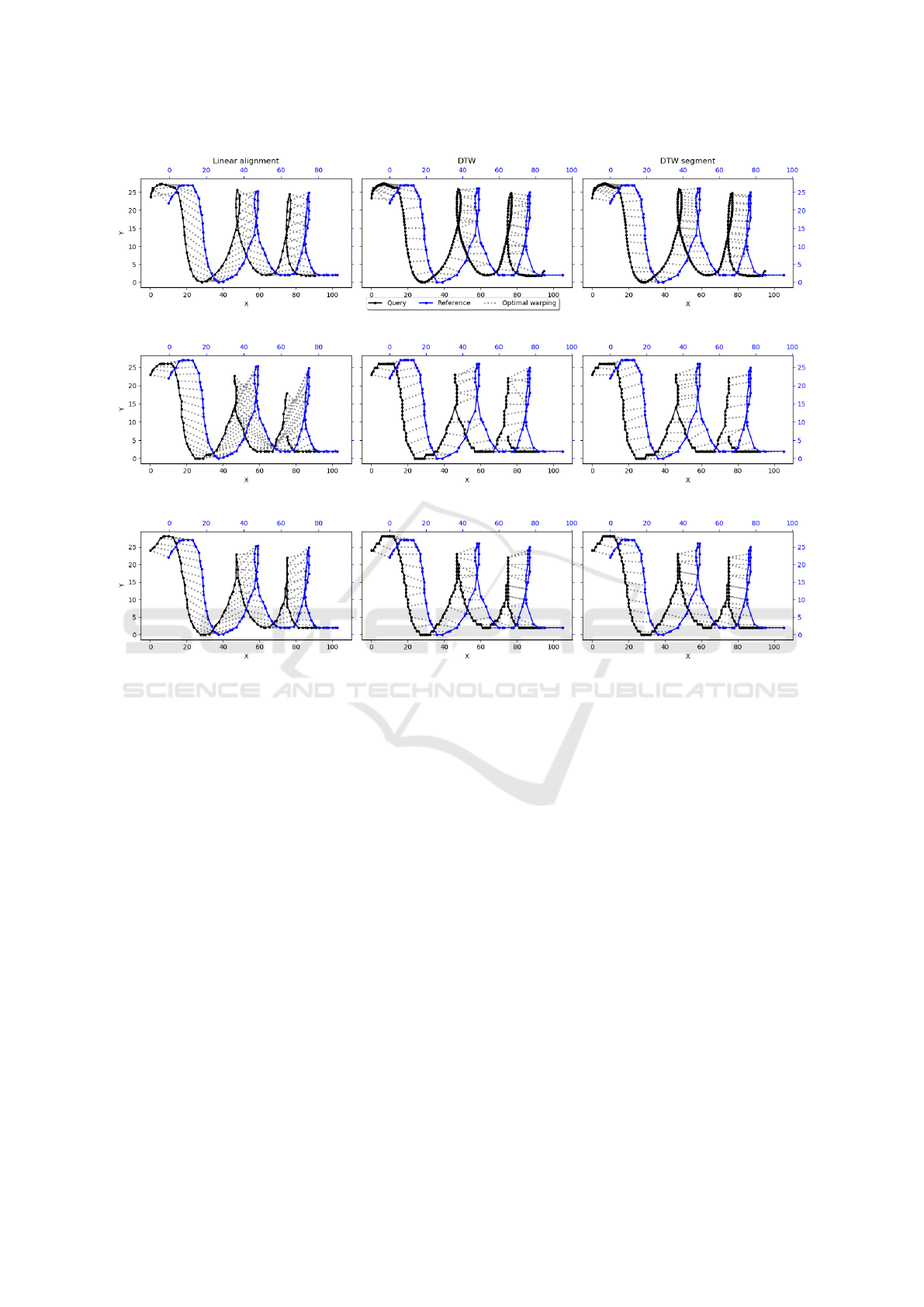
(a) (Archibald et al., 2021). RMSE = 3.09, DTW = 1.08, DTW

seg

= 0.58.

(b) (Chan, 2020). RMSE = 7.32, DTW = 1.88, DTW

seg

= 1.65.

seg

= 1.01.

Figure 5: Comparison of SoTA methods for online signal reconstruction from ofﬂine. Inferences are in black, ground truth is

in blue.

proach was performed for a fairer comparison. Fig-

ure 5 illustrates inference results for different SoTA

approaches. Figure 5a shows that (Archibald et al.,

2021) prediction is overall the best in this particular

instance. In fact, ﬁgures 5c and 5b tend to oversim-

plify small loops, the latter is also missing a portion

of the last small ending. Since all of the mentioned

methods infer oversampled signals, DTW

seg

is shown

to be the metric that best evaluates the inherent sig-

nal directions and spatial arrangement with minimal

regard to sampling frequencies.

5 DISCUSSION

This work focuses on improving the matching of simi-

lar online handwriting signals with different sampling

frequencies. This variability occurs when recording

simultaneously on multiple devices or due to the natu-

ral variance in human writing velocity. Another chal-

lenging extension, which is out of the scope of this pa-

per, is the invariance to stroke direction inversion (e.g.

crossing a t with a left-to-right or right-to-left stroke)

and stroke permutation (e.g. letter x in Figure 2). In

fact, DTW’s strict continuity constraints make it such

that those small handwriting preferences are assigned

a very important alignment cost which can hinder the

performance of downstream tasks. (Archibald et al.,

2021) employs a DTW loss function that ﬁnds the per-

mutation of consecutive pairs of strokes and stroke

direction that minimizes the alignment cost. This ap-

proach does not deal with longer-range permutations

such as crossing or dotting. (Li et al., 2013) proposed

a more complete multi-stroke DTW based on the A*

star algorithm to overcome the combinatorial explo-

sion of alignment hypothesis. However, it is still dif-

ﬁcult to upscale to the word level and beyond.

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

854

6 CONCLUSIONS

In this paper, we presented DTW

seg

, a modiﬁed

DTW algorithm based on a segment-to-point cost

function dedicated to online handwriting matching.

We showed that classical matching approaches such

as RMSE and DTW distance overstate the sam-

pling rate’s importance. DTW

seg

, on the other hand,

matches more closely signals differing in sampling

rates. We also benchmark SoTA for ofﬂine to on-

line conversion with DTW

seg

. In future work, we

will study the deﬁnition of a loss function (Cuturi and

Blondel, 2018) based on DTW

seg

to train a neural net-

work for the ofﬂine to online conversion online task.

We hypothesize that DTW

seg

provides more meaning-

ful information as its gradient pushes the network’s

predictions to be closer to the signal as a whole rather

than a single point from the signal.

REFERENCES

Aksan, E., Pece, F., and Hilliges, O. (2018). DeepWrit-

ing: Making Digital Ink Editable via Deep Generative

Modeling. In Proceedings of the 2018 CHI Confer-

ence on Human Factors in Computing Systems, CHI

’18, pages 1–14, New York, NY, USA. Association

for Computing Machinery.

Archibald, T., Poggemann, M., Chan, A., and Martinez, T.

(2021). TRACE: A Differentiable Approach to Line-

Level Stroke Recovery for Ofﬂine Handwritten Text.

In Llad

os, J., Lopresti, D., and Uchida, S., editors,

Document Analysis and Recognition – ICDAR 2021,

volume 12823, pages 414–429. Springer International

Publishing, Cham.

Awal, A.-M., Feng, G., Mouch

ere, H., and Viard-Gaudin,

C. (2011). First experiments on a new online hand-

written ﬂowchart database. In Agam, G. and Viard-

Gaudin, C., editors, IS&T/SPIE Electronic Imag-

ing, page 78740A, San Francisco Airport, California,

USA.

Bahlmann, C., Haasdonk, B., and Burkhardt, H. (2002).

Online handwriting recognition with support vector

machines - a kernel approach. In Proceedings Eighth

International Workshop on Frontiers in Handwriting

Recognition, pages 49–54.

Chan, C. (2020). Stroke Extraction for Ofﬂine Handwritten

Mathematical Expression Recognition. IEEE Access,

8:61565–61575.

Cuturi, M. and Blondel, M. (2018). Soft-DTW: A Differen-

tiable Loss Function for Time-Series.

Diaz, M., Crispo, G., Parziale, A., Marcelli, A., and Ferrer,

M. A. (2022). Writing Order Recovery in Complex

and Long Static Handwriting. International Journal

of Interactive Multimedia and Artiﬁcial Intelligence,

7(4):171.

Dinh, M., Yang, H.-J., Lee, G.-S., Kim, S.-H., and Do, L.-

N. (2016). Recovery of drawing order from multi-

stroke English handwritten images based on graph

models and ambiguous zone analysis. Expert Systems

with Applications, 64:352–364.

Graves, A. (2014). Generating Sequences With Recurrent

Neural Networks.

Hassa

ıne, A., Al Maadeed, S., and Bouridane, A. (2013).

ICDAR 2013 Competition on Handwriting Stroke Re-

covery from Ofﬂine Data. In 2013 12th International

Conference on Document Analysis and Recognition,

pages 1412–1416.

Ji, B. and Chen, T. (2020). Generative Adversarial Network

for Handwritten Text.

Kato, Y. and Yasuhara, M. (2000). Recovery of drawing

order from single-stroke handwriting images. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 22(9):938–949.

Li, J., Mouchere, H., Viard-Gaudin, C., and Chen, Z.

(2013). A Multi-stroke Dynamic Time Warping Dis-

tance Based on A* Optimization. In 2013 12th In-

ternational Conference on Document Analysis and

Recognition, pages 1330–1334.

Marti, U.-V. and Bunke, H. (2002). The IAM-database:

An English sentence database for ofﬂine handwrit-

ing recognition. International Journal on Document

Analysis and Recognition, 5(1):39–46.

Mohamed Moussa, E., Lelore, T., and Mouch

ere, H. (2021).

Applying End-to-End Trainable Approach on Stroke

Extraction in Handwritten Math Expressions Images.

In Llad

os, J., Lopresti, D., and Uchida, S., editors,

Document Analysis and Recognition – ICDAR 2021,

Lecture Notes in Computer Science, pages 445–458,

Cham. Springer International Publishing.

Phan, D., Na, I.-S., Kim, S.-H., Lee, G.-S., and Yang, H.-J.

(2015). Triangulation Based Skeletonization and Tra-

jectory Recovery for Handwritten Character Patterns.

KSII Transactions on Internet and Information Sys-

tems (TIIS), 9(1):358–377.

Sakoe, H. and Chiba, S. (1978). Dynamic programming

algorithm optimization for spoken word recognition.

IEEE Transactions on Acoustics, Speech, and Signal

Processing, 26(1):43–49.

Sharma, A. and Sundaram, S. (2018). On the Exploration

of Information From the DTW Cost Matrix for Online

Signature Veriﬁcation. IEEE Transactions on Cyber-

netics, 48(2):611–624.

Szoke, I., Schwarz, P., Matejka, P., Burget, L., Karaﬁat, M.,

Fapso, M., and Cernocky, J. (2005). Comparison of

keyword spotting approaches for informal continuous

speech. In Interspeech 2005, pages 633–636. ISCA.

Viard-Gaudin, C., Lallican, P. M., Knerr, S., and Binter, P.

(1999). The IRESTE On/Off (IRONOFF) dual hand-

writing database. In Proceedings of the Fifth Interna-

tional Conference on Document Analysis and Recog-

nition. ICDAR ’99 (Cat. No.PR00318), pages 455–

458.

Wehbi, M., Luge, D., Hamann, T., Barth, J., Kaempf, P.,

Zanca, D., and Eskoﬁer, B. M. (2022). Surface-Free

Multi-Stroke Trajectory Reconstruction and Word

Recognition Using an IMU-Enhanced Digital Pen.

Sensors, 22(14):5347.

Point to Segment Distance DTW for Online Handwriting Signals Matching

855