Unsupervised Tree Detection and Counting via Region-Based Circle

Fitting

Smaragda Markaki

and Costas Panagiotakis

Department of Management Science and Technology, Hellenic Mediterranean University, Agios Nikolaos, 72100, Greece

Keywords:

Remote Sensing, Tree Detection, Tree Counting, Circle Fitting, Vegetation Index, UAV Images, AIC.

Abstract:

Automatic tree detection and counting is a very important task for many areas such as environmental protec-

tion, agricultural planning, crop yield estimation and monitoring of replanted forest areas. This paper presents

an unsupervised method for tree detection from high resolution UAV imagery based on a modiﬁed version of

the Decremental Ellipse Fitting Algorithm DEFA. The proposed Decremental Circle Fitting Algorithm (DCFA)

works similarly to DEFA with the main difference that DCFA uses circles instead of ellipses. According to

DCFA, the skeleton of the 2D shape is calculated ﬁrst, followed by the initialization of the circle hypotheses

and the application of the Gaussian Mixture Model Expectation Maximization algorithm. Finally, model eval-

uation is performed based on the Akaike Information Criterion. The DCFA method was tested on the Acacia-6

dataset, which depicts six months acacia trees, collected with Unmanned Aerial Vehicles in Southeast Asia

and it exhibits high performance compared with the state-of-the art unsupervised and supervised methods.

1 INTRODUCTION

Automatic tree detection and counting is a very im-

portant task for many areas such as environmental

protection, agricultural planning, crop yield estima-

tion and monitoring of replanted forest areas. The dif-

ferent characteristics of various species of trees also

make it a challenge. However, with the increasing

availability of remote sensing data with high and very

high spatial resolution, we are now able to collect in-

formation at the level of individual trees. Especially,

nowadays, Unmanned Aerial Vehicle (UAV) has be-

come a promising tool for tree detection due to its

high spatial resolution and low cost. The majority of

the studies use high-resolution aerial or satellite im-

agery or LiDAR data from a relatively open forest,

such as oil palms, olive trees, and fruit trees (Osco

et al., 2020; Salam

ı et al., 2019). Numerous unsu-

pervised methods, based on the spectral and textural

features of high-resolution imagery or the elevation

features of the Li-DAR data were developed for tree

detection. Recently, Deep Learning based algorithms

have an increasing potential in developing an auto-

mated approach to tree detection and counting with

excellent performance.

Unsupervised tree detection methods are based

https://orcid.org/0000-0002-9821-7499

https://orcid.org/0000-0003-3680-7087

on the spectral and textural characteristics of high-

resolution imagery or the altitude factor of LIDAR

data. Numerous methods, such as watershed seg-

mentation (Chen et al., 2006), region growing (Erik-

son, 2003), polynomial ﬁtting (Wu et al., 2019), dis-

tance discriminant clustering (Li et al., 2012), adap-

tive mean shift (Yan et al., 2020), template matching

(Vibha et al., 2009), and object-oriented image seg-

mentation (Qiu et al., 2020) are developed to detect

individual trees (Duncanson et al., 2014). Recently,

deep learning based algorithms show an increasing

potential in developing automated approaches to tree

detection and counting with excellent performance.

In this paper, the problem of unsupervised tree

detection is studied, since this is still an open prob-

lem available for further research and in which the

scientiﬁc community shows great interest. The pro-

posed method, called Decremental Circle Fitting Al-

gorithm (DCFA), is a modiﬁed and simpliﬁed version

of the Decremental Ellipse Fitting Algorithm (DEFA)

presented by (Panagiotakis and Argyros, 2016). In

(Panagiotakis and Argyros, 2016), an augmentative

approach AEFA (Augmentative Ellipse Fitting Algo-

rithm) has been also proposed and compared with

DEFA. DEFA outperforms AEFA especially for mid-

dle and high complexity shapes. The goal of DEFA

is to represent a given 2D shape with an automati-

cally determined number of ellipses such that the to-

tal area covered by the ellipses is equal to the area of

Markaki, S. and Panagiotakis, C.

Unsupervised Tree Detection and Counting via Region-Based Circle Fitting.

DOI: 10.5220/0011672700003411

In Proceedings of the 12th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2023), pages 95-106

ISBN: 978-989-758-626-2; ISSN: 2184-4313

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

100 200 300 400 500

100

200

300

400

500

(a)

100 200 300 400 500

100

200

300

400

500

0.1

0.2

0.3

0.4

0.5

(b)

100 200 300 400 500

100

200

300

400

500

(c)

100 200 300 400 500

100

200

300

400

500

(d)

Figure 1: An example of execution of the proposed framework. (a) Original image. (b) RGBVI image (c) Binary image (d)

Tree Detection.

the original shape, without any assumptions or prior

knowledge about the object structure. The ﬁrst step,

is the creation of the 2D shape’s skeleton. DEFA

starts with a large number of ellipses deﬁned automat-

ically (complex model) and eliminates them gradually

(model simpliﬁcation). Different solutions involv-

ing different numbers of ellipses are evaluated based

on the Akaike Information Criterion (AIC) (Akaike,

1974). Similarly, the goal of DCFA is to represent

a given 2D shape with an automatically determined

number of circles having the same constraints and

steps as DEFA. Figure 1 depicts an example of the

execution of the proposed framework and its interme-

diate results. The input of DCFA is a binary image

(see Fig. 1(c)) that is computed using the vegetation

index image (see Fig. 1(b)) of the given aerial image

(see Fig. 1(a)).

In (Panagiotakis and Argyros, 2016), DEFA has

been applied on more than 4,000 2D shapes showing

its effectiveness on a variety of shapes, shape transfor-

mations, noise models and noise contamination lev-

els. DEFA has also been successfully applied in the

problem of cell segmentation and counting (Panagio-

takis and Argyros, 2018; Panagiotakis and Argyros,

2020). In (Panagiotakis and Argyros, 2018), the ap-

plication of DEFA provides good performance results

on segmentation and counting of cell nuclei. Better

results on segmentation of touching-overlapping cells

were achieved in (Panagiotakis and Argyros, 2020),

by using an extension of the existing method via ﬁt-

ting of overlapping ellipses. Experimental results

demonstrated the effectiveness of DEFA in segment-

ing potentially overlapping cells.

On the tree detection problem, due to the fact that

trees have a circular shape, the modiﬁcation of ellipse

ﬁtting to circle ﬁtting provides more robust results.

It holds that if two or more trees are connected in

the binary image (same detected object), then ellipse

ﬁtting DEFA may provide lower AIC using less el-

lipses (under-segmentation) or higher number of el-

lipses (over-segmentation) than the true number of

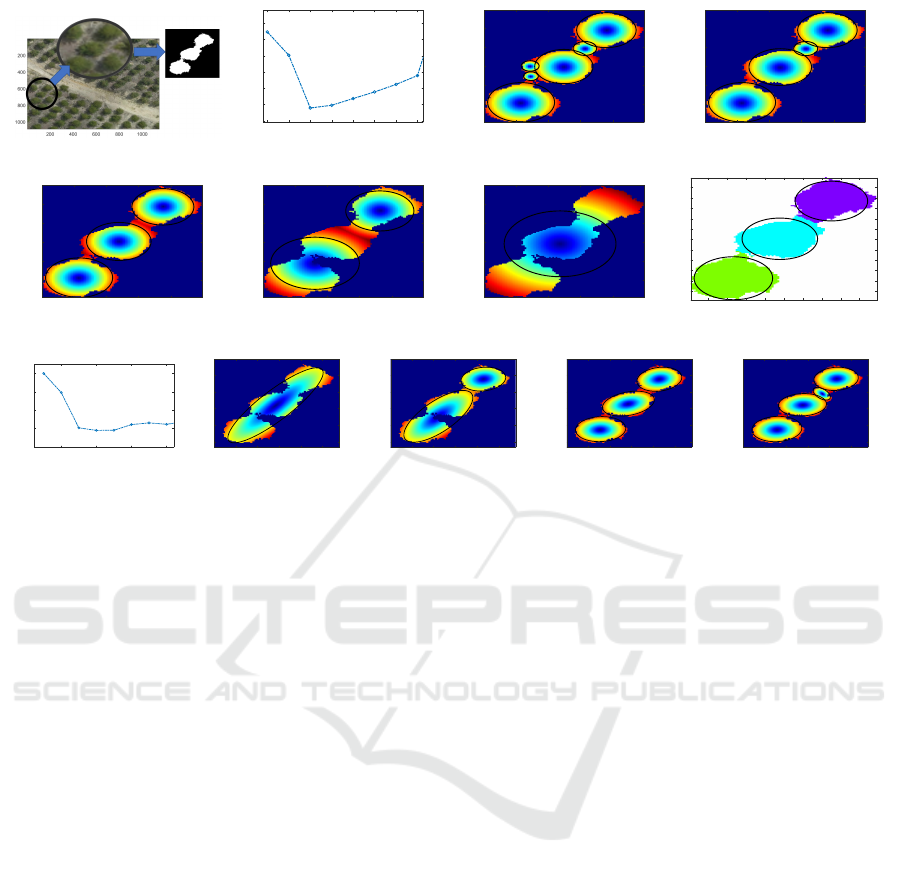
trees. Such typical example is depicted in Fig. 2. In

this example, when DEFA is used, AIC is minimized

using four ellipses resulting over-segmentation (see

Fig. 2(i)). Additionally, the global minima of AIC

under DEFA is not so clear. On the other side, under

DCFA, it holds that AIC is clearly minimized under

the true number of trees (see Fig. 2(b)). Additionally,

according to our experimental results, due to the sim-

pliﬁed model of circle, that requires less computations

than ellipse model, DCFA is 40% faster than DEFA on

tree detection problem. Detailed experimental results

and comparisons of DCFA and DEFA are also pro-

vided in Section 4.

The main contribution of this work is the develop-

ment of a fully unsupervised method for tree detection

from high resolution UAV imagery which exhibits

high performance compared with the state-of-the art

unsupervised or supervised methods. Another contri-

bution, is that we show that circle ﬁtting (DCFA) is

more suitable than ellipse ﬁtting (DEFA) on tree de-

tection problem. DCFA has several advantages over

other existing methods:

• DCFA is a parameter free method.

• DCFA is a region-based method, so it is more ro-

bust and tolerant to noise and boundary segmen-

tation errors than boundary-based methods (e.g.

(Khan et al., 2018)).

• DCFA automatically identiﬁes the number of trees

by considering different numbers of circles and

evaluating them based on the AIC.

The remainder of the paper is organized as fol-

lows: Section 2 describes the related work with

emphasis on the unsupervised and supervised tech-

niques. Section 3 discusses the problem formulation

and describes thoroughly the main steps of the DCFA.

Section 4 presents our experimental results. Section

5 presents the summary and conclusion of the paper

followed by our proposals for future research.

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

2 RELATED WORK

2.1 Unsupervised Techniques

A segmentation method for tree canopies in aerial im-

ages based on region growing was presented by (Erik-

son, 2003). By simultaneously using a decision func-

tion to include or not include a pixel in the spatial do-

main and in the colour domain, the irregular contour

of the tree canopies is preserved in the segmentation

result. In 2004, another approach for automatic ex-

traction of olive trees from satellite images was intro-

duced by (Karantzalos and Argialas, 2004). Their im-

age processing scheme consisted of two steps. Firstly,

enhancement and smoothing of the image take place

using nonlinear diffusion and then extraction of the

local spatial maxima of the Laplacian which leads to

olive tree extraction.

In 2006, (Chen et al., 2006) presented a method

for individual tree canopies detection from LiDAR

data. This method applied marker-driven water-

shed segmentation to isolate individual trees. Tree

canopies were detected by searching for local max-

ima in a canopy maxima model (CMM) with variable

window sizes. Unlike previous methods, the variable

window sizes were determined by the lower bound

of the prediction intervals of the regression curve be-

tween canopy size and tree height. The canopy max-

ima model was developed to reduce commission er-

rors of tree canopy detection. Tree canopies were also

detected based on the fact that they are usually located

in the centre of the crowns.

An algorithm for individual trees segmentation

from the LiDAR point cloud was developed by (Li

et al., 2012). Their algorithm uses a top-down grow-

ing approach that segments trees individually and se-

quentially from the tallest tree to the shortest one. The

method showed good results in segmenting trees from

the LiDAR point cloud in complex mixed conifer

forests in rugged terrain. LiDAR data were also used

by (Duncanson et al., 2014) as well for single tree de-

tection. Their method used a watershed-based delin-

eation of a canopy height model, (CHM), which was

then reﬁned using the LiDAR point cloud.

In 2018, a method of automatic delineation of tree

canopies based on very high-resolution satellite im-

agery, was presented by (Wagner et al., 2018). This

method was applied to a forest with a very hetero-

geneous tropical canopy cover and includes prepro-

cessing, selection of forested pixels, boundary en-

hancement, detection of pixels in the canopy bound-

aries, correction of shadows for large trees and, ﬁ-

nally, canopy segmentation. Another approach for au-

tomatic citrus trees extraction using multispectral im-

agery from UAVs and digital surface models (DSMs)

was proposed in the same year by (Koc-San et al.,

2018). In this method, tree boundaries were extracted

using sequential thresholding, Canny edge detection

and circular Hough transformations. A combination

of object-oriented image segmentation and regression

analysis was proposed by (Rizeei et al., 2018) for oil

palm trees detection and counting using satellite im-

agery and LiDAR data. The Circular Hough Trans-

form CHT method was presented by (Khan et al.,

2018). Their method was unsupervised and it was

consisted of two steps. The ﬁrst step was the prepro-

cessing of the satellite imagery with unsharp mask-

ing followed by enhanced multilevel threshold based

segmentation. Taking advantage of circular geometry,

circular blobs among these segments were ﬁltered out

and counted using the Circular Hough Transform.

In 2019, (Wu et al., 2019) proposed a method

to estimate the canopy cover of a pure Ginkgo

biloba L. planted forest in China. Their method was

consisted of an individual tree segmentation-based

method using LiDAR data, a canopy height model-

based method, and a statistical model method. An-

other automated method for individual tree detec-

tion was presented by (Marques et al., 2019). Their

method was based on the calculation of vegetation

indices using visible (RGB) and near-infrared (NIR)

bands combined with the tree canopy height model.

2.2 Supervised Techniques

In recent years, Deep Learning based algorithms have

shown increasing potential for developing automated

approaches to tree detection and counting with ex-

cellent performance. A Multi-level Attention Do-

main Adaptation Network for oil palm tree detection

and counting was developed by (Zheng et al., 2020).

They used a classiﬁcation method with various post-

processing steps. Semantic segmentation is used to

classify image regions into distinct groups based on

their content. The Fully Convolutional Network FCN

(Long et al., 2015), SegNet (Badrinarayanan et al.,

2017), Unet (Ronneberger et al., 2015), Deeplab

(Chen et al., 2017), and PSPNet (Chen et al., 2017)

are commonly used networks. Yao et al. (Yao et al.,

2021) used four networks, including CNNs and FCNs,

for tree counting. They reported that the encoder-

decoder FCNs showed better results than the CNNs.

A similar study was conducted by (Tong et al., 2021).

Their Point-Wise Supervised Segmentation Network

PWSSN is able to complete the detection and create a

mask for each tree.

Semantic segmentation cannot separate individual

objects from the same category. However, object de-

Unsupervised Tree Detection and Counting via Region-Based Circle Fitting

(a)

1 2 3 4 5 6 7 8

-70

-60

-50

-40

-30

-20

-10

AIC - DCFA

(b)

20 40 60 80

100

20 40 60 80

100

(d) a = 90.5%

20 40 60 80

100

(e) a = 89.3%

20 40 60 80

100

(f) a = 68.7%

20 40 60 80

100

(g) a = 44.8%

10 20 30 40 50 60 70 80 90

100

110

(h)

2 4 6 8

-100

-90

-80

-70

-60

AIC - DEFA

(i)

20 40 60 80 100

100

(j) a = 81.0%

20 40 60 80 100

100

(k) a = 86.3%

20 40 60 80 100

100

(l) a = 92.2%

20 40 60 80 100

100

(m) a = 92.9%

Figure 2: (a) Original image and the binary object that is given to the DCFA as input. (b) the AIC criterion for different values

of circles. (c)-(g) The intermediate solutions proposed by DCFA using 6, 4, 3, 2 and 1 circles. Captions show the estimated

values of shape coverage. (h) The association of pixels to three circles which is the ﬁnal solution estimated by DCFA. (i) The

AIC criterion for different values of ellipses DEFA. (j)-(m) The intermediate solutions proposed by DEFA using 1, 2, 3, 4

ellipses. Captions show the estimated values of shape coverage a.

tection is able to recognise each object in the input

image and categorize it accordingly. A bounding box

can be used for the individual object detection. Com-

mon algorithms include Region-based Convolutional

Neural Networks RCNNs (Girshick et al., 2014), SPP-

Net (He et al., 2015), and Fast RCNNs (Ren et al.,

2015). These methods consist of two steps. First, the

proposed areas are deﬁned, and then, the bounding

box is created and the categorization is performed.

A DeepForest network for detecting individual trees

was proposed by (Weinstein et al., 2020). A deep-

learning method for palm trees detection and counting

on aerial geotagged imagery was proposed by (Am-

mar et al., 2021). Their method involved three object

detection networks. However, the tree canopies could

not be delineated.

Instance segmentation is a combination of seman-

tic segmentation and object detection and it is able to

detect objects and demarcating their boundaries (He

et al., 2017). Instance segmentation is used for count-

ing trees by demarcating their canopies. A Mask R-

CNN model and feature pyramid network FPN were

used by (Ocer et al., 2020) for tree extraction from

high-resolution UAV data with different scales and

tree contents.

In 2019, a deep learning approach to predict and

count oil palm trees in satellite imagery was presented

by (Mubin et al., 2019). The proposed method con-

sisted of two different convolutional neural networks

CNNs to detect young and mature oil palm trees and

GIS during data processing and result storage. A

method for detecting diseased pinus trees that com-

bines deep convolutional neural networks DCNNs,

deep convolutional generative adversarial networks

DCGANs, and an AdaBoost classiﬁer was presented

by (Hu et al., 2020). A convolutional neural network

CNN approach for citrus tree counting from multi-

spectral UAV imagery was presented by (Osco et al.,

2020). The method estimates a dense map with the

certainty that every pixel contains a tree. A mask

region-based convolutional neural network Mask R-

CNN for detecting discontinuous canopy and height

of Chinese ﬁr was presented by (Hao et al., 2021).

In 2022, a deep-learning method based on in-

stance segmentation for tree counting was developed

by (Sun et al., 2022). They used the cascade mask

regions with convolutional neural networks CMask

R-CNN and added three types of attention modules

to build the derivatives of CMask R-CNN. A deep

learning model for detecting and counting olive trees

on satellite images was proposed by (Abozeid et al.,

2022). The proposed SwinTUnet model is a Unet-like

network consisting of an encoder, a decoder, and skip

connections. The Swin Transformer block is the basic

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

unit of SwinTUnet to learn local and global semantic

information.

3 TREE DETECTION AND

COUNTING

In this Section, we present the Decremental Circle

Fitting Algorithm (DCFA) for unsupervised tree de-

tection and counting based on a modiﬁed version of

the Decremental Ellipse Fitting Algorithm (DEFA)

(Panagiotakis and Argyros, 2016). The main differ-

ence with DEFA is that the proposed method DCFA

approximates an arbitrary 2D shape with a number of

circles instead of ellipses. DCFA is simpler and faster

(40% according to our experiments) than DEFA due

to the simpliﬁed model of circle, that requires the es-

timation of three parameters, instead of ﬁve parame-

ters model of ellipse. The input to DCFA is a binary

image representing the shape to be modelled by cir-

cles. DCFA starts with an automatically deﬁned, large

number of circles (complex model) and progressively

eliminates some of them (model simpliﬁcation). Dif-

ferent models are evaluated based on the AIC.

3.1 Problem Formulation of Circle

Fitting

Similarly with the problem formulation of ellipse ﬁt-

ting presented in (Panagiotakis and Argyros, 2016),

hereafter we present the proposed problem formula-

tion of circle ﬁtting so that the total area covered by

the circles is equal to the area of the original shape

without any assumption or prior knowledge about the

object structure (Equal Area Constraint).

We assume a binary image I that represents a 2D

shape. A pixel p of I belongs either to the foreground

FG (I(p) = 1) or to the background BG (I(p) = 0).

The area A of the 2D shape is given by

A =

∑

p∈FG

I(p) (1)

We also assume a set C of k circles C

, each with

an individual area

. A binary image U

is also

deﬁned such that U

(p) = 1 at points p that are inside

any of the circles C

∈ C and U

(p) = 0, otherwise.

Then, we deﬁne the coverage α(C) of the 2D shape

by the given set of circles C as:

α(C) =

∑

p∈FG

I(p) ·U

(p) (2)

In essence, α(C) is the percentage of 2D shape

points that are below some of the circles in C. Let

denote the sum of the areas of all circles

∑

i=1

(3)

The problem of Maximum Coverage MAX-α

amounts to computing the parameters of a set C

∗

k circles C

, so that α(C

∗

) as deﬁned in Equation 2 is

maximised, under the constraint that the sum of the

areas of all circles is equal to the area of the 2D shape

(Equal Area Constraint). Formally,

∗

= arg max

α(C) s.t.

= A (4)

According to Equation 4, different models of the

same number of circles can be evaluated. However,

in tree detection problem, the number of circles that

better ﬁt on a segmented object is generally unknown.

Therefore, in this work we have used AIC to evaluate

models with different number of circles (see Section

3.3.3).

3.2 Image Segmentation

We assume a high-resolution UAV aerial image con-

taining a large number of trees. Each tree has no

holes and stands out from its local background with

its green color and round shape.

The ﬁrst step in our approach is to compute the

vegetation index (see Fig. 1(b)). Vegetation indices

maximize sensitivity to vegetation characteristics and

minimize interfering factors such as background soil

reﬂection, directional effects, or atmospheric effects.

Speciﬁcally, we used the red-green-blue vegetation

index RGBVI introduced by (Bendig et al., 2015).

The RGBVI is deﬁned as the normalized difference of

the squared green reﬂectance and the product of blue

and red reﬂectance:

RGBV I =

)

− (R

∗ R

)

+ (R

∗ R

)

(5)

where R

, R

and R

denote the red, blue and green

reﬂectance respectively.

The following step is to create a binary image I

using the Otsu method (Otsu, 1979) and then ﬁll the

holes and reject very low are objects (see Fig. 1(c)).

The binary image I represents a set of 2D shapes to

be modelled by circles. Then for each detected object

(2D shape), DCFA is applied as described below.

3.3 DCFA Algorithm

The DCFA works similarly to DEFA (Panagiotakis

and Argyros, 2016) with the main difference that

DCFA uses circles instead of ellipses. The main steps

Unsupervised Tree Detection and Counting via Region-Based Circle Fitting

Figure 3: The schema of the main steps of the DCFA.

of the DCFA are depicted in Fig. 3 and are explained

thoroughly below:

3.3.1 Initialization of Circle Hypothesis

First, the medial axis (skeleton) S of the 2D shape is

calculated. Then follows the initialization of the circle

hypotheses. DCFA deﬁnes a set CC of circles that are

used as initial circle hypotheses. The centers of these

circles lie on S and their radius is deﬁned by the min-

imum distance of these centers from the contour of

the shape. The circles are considered for inclusion in

CC in decreasing order of radius. Initially, CC = ∅.

Each considered circle is included in CC if its over-

lap with the already selected circles is below a certain

threshold.

3.3.2 Evolution of Circle Hypothesis

The Gaussian Mixture Model Expectation Maximiza-

tion GMMEM algorithm is responsible for computing

the parameters of a ﬁxed number k of circles in C with

the best coverage α(C) of the given 2D shape. This

is achieved by the repeated application of two steps.

The assignment of the shape points to the circles and

the estimation of the circle parameters.

3.3.3 Solving for the Optimal Number of Circles

Different models (i.e., solutions with different num-

bers of circles) are evaluated based on the AIC crite-

rion (see Eq. 6), which weighs the trade off between

model complexity and approximation error. The AIC-

based model selection criterion amounts to minimiz-

ing the following quantity for all possible numbers of

circles, k:

AIC(C) = SC · ln(1 − α(C)) + 2 · k (6)

where SC denotes a shape complexity measure (SC)

deﬁned in (Panagiotakis and Argyros, 2016). SC is

calculated based on the radius of the circles centered

on and maximally inscribed in the 2D skeleton of the

shape. Intuitively, this attains a good balance between

the increased shape coverage achieved when more cir-

cles are used to approximate a particular shape and the

associated increased complexity of that model (due to

the increase in the number of circles used).

To minimize the AIC criterion, DCFA reduces the

number of circles considered starting from a large,

automatically deﬁned set (the set CC of circles de-

ﬁned in the initialization step). Since there is no lower

bound on the AIC as the number of circles decreases,

this process continues until the set of all circles con-

tains a single circle. In each iteration (each candidate

number of circles from

down to 1), a pair of cir-

cles is selected as candidates for merging. The pair

that is ﬁnally merged is the one that gives the lowest

AIC. Of all possible models (with a minimum of 1 to a

maximum of

circles), the one with the minimum

AIC is ﬁnally reported.

Figure 2 illustrates an example run of DCFA. The

colour-map of Figure 2(c)–2(g) corresponds to the

distance of foreground pixels from the center of the

circles introduced so far (cold and warm colours de-

note small and large distances, respectively). As

shown in Fig. 2(c) and 2(d), the circles that are lo-

cated in the most over-segmented regions are selected

so as to maximise the expected coverage. Figure 2(b)

shows the AIC criterion for different values of circles.

The solution with three circles clearly minimizes AIC.

Figure 2(e) and 2(h) shows the ﬁnal solution and the

clustering of pixels, respectively.

4 EXPERIMENTAL EVALUATION

4.1 Dataset

For the assessment of the proposed methodology we

used the Acacia-6 dataset introduced by (Tong et al.,

2021). The dataset was created by Unmanned Aerial

Vehicles in an area covered by acacia trees in South-

east Asia. The size and morphological characteris-

tics of these trees change greatly during the grow-

ing season, resulting in obscurations and overlaps.

Therefore, the Acacia dataset is created with different

months such as 6 and 12 months (Tong et al., 2021).

For this work, the Acacia-6 dataset was used which

contain acacia trees at the age of six months (see Fig.

4). The shape of trees in Acacia-6 is complete, and

there are clear boundaries between objects. In the ex-

periment, we divided the original Acacia-6 image into

247 sub-images of the same size.

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

100

Figure 4: Acacia-6 Dataset (Tong et al., 2021).

4.2 Evaluation Metrics

To evaluate the proposed method, we used the metrics

True Positive Rate (T PR) also knows as Recall, Pre-

cision (Prec) and F

-score (F

). The following equa-

tions are used to deﬁne the above mentioned metrics:

T PR =

T P

T P + FN

(7)

Prec =

T P

T P + FP

(8)

2T P

2T P + FP + FN

(9)

where T P is the value of true positives meaning the

correctly identiﬁed trees, FN is the value of false neg-

atives meaning the number of trees that are not recog-

nized by the algorithm and FP is the value of false

positives meaning the number of tree predictions that

contain no trees.

High precision means that almost every prediction

is a tree, regardless the number of trees that are not

recognized by the algorithm. In contrast, a high recall

means that almost all trees were found, regardless the

number of tree predictions that contain no trees. The

-score is the harmonic mean of precision and recall.

4.3 Baseline Methods

The proposed method is compared with the following

unsupervised methods:

• CHT method proposed by (Khan et al., 2018) is

based on Circular Hough Transform as described

in Section 2.1.

• CHT++ method, an improved version of the

CHT method that reduce false positives of CHT.

The CHT++ method overcomes this drawback by

adding an area constraint that excludes spurious

tree predictions. This is done by removing the de-

tected circles having low the number of pixels that

belong to the binary image I (green area).

• DEFA method proposed by (Panagiotakis and Ar-

gyros, 2016) as described thoroughly in Section

In order to show the robustness of the proposed

method, it is also compared with the following state-

of-the art supervised and weakly supervised methods:

• Point-Wise Supervised Segmentation Network

PWSSN proposed by (Tong et al., 2021) which

was described in Section 2.2.

• Weakly Supervised Deep Detection Network WS-

DDN introduced by (Bilen and Vedaldi, 2016)

which performs simultaneously region selection

and classiﬁcation.

• Proposal Cluster Learning PCL introduced by

(Tang et al., 2018) which generates proposal clus-

ters to learn reﬁned instance classiﬁers by an iter-

ative process.

• Continuation Multiple Instance Learning C-MIL

method presented by (Wan et al., 2019) which

targets alleviating the non-convexity problem

of multiple instance learning using a series of

smoothed loss functions.

4.4 Experimental Results

Tables 1 and 2 summarize the results of the unsu-

pervised and supervised methods, respectively, ob-

tained with the Acacia-6 dataset for the original im-

age. The results of the supervised methods (PWSSN,

WSDDN, PCL and C-MIL) are presented according

to the experimental evaluation of (Tong et al., 2021).

In our experiments, we have also divided the original

Acacia-6 image into 247 sub-images. By dividing the

original image into sub-images we are able to calcu-

late the average scores of the individual scores per im-

age of the 247 sub-images. This is done to perform an

experiment where all images have the same weight in

the metric calculations (equal weight per area). Thus,

Table 3 shows the average values calculated for the

247 sub-images of the Acacia-6 dataset from the indi-

vidual results per image.

As expected Tables 1 and 3 show the same rank-

ing of methods with very little difference between the

results of the original image (see Table 1) and the

average results of the 247 sub-images (see Table 3).

The DCFA method clearly outperforms all the unsu-

pervised methods under any metric. CHT++ ranks

second in terms of F

-score. It ranks third in terms

of the T PR value (but with a very slight difference

Unsupervised Tree Detection and Counting via Region-Based Circle Fitting

101

from the CHT method), however, has a much higher

Prec value. This points to the main drawback of the

CHT method, which is that it leads to many false pos-

itives and low Prec value. The CHT method is sec-

ond in terms of T PR value, but has a very low Prec

value yielding the lowest F

-score over all methods.

The CHT++ method, on the other hand, overcomes

this drawback by adding an area constraint that rejects

false tree predictions, resulting in a higher Prec value.

DEFA is the third top performing method in terms of

-score, that shows the lowest T PR value, while its

Prec value is sufﬁciently high. This shows that DEFA

is not able to identify all trees. Its main disadvantage

is the higher fusion, which means that two adjacent

trees can be identiﬁed as one.

Table 1: Results of the unsupervised methods obtained on

the Acacia -6 dataset for the original image.

Method TPR Prec F1

CHT 0.875 0.556 0.680

CHT++ 0.861 0.853 0.857

DEFA 0.826 0.897 0.860

DCFA 0.876 0.908 0.892

Table 2: Results of the supervised methods and DCFA ob-

tained on the Acacia -6 dataset for the original image.

Method TPR Prec F1

PWSSN 0.975 0.983 0.979

WSDDN 0.702 0.776 0.715

PCL 0.751 0.785 0.773

C-MIL 0.826 0.879 0.868

DCFA 0.876 0.908 0.892

Table 3: Average scores of the unsupervised methods com-

puted over individual scores per image of the 247 sub-

images obtained from the Acacia-6 dataset.

Method TPR Prec F1

CHT 0.870 0.602 0.694

CHT++ 0.861 0.859 0.852

DEFA 0.849 0.889 0.818

DCFA 0.870 0.904 0.883

As it is explained above, the proposed method

clearly outperforms all the unsupervised methods un-

der any metric either in the original image (Table

1) or in the sub-images (Table 3). Between the

supervised methods (see Table 2), PWSSN method

proposed by (Tong et al., 2021) is the top-ranking

method. The proposed method outperforms the rest

of the supervised methods, showing that a fully un-

supervised technique can be compared with super-

vised techniques with satisfactory results. The C-MIL

method ranks third. The PCL and the WSDDN meth-

ods fail to provide satisfactory results.

Figure 5 shows three example results of the DCFA,

the CHT++, and the DEFA methods, respectively,

from the Acacia-6 dataset. In all cases, the proposed

method successfully detects the vast majority of trees

and achieves a higher F

-score value than the other

methods. In most of the cases, the detections of the

DCFA agree with the human intuition. More specif-

ically, Figures 5(a) and 5(b) show that the DCFA

method correctly identiﬁes all trees, and in Figure

5(b) the vast majority of trees are correctly detected.

In these examples, the CHT++ method is second in

terms of F

-score due to lower T PR value especially

in Fig. 5(f). Concerning the DEFA, in some cases fails

to discriminate adjacent trees, since they may be iden-

tiﬁed as one due to used ellipse model. Such cases are

depicted in the bottom right of Fig. 5(g), in the bottom

left of Fig. 5(h) and in the top right of Fig. 5(i).

Figure 6 shows an example of the results of the

CHT and CHT++ methods. As shown, the T PR value

is the same and sufﬁciently high for both methods.

Figure 6(a) shows the main drawback of the CHT

method, which is that it leads to many false positives

and thus a low Prec value. The CHT++ method, on

the other hand, overcomes this drawback by adding

an area constraint that rejects false tree predictions,

resulting in a higher Prec value.

According to our experiments there exist some

cases where the proposed framework provides low

performance results that are mainly due to the fail-

ure of the image segmentation step, as depicted in

Figure 7. Figures 7(a) and 7(b) depict two sample

results of the DCFA with low performance on TPR

and Prec metrics, respectively. In the Figure 7(a), the

used RGBVI index fails to segment some small trees

on the right part of the image due to the low image

quality. In the Figure 7(b), the used RGBVI index de-

tects dense vegetation (plants) as tree region, resulting

false alarms. Therefore, even in false detections there

is green color that could be confusing even to the hu-

man eye. In both cases, the DCFA well detects the

rest segmented trees.

5 CONCLUSIONS AND FUTURE

RESEARCH DIRECTIONS

An unsupervised method (DCFA) for accurate and au-

tomatic tree detection and counting was presented in

this work. DCFA is a modiﬁed version of the ellipse

ﬁtting algorithm (DEFA) introduced by (Panagiotakis

and Argyros, 2016) with the main difference that

it uses circles instead of ellipses. Different models

are evaluated based on the Akaike Information Crite-

rion (AIC). The experimental results on the Acacia-

6 dataset showed the effectiveness of the proposed

method as well as its superiority in comparison to

relevant unsupervised state-of-the-art methods. Ad-

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

102

(a) DCFA (b) DCFA (c) DCFA

(d) CHT++ (e) CHT++ (f) CHT++

(g) DEFA (h) DEFA (i) DEFA

Figure 5: Sample results of the unsupervised methods on the Acacia-6 dataset. The detected and the ground truth trees are

plotted with white-red circles and yellow pluses respectively. (a),(b),(c) The results of the DCFA method. (d),(e),(f) The

results of the CHT++ method. (g),(h),(i) The results of the DEFA method.

(a) CHT (b) CHT++

Figure 6: A sample results of the CHT (a) and the CHT++

(b) method on the Acacia-6 dataset. The detected and the

ground truth trees are plotted with white-red circles and yel-

low pluses respectively.

ditionally, the DCFA has been compared with state of

the supervised methods yielding comparable results

on the Acacia-6 dataset. In this work, we also show

that the simpler and faster method DCFA is more suit-

able than DEFA on tree detection problem due to the

circular tree shapes.

There is no doubt that automatic tree detection has

been extensively explored by the scientiﬁc commu-

nity, but there are still some challenges ahead. Auto-

matic tree detection and counting is an evolving ﬁeld

of research and can effectively contribute to the study

of many areas such as environmental protection, agri-

cultural planning, crop yield estimation and monitor-

ing of replanted forest areas. Our goal is not only to

improve our method but also to develop such meth-

ods for automatic tree detection that can be used as

input in a second step for green and agriculture plan-

ning. Forest road network planning is an important

and challenging task since its spatial arrangement re-

duces the incidence of ﬁres and prevents the spread of

ﬁres on larger areas (Stefanovi

c et al., 2016).

Unsupervised Tree Detection and Counting via Region-Based Circle Fitting

103

(a) DCFA

(b) DCFA

Figure 7: Two sample results of the DCFA with low perfor-

mance on (a) TPR and (b) Prec metrics. The detected and

the ground truth trees are plotted with white-red circles and

yellow pluses respectively.

ACKNOWLEDGMENTS

This research has been co-ﬁnanced by the European

Union and Greek national funds through the Oper-

ational Program Competitiveness, Entrepreneurship

and Innovation, under the call RESEARCH - CRE-

ATE - INNOVATE B cycle (project code: T2EDK-

03135).

REFERENCES

Abozeid, A., Alanazi, R., Elhadad, A., Taloba, A. I., El-

Aziz, A., and Rasha, M. (2022). A large-scale dataset

and deep learning model for detecting and counting

olive trees in satellite imagery. Computational Intelli-

gence and Neuroscience, 2022.

Akaike, H. (1974). A new look at the statistical model iden-

tiﬁcation. IEEE transactions on automatic control,

19(6):716–723.

Ammar, A., Koubaa, A., and Benjdira, B. (2021). Deep-

learning-based automated palm tree counting and ge-

olocation in large farms from aerial geotagged images.

Agronomy, 11(8):1458.

Badrinarayanan, V., Kendall, A., and Cipolla, R. (2017).

Segnet: A deep convolutional encoder-decoder ar-

chitecture for image segmentation. IEEE transac-

tions on pattern analysis and machine intelligence,

39(12):2481–2495.

Bendig, J., Yu, K., Aasen, H., Bolten, A., Bennertz, S.,

Broscheit, J., Gnyp, M. L., and Bareth, G. (2015).

Combining uav-based plant height from crop surface

models, visible, and near infrared vegetation indices

for biomass monitoring in barley. International Jour-

nal of Applied Earth Observation and Geoinforma-

tion, 39:79–87.

Bilen, H. and Vedaldi, A. (2016). Weakly supervised deep

detection networks. In Proceedings of the IEEE con-

ference on computer vision and pattern recognition,

pages 2846–2854.

Chen, L.-C., Papandreou, G., Kokkinos, I., Murphy, K., and

Yuille, A. L. (2017). Deeplab: Semantic image seg-

mentation with deep convolutional nets, atrous convo-

lution, and fully connected crfs. IEEE transactions on

pattern analysis and machine intelligence, 40(4):834–

848.

Chen, Q., Baldocchi, D., Gong, P., and Kelly, M. (2006).

Isolating individual trees in a savanna woodland using

small footprint lidar data. Photogrammetric Engineer-

ing & Remote Sensing, 72(8):923–932.

Duncanson, L., Cook, B., Hurtt, G., and Dubayah, R.

(2014). An efﬁcient, multi-layered crown delineation

algorithm for mapping individual tree structure across

multiple ecosystems. Remote Sensing of Environment,

154:378–386.

Erikson, M. (2003). Segmentation of individual tree crowns

in colour aerial photographs using region growing

supported by fuzzy rules. Canadian Journal of For-

est Research, 33(8):1557–1563.

Girshick, R., Donahue, J., Darrell, T., and Malik, J. (2014).

Rich feature hierarchies for accurate object detec-

tion and semantic segmentation. In Proceedings of

the IEEE conference on computer vision and pattern

recognition, pages 580–587.

Hao, Z., Lin, L., Post, C. J., Mikhailova, E. A., Li, M.,

Chen, Y., Yu, K., and Liu, J. (2021). Automated tree-

crown and height detection in a young forest plan-

tation using mask region-based convolutional neural

network (mask r-cnn). ISPRS Journal of Photogram-

metry and Remote Sensing, 178:112–123.

He, K., Gkioxari, G., Doll

ar, P., and Girshick, R. (2017).

Mask r-cnn. In Proceedings of the IEEE international

conference on computer vision, pages 2961–2969.

He, K., Zhang, X., Ren, S., and Sun, J. (2015). Spatial pyra-

mid pooling in deep convolutional networks for visual

recognition. IEEE transactions on pattern analysis

and machine intelligence, 37(9):1904–1916.

Hu, G., Yin, C., Wan, M., Zhang, Y., and Fang, Y. (2020).

Recognition of diseased pinus trees in uav images us-

ing deep learning and adaboost classiﬁer. Biosystems

Engineering, 194:138–151.

Karantzalos, K. and Argialas, D. (2004). Towards automatic

olive tree extraction from satellite imagery. In Geo-

Imagery Bridging Continents. XXth ISPRS Congress,

pages 12–23. Citeseer.

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

104

Khan, A., Khan, U., Waleed, M., Khan, A., Kamal, T., Mar-

wat, S. N. K., Maqsood, M., and Aadil, F. (2018).

Remote sensing: an automated methodology for olive

tree detection and counting in satellite images. IEEE

Access, 6:77816–77828.

Koc-San, D., Selim, S., Aslan, N., and San, B. T. (2018).

Automatic citrus tree extraction from uav images and

digital surface models using circular hough transform.

Computers and electronics in agriculture, 150:289–

301.

Li, W., Guo, Q., Jakubowski, M. K., and Kelly, M. (2012).

A new method for segmenting individual trees from

the lidar point cloud. Photogrammetric Engineering

& Remote Sensing, 78(1):75–84.

Long, J., Shelhamer, E., and Darrell, T. (2015). Fully con-

volutional networks for semantic segmentation. In

Proceedings of the IEEE conference on computer vi-

sion and pattern recognition, pages 3431–3440.

Marques, P., P

adua, L., Ad

ao, T., Hru

ska, J., Peres, E.,

Sousa, A., and Sousa, J. J. (2019). Uav-based auto-

matic detection and monitoring of chestnut trees. Re-

mote Sensing, 11(7):855.

Mubin, N. A., Nadarajoo, E., Shafri, H. Z. M., and Ha-

medianfar, A. (2019). Young and mature oil palm tree

detection and counting using convolutional neural net-

work deep learning method. International Journal of

Remote Sensing, 40(19):7500–7515.

Ocer, N. E., Kaplan, G., Erdem, F., Kucuk Matci, D., and

Avdan, U. (2020). Tree extraction from multi-scale

uav images using mask r-cnn with fpn. Remote sens-

ing letters, 11(9):847–856.

Osco, L. P., De Arruda, M. d. S., Junior, J. M., Da Silva,

N. B., Ramos, A. P. M., Moryia,

E. A. S., Imai, N. N.,

Pereira, D. R., Creste, J. E., Matsubara, E. T., et al.

(2020). A convolutional neural network approach for

counting and geolocating citrus-trees in uav multi-

spectral imagery. ISPRS Journal of Photogrammetry

and Remote Sensing, 160:97–106.

Otsu, N. (1979). A threshold selection method from gray-

level histograms. IEEE transactions on systems, man,

and cybernetics, 9(1):62–66.

Panagiotakis, C. and Argyros, A. (2016). Parameter-free

modelling of 2d shapes with ellipses. Pattern Recog-

nition, 53:259–275.

Panagiotakis, C. and Argyros, A. (2020). Region-based

ﬁtting of overlapping ellipses and its application to

cells segmentation. Image and Vision Computing,

93:103810.

Panagiotakis, C. and Argyros, A. A. (2018). Cell segmen-

tation via region-based ellipse ﬁtting. In 2018 25th

IEEE International Conference on Image Processing

(ICIP), pages 2426–2430. IEEE.

Qiu, L., Jing, L., Hu, B., Li, H., and Tang, Y. (2020).

A new individual tree crown delineation method for

high resolution multispectral imagery. Remote Sens-

ing, 12(3):585.

Ren, S., He, K., Girshick, R., and Sun, J. (2015). Faster

r-cnn: Towards real-time object detection with region

proposal networks. Advances in neural information

processing systems, 28.

Rizeei, H. M., Shafri, H. Z., Mohamoud, M. A., Pradhan,

B., and Kalantar, B. (2018). Oil palm counting and age

estimation from worldview-3 imagery and lidar data

using an integrated obia height model and regression

analysis. Journal of Sensors, 2018.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-net:

Convolutional networks for biomedical image seg-

mentation. In International Conference on Medical

image computing and computer-assisted intervention,

pages 234–241. Springer.

Salam

ı, E., Gallardo, A., Skorobogatov, G., and Barrado, C.

(2019). On-the-ﬂy olive tree counting using a uas and

cloud services. Remote Sensing, 11(3):316.

Stefanovi

c, B., Stojni

c, D., and Danilovi

c, M. (2016).

Multi-criteria forest road network planning in ﬁre-

prone environment: a case study in serbia. Jour-

nal of Environmental Planning and Management,

59(5):911–926.

Sun, Y., Li, Z., He, H., Guo, L., Zhang, X., and Xin, Q.

(2022). Counting trees in a subtropical mega city us-

ing the instance segmentation method. International

Journal of Applied Earth Observation and Geoinfor-

mation, 106:102662.

Tang, P., Wang, X., Bai, S., Shen, W., Bai, X., Liu, W.,

and Yuille, A. (2018). Pcl: Proposal cluster learning

for weakly supervised object detection. IEEE trans-

actions on pattern analysis and machine intelligence,

42(1):176–191.

Tong, P., Han, P., Li, S., Li, N., Bu, S., Li, Q., and Li,

K. (2021). Counting trees with point-wise supervised

segmentation network. Engineering Applications of

Artiﬁcial Intelligence, 100:104172.

Vibha, L., Shenoy, P. D., Venugopal, K., and Patnaik, L.

(2009). Robust technique for segmentation and count-

ing of trees from remotely sensed data. In 2009 IEEE

International Advance Computing Conference, pages

1437–1442. IEEE.

Wagner, F. H., Ferreira, M. P., Sanchez, A., Hirye, M. C.,

Zortea, M., Gloor, E., Phillips, O. L., de Souza Filho,

C. R., Shimabukuro, Y. E., and Arag

ao, L. E. (2018).

Individual tree crown delineation in a highly diverse

tropical forest using very high resolution satellite im-

ages. ISPRS journal of photogrammetry and remote

sensing, 145:362–377.

Wan, F., Liu, C., Ke, W., Ji, X., Jiao, J., and Ye, Q. (2019).

C-mil: Continuation multiple instance learning for

weakly supervised object detection. In Proceedings

of the IEEE/CVF Conference on Computer Vision and

Pattern Recognition, pages 2199–2208.

Weinstein, B. G., Marconi, S., Aubry-Kientz, M., Vincent,

G., Senyondo, H., and White, E. P. (2020). Deep-

forest: A python package for rgb deep learning tree

crown delineation. Methods in Ecology and Evolu-

tion, 11(12):1743–1751.

Wu, X., Shen, X., Cao, L., Wang, G., and Cao, F. (2019).

Assessment of individual tree detection and canopy

cover estimation using unmanned aerial vehicle based

light detection and ranging (uav-lidar) data in planted

forests. Remote Sensing, 11(8):908.

Yan, W., Guan, H., Cao, L., Yu, Y., Li, C., and Lu, J. (2020).

Unsupervised Tree Detection and Counting via Region-Based Circle Fitting

105

A self-adaptive mean shift tree-segmentation method

using uav lidar data. Remote Sensing, 12(3):515.

Yao, L., Liu, T., Qin, J., Lu, N., and Zhou, C. (2021). Tree

counting with high spatial-resolution satellite imagery

based on deep neural networks. Ecological Indicators,

125:107591.

Zheng, J., Fu, H., Li, W., Wu, W., Zhao, Y., Dong, R., and

Yu, L. (2020). Cross-regional oil palm tree count-

ing and detection via a multi-level attention domain

adaptation network. ISPRS Journal of Photogramme-

try and Remote Sensing, 167:154–177.

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

106