Deep Minutiae Fingerprint Extraction Using Equivariance Priors

Margarida Gouveia

1,2 a

, Eduardo Castro

1,2 b

, Ana Rebelo

1 c

, Jaime S. Cardoso

1,2 d

and Bruno Patr

3,4 e

Instituto de Engenharia de Sistemas e Computadores, Tecnologia e Ci

encia, Porto, Portugal

Faculdade de Engenharia, Universidade do Porto, Porto, Portugal

Imprensa Nacional-Casa da Moeda, Lisbon, Portugal

Department of Electrical and Computer Engineering, University of Coimbra, Coimbra, Portugal

Keywords:

Biometrics, Convolution Neural Network, Equivariance, Fingerprints, Group Convolutional Network,

Minutiae, Multi-Task Learning, U-Net.

Abstract:

Currently, ﬁngerprints are one of the most explored characteristics in biometric systems. These systems typi-

cally rely on minutiae extraction, a task highly dependent on image quality, orientation, and size of the ﬁnger-

print images. In this paper, a U-Net model capable of performing minutiae extraction is proposed (position,

angle, and type). Based on this model, we explore two different ways of regularizing the model based on

equivariance priors. First, we adapt the model architecture so that it becomes equivariant to rotations. Second,

we use a multi-task learning approach in order to extract a more comprehensive set of information from the

ﬁngerprints (binary images, segmentation, frequencies, and orientation maps). The two approaches improved

accuracy and generalization capability in comparison with the baseline model. On the 16 test datasets of the

Fingerprint Veriﬁcation Competition, we obtained an average Equal-Error Rate (EER) of 2.26, which was

better than a well-optimized commercial product.

1 INTRODUCTION

A ﬁngerprint is an impression formed by the con-

tact of the friction ridges on the ﬁngertips with a

surface (Adiga V and Sivaswamy, 2019). Friction

ridges are described as “three-dimensional surfaces

with irregular structures separated by narrow fur-

rows valleys” (Hicklin, 2009). A detailed and dis-

tinct pattern of ridges and valleys exists for each hu-

man, which cannot be changed during the individual’s

life (Adiga V and Sivaswamy, 2019). These charac-

teristics explain why ﬁngerprints are useful as a pri-

mary biometric modality in our daily lives (Adiga V

and Sivaswamy, 2019; Peralta et al., 2015; Joshi et al.,

2019).

Experts can recognize ﬁngerprints by comparing

two ﬁngerprint images and matching the structures

present in them. One of the most important steps

https://orcid.org/0000-0002-0268-7921

https://orcid.org/0000-0003-4144-695X

https://orcid.org/0000-0003-4776-6057

https://orcid.org/0000-0002-3760-2473

https://orcid.org/0000-0002-0251-9047

is minutiae extraction, in which friction ridge skin

features are detected. The combination of these fea-

tures results in different minutiae types in different

positions and orientations, which are unique to each

individual (Hicklin, 2009). Minutiae extraction is

inﬂuenced by conditions such as humidity or skin

dryness, the presence of dirt, or the existence of

wounds (Adiga V and Sivaswamy, 2019). Also, the

variety of sensors available to capture ﬁngerprints re-

sults in images with different characteristics (Adiga V

and Sivaswamy, 2019). As a result, ﬁngerprint images

may have different levels of noise, orientations, and

scale. To address this variability, various deep learn-

ing methods, such as Convolutional Neural Networks

(CNNs), have been tested, for minutiae extraction and

pre-processing or matching ﬁngerprints.

Minutiae can be extracted using deep learning

methods that learn feature representations directly

from data (Rebelo et al., 2019; Tang et al., 2017). The

result is a probability map of minutiae positions, that

needs to be post-processed to precise positions and

orientations of minutiae (Rebelo et al., 2019). These

methods have shown promise in tackling ﬁngerprint

image complexity, especially artefacts. Despite this,

Gouveia, M., Castro, E., Rebelo, A., Cardoso, J. and Patrão, B.

Deep Minutiae Fingerprint Extraction Using Equivariance Priors.

DOI: 10.5220/0011673500003414

In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 4: BIOSIGNALS, pages 241-251

ISBN: 978-989-758-631-6; ISSN: 2184-4305

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

241

the use of CNNs for minutiae extraction is restricted

by the scarcity of real ﬁngerprint datasets with ade-

quate minutiae marking, as well as privacy concerns.

Alternatively, synthetic ﬁngerprint generators capable

of creating large databases that mimic inter-class and

intra-class variations can be used. Although helpful,

mimicking the natural degradation that occurs in natu-

rally enrolled ﬁngerprints or naturally acquired latent

ﬁngerprints is difﬁcult. This emphasizes the impor-

tance of developing models with strong generalization

capabilities, even when trained with small amounts of

data. The ﬁeld of Geometric Deep Learning proposes

the use of equivariant CNNs to obtain networks robust

to input transformations, and with a greater capacity

for generalization to unseen data. The equivariance

priors used are motivated by prior knowledge of the

data and task at hand. In the case of ﬁngerprint im-

ages, due to the importance of minutiae orientation,

rotation-equivariant CNNs are worth investigating.

The aim of this paper is to investigate how a CNN

model can be used to extract minutiae (position, an-

gle, and type) from various types of ﬁngerprint im-

ages. Speciﬁcally, how the model optimization can

be regularized by incorporating rotation equivariance

properties into the model architecture, and how the

use of additional ground-truth information can impact

network performance in the main task of minutiae ex-

traction for ﬁngerprint images from various sources.

The main contributions of our paper are the follow-

ing:

• We propose a deep learning approach for minu-

tiae extraction trained on synthetic data but with

excellent performance in real ﬁngerprint images.

• We demonstrate how regularization with addi-

tional ground-truth information results in a better

performance in the minutiae extraction task and

allows also the recovery of extra ﬁngerprint infor-

mation.

• We demonstrate how equivariance priors can be

incorporated into the model architecture and train-

ing to improve generalization.

2 RELATED WORK

2.1 CNNs for Minutiae Extraction

Deep learning for minutiae extraction can take two

forms: building a neural network from scratch or

combining domain knowledge with neural networks

to improve structure design (Rebelo et al., 2019).

The FingerNet (Tang et al., 2017) and the Minuti-

aeNet (Nguyen et al., 2017) are two of those exam-

ples where domain knowledge is combined with deep

learning.

As a rule, the methods ﬁrst generate a proposal

for the minutiae points and then extract the exact po-

sition, orientation, or type of minutiae (Jiang et al.,

2016; Tang et al., 2017; Zhou et al., 2020; Jiang

and Liu, 2017). Other methods consider the minu-

tiae extraction problem to be a segmentation task

where a U-Net model encodes the minutiae positions

using a binary mask (Pinetz et al., 2017) or the

positions and orientations using a mask with multi-

ple classes, according to the angle intervals (Nguyen

et al., 2020). In addition to minutiae information,

multi-task learning and transfer learning can be used

to extract frequency and texture information (Taka-

hashi et al., 2020; Zhang et al., 2021).

In our proposal, the minutiae information (posi-

tion, angle, and type) is encoded in different target

masks, with the U-Net model being trained in a multi-

task approach. The model’s outputs are then post-

processed to produce the typical minutiae template.

Our work is most similar to the approaches based on

the use of the U-Net (Pinetz et al., 2017; Nguyen

et al., 2020). We encode the minutiae positions and

orientations in different masks and obtain also the

minutiae type. Our work differs from the state-of-the-

art since we only use synthetic data in the training in-

stead of real ﬁngerprints (Tang et al., 2017) to obtain

a larger training set. In addition, our proposed models

were tested in diverse datasets to test the generaliza-

tion capability of the models.

2.2 Equivariant CNNs

A CNN is equivariant when a speciﬁc transformation

in the network’s input results in a predictable change

in network output.

For instance, traditional CNNs are translation

equivariant: shifting the input of a layer yields the

same feature map as feeding the original image (with-

out shifting) to that layer and shifting the feature map.

This results from the weight sharing and local con-

nectivity properties of these models, which are con-

tributing factors to the high performance when pro-

cessing natural images (Castro et al., 2020). A CNN

can be classiﬁed as translation equivariant when fea-

ture extraction is identical regardless of the image re-

gion being processed (Castro et al., 2020; Cohen and

Welling, 2016). The importance of equivariance to

translations in traditional CNNs motivates the study

of additional types of equivariances that could be used

to enhance the accuracy of these models in other com-

puter vision tasks. In other words, the application of

symmetries was a fundamental design principle for

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

242

network architectures and can result in more precise

models (Gerken et al., 2021). For the speciﬁc case of

minutia extraction, ﬁngerprint image characteristics

motivate the search for rotation-equivariant CNNs.

The most common way to address scale and ro-

tation equivariance in CNNs is to use data augmen-

tation, which involves rotating the data or changing

the scale (Castro et al., 2020; Naderi et al., 2020;

Worrall et al., 2017). This method ensures the ca-

pability of generalization of CNNs but does not en-

sure equivariance at all network layers (Worrall et al.,

2017). Data augmentation results in a heavy training

cost and complex model parameters, which may re-

duce network performance (Naderi et al., 2020). In

this way, several methods have been proposed to in-

corporate geometric transformation information into

network architectures.

One approach is to use four operations (slice,

pool, roll, and stack) to allow parameter sharing be-

tween different orientations via feature map rota-

tions to obtain equivariance to rotations (Dieleman

et al., 2016). The same property is obtained in the

Deep Rotation Equivariant Networks (DRENs) by re-

placing the rotations of the features maps with rota-

tions of the ﬁlters (Li et al., 2018). Another pro-

posal is the Group Equivariant Convolutional Neu-

ral Networks (G-CNNs), which allows the rotation

equivariance by deﬁning the operation G-convolution

(Group-equivariant convolution) (Cohen and Welling,

2016). This operation exploits the known symmetries

of the data and is responsible for the generalization of

the common convolution operator to deal with rota-

tions and reﬂections. The limitation presented in this

method is the capability of dealing only with discrete

groups, and only rotations of multiple of 90°are con-

sidered. The Harmonic Networks (H-Nets) general-

ize the rotation equivariance for continuous groups of

360°rotations by replacing regular CNN ﬁlters with

circular harmonics (Worrall et al., 2017). This prop-

erty is the result of the replacement of regular CNN

ﬁlters with circular harmonics that return a maxi-

mal response and orientation. Circular harmonics are

steerable ﬁlters as the ones used to obtain scale equiv-

ariance in the Scale Equivariant Convolutional Neu-

ral Networks (SE-CNNs) (Naderi et al., 2020). The

Group Equivariant Capsule Networks also achieve ro-

tation equivariance by using group equivariant cap-

sule layers (Lenssen et al., 2018).

The aforementioned proposals use diverse tech-

niques to address the problem of scale and/or rota-

tion equivariance, and all demonstrated superior per-

formance in classiﬁcation tasks compared to baseline

models. This indicates that the integration of scale

and/or rotation equivariance priors should be consid-

ered when designing different networking architec-

tures. The purpose of introducing these equivariances

was to improve the robustness and generalization of

the networks to unseen data. In this paper, the rotation

equivariance was embedded using G-convolutions to

replace the conventional convolutions of the U-net

model and obtain a Group Equivariant U-Net that can

be used for minutiae extraction.

3 METHODS

3.1 U-Net Architecture

To allow an image-to-image mapping between a ﬁn-

gerprint image and a map with the same dimensions

of the minutiae positions, a U-Net model was em-

ployed (Ronneberger et al., 2015). It consists of an

encoder-decoder structure that uses as the main block

(ConvBlock) a sequence of a 3 by 3 Convolutional

layer (3x3 Conv), a Batch Normalization layer (BN)

and a Rectiﬁed Linear Unit (ReLU) as the activation

function. The Encoding Layer consists of four repe-

titions of two blocks ConvBlocks followed by a max-

pooling operation of stride 2. The Decoder consists

of four repetitions of two ConvBlocks followed by an

up-sampling operation with stride 2. The ﬁnal out-

put is obtained by a 1 by 1 Convolutional layer. An-

other important detail is the use of skip connections,

which provide the decoder with information typically

lost during down-sampling. These consist of concate-

nating the feature maps after up-sampling in the de-

coder with feature maps before down-sampling in the

encoder.

3.2 Multi-Task Learning

We modify the U-Net model to perform multiple tasks

concurrently via a hard parameter-sharing strategy,

i.e., different tasks share hidden layers and have dis-

tinct output layers (Ruder, 2017). Through the use of

these share representations, the model focuses on the

most crucial aspects. The optimization of the multi-

task model is performed using a linear combination

of multiple loss functions for each task, following the

general equation presented in Equation 1. L

total

cor-

responds to the total value of the loss function with

N partial losses, L

corresponds to the value of each

partial loss, and λ

to the respective weight.

total

∑

i=1

(λ

· L

) (1)

Deep Minutiae Fingerprint Extraction Using Equivariance Priors

243

3.3 Baseline Model

The baseline model was designed to extract only in-

formation regarding the minutiae: position (x

, y

angle (θ

) and type (type 1 for a termination point or

type 2 for a bifurcation). The model uses the above-

mentioned U-Net architecture with four output chan-

nels that encode the minutiae information.

The spatial information of each minutia is en-

coded using a 2D Gaussian centered on the minutia’s

position. Two channels were used for encoding, one

for endpoints (Mask XY 1) and one for bifurcations

(Mask XY 2). A 21 × 21 Gaussian window, with a

standard deviation of 2 was used and normalized so

that the maximum value is 1. These two channels

can be seen as probability maps where the maximum

probability of 1, corresponds to the exact position of

the minutiae. For this reason, the sigmoid was used

as the output activation function.

For encoding the angle of each minutia, two more

channels were used. A box centered in each minu-

tia with the values of the sine (Mask A Sen) and the

cosine (Mask A Cos) encode the minutia angle. Us-

ing the trigonometric functions ensures there are no

discontinuities. For instance, when the model’s pre-

diction is 360°and the actual value of the angle is 0°,

the difference would be high even though the model

is accurate. Due to the range of these trigonometric

functions ([-1, 1]) the Hyperbolic Tangent (Tanh) was

used as the output activation function.

The loss function (L

minutiae

) for the baseline model

is presented in Equation 2, and consists of a sum of

four partial losses. The ﬁrst two relate to the minu-

tiae position encoding and the two relate to orienta-

tion encoding were based on the Mean-Squared Error

(MSE). Notice that for the angle encoding losses, a

mask is used to ensure only regions around minutiae

(21 × 21 boxes) contribute to the loss since other re-

gions do not have a deﬁned minutiae orientation. The

same weight is attributed to each partial loss. The

combination of the partial loss functions used for each

output channel of the model, the respective activation

function, and the range of output values are presented

in Table 1.

minutiae

= MSE

XY 1

+ MSE

XY 2

+ MSE

A Sen

+MSE

A Cos

(2)

3.4 Regularization with Additional

Ground-Truth Information

Five additional output channels were added to the

baseline model to act as model regularization. These

outputs are used to learn additional tasks, such as

the position, orientation, and frequency of the ridge

patterns, as well as a binary segmentation of the ﬁn-

gerprint. These are not required for minutiae extrac-

tion but serve as a regularization of the learning pro-

cess. The proposed loss based on these extra chan-

nels (L

extra

) is combined with the loss of the main task

of minutiae extraction (L

minutiae

), using the parameter

total

to weight the sum (Equation 3). The parameter

total

was tuned to provide the best performance in the

task of minutiae extraction.

total

= λ

total

· L

minutiae

+ (1 − λ

total

) · L

extra

(3)

The ﬁrst two channels added correspond to the

masks containing information about the binary ridge

pattern (Mask Bin) and the segmentation map (Mask

Seg). These two channels allow obtaining addi-

tional information about different regions in the im-

age: foreground/ﬁngerprint, background, and ridge

lines. A sigmoid activation is used in each of these

channels, and the BCE serves as the loss function for

the corresponding additional tasks.

Two more channels were added to reconstruct the

orientation map, sine (Mask O Sen) and cosine (Mask

O Cos) masks. Due to the range of the sine and cosine

functions ([-1, 1]), we used a Tanh activation function

and the MSE loss function for optimization. To re-

cover the ridge pattern’s frequency, another channel

with normalized values between 0 and 1 was added

(Mask Frq). Normalized frequency map limits al-

lowed for Sigmoid activation and MSE loss. The total

loss of these auxiliary tasks was calculated by adding

the ﬁve individual losses, giving equal weight to each

partial loss (Equation 4).

extra

= BCE

Bin

+ BCE

Seg

+ MSE

O Sen

+MSE

O Cos

+ MSE

Frq

(4)

3.5 Equivariant Model

Motivated by the importance of translation equiv-

ariance in CNNs and by the ﬁngerprint character-

istics, the goal was to obtain a Group Equivariant

CNN (Cohen and Welling, 2016), equivariant to ro-

tations and capable of performing the minutiae ex-

traction. This led to the implementation of a Group

Equivariant U-Net. The created model differs from

the baseline model in the U-Net architecture, where

G-convolutions replaced typical convolutions to cre-

ate an equivariant model. To avoid duplicate out-

put channels, the output layer convolutions were not

replaced. This work used the group p4 in the G-

convolutions.

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

244

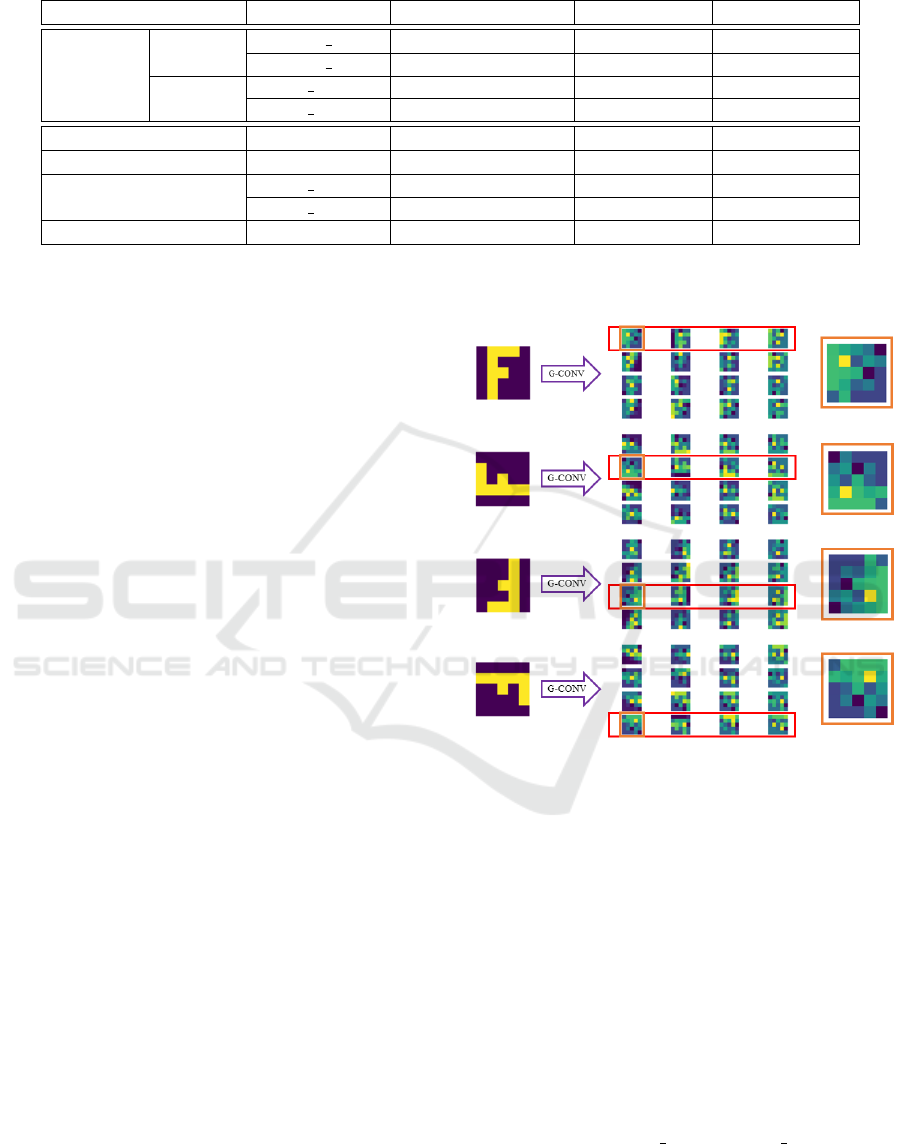
Table 1: Output channels from the U-Net model: task, activation function, loss function and channel range.

Task Channel Name Activation Function Loss Function Channel Range

Minutiae

Extraction

Position

and Type

XY 1 Sigmoid MSE [0 - 1]

XY 2 Sigmoid MSE [0 - 1]

Angle

A Cos Tanh MSE

∗

[-1 - 1]

A Sen Tanh MSE

∗

[-1 - 1]

Binary Image Bin Sigmoid BCE [0 - 1]

Segmentation Map Seg Sigmoid BCE [0 - 1]

Orientation Map

O Cos Tanh MSE

∗∗

[-1 - 1]

O Sen Tanh MSE

∗∗

[-1 - 1]

Frequency Map Frq Sigmoid MSE

∗∗

[0 - 1]

* Only computed in 21x21 boxes centered around each minutia.

** Only computed in the ﬁngerprint region from the segmentation map.

The G-convolution can be understood as the use of

the same ﬁlter in different orientations such that a fea-

ture map is generated for each orientation. The collec-

tion of feature maps is concatenated such that a rota-

tion on the input causes a rotation and a shift on the

output (see Figure 1). The subsequent G-convolution

layers account for this shift when transforming their

ﬁlters, such that, when multiple layers are stacked,

this input-output relationship is maintained. As such,

the model can maintain equivariance to rotation. The

G-convolutions can be deﬁned according if they are

in the ﬁrst layer of a CNN being applied to an in-

put image (Equation 5) (ﬁrst-layer G-convolution) or

if they are applied to a feature map in a hidden layer

of the CNN (Equation 6) (full G-convolution) (Cohen

and Welling, 2016). The convolution deﬁned in Equa-

tion 5 receives an input image f and a ﬁlter ψ, both

functions of the plane Z

, and outputs a feature map

( f ∗ ψ) function of the discrete group G. For the con-

volution deﬁned in Equation 6, the ﬁlters ψ need also

to be functions on G.

[ f ∗ ψ](g) =

∑

y∈Z

∑

(y)ψ

−1

y) (5)

[ f ∗ ψ](g) =

∑

h∈G

∑

(h)ψ

−1

h) (6)

When replacing convolutions with their equivari-

ant counterpart, we maintained the same number of

channels. This ensures that the models are equivalent

in terms of the number of operations resulting in a re-

duction of the network’s trainable parameters. This

reduction corresponds to using four rotated copies of

each ﬁlter for the G-convolutions layers and is equiva-

lent to a reduction of approximately one-quarter (from

17.3 million to 4.3 million trainable parameters). In

addition, to ensure rotation-equivariance the batch

normalization was implemented with a single scale

and bias parameter per each p4 G-feature map.

Figure 1: Graphical representation of the G-convolution

equivariance, considering a convolution with 1 input chan-

nel and 16 output channels.

3.6 Post-Processing

A correlation between the masks with the outputs and

the Gaussian template is performed in the ﬁrst step

of the post-processing method. For the correlation,

it was used a window with the same size and stan-

dard deviation as the one used for the target construc-

tion. The peaks of the correlation result with a value

above the threshold of 1.0 were selected. In addi-

tion, the maximum number of peaks possible to ex-

tract was 100. When two peaks were very close (less

than 5 pixels apart), the peak with the higher inten-

sity was always chosen. The mask in which the peak

was veriﬁed (Mask XY 1 or Mask XY 2) determined

the minutia type (type 1 or type 2). After identify-

ing the points with minutia, the angle sine and cosine

outputs were used to calculate the angle. A circular

Deep Minutiae Fingerprint Extraction Using Equivariance Priors

245

mean is computed for each minutia position to cal-

culate the mean angle in a 5 × 5 window around the

minutia. The formula for the circular mean is pre-

sented in Equation 7, where a corresponds to the av-

erage angle value calculated over N sine and cosine

sample values. Each minutia was also assigned a rel-

ative quality based on the intensity of the correlation

map.

a = arctg(

∑

i=1

sen(a

∑

i=1

(cos(a

)) (7)

4 EXPERIMENTAL SETUP

The work proposed in this paper began with the im-

plementation of a basic U-Net model design to ex-

tract only the minutiae information from a grayscale

ﬁngerprint image, as described in Section 3.3. The

model was then modiﬁed to use a more complex

multi-task learning approach, in which the methodol-

ogy extracts more information from the image, such

as binary image, segmentation, frequency, and orien-

tation maps (Section 3.4). Alternatively, the equivari-

ant architecture described in Section 3.5 was imple-

mented to obtain a Group Equivariant U-Net. Finally,

we combine the two strategies in the same model.

All the model’s outputs were post-processed using the

same method (Section 3.6).

The optimization of the models followed the

pipeline presented in Figure 2. The models were

trained for 100 epochs, using the Adam optimizer al-

gorithm, with a learning rate of 1e

−1

and using a batch

size of 8. The datasets used for training, validation,

and testing are described in Section 4.1 and the mod-

els were evaluated using the metrics presented in Sec-

tion 4.2

4.1 Data

4.1.1 Synthetic Fingerprint Databases

The training of CNNs, for minutiae extraction, de-

mands a large number of ﬁngerprint images with cor-

rect annotations for the minutiae information. Due

to the difﬁculty in annotation and privacy concerns,

synthetic databases were used. These databases were

created using the Synthetic Fingerprint Generator

(SFinGe) available in

(Maltoni et al., 2022). The

generator tries to mimic inter-class and intra-class

variations of real ﬁngerprints, i.e., creates examples

https://bit.ly/3ysNNej

of the “same individual” and from “different individ-

uals”. This software generates:

1. Grayscale image of the ﬁngerprint;

2. Binary image with the pattern of ﬁngerprint’s

ridges and valleys pattern.;

3. Frequency map with the frequency of the ridges

and valleys pattern;

4. Orientations map with the angle of the ridges and

valleys;

5. Segmentation map with information on the region

of the ﬁngerprint versus the background;

6. Minutiae template with information about the

minutiae coordinates, angle and type (type 1 for a

termination point or type 2 for a bifurcation point)

A total number of 21600 synthetic images (8 dif-

ferent images from 2700 different individuals) were

used for training the models and 7200 synthetic im-

ages (8 different images from 900 different individu-

als) were used to validate the models.

4.1.2 Real Fingerprint Databases

For testing the different models, the real ﬁngerprint

images provided by the Fingerprint Veriﬁcation Com-

petition (FVC) were chosen. These databases con-

tain ﬁngerprint images obtained with various sensors,

resulting in different features, which are useful for

testing the universality and robustness of the vari-

ous steps of a Fingerprint Recognition System (Maio

et al., 2002a; Maio et al., 2002b; Cappelli et al., 2005;

Cappelli et al., 2007).

4.1.3 Data Augmentation

Different data augmentation techniques were simul-

taneously applied to approximate the synthetic train-

ing images to real ones. The ﬁrst set of transforma-

tions tried to mimic image textures when acquired by

different sensors with low noise levels. They were

only adopted in grayscale images. It includes con-

trast, brightness, saturation, blurring, sharpening, and

inversion. The second set randomly crops and trans-

lates the image. It mimics the need to process non-

centered partial ﬁngerprints. The last set included

random ﬁngerprint rotations (from 0°and 360°) and

ﬂips (horizontal and vertical). They were applied to

provide the model ﬁngerprints in diverse orientations,

not just vertically, but also to provide minutiae in di-

verse orientations. Data augmentation was performed

online and for each image was applied simultaneously

one transformation from each set.

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

246

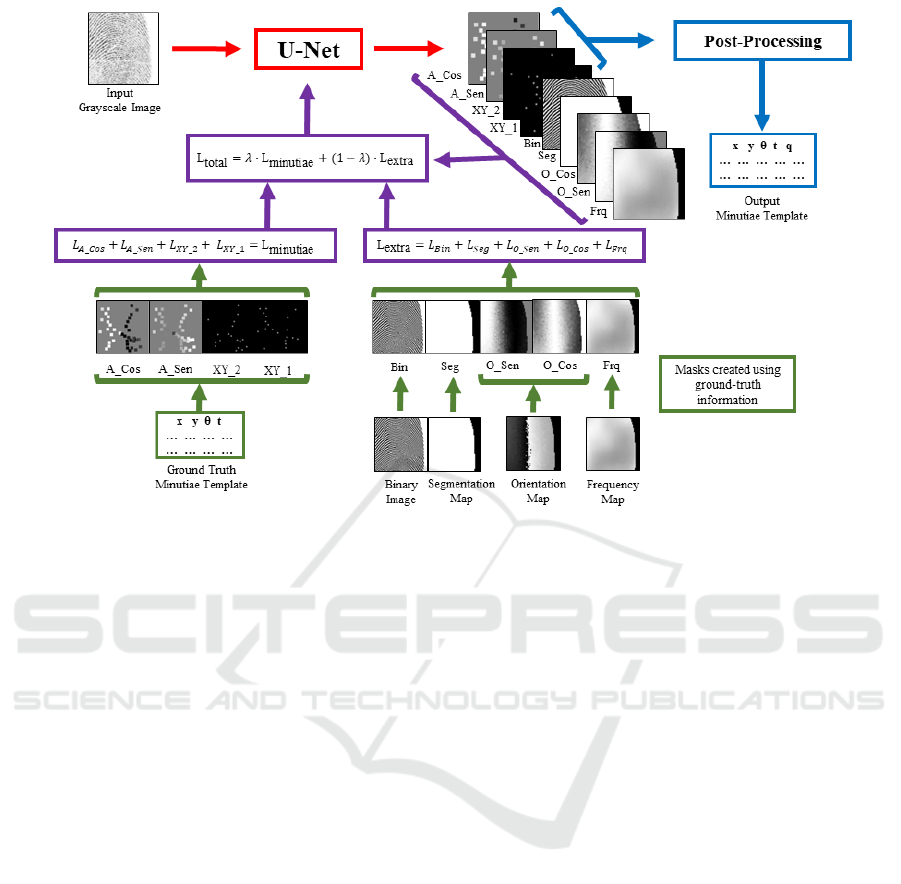
Figure 2: The complete pipeline used for the U-Net models training.

4.2 Minutiae Extraction Evaluation

The evaluation of the different models for minutiae

extraction was centred on two main objectives: 1) the

ability to obtain the correct information of each minu-

tia - coordinates, angle, and type; and 2) the ability to

distinguish ﬁngerprints of different individuals when

the extracted templates are used by a matching algo-

rithm.

The Goodness Index (GI) was used to evaluate

the proportion of the minutiae that were well de-

tected, spurious, and not detected (Peralta et al., 2014;

Bhattacharjee and Lee, 2010). To the GI calculus,

a minutia was considered well-detected when inside

a 13 × 13 box centered on the closest ground-truth

minutiae. In addition to the standard GI, more strict

criteria to classify a minutia as well-detected were

considered. It was also considered in addition to the

position that the minutia angle must be within ±20°of

the ground truth minutiae to be considered as well de-

tected (GI (w/a)). This metric measures the model’s

ability to identify the minutia angle. To evaluate the

model’s ability to extract the minutiae type correctly,

the GI (w/t) was used, in this situation the minutia

type was used in addition to the minutia position as

criteria. The GI (w/at) considers all three criteria dur-

ing the minutia classiﬁcation.

The Equal Error Rate (EER) calculus in accor-

dance with the FVC protocol (Maio et al., 2002a;

Maio et al., 2002b; Cappelli et al., 2005; Cappelli

et al., 2007) was used to evaluate the quality of the

model when used in conjunction with a matching

algorithm for ﬁngerprint veriﬁcation. The match-

ing algorithm was based on the Minutia Cylinder-

Code (MCC) representation combined with the Local

Similarity Assignment with Relaxation (LSA-R) was

used (Cappelli et al., 2010; Rebelo et al., 2019).

The models were compared against two baseline

minutiae extraction solutions: a well-optimized, tra-

ditional commercial method for minutiae extraction -

the ﬁngerIDALg (Rebelo et al., 2019); and a state-of-

the-art method based on deep learning combined with

domain knowledge- the FingerNet (Tang et al., 2017).

5 RESULTS AND DISCUSSION

The results for the validation set that contains only

synthetic images were based on the GI values and are

depicted in Table 2. To evaluate the performance of

the models in test sets, due to the lack of ground-truth

annotations, the results were based on EER values and

are presented in Table 3.

5.1 Baseline Model

In the validation set with synthetic images, the non-

equivariant model with lambda

total

of 1.0 performs

better than the ﬁngerIDALg (a GI of 0.01 versus -

Deep Minutiae Fingerprint Extraction Using Equivariance Priors

247

Table 2: Results for the validation set of the reference system and all the four models: GI, Percentage missing minutiae (%M),

percentage of spurious minutiae (%S), and the GI considering the angle (w/a), the type (w/t) and both (w/at) as a criterion for

classiﬁcation of a minutia as well detected.

Model GI %M

∗

∗∗

GI (w/a) GI (w/t) GI (w/at)

Reference ﬁngerIDALg -0.05 34.53 37.77 -0.24 -0.32 -0.47

Non-Equivariant

total

= 1.0 0.01 30.71 40.73 -0.19 -0.27 -0.43

total

= 0.8 0.01 30.51 42.55 -0.21 -0.26 -0.43

Equivariant

total

= 1.0 0.02 30.27 41.18 -0.18 -0.26 -0.42

total

= 0.8 0.02 30.40 40.21 -0.18 -0.23 -0.39

* Calculated in relation to the ground truth minutiae set.

** Calculated in relation to the extracted minutiae set.

Table 3: EER (%) values for the reference systems and the four models for the different FVC databases; and the average of

the EER (%) for all the FVC databases.

FVC Database

Reference

Model

Non-Equivariant Equivariant

ﬁngerIDALg FingerNet

total

1.0

total

0.8

total

1.0

total

0.8

2000

DB1 1.01 0.44 0.36 0.30 0.36 0.40

DB2 0.59 0.55 1.76 1.70 1.74 0.44

DB3 2.44 2.40 3.84 4.08 4.65 3.72

DB4

∗

1.33 1.84 0.79 0.79 0.65 0.69

2002

DB1 0.65 0.65 0.55 0.69 0.44 0.63

DB2 0.30 0.32 0.30 0.40 0.26 0.18

DB3 2.83 1.29 2.18 1.86 1.76 1.58

DB4

∗

0.99 0.85 0.30 0.40 0.32 0.18

2004

DB1 3.94 3.01 3.15 3.37 3.19 2.79

DB2 3.01 3.39 3.58 4.79 3.09 3.84

DB3 2.73 2.18 3.92 3.15 3.39 3.23

DB4

∗

2.08 1.86 1.01 0.97 0.73 0.79

2006

DB1 11.41 21.96 14.77 12.00 13.66 12.63

DB2 0.55 0.10 1.37 1.70 1.01 1.25

DB3 5.25 3.76 4.26 4.22 3.98 3.29

DB4

∗

2.91 1.29 0.83 0.73 0.69 0.59

Average EER(%) 2.63 2.87 2.69 2.57 2.49 2.26

* Synthetic Databases

0.05). The GI (w/a) results show that the baseline

model misses some minutia angles, but it outperforms

the commercial solution. The model fails to identify

some minutia types but performs better than the ref-

erence system. GI (w/at) results show that the model

can fail in minutia type and predict minutia orienta-

tion and vice versa.

Table 3 shows the EER (%) values for all the

16 FVC test sets using the ﬁngerIDALg, the Finger-

Net, and the models proposed in this work. Com-

paring both reference systems, one based on tradi-

tional methods and the other on deep learning com-

bined with domain knowledge, the traditional method

has a lower average EER value: 2.63% versus 2.87%.

The ﬁngerIDALg had the lowest EER for the 2002 2

database and the highest for the 2006 1 database. This

results in a range from 0.30% to 11.41% which shows

a high-performance range for the test datasets.

The baseline model’s lower EER value was 0.30%

in the 2002 2 database and 14.77% in the 2006 1

database. EER averaged 2.69%. These results show

that the baseline model is competitive in compari-

son with a well-optimized commercial system, sur-

passing it in 10 of 16 test databases: 4 synthetic

databases (2000 4; 2002 4; 2004 4; and 2006 4)

and 6 databases with real images (2000 1; 2002 1;

2002 2; 2002 3; 2004 1; and 2006 3). The baseline

model outperforms the state-of-the-art reference, the

FingerNet, in 8 test sets (4 synthetic and 4 real test

sets). Notice that 12 real test sets contain images out-

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

248

domain in comparison with the 4 synthetic test sets

that are from a domain similar to the training domain.

This explains the high variability in results and the

higher accuracy in the synthetic sets, as expected.

5.2 Regularization with Additional

Ground-Truth Information

Considering the lambda

total

optimization, the results

indicate that the performance of the validation set

models was independent of lambda

total

. Using a

lambda

total

value of 0.8 resulted in a similar GI value

than using a lambda

total

value of 1.0, and when the

percentage of missing and suspicious data is consid-

ered, the performance of both models is also compa-

rable.

The EER values for the test set shown in Table 3,

indicate that a lambda

total

value of 0.8 can reduce the

average EER value to 2.57%. This value falls below

the average value of the reference systems. In 11 of

the test sets, the EER value was decreased due to the

reduction of lambda

total

These results show that adding extra tasks to the

model can act as regularization during optimization,

leading to better minutiae extraction. This model can

also extract more information from a greyscale ﬁn-

gerprint image, which can be useful for some more

sophisticated matching algorithms.

5.3 Equivariant Models

Regarding the introduction of equivariance, the equiv-

ariant model with a lambda

total

of 1.0 has a slightly

higher GI value (0.02) than the baseline model, but

their performance in the validation set is very similar

(see Table 2). The same occurs for the models with a

lambda

total

of 0.8.

The use of an equivariant architecture leads to

more robust models allowing both equivariant models

to outperform the reference systems. In particular, the

EER decreased from 2.69% to 2.49% when no addi-

tional regularization was used (lambda

total

= 1.0) and

was comparable for the scenario when lambda

total

0.8 (reduction from 2.57% to 2.26%). These results

showed that the best model performance occurs with

the combination of an equivariant architecture with a

regularization with extra ground-truth information.

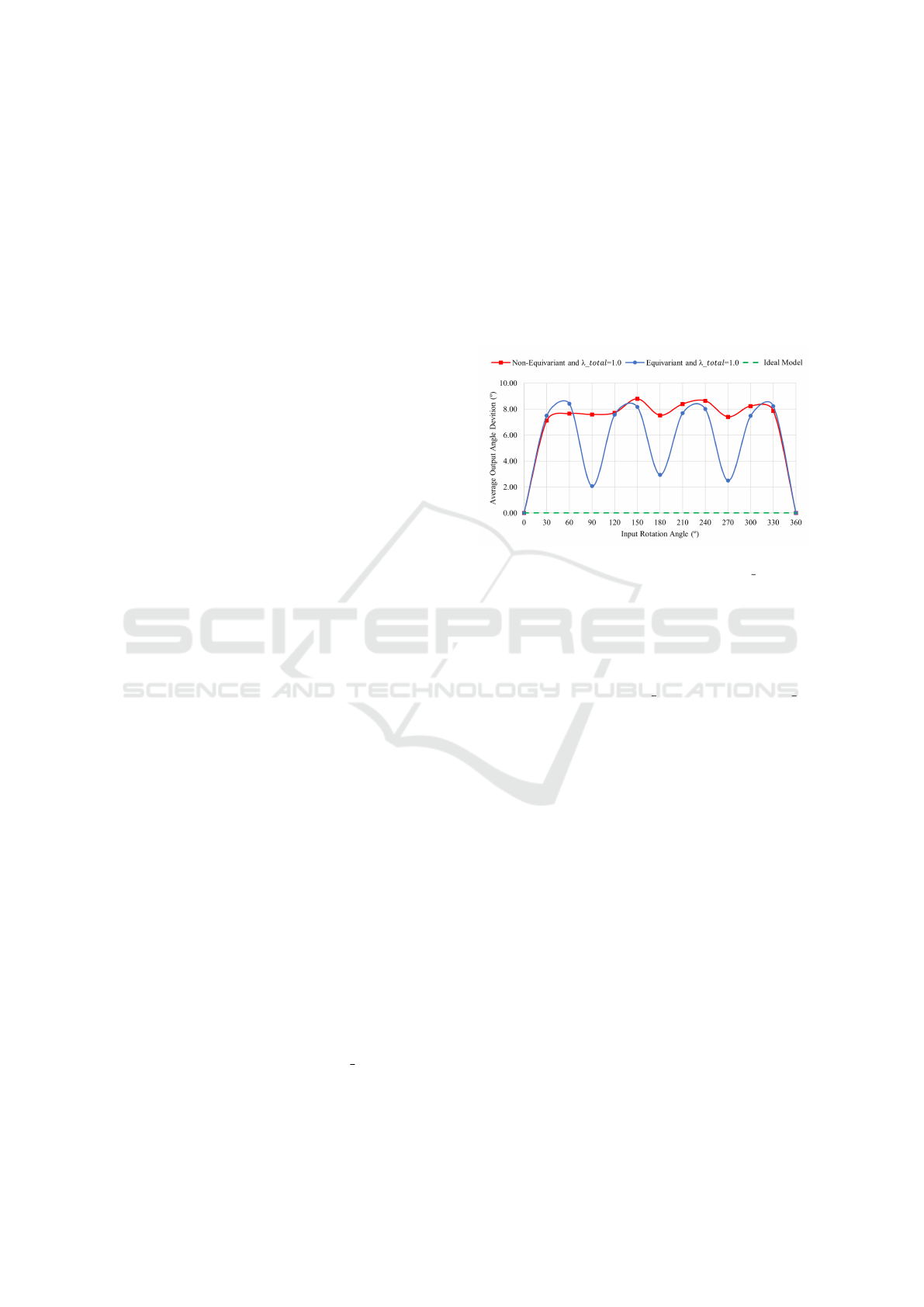
We conducted an additional test to assess the

impact of the proposed architectural change on the

model’s rotation equivariance property. For this, we

rotated all the test images in the 2000 1 FVC dataset

by a constant angle before being fed to the model.

Then, the output minutiae were readjusted to the orig-

inal position and compared to the ones obtained with

the initial images (with no rotation). The average

difference between these outputs for different input

angles is shown in Figure 3. The results show a

lower average output angle deviation for the equiv-

ariant model. This is more meaningful for the input

rotation angles multiple from 90°, as expected since

the rotation equivariance of the network was assured

for the p4 group. Despite this, a deviation of 0°is only

achieved to input rotations of 0°since the output layer

of the Group Equivariant U-Net uses a typical convo-

lution that does not assure rotation equivariance.

Figure 3: Average output angle deviation in the function

of the ﬁxated input rotation angle, for the 2000 1 dataset,

computed for the models with λ

total

= 1, and for an ideal

model with a constant angle deviation of 0°.

The ﬁnal model (equivariant and with lambda

total

of 0.8) presented the lower average ERR with the

value of 2.26%. However, a large interval of EER

values from 0.18% (2002 2) to 12.63% (2006 1)

was veriﬁed. Figure 4 shows one image from each

database with the minutiae set extracted by the ﬁnal

model. The images are examples of the diversity of

the ﬁngerprint images used to test the models and

how the acquisition conditions can change the char-

acteristics of the ﬁngerprint images and by that the

ﬁngerprint domain. This also shows that the synthetic

generator even when combined with the data augmen-

tation techniques during the training process, is not

capable of mimicking, with the same quality the dif-

ferent ﬁngerprints domain. In the case of Figure 4a,

the pattern of ridges and valleys is well-deﬁned which

allows the correct minutiae extraction, this image be-

longs to a dataset with a domain close to the synthetic

domain. For the case, of Figure 4b, the model par-

tially fails to detect the ﬁngerprint pattern with the

quality needed for a correct minutiae extraction, the

degradation, and the poor quality of this kind of im-

ages from this domain cannot be mimicked syntheti-

cally with the quality need to obtain a good general-

ization of the models to this domain.

Deep Minutiae Fingerprint Extraction Using Equivariance Priors

249

(a) (b)

Figure 4: Test images with the minutiae sets extracted by

the equivariant model with lambda

total

of 0.8: image 100 1

from the 2002 2 (a) and 2006 1 (b) datasets.

6 CONCLUSIONS

The model developed in this paper outperformed a

well-optimized commercial solution, resulting in a

lower EER average for ﬁngerprint images from var-

ious sensors. Rotation equivariance improved results,

especially model generalization. Furthermore, this

paper demonstrated that including equivariance pri-

ors into the network architecture based on the ﬁnger-

print’s prior knowledge can help deep learning meth-

ods match or exceed the performance of traditional

systems. The introduction of extra tasks enabled reg-

ularization and knowledge transfer, resulting in better

results. This allows the development of a model that

extracts more information from the same ﬁngerprint

image without jeopardizing the main task of minutiae

extraction.

Taking the ﬁnal architecture into account, future

research can be conducted to improve generaliza-

tion. This paper focused on discrete rotation equiv-

ariance. A future model may include the incorpora-

tion of equivariance to a continuous range of rotations

and equivariance to scale transformations. In addi-

tion, with the goal of achieving a more competitive

model, the computational cost must be reduced, with

special attention to the processing time.

ACKNOWLEDGEMENTS

This work is ﬁnanced by National Funds through

the Portuguese funding agency, FCT - Fundac¸

para a Ci

encia e a Tecnologia, within project

UIDB/50014/2020.

REFERENCES

Adiga V, S. and Sivaswamy, J. (2019). FPD-M-net:

Fingerprint Image Denoising and Inpainting Us-

ing M-Net Based Convolutional Neural Networks.

arXiv:1812.10191 [cs]. arXiv: 1812.10191.

Bhattacharjee, N. and Lee, C. E. (2010). Fingerprint Image

Processing And Fuzzy Vault Implementation. Journal

of Mobile Multimedia, pages 314–338.

Cappelli, R., Ferrara, M., Franco, A., and Maltoni, D.

(2007). Fingerprint veriﬁcation competition 2006.

Biometric Technology Today, 15(7-8):7–9.

Cappelli, R., Ferrara, M., and Maltoni, D. (2010). Minutia

Cylinder-Code: A New Representation and Matching

Technique for Fingerprint Recognition. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

32:2128–41.

Cappelli, R., Maio, D., Maltoni, D., Wayman, J. L., and

Jain, A. K. (2005). Performance evaluation of ﬁnger-

print veriﬁcation systems. IEEE transactions on pat-

tern analysis and machine intelligence, 28(1):3–18.

Castro, E., Pereira, J. C., and Cardoso, J. S. (2020). Soft Ro-

tation Equivariant Convolutional Neural Networks. In

2020 International Joint Conference on Neural Net-

works (IJCNN), pages 1–8. ISSN: 2161-4407.

Cohen, T. S. and Welling, M. (2016). Group Equivariant

Convolutional Networks. arXiv:1602.07576 [cs, stat].

arXiv: 1602.07576.

Dieleman, S., Fauw, J. D., and Kavukcuoglu, K. (2016).

Exploiting Cyclic Symmetry in Convolutional Neural

Networks. In Proceedings of The 33rd International

Conference on Machine Learning, pages 1889–1898.

PMLR. ISSN: 1938-7228.

Gerken, J. E., Aronsson, J., Carlsson, O., Linander, H.,

Ohlsson, F., Petersson, C., and Persson, D. (2021).

Geometric Deep Learning and Equivariant Neural

Networks. arXiv:2105.13926 [hep-th]. arXiv:

2105.13926.

Hicklin, R. A. (2009). Anatomy of Friction Ridge Skin. In

Li, S. Z. and Jain, A., editors, Encyclopedia of Bio-

metrics, pages 23–28. Springer US, Boston, MA.

Jiang, H. and Liu, M. (2017). Fingerprint Minutiae De-

tection Based on Multi-scale Convolution Neural Net-

works. In Zhou, J., Wang, Y., Sun, Z., Xu, Y., Shen,

L., Feng, J., Shan, S., Qiao, Y., Guo, Z., and Yu, S., ed-

itors, Biometric Recognition, Lecture Notes in Com-

puter Science, pages 306–313, Cham. Springer Inter-

national Publishing.

Jiang, L., Zhao, T., Bai, C., Yong, A., and Wu, M. (2016). A

direct ﬁngerprint minutiae extraction approach based

on convolutional neural networks. In 2016 Interna-

tional Joint Conference on Neural Networks (IJCNN),

pages 571–578. ISSN: 2161-4407.

Joshi, I., Anand, A., Vatsa, M., Singh, R., Roy, S. D., and

Kalra, P. (2019). Latent Fingerprint Enhancement Us-

ing Generative Adversarial Networks. In 2019 IEEE

Winter Conference on Applications of Computer Vi-

sion (WACV), pages 895–903. ISSN: 1550-5790.

Lenssen, J. E., Fey, M., and Libuschewski, P. (2018). Group

Equivariant Capsule Networks. In Advances in Neural

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

250

Information Processing Systems, volume 31. Curran

Associates, Inc.

Li, J., Yang, Z., Liu, H., and Cai, D. (2018). Deep Rotation

Equivariant Network. Neurocomputing, 290:26–33.

Maio, D., Maltoni, D., Cappelli, R., Wayman, J. L., and

Jain, A. K. (2002a). Fvc2000: Fingerprint veriﬁcation

competition. IEEE transactions on pattern analysis

and machine intelligence, 24(3):402–412.

Maio, D., Maltoni, D., Cappelli, R., Wayman, J. L., and

Jain, A. K. (2002b). Fvc2002: Second ﬁngerprint ver-

iﬁcation competition. In 2002 International Confer-

ence on Pattern Recognition, volume 3, pages 811–

814. IEEE.

Maltoni, D., Maio, D., Jain, A. K., and Feng, J. (2022).

Fingerprint Synthesis. In Maltoni, D., Maio, D., Jain,

A. K., and Feng, J., editors, Handbook of Fingerprint

Recognition, pages 385–426. Springer International

Publishing, Cham.

Naderi, H., Goli, L., and Kasaei, S. (2020). Scale Equiv-

ariant CNNs with Scale Steerable Filters. In 2020 In-

ternational Conference on Machine Vision and Image

Processing (MVIP), pages 1–5. ISSN: 2166-6784.

Nguyen, D.-L., Cao, K., and Jain, A. K. (2017). Robust

Minutiae Extractor: Integrating Deep Networks and

Fingerprint Domain Knowledge. arXiv:1712.09401

[cs]. arXiv: 1712.09401.

Nguyen, V. H., Liu, J., Nguyen, T. H. B., and

Kim, H. (2020). Universal ﬁngerprint minu-

tiae extractor using convolutional neural net-

works. IET Biometrics, 9(2):47–57. eprint:

https://onlinelibrary.wiley.com/doi/pdf/10.1049/iet-

bmt.2019.0017.

Peralta, D., Galar, M., Triguero, I., Miguel-Hurtado, O.,

Benitez, J. M., and Herrera, F. (2014). Minutiae ﬁlter-

ing to improve both efﬁcacy and efﬁciency of ﬁnger-

print matching algorithms. Engineering Applications

of Artiﬁcial Intelligence, 32:37–53.

Peralta, D., Galar, M., Triguero, I., Paternain, D., Garc

ıa,

S., Barrenechea, E., Ben

ıtez, J. M., Bustince, H., and

Herrera, F. (2015). A survey on ﬁngerprint minutiae-

based local matching for veriﬁcation and identiﬁca-

tion: Taxonomy and experimental evaluation. Infor-

mation Sciences, 315:67–87.

Pinetz, T., Huber-M

ork, R., Soukop, D., and Sablatnig, R.

(2017). Using a U-Shaped Neural Network for minu-

tiae extraction trained from reﬁned, synthetic ﬁnger-

prints. In 2017 Proceedings of the OAGM & ARW

Joint Workshop Vision, Automation and Robotics.

Rebelo, A., Oliveira, T., Correia, M. E., and Cardoso,

J. S. (2019). Are Deep Learning Methods Ready for

Prime Time in Fingerprints Minutiae Extraction? In

Vera-Rodriguez, R., Fierrez, J., and Morales, A., edi-

tors, Progress in Pattern Recognition, Image Analysis,

Computer Vision, and Applications, Lecture Notes in

Computer Science, pages 628–636, Cham. Springer

International Publishing.

Ronneberger, O., Fischer, P., and Brox, T. (2015). U-Net:

Convolutional Networks for Biomedical Image Seg-

mentation. In Navab, N., Hornegger, J., Wells, W. M.,

and Frangi, A. F., editors, Medical Image Computing

and Computer-Assisted Intervention – MICCAI 2015,

Lecture Notes in Computer Science, pages 234–241,

Cham. Springer International Publishing.

Ruder, S. (2017). An Overview of Multi-Task Learning

in Deep Neural Networks. http://arxiv.org/abs/1706.

05098. arXiv:1706.05098 [cs, stat].

Takahashi, A., Koda, Y., Ito, K., and Aoki, T. (2020). Fin-

gerprint Feature Extraction by Combining Texture,

Minutiae, and Frequency Spectrum Using Multi-Task

CNN. In 2020 IEEE International Joint Conference

on Biometrics (IJCB), pages 1–8. ISSN: 2474-9699.

Tang, Y., Gao, F., Feng, J., and Liu, Y. (2017). FingerNet:

An uniﬁed deep network for ﬁngerprint minutiae ex-

traction. In 2017 IEEE International Joint Conference

on Biometrics (IJCB), pages 108–116. ISSN: 2474-

9699.

Worrall, D. E., Garbin, S. J., Turmukhambetov, D.,

and Brostow, G. J. (2017). Harmonic Net-

works: Deep Translation and Rotation Equivariance.

arXiv:1612.04642 [cs, stat]. arXiv: 1612.04642.

Zhang, Z., Liu, S., and Liu, M. (2021). A multi-task

fully deep convolutional neural network for contact-

less ﬁngerprint minutiae extraction. Pattern Recogni-

tion, 120:108189.

Zhou, B., Han, C., Liu, Y., Guo, T., and Qin, J. (2020).

Fast minutiae extractor using neural network. Pattern

Recognition, 103:107273.

Deep Minutiae Fingerprint Extraction Using Equivariance Priors

251