Search for Rotational Symmetry of Binary Images via Radon Transform
and Fourier Analysis
Nikita Lomov
1,2 a
, Oleg Seredin
3 b
, Olesia Kushnir
3 c
and Daniil Liakhov
3 d
1
Office of Research and Development, Tula State University, Tula, Russian Federation
2
Complex Systems Department, Federal Research Center “Computer Science and Control” of the Russian Federation
Academy of Sciences, Moscow, Russia
3
Cognitive Technologies and Simulation Systems Lab, Tula State University, Tula, Russian Federation
Keywords:
Rotational Symmetry, Jaccard Index, Affine Transformations, Radon Transform, Fourier Transform.
Abstract:
We considered the optimization of such rotational symmetry properties in 2D shapes as the focus position,
symmetry degree, and measure expressed as the Jaccard index generalized to a group of two or more shapes.
We proposed to reduce the symmetry detection to the averaging of Jaccard indices for all possible pairs of
rotated shapes. It is sufficient to consider a number of pairs linearly proportional to the degree of symmetry. It
is shown that for a class of plane affine transformations translating lines into lines, and rotations in particular,
the upper estimate of the Jaccard index can be directly derived from the Radon transform of the shape. We
proposed a fast estimation of the shape degree of symmetry by applying the Fourier analysis of the secondary
features derived from the Radon transform. The proposed methods were implemented as a highly efficient
computational procedure. The results are consistent with the expert judgment of the qualities of symmetry.
1 INTRODUCTION
Detection of symmetrical objects is important for vi-
sual information processing by both humans and com-
puters. It is also widely used in many manufactur-
ing processes. It is significantly faster and cheaper to
weld plastic parts by a laser when they are symmetric.
The processing and storage of symmetric shapes in
computer graphics applications can be greatly simpli-
fied. In environmental studies, the asymmetry factor
of plant leaves is a good environmental health metric.
Rotational and reflectional symmetries are the
most common types and most familiar to humans.
Many rotational symmetry detection problem state-
ments were considered. They differ in the quality cri-
teria used to find the best points of rotation, shape pa-
rameterization approaches, and processing either the
contour or interior of the shape.
The detection of reflectional and rotational sym-
metry in weak perspective projection images was pro-
posed in (Lei and Wong, 1999). The method uses
the Hough transform to detect the skewed symmetric
a
https://orcid.org/0000-0003-4286-1768
b
https://orcid.org/0000-0003-0410-7705
c
https://orcid.org/0000-0001-7879-9463
d
https://orcid.org/0000-0003-1105-9780
axes and their skew angles. For each of the detected
skewed axes and their angles an equation for the re-
flectional and rotational symmetry estimation was ob-
tained. The Hough transform concepts were further
advanced in (Yip, 1999), where the groups of sym-
metric points, i.e., coinciding with each other as they
rotate in parallel projections, are considered. When
the initial points in the groups are known, the au-
thor identifies the subsequent points and the group’s
focus of symmetry with geometric invariants. With
multiple Hough transforms, the symmetry focus, par-
allel projection properties, and degree of symmetry
are consistently determined as values found in most
groups. Another work (Yip, 2007) describes a genetic
Fourier descriptor for rotational symmetry detection.
A closed curve can be represented by a periodic func-
tion or a set of the function’s Fourier coefficients. The
genetic algorithm is used to fit the coefficients to the
solution. The resulting function is analyzed to find the
rotational symmetry.
Symmetry detection by analyzing object contour
chains consisting of small segments was described
in (Aguilar et al., 2020). The chains are divided
into fragments to be compared to detect the symme-
try. The method offers excellent performance for de-
tecting the object symmetry and its order, and good
performance when handling quasi-symmetric objects.
280
Lomov, N., Seredin, O., Kushnir, O. and Liakhov, D.
Search for Rotational Symmetry of Binary Images via Radon Transform and Fourier Analysis.
DOI: 10.5220/0011679900003417
In Proceedings of the 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 4: VISAPP, pages
280-289
ISBN: 978-989-758-634-7; ISSN: 2184-4321
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

Another contour-based approach (Llados et al., 1997)
represents the shape boundary as substrings and sub-
sequently uses their cyclic comparison to detect rota-
tional symmetry. The key concept is that the boundary
of a rotationally symmetric shape consists of identi-
cal substrings. The number of such substrings indi-
cates the degree of rotational symmetry. The method
works fine for perfect shapes, but requires adjusting
the distortion factor when handling quasi-symmetric
objects. A correlation measure to find various types of
symmetry is used in (Kondra et al., 2013). The mea-
sure’s maximum value characterizes the symmetry re-
gion. This approach makes it possible to search for
symmetries even when there are multiple objects in
the image. It was proposed in (Lee and Liu, 2010) to
analyze the patterns occurring as the polar coordinate
system with its origin at the possible center of sym-
metry is converted into a Cartesian coordinate system
with the Fourier analysis.
Symmetry detection in full-color and grayscale
images are also of considerable interest. The anal-
ysis of a so-called Gradient Vector Flow image was
proposed in (Shiv Naga Prasad and Davis, 2005). A
graph linking the image pixels similar to the rotated
versions of each other in terms of the flow is gener-
ated. A presence of n-size cycles in the graph indi-
cates the presence of a n-degree symmetry with its
focus at the mean of cycle points. There are neural
network-based rotational symmetry detection meth-
ods. A notable example of such an approach (Krip-
pendorf and Syvaeri, 2020) assumes that the points
symmetrical with respect to a complex transforma-
tion will have similar representation in the last hidden
layer. It is also possible to develop special layers for
neural networks in order to make these networks par-
tially equivariant to rotations (Dieleman et al., 2016).
For this work, symmetry detection algorithms
based on image projections are especially relevant.
They consider not individual points, but groups of
points behaving similarly during the transformation.
The illustrative approach (Nguyen, 2019) uses a
Radon transform of a 2D shape and its derivative R-
signature as an integral over the squared Radon trans-
form. The method core is the obvious consideration
that the Radon transform along the lines parallel to the
symmetry axis is also symmetric. The author further
expanded this approach in (Nguyen et al., 2022), pro-
viding a large theoretical background and presenting
a new binary image dataset to assess the symmetry
detection strategies. This study uses the so-called LIP
(the Largest Intersection and Projection) proposed in
(Nguyen and Nguyen, 2018). It is a function of the
angle expressing the ratio of the largest intersection
with a shape selected from all the lines having a given
angular direction to the shape’s projection onto a per-
pendicular straight line.
These works deal with reflection symmetry, but
similar theorems about the properties of symmetric
shapes can be also derived for rotational symmetry.
Note that although the above-mentioned works con-
tain some important insights concerning the proper-
ties of symmetric shapes, for non-strict symmetry we
face a problem of selecting from a set of “non-ideal”
lines. We should somehow compare such lines with
each other. The answer usually relies on statistical
(e.g., the χ
2
criterion) or computationally defined (the
Hough accumulator array analysis) criteria with no
explicit geometric interpretation. Subsequently we
will show that this problem can be solved by using
the Jaccard index, a special shape comparison mea-
sure. The Radon transform applied to it produces ex-
plicit upper estimates of the measure and gives an up-
per approximation of the function to be optimized.
2 ROTATIONAL SYMMETRY
MEASURE BASED ON THE
JACCARD INDEX
In a strict sense, a planar shape A has a degree k ≥ 2
rotational symmetry with its focus at c = (x
c
,y
c
) if the
shape does not change when rotated around the focus
by {
2πi
k
}
k−1
i=1
angles. In other words, we can assume
that we have a set of k shapes {A
0
,... A
k−1
}, where
the shape A
i
is obtained from the shape A by rotat-
ing it by
2πi
k
. The symmetry criterion is that all these
shapes coincide with each other. However, despite
its exceptional value for geometry and group theory,
such a definition is hardly applicable to the recogni-
tion of real-world images. There are two reasons for
this. First, such objects are rare. The second reason is
the ways images are stored in computer memory and
the transformation algorithms are implemented. For
instance, rotations of a raster image around a given
point, generally speaking, do not generate a group.
Moreover, for real-world applications we need not
just to divide shapes in the images into ”symmetrical”
and ”asymmetrical” ones, but to quantitatively esti-
mate the symmetry measure as closeness to an abso-
lutely symmetrical standard for all shapes, including
those that are unambiguously estimated as asymmet-
rical in terms of common sense.
A symmetry measure based on Jaccard index
(Kushnir et al., 2017) is of particular interest for the
reflection symmetry analysis. The shape A is com-
pared to its version A
′
reflected from its symmetry
Search for Rotational Symmetry of Binary Images via Radon Transform and Fourier Analysis
281

axis:
J(A) =
|A ∩ A
′
|
|A ∪ A
′
|
. (1)
This value range is [0, 1], which meets the defi-
nition of a measure. We will call the shapes quasi-
symmetric if their symmetry measure is close to 1.
Such a measure can be applied to degree 2 rotational
(central) symmetry, since only two shapes are com-
pared. The paper (Seredin et al., 2022) investigates
the search for the symmetry focus point where the
Jaccard index as a function of the focus position is
approximated by a quadratic function, and then the
search covers the neighborhood of the paraboloid ver-
tex.
As the Jaccard index is generalized to rotational
symmetry of any degree, more than two shapes are to
be compared. An obvious solution would be to aver-
age the measures over all possible pairs:
J
(k)
(A) =
2
k(k − 1)
k−2
∑
i=0
k−1
∑
j=i+1
|A
i
∩ A
j
|
|A
i
∪ A
j
|
=
=
2
k(k − 1)
k−2
∑
i=0
k−1
∑
j=i+1
J
i j
(A). (2)
At first glance, this requires to process
k(k−1)
2
number of pairs quadratic in k, which will negatively
affect the computational efficiency. The following
theorem shows that it is sufficient to consider a num-
ber of pairs linearly proportional to k.
Theorem 1. Let min(|i − j|,k − |i − j|) =
min(|p−q|,k − |p−q|) for 0 ≤ i, j, p,q ≤ k −1. Then
|A
i
∩ A
j
| = |A
p
∩ A
q
|, and |A
i
∪ A
j
| = |A
p
∪ A
q
|.
Proof. It follows that either q ≡
k
p + ( j − i), or
q ≡
k
p − ( j − i) and p ≡
k
q + ( j − i). In the first case,
A
p
is obtained from A
i
by rotating it by
2π(p−i)
k
, and
A
q
is obtained from A
j
by rotating it by same angle
around the same point. Therefore, A
p
∩A
q
and A
p
∪A
q
are obtained from A
i
∩ A
j
and A
i
∪ A
j
respectively by
the same rotation, and the areas of these sets are main-
tained. The equality of areas in the second case fol-
lows from the commutativity of the intersection and
union operations, so we can swap p and q. □
It is sufficient to consider a pair of shape num-
bers (i, j) for each d = min(|i − j|,k − |i − j|), 1 ≤
d ≤
k
2
, for example, (0,d) pairs. Let us introduce
the coefficients into the final equation. For con-
venience, the pairs (i, j) and ( j, i) are assumed to
be identical, and modulo k numbers are processed.
If d <
k
2
, each (0,d) pair covers k of the original
pairs: (0,d),(1, d + 1),...(k − 1,k − 1 + d). When
d =
k
2
, the pair (0,d) covers
k
2
of the original pairs:
J(A
0
,A
1
) = 0.8223 J(A
0
,A
2
) = 0.8110
J(A
0
,A
3
) = 0.8324 J(A
0
,A
4
) = 0.7941
Figure 1: Rotations to estimate the Jaccard index of a sym-
metry degree 8 shape. The original shape is filled with black
and blue, the rotate one, in black and red.
(0,d),(1,d + 1),. .. (d − 1, k − 1), since (d,k) coin-
cides with the pair (0, d) and then the pairs are re-
processed. The resulting transformation of the equa-
tion 2 is as follows:
J
(k)
(A) =

















2
k(k−1)

∑
k−1
2
i=1
k
|A
0
∩A
i
|
|A
0
∪A
i
|

,
if k is odd;
2
k(k−1)

∑
k
2
−1
i=1
k
|A
0
∩A
i
|
|A
0
∪A
i
|

+
k
2
|A
0
∩A
k
2
|
|A
0
∪A
k
2
|

,
if k is even.
(3)
Note that the sum of the coefficients in parentheses in
the equation above equals to
k(k−1)
2
in both cases.
The average Jaccard index estimation flow for ro-
tated shapes is shown in Fig. 1. For exact symmetry,
the focus point coincides with the center of gravity.
For quasi-symmetric shapes, finding a focus point op-
timal in terms of Jaccard index is a separate problem.
Note that for shapes with a sufficiently high symme-
try measure, the focus is often close to the center of
gravity. It prompts to limit the area of possible fo-
cus positions. The following section investigates the
exact focus location problem.
3 UPPER JACCARD INDEX
ESTIMATES BASED ON THE
RADON TRANSFORM
Rotation, just like reflection, is a special case of a pro-
jective transformation that converts straight lines into
VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications
282

straight lines. We define lines by a two parameters
(r,θ): line to the origin distance, and the angle be-
tween the normal to the line (cos θ,sin θ) and the axis
X. Such a line is defined by the equation
x cos θ + y sin θ = r. (4)
We consider an affine transformation with the matrix
C =


c
11
c
12
c
13
c
21
c
22
c
23
0 0 1


, det C ̸= 0.
Note that this transformation converts
(−sin θ,cos θ), the directional vector of the line
l(r,θ) into a vector
(−λsin θ
′
,λ cosθ
′
) =
= (−c
11
sinθ +c
12
r cos θ, −c
21
sinθ +c
22
cosθ) .
Therefore, the line l(r,θ) is converted into the line
l(r
′
,θ
′
), where
θ
′
= atan2(c
11
sinθ − c
12
cosθ,−c
21
sinθ + c
22
cosθ),
r
′
= cosθ
′
(c
11
r cosθ + c
12
r sinθ + c
13
)+
+sin θ
′
(c
21
r cosθ + c
22
r sinθ + c
23
). (5)
(a) (b)
0
/6 /3 /2 2 /3 5 /6
- /2
- /3
- /6
0
/6
/3
/2
2 /3
0
/6 /3 /2 2 /3 5 /6
0.8
0.9
1
1.1
1.2
1.3
1.4
(c) (d)
Figure 2: The lines before (a) and after (b) the affine trans-
formation (color-coded). (c) θ
′
(θ) and (d) λ(θ) curves.
Also note that under the transformation the dis-
tances along the parallel lines are scaled uniformly,
regardless of position on the line. The scale factor is:
λ(θ) =
q
(−c
11
sinθ + c
12
cosθ)
2
+ (−c
21
sinθ + c
22
cosθ)
2
.
It follows from the change in the directional vector
length. Fig. 2 shows an example of the line affine
transformation C.
It may be possible to estimate the Jaccard index
from the corresponding characteristics of the line be-
fore and after transformations. One of the most com-
mon such characteristics is the Radon transform. It
specifies the length of the intersection of all possible
lines with a shape. It is expressed as
T
A
(r,θ) =
+∞
Z
−∞
χ
A
(r cos θ − zsin θ,r sin θ + zcosθ)dz.
(6)
Where χ
A
is the characteristic function of the shape
A:
χ
A
(x,y) =
(
1, if (x,y) ∈ A;
0, if (x,y) /∈ A.
(7)
The Radon transform gives natural upper esti-
mates of the Jaccard index.
Theorem 2. Let the shape A
′
is obtained
from A by an affine transformation. Let us denote
r
′−1
(r,θ) and θ
′−1
(θ) such r
′′
and θ
′′
that r
′
(r,θ
′′
) = r
and θ
′
(θ
′′
) = θ. Then for any given θ
|A ∩ A
′
| ≤
R
+∞
−∞
min

T (r,θ), λ(θ
′−1
(θ))T (r
′−1
(r,θ), θ
′−1
(θ)

dr = B
∩
(A),
(8)
|A ∪ A
′
| ≥
R
+∞
−∞
max

T (r,θ), λ(θ
′−1
(θ))T (r
′−1
(r,θ), θ
′−1
(θ)

dr = B
∪
(A).
(9)
Proof. Let us consider the intersection area
expressed as an integral over the l(r,θ) lines when θ
is fixed:
|A ∩ A
′
| =
=
+∞
R
−∞
+∞
R
−∞
χ
A
(x(r,θ,z),y(r,θ,z))χ
A
′
(x(r,θ,z),y(r,θ,z))dzdr ≤
≤
+∞
R
−∞
min(T
A
(r,θ),T
A
′
(r,θ))dr, (10)
where x(r,θ, z) = r cosθ − z sinθ, y(r,θ,z) = r sin θ +
zcos θ.
Similarly,
|A ∪ A
′
| ≥
Z
+∞
−∞
max(T
A
(r,θ),T
A
′
(r,θ)). (11)
Since the line l(r,θ) is converted into the line l(r
′
,θ
′
)
and the distances are stretched λ(θ) times,
T
A
′
(r
′
,θ
′
) = λ(θ)T
A
(r,θ),
T
A
′
(r,θ) = λ(θ
′−1
(θ))T
A
(r
′−1
(r,θ),θ
′−1
(θ)). (12)
By substituting the expression for T
A
′
(r,θ), we obtain
the sought equations. The theorem is now proved. □
Since |A
′
| = detC|A|, |A ∪ A
′
| = |A| + |A
′
| − |A ∩
A
′
|,
min(T
A
(r,θ),T
A
′
(r,θ)) + max (T
A
(r,θ),T
A
′
(r,θ)) =
= T
A
(r,θ) + T
A
′
(r,θ), (13)
therefore, B
∪
(A) + B
∩
(A) = (1 + det C)|A|. This re-
sults in the final upper estimate of the Jaccard index:
J(A) ≤ J(A) =
B
∩
(A)
(1 + det C)|A| − B
∩
(A)
. (14)
Search for Rotational Symmetry of Binary Images via Radon Transform and Fourier Analysis
283

4 SEARCH FOR SYMMETRY
FOCUS USING UPPER
ESTIMATES
When we rotate a shape by the angle α, the l(r,θ)
lines are converted into the l(r
′
,θ + α) lines. Let us
first show that as shapes are rotated, the distance be-
tween the point projections along the corresponding
lines is preserved. Note that the matrix of rotation
about the point (x
c
,y
c
) is


cosα −sin α d
x
sinα cosα d
y
0 0 1


,
where d
x
= −x
c
cosα + y
c
sinα + x
c
, d
y
= −x
c
sinα −
y
c
cosα +y
c
.
Consider the points a = (x
a
,y
a
) and b = (x
b
,y
b
).
Let their projections along the lines l(r,θ) are d away
from each other:
x
b
cosθ +y
b
sinθ −x
a
cosθ +y
a
sinθ = d.
Then, after rotating by α, the distance between their
projections along the l(r,θ+α) lines will be the same:
(x
b
cosα − y
b
sinα − x
c
cosα + y
c
sinα + x
c
)cos(θ + α)+
+(x
b
sinα + y
b
cosα − x
c
sinα − y
c
cosα + y
c
)sin(θ + α)+
−(x
a
cosα − y
a
sinα − x
c
cosα + y
c
sinα + x
c
)cos(θ + α)+
−(x
a
sinα + y
a
cosα − x
c
sinα − y
c
cosα + y
c
)sin(θ + α) =
=((x
b
− x
a
)cosα − (y
b
− y
a
)sinα)cos(θ + α)+
+((x
b
− x
a
)sinα + (y
b
− y
a
)cosα)sin(θ + α) =
=(x
b
− x
a
)(cosαcosθ cos α − cosα sin θ sin α)+
+(x
b
− x
a
)(sinαsinθ cos α + sinα cos θ sin α)+
+(y
b
− y
a
)(−sin α cos θ cos α + sinα sin θ sin α)+
+(y
b
− y
a
)(cosαsinθ cos α + cosα cos θ sin α) =
=(x
b
− x
a
)cosθ + (y
b
− y
a
)sinθ = d.
Thus, r
′
is obtained from r by adding a value that
depends on θ but not on r as the center of rotation is
fixed:
d(θ)= ((x
a
− x
c
)cos α − (y
a
− y
c
)sin α + x
c
)cos(θ + α)+
+((x
a
− x
c
)sin α + (y
a
− y
c
)cos α + y
c
)sin(θ + α) − x
a
cosθ − y
a
sinθ =
= x
c
cos(α + θ) + y
c
sin(α + θ) − x
c
cosθ − y
c
sinθ =
= x
c

2sin
α+2θ
2
sin
−α
2

+ y
c

2sin
α+2θ
2
cos
−α
2

=
= 2sin
α+2θ
2

x
c
cos

π
2
+
α
2

+ y
c
sin

π
2
+
α
2

.
(15)
As a result, all the centers of rotation on the
l(r,
π
2
+
α
2
) line produce an identical shift. We ob-
tain r
′
(r,θ) = r + d(θ), and since θ
′−1
(θ) = θ − α,
r
′−1
(r,θ) = r − d(θ − α). Given that for a λ(θ) ≡ 1
rotation, the equation 12 takes the form:
T
A
′
(r,θ) = T
A
(r − d(θ − α),θ − α), (16)
B
∩
1
(A|0) B
∩
1
(A|π/6) B
∩
1
(A|π/3) B
∗
1
(A) Image
B
∩
2
(A|0) B
∩
2
(A|π/6) B
∩
2
(A|π/3) B
∗
2
(A) J
(6)
(A)
B
∩
3
(A|0) B
∩
3
(A|π/6) B
∩
3
(A|π/3) B
∗
3
(A) J
(6)
(A)
Figure 3: Upper Estimates of the Jaccard Index.
which results in a general upper estimate of the inter-
section, shown in Fig. 3.
B
∩
i
(A|θ) =
R
+∞
−∞
min

T
A
(r,θ),T
A

r − d

θ −
2πi
k

,θ −
2πi
k

dr.
(17)
Note that the θ angle in these estimates is arbitrary,
and B
∩
i
(A|θ) = B
∩
i
(A|θ+π), since T
A
(r,θ) = T
A
(r,θ+
π). We will use θ from the {
2π j
k
}
k−1
j=0
set to refine the
estimates taking into account all the rotation angles:
B
∗
i
(A) = min
0≤ j≤k−1
{B
∩
i
(A|2π j/k)}. (18)
Therefore, we can express the final estimates for
all the k images:
J
(k)
(A) =













2
k−1
∑
k−1
2
i=1
B
∗
i
(A)
2|A|−B
∗
i
(A)
,
if k is odd;
1
k−1

B
∗
k/2
(A)
2|A|−B
∗
k/2
(A)
+ 2
∑
k−1
2
i=1
B
∗
i
(A)
2|A|−B
∗
i
(A)

,
if k is even.
(19)
Note that so far the (x
c
,y
c
) center of rotation was
assumed to be known, although the problem state-
ment implies it is not. Let us denote the Jaccard index
averaged over k images as by J
(k)
(A|x
c
,y
c
) for a ro-
tation around the (x
c
,y
c
) point. Then we come to the
following optimization problem:
maximize
x
c
,y
c
J
(k)
(A|x
c
,y
c
).
To solve it, we apply the following algorithm with
upper estimates:
1. Let the center of gravity of the A shape be the ini-
tial position of the (x
∗
,y
∗
) center of rotation.
2. Generate a list L = {(x,y) |(x, y) ∈
conv(A), J
(k)
(A|x,y) > J
(k)
(A|x
∗
,y
∗
)}, and
sort it in the descending by J
(k)
(A|x,y) order.
VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications
284

3. Enumerate the L values while J
(k)
(A|x,y) >
J
(k)
(A|x
∗
,y
∗
), calculate J
(k)
(A|x,y), replacing
(x
∗
,y
∗
) with (x,y) if J
(k)
(A|x,y) > J
(k)
(A|x
∗
,y
∗
).
5 ORDER OF SYMMETRY
ESTIMATION USING THE
FOURIER TRANSFORM OF
THE SHAPE PROJECTION
FEATURES
So far, the symmetry order k was assumed to be
known, and was not questioned. An obvious approach
would be to turn k into an optimization parameter:
maximize
k,x
c
,y
c
J
(k)
(A|x
c
,y
c
) ≡ maximize
k
max
x
c
,y
c
J
(k)
(A|x
c
,y
c
).
Let us note that a shape with an order k symmetry is
also considered as symmetric with the m order, where
m is the divisor of k. The problem statement above in
some cases leads to giving the priority to one of the
divisors if its symmetry measure is slightly higher.
It does not agree well with the human concept of
symmetry. A possible solution is to modify the es-
timates with the R(v,k) regularization function which
increases for both arguments:
maximize
k,x
c
,y
c
R

J
(k)
(A|x
c
,y
c
),k

,
or use the max divisor with the measure close to the
max value as the degree of symmetry (Yip, 1999):
k
∗
= max{n : n
.
.
. arg max
k
max
x
c
,y
c
J
(k)
(A|x
c
,y
c
),
max
x
c
,y
c
J
(n)
(A|x
c
,y
c
) ≥ µ max
k,x
c
,y
c
J
(k)
(A|x
c
,y
c
)}.
However, such a solution still requires to search
for the optimal focus for each order of symmetry. It
would be computationally expensive. We used a fast
order of symmetry estimation when the focus position
is not known. Note that for a strictly symmetric shape
with the k degree of symmetry its Radon transform is
periodic:
T
A
(r + d(θ|x
c
,y
c
,2π/k),θ +2π/k) = T
A
(r,θ). (20)
Therefore, T
A
(r,θ +
2π
k
) as a function of r is iden-
tical to T
A
(r,θ) up to the shift value. We will de-
scribe the function with features independent of these
shifts. A similar approach is also used to estimate
the LIP-signature (Nguyen and Nguyen, 2018), where
the following values are calculated: max
r
T
A
(r,θ),
R
+∞
−∞
[T
A
(r,θ) > 0]dr. They are invariant to shifts of
r. Since the Fourier transform is well suited to detect
the periodicity of a function, we use a single feature,
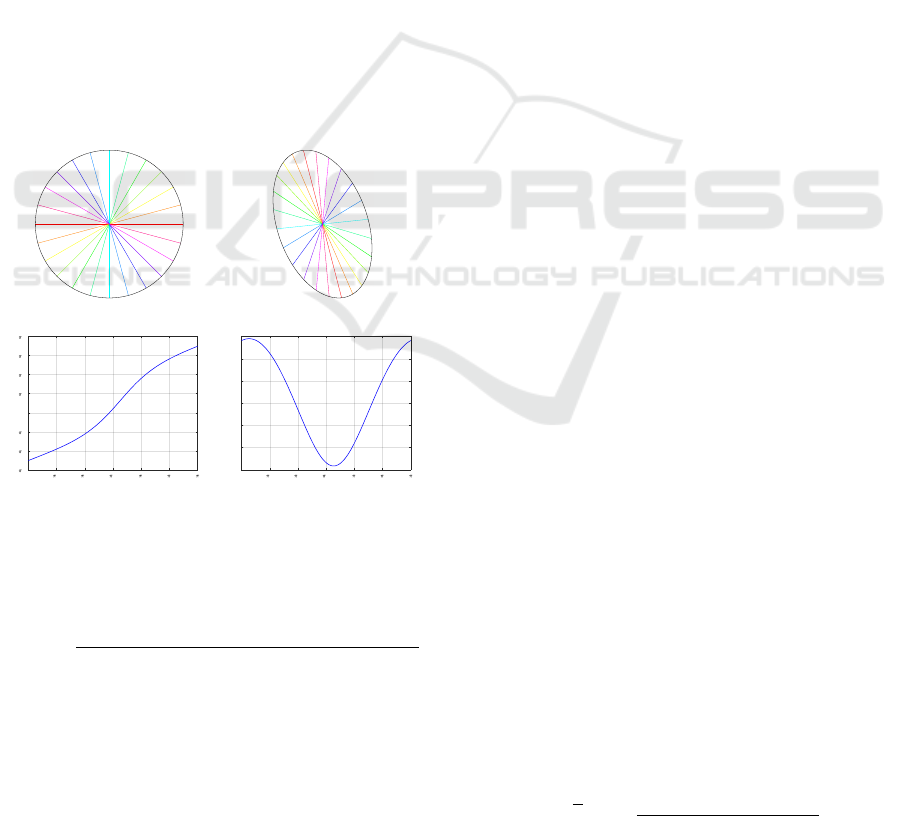
a complex number:
W
A
(θ) = (T
A,0.5
(θ) − T
A,0.5−δ
(θ)) + i(T
A,0.5+δ
(θ) − T
A,0.5
(θ)),
(21)
where T
A,γ
(θ) is the corresponding quantile of the A
shape projections along the lines at the θ angle:
T
A,γ
(θ) = r, such that
1
|A|
Z
r
−∞
T
A
(s,θ)ds = γ. (22)
The F
A
(k) discrete complex-valued Fourier trans-
form is calculated for the W
A
(θ) − mean
θ
W
A
(θ) func-
tion and then normalized:
b
F
A
(k) =
F
A
(k)
∑
k
(F
A
(k))
2
. (23)
The final degree of symmetry is the max modulus am-
plitude:
k
∗
= max
k
|
b
F
A
(k)|, (24)
then the optimal center of rotation (x
c
,y
c
) is deter-
mined by the algorithm presented in the previous sec-
tion.
0 50 100 150 200 250 300 350
Angle, degrees
60
70
80
90
100
110
120
130
140
150
Deviation, pixels
Left
Right
0 2 4 6 8 10 12 14 16 18 20
Frequency
0
1000
2000
3000
4000
5000
6000
7000
8000
9000
Amplitude
(a) (b) (c)
Figure 4: Image degree of symmetry estimation (a) with
the Fourier transform (c) of the projection quantiles (b) for
α = 0.25.
Fig. 4 shows an example of determining the de-
gree of symmetry with the proposed algorithm.
6 EXPERIMENTS
2 (19) 3 (8) 4 (23) 5 (5) 6 (16) 8 (21)
9 (1) 10 (2) 12 (3) 18 (1) 22 (1)
Figure 5: UTLN-MRA dataset images. The number of
images in the dataset is indicated in parentheses after the
degree of symmetry.
The algorithm was implemented in C++ using Mi-
crosoft Visual Studio 2019 and the OpenCV 4.5.5 li-
brary. We ran it on a laptop with an Intel® Core
TM
Search for Rotational Symmetry of Binary Images via Radon Transform and Fourier Analysis
285

i7-9750H CPU, 16 Gb RAM, and a NVIDIA GeForce
GTX 1660 Ti video card. For comparison, we also
implemented a Hough detector-based method which
follows the concepts presented in (Yip, 1999). Since
the search for symmetry in parallel projections is be-
yond the scope of this work, we skipped the projec-
tion parameter estimation step. We considered only
the points that pass into each other after a “perfect”
rotation. As a result, we produced Algorithm 1. It is
worth mentioning how to scale the measure values for
each degree of symmetry. Suppose we have an image
with the k degree of symmetry. Then n of its pixels
are split into
n
k
orbits, each of which has
k(k−1)
2
pairs
of points that pass into each other after various rota-
tions. Then, the maximum number of possible pairs
is
n(k−1)
2
. If we divide the number of pairs found by
this value, we get a fraction of the maximum. Note
that the original paper proposes to consider only the
boundary points of the image. We can assume the al-
gorithm produces an approximate Jaccard index for
these points.
We used the UTLN-MRA (Multiple Reflection
Axis) image dataset presented in (Nguyen et al.,
2022) and available at http://tpnguyen.univ-tln.fr/
download/UTLN-Reflection/ to evaluate the effi-
ciency of the proposed method. Although the dataset
is originally designed to detect reflective symmetry,
most images have multiple symmetry axes and the
axes have a common point. Each image is divided by
these axes into equal parts which can be transformed
into each other by rotating the image around the com-
mon point. For this reason, the dataset is suitable for
rotational symmetry experiments. The dataset con-
tains 100 images. Their degree of symmetry, as evalu-
ated by the authors, ranges from 2 to 22. Examples of
the images with each degree of symmetry are shown
in Fig. 5.
0 5 10 15 20 25
Order of symmetry
0
0.2
0.4
0.6
0.8
1
1.2
Measure of symmetry
Radon
Hough
Figure 6: Comparison of the Radon transform and Hough
detector-based methods.
Fig. 6 shows an example of the results for the pro-
posed method based on the Radon transform and the
method based on the Hough detector. Obviously, for
both methods, the comparison of the estimates for dif-
ferent degrees of symmetry is complicated, especially
Algorithm 1: Search for rotational symmetry parameters.
Require: Image I
Ensure: The degree of symmetry k
∗
and its center
(x
∗
,y
∗
)
for k = 2,...,k
max
do
Fill the A accumulator array with zeros. The
array size is the same as I
for t = 2,...,k do
for (p, q) from the set of all pairs formed by
n boundary points of I do
Define the affine similarity transforma-
tion T that converts the first point of a regular k-gon
to p, and the t-th point, to q
(x,y) = T (0,0) (the center point for a
rotation which transforms p to q)
Increment A[int(y),int(x)]
end for
end for
Determine the k-symmetry center (x
k
,y
k
) =
argmaxA and the symmetry measure m
k
=
2max A
n(k−1)
end for
Determine the center of symmetry (x
∗
,y
∗
) and
thedegree of symmetry k
∗
as the best value over all
degrees.
if the “correct” degree is not a prime number. Note
that the Hough-based method is more prone to over-
rate the estimates for smaller degrees of symmetry.
Therefore, a more stringent regularization is required.
By modifying the estimates according to the rule
R(v,k) =
v
1+λ/k
the degree is correctly determined in
90% cases for the Hough detector (the optimal value
λ = 3.2) and in 95% cases for the Radon transform-
based method (the optimal value λ = 0.28).
The Fourier transform-based fast degree of sym-
metry estimation described in section 5 significantly
reduces the run time and simplifies the regularizer se-
lection. We will use it as follows. Since the differ-
ences characterizing the degree of symmetry can be
found both at the edges and in the middle of a shape,
we need to perform a quantile analysis across the en-
tire [0,1] range. Therefore, we calculate the degree
of symmetry k(δ) for multiple quantiles: δ ∈ ∆ =
{0.1,0.2, 0.3,0.4}, and the final degree is estimated
as the argument of the max Jaccard index with regu-
larization:
k
∗
= argmax
k∈{k(δ)|δ∈∆}
J
(k)
(A)
1 + λ/k
. (25)
This approach correctly determines the degree of
symmetry for 98 of 100 images, while the total run
time is reduced by two orders of magnitude: from 12
to 0.12 second on average per image. Note that with-
out using a GPU, the Hough detector-based method
VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications
286

is about 10x slower than the Radon transform-based
method without the fast degree of symmetry estima-
tion. This is largely due to the presence of multiple
contours in a number of images. For example, pay at-
tention to the images with 5, 6, 8, 12, and 22 degrees
of symmetry, that are shown in Fig. 5.
0 50 100 150 200 250 300 350
Angle, degrees
0
20
40
60
80
100
120
Deviation, pixels
= 0.1
= 0.2
= 0.3
= 0.4
(a) (b) (c) (d)
Figure 7: Degree of symmetry estimation errors. (a) A 2
degree of symmetry image, (b) the quantiles of its Radon
transform, (c) a 8 degree image, (d) its comparison with the
imaged rotated by 45
◦
.
Let us conclude the study on this database with
an error analysis. Fig. 7 shows the images for which
the proposed method is unable to correctly determine
the degree of symmetry. In the first case (Fig. 7ab)
the shape in the image is a composition of symmet-
ric shapes with the 6 and 8 orders of symmetry, and
its degree of symmetry is equal to the greatest com-
mon divisor of these numbers: 2. A Fourier analy-
sis does not identify that the shape is composite and
predicts the degree of 6 for all the quantiles. In the
second case (Fig. 7cd), the shape consists of thin ele-
ments that do not overlap well when rotated, although
the human perception identifies 8 equal sections in the
shape. As a result, the measure for degree 8 vs. de-
grees 2 and 4 drops too much to be corrected by the
regularizer: 0.9012 vs. 0.9986 and 0.9988, respec-
tively. The errors indicate that it is difficult to find
a general symmetry measure for all shapes. When
the shape is based on a wide circle, as in Fig. 6, the
measures are close to each other for many degrees of
symmetry, and the differences that distinguish the de-
gree are expressed only in a small fraction of the Jac-
card index. On the other hand, a shape formed by
thin elements may poorly overlap itself after rotation.
It makes us think about further modifications of the
symmetry measure, such as using pixel weights and
non-affine transforms.
Although the R and LIP signatures (Nguyen et al.,
2022) are used to detect only reflection symmetry,
they can be naturally adapted to analyze rotational
symmetry. Recall that the R-signature is defined as
follows:
R
A
(θ) =
Z
+∞
−∞
T
2
A
(r,θ)dr. (26)
In turn, the LIP-signature is
L
A
(θ) =
max
r
T
A
(θ,r)
sup{R
+
(θ +
π
2
)} − inf{R
+
(θ +
π
2
)}
, (27)
R
+
(θ) = {r : T
A
(θ,r) > 0}.
Note that for a figure with rotational symmetry of de-
gree k, the corresponding signatures are periodic:
S
A

θ +
2π
k

= S
A
(θ), S
A
∈ {R
A
,L
A
}. (28)
It is on this property that our procedure for determin-
ing the quality measure of rotational symmetry will
be based using correlation as in the original article:
G
A
(k) =
1
⌈
k
2
⌉ − 1
⌈
k
2
⌉−1
∑
i=1
corr
θ∈[0,2π]

S
A
(θ),S
A
(θ +
2π
k
)

.
(29)
At the same time, these signatures are π-periodic
by design, so corr
θ∈[0,2π]
(S
A
(θ),S
A
(θ + π)) = 1, and
G
A
(2k) = G
A
(k) if k is odd.
0 50 100 150 200 250 300 350
Angle, degrees
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
R-signature value
(a) (b)
0 50 100 150 200 250 300 350
Angle, degrees
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
LIP-signature value
0 5 10 15 20 25
Order of symmetry
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
Measure of symmetry
R
LIP
(c) (d)
Figure 8: Detection of rotational symmetry using Nguyen
signatures. (a) Initial image; (b) its R-signature; (c) its LIP-
signature; (d) symmetry measures for various degrees.
For the final experiment, 57 binarized
starfish images were prepared from the repos-
itories available at https://australian.museum/
learn/animals/sea-stars/sydney-seastars/ and
http://www.jaxshells.org/starfish.htm. For each
image, the number of rays per individual was man-
ually determined, which varied from 5 to 11 in the
entire set. The determination of the degree of sym-
metry was considered correct if the corresponding
measure of symmetry based on signatures was among
the four largest values. Note that this is a looser
setting than in the method proposed by us, since it
does not require identifying the best degree among
the four in additional indicators. As a result, the
number of individuals with correctly counted rays
was 32 (56.14%) for the R-signature, 40 (70.18%)
for the LIP-signature, and 49 (85.96%) when using
proposed Fourier-based signature. This indicates that
the Nguyen signatures, depicted in Fig. 8, are less
Search for Rotational Symmetry of Binary Images via Radon Transform and Fourier Analysis
287

suitable for rotational symmetry detection, possibly
due to the inability to distinguish directions at angles
θ and θ+ π.
J
(7)
(A|x
c
,y
c
) = 0.7828 J
(7)
(A|x
∗
,y
∗
) = 0.8381
J
(5)
(A|x
c
,y
c
) = 0.7637 J
(5)
(A|x
∗
,y
∗
) = 0.7738
Figure 9: Comparison of Jaccard measures at the center of
mass (left column) and at the optimal point (right column).
Images averaged over all rotations are shown. The original
images are highlighted in red.
Finally, we note that for all images the center of
symmetry found from the upper estimates of the Jac-
card index coincides with the center found by com-
plete enumeration. This is due to the very nature of
the algorithm. It ensures that the optimal center point
is not be excluded at the point filtering stage since
the upper estimate is high, and eventually the symme-
try measure for it will be explicitly checked. At the
same time, the process of searching for the optimal
focus can sometimes significantly improve the initial
approximation in the form of the center of mass, but
sometimes this approximation turns out to be quite
successful (Fig. 9).
7 CONCLUSION
Finding reflective and rotational symmetry parame-
ters is an optimization problem. Its solution has a
significant computational cost, since it is reduced to
comparing a group of images for each set of possible
parameters. There is a need to develop a more effi-
cient optimization algorithm. For example, the search
space should be reduced. This study shows that for a
preliminary estimation of the optimum it is sufficient
to compare not the images, but the simplest statistical
parameters of their projections which can be obtained
with the Radon transform. It is shown that such sta-
tistical parameters are closely related to the Jaccard
index extensively used for comparing the shapes in
images since it directly produces the upper estimates
for each measure.
It is assured that the number of image comparisons
in a group can be significantly reduced by providing a
suitable mathematical expression for the generalized
Jaccard index. We presented a theoretical rationale
for the proposed method. It is shown that its underly-
ing principle is applicable to the analysis of many re-
flective and rotational symmetries expressed by affine
transformations. We also developed an original fast
algorithm based on the Fourier analysis of quantile
distribution of the shape’s pixel projections on vari-
ous lines.
The experiments show that the proposed method
is highly efficient which makes it suitable for real-
time applications. It is better than the similar Hough
transform-based method not only because it is an or-
der of magnitude faster, but also because it is easier
to interpret and more versatile. The method correctly
identifies the degree of symmetry for almost any im-
age, and the found center of symmetry is guaranteed
to be the global maximum of the Jaccard index.
Further research may be focused on developing an
efficient algorithm for affine transforms that are not
similarity transforms, such as skews and stretchings.
ACKNOWLEDGEMENTS
This study is supported by the Russian Science Foun-
dation grant No. 22-21-00575, https://rscf.ru/project/
22-21-00575/.
REFERENCES
Aguilar, W., Alvarado-Gonzalez, M., Garduno, E., Velarde,
C., and Bribiesca, E. (2020). Detection of rotational
symmetry in curves represented by the slope chain
code. Pattern Recognition, 107:107421.
Dieleman, S., De Fauw, J., and Kavukcuoglu, K. (2016).
Exploiting cyclic symmetry in convolutional neu-
ral networks. In Proceedings of the 33rd Interna-
tional Conference on Machine Learning - Volume 48,
ICML’16, pages 1889–1898. JMLR.org.
Kondra, S., Petrosino, A., and Iodice, S. (2013). Multi-scale
kernel operators for reflection and rotation symme-
try: Further achievements. In IEEE Computer Society
Conference on Computer Vision and Pattern Recogni-
tion Workshops, pages 217–222.
Krippendorf, S. and Syvaeri, M. (2020). Detecting symme-
tries with neural networks. Machine Learning: Sci-
ence and Technology, 2(1):015010.
VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications
288

Kushnir, O., Fedotova, S., Seredin, O., and Karkishchenko,
A. (2017). Reflection symmetry of shapes based on
skeleton primitive chains. Communications in Com-
puter and Information Science, 661:293–304.
Lee, S. and Liu, Y. (2010). Skewed rotation symmetry
group detection. IEEE Transactions on Pattern Anal-
ysis and Machine Intelligence, 32(9):1659–1672.
Lei, Y. and Wong, K. C. (1999). Detection and locali-
sation of reflectional and rotational symmetry under
weak perspective projection. Pattern Recognition,
32(2):167–180.
Llados, J., Bunke, H., and Marti, E. (1997). Finding rota-
tional symmetries by cyclic string matching. Pattern
Recognition Letters, 18(14):1435–1442.
Nguyen, T. P. (2019). Projection based approach for reflec-
tion symmetry detection. In 2019 IEEE International
Conference on Image Processing (ICIP), pages 4235–
4239.
Nguyen, T. P. and Nguyen, X. S. (2018). Shape measure-
ment using LIP-signature. Computer Vision and Im-
age Understanding, 171:83–94.
Nguyen, T. P., Truong, H. P., Nguyen, T. T., and Kim, Y.-
G. (2022). Reflection symmetry detection of shapes
based on shape signatures. Pattern Recognition,
128:108667.
Seredin, O., Liakhov, D., Kushnir, O., and Lomov, N.
(2022). Jaccard index-based detection of order 2 rota-
tional quasi-symmetry focus for binary images. Pat-
tern Recognition and Image Analysis, 32(3):672–681.
Shiv Naga Prasad, V. and Davis, L. (2005). Detecting rota-
tional symmetries. In Tenth IEEE International Con-
ference on Computer Vision (ICCV’05) Volume 1, vol-
ume 2, pages 954–961.
Yip, R. K. (1999). A Hough transform technique for the de-
tection of parallel projected rotational symmetry. Pat-
tern Recognition Letters, 20(10):991–1004.
Yip, R. K. (2007). Genetic Fourier descriptor for the de-
tection of rotational symmetry. Image and Vision
Computing, 25(2):148–154. Soft Computing in Im-
age Analysis.
Search for Rotational Symmetry of Binary Images via Radon Transform and Fourier Analysis
289