Study of Uncertainty Quantiﬁcation Using Multi-Label ECG in

Deep Learning Models

Raquel Sim

1,2,∗ a

, Mar

ılia Barandas

1,2,∗ b

, David Belo

2 c

and Hugo Gamboa

1,2 d

LIBPhys (Laboratory for Instrumentation, Biomedical Engineering and Radiation Physics),

NOVA School of Science and Technology, Campus da Caparica, 2829-516, Portugal

Associac¸

ao Fraunhofer Portugal Research, Rua Alfredo Allen 455/461, 4200-135 Porto, Portugal

Keywords:

Uncertainty Quantiﬁcation, Monte Carlo Dropout, Deep Ensemble, Dataset Shift, Active Learning.

Abstract:

Machine Learning (ML) models can predict diseases with noteworthy results. However, when implemented,

their generalization are compromised, resulting in lower performances and render healthcare professionals

more susceptible into delivering erroneous diagnostics. This study focuses on the use of uncertainty measures

to abstain from classifying samples and use the rejected samples as a selection criterion for active learning.

For the multi-label classiﬁcation of cardiac arrhythmias different methods for uncertainty quantiﬁcation were

compared using three Deep Learning (DL) models: a single model and two pseudoensemble models using

Monte-Carlo (MC) Dropout and Deep Ensemble (DE) techniques. When tested with an external dataset, the

models’ performances dropped from a F1-Score of 96% to 70%, indicating the possibility of dataset shift. The

uncertainty measures for classiﬁcation with rejection resulted in an increase of the rejection rate from 10% in

the training set to a range between 30% to 50% on the external dataset. For the active learning approach, 10%

of the highest uncertainty samples were used to retrain the models and their performance increased by almost

5%. Although there are still challenges to the implementation of ML models, the results show that uncertainty

quantiﬁcation is a valuable method to employ in safety mechanisms under dataset shift conditions.

1 INTRODUCTION

Over the years, medical technology has been devel-

oped and improved in order to ensure the most effec-

tive healthcare to the general public. Artiﬁcial Intel-

ligence (AI) is quickly evolving due to its potential

to assist evidence-based clinical decision-making and

achieve value-based care (Chen and Decary, 2020).

As a result, there has been a growing amount of sci-

entiﬁc research regarding the use of ML algorithms

in the medical domain. ML models have progressed

to the point that they can predict a variety of dis-

eases, with performances that can be superior to those

achieved by healthcare professionals. This is achiev-

able because ML models are trained with patient data

in order to identify patterns that would otherwise be

undetected and, thereby, produce an estimate of a pa-

tient’s current or future clinical state.

However, while showing promising results, these

models still have some limitations for their deploy-

https://orcid.org/0000-0002-1678-5709

https://orcid.org/0000-0002-9445-4809

https://orcid.org/0000-0002-5337-0430

https://orcid.org/0000-0002-4022-7424

∗

These authors contributed equally to this work

ment on clinical settings since their generalization ca-

pabilities are often compromised, resulting in lower

performances and rendering healthcare professionals

more susceptible into delivering erroneous diagnos-

tics. This occurs since conditions in which we use the

medical systems diverge from the conditions in which

these systems were created, leading to mismatches

between the training data and the data intended to be

classiﬁed. This problem is called dataset shift and, in

general, the greater the degree of shift, the poorer is

the model’s performance (Malinin et al., 2021). This

is one of many problems that contribute to the limited

number of models implemented in real life setting,

with only 64 AI/ML medical systems approved by the

FDA up until 2020 (Benjamens et al., 2020). As a re-

sult, it is critical that ML models include safety mech-

anisms to mitigate the dataset shift problem and im-

prove the trustworthiness of these models. If AI/ML

models fail to possess these mechanisms, they will be

unable to be effectively implemented with FDA ap-

proval, leading AI/ML models to oblivion as decision

support models.

Quantifying the uncertainty of models’ predic-

tions is a key method to assess the model’s conﬁ-

dence in their decisions. Although uncertainty quan-

252

Simão, R., Barandas, M., Belo, D. and Gamboa, H.

Study of Uncertainty Quantiﬁcation Using Multi-Label ECG in Deep Learning Models.

DOI: 10.5220/0011680700003414

In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 4: BIOSIGNALS, pages 252-259

ISBN: 978-989-758-631-6; ISSN: 2184-4305

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

tiﬁcation has already demonstrated promising results

in different ﬁelds, the literature on ECG classiﬁcation

is scarce. The works of (Vranken et al., 2021) and

(Aseeri, 2021) are relevant works under this topic,

however a single-label classiﬁcation is applied, even

though multi-label datasets are used.

In this paper, we develop a classiﬁcation approach

with rejection option based on uncertainty measures

and evaluate the uncertainty as a selection method for

active learning. Although the main purpose is to de-

velop an agnostic framework for the classiﬁcation of

cardiac arrhythmias, this work will concentrate on es-

tablishing the practical value of the uncertainty quan-

tiﬁcation applied in three types of DL models in dif-

ferent medical datasets and their role in the referred

methods. This research aims at providing a better

understanding of the capacity of the model’s gener-

alization through uncertainty estimation as well as

demonstrate that uncertainty aware models are capa-

ble of containing safety mechanisms and, therefore,

be considered trustworthy systems to be implemented

in clinical settings.

2 RELATED WORK

2.1 Uncertainty Estimation Measures

In the general literature (Shaker and H

ullermeier,

2020; Barandas et al., 2022), a distinction between

two intrinsically different sources of uncertainty is

done: aleatoric and epistemic. Aleatoric Uncertainty

(AU) is associated with the variability in the outcome

of an experiment which is due to intrinsic random-

ness of the data generating process that cannot be ex-

plained away given more observations or data sam-

ples (Shaker and H

ullermeier, 2020). Epistemic Un-

certainty (EU) refers to the lack of knowledge of the

model and usually is caused by incomplete domain

coverage since unknown regions of the data space will

always be presented. The presence of new classes that

were not contemplated in the training of the model,

are an example of high EU. This uncertainty can be

reduced by increasing the training data, better model-

ing or better data analysis (Barandas et al., 2022).

In traditional probabilistic modeling and Bayesian

inference, the uncertainty of a prediction is given by

the posterior distribution. Considering a ﬁnite dataset

D composed of instances x ans labels y, where y

∈

, ..., y

} is a set of K class labels, an hypothesis h

maps the instances x to the outcomes y. The posterior

P(h|D) can be obtained via the Bayes rule:

P(h|D) =

P(D|h)P(h)

P(D)

(1)

where P(D|h) is the probability of data given h and

P(h) is a prior distribution. For a single probabil-

ity distribution, an uncertainty measure that combines

both aleatoric and epistemic uncertainty can be cal-

culated through the probability of the predicted class,

given by:

p( ˆy|x) = max

p(y

|x, D) (2)

The entropy of the predictive posterior modeled

by Shannon’s entropy is also an uncertainty measure

for single probability distribution deﬁned by:

H[p(y|x)] = −

∑

k=1

p(y

|x)log

p(y

|x) (3)

In DL the randomness induced during training and

inference can be used to obtain an uncertainty esti-

mation (Mi et al., 2019). DE and MC Dropout are

techniques commonly used for this quantiﬁcation. DE

consists of training repeatedly the same neural net-

work with different parameters due to the randomness

in the initialization and training process (St

ahl et al.,

2020). Each model makes its own prediction and the

ﬁnal prediction is derived from the composition of all

models in the ensemble. MC Dropout is a method that

omits a certain percentage of neurons at each layer

of a neural network during training and testing, with

the missed neurons randomly selected for each itera-

tion and each test time (Gal et al., 2016). The ﬁnal

prediction is obtained from the composition of all the

predictions with distinct dropouts.

For these methods, the approximation proposed

by Depeweg et al (Depeweg et al., 2018) can be used

to obtain a measure of total, aleatoric and epistemic

uncertainty:

total

(x) := H[

∑

i=1

p(y|x, h

) (4)

aleat

(x) :=

∑

i=1

H[p(y|x, h

)] (5)

epist

(x) := u

total

(x) − u

aleat

(x) (6)

2.2 Classiﬁcation with Rejection Option

When a classiﬁer is not sufﬁciently conﬁdent in the

prediction, the model can abstain from producing an

answer or discard a prediction if the uncertainty is

sufﬁciently high. Therefore, a classiﬁer with rejec-

tion can cope with unknown information, reducing

the threat caused by the existence of unknown sam-

ples or mislabeled training samples that can compro-

mise the performance of the model. The standard

Study of Uncertainty Quantiﬁcation Using Multi-Label ECG in Deep Learning Models

253

approach for classiﬁcation with rejection option, also

known as Chow’s theory (Chow, 1970), is the calcula-

tion of a rejection threshold that minimises the classi-

ﬁcation risk. One approach to achieve this is through

the uncertainty associated with every prediction. The

empirical evaluation of methods for quantifying un-

certainty is a non-trivial problem, due to the lack of

ground truth uncertainty information. A common ap-

proach for indirectly evaluating the predicted uncer-

tainty measures is using Accuracy-Rejection Curve

(ARC). The ARC represents the accuracy of a clas-

siﬁer against its rejection rate, varying from 0 to 1

(Nadeem et al., 2009).

2.3 Active Learning

ML models, particularly DL models, demand a vast

labelled dataset to learn properly. The number of la-

belled data required grows with the complexity of the

problem or the complexity of the input data. This

issue is particularly dominant in the medical ﬁeld.

In order to automate the analysis of a given medical

exam, it would be necessary an expert to annotate a

large number of exams, labelling them to indicate if

the patient has certain condition or not. However, ob-

taining the amount of the needed labelled data is time-

consuming and expensive. One possible solution to

this problem is active learning. In this approach, the

model chooses what unlabelled data is appropriate for

training, and request an external “oracle”, for example

a medical work, for the label of the selected data (Set-

tles, 2009). The choice of the data to be labelled is se-

lected by an acquisition function, which ranks points

based on their potential informativeness (Gal et al.,

2016). There are a variety of acquisition functions

and many of them rely on model uncertainty to eval-

uate the potential informativeness of the unlabelled

data points. The more informative is the selected data,

the fewer labelled training examples are necessary to

achieve a greater classiﬁer accuracy. Therefore, the

quantiﬁcation of uncertainty plays a central role in

active learning and can be valuable to improve the

model’s performance when implemented in clinical

settings.

3 METHODOLOGIES

3.1 Databases

Four public multi-label cardiac arrhythmia datasets

from various countries were employed, having been

provided by the PhysioNet/Computing in Cardiology

Challenge 2020, as proposed by Perez Alday et. al

(Alday et al., 2020). A subset of ﬁve classes were

selected for classiﬁcation: Atrial ﬁbrillation (AF),

First-degree atrioventricular block (IAVB), Left bun-

dle branch block (LBBB), Right bundle branch block

(RBBB) and Sinus rhythm (NSR). These classes were

chosen since almost all of them are presented in each

dataset and are the most frequent classes overall. The

training database is composed of the CPSC2018 and

PTB-XL dataset. The PTB and G12EC databases are

used as external data in this research.

3.2 Data Preparation

To reduce the computational costs, only the ECG aVR

lead was used since this lead produced the best results

in the work of Chen et al. (Chen et al., 2020). The

data was downsampled to 125 Hz and a 10 seconds

window size was used. Data with length below that

value were excluded and data above 10 seconds were

truncated, so that all the samples have 1250 sample

data points. The ECG signals were ﬁltered using a

2nd order band-pass Butterworth ﬁlter between 1 and

40 Hz and it was also employed a smooth function

using a window of 10 samples. Lastly, the data was

normalised through a z-normalisation.

3.3 Proposed Algorithm

The model developed is a one-dimensional CNN. The

architecture consists of three convolutional blocks,

each with a convolutional layer followed by a batch

normalization layer, a PRelu activation function with

an initializer of 0.25, a max pooling layer and a

dropout layer with rate of 0.25. Each convolutional

layer has the same kernel size (31x31) but different

number of ﬁlters (the ﬁrst has 512 ﬁlters, the second

has 256 and the last one has 128 ﬁlters). After the

convolutional blocks, a ﬂatten layer was applied, re-

sulting in a Latent Vector. Three fully connected lay-

ers are added and the last one has a sigmoid activation

function with the same number of neurons as classes.

The ﬂowchart of the proposed algorithm is shown in

Figure 1.

The model was trained in 30 epochs with a batch

size of 64. The loss function employed was the binary

cross-entropy and an Adam optimizer with a learning

rate of 0.1. Since the model is trained with imbal-

anced datasets, it was added the class weight param-

eter that deﬁnes the weighting to adopt for each class

when ﬁtting the model.

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

254

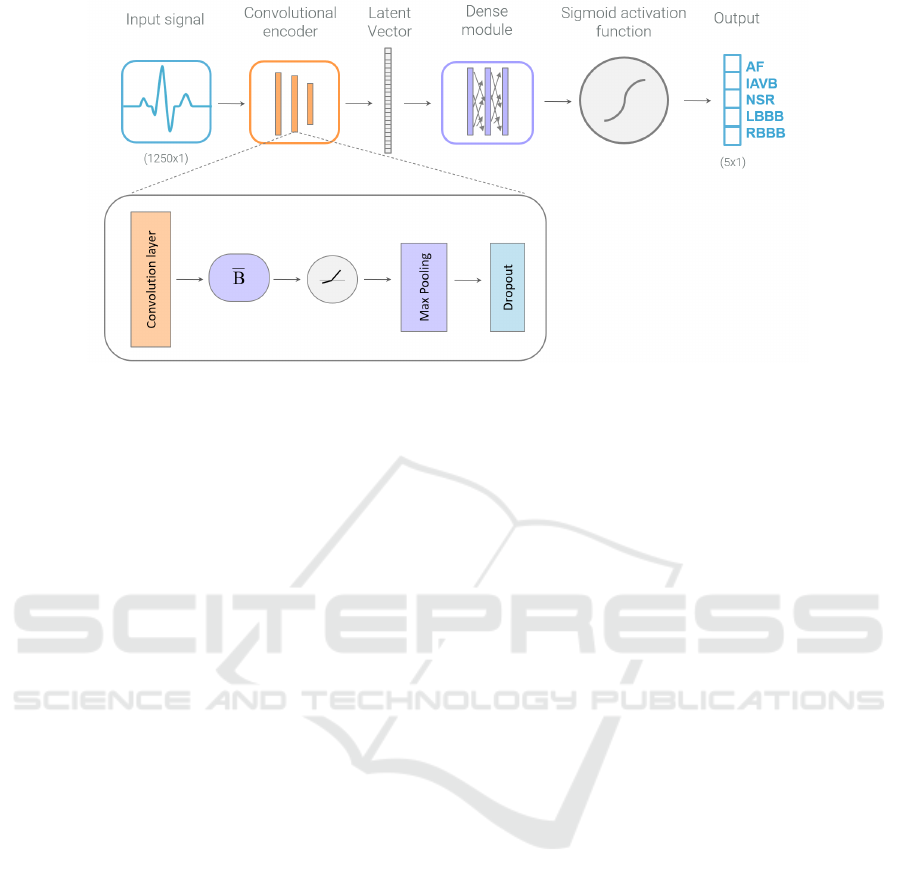
Figure 1: The ﬂowchart of the designed algorithm. The algorithm architecture consists of three convolutional blocks, each

with a convolutional layer followed by a batch normalization layer (

B), a PRelu activation function with an initializer of 0.25,

a max pooling layer and a dropout layer with rate of 0.25. A ﬂatten layer was applied, resulting in a Latent Vector. Three fully

connected layers are added and the last one has a sigmoid activation function with the same number of neurons as classes.

3.4 Training and Testing

The data from CPSC2018 and PTB-XL database was

split into 60% training, 20% validation and 20% test-

ing. The test set from this database was used as an

in-distribution set and will be referred as test-in from

now on. The test set composed from all the samples in

the PTB and G12EC datasets is named test-out. Two

approaches were employed: the MC dropout and the

DE. Both approaches were applied 30 times to both

test sets, resulting in 30 models for each. To obtain

the ﬁnal prediction with both MC Dropout and DE

approach, it was applied the majority vote for each

class.

3.5 Uncertainty Approaches

For the single CNN, the predicted posterior proba-

bility, also known as maximum probability, and the

Shannon entropy of the predicted probabilities were

used as uncertainty measures. In the case of MC

Dropout and DE, the total uncertainty, EU and AU

measures were estimated. Since a prediction in a

multi-label classiﬁcation can return more than one

class, the network sigmoid values do not sum 1. For

this reason, in this multi-label scenario, each class

was assumed as an independent binary case and the

uncertainty calculated by each class. Besides the un-

certainty by class, an aggregation mechanism based

on the sum of all class uncertainties was employed as

the ﬁnal prediction uncertainty.

Regarding the uncertainty evaluation, a common

approach for evaluating the predicted uncertainty is

by using ARC. However, due to the imbalance data,

instead of using accuracy as a performance measure,

the F1-score was used and the F1-Rejection curve was

computed to evaluate the behaviour of the developed

models. These curves were performed for the uncer-

tainty measures mentioned previously with the rejec-

tion occurring from the sample with the highest un-

certainty in its classiﬁcation to the sample with the

lowest uncertainty. This evaluation was performed

considering the overall performance. Since the data

is multi-label, the uncertainty of an ECG sample is

the sum of each class uncertainty and, therefore, each

sample uncertainty is represented by a value between

0 and 5.

3.6 Active Learning

Uncertainty estimation can be used to select the sam-

ples with higher uncertainty, taking advantage of the

separation between epistemic and aleatoric uncer-

tainty, where the former is more relevant as a selection

criterion (H

ullermeier and Waegeman, 2021). Fol-

lowing this idea, the retraining process was performed

for the single model and the DE model, where a new

set was added to the previous training set for the re-

training process. Each model was retrained for four

more epochs using the newly dataset and the same pa-

rameters previously used to train the initial models.

To validate if samples with high epistemic uncer-

tainty are more informative to the DE model, three

different sets composed by 10% of the test-out were

deﬁned to the retraining process, namely: 1) random

samples; 2) samples with the highest epistemic uncer-

tainty; 3) samples with the highest total uncertainty.

For the single model, the retraining was done with

Study of Uncertainty Quantiﬁcation Using Multi-Label ECG in Deep Learning Models

255

samples with the highest Shannon Entropy and for

random samples as well.

4 RESULTS

In order to access the models’ generalization capaci-

ties, it was compared the performance of the single,

MC Dropout and DE models tested with test-in and

tested with test-out.

Figure 2: Micro average F1-score results for the three de-

veloped models tested in test-in and test-out sets.

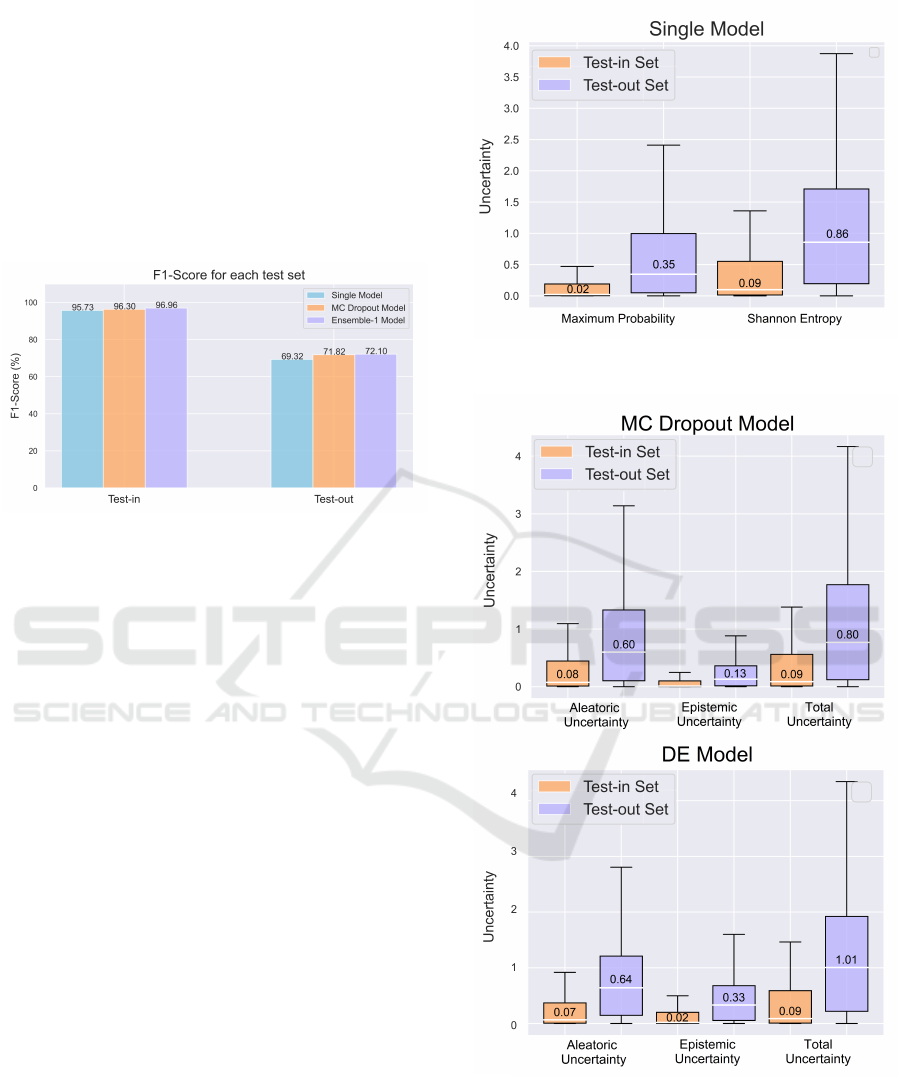
As it can be seen in Figure 2, the three models,

when tested with the test-in set, have similar perfor-

mances, with micro average F1-score around 96%-

97%, being comparable to the state of the art results.

However, when the models are tested with the test-

out set, their performances decrease signiﬁcantly in

all three models, having a micro-average F1-Score

of approximately 70%. The DE model obtained the

highest F1-score in both test sets with a maximum dif-

ference of 3% from the other models.

Regarding the classiﬁcation with rejection option,

even though this method does not solve the problem

of model’s generalization that leads to poor perfor-

mance results under data shift, it can be a viable ap-

proach to abstain to predict a class under high uncer-

tainty conditions. For each model, the uncertainties

measures presented in Section 2.1 were calculated for

the test-in and test-out sets and the results can be

seen in Figures 3 and 4. For the single model, the be-

haviour of both uncertainties measures in test-in and

test-out are similar. However, both uncertainty mea-

sures obtain higher uncertainty in the test-out set.

As for the results in Figure 4, for the test-in set,

the MC Dropout and DE models estimate similar val-

ues of uncertainty, presenting the same median and

the same range of total uncertainty. The MC Dropout

presents a higher range of AU while the DE detects

higher EU. As for the test-out set, both models cap-

ture higher uncertainty than for the test-in set in all

the three types of uncertainty measures.

Figure 3: Uncertainty Estimation for both test sets in the

single model.

Figure 4: Uncertainty Estimation for both test sets in the

MC Dropout(up) and DE(down) models.

To investigate the role of uncertainty in rejection,

the F1-rejection curve was produced for the three

models, rejecting the samples according to the highest

calculated uncertainties. To validate the rejection rate

in both sets, a 10% rejection in the training set was ap-

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

256

plied and the uncertainty thresholds obtained. Using

the same thresholds on test-in and test-out, the rejec-

tion rates increased to approximately 12% and 40%,

respectively, using the single model for both maxi-

mum probability and entropy measures. For the MC

Dropout the rejection in test-in was 9% and vary be-

tween 31% and 34% for test-out depending on the un-

certainty measure used. The DE model vary the rejec-

tions rates between the intervals 13%-16% and 45%-

51% for test-in and test-out, respectively. Further-

more, as it can be deducted for the micro average F1-

Scores presented in the Table 1, for all the three mod-

els and for all uncertainty measures, the more samples

rejected, the better is the models’ performance. Even

though the curves based on the different uncertainty

methods are quite similar, throughout the rejection,

the DE model presents better micro average F1-Score

results for the same rejection rate.

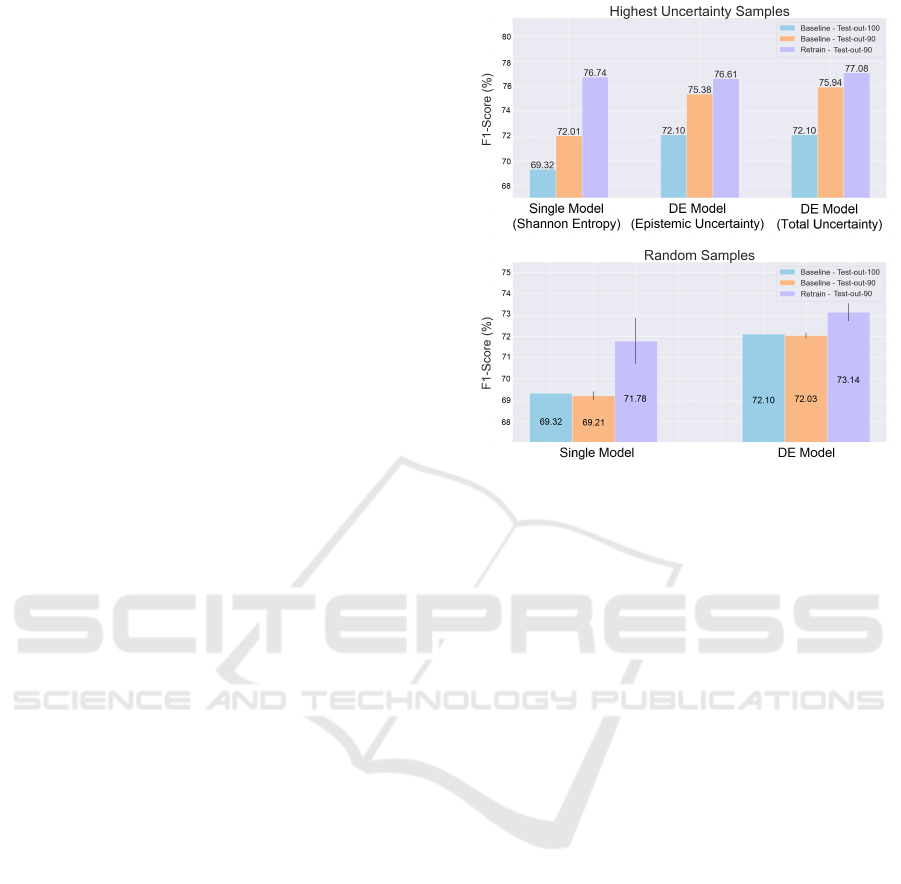
Apart from employing the rejection option, a pos-

sible method to deal with dataset shift is by retraining

the model with samples that have crucial information

to help improve its performance. A potential solution

is the active learning approach, in which the samples

used to retrain the model contain the highest uncer-

tainty associated with their classiﬁcations. To eval-

uate the three uncertainties in this approach, the re-

trained models were tested with the test-out set with-

out the 10% samples to fairly compare the increase

between the retrained model and the baseline model.

Thus, the following nomenclature was used: 1) Pre-

vious trained model using the complete test-out set

(Baseline - test-out-100); 2) Previous trained model

tested only on 90% of test-out, i.e 10% of test-out

was used to retrain the model (Baseline - test-out-

90); 3) Retrained model using the selected 10% data

and tested on the remaining 90% (Retrain - test-out-

90). Furthermore, to serve as control, this process

was performed for 10% of random samples in order

to observe the role of uncertainty in this approach.

This procedure was conducted 10 times and the mean

and standard deviation of the results are represented

in Figure 5.

As it can be observed in Figure 5, when the sam-

ples with the highest uncertainty are removed from

the test-out, the model performance increases slightly,

from 2%-4%. After retraining the two models with

these samples and evaluating it without them, a max-

imum increase of almost 5% is observed when com-

pared to the baseline models that are tested with all

the samples of test-out. These conclusions are sup-

ported through the results served as a control, where

the samples selected are random and the trained mod-

els have similar performance as the original models.

Figure 5: Micro average F1-score for the Active learning

approach for the highest uncertainties and for random sam-

ples.

5 DISCUSSION

To make the decision support systems as trustwor-

thy as possible, it is critical to access the conﬁdence

that ML models have in their classiﬁcations. This

work studied these concepts using four large public

ECG databases for the classiﬁcation of cardiac ar-

rhythmias. As multiple cardiac arrhythmias can be

presented within the same recording, a multi-label

classiﬁcation setting was adopted for the development

of DL models.

The performance of the three models developed

were assessed for two test sets, where the test-in has

data from the same database as the training and the

test-out presents data from a different database. Al-

though these models produced similar performance

results for the same test set, the DE and MC Dropout

outperform the single model, as expected since these

models assist in reducing models’ high conﬁdence in

incorrect classiﬁcations. The DE model revealed has

the better performance in both test sets, which it is

consistent with the literature. When tested with the

test-out set, the performance of all the three mod-

els drops signiﬁcantly, conﬁrmed by the decrease of

F1-Score from around 96% to 70%. These results

indicate the possible presence of dataset shift since

the data from test-out has different characteristics and

distributions than the data used for training.

Study of Uncertainty Quantiﬁcation Using Multi-Label ECG in Deep Learning Models

257

Table 1: Rejection rate results and the respective F1-Score values for each uncertainty.

Model Uncertainty

Test-in Test-out

Rejection F1-Score Rejection F1-Score

Single CNN

Maximum Probability 12.24% 98.54% 39.81% 79.14%

Shannon Entropy 12.16% 98.38% 41.70% 79.89%

MC Dropout

Aleatoric 9.51% 98.46% 31.92% 82.25%

Epistemic 9.35% 98.29% 33.68% 83.07%

Total 9.41% 98.47% 34.30% 83.33%

Aleatoric 16.21% 99.34% 51.03% 86.26%

Epistemic 13.46% 99.10% 45.05% 85.25%

Total 15.75% 99.41% 49.95% 87.00%

Regarding the uncertainty estimations, the Shan-

non entropy and maximum probability were esti-

mated for the single model and the aleatoric, epis-

temic, and total uncertainty for the MC Dropout and

DE models. For the single model, both maximum

probability and entropy obtained similar results, while

for the MC Dropout and DE the total uncertainty pre-

sented slightly better result. This suggests the ben-

eﬁt of estimating uncertainty using the combination

of epistemic and aleatoric uncertainty. Additionally,

all uncertainties computed for the test-out were sig-

niﬁcantly higher than for the test-in set. This shows

that the model is less conﬁdent on the classiﬁcation of

cardiac arrhytmias and as result there is higher prob-

ability of misclassiﬁed samples. This is an indication

of dataset shift and the main reason of models’ perfor-

mance drop in test-out set. Furthermore, it is impor-

tant to mention that it was expected that the EU would

be higher than the AU in test-out since the data comes

from a different source and might be a different dis-

tribution. This reveals that there are still challenges in

capturing these two uncertainties correctly.

In order to improve the trustworthiness of the

models, the classiﬁcation with rejection option was

applied. For both test sets, the models performance

increased with rejection, revealing that the higher the

uncertainty in a given classiﬁcation, the higher is the

probability of the models to misclassify the samples.

Additionally, the uncertainty threshold, selected from

the training data, increased from 10% to a range be-

tween 30% to 50% depending on the model or un-

certainty measure employed. The increase in rejec-

tion rate conﬁrms that high uncertainty is presented in

the classiﬁcations and the uncertainty is higher in the

test-out set. This is another evidence of the dataset

shift effect and that the models are not as prepared to

classify data with different distributions.

Another alternative to improve the models’ per-

formance and reliability is through the retraining of

models with unseen data. In this manner, it was em-

ployed an active learning approach, using 10% of the

samples with the highest uncertainty in the test-out

set. The results showed that the models improved

their performance by a maximum of almost 5% when

using uncertainty versus 2% when using a random

selection. These results demonstrate that data with

high uncertainty has information that the model has

not yet learned and hence the models beneﬁt from

the retraining with this selection method. Moreover,

when removing the 10% of the samples with the high-

est uncertainty and test 90% of the test-out in the

baseline models, the performance improved, showing

that the samples with highest uncertainty are misclas-

siﬁed. This underlines the importance of the uncer-

tainty quantiﬁcation in detecting incorrect classiﬁca-

tions.

6 CONCLUSIONS

The evaluation and comparison of uncertainty mea-

sures has proven to be essential in an in-depth anal-

ysis of ML models, allowing us to understand their

limitations. Furthermore, the preliminary results re-

veal that the quantiﬁcation of uncertainty should be

considered a key feature of any ML model as a safety

mechanism.

Although there are still no ground truth for the es-

timation of uncertainty, all the metrics used were ca-

pable to detect uncertainty in multi-label data. Never-

theless, there are still challenges in capturing the un-

certainty through the employed measures, specially in

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

258

the separation of epistemic and aleatoric uncertainty.

It is also possible to infer the role of uncertainty as a

valuable method under dataset shift conditions and in

strategies such classiﬁcation with rejection option and

active learning approaches.

Thus, the development of uncertainty aware mod-

els will provide healthcare professionals with access

to the model’s conﬁdence in its predictions but also

refrain the model from delivering classiﬁcations with

high uncertainty. Furthermore, samples that have dif-

ferent characteristics and distributions than the ones

learned by the models have higher uncertainty asso-

ciated with their classiﬁcations and, therefore, can be

used to retrain the ML models and improve its gen-

eralization and robustness. The active learning ap-

proach is a reliable method for this purpose, demon-

strating that it is a technique capable to self-regulate

the learning of the models in a real life setting, with a

reduction in computational cost as well as in the cost

of labelling the data usually required. Despite the en-

couraging results, much more research is needed in

the area of clinical data uncertainty, particularly in

multi-label data.

To conclude, data with different characteristics

and distributions from those learnt by the ML mod-

els will always exist, so it is imperative that AI sys-

tems possess uncertainty associated methods as safety

mechanisms to produce reliable models to implement

as a decision support system in clinical settings.

REFERENCES

Alday, E. A. P., Gu, A., Shah, A. J., Robichaux, C., Wong,

A.-K. I., Liu, C., Liu, F., Rad, A. B., Elola, A., Seyedi,

S., et al. (2020). Classiﬁcation of 12-lead ecgs: the

physionet/computing in cardiology challenge 2020.

Physiological measurement, 41(12):124003.

Aseeri, A. O. (2021). Uncertainty-aware deep learning-

based cardiac arrhythmias classiﬁcation model of

electrocardiogram signals. Computers, 10(6):82.

Barandas, M., Folgado, D., Santos, R., Sim

ao, R., and Gam-

boa, H. (2022). Uncertainty-based rejection in ma-

chine learning: Implications for model development

and interpretability. Electronics, 11(3).

Benjamens, S., Dhunnoo, P., and Mesk

o, B. (2020).

The state of artiﬁcial intelligence-based fda-approved

medical devices and algorithms: an online database.

NPJ digital medicine, 3(1):1–8.

Chen, M. and Decary, M. (2020). Artiﬁcial intelligence

in healthcare: An essential guide for health leaders.

Healthcare Management Forum, 33(1):10–18. PMID:

31550922.

Chen, T.-M., Huang, C.-H., Shih, E. S., Hu, Y.-F., and

Hwang, M.-J. (2020). Detection and classiﬁcation of

cardiac arrhythmias by a challenge-best deep learning

neural network model. Iscience, 23(3):100886.

Chow, C. (1970). On optimum recognition error and reject

tradeoff. IEEE Transactions on Information Theory,

16(1):41–46.

Depeweg, S., Hernandez-Lobato, J.-M., Doshi-Velez, F.,

and Udluft, S. (2018). Decomposition of uncer-

tainty in Bayesian deep learning for efﬁcient and risk-

sensitive learning. In Dy, J. and Krause, A., editors,

Proceedings of the 35th International Conference on

Machine Learning, volume 80 of Proceedings of Ma-

chine Learning Research, pages 1184–1193. PMLR.

Gal, Y. et al. (2016). Uncertainty in deep learning.

ullermeier, E. and Waegeman, W. (2021). Aleatoric and

epistemic uncertainty in machine learning: An intro-

duction to concepts and methods. Machine Learning,

110(3):457–506.

Malinin, A., Band, N., Chesnokov, G., Gal, Y., Gales,

M. J., Noskov, A., Ploskonosov, A., Prokhorenkova,

L., Provilkov, I., Raina, V., et al. (2021). Shifts:

A dataset of real distributional shift across multiple

large-scale tasks. arXiv preprint arXiv:2107.07455.

Mi, L., Wang, H., Tian, Y., and Shavit, N. (2019). Training-

free uncertainty estimation for neural networks.

Nadeem, M. S. A., Zucker, J.-D., and Hanczar, B. (2009).

Accuracy-rejection curves (arcs) for comparing clas-

siﬁcation methods with a reject option. In D

zeroski,

S., Guerts, P., and Rousu, J., editors, Proceedings of

the third International Workshop on Machine Learn-

ing in Systems Biology, volume 8 of Proceedings of

Machine Learning Research, pages 65–81, Ljubljana,

Slovenia. PMLR.

Settles, B. (2009). Active learning literature survey. Com-

puter Sciences Technical Report 1648, University of

Wisconsin–Madison.

Shaker, M. H. and H

ullermeier, E. (2020). Aleatoric and

epistemic uncertainty with random forests. In Interna-

tional Symposium on Intelligent Data Analysis, pages

444–456. Springer.

ahl, N., Falkman, G., Karlsson, A., and Mathiason, G.

(2020). Evaluation of uncertainty quantiﬁcation in

deep learning. In International Conference on Infor-

mation Processing and Management of Uncertainty in

Knowledge-Based Systems, pages 556–568. Springer.

Vranken, J. F., van de Leur, R. R., Gupta, D. K.,

Juarez Orozco, L. E., Hassink, R. J., van der Harst, P.,

Doevendans, P. A., Gulshad, S., and van Es, R. (2021).

Uncertainty estimation for deep learning-based auto-

mated analysis of 12-lead electrocardiograms. Euro-

pean Heart Journal-Digital Health, 2(3):401–415.

Study of Uncertainty Quantiﬁcation Using Multi-Label ECG in Deep Learning Models

259