The Subspace Regularization Method Improves ErrP Detection by

EEGNET in BCI Experiments

Andrea Farabbi

and Luca Mainardi

Dipartimento di Elettronica, Informatica e Bioingegneria, Politecnico di Milano, Milan, Italy

Keywords:

Brain-Computer Interface, Electroencephalography, Biosignal Processing, Error Potential, Deep Learning.

Abstract:

In this study, the subspace regularization method was applied on the Electroencephalographic (EEG) signal

recorded during stimulation of the Error Potential (ErrP) in order to improve the detection of the latter. The

ErrP is stimulated through the presentation of an erroneous event to the subject. The recorded signals were

processed with the subspace regularization method to remove the background EEG not related to the erroneous

event. Then, the ErrP and Non–ErrP epochs (both raw and processed with the proposed method) were clas-

siﬁed using EEGNET, a Convolutional Neural Network considered golden standard for EEG classiﬁcation.

The results show that elaborating the signals with the proposed method highlight the typical characteristics of

the ErrP epochs both in temporal and frequency domain. Moreover, the classiﬁcation metrics evaluated, al-

ways increase if compared to not processed signal (i.e. maximum increase in accuracy, balanced accuracy and

F1-score are of 7.7%, 10.1% and 11% respectively). These ﬁndings suggest that the subspace regularization

method can improve the performance of ErrP-based Brain Computer Interfaces (BCI) and can be used also in

real time application and for asynchronous classiﬁcation of erroneous events.

1 INTRODUCTION

Brain Computer Interfaces (BCI) are technologies

that allow to control an external device using subject’s

brain activity (Wolpaw et al., 2000). BCI are partic-

ularly used for rehabilitation in subjects that experi-

enced the loss of motor or cognitive skills.

To have a representation of the activity present

at the scalp level, the Electroencephalographic signal

(EEG) is usually recorded due to its intrinsic non in-

vasive nature and its high temporal resolution. De-

pending on the kind of stimulus presented to the sub-

ject, different EEG responses can be obtained and,

therefore, different EEG-based BCI systems can be

designed. In this paper the focus is set on the Error

Potential (ErrP), an event-related potential that arises

whenever an error is detected by a user, both if the

error is committed by an external device or by the

user itself (Falkenstein et al., 2000). The activity is

located in the medio–frontal areas of the brain, in par-

ticular in the anterior cingulate cortex (Holroyd and

M.Coles, 2002), and, depending on the task, differ-

ent ErrPs types can be distinguished. The realization

https://orcid.org/0000-0001-5582-4654

https://orcid.org/0000-0002-6276-6314

follows a stereotypical shape characterized by a neg-

ative peak occurring at 250 ms after the error, a pos-

itive peak at 320 ms and a negative peak at 450 ms

(Ferrez and del R. Millan, 2008). In the frequency

domain the EEG signal recorded after the erroneous

event is particularly localized in the δ(1 − 3Hz) and

θ(5 − 8Hz) brain rhythms (Spuler and Niethammer,

2015)(Abhang et al., 2016).

In literature, the ErrP detection in BCI application

is mainly employed to correct the output of BCIs that

are based on other paradigms. For example in (Seno

et al., 2010), the authors developed a P300 speller, a

BCI able to detect the letter chosen by the user from

a grid of letters. The detection of the ErrP in this case

is used for correcting the letter identiﬁed by the sys-

tem if it is not the one intended by the user. Since

the feedback given to the subject is crucial in any BCI

experiment, the detection of an ErrP during a correct

trial may lead to frustration and, thus, to less involve-

ment of the participant during the trial (Lotte, 2012).

Moreover, the detection of erroneous events is

ﬁnding application also in other ﬁelds, where the cor-

rection of an external device can drastically improve

the effectiveness of the device itself (e.g. autonomous

driving (Belcher et al., 2022)). These examples high-

light the importance of having a correct classiﬁcation

260

Farabbi, A. and Mainardi, L.

The Subspace Regularization Method Improves ErrP Detection by EEGNET in BCI Experiments.

DOI: 10.5220/0011682400003414

In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 4: BIOSIGNALS, pages 260-264

ISBN: 978-989-758-631-6; ISSN: 2184-4305

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

of the ErrP and excluding false postives as much as

possible. The advances in machine learning and deep

learning algorithms have enhanced the detection of

Evoked Potentials (EP) (Z.Cao, 2020), but still re-

mains difﬁcult to separate the signal of interest from

the background EEG in the single sweep analysis.

These difﬁculties is reﬂected in unsatisfactory perfor-

mances and high values of false positives during clas-

siﬁcation.

In this study, we applied a method used in litera-

ture (i.e. subspace regularization (Karjalainen et al.,

1999)) for estimating the sources of the ErrP sin-

gle sweeps and we analyzed whether this elaboration

of the signal may improve the classiﬁcation perfor-

mance in distinguishing between erroneous and cor-

rect events. Moreover, the elaborated signal has also

been analyzed in order to assess if the characteristics

of the ErrP are preserved, or even enhanced, by this

method.

2 METHODS

2.1 Dataset

The dataset used in this project is the open access BCI

dataset of BNCI Horizon 2020: Monitoring error-

related potentials (BNCI, 2020). It consists of EEG

recordings obtained during an ErrP-speciﬁc experi-

ment performed on six subjects (mean age 27.83 ±

2.23) in two recording sessions (Chavarriaga and Mil-

lan, 2010).

The experimental paradigm consists of reaching a

target (i.e. a coloured square) through a moving cur-

sor. The working area is constituted by 20 possible

horizontal positions where the cursor and the target

square may be located. At each time step (2 seconds

each), the cursor moves a step toward the location

of the square. Once the target is reached, the cursor

remains in place and a new target location appears.

Subjects are asked to monitor the position of the cur-

sor (without having any control over it), knowing that

the objective is to reach the target. In order to elicit

the ErrP, at each time step, the cursor is moved in the

wrong direction with 20% of probability.

The recording session consists of 10 blocks of

3 minutes each, including approximately 50 cur-

sor movements per block. Subjects performed two

recording sessions with a gap of several weeks.

For each session, the EEG signal is recorded (512

Hz sampling frequency) with 64 electrodes using a

BioSemi ActiveTwo system. Electrodes are placed

according to the 10-20 International System. More

details about the experimental setup and the recorded

signals are published in (Chavarriaga and Millan,

2010).

The data–set is largely unbalanced: it is consti-

tuted by 6437 epochs of which 1322 include the ErrP.

2.2 Preprocessing

The raw EEG data are spatially ﬁltered with the Com-

mon Average Rereferencing (CAR) method and then

band passed ﬁltered between 1-40 Hz in order to re-

move the noise at higher frequencies. Data are then

downsampled at 64Hz and divided in epochs of in-

terval [0 1]s from stimulus onset in order to cover

the expected ErrP latencies. No artifact removal

(e.g. Indipendent Component Analysis) algorithm has

been applied in view of a real-time application of the

method. The preprocessing pipeline has been imple-

mented in Python with the MNE library (Gramfort

et al., 2013).

2.3 Subspace Regularization Method

The subspace regularization method has been pre-

sented in (Karjalainen et al., 1999) and has been used

for single trial estimation of P300 EP.

The recorded signal can be described as a linear

combination of the EP of interest (i.e. source) and

some noise introduced with the measurements. The

EEG signal z is described as:

z = s + v = Hθ + v (1)

where s is the source signal and v is the backgorund

EEG. In particular the source is described as a linear

combination of some basis vectors (i.e. H) depending

on the measurements and so, in linear algebra, s lie in

the subspace described by these basis vectors.

The subspace regularization method aims to ﬁnd

the optimal parameters θ by searching the optimal ba-

sis vectors and minimizing the contribution given by

an estimated v.

In our study we decided to use as noise the back-

ground EEG not related to the stimulation and esti-

mated during the second before the stimulation. Thus,

the estimation of s is reduced to the solution of follow-

ing formula:

s = H(H

∗ C

−1

H + α

(I − K

)H)

−1

(2)

where H is a set of basis vector (Gaussian waveforms)

than span along the signal, K

is the eigenvector ma-

trix of the correlation matrix of z, C

is the covariance

matrix of the noise v and α is deﬁned as the regular-

ization parameter that can be chosen experimentally.

From the preprocessed ErrP and Non–ErrP

epochs, the sources are extracted with this method and

used for classiﬁcation purposes.

The Subspace Regularization Method Improves ErrP Detection by EEGNET in BCI Experiments

261

Figure 1: Pipeline of the preprocessing and classiﬁcation of the ErrP and Non-ErrP EEG measurements.

2.4 ErrP Classiﬁcation

In order to classify the extracted epochs, the EEGNET

(Lawhern et al., 2018) Convolutional Neural Network

have been employed. The authors of this CNN proved

that it has good generalize ability in different BCI

paradigms and that is why it has been chosen also in

this paper. The architecture is composed by the pe-

culiar Depthwise and Separable Convolutional layers

in combination with the classical dropout and batch

normalization layers. The last layer is a typical fully

connected layer for classiﬁcation output. A majority

vote approach is employed to obtain the prediction la-

bel for the test set: it has been chosen since it would

outperform the best classiﬁer if the classiﬁers make

independent errors (Orrite et al., 2008). As input of

EEGNET both the subspace regularized and not pro-

cessed EEG signals coming from all channels were

used. It has been decided to consider all the electrodes

in order to not lose any information.

The dataset of each subject was shufﬂed to ensure

heterogeneous distribution of data an then it was di-

vided, using 20% of the data as test set, while the re-

maining data were divided in training (80%) and val-

idation set (20%). The performance in test was as-

sessed ﬁrst with the raw data and then the network

was re-trained and tested with the subspace regular-

ized epochs and differences in performances was ana-

lyzed. Stratiﬁed 5-folds cross-validation is performed

on the validation set. The results will be presented

in terms of test accuracy, balanced accuracy and F1-

score for assessing the classiﬁer performance.

Due to the high unbalance of the two classes,

for both training processes a data augmentation algo-

rithm has been used: in particular we decided to use

the ARX-based method proposed in (Farabbi et al.,

2021).

The performance of the classiﬁer has been anal-

ysed both in two ways: subject-wise, where the clas-

siﬁer has been trained and tested separately for each

subject in order to assess the individual performance;

population-wise, where data coming from all subjects

were considered as one in order to assess an overall

generalize ability of the classiﬁer.

The complete pipeline of the preprocessing and

classiﬁcation is reported in Fig.1.

3 RESULTS

3.1 Sources Estimation

In Fig.2.A are reported the Grand Average of the ErrP

signal without (blue) and with subspace regulariza-

tion (orange) at the electrode FCz (the most involved

in ErrP stimulation) for one subject as an example. It

is worth to notice that the source estimated with the

proposed method, follows the original waveform, ex-

cluding the high frequency components and reducing

the peaks given by the background EEG that is not

related with the EP of interest. Moreover, the main

characteristics of the ErrP are preserved with the typ-

ical negative and positive peaks.

This can be noticed also in the frequency domain

(Fig.2.B): the PSD of the estimated source (blue) is

mostly activated in the δ and θ bands and no compo-

nent after 10Hz.

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

262

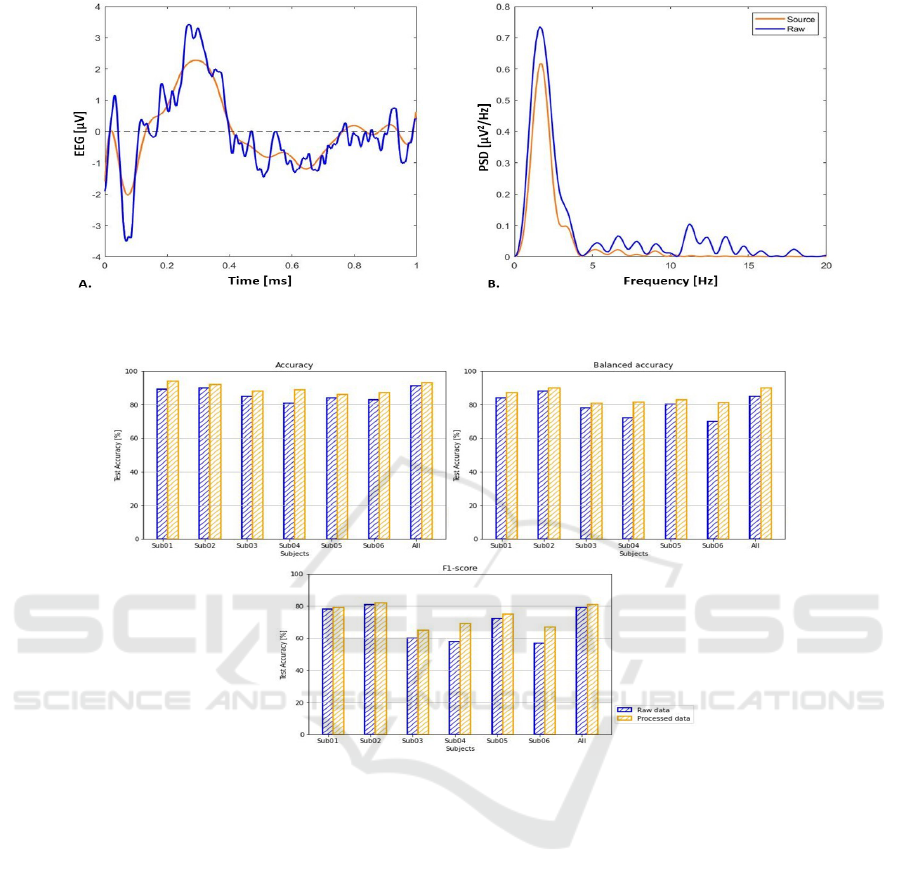
Figure 2: ErrP epoch in time domain (A) and the PSD in frequency domain (B) for electrode FCz. In blue is reported the ErrP

signal processed with the subspace regularization method, while in orange the signal with no processing.

Figure 3: EEGNET performance in terms of accuracy, balanced accuracy and F1 score. The score for each subject and of the

whole participants considered as one are reported. In blue the metrics with non processed signals used as input for EEGNET,

while in orange the signals with subspace regularization.

3.2 EEGNET Performances

Concerning the performance of the EEGNET classi-

ﬁer, we reported in Fig.3 the results in terms of ac-

curacy, balanced accuracy and F1-score using signals

processed with the subspace regularization method

(in orange) and the ones with no processing (in blue).

In the ﬁgure are reported the metrics obtained

for each subject and the ones considering the signals

coming from all participants as one.

We can observe that in all cases the metrics get

higher values, with maximum increases of 10.1% for

the balanced accuracy, 7.7% for the accuracy and

11% for the F1-score. Moreover, it is worth to notice

that the subjects that achieved lower performances us-

ing not elaborated signals are the ones that resulted in

a larger increment of the metrics.

4 DISCUSSION

The obtained results suggest that the subspace regu-

larization method may be optimal in ErrP signal pro-

cessing in order to improve the classiﬁcation perfor-

mances of the ErrP detector. It is interesting to ob-

serve that also subjects with low accuracy metrics (i.e.

subjects #3, #4 and #6) when no processing was im-

plemented, resulted in good performance when pro-

cessed with the proposed method.

Moreover, the signals obtained after the subspace

regularization enhance the main characteristics of the

subject, highlighting positive and negative peaks at

the expected latencies and focusing the brain rhythm

in the δ band, suggesting that the activation of higher

frequencies (observable in the non processed signal)

The Subspace Regularization Method Improves ErrP Detection by EEGNET in BCI Experiments

263

are not related to the ErrP-stimulated response, but to

background EEG. Thus, not only the method seems to

give a good estimate of the sweep of interest, but also

seems appropriate to estimate the background EEG

from the second before the onset of the stimulus.

5 CONCLUSION

In this paper we presented a study on the effect of

applying subspace regularization method to ErrP in

terms of signal processing and of classiﬁcation met-

rics using a Convolutional Neural Network for distin-

guishing between ErrP and Non–ErrP realizations.

The proposed pre-processing method enhances the

main characteristics of the ErrP signal and improves

the classiﬁcation performance in each subject and for

each evaluated metric.

Since the subspace regularization method is fast in

terms of computational time, it can be adopted also in

real time BCI classiﬁcation based on the ErrP Evoked

Potential. Moreover, the proposed method can be ap-

plied also to enhance asynchronous classiﬁcation of

ErrP events (or in general of Evoked Potentials).

REFERENCES

Abhang, P., Gawali, B., and Mehrotra, S. (2016). Techno-

logical basics of eeg recording and operation of appa-

ratus. Introduction to EEG- and Speech-Based Emo-

tion Recognition.

Belcher, M., I.Hwuang, S.Bhattacharya, Hairston, W., and

Metcalfe, J. (2022). Eeg-based prediction of driv-

ing events from passenger cognitive state using morlet

wavelet and evoked responses. Transportation Engi-

neering, 8:100–107.

BNCI (2020). http://bnci-horizon-2020.eu/database/data-

set.

Chavarriaga, R. and Millan, J. d. R. (2010). Learning

from eeg error-related potentials in noninvasive brain-

computer interfaces. IEEE Transactions on Neural

Systems and Rehabilitation Engineering, 18(4):381–

388.

Falkenstein, M., Hoormann, J., Christ, S., and J.Hohnsbein

(2000). Erp components on reaction errors and their

functional signiﬁcance: a tutorial. Biological psychol-

ogy, 51(2-3):87–107.

Farabbi, A., Aloia, V., and Mainardi, L. (2021). Arx-based

eeg data balancing for error potential bci. Journal of

Neural ENgineering, 19(3):1741–2552.

Ferrez, W. and del R. Millan, J. (2008). Error-related eeg

potentials generated during simulated brain-computer

interaction. ieee transactions on biomedical engineer-

ing. IEEE transactions on bio-medical engineering,

55.3:923–929.

Gramfort, A., Luessi, M., Larson, E., Engemann, D.,

Strohmeier, D., Brodbeck, C., Goj, R., Jas, M.,

Brooks, T., Parkkonen, L., and H

ainen, M.

(2013). MEG and EEG data analysis with MNE-

Python. Frontiers in Neuroscience, 7(267):1–13.

Holroyd and M.Coles (2002). The neural basis of human

error processing: Reinforcement learning, dopamine

and the error-related negativity. Psychological Re-

view, pages 679–709.

Karjalainen, P., Kaipio, J., Koistinen, A., and Vauhkonen,

M. (1999). Subspace regularization method for the

single-trial estimation of evoked potentials. IEEE

Transactions on Biomedical Engineering, 46:849–

860.

Lawhern, V. J., Solon, A. J., Waytowich, N. R., Gordon,

S. M., Hung, C. P., and Lance, B. J. (2018). Eegnet: a

compact convolutional neural network for eeg-based

brain-computer interfaces. Journal of Neural Engi-

neering, 15(5).

Lotte, F. (2012). On the need for alternative feedback train-

ing approaches for bci. Berlin Brain-Computer Inter-

face Workshop.

Orrite, C., Rodr

ıguez, M., Francisco, Mart

ınez, and

Michael Fairhurst, M. (2008). Classiﬁer ensemble

generation for the majority vote rule. Progress in Pat-

tern Recognition, Image Analysis and Applications,

5197:340–347.

Seno, B. D., Matteucci, M., and Mainardi, L. (2010). Online

detection of p300 and error potentials in a bci speller.

Computational intelligence and neuroscience, 2010.

Spuler, M. and Niethammer, C. (2015). Error-related poten-

tials during continuous feedback: using eeg to detect

errors of different type and severity. Frontiers in hu-

man neuroscience, 9:155.

Wolpaw, J., Birbaumer, N., Heetderks, W., D.J.McFarland,

Peckham, P., Schalk, G., Donchin, E., Quatrano,

L., Robinson, C., and Vaughan, T. (2000). Brain-

computer interface technology: a review of the ﬁrst

international meeting. IEEE transactions on rehabil-

itation engineering : a publication of the IEEE En-

gineering in Medicine and Biology Society, 8(2):164–

173.

Z.Cao (2020). A review of artiﬁcial intelligence for

eeg based brain computer interfaces and applications.

Brain Science Advances, 6(3):162–170.

BIOSIGNALS 2023 - 16th International Conference on Bio-inspired Systems and Signal Processing

264