Robust Semi-Supervised Anomaly Detection via

Adversarially Learned Continuous Noise Corruption

Jack W. Barker

, Neelanjan Bhowmik

, Yona Falinie A. Gaus

and Toby P. Breckon

1,2

Department of Computer Science, Durham University, Durham, U.K.

Department of Engineering, Durham University, Durham, U.K.

Keywords:

Novelty Detection, Denoising Autoencoder, Semi-supervised Anomaly Detection.

Abstract:

Anomaly detection is the task of recognising novel samples which deviate signiﬁcantly from pre-established

normality. Abnormal classes are not present during training meaning that models must learn effective rep-

resentations solely across normal class data samples. Deep Autoencoders (AE) have been widely used for

anomaly detection tasks, but suffer from overﬁtting to a null identity function. To address this problem, we

implement a training scheme applied to a Denoising Autoencoder (DAE) which introduces an efﬁcient method

of producing Adversarially Learned Continuous Noise (ALCN) to maximally globally corrupt the input prior

to denoising. Prior methods have applied similar approaches of adversarial training to increase the robustness

of DAE, however they exhibit limitations such as slow inference speed reducing their real-world applicability

or producing generalised obfuscation which is more trivial to denoise. We show through rigorous evaluation

that our ALCN method of regularisation during training improves AUC performance during inference while

remaining efﬁcient over both classical, leave-one-out novelty detection tasks with the variations-: 9 (normal)

vs. 1 (abnormal) & 1 (normal) vs. 9 (abnormal); MNIST - AUC

avg

: 0.890 & 0.989, CIFAR-10 - AUC

avg

: 0.670

& 0.742, in addition to challenging real-world anomaly detection tasks: industrial inspection (MVTEC-AD -

AUC

avg

: 0.780) and plant disease detection (Plant Village - AUC: 0.770) when compared to prior approaches.

1 INTRODUCTION

The task of anomaly detection is challenging due to

deviations from normality being continuous and spo-

radic by nature. Anomalous space is open-set con-

tinuous, meaning that strictly supervised classiﬁers,

although performing well across tasks in anomaly de-

tection (Gaus et al., 2019; Bhowmik et al., 2019) are

restricted by their limited exposure to abnormal ex-

amples during training. It is impossible for datasets

to contain every possible deviation in the anoma-

lous data thus supervised (classiﬁcation-based) ap-

proaches cannot generalise to the continuous nature in

which anomalous samples may deviate from normal-

ity. This means that there will always exist anomalous

deviations in anomaly space which present as adver-

sarial examples to supervised methods.

Generative-based anomaly detection methods

(Schlegl et al., 2017; Schlegl et al., 2019; Zenati et al.,

2018; Akcay et al., 2019b; Akcay et al., 2019a) train

solely across normal examples in order to approxi-

mate the underlying distribution of normality. They

work by learning meaningful features to solely rep-

resent normal samples which will cause a relatively

small reconstruction error after decoding; conversely,

the model will fail to reconstruct anomalous samples

fully due to null exposure of the anomalous parts dur-

ing training. As such, the reconstruction error be-

tween input and output provides a sound metric to

measure anomalous deviation of presented samples.

The beneﬁt of this (semi-supervised) training is that

normal (non-anomalous) data is often relatively in-

expensive and plentiful to obtain within real-world

anomaly detection tasks.

Autoencoders (AE) are well-suited to the ap-

proximation of the the underlying data distribution

across the normal class. They exhibit stability dur-

ing training unlike their Generative Adversarial Net-

work (GAN) (Goodfellow et al., 2014) based counter-

parts which exhibit training difﬁculties such as mode-

collapse or convergence instability (Zhang et al.,

2018). AE do however risk converging to a pass-

through identity function ( ) (Bengio et al., 2013) for

which the mapping from input x to output x

′

is a null

function such that lim

y→0

y = L (x,x

′

) ⇒ x ≃ x

′

where

L is the reconstruction error. Although this can still

learn limited underlying information about the distri-

bution of the training data, this over-ﬁtting allows the

reconstruction of anomalous regions within the input

which negatively affects performance in the task of

Barker, J., Bhowmik, N., A. Gaus, Y. and Breckon, T.

Robust Semi-Supervised Anomaly Detection via Adversarially Learned Continuous Noise Corruption.

DOI: 10.5220/0011684700003417

In Proceedings of the 18th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2023) - Volume 5: VISAPP, pages

615-625

ISBN: 978-989-758-634-7; ISSN: 2184-4321

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

615

semi-supervised anomaly detection. To prevent this,

Denoising Autoencoders (DAE) (Bengio et al., 2013)

are trained to produce unperturbed reconstructions

from purposefully noised input. This applies a level

of regularisation to the AE such that convergence to a

trivial solution is not straightforward. It allows an AE

to learn more robust and meaningful features across

normality as well as remain invariant of noise present

in the input (Salehi et al., 2021; Jewell et al., 2022).

Adding noise to input images in the task of semi-

supervised anomaly detection has been explored pre-

viously (Salehi et al., 2021; Jewell et al., 2022; Pathak

et al., 2016). The Adversarially Robust Autoencoder

(ARAE) (Salehi et al., 2021) works by forcing per-

ceptually similar samples closer in their latent repre-

sentations by crafting adversarial examples that are

constrained to be 1) perceptually similar to the in-

put, but have 2) maximally distant latent encoding.

The adversarial samples are produced by traversing

the latent space at each training epoch to ﬁnd samples

which optimally satisfy conditions 1 and 2. This pro-

cess signiﬁcantly increases computational overhead

of the model due to the demands of satisfying such

constraints. As such, the latency of ARAE (Salehi

et al., 2021) is slow during training.

The One-Class Learned Encoder-Decoder

(OLED) (Jewell et al., 2022) partially obfuscates the

input data with a mask produced by an additional

autoencoder network called the Mask Module (MM).

The MM is optimised to produce masks which max-

imise the reconstruction error of the DAE module. A

limitation of this method is that the produced masks

are visually similar across all datasets, becoming,

in-essence, a one-size-ﬁts-all type of obfuscation.

In this work, we address the limitations of prior

work (Salehi et al., 2021; Jewell et al., 2022) by pro-

ducing tailored noise to the given task efﬁciently by

extending the notion of optimised adversarial noise

for robust training with the Adversarially Learned

Continuous Noise (ALCN) method. Our method

has two parts which are trained simultaneously: 1)

The Noise Generator G

noise

module which produces

maximal and continuous noise which is bespoke to

the training data and 2) The Denoising Autoencoder

denoise

module which is trained to reconstruct input

images corrupted (by weighted sum) by the output of

noise

In this work, we propose the following contributions:

– A novel method of adding continuous adversar-

ially generated noise to input images which are

optimised to be maximally challenging for a de-

noising autoencoder to reverse.

– Exhaustive evaluation of this approach against

prior noising methods (Salehi et al., 2021; Jew-

ell et al., 2022; Pathak et al., 2016) as well as

against manually deﬁned noise (Random Speckle

and Gaussian) across ‘leave-one-out’ anomaly de-

tection tasks formulated via the MNIST (LeCun

et al., 2010) and CIFAR-10 (Krizhevsky and Hin-

ton, 2009) benchmark datasets.

– Extended evaluation over real-world anomaly

detection tasks including industrial inspection

(MVTEC (Bergmann et al., 2019)) and the plant

leaf disease detection (Plant Village (Hughes and

Salath’e , 2015)) with side-by-side comparison

against leading state-of-the-art methods (Akcay

et al., 2019b; Akc¸ay et al., 2019; Vu et al., 2019a;

Zenati et al., 2018; Schlegl et al., 2017; Ruff

et al., 2018a; Perera et al., 2019; Abati et al.,

2019; Salehi et al., 2021; Jewell et al., 2022) via

the Area Under Receiver Operator Characteristic

(AUC) metric.

2 RELATED WORK

Existing anomaly detection methods have gained

exceptional success in identifying data instances

which deviate signiﬁcantly from established normal-

ity. However, the current methods struggle to ad-

dress fully the two enduring anomaly detection chal-

lenges. Firstly, data availability and coverage is al-

ways limited for the anomalous class such that those

limited anomaly examples present provide poor cov-

erge of the full sprectrum of possible anomalous de-

viations. Second, is the challenge of a high-skewed

dataset distribution such that normal instances dom-

inate but with anomaly contamination (Pang et al.,

2019). In order to combat these challenges, deep

anomaly detection methods operate in a domain of

a binary-class, semi-supervised learning paradigm.

These are typically trained to solely represent nor-

mal class data with varying representations spanning

the latent space of Generative Adversarial Networks

(GAN) (Schlegl et al., 2017; Akcay et al., 2018;

Zenati et al., 2018), distance metric spaces within

(Pang et al., 2018; Ruff et al., 2018b) or intermediate

representations via autoencoders (Zhou and Paffen-

roth, 2017). Subsequently, these learned representa-

tions are used to deﬁne normality as an anomaly score

correlated to reconstruction error (Schlegl et al., 2017;

Akcay et al., 2018; Zenati et al., 2018) or distance-

based measures (Pang et al., 2018; Ruff et al., 2018b).

Generally, semi-supervised anomaly detection ap-

proaches (Schlegl et al., 2017; Akcay et al., 2018;

Akc¸ay et al., 2019) are based on learning a close

approximation to the true distribution of normal in-

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

616

stances by using generative methods, such as (Akcay

et al., 2018; Akc¸ay et al., 2019; Barker and Breckon,

2021). The initial strategy uses autoencoder (LeCun

et al., 2015) architectures such as a variational au-

toencoder (VAE) (Kingma and Welling, 2014), where

a latent representation z is learned from the image

space X via an encoder mapping via Pr(z|x). Sequen-

tially, a decoder maps from z back to image space

via Pr(i

′

|x) to produce x

′

. The encoder and decoder

is trained to minimise reconstruction error between

the original image x ∈ X and the reconstruction im-

age x

′

. However, in general, they do not closely

capture the data distribution over X due to the over-

simpliﬁcation of the learned prior probability p(z|x).

VAE (Kingma and Welling, 2014) are only capable of

learning a uni-modal distribution, which fails to cap-

ture complex distributions that are commonplace in

real world anomaly detection scenarios (Barker and

Breckon, 2021).

AnoGAN (Schlegl et al., 2017) combats this sim-

pliﬁcation by adopting GAN in the anomaly detec-

tion approach. AnoGAN (Schlegl et al., 2017) is the

ﬁrst GAN-based method, where the model is trained

to learn the manifold z only on normal data. When

anomalous x

is going through the generator network

(G), it produces an l

reconstruction error which,

if large enough from learned normal data distribu-

tion will be ﬂagged anomalous. Although effectively

proven, the computational performance is prolonged

hence limiting real-world applicability. GANomaly

(Akcay et al., 2019b) solves this issue by training an

encoder-decoder-encoder network with the adversar-

ial scheme to capture the normal distribution within

the image and latent space. It is achieved by training a

generator network and a secondary encoder in order to

map the generated samples into a second latent space

ˆz which is then used to better learn the original latent

priors z, mapping between latent values efﬁciently at

the same time as the generator G learns the distri-

bution manifold over data x. Efﬁcient GAN Based

Anomaly Detection (EGBAD) also addresses the per-

formance issue in AnoGAN by adopting a Bidirec-

tional GAN (Donahue et al., 2019) into its architec-

ture. The primary idea is to solve, during training, the

optimisation problem min

G,E

max

V (D,G,E) where

the features of X are learned by the network E to pro-

duce the pair of (x,E(x)). The main contribution is to

allow EGBAD to compute the anomaly score without

Γ optimisation steps during inference as it happens in

AnoGAN (Schlegl et al., 2017).

Although GAN-based methods for anomaly de-

tection have risen to prominence and gained signiﬁ-

cant results, they suffer from volatile training issues

such as mode collapse (Thanh-Tung and Tran, 2020),

leading to potential inability for the generator to pro-

duce meaningful output. On the other hand, autoen-

coder (LeCun et al., 2015) based architectures are

much more stable than GAN-based approaches, but

can overﬁt to a pass-through identity (null) function

as previously discussed. To combat this, regularisa-

tion in the form of adding deliberate corruption to the

input data often takes place (Adey et al., 2021; Salehi

et al., 2021; Jewell et al., 2022).

The work of (Adey et al., 2021) adds purposeful

corruption to the normal input data and subsequently

forces the autoencoder to reconstruct it, or denoise it.

It enables the model to compress anomaly score to

zero for normal pixel, resulting clean anomaly seg-

mentation which signiﬁcantly improve performance.

ARAE (Salehi et al., 2021) works by injecting adver-

sarial samples into the training set so that the model

can ﬁt the original sample and the adversarial sample

at the same time. It is shown that ARAE (Salehi et al.,

2021) learns more semantically meaningful features

of normal class by training an adversarially robust au-

toencoder in a latent space, resulting competitive per-

formance with state-of-the-art in novelty detection.

The work of OLED (Jewell et al., 2022) offers

another approach in noise perturbation in input data,

where instead of being perturbed by noise, input im-

ages are subjected to masking through the use of

Mask Module (MM). The masks generated by MM

are optimized to cover the most important parts of the

input image, resulting in a comparable reconstruction

score across sample. Through optimal masking, the

proposed approach learns semantically richer repre-

sentations and enhances novelty detection at test time.

Motivated by the idea intention pre-encoding in-

put corruption, we propose a novel approach for ad-

versarially generated noise which, when added to the

input data, is very challenging for the denoising au-

toencoder to reverse. Our approach, Adversarially

Learned Continuous Noise (ALCN), it consists of two

parts, Noise Generator G

noise

and Denoising Autoen-

coder G

denoise

. The former produces maximal and

continuous noise which is bespoke to the training data

while the latter trained to reconstruct input images

perturbed (by weighted sum) with this maximal noise.

3 PROPOSED APPROACH

Our proposed method is outlined in Figure 1. In our

approach, we utilise a Denoising Autoencoder Gen-

erator (G

denoise

) network together with a GAN-like

Noise Generator (G

noise

) network. These are concur-

rently adversarially trained using the process outlined

in Algorithm 1. In a given step, the weights of G

noise

Robust Semi-Supervised Anomaly Detection via Adversarially Learned Continuous Noise Corruption

617

Noise Generator

x ~ N(0, 1)

B x 256 x 12,800

ReLU

Encoder

(3, 16, 5 )

Encoder

(16, 32, 5 )

Decoder

(32, 16, 5 )

Decoder

(16, 3, 5 )

Decoder

(32, 16, 5 )

Decoder

(16, 3, 5 )

Adversarial Noise

Reconstructed Images

Input Images

Sigmoid

(256, 12800)

Denoising Autoencoder

Figure 1: Overview of adversarial noise learning architecture featuring: top-Noise Generator Module G

noise

, bottom- Denois-

ing module G

denoise

are updated ﬁrst with gradient ascent with respect

to the reconstruction error so that at any given step,

noise

produces differing corruption from the previ-

ous step which G

denoise

then attempts to reverse by

optimising the reconstruction error with gradient de-

scent.

Training across dataset x ∈ R

B×C×H×W

∈ X where

{B,C,H,W} represent the batch size, number of

channels, height and width, respectively, starts by

training the noise generator G

noise

. A linear vector

of size B × 256 random variables φ is sampled from

a standard Gaussian normal distribution φ ∼ N(µ :

0,σ : 1) and fed through G

noise

to produce noise n of

shape R

B×C×H×W

. The added Sigmoid layer (

1+e

−l

)

on the ﬁnal layer of G

noise

binds the noise values con-

tinuously between [0,1]. We combine the noise n

to the input image x using a weighted sum by utilis-

ing the linear blending operator noise(x,n) = α(x) +

(1 − α)(n) where α is randomly sampled on each step

within bounds α → [0.2, 0.9] ∈ R

. The linear blend

operator ensures that the magnitude of the values of

noise(x,n) match with the pixel intensities of x and n.

Values of x are normalised with 0 mean and unit vari-

ance meaning that the values of noise(x,n) are such

that G

denoise

is prevented from discriminating between

the noise corrupted pixels and the original image pix-

els based on differing pixel intensity.

If alpha is static during training, G

noise

can

theoretically perfectly optimise the generated noise

n to destroy all information in image x ∈ X such

that all values in noise(x , n) are set to 1 such that

Algorithm 1: Adversarial Noise Training.

W{G} ← init ▷ Initialise G randomly

W{N

} ← init ▷ Initialise N

randomly

Train One Epoch:

for mini-batch: x ⊂ X do

weights{G

noise

} ← True

weights{G

denoise

} ← False

α ← [0.2,0.9] ▷ Randomly select α

z ← N(µ = 0, σ = 1) ▷ |z| = {|x|, 256}

′

← G

denoise

((1 − α)G

noise

(z) + αx)

W{G

noise

}

backpropagate

←−−−−−−−− Optim

noise

(−L (x,x

′

))

weights{G

noise

} ← False

weights{G

denoise

} ← True

′

← G

denoise

noise

(z) + x)

W{G

denoise

}

backpropagate

←−−−−−−−− Optim

denoise

(L (x,x

′

))

end for

n = (

1−α·x∈X

1−α

). The noise(x,n) cannot converge to

all zeros where n = −(

α·x∈X

1−α

) due to the logical ar-

gument that the values of noise n produced by G

noise

are bound to [0,1] ∈ R

because of the Sigmoid layer

on the output of G

noise

and x is such that ∀x

∈ x →

{0,1},∃x

∈ x | x

= 1 implying that if (x

∈ x = 1)

then n =

−α

1−α

⇒ n < 0 ∀α ∴ n /∈ R

. To prevent con-

vergence to the trivial solution n = (

1−α·x∈X

1−α

) in our

experiments, we: 1) Set the value of α to be randomly

continuously sampled for each step during training

and 2) The input of G

noise

is sampled from the Gaus-

sian distribution N(0, 1) which applies some level of

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

618

randomness during sampling.

The noise(x, n) is then used as input to G

denoise

reconstruct x from noise(x,n), reversing the corrup-

tion caused by G

noise

. The corrupted image noise

x,n

encoded to the latent vector z and then subsequently

decoded into a synthetic reconstruction x

′

Adversarial learning is accomplished by the mini-

max optimisation between the G

denoise

and G

noise

modules. Weights of G

denoise

are optimised to min-

imise L, the reconstruction error between x and x

′

whereas the weights of G

noise

are conversely opti-

mised to maximise L . Loss terms in the overall loss

are given scalar regularisation terms λ

and λ

for

losses L

denoise

and L

noise

respectively. The overall

optimisation function in this work is:

argmin argmax

denoise

noise

= L

denoise

(x,x

′

)λ

noise

(x,x

′

)λ

(1)

This method of training encourages the noise gen-

erator to produce masks which optimally corrupt the

input. Such optimal noise makes the denoising pro-

cess more difﬁcult as the denoising module must not

only learn meaningful features of the input data, but

such learned representations should not carry forward

out-of-distribution (anomalous) features to the syn-

thetic reconstruction.

3.1 Loss Function

In our experiments, we ﬁnd that the use of Focal Fre-

quency Loss (FFL) (Jiang et al., 2021) created higher-

ﬁdelity reconstructions and a slight increase in AUC

performance. FFL is based on the L2 distance (loss)

between the real image x and the generated image x

′

in the Fourier (frequency) domain. Pixel coordinates

of x (x

) and x

′

) are used in conjunction to their

respective frequency spectrum coordinates (x

f req

′

f req

) from the Discrete Fourier Transform (DFT) as

follows:

F(ϑ) = (

· ϑ

f req

|H|

)|ϑ = {x,x

′

} (2)

The loss is deﬁned as the total distance in fre-

quency domain with respect to amplitude and phase

in the following formula:

L (x,x

′

) = ||e

−i2π(F(x))

− e

−i2π(F(x

′

))

(3)

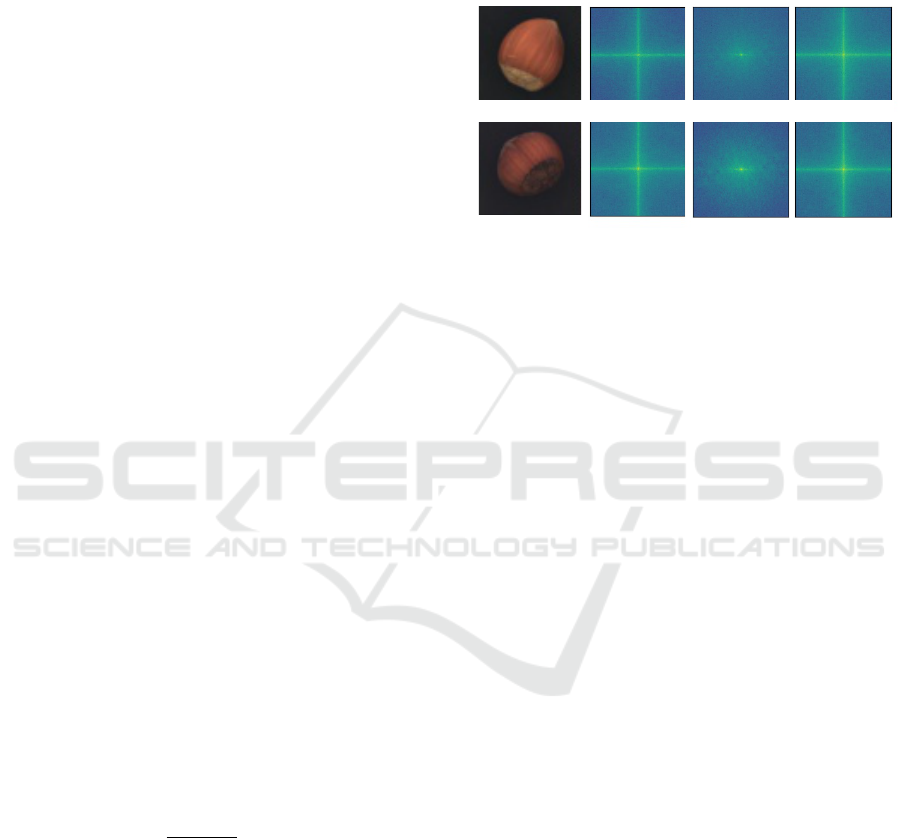
Figure 2 shows visually how using an L2 loss

loosely approximates the frequency representation of

x, but fails to capture high-frequency information

present in the image. FFL (Jiang et al., 2021) how-

ever, can more closely approximate the frequency do-

main as seen in this ﬁgure, the frequency representa-

tions of x and x

′

are closely matched. This property

makes it highly suitable for use in our reconstruction-

driven anomaly detection approach.

Original Image (x)

MVTEC (Hazelnut)

Fourier Transform (x)

Fourier Transform (x')

Training using L2 Loss

Fourier Transform (x')

Training using FFL

Figure 2: Visualisation of frequency domain after Fourier

Transform operation of reconstruction x

′

from input image x

both with and without using FFL (Jiang et al., 2021) during

training.

4 EXPERIMENTAL SETUP

We present our experimental setup in terms of the

benchmark datasets used for evaluation (Section 4.1)

and the implementation details of our approach (Sec-

tion 4.2).

4.1 Datasets

We make use of four established benchmark datasets

that are commonplace for evaluation within the

anomaly detection domain:

• MNIST (LeCun et al., 2010): A collection of

69,018 hand-written single digits from 0 to 9 of

resolution 28 × 28. For this dataset we utilise a

80 : 20 (55,209 : 13,807) split between training

and testing respectively across the data.

• CIFAR-10 (Krizhevsky and Hinton, 2009): A

set of 50,026 low-resolution (32 × 32) images

split into ten classes of common objects. A 80 : 20

(40,012 : 10,012) split between training and test-

ing sets are utilised across this dataset.

• MVTEC-AD (Bergmann et al., 2019): Bench-

mark dataset of 6,809 images for quality control

in industrial visual inspection. The data is com-

posed of ﬁfteen classes of both non-anomalous,

defect free objects as well as a set of defective

anomalous counter-parts. A 70 : 30 split for

training and testing respectively is applied for

each class.

Robust Semi-Supervised Anomaly Detection via Adversarially Learned Continuous Noise Corruption

619

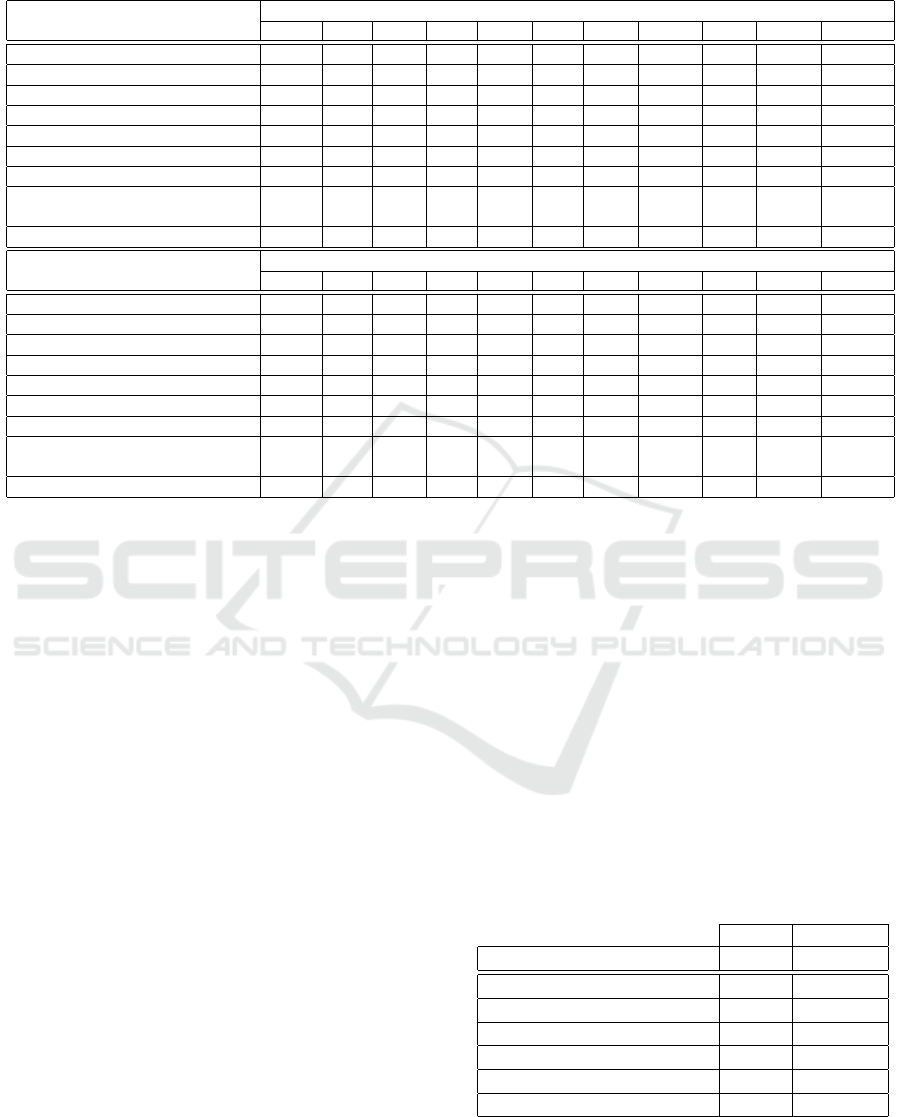
Table 1: Quantitative results (class name indicates AUC, AUC

avg

of all classes) of models across MNIST (LeCun et al., 2010)

(upper) and CIFAR-10 (Krizhevsky and Hinton, 2009) (lower) datasets (Protocol 1).

Model

MNIST

0 1 2 3 4 5 6 7 8 9 AUC

avg

VAE (Kingma and Welling, 2014) 0.55 0.10 0.63 0.25 0.35 0.30 0.43 0.18 0.50 0.10 0.34

AnoGAN (Schlegl et al., 2017) 0.61 0.30 0.54 0.44 0.43 0.42 0.48 0.36 0.40 0.34 0.43

EGBAD (Zenati et al., 2018) 0.78 0.29 0.67 0.52 0.45 0.43 0.57 0.40 0.55 0.35 0.50

GANomaly (Akcay et al., 2019b) 0.89 0.65 0.93 0.80 0.82 0.85 0.84 0.69 0.87 0.55 0.79

ADAE (Vu et al., 2019b) 0.95 0.82 0.95 0.89 0.82 0.91 0.89 0.80 0.93 0.63 0.86

DAE 0.84 0.97 0.79 0.64 0.53 0.61 0.66 0.55 0.71 0.57 0.69

DAE+Random Noise 0.84 0.93 0.66 0.66 0.52 0.62 0.72 0.56 0.75 0.53 0.68

DAE+Gaussian Noise

∼ N(0, 0.5)

0.88 0.97 0.77 0.66 0.55 0.62 0.75 0.55 0.71 0.57 0.70

DAE + ALCN 0.97 0.97 0.96 0.89 0.85 0.88 0.92 0.80 0.93 0.76 0.89

Model

CIFAR-10

Plane Car Bird Cat Deer Dog Frog Horse Ship Truck AUC

avg

VAE (Kingma and Welling, 2014) 0.59 0.40 0.52 0.44 0.46 0.50 0.38 0.51 0.64 0.49 0.49

AnoGAN (Schlegl et al., 2017) 0.51 0.49 0.41 0.40 0.34 0.39 0.34 0.41 0.56 0.51 0.44

EGBAD (Zenati et al., 2018) 0.58 0.52 0.39 0.45 0.37 0.49 0.36 0.54 0.42 0.55 0.47

GANomaly (Akcay et al., 2019b) 0.63 0.63 0.51 0.58 0.59 0.62 0.68 0.61 0.62 0.62 0.61

ADAE (Vu et al., 2019a) 0.63 0.73 0.55 0.58 0.50 0.60 0.60 0.61 0.62 0.67 0.61

DAE 0.50 0.68 0.61 0.55 0.69 0.53 0.62 0.60 0.63 0.71 0.61

DAE+Random Noise 0.63 0.53 0.54 0.54 0.65 0.59 0.64 0.55 0.66 0.63 0.60

DAE+Gaussian Noise

∼ N(0, 0.5)

0.57 0.68 0.57 0.54 0.65 0.54 0.55 0.52 0.57 0.53 0.57

DAE + ALCN 0.77 0.71 0.62 0.57 0.72 0.62 0.72 0.60 0.66 0.69 0.67

• Plant Village (Hughes and Salath’e , 2015):

Visual images of the leaves of vital agricultural

edible plants together with anomalies containing

common visual leaf diseases for each respective

plant.

4.2 Implementation Details

Our method is compared across the MNIST (LeCun

et al., 2010) and CIFAR-10 (Krizhevsky and Hinton,

2009) datasets due to their inherent simplicity while

training as well as giving sufﬁcient bench-marking

for the evaluation between the techniques included in

this work. Evaluation is conducted in two protocols

following from established methods for ‘leave-one-

out’ anomaly detection tasks. During protocol 1 (1

vs. rest), one digit is regarded as anomalous and re-

maining classes are normal as performed by: (Akcay

et al., 2018; Akc¸ay et al., 2019; Barker and Breckon,

2021; Zenati et al., 2018; Schlegl et al., 2017; Schlegl

et al., 2019). Protocol 2 (rest vs. 1) as performed by:

(Ruff et al., 2018a; Perera et al., 2019; Abati et al.,

2019; Salehi et al., 2021; Jewell et al., 2022) is the

opposite in that one digit is normal and the nine re-

maining classes are anomalous.

The split ratio for the data is 80 : 20 for train-

ing and testing respectively as conducted by (Zenati

et al., 2018; Akcay et al., 2019b). During training, the

Adam optimiser is used for both G

denoise

and G

noise

with learning rates of 1 × 10

−5

and 8 × 10

−3

respec-

tively. An image resolution of 28×28 is implemented

throughout ‘leave-one-out’ anomaly detection tasks

(LeCun et al., 2010; Krizhevsky and Hinton, 2009).

We implement a larger resolution of 256 × 256 across

MVTEC (Bergmann et al., 2019) and Plant Village

(Hughes and Salath’e , 2015) however. A batch size

of 4096 is employed across MNIST and CIFAR-10

and a batch size of 16 is used across MVTEC and

plant village during training on an NVidia GTX 1080

TI GPU. We evaluate our method using the Area Un-

der Receiver Operator Characteristic (AUC) metric.

Table 2: Quantitative results (AUC

avg

) of models including

ARAE (Salehi et al., 2021) and OLED (Jewell et al., 2022)

across MNIST (LeCun et al., 2010) (left) and CIFAR-10

(Krizhevsky and Hinton, 2009) (right) datasets (Protocol 2).

MNIST CIFAR-10

Method AUC

avg

AUC

avg

DSVDD (Ruff et al., 2018a) 0.948 0.648

OCGAN (Perera et al., 2019) 0.975 0.733

LSA(Abati et al., 2019) 0.975 0.731

ARAE (Salehi et al., 2021) 0.975 0.717

OLED (Jewell et al., 2022) 0.985 0.671

DAE + ALCN 0.989 0.742

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

620

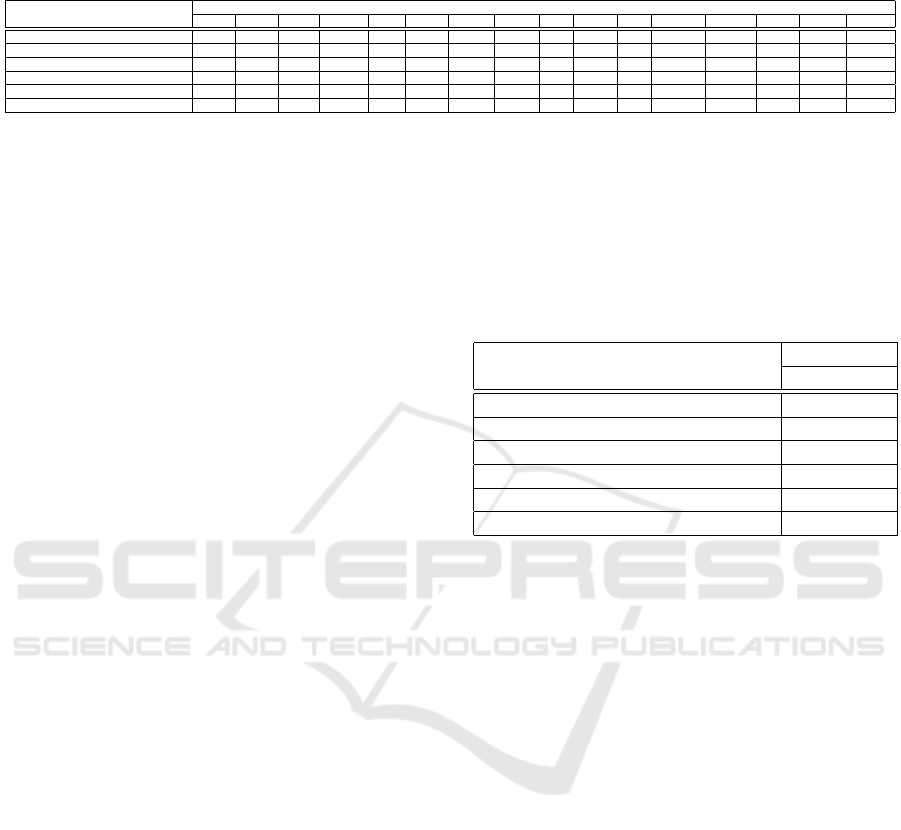
Table 3: Quantitative results (class name indicates AUC, AUC

avg

of all classes) of models across MVTEC-AD (Bergmann

et al., 2019) dataset.

Model

MVTEC-AD

Bottle Cable Caps. Carpet Grid H’nut Leath. M’nut Pill Screw Tile T’brush T’sistor Wood Zipper AUC

avg

VAE (Kingma and Welling, 2014) 0.66 0.63 0.61 0.51 0.52 0.30 0.41 0.66 0.51 1 0.21 0.30 0.65 0.87 0.87 0.58

AnoGAN (Schlegl et al., 2017) 0.80 0.48 0.44 0.34 0.87 0.26 0.45 0.28 0.71 1 0.40 0.44 0.69 0.57 0.72 0.56

EGBAD (Zenati et al., 2018) 0.63 0.68 0.52 0.52 0.54 0.43 0.55 0.47 0.57 0.43 0.79 0.64 0.73 0.91 0.58 0.60

GANomaly (Akcay et al., 2019b) 0.89 0.76 0.73 0.70 0.71 0.79 0.84 0.70 0.74 0.75 0.79 0.65 0.79 0.83 0.75 0.76

Skip-GANomaly (Akc¸ay et al., 2019) 0.93 0.67 0.71 0.79 0.65 0.90 0.90 0.79 0.75 1 0.85 0.68 0.81 0.91 0.66 0.80

DAE+ALCN

0.94 0.84 0.86 0.84 0.97 0.92 0.62 0.86 0.75 1 0.79 0.65 0.73 0.93 0.70 0.83

5 RESULTS

Extensive comparison of the results of our method

compared to prior methods are outlined in Tables 1, 2,

3, 4 and 5. Tables 1 and 2 outline the quantitative re-

sults of the DAE+ALCN method across both MNIST

(LeCun et al., 2010) and CIFAR-10 (Krizhevsky and

Hinton, 2009) ‘leave-one-out tasks’ across both pro-

tocol 1 (9 normal/1 anomalous) and protocol 2 (1 nor-

mal/9 anomalous). Across the real-world anomaly de-

tection tasks outlined in this paper (Bergmann et al.,

2019; Hughes and Salath’e , 2015), Table 3 out-

lines the quantitative results of our method across

the MVTEC-AD (Bergmann et al., 2019) industrial

inspection dataset and Table 4 presents the results

across the Plant Village dataset (Hughes and Salath’e

, 2015).

5.1 Leave One Out Anomaly Detection

5.1.1 Protocol 1

Table 1 outlines the results of each approach across

the MNIST and CIFAR-10 datasets. We begin by

comparing our vanilla DAE approach without any

noise regularisation and this results in an AUC

avg

0.69 across MNIST and 0.61 across CIFAR-10. This

is weak compared to other methods in the table. Ap-

plying Gaussian noise obtains an AUC

avg

of 0.70 on

MNIST and 0.57 on CIFAR-10. Our DAE+ALCN

approach applied to the DAE architecture achieves the

best AUC score on 90% of the classes with an aver-

age AUC of 0.89 and produces the best scores on 60%

classes of CIFAR-10 with an average AUC score of

0.67.

5.1.2 Protocol 2

Table 2 presents the results across the protocol 2

variant (1 normal/9 anomalous) across both MNIST

and CIFAR-10. Our DAE+ALCN method obtains

an AUC

avg

of 0.989 across MNIST and an AUC

avg

of 0.742 across CIFAR-10, outperforming all prior

methods including OLED (Jewell et al., 2022) which

uses discrete noise, as previously stated in this work.

This gives illumination as to the beneﬁt of using be-

spoke continuous noise while training.

5.2 Real-world Tasks

Table 4: Quantitative results (AUC

avg

) of models across

Plant Village (Hughes and Salath’e , 2015) dataset.

Model

Plant Village

AUC

avg

VAE (Kingma and Welling, 2014) 0.65

AnoGAN (Schlegl et al., 2017) 0.65

EGBAD (Zenati et al., 2018) 0.70

GANomaly (Akcay et al., 2019b) 0.73

Skip-GANomaly (Akc¸ay et al., 2019) 0.77

DAE+ALCN 0.77

5.2.1 MVTEC-AD Industrial Inspection Dataset

In this experiment we compare our DAE+ALCN

method against prior semi-supervised anomaly detec-

tion methods across the MVTEC-AD task (Bergmann

et al., 2019) to verify that we can apply our method to

a real-world example rather than solely across syn-

thetic and trivial leave-one-out tasks.

The results of this experiment are shown in Table

3. It can be observed that DAE+ALCN obtains the

highest average AUC score of 0.83, outperforming all

other methods on 10 out of the 15 classes in MVTEC-

AD dataset.

5.2.2 Plant Village Dataset

The Plant Village dataset (Bergmann et al., 2019)

is challenging due to the large intra-class variance

present in this dataset. Leaves of a given plant can

vary vastly in appearance with respect to shape and

colour. As such, it is challenging to map the underly-

ing distribution of the leaves. The quantitative results

of methods across this dataset are presented in Table

4. Our DAE+ALCN method obtains an AUC

avg

0.77 which is the same as that of Skip-GANomaly

(Akc¸ay et al., 2019). Both methods far-outperform

prior methods across this dataset.

Robust Semi-Supervised Anomaly Detection via Adversarially Learned Continuous Noise Corruption

621

Table 5: Comparison of model complexity (number of parameters (millions)) and inference time (milliseconds).

Model

DAE AnoGAN EGBAD GANomaly DAE + ALCN

Parameters (Million) 1.12 233.04 8.65 3.86 9.87

Inference Time/Batch MNIST 2.36 667 8.02 9.7 4.54

(Millisecond) CIFAR-10 2.73 611 9.55 10.53 5.23

Cable

Anomaly Score: 0.15

Bottle

Skip-GANomaly DAE+Adversarial Noise

Input Output Input Output

Training

Class

Anomaly Score: 0.07Anomaly Score: 0.05

Anomaly Score: 0.12

Figure 3: Comparison between Skip-GANomaly(Akcay

et al., 2019a) and DAE+Adversarial Noise of feeding vastly

out-of-distribution (Hazelnut and Grid) examples through

models trained on a different class (Cable and Bottle).

Figure 3 illustrates the results of an input which is

an out-of-distribution example through both the Skip-

GANomaly (Akc¸ay et al., 2019) and DAE+ALCN

into models trained on only another speciﬁc class

singular (Figure 3, left label). The objective be-

ing that Skip-GANomaly (Akc¸ay et al., 2019) and

DAE+ALCN should reconstruct out-of-distribution

examples within the original class distribution. How-

ever, it can be seen in Figure 3 that Skip-GANomaly

(Akc¸ay et al., 2019) successfully reconstructs an out-

of-distribution example given weight to the conclu-

sion that it has converged to a pass-though identity

function and just copies information from input to

output (i.e. hazelnut/grid observed in both input +

output), despite the fact the model has never been

exposed to these class examples in training. For

Skip-GANomaly this leads to low anomaly scores

of 0.05 and 0.12 for Cable and Bottle respectively.

By contrast, our DAE+ALCN architecture, man-

ages to reconstruct such out-of-distribution exam-

ples back into the training classes thus resulting in

the anomaly scores 0.07 for Cable (0.02 larger than

Skip-GANomaly (Akcay et al., 2019a)) and 0.15

for Bottle (0.03 higher than Skip-GANomaly (Akcay

et al., 2019a)). This shows that given vastly out-of-

distribution examples, the DAE+ALCN network is

more robust to misclassiﬁcation and less prone to a

pass-through identity-like reconstruction output.

Overall these experiments show that using our ad-

versarial noise as a regularisation technique can en-

able even a simple architecture such as the Denoising

Autoencoder outlined in Figure 1 to obtain better re-

sults than more complex model architectures.

5.3 Model Complexity

An outline of model complexity together with in-

ference time per batch is outlined in Table 5. The

DAE+ALCN architecture has 9.87 Million param-

eters which is slightly larger than EGBAD (Zenati

et al., 2018) which is at 8.65 Million but still or-

ders of magnitude smaller relative to that of AnoGAN

(Schlegl et al., 2017). The magnitude of our model

comes from the noise generation module (ALCN)

in addition to the DAE module which is fairly light

weight at 1.12 million parameters. This means that

during training, the adversarial noising approach out-

lined in this paper adds a signiﬁcant memory over-

head to the model during training however, has an in-

ference speed of 4 milliseconds per batch which is

signiﬁcantly faster than the other methods, but gener-

ating the noise during inference adds a slight overhead

of 2.5ms over the standard DAE architecture.

5.3.1 Qualitative Results

Figure 4 illustrates the qualitative results of

DAE+ALCN across different datasets. The ﬁrst

column for each example shows the input images

to the model. The second column illustrates the

adversarial noise which is added to the input resulting

in those images (3rd column). This adversarial noise

+ input is then fed into DAE and the resulting output

after denoising (4th column). Of particular interest

are the noise examples across the MNIST (LeCun

et al., 2010) and Plant Village (Hughes and Salath’e

, 2015) datasets. From Figure 4 we can observe that

the adversarial noise tends towards the style/shape of

the input data which, when added to the image, adds

a large level of input obfuscation (Figure 4 - Input +

Noise columns). Despite this, the DAE architecture

is able to successfully reconstruct the original input

images from this maximally noised version with

signiﬁcant ﬁdelity (Figure 4 - Output columns).

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

622

Input

Image

Adversarial

Noise

Image + Noise Output

Input

Image

Adversarial

Noise

Image + Noise Output

MNIST

CIFAR-10

MVTEC-AD

(Bottle)

MVTEC-AD

(Cable)

Plant Village

Figure 4: Examples of input image, generated adversarial noise, input + noise addition and resulting reconstructed output (left

→ right).

Robust Semi-Supervised Anomaly Detection via Adversarially Learned Continuous Noise Corruption

623

6 CONCLUSION

In this work we introduce a novel approach for im-

proved robustness semi-supervised anomaly detection

by adversarially training a noise generator to produce

maximal continuous noise which is then added to in-

put data. In the same training step, a simple Denois-

ing Autoencoder (DAE) is optimised to reconstruct

the denoised, unperturbed input from the noised in-

put. Through this simple approach, we vastly improve

performance on semi-supervised anomaly detection

tasks across both benchmark ‘leave-one-out’ anomaly

and challenging real-world anomaly detection tasks,

outperforming prior work in the ﬁeld. Via abla-

tion, we also show the DAE with adversarial noise

approach demonstrates superior performance against

prior ﬁxed-parameter noising strategies (random and

Gaussian) across the leave-one-out benchmark tasks.

REFERENCES

Abati, D., Porrello, A., Calderara, S., and Cucchiara, R.

(2019). Latent space autoregression for novelty detec-

tion. In Conference on Computer Vision and Pattern

Recognition (CVPR), pages 481–490. IEEE Computer

Society.

Adey, P. A., Akc¸ay, S., Bordewich, M. J., and Breckon, T. P.

(2021). Autoencoders without reconstruction for tex-

tural anomaly detection. In 2021 International Joint

Conference on Neural Networks (IJCNN), pages 1–8.

IEEE.

Akcay, S., Atapour-Abarghouei, A., and Breckon, T.

(2019a). Skip-ganomaly: Skip connected and adver-

sarially trained encoder-decoder anomaly detection.

Proceedings of the International Joint Conference on

Neural Networks, July.

Akcay, S., Atapour-Abarghouei, A., and Breckon, T. P.

(2018). Ganomaly: Semi-supervised anomaly detec-

tion via adversarial training. In Asian conference on

computer vision, pages 622–637. Springer.

Akcay, S., Atapour-Abarghouei, A., and Breckon, T. P.

(2019b). Ganomaly : semi-supervised anomaly detec-

tion via adversarial training. In 14th Asian Conference

on Computer Vision, number 11363 in Lecture notes

in computer science, pages 622–637. Springer.

Akc¸ay, S., Atapour-Abarghouei, A., and Breckon, T. P.

(2019). Skip-ganomaly: Skip connected and adversar-

ially trained encoder-decoder anomaly detection. In

2019 International Joint Conference on Neural Net-

works (IJCNN), pages 1–8. IEEE.

Barker, J. W. and Breckon, T. P. (2021). Panda: Perceptually

aware neural detection of anomalies. In International

Joint Conference on Neural Networks, IJCNN.

Bengio, Y., Yao, L., Alain, G., and Vincent, P. (2013). Gen-

eralized denoising auto-encoders as generative mod-

els. arXiv preprint arXiv:1305.6663.

Bergmann, P., Fauser, M., Sattlegger, D., and Steger, C.

(2019). Mvtec ad–a comprehensive real-world dataset

for unsupervised anomaly detection. In Proceedings

of the IEEE/CVF Conference on Computer Vision and

Pattern Recognition, pages 9592–9600.

Bhowmik, N., Gaus, Y., Akcay, S., Barker, J. W., and

Breckon, T. P. (2019). On the impact of object and

sub-component level segmentation strategies for su-

pervised anomaly detection within x-ray security im-

agery. In 18th IEEE International Conference on

Machine Learning and Applications (ICMLA 2019).

IEEE.

Donahue, J., Darrell, T., and Philipp, K. (2019). Adver-

sarial feature learning. In 5th International Confer-

ence on Learning Representations, ICLR 2017 - Con-

ference Track Proceedings. International Conference

on Learning Representations, ICLR.

Gaus, Y. F. A., Bhowmik, N., Akc¸ay, S., Guill

en-Garcia,

P. M., Barker, J. W., and Breckon, T. P. (2019). Eval-

uation of a dual convolutional neural network archi-

tecture for object-wise anomaly detection in cluttered

x-ray security imagery. In 2019 International Joint

Conference on Neural Networks (IJCNN), pages 1–8.

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,

Warde-Farley, D., Ozair, S., Courville, A., and Ben-

gio, Y. (2014). Generative adversarial nets. In Ghahra-

mani, Z., Welling, M., Cortes, C., Lawrence, N., and

Weinberger, K. Q., editors, Advances in Neural Infor-

mation Processing Systems, volume 27. Curran Asso-

ciates, Inc.

Hughes, D. P. and Salath’e , M. (2015). An open ac-

cess repository of images on plant health to en-

able the development of mobile disease diagnostics

through machine learning and crowdsourcing. CoRR,

abs/1511.08060.

Jewell, J. T., Reza Khazaie, V., and Mohsenzadeh, Y.

(2022). One-class learned encoder-decoder network

with adversarial context masking for novelty detec-

tion. In 2022 IEEE/CVF Winter Conference on Ap-

plications of Computer Vision (WACV), pages 2856–

2866.

Jiang, L., Dai, B., Wu, W., and Loy, C. C. (2021). Focal

frequency loss for image reconstruction and synthesis.

In ICCV.

Kingma, D. and Welling, M. (2014). Auto-encoding vari-

ational bayes. In 2nd International Conference on

Learning Representations.

Krizhevsky, A. and Hinton, G. (2009). Learning multiple

layers of features from tiny images. Master’s the-

sis, Department of Computer Science, University of

Toronto.

LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learn-

ing. nature, 521(7553):436–444.

LeCun, Y., Cortes, C., and Burges, C. (2010). Mnist hand-

written digit database. ATT Labs [Online]. Available:

http://yann.lecun.com/exdb/mnist, 2.

Pang, G., Cao, L., Chen, L., and Liu, H. (2018). Learning

representations of ultrahigh-dimensional data for ran-

dom distance-based outlier detection. In Proceedings

of the 24th ACM SIGKDD international conference

VISAPP 2023 - 18th International Conference on Computer Vision Theory and Applications

624

on knowledge discovery & data mining, pages 2041–

2050.

Pang, G., Shen, C., Jin, H., and Hengel, A. v. d. (2019).

Deep weakly-supervised anomaly detection. arXiv

preprint arXiv:1910.13601.

Pathak, D., Krahenbuhl, P., Donahue, J., Darrell, T., and

Efros, A. A. (2016). Context encoders: Feature learn-

ing by inpainting. In Proceedings of the IEEE con-

ference on computer vision and pattern recognition,

pages 2536–2544.

Perera, P., Nallapati, R., and Xiang, B. (2019). Ocgan: One-

class novelty detection using gans with constrained

latent representations. In Conference on Computer

Vision and Pattern Recognition (CVPR). IEEE Com-

puter Society.

Ruff, L., Vandermeulen, R., Goernitz, N., Deecke, L., Sid-

diqui, S. A., Binder, A., M

uller, E., and Kloft, M.

(2018a). Deep one-class classiﬁcation. In Dy, J. and

Krause, A., editors, Proceedings of the 35th Interna-

tional Conference on Machine Learning, volume 80

of Proceedings of Machine Learning Research, pages

4393–4402. PMLR.

Ruff, L., Vandermeulen, R., Goernitz, N., Deecke, L., Sid-

diqui, S. A., Binder, A., M

uller, E., and Kloft, M.

(2018b). Deep one-class classiﬁcation. In Interna-

tional conference on machine learning, pages 4393–

4402. PMLR.

Salehi, M., Arya, A., Pajoum, B., Otooﬁ, M., Shaeiri, A.,

Rohban, M. H., and Rabiee, H. R. (2021). Arae: Ad-

versarially robust training of autoencoders improves

novelty detection. Neural Networks, 144:726–736.

Schlegl, T., Seeb

ock, P., Waldstein, S., Langs, G., and

Schmidt-Erfurth, U. (2019). f-anogan: Fast unsuper-

vised anomaly detection with generative adversarial

networks. Medical Image Analysis, 54:30–44.

Schlegl, T., Seeb

ock, P., Waldstein, S. M., Schmidt-Erfurth,

U., and Langs, G. (2017). Unsupervised anomaly de-

tection with generative adversarial networks to guide

marker discovery. In International conference on in-

formation processing in medical imaging, pages 146–

157. Springer.

Thanh-Tung, H. and Tran, T. (2020). Catastrophic forget-

ting and mode collapse in gans. In International Joint

Conference on Neural Networks (IJCNN 2020), pages

1–10.

Vu, H. S., Ueta, D., Hashimoto, K., Maeno, K., Pranata, S.,

and Shen, S. (2019a). Anomaly detection with adver-

sarial dual autoencoders.

Vu, H. S., Ueta, D., Hashimoto, K., Maeno, K., Pranata, S.,

and Shen, S. (2019b). Anomaly detection with adver-

sarial dual autoencoders. ArXiv, abs/1902.06924.

Zenati, H., Foo, C., Lecouat, B., Manek, G., and Chan-

drasekhar, V. (2018). Efﬁcient gan-based anomaly de-

tection. arXiv, abs/1802.06222.

Zhang, Z., Li, M., and Yu, J. (2018). On the convergence

and mode collapse of gan. In SIGGRAPH Asia 2018

Technical Briefs, SA ’18, New York, NY, USA. Asso-

ciation for Computing Machinery.

Zhou, C. and Paffenroth, R. C. (2017). Anomaly detec-

tion with robust deep autoencoders. In Proceedings

of the 23rd ACM SIGKDD international conference

on knowledge discovery and data mining, pages 665–

674.

Robust Semi-Supervised Anomaly Detection via Adversarially Learned Continuous Noise Corruption

625