So Can We Use Intrinsic Bias Measures or Not?

Sarah Schr¨oder

, Alexander Schulz

, Philip Kenneweg

and Barbara Hammer

CITEC, Bielefeld University, Inspiration 1, 33619 Bielefeld, Germany

Keywords:

Intrinsic Bias Measures, Pretrained Language Models, Template-Based Evaluation.

Abstract:

While text embeddings have become the state-of-the-art in many natural language processing applications, the

presence of bias that such models often l earn from training data can become a serious problem. As a reaction,

a l arge variety of measures for detecting bias has been proposed. However, an extensive comparison between

them does not exists so far. We aim to close this gap for the class of intrinsic bias measures in the context

of pretrained language models and propose an experimental setup which allows a fair comparison by using a

large set of templates for each bias measure. Our setup is based on the idea of simulating pretraining on a set

of differently biased corpora, thereby obtaining a ground truth for the present bias. This allows us to evaluate

in how far bias is detected by different measures and also enables to j udge the robustness of bias scores.

1 INTRODUCTION

Biases in machine learning mode ls, but especially in

pretrained lang uage models (PLM) are complex in na-

ture and difﬁcult to assess with respect to all po ssi-

ble bias orig ins and potential harms in applications

(Shah et al., 20 19). While th e ability to detect bias in

such PLMs is crucial for transpare ncy and also consti-

tutes a ﬁrst step for mitigating bias related proble ms,

there exists a variety of d ifferent methods for measu r-

ing bias in such models (Caliskan et al., 2017; May

et al., 201 9; Bolukbasi et al. , 2016; Gonen and Gold-

berg, 2019; De-Arteaga et al., 2019). In particular,

they can be grouped b y intrinsic and extrinsic evalu-

ation strategies, where the former ones dir e ctly work

with the intrinsic text embeddings while the latter aim

for evaluation with an additional down stream task.

In this work we f ocus on intrinsic bias measures

and biases that are learned during pretraining, because

such pretrained models are the basis in many applica-

tions and biases lear ned in the pretraining phase can

persist in later applications. The class of intrinsic bias

measures is, however, diverse, including different co-

sine based scores (Caliskan et al., 2017; May et al.,

2019; Bolukbasi et al. , 2016) and Neighbor, Clus-

tering and Classiﬁcation tests (Gonen and Goldberg,

2019) among others. A uniﬁed, systematic and fair

compariso n between them remains challenging.

https://orcid.org/0000-0002-7954-3133

https://orcid.org/0000-0002-0739-612X

https://orcid.org/0000-0002-7097-173X

https://orcid.org/0000-0002-0935-5591

In the present work, we conduct an experiment

where we simulate pretraining o n a variety of bi-

ased corpora and assess how these biases manifest in

the model. Not only do we consider binary gende r

bias, as frequently done in relate d work, but also as-

sess multi-attribute biases at the example of religious

and ethnicity b ia ses. We evaluate many intrinsic bias

measures from the literature in terms of their abil-

ity to capture biases in the model, compatibility to

each other and their robustness. Compatibility is of-

ten impacted by different testing scenarios (e.g. target

words, templates) of the different bias measures (Se-

shadri et al., 2022). We rem ove this variable by using

a uniﬁed test case for all measures, to speciﬁcally ﬁnd

out how the scores themselves rela te to each other.

Our con tributions are: (i) We propose a novel test

framework for intrinsic bias m easures w.r.t. pretrain-

ing of language models, which enables a fair com-

parison between different measures, regarding their

performance to measure bias and their stability. (ii)

Thereby, we create and publish a benchmark that is

signiﬁcantly larger and has more variety than other

template-based approaches like BEC-Pro (Bartl et al.,

2020) or the SEAT test cases (May et al., 2019).

(iii) Our b e nchmark includes the possibility of using

multi-group attributes, which we demonstrate for eth-

nicity an d religion. Thereby we gain insights into how

binary and multi-gr oup biases manifest in the models

and are captured by intrinsic measures. (iv) We per-

form an experimental evaluation, demonstrating dif-

ferences in stability and overall performance.

Schröder, S., Schulz, A., Kenneweg, P. and Hammer, B.

So Can We Use Intrinsic Bias Measures or Not?.

DOI: 10.5220/0011693700003411

In Proceedings of the 12th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2023), pages 403-410

ISBN: 978-989-758-626-2; ISSN: 2184-4313

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

403

For reproducibility’s sake we publish our co de, in-

cluding templates, target words and conﬁg ﬁles

2 RELATED WORK

In literature, the re exist many intrinsic bias measures,

including WEAT (Caliskan et al., 2017), SEAT, (May

et al., 2019), Direct Bias (Bolukbasi et al., 2016),

RIPA, (Ethayar a jh et al., 2019), Neighbor, Clustering

and Classiﬁcation tests (Gonen and Goldberg, 2019)

as well as the log probability bias scor e (Kurita et al.,

2019). We recap those in the next section as their

evaluation is at the core of the present work. Furth er,

there also do exist extrinsic bias measures which aim

to evaluate bias in a downstream task such a s occu pa-

tion classiﬁcation, wher e an example is Bias in Bios

(De-Arteaga et al., 2019).

A family of work investigates in how far observa-

tions with intrinsic measures transfer to downstream

tasks. For instance, it has been shown that WEAT

correlates with extrinsic bias metrics only in very re-

stricted settings (Goldfarb-Tarrant et al., 2020) or that

intrinsic bias measures in gener a l have a limited cor-

related with extrinsic metrics (Kaneko et al., 2022).

Similarly debiasing before ﬁne-tuning does not effec-

tively reduce biases in the downstream task (Kan eko

et al., 2022). As reasons they state that the lan-

guage models re-learn bias in the ﬁne-tuning step du e

to ﬂawed training data . Another work (Steed et al.,

2022) investigates the bias tra nsfer hypothesis (that

biases from PLM affect downstream tasks) using two

downstream data sets. The authors show that most

of the downstream bias can be explained b y ﬁne-

tuning. On the other hand, certain debiasing mea-

sures (re-sampling and scrubbing of identity te rms)

w.r.t. the downstream tasks only effectively removes

biases w hen the model was not pretrained (i.e . never

contained biases from the start). This in turn indi-

cates that mitigating biases in PLM is not sufﬁcient

but must also not be neglected.

It has been shown that templates used for bias

measurements have a large impact on the results, i.e.

modify ing a temp la te without ch anging the seman-

tic meaning can alter the measured bias sign iﬁca ntly

(Seshadri et al., 2022). The authors point out that

many works use a limited amou nt of templates, which

makes scientiﬁc claims less reliable.

Similarly, the compatibility of bias mea sures from

the literature, including the test scenario (used words,

templates, attributes) has been found limited. (Delo-

belle et a l., 2 021). This authors argue that the ”seman-

https://github.com/HammerLabML/PLMBiasMeasur

eBenchmark

tically bleached” templates suggested by other work

do in fact inﬂuence th e biases measure d when insert-

ing the targets/attributes of interest, hence are not as

”bleached”. Furthermore, the way sentence represen-

tations are created (e.g. CLS embedding vs. mean

pooling) inﬂuences bias measurements.Basically, a

major issue with (intrinsic) bias mea sures are the in-

compatible testing conditions.

To summarize bias deﬁn tions from other works,

a unifying bias framework has been proposed (Shah

et al., 2019) that includes four deﬁnitions of bias ori-

gins (semantic bias in embeddin gs, selection bias,

over-ampliﬁcation by the model and label bias) and

two deﬁnition s of predictive biases/ bias conse-

quences (outcome disparity and e rror disparity).

While (Schr ¨oder et al., 2021) aim to compare dif-

ferent bias measures, they focus more on theore tica l

aspects of bias scores and are, fu rthermor e, restricted

to cosine based scores.

3 BIAS EVALUATION METHO DS

In th e following, we depict the intrinsic bias scores

from the literature which w e compare in our expe r-

iments. Some of these offer both a bias score for

single words (e.g. the gender bias of secretary), oth-

ers only a bias score that determin es bia s over sets of

words. This is often a mea n word bias or some con-

trasting bias measure that checks whether stereoty pi-

cal grou ps exist.

3.1 SEAT

SEAT (May et al., 2019) is an extensio n of the

Word Embedding Association Test (Caliskan et al. ,

2017) for sentence representations. WEAT and

SEAT are among the most commo nly used intrin-

sic bias measures. In our experiments we apply

SEAT since we use contextualized em bedding s and

hence need to compar e bias measures in the context

of sentences. We evaluate both the word dissimilar-

ity score s(~w,A,B) and the effect size d(X,Y,A,B).

Since WEAT and SEAT are only deﬁned for bi-

nary bias evaluations, we also use the generalized

WEAT (GWEAT) (Swinger et al., 2019), which pro-

poses a scor e for an arbitrary number of groups

g(X

,...,X

). Again we apply it to sen te nce

representations in the way of SEAT.

3.2 DirectBias and RIPA

The DirectBias (DB) (Bolukbasi et al., 2016) deter-

mines a bias subspace in the embe dding space, which

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

404

is deﬁned by bias attributes, such a s gender words.

Then any correlation of neutral words with this sub-

space is con sid ered a bias. RIPA (Ethayarajh et al.,

2019) is closely related to the DirectBias as it uses

the same strategy. Con trary to the DirectBias, which

normalizes word vectors, RIPA considers the vector

length. In our experiments we apply both measures to

sentence r epresentations instead of words, in the same

way as SEAT. Bo th can report a word-wise bias score

as well as a mean bias for a set of words.

3.3 Clustering, Cl a ssiﬁcation a nd

Neighbor Test

In order to evaluate the effect of debiasing on word

embedd ings, the clustering, classiﬁcation and ne igh-

bor test (Gonen and Goldberg, 201 9) were introduced.

These bias tests detect whether words with similar

gender stereotypes cluster together in the embeddings

space. The neighbor test evaluates how many of the

closest k n eighbors of a word have the same stereo-

type. The clustering and classiﬁcation test measure

the accuracy of k-Means clustering and a SVM classi-

ﬁer for separating two groups of stereotypical words.

All of these test require the user to deﬁne stereotypi-

cal groups beforehand. In the paper, the authors sort

words by WEAT’s dissimilarity score s(~w,A,B) into

stereotypical male/female groups. We extend the clas-

siﬁcation and neighbor test to cases with multi-group

biases. For the classiﬁcation test, we simply use a

multi-class classiﬁer, for the neighbo r test we count

the amount of neighbors that are part of the same

stereotypical group. While k-Means itself could also

handle multiple clusters, the a uthors used accuracy to

evaluate the clustering perfor mance, which cannot be

used with more than two groups.

3.4 Log Probability Scores

There exist a variety of log probability scores, which

are closely related to the masked language objective

of BERT. Initially (Kurita et al., 2019) proposed the

log probability bias score (LPBS), which queries the

probability of BERT to replace a ma sk token with

a male over a female term (or vice versa) given a

context like a stereotypical male/female occupation.

Thereby, the authors could show that BERT does c on-

tain human-like biases. Similar sco res in literature are

the CrowS-Pairs Score (Nangia et al., 2020), Stere-

oSet Score (Nadeem et al., 2021) or All Unmasked

Likelihood score (Kaneko and Bollegala, 2021) .

4 EXPERIMENTAL DESIGN

Our goal in the following is to be able to c ompare and

judge different intrinsic bias measures regarding their

performance to measure bias and their robustness. For

this purpose, we aim to achieve a setting, where bi-

ases are fully observable: We simulate various demo-

graphic distributions from which we derive pretrain-

ing corpora and train LMs. To keep computation time

minimal and enable training of many models, we use

a pretrained Hugginface model (bert-base-uncased)

for Masked Language Mo deling (MLM) and train it

on each of our corpora for a few epochs. Figure 1 il-

lustrates our approach. As a baseline for biases m an-

ifesting in the PLM, we directly query our model for

the probabilities to replace mask tokens with certain

demographic attributes. The details are explained in

Section 4.3. Our test cases in c lude gender, ethnic-

ity and religious biases regarding occupations. For

ethnicity we consider 5 and for religion 4 different

groups, which is crucial because re la te d work often

neglects settings with more than two groups.

4.1 Generating Training Data

Many works tha t evaluate bias measures either only

use one or few PLMs or, based on one PLM, miti-

gate or amplify existing biases to gener a te a variety

of biased models. To achieve a more diverse setting

and simulate the whole cycle of data acquisition, pre-

training a nd bias manifestation, we generate demo-

graphic distributions, speciﬁcally the probabilities of

certain demog raphic group s being a ssoc iate d with oc-

cupations. These associations are randomized and do

not have to align with actual b iases in humans and so-

ciety. This has the advantage that we can distinguish

if the PLM actually learns the biases presented du r-

ing our training instead of sticking to bia ses it learned

beforehand.

Given a list of target words (here occupations),

attributes (gender, religion, ethnicity) and grou ps

per attribute (e.g. male/female for gender), we cre-

ate a probability distribution per target and attribute

p(group|target,attribute), e.g. how likely does a

cook belong to a certain ethnicity (if ethnicity is men-

tioned). Algorithm 1 d escribes our approach. We

used the groups mentioned in Table 1 .

Table 1: Demographic groups used in our experiments.

Attributes Groups per Attribute

Gender male, female

Ethnicity black, white, asian, hispanic, a rab

Religion christian, muslim, jewish, hindu

So Can We Use Intrinsic Bias Measures or Not?

405

Pretraining Corpus

Demographic biases

p(ATTRIBUTE=ai | TARGET)

Test Corpus

Demographic attributes

masked out/ removed

PLM

Pretraining Biases

Query PLM for

p(ATTRIBUTE=ai | TARGET)

Model-intrinsic Biases

cosim/ inner product-based

clustering-based

log probability based

Figure 1: Our experimental setup to evaluate intrinsic bias measures with regard to the pretraining of language models.

Data: groups,minP < maxP

Result: groups, probs

n ← size(groups);

minP ← minP/n;

maxP ← maxP/n;

P ← 1.0;

groups ← shu f f le(groups);

probs = [];

while i < n − 1 do

maxBound ← min(maxP, P − minP ∗ n);

p ← randomU ni f orm(minP,maxBound);

P ← P − p;

AddItem(probs, p);

end

AddItem(probs,P);

Algorithm 1: This algorithm generates a random demo-

graphic distribution for a list of groups. minP < 1.0 is a

strict lower bound for the group probabilities. The higher,

the less likely are extreme differences between the demo-

graphic groups. maxP is the maximal upper bound. If

maxP < 1.0 an equal distribution is impossible and there

will be exactly one majority group with p(group) >

We create a u nique demographic distribution for

each combination of minP ∈ {0.05, 0.1,0.15,0.2} and

maxP ∈ {0.8,0.85,0.9,0.95}. Due to the choice of

both pa rameters, each group will be represented with

p(group) > 0 and there will be exactly one ma jor-

ity gr oup (the la st one chosen by the algorithm) w ith

p(group) >

given n groups.

To create datasets based on th e se distributions, we

use a selection of template sentences, containing a

placeholder for target words and at least on e place-

holder for a protected attribute. The re might be mul-

tiple attributes or multiple mentions of the same at-

tribute in one template. Formally, a template sentence

S contains a target placeholder and attribute place-

holders A

with i denoting the type of attribute (e .g.

gender /ethnicity). Con trary to other works, we do

not limit ourselves with ”sema ntically bleached” tem-

plates, as it has been shown that even those te mplates

inﬂuence the measured biases (Seshadri et al., 2022).

Instead, we chose a larger number of templates in-

cluding many with additional context, assuming that

averaging over a variety of templates improves the

Table 2: Exemplary templates and the terms that can be

inserted as attributes.

i saw the OCCUPATION at th e RELIGION2

(church, mosque, synagogue, mandir)

the OCCUPATION enjoyed GENDER1 lunch

(his, her)

the OCCUPATION often visits GENDER1

family in E THNICITY8

(his, her)/(africa, europe, asia, mexico, qa ta r)

stability of bias measurements. Some exemplary tem-

plates are shown in Table 2.

Given a template S and a list of target words T , we

create sentences S

∀t ∈ T . For each attribute place-

holder A

in S

we choose a ﬁtting group j and in-

sert the corresponding group attribute a

i, j

based on

p(a

i, j

|t, A

). For MLM training we mask out on e at-

tribute instead of random words to ensure that BERT

speciﬁcally learns to infer these. If multiple attributes

are present, we create a training sample per attribute,

where this one is masked out. The resulting corpora

contain 29800 trainin g samples derived from 100 oc-

cupations as target words and 165 templates. Among

our training templates, 60 include an ethnicity refer-

ence, 145 a gender and 45 a religion reference.

4.2 Training and Model Va lidation

On each o f our generated tr a ining datasets, we retrain

BERT for 5 epochs using the Masked Language Ob-

jective. We repe a t this for 5 iterations, resulting in

5 BERT in stances trained on the same demographic

distribution, which will be relevant in our robustness

experiments. To ensure that our models learned the

biases well enough, we test th e Pearson corr elation

of the unmasking probabilities p

unmask

i, j

|t, A

) (see

Section 4.3) with the group probabilities in the train-

ing data p

data

i, j

|t, A

). If the correla tion is below

a threshold of 0.85, we repeat the training (starting

from the pretrained BERT again). After a maximum

of 5 training runs, we keep the best performing model,

to keep computation time lim ited.

We utilize 113 test templates to generate our test

data similarly to th e training data, i.e. inserting each

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

406

target word into eac h template. However, we do not

insert any demog raphic attributes, but instead mask

out on e attribute that was tested for and replace all

other attributes by a neutral term. This results in

17600 test sentences. Given these, we query the un -

masking probabilities of all groups and average over

each target. The exact same test sentences are used

for the evaluation of the different intrinsic bias scores

(see Section 5.2).

4.3 Baseline: Unmasking Bias

To evaluate intrinsic bias scores in terms of a pre-

trained model, we choose a measure directly linked

to the MLM objective and hence similar to the LPBS,

called unmasking bias. Given a templa te such as

”GENDER is a TARGET”, we replace GENDER by a

mask token an d TARGET by a target word for which

we want to determine the gende r bias. Instead of gen-

der one could also use a protected attribute with more

than two groups such as religion or ethnicity. Then,

we query BERT for the p robabilities of certain pro-

tected g roups to replace the mask token normalized

by the probability to choose any of group a ssocia te d

with th a t attribute. In this example, one could com-

pare the probabilities of ”he” and ”she”.

More formally, given a template s, a target words

t and an attribute A

(e.g. ethnicity), we are interested

in the probability that our trained language model as-

sociates this target with a g roup j ∈ [1,n] (e.g. black),

where n is the number of group s f or A

(e.g. 5 for eth-

nicity, in our case). For this purpose, we insert t and

query the mode l for the probability of the correspond-

ing group attribute a

i, j

to be inserted into s:

unmask

i, j

|s,t,A

) =

P([MASK] = a

i, j

|s,t,A

)

∑

k=1

P([MASK] = a

i,k

|s,t,A

)

(1)

By using a large set of templates S, we achieve a ro-

bust estimate of the probability that group j is associ-

ated with target t in the model:

unmask

i, j

|t, A

) =

|S|

∑

s∈S

unmask

i, j

|s,t,A

). (2)

One advantage of this formulation over LPBS is that

unmask

i, j

|t, A

) does not depend on the nu mber of

protected groups.

Now we can use this probability in orde r to judge

in how far our model has learned the biases p resent

in the d a ta : From our training data, we estimate

data

i, j

|t, A

) by the relative frequen cies of the ac-

cording grou p attribute and target word occurring to-

gether (we have generated the training using such

templates). Then we c ould measure the dissimilarity

between p

unmask

i, j

|t, A

) and p

data

i, j

|t, A

Most bias scores, however, report only an aggre-

gated score for one attribute, aggregating over the

groups. In order to be comparable to this setup,

we also aggr egate over the groups using the Jensen-

Shannon divergence (Lin, 1991) between p(a

i, j

|t, A

)

and the uniform distribution which represents no bias.

We don’t use KL because we want symmetry.

Calculating this for both p

unmask

i, j

|t, A

) and

data

i, j

|t, A

), we obtain scalar scores for ea ch of

the two and for each t. We ﬁnally utilize the Pearson

correlation over all t for a measure of similarity be-

tween the bias in the data a nd the bias learned by the

model. Accordingly, we also compare the similarity

between the bias in the data and a bias score.

5 EXPERIMENTAL RESULTS

In our experiments, we ﬁrst evaluate the re liability of

our template-based approach w.r.t. the nu mber of tem-

plates. Afterwards, we apply our setup to compare

different bias measures, ﬁrst when considering only

biases of individual target words, then using the full

bias scores. Finally we investigate the robustness of

our sche me and some bias scores whe n training dif-

ferent models on the same biased data set.

5.1 Assessing the Reliability of Our

Template-Based Evaluation

There is work suggesting tha t template based ap-

proach e s for bias evaluation are unreliable (Seshadri

et al., 2022), which is mostly due to the fact that a

limited amount of templates is used. For instance,

(Bartl et al., 2020) propose BEC-Pro, a dataset for

bias evaluation which is created from only 5 differ-

ent templates. To circumvent this problem, we use a

much larger numbe r of over 100 tem plates (see Sec-

tion 4) for training a nd testing, respectively.

Furthermore, we evaluate the reliability of our

evaluation with respect to changing template num-

bers in the following. We run a statistical test to esti-

mate the signiﬁcance of biases obtained with our tem-

plates: We com pute the unmasking probabilities for

Table 3: Mean and standard deviation of p-values reported

by our permutation test over all models compared to number

of test templates with the respective attribute.

Gender Religion Ethnicity

p-value 0.01 0.08 0.14

±0.01 ±0.03 ±0.03

templates 82 34 53

So Can We Use Intrinsic Bias Measures or Not?

407

Figure 2: Pearson Correlation of word bias scores for ethnicity, gender and religious bias.

each combin a tion of te mplate sentence, target word

and protected a ttribute and take the mean probabili-

ties per target and attribute combination. Then we run

a permutation test for 1000 iterations under the hy-

pothesis that the ranking of grou p probabilities does

not change if computed over a subset (90%) of tem-

plates. We report the p-values in Table 3.

These show that in the gender case, which in-

volved the largest number of templates, we achieve

statistical signiﬁca nt results. In the multi group cases

we observe p-values larger than 0.05. Hence results

are not as reliable. We assume that this is due to the

smaller number of test templates and the increased

complexity of bias f or more than two groups.

5.2 Comparison of Bias Measures

5.2.1 Word Biases

For eac h protected attribute, we ﬁrst evaluate the cor-

relation o f different word bias scores. This includes

only the cosine scores and the da ta and unmasking

probability, where we report the Jensen-Shannon di-

vergence (see Section 4.3).

The results are illustrated in Figure 2. We re port

relatively high correlations with the data biases for

our baseline (’unmask’) with any attribute. The co-

sine scores c orrelate rather well with the baseline a nd

data biases in the gender case, but not in the multi at-

tribute cases (SEAT is only deﬁned for the binary gen-

der case). Furtherm ore, the DirectBias and RIPA cor-

relate strongly with each other, wh ic h was expected

due to their similar deﬁnitions.

This contradicts observations from previous work,

which reports that cosine scores failed to capture bi-

ases in some scenar ios ( G oldfarb-Tarrant et al., 2020;

Kurita et al., 2019) or produced inconsistent results

(May et al., 2019). However, it has be en observed

that the compatibility of different bias measures is

strongly limited by the different test cases, i.e. whe n

comparing word biases to sentence biases or comput-

ing bia ses with different kinds of templates (Delobelle

et al., 2021). Our ﬁndings underline that unifying test

cases makes different bias scores more compatible.

The fact that we report muc h higher correlations

in the gender case could mean that a binary concept

such as gender bias is in fact represented in a lin-

ear way, which satisﬁes the assumptions of cosine

based scores, while non-binary concepts could be rep-

resented in a more complex way which cosine based

scores cannot account for entirely.

5.2.2 Overall Bias Scores

In practice, often a bias score over whole concepts

(set(s) of words) instead of single words is reported,

which is the case e.g . for WEAT/SEAT. Hence, we

evaluate these bias scores compared to the mean un-

masking bias over all target words (see Section 4.3).

The DirectBias and RIPA apply an ”objective” mean

word bias. On the other hand, SEAT, GWEAT, the

clustering, classiﬁcation and neighbor test require the

target words to be sorted into grou ps based on their

stereotypes. When users choose suc h groups one can

assume that they have certain knowledge about the

stereotypes that can be expected . However, their ex-

pectations might not exactly align with the biases in

the data/model, either du e to subjective views, lim-

ited knowledge or sampling bias of the dataset com-

pared to biases in the real world. To model this,

we derive the groups from the actual demographic

probabilities in our datasets after adding Gaussian

noise (µ = 0,σ = 0.3). For each occupation, we sim-

ply choose the gro up with the highest co-occurrence

probability in the dataset.

Figure 3 shows the corre la tions of the bia s mea-

sures and the data biases. Overall, correlations are

slightly lower than for th e word bias scores. Other

than that the results are similar in the sense that we

observe stable correlations with the data bias for the

baseline (’unmask’) for all thr ee attributes and ob-

serve the best correlations in the gender ca se. We

ﬁnd that SEAT and the neighbor bias achieve the

best Pearson correlation both with the data and un-

masking bias and also correlate with each other.

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

408

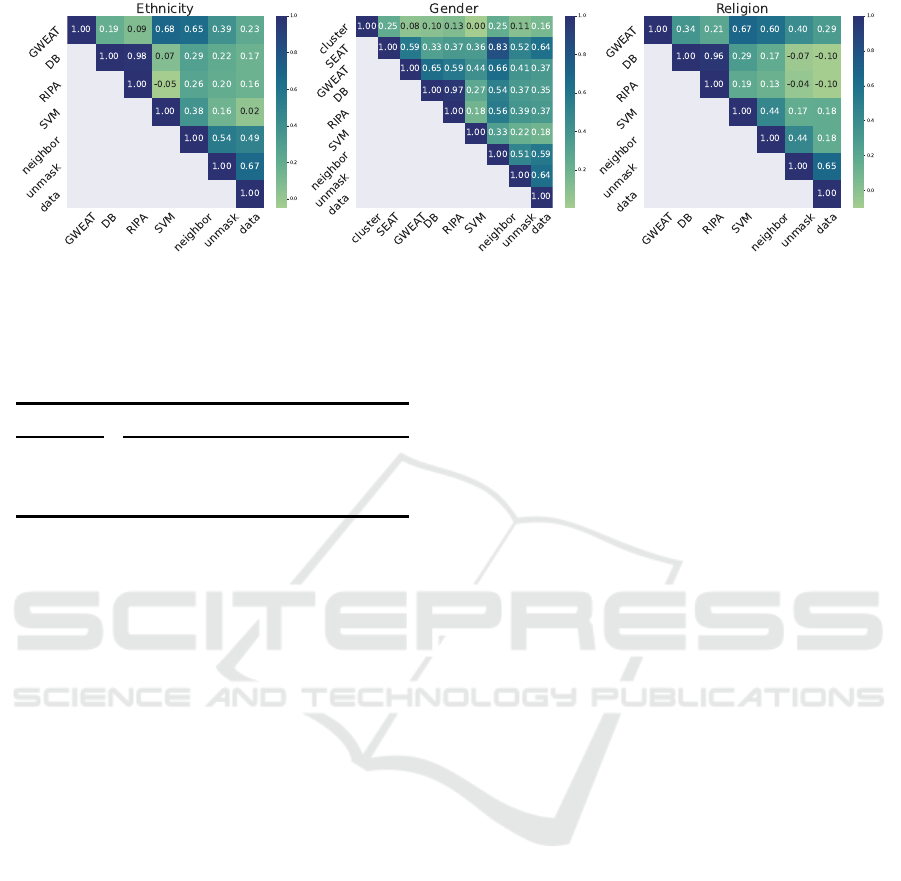
Figure 3: Pearson Correlation of bias scores for ethnicity, gender and rel igious bias.

Table 4: C onsistency over experiment iterations. Mean

percentage differences of scores reported in models with

the same demographic distributions. Lower values indicate

consistency.

SEAT DB RIPA unmask

Ethnicity - 0.501 0.518 0.111

Gender 1.358 0.358 0.361 0.291

Religion - 0.486 0.483 0.147

GWEAT shows a similar behavior to SEAT, but over-

all lower correlations. The clustering and classiﬁca-

tion (’SVM’) achieve the lowest correlations with the

data biases. No teworthy the differences be tween gen-

der and the multi group cases are compara bly low for

GWEAT and the neighbor test. Other than that, we

ﬁnd high correlations between GWEAT an d the clas-

siﬁcation (’SVM’) bias.

5.3 Robustness of Bias Measures

In addition to the general performance and c ompat-

ibility of bias measures, we also want to investigate

their robustness. For this purpose, we test how stable

bias measures are, given the same initial bias distribu-

tion. We compare the word bias measure s over the 5

iterations (5 different models) trained with the same

bias distribution. Results ar e aggregated over all bias

distributions and shown in Table 4.

The fact that the unmask baseline achieves very

small percentage differences indicates that the differ-

ent model instances have learned the according bias

robustly. Overall the con sid ered bias measures vary

more than the baseline, where SEAT varies more than

DirectBias and RIPA. For DirectBias and RIPA we

see slightly more stable results in the gender case,

which could indicate that an increasing number of

groups also makes bias measurements more difﬁcult

and thus less robust. For SEAT we see large discrep-

ancies between biases measures over similar models,

which is due to the fact that SE AT rep orts rather low

biases in general. However, we also observe tha t the

signs of biases reported by SEAT frequently change.

6 CONCLUSION

In the present work w e have proposed a novel test

scenario where different bias measures can be com-

pared using the same test sentences. We have showed

that template-based a pproaches can pr oduce reliable

results if a sufﬁcient number of templates is em-

ployed. In addition to binary attribute cases, w e

have also evaluated multi-attribute cases and showed

large differences between them regarding the detec-

tion of bias. Furthermore, we showed that cosine

and intrinsic scores actually can attest for biases quite

well, given our speciﬁc pretraining scenario. We have

shown that the more complex bias tests based on clas-

siﬁcation and clustering do not perform better in de-

tecting bias than the simple SEAT score. We have

further investigated the robustness of word biases and

have shown that SEAT perf ormed inferior as com-

pared to DirectBias and RIPA.

Limitations of our work includ e the not perfect

baseline performance of the pretrained model, i.e. our

trained models do represent the bias perfectly (the un-

mask correlation does not go over 70%). This could

make it somewhat more difﬁcult for bias methods

to d etect the bias. Here, more training data could

yield an improvement. Further, our evaluation is lim-

ited to pretraining as such and implications for down-

stream tasks cann ot be directly transferred. However,

pretrained m odels can be used directly without ﬁne-

tuning, so this setup remains valid.

This work ope ns up new interesting directions of

investigations, including direct evaluations in settings

where ﬁne-tuning the embedding is n ot possible, such

as similarity ran king or training o nly a classiﬁcation

head. Here biases from pretraining are likely to per-

sist. The investigation of in te rsectional groups is a

So Can We Use Intrinsic Bias Measures or Not?

409

further promising application of our setup, be c ause

our template-based approach naturally allows to in-

clude multiple protected group s also in the test set.

Finally, a further extension of the benchmark, w.r.t.

templates for the multi-attribute attributes or other tar-

gets than occupations cou ld improve the evaluation

further.

ACKNOWLEDGEMENTS

We gratefully acknowledge the funding by the Ger-

man Federal Ministry of Economic Affairs and En-

ergy (01MK20007E) and by the Ministry of Culture

and Science of the state of North Rhine-Westp halia in

the project ”Bias aus KI-Modellen”.

REFERENCES

Bartl, M., Nissim, M., and Gatt, A. (2020). Unmasking con-

textual stereotypes: Measuring and miti gating bert’s

gender bias. arXiv preprint arXiv:2010.14534.

Bolukbasi, T., Chang, K.-W., Zou, J. Y., Saligrama, V., and

Kalai, A. T. (2016). Man is to computer programmer

as woman is to homemaker? debiasing word embed-

dings. Advances in neural information processing sys-

tems, 29:4349–4357.

Caliskan, A., Bryson, J. J., and Narayanan, A. (2017). Se-

mantics derived automatically from language corpora

contain human-like biases. Science, 356(6334):183–

186.

De-Arteaga, M., Romanov, A., Wallach, H., Chayes, J.,

Borgs, C ., Chouldechova, A., Geyik, S., Kenthapadi,

K., and Kalai, A. T. (2019). Bi as in bios: A case study

of semantic representation bias in a high-stakes set-

ting. In proceedings of the Conference on Fairness,

Accountability, and Transparency, pages 120–128.

Delobelle, P., Tokpo, E. K., Calders, T., and Berendt, B.

(2021). Measuring fairness with biased rulers: A sur-

vey on quantifying biases in pretrained language mod-

els. arXiv preprint arXiv:2112.07447.

Ethayarajh, K., Duvenaud, D., and Hirst, G. (2019). Under-

standing undesirable word embedding associations.

arXiv preprint arXiv:1908.06361.

Goldfarb-Tarrant, S., Marchant, R., S´anchez, R. M.,

Pandya, M., and Lopez, A. (2020). Intrinsic bias

metrics do not correlate with application bias. arXiv

preprint arXiv:2012.15859.

Gonen, H. and Goldberg, Y. (2019). Lipstick on a pig: De-

biasing methods cover up systematic gender biases in

word embeddings but do not remove them. CoRR,

abs/1903.03862.

Kaneko, M. and Bollegala, D. (2021). Unmasking the mask

- evaluating social biases in masked language models.

CoRR, abs/2104.07496.

Kaneko, M., Bollegala, D., and Okazaki, N. (2022). De-

biasing isn’t enough!–on the effectiveness of debias-

ing mlms and their social biases in downstream tasks.

arXiv preprint arXiv:2210.02938.

Kurita, K., Vyas, N., Pareek, A., Black, A. W., and

Tsvetkov, Y. (2019). Measuring bias in con-

textualized word representations. arXiv preprint

arXiv:1906.07337.

Lin, J. (1991). Divergence measures based on the shannon

entropy. IEEE Transactions on Information Theory,

37(1):145–151.

May, C ., Wang, A., Bordia, S., Bowman, S. R., and

Rudinger, R. (2019). On measuring social biases in

sentence encoders. CoRR, abs/1903.10561.

Nadeem, M., Bethke, A., and Reddy, S. (2021). StereoSet:

Measuring stereotypical bias in pretrained language

models. In Proceedings of the 59th Annual Meet-

ing of the Association for Computational Linguistics

and the 11th International Joint Conference on Nat-

ural Language Processing (Volume 1: Long Papers),

pages 5356–5371, Online. Association for Computa-

tional Linguistics.

Nangia, N., Vania, C., Bhalerao, R., and Bowman, S. R.

(2020). CrowS-pairs: A challenge dataset for measur-

ing social biases in masked language models. In Pro-

ceedings of the 2020 Conference on Empirical Meth-

ods in Natural Language Processing (EMNLP), pages

1953–1967, Online. Association for Computational

Linguistics.

Schr¨oder, S., Schulz, A. , Kenneweg, P., Feldhans, R., Hin-

der, F., and Hammer, B. (2021). Evaluating metri cs

for bias in word embeddings. CoRR, abs/2111.07864.

Seshadri, P., Pezeshkpour, P., and Singh, S. (2022). Quanti-

fying social biases using templates is unreliable. arXiv

preprint arXiv:2210.04337.

Shah, D., Schwartz, H. A., and Hovy, D. (2019). Predic-

tive biases in natural language processing models: A

conceptual framework and overview. arXiv preprint

arXiv:1912.11078.

Steed, R., Panda, S., Kobren, A., and Wick, M. (2022). Up-

stream mitigation is not all you need: Testing the bias

transfer hypothesis in pre-trained language models. In

Proceedings of the 60th Annual Meeting of the Associ-

ation for Computational Linguistics (Volume 1: Long

Papers), pages 3524–3542.

Swinger, N. , De-Arteaga, M., Heffernan IV, N. T., Leiser-

son, M. D., and Kalai, A. T. (2019). What are the

biases in my word embedding? In Proceedings of the

2019 AAAI/ACM Conference on AI, Ethics, and Soci-

ety, pages 305–311.

ICPRAM 2023 - 12th International Conference on Pattern Recognition Applications and Methods

410