An Application of Priority-Based Lightweight Ontology Merging
Rim Mohamed
1
, Truong-Thanh Ma
2
and Zied Bouraoui
3
1
University of Sfax, Miracl Laboratory, Isims, Tunisia
2
CICT, Can Tho University, Can Tho, Vietnam
3
CRIL, Universit
´
e d’Artois & CNRS, Lens, France
Keywords:
OWL-EL, E L Description Logics, Information fusion, Possibility theory, Uncertainty Handling.
Abstract:
Merging multiple and frequently contradictory sources of information has been identified as a significant
issue in the semantic web community. In addition, pieces of information to be combined are provided with
uncertainty due, for instance, to the reliability of sources. To solve this, possibility theory offers a useful
tool for representing and reasoning with uncertain, partial, and inconsistent information. In this paper, we
concentrate on dance video processing, in which many inconsistent information sources exist. Therefore,
we propose possibilistic merging operators for the dance OWL2-EL ontologies to deal with the conflicting
dance sources. We represent an extension of E L within a possibility theory setting. It leverages a min-based
operator to merge the ontologies based on possible distributions. Furthermore, the semantic fusion of these
distributions has a natural syntactic counterpart when dealing with E L ontologies. The min-based fusion
operator is recommended when distinct dance sources that provide information are dependent.
1 INTRODUCTION
Various sorts of knowledge originating from con-
flicting (or inconsistent) sources are affected by un-
certainty. The problem of merging this knowledge
is a key challenge in several applications, including
distributed databases, multi-agent systems, and dis-
tributed information systems, i.e., (Konieczny and
P
´
erez, 2002; Everaere et al., 2010; Hue et al., 2007;
Konieczny and P
´
erez, 2011; Patricia et al., 2008;
Haret and Woltran, 2019). Additionally, a knowledge
base is composed of a set of pieces of information
provided by sources. A set of formulas syntactically
formulates the pieces of information. Normally, they
are semantically represented by a set of interpreta-
tions. Therein, the syntactical approaches merge all
the formulas to obtain one knowledge base that repre-
sents various different sources. Otherwise, the views
of semantics consist of ranking all the interpretations
and merging them using merging operators in order
to obtain a unique order for all sources of information
(Konieczny and P
´
erez, 2002).
Indeed, in terms of the problem of culture and
its hesitant preservation, traditional dance manage-
ment has attracted scientists’ attention in recent years.
Namely, we concentrate on Vietnamese traditional
dances (for short, VTDs). Most VTDs are crucially
stored in numerous distinct video sources that are in
conflict. (Lam, 1994). Indeed, in the same dance,
each different video has distinct movements. Fur-
thermore, they manage the resulting large amount of
heterogeneous digital content. Therefore, preserving
VTDs is a remarkable problem that needs to be han-
dled. This paper concentrates on merging the dance
ontologies distributed from different sources. For this
purpose, we realize that an application to manage
those data sources is necessary and desirable. As a
result, the approach of the OWL2-EL ontology is rea-
sonably expected, as OWL2-EL is one of the essen-
tial tractable profiles of the W3C Ontology Web Lan-
guage, which provides a powerful framework to com-
pactly encode structured knowledge with low com-
putational complexity. Notably, we are interested in
E L Description Logics to represent VTD’s ontol-
ogy sources, perceiving further what is the motivation
behind building an application (semantic web using
OWL2-EL).
On the other hand, possibility theory (Dubois and
Prade, 2012), especially the qualitative possibility
theory offers a natural framework to deal with ordi-
nal uncertainty. It holds when there exists a prefer-
ence ranking between pieces of information that re-
flects their reliability or compatibility with the avail-
able knowledge or when there exists a total preorder
268
Mohamed, R., Ma, T. and Bouraoui, Z.
An Application of Priority-Based Lightweight Ontology Merging.
DOI: 10.5220/0011699200003393
In Proceedings of the 15th International Conference on Agents and Artificial Intelligence (ICAART 2023) - Volume 2, pages 268-276
ISBN: 978-989-758-623-1; ISSN: 2184-433X
Copyright
c
 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

between them. Merging the pieces of information de-
pends on the nature of the knowledge base such as the
propositional knowledge bases (Konieczny and P
´
erez,
2002), prioritized knowledge bases (Delgrande et al.,
2006), or weighted knowledge bases(Benferhat et al.,
1993; Qi et al., 2006). Indeed, there exist several ap-
proaches to merge possibilistic logic bases (Benferhat
et al., 1993; Benferhat et al., 1999; Benferhat et al.,
2000). However, there exists a few works that merge
possibilistic DLs, more precisely the lightweight DLs
DL-Lite (Benferhat et al., 2013). Note that, there is to
the best of our knowledge, no approaches for fusing
possibilistic E L ontology. Therefore, merging E L
ontology combine with possibility theory to handle
inconsistent and uncertain problems is quite essential,
especially, in the case of the dance video processing
from several sources.
Moreover, one of the big problems regarding
dance video processing is that the motions (postures
and gestures) from performers/dancers are only par-
tially specific and accurate. They have a range of
approximations. For example, as a piece of evi-
dence, Posture:“the left hand is horizontal at shoul-
der level”, meaning that the left hand of the dancer is
horizontal with the shoulder (creating an angle of 90
degrees from the body), however, in fact, the dancer
performed the left-hand posture with a different de-
gree. Therefore, utilizing possibility theory in the
dance domain is appropriate.
In this paper, we take advantage of the qualita-
tive possibility theory in order to deal with quali-
tative and ordinal uncertainty. We concentrate on
the lightweight description logics named EL (Baader
et al., 2010), which offer a powerful expressiveness
in expressing ontological knowledge and guarantee
the tractability of reasoning processes, especially for
instance and subsumption checking (Kazakov et al.,
2012; Kazakov et al., 2003). This logic underlies the
OWL2 EL profile, one of the three profiles proposed
as sublanguages of the full OWL2. The E L descrip-
tion logic is suitable especially for medical applica-
tions such as based on using general core terminology
of SNOMED CT
1
, GALEN
2
and for biology appli-
cations such as Gene Ontology
3
. However, we con-
centrate primarily on the dance domain in this paper
by representing a prominent example of VTD video
processing. First, we will investigate the possibility
theory with an extended fragment of E L. Then, we
will focus on the minimum operator for merging pos-
sibilistic E L ontologies.
The remainder of this paper is structured as fol-
1
http://www.snomed.org/
2
http://www.opengalen.org/index.html
3
http://geneontology.org/
lows: we describe a prominent example in Section
2 briefly. In the next section, (Section 3, we give a
refresher on the E L logic. After that, we condense
the possibility theory over EL interpretations in Sec-
tion 4. Section V discusses the fragment of E L com-
bined with possibility distribution. A presentation of
the min-based merging of π-EL
+
⊥
possibility distribu-
tions and syntactical merging of π-E L
+
⊥
are in section
6 and section 7, respectively. To illustrate our pro-
posal, a noticeable example related to merging E L
ontologies for dance video processing is presented in
Section 8. Finally, Section 9 concludes the paper.
2 DESCRIPTION OF A
PROMINENT DANCE
EXAMPLE
This section contains a brief description of a poten-
tial (prominent) example of our approach to classify-
ing and merging a collection of dance videos issued
from different sources. More preciously, we concen-
trated on Vietnamese traditional dances (VTDs), in
which existing a large number of fundamental mo-
tions in dance videos. Motions carry important in-
formation which is of a multi-fold nature. At present,
there are many different dataset sources to represent a
Vietnamese dance, hence, merging the dance video
remains to be an active research area. A question
arises as to how to merge dance knowledge (motions,
stories in dances, others) from several different video
sources.
As known, a video is a sequence of frames (im-
ages). Moreover, a set of frames can be referred to
as a dance segment (or a dance step) in a compos-
ing dance. Each motion corresponds to an image ex-
tracted from a video. In this section, we present the
fundamental features of VTDs to represent merging
dance E L ontologies. In this example, we focused
on representing VTDs motions through dance orien-
tations
Regarding orientation features (Lam, 1994)(Tran
et al., 2003), it is one of the most significant charac-
teristics in VTDs because the motions, postures, and
gestures are always described explicitly through the
orientations with body parts written in almost of all
documents. For instance, the left hand has a direction
in orientation 7, the right hand is in orientation 1. In
(Tran et al., 2003), the experts of the dance domain in
Vietnam are split fundamental orientations into eight
directions as Figure 1, denoted by VNOri{i} with
i = [1, 8]. Namely, VNOri1 is the direction of the
dancer opposite the spectator (in front of the audi-
An Application of Priority-Based Lightweight Ontology Merging
269

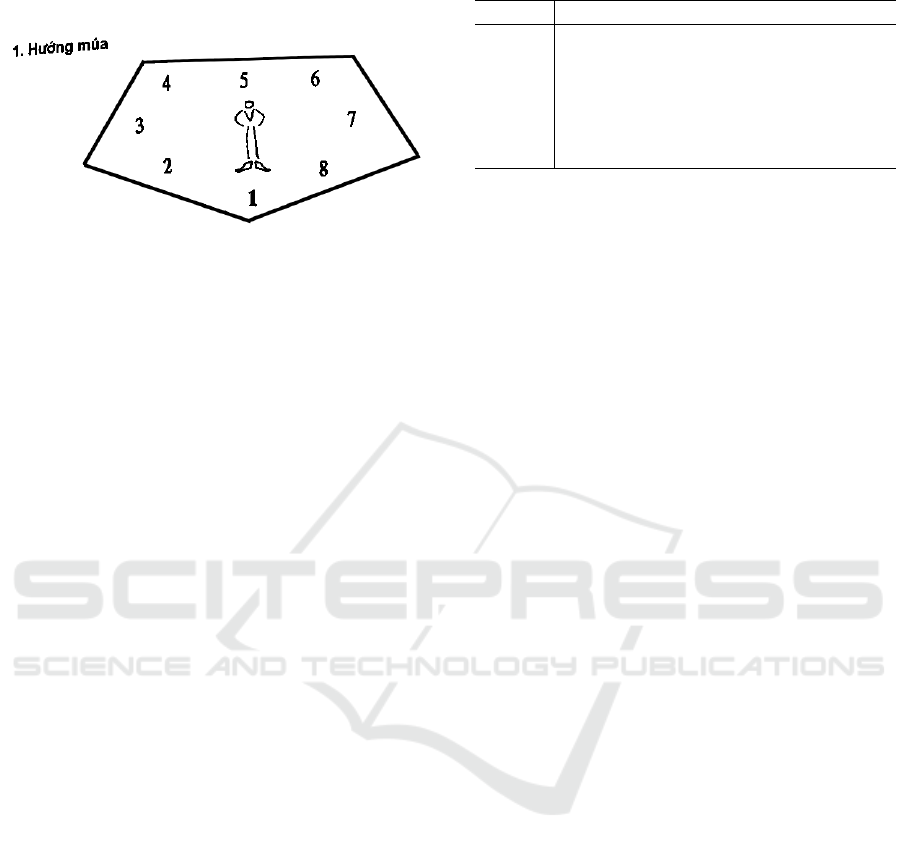
ence), it is also used for the first preparation step of
performing.
Figure 1: Orientation (direction) features of VTDs.
In this paper, we concentrate primarily on repre-
senting orientation characteristics in VTDs into the
merging operators proposed. Therefore, we would
use these features to model and illustrate the merg-
ing operators throughout the examples of this paper.
Our main purpose is to represent how to merge pos-
sibilistic ontologies with dance video processing, in
this case Vietnamese traditional dances with orienta-
tion features.
3 A REFRESHER ON E L LOGICS
Our approach is built on a foundation of a lightweight
Description Logic (DL) framework to encode the on-
tology. We now provide a brief description of the DL
E L (Baader et al., 2005).
Let N
C
, N
R
, N
I
be three pairwise disjoint sets
where N
C
denotes a set of atomic concepts, N
R
de-
notes a set of atomic roles and N
I
denotes a set of
individuals. The EL concept expressions are built ac-
cording to the following syntax:
C ::= ⊤ | N
C
| C ⊓C | ∃r.C.
where C, D ∈ N
C
, a, b ∈ N
I
, and r ∈ N
R
.
An E L ontology O = ⟨T , A⟩ (a.k.a. knowledge
base) comprises two components, the TBox (Termi-
nological Box denoted by T ) and ABox (denoted by
A). The TBox consists of a set of General Concept
Inclusion (GCI) axioms of the form C ⊑ D, meaning
that C is more specific than D or simply C is sub-
sumed by D, C ≡ D which is a shortcut for C ⊑ D
and D ⊑ C. The ABox is a finite set of assertions on
individual objects of the form C(a) or r(a, b).
The semantics is given in terms of interpretations
I = (∆
I
, ·
I
), which consist of a non-empty interpreta-
tion domain ∆
I
and an interpretation function ·
I
that
maps each individual a ∈ N
I
into an element a
I
∈ ∆
I
,
each concept A ∈ N
C
into a subset A
I
⊆ ∆
I
, and each
role r ∈ N
R
into a subset r
I
⊆ ∆
I
× ∆
I
.
Table 1: Syntax and semantics of E L.
Syntax Semantics
C ⊑ D C
I
⊆ D
I
r r
I
⊆ ∆
I
× ∆
I
a a
I
∈ ∆
I
C ⊓ D
C
I
∩ D
I
⊤ ∆
I
∃r.C {x ∈ ∆
I
| ∃y ∈ ∆
I
s.t.(x, y) ∈ r
I
, y ∈ C
I
}
A summary of the syntax and semantics of E L is
shown in Table 1. An interpretation I is said to be a
model of (or satisfies) an axiom φ in the form of the
left column in the table, denoted by I |= φ, when the
corresponding condition in the right column is satis-
fied. For instance, I |= C ⊑ D if and only if C
I
⊆ D
I
.
Similarly, I satisfies a concept (resp. role) assertion,
denoted by I |= C(a) (resp. I |= r(a, b)), if a
I
∈ C
I
(resp. (a
I
, b
I
) ∈ r
I
). An interpretation I is a model
of an ontology O if it satisfies all the axioms and as-
sertions in O. An ontology is said to be consistent if
it has a model. Otherwise, it is inconsistent. An ax-
iom φ is entailed by an ontology, denoted by O |= φ,
if φ is satisfied by every model of O. We say that C is
subsumed by D w.r.t. an ontology O iff O |= C ⊑ D.
Similarly, we say that a is an instance of C w.r.t. O iff
O |= C(a).
In this work, we assume that the input ontologies
are provided in a specific normal form, to which we
apply completion rules for classification. We assume
that each source is in the normal form (Baader et al.,
2005). We define it as follows:
Definition 1 (Normal form of E L): An E L T Box is
in normal form if all concept inclusions have one of
the following forms:
A ⊑ B, A ⊓ B ⊑ C, A ⊑ ∃r.B, ∃r.A ⊑ B
where A, B ∈ N
C
.
Note that, this assumption will transform the com-
plex concept into the E L normal form (with the
atomic concept) before the merging process is per-
formed.
4 POSSIBILITY THEORY OVER
E L INTERPRETATIONS
Possibility theory (Dubois and Prade, 2012) is a the-
ory devoted to representing and reasoning with uncer-
tain and inconsistent ontologies. In the following, we
define the basic notions of this theory. Let Ω be a uni-
verse of discourse and I = (∆
I
, .
I
) ∈ Ω be the E L
interpretations.
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
270

4.1 Possibility Distribution
A possibility distribution is the main block of the pos-
sibility theory, which is a function denoted by π. It is
a mapping from Ω to the unit interval [0, 1]. It as-
signs to each interpretation I ∈ Ω a possibility degree
π(I ) ranged between 0 and 1, reflecting its compat-
ibility or consistency w.r.t the available knowledge.
We say that I is totally possible (i.e., fully consis-
tent with available knowledge) when π(I ) = 1 and is
impossible (i.e., fully inconsistent) when π(I ) = 0.
Finally, given two interpretations I and I
′
, we say
that I is more consistent or more compatible than I
′
if π(I ) > π(I
′
). A possibility distribution π is nor-
malized if ∃I ∈ Ω s.t π(I ) = 1, otherwise, π is sub-
normalized. The concept of normalization is impor-
tant since it reflects the presence of conflicts in the set
of available information.
4.2 Possibility and Necessity Measures
Given a possibility distribution π, standard possibility
theory offers two measures from 2
Ω
to the interval
(0, 1] which discriminate between the plausibility and
the certainty regarding an event A ⊆ Ω.
A possibility measure Π(A) = sup{π(I ) : I ∈ A}
evaluates to what extent A is compatible or plausi-
ble w.r.t available knowledge encoded by π. When
Π(A) = 1 and Π(
¯
A) = 0, we say that event A is cer-
tainly true. Furthermore, when Π(
¯
A) ∈]0.1[ we say
that A is somewhat certain. Finally, we say that there
exists a total ignorance about A if Π(M) = 1 and
Π(
¯
A) = 1. The possibility measure satisfies the fol-
lowing properties:
∀A ∈ Ω, ∀F ∈ Ω, Π(A ∪ F) = max(Π(A), Π(F))
and
∀A ∈ Ω, ∀F ∈ Ω, Π(A ∩ F) ≤ min(Π(A), Π(F))
A necessity measure N(A) = 1 − Π(
¯
A), which is
the dual function of the possibility measure Π, evalu-
ates to what extent A is certainty entailed from avail-
able knowledge encoded by π. When N(A) = 1, we
say that A is certain. When N(A) ∈ ]0, 1[, we say that
A is somewhat certain. When N(A) = 0 and N(
¯
A) = 0,
we say that there is a total ignorance about A.
A necessity measure N satisfies the following
properties:
∀A ⊆ Ω, ∀L ⊆ Ω, N(A ∩ L) = min(N(A), N(L))
and
∀A ⊆ Ω, ∀L ⊆ Ω, N(A ∪ L) ≥ max(N(A), N(L))
It is faithful to note that not all the subsets of Ω
represent axioms in EL, indeed the disjunction is not
allowed in E L language. Now, we are able to deter-
mine the possibility and the necessity measures asso-
ciated with the axioms (φ) of E L language. Where
the possibility measure of φ is defined as follow:
∀I ∈ Ω, Π(φ) = max{π(I ) : I |= φ}
and its associated necessity measure is defined as fol-
lows:
∀I ∈ Ω, Π(φ) = max{π(I ) : I ̸|= φ}
with I ̸|= φ means that I is not a model of the axioms
φ.
5 POSSIBILISTIC E L
Since the practical knowledge of the VTD has some
opposing statements. i.e., Hand and Leg is separate,
Le f tHand is disjoint with RightHand. Hence, in this
section, we take advantage of the EL
+
⊥
(Giordano
et al., 2009; Kazakov et al., 2014) as a fragment of
E L. The set of E L
+
⊥
concepts can be extended as
follows:
C ::= ⊤ | ⊥ | N
C
| C ⊓C | ∃r.C
where r ∈ N
R
. Namely, the E L
+
⊥
is added by a bottom
concept (⊥) that its semantics is an empty set (
/
0). i.e.,
Le f tHand ⊓RightHand ⊑ ⊥. Moreover, it extends in
role inclusions r
1
◦ . . . ◦ r
n
⊑ r, where r
1
, . . . , r
n
, and
r ∈ N
r
(see (Giordano and Dupr
´
e, 2020) for more de-
tails). For this setting, we use the “strict” E L
+
⊥
nor-
mal form that is extended with the axioms as follows:
A ⊑ B, A⊓B ⊑ C, A ⊑ ∃r.B, ∃r.A ⊑ B, A⊓B ⊑ ⊥ where
A, B ∈ N
C
.
Now, we define the syntax and semantics of the
possibilitic extension of E L
+
⊥
, denoted by π-EL
+
⊥
.
Moreover, we also present an illustration of the posi-
bilistic ontology based on Figure 1.
5.1 Possibilistic π-E L
+
⊥
Ontology
A possibilistic E L
+
⊥
ontology, denoted by O
π
, is de-
fined by O
π
= {(φ
i
, α
i
), i = 1..n} where φ is E L
+
⊥
axioms and α ∈ (0, 1] its certainty degree, meaning
that N(φ
i
) ≥ α
i
. Note that the higher is α the more
the axiom is certain. Only the axioms having a de-
gree strictly greater than 0 are explicitly represented
in the ontology. However, when the axioms have a
degree equal to 1 then O
π
coincides with the stan-
dard E L
+
⊥
ontology, which is denoted by O, with
O = {φ
i
, i = 1..n}.
An Application of Priority-Based Lightweight Ontology Merging
271

Example 1: In order to illustrate explicitly ontology
merging, we take advantage of existing operators of
the E L
+
⊥
setting to represent the orientation char-
acteristics of VTDs and relevant primary concepts
(body-parts concepts).
Firstly, we take an account of TBox of VTDs On-
tology 1 denoted by T O
π
1
, including:
T O
π
1
=





































































































Orientations ⊑ V T D − Movements, 0.8
V NOri1 ⊑ Orientations, 0.9
V NOri2 ⊑ Orientations, 0.95
V NOri7 ⊑ Orientations, 0.87
V NOri8 ⊑ Orientations, 0.93
Hands ⊑ BodyParts, 1.0
Le f tHand ⊑ Hands, 0.78
RightHand ⊑ Hands, 0.89
Le f tHand ∩ RightHands ⊑ ⊥, 0.85
Shoulders ⊑ BodyParts,0.98
RightShoulder ⊑ Shoulders, 1.0
Le f tShoulder ⊑ Shoulders, 0.89
Le f tHand ⊑ ∃hasPosIn.V NOri8, 0.75
RightHand ⊑ ∃hasPosIn.V NOri2, 0.83
Le f tShoulder ⊑ ∃hasPosIn.V NOri7, 0.8
RightShoulder ⊑ ∃hasPosIn.V NOri3, 0.9
RightLeg ⊑ ∃hasPosIn.V NOri1, 1.0
Based on the description of section II regarding
orientations features, we implement the concepts of
VTD as in T O
π
1
and also implement one relation (a
role) between body parts concepts and dance orienta-
tions concepts such as:
• hasPosIn: gives for each body part correspond-
ing to a specific orientation, for example, the left
shoulder has a posture in orientation 3.
In this ontology, each axiom is attached with
a necessity degree reflecting its certainty with the
available knowledge. The axiom (Orientations ⊑
V T D − Movements, 0.8), means that dance orienta-
tions may be considered as one of the fundamental
motions (movements) of VTD with a possibilistic de-
gree greater or equal to 0.7. Furthermore, the axiom
(RightLeg ⊑ ∃hasPosIn.V NOri1, 1.0) is a fully cer-
tain axiom because the possibility of this motion is
attached to a degree equal to 1.0, meaning that the
right leg of the performer has a posture in orientation
1 that is undoubting.
5.2 From π-E L
+
⊥
Ontology to π-E L
+
⊥
Possibility Distribution
As in standard E L, the semantics of the possibility
E L
+
⊥
ontology is defined by the possibility distribu-
tion, denoted by π
O
π
, defined over the set of all in-
terpretations of E L language. The possibility distri-
bution can be interpreted in two ways: i) a numerical
interpretation when there is a real sense, ii) an ordinal
interpretation when there exists a preference ranking
between pieces of information. In this paper, we will
focus on the latter interpretation which is appropriate
when there exists a total pre-order or preference rank-
ing between pieces of information reflecting their re-
liability or consistency with the available knowledge.
The possibility distribution π
O
π
assigns to each inter-
pretation I ∈ Ω a possibility degree π(I ) ∈ (0, 1] re-
flecting what extent this latter satisfies the axioms of
the ontology. In the following, we will define the pos-
sibility distribution associated with EL
+
⊥
ontology.
Definition 2: ∀I ∈ Ω
π
O
π
(I ) =
(
1 if ∀(φ
i
, α
i
) ∈ O
π
, I |= φ
i
1 − max{α
i
: (φ
i
, α
i
) ∈ O
π
, I ̸|= φ} ow.
where ow is otherwise.
Example 2: We will continue with the Example 1 to
illustrate explicitly for Definition 2. Let π
1
be the
possibility distribution associated with T O
π
1
and let
{I
1
, I
2
, I
3
} be three interpretations in T O
π
1
. Assum-
ing that I
1
, I
2
, I
3
are satisfied most of the axioms ex-
cept some axioms as follows:
• For I
1
is NOT satisfied (unsatisfied) following ax-
ioms: I
1
̸|= (Le f tHand ⊑ ∃hasPosIn.V NOri8, 0.75)
I
1
̸|= (Le f tShoulder ⊑ ∃hasPosIn.V NOri7, 0.8)
• For I
2
is NOT satisfied (unsatisfied) following ax-
ioms: I
2
̸|= (RightHand ⊑ ∃hasPosIn.V NOri2, 0.83)
I
2
̸|= (RightLeg ⊑ ∃hasPosIn.V NOri1, 1.0)
• For I
3
is SATISFIED ALL of the axioms
From Definition 2, possibility distributions of
I
1
, I
2
, I
3
as follows:
⇒









π
T O
π
1
(I
1
) = (1 − max(0.8, 0.75) = 0.2)
π
T O
π
1
(I
2
) = (1 − max(0.83, 1.0) = 0)
π
T O
π
1
(I
3
) = 1.0 , f or I
3
|= φ
i
(1)
An ontology is said to be consistent if there ex-
ists at least one interpretation that satisfies all the ax-
ioms of the ontology, i.e., π
O
π
(I ) = 1. Otherwise, the
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
272

ontology is inconsistent and their inconsistency is de-
fined by the following expression:
∀I ∈ Ω, Inc(O
π
) = 1 − max{π(I )}
Therefore, from Example 2 and (1), we also said
that the VTD ontology T O
π
1
is consistent because as
the above expression is π
T O
π
1
(I
3
) = 1.0 as well as
Inc(T O
π
1
) = 1 − max(0.2, 0, 1) = 0
⇒ T O
π
1
is consistent
6 MIN-BASED MERGING OF
π-E L
+
⊥
POSSIBILITY
DISTRIBUTIONS
Several fusion operators have been proposed in or-
der to manage the problem of merging n uncertain
pieces of information represented by n possibility dis-
tributions (Benferhat et al., 1997; Benferhat and Kaci,
2003; Benferhat et al., 2013), these fusion operators
aim to obtain a unique possibility distribution from
the set of possibility distributions. As we cited above,
the pieces of information can be represented syntacti-
cally by a set of weighted formulas and semantically
by a set of interpretations.
In this paper, we focus on the fusion operators,
i.e., we will study the syntactic approach which con-
sists of merging possibilistic EL
+
⊥
ontology. How-
ever, in this section, we will focus on the semantic
approach which consists of combining the possibility
distributions associated with each possibilistic E L
+
⊥
ontology using the min-based operator. Note that the
min-based operator holds when the sources of infor-
mation are dependent. Let {π
1
, ..., π
n
} be a set of pos-
sibility distributions provided by n sources of infor-
mation. All the sources use the same scale to repre-
sent uncertainty and share the same domain of inter-
pretations {∆
1
= . . . = ∆
n
}.
Definition 3: Let list(I ) = {π
1
(I ), . . . , π
n
(I )} be a
list that contains n possibility values. The min-based
operator is a mapping from list(I ) to the unit interval
[0.1] and it is defined as follow:
∀I ∈ Ω, π
⊕
(I ) = min(list(I ))
Example 3: To demonstrate a case of inconsistency,
we represent the TBox of VTDs Ontology 2 identified
by T O
π
2
with specific probabilities as follows:
T O
π
2
=





































Orientations ⊑ V T D − Movements, 0.8
V NOri2 ⊑ Orientationsm, 0.95
V NOri3 ⊑ Orientations, 0.80
V NOri8 ⊑ Orientations, 0.93
Hands ⊑ BodyParts, 1.0
Le f tHand ⊑ Hands, 0.78
RightHand ⊑ Hands, 0.89
T O
π
2
=

















































Le f tHand ∩ RightHands ⊑ ⊥, 0.85
Shoulders ⊑ BodyParts,0.98
RightShoulder ⊑ Shoulders, 1.0
Le f tShoulder ⊑ Shoulders, 0.89
Le f tHand ⊑ ∃hasPosIn.V NOri8, 0.75
RightHand ⊑ ∃hasPosIn.V NOri2, 0.85
Le f tShoulder ⊑ ∃hasPosIn.V NOri7, 0.8
RightShoulder ⊑ ∃hasPosIn.V NOri3, 0.3
Le f tLeg ⊑ ∃hasPosIn.V NOri1, 0.78
In the same way, regarding the possibilistic
E L
+
⊥
ontology T O
π
2
, let consider the three interpre-
tations, namely I
1
, I
2
, and I
3
being the axioms in
T O
π
2
. Assuming that I
1
, I
2
, I
3
are satisfied most of
the axioms except some axioms as follows:
• For I
1
is NOT satisfied (unsatisfied) a following
axiom: I
2
̸|= Le f tHand ⊑ ∃hasPosIn.V NOri8, 0.75
• For I
2
is NOT satisfied (unsatisfied) following
axioms:
I
2
̸|= Le f tShoulder ⊑ Shoulders, 0.89
I
2
̸|= Le f tShoulder ⊑ ∃hasPosIn.V NOri7, 0.8
• For I
3
is NOT satisfied (unsatisfied) a following
axioms: I
2
̸|= Le f tLeg ⊑ ∃hasPosIn.V NOri1, 0.78
From Definition 2, possibility distributions of
I
1
, I
2
, I
3
as follows:
⇒









π
T O
π
2
(I
1
) = (1 − max(0.75) = 0.25)
π
T O
π
2
(I
2
) = (1 − max(0.89, 0.8) = 0.11)
π
T O
π
2
(I
3
) = (1 − max(0.78) = 0.22)
(2)
From the expression as Example 2, we also said
that the VTD ontology T O
π
2
is inconsistent because
as the above expression is
An Application of Priority-Based Lightweight Ontology Merging
273

Inc(T O
π
2
) = 1 − max(0.25, 0.11, 0.22) = 0.75
⇒ T O
π
2
is inconsistent
According to Definition 3 with min-based opera-
tor, we can merge the two possibility distributions
represented respectively in Example 2 and Example 3.
Example 4: We continue with Example 2 and Exam-
ple 3. The merged possibility distribution, denoted by
(π
⊕V T D
), is the act of merging two possibility distri-
butions (π
T O
π
1
) and (π
T O
π
2
) represented respectively
in Example2 and Example3. Let {I
1
, I
2
, I
3
} be three
interpretations. The result of the min-base operator
is
⇒ π
⊕
(I
1
) = min(list(I
1
)) = min(0.2, 0.25) = 0.2,
and π
⊕
(I
2
) = min(list(I
2
)) = min(0, 0.11) = 0, and
π
⊕
(I
3
) = min(list(I
3
)) = min(1.0, 0.22) = 0.22.
The merged possibility distribution should satisfy
the following properties: Let consider the two
interpretations I ∈ Ω and I
′
∈ Ω,
∀I , I
′
∈ Ω,
(
When π(I ) ≤ π(I
′
), then π
⊕
(I ) ≤ π
⊕
(I
′
)
When π(I ) = 1, then π
⊕
(I ) = 1.
Based on the Example 4, note that the use of a
minimum operator for merging two normalized pos-
sibility distributions leads to sub-normalized possibil-
ity distribution. Indeed, to solve this problem, let’s
consider the following expression: ∀I ∈ Ω, L(π
⊕
) =
max{π
⊕
(I )}. This function states that there exists at
least one interpretation that is satisfied by all sources.
Let (π
O
π
) be a possibility distribution and (π
N
⊕
) be
their normalized possibility distribution.
Definition 4: The normalized possibility distribution
is defined by the following expression:
∀I ∈ Ω and L(π
⊕
) > 0, π
N
⊕
(I ) =
(
1 if π
⊕
(I ) = L(π
⊕
)
π
⊕
(I ) otherwise.
In the following, we will use the Definition 4 to
represent the normalized possibility distributions.
Example 5: Let us continue with Example 4. Let
I
1
, I
2
, I
3
be three interpretations. Let π
N
⊕
be the
normalized possibility distribution of π
⊕
. Then
⇒ π
N
⊕
(I
1
) = 0.2, π
N
⊕
(I
2
) = 0 and π
N
⊕
(I
3
) = 1.0.
Therein, π
N
⊕
(I
3
) = 1.0 since L(π
⊕
) =
max{0.2, 0, 0.22} = 0.22 and π
⊕
(I
3
) = L(π
⊕
) =
0.22.
Intuitively, the normalized possibility distribution
consists of comparing the merged possibility distribu-
tions with the function L(π
⊕
). When π
⊕
(I ) is equal
to L(π
⊕
), then the normalized possibility distribution
is equal to 1.0. However, when π
⊕
(I ) is different to
L(π
⊕
), then the normalized possibility distribution is
equal to the merged possibility distribution.
7 SYNTACTICAL MERGING OF
π-E L
+
⊥
ONTOLOGY
In this section, we will define the syntactical counter-
part of merging π-E L
+
⊥
ontology. Let {O
π
1
, ..., O
π
n
}
be a set of π-E L
+
⊥
ontology provided by n different
sources. Each O
π
i
is associated with a possibility dis-
tribution π
i
.
Definition 5: Let (φ
i
, α
i
) ∈ O
π
1
and (ϕ
i
, β
i
) ∈ O
π
2
.
The syntax of the min-based operator ⊕ is defined by
the following expression:
O
⊕
= O
π
1
∪ O
π
2
∪ {φ
i
∧ ϕ
i
, max(α
i
, β
i
)}
= O
π
1
∪ O
π
2
Now, based in Definition 5, we are able to merge
T O
π
1
and T O
π
2
represented respectively in Example
2 and Example 3 in order to obtain O
⊕V T D
. Further-
more, their semantics is defined in Example 4. The
result of merging possibilistic E L
+
⊥
ontology will be
presented in the next section.
Note that the merged possibilistic EL
+
⊥
ontology
can be an inconsistent ontology, since merging two
consistent possibilistic E L
+
⊥
ontologies does not al-
ways lead to a consistent merged ontology. In the fol-
lowing, we will define how to determine the consis-
tency degree of the merged possibilistic E L
+
⊥
ontol-
ogy:
Definition 6: Let O
π>α
be a sub-ontology that
contains axioms having a degree greater than alpha.
The consistency degree of E L
+
⊥
ontology, denoted
by Inc(O
π
), is syntactically defined by the following
expression:
Inc(O
π
) = max{α : O
π
α
is the inconsistency}
8 THE RESULT OF MERGING
DANCE E L ONTOLOGIES
In this section, we present the result of merging EL
+
⊥
ontologies based on a potential example introduced
in section 2 and represented their possibility distribu-
tions in Example 2 and Example 3. We would also
present a condensed summary of the result of min-
based merging through Table 2.
To sum up, from Definition 3 and 4, we have a
merged possibilistic distribution table (semantics) of
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
274

the result min-based merging of π-E L
+
⊥
possibility
distributions as follows:
Table 2: The result of min-based merging.
Min-based merging of
π-E L possibility distributions
I
i
π
T O
π
1
π
T O
π
2
π
⊕V T D
π
N
⊕V TD
(1) (2) min(list(I ))
I
1
0.2 0.25 0.2 0.2
I
2
0 0.11 0 0
I
3
1.0 0.22 0.22 1.0
The following is an unambiguous explanation re-
garding Table 2 of processing min-based merging EL
ontologies including: first of all, possibilistic distri-
butions (π
T O
π
) of T O
π
1
and T O
π
2
presented in Col-
umn 1 and Column 2. Secondly, Column 3 is the
merged possibilistic distribution based on the min-
based merging operator (π
⊕V T D
) in Definition 3. Fi-
nally, (3) Column 4 is the normalized possibility dis-
tribution with
L(π
⊕V T D
) = max(π
⊕V T D
(I ))
= max(0.2, 0, 0.22) = 0.22
introduced in Definition 4, therefore, axiom I
3
, in this
case, is equal to 1.0 (normalization) because
π
⊕V T D
(I ) = L(π
⊕V T D
) = 0.22
In terms of the syntactical merging of
E L
+
⊥
ontologies, we have the following merged
results:
Let O
⊕V T D
be a merged possibilitic E L
+
⊥
ontol-
ogy in which based on merging VTD probabilistic
Ontology 1 (T O
π
1
) and VTD probabilistic Ontology
2 (T O
π
2
) represented in above parts of this paper. We
here apply Definition 5 to consider syntactical merg-
ing of π-E L
+
⊥
Ontology, we then obtain the results
defined O
⊕V T D
as follows:
T O
⊕V T D
=































































































Orientations ⊑ V T D − Movements, 0.8
V NOri1 ⊑ Orientations, 0.9
V NOri2 ⊑ Orientationsm, 0.95
V NOri3 ⊑ Orientations, 0.80
V NOri7 ⊑ Orientations, 0.87
V NOri8 ⊑ Orientations, 0.93
Hands ⊑ BodyParts, 1.0
Le f tHand ⊑ Hands, 0.78
RightHand ⊑ Hands, 0.89
Le f tHand ∩ RightHands ⊑ ⊥, 0.85
Shoulders ⊑ BodyParts,0.98
RightShoulder ⊑ Shoulders, 1.0
Le f tShoulder ⊑ Shoulders, 0.89
Le f tHand ⊑ ∃hasPosIn.V NOri8, 0.75
RightHand ⊑ ∃hasPosIn.V NOri2, 0.85
Le f tShoulder ⊑ ∃hasPosIn.V NOri7, 0.8
T O
⊕V T D
=









RightShoulder ⊑ ∃hasPosIn.V NOri3, 0.9
RightLeg ⊑ ∃hasPosIn.V NOri1, 1.0
Le f tLeg ⊑ ∃hasPosIn.V NOri1, 0.78
Following the Definition 5, a merged possibilistic
E L
+
⊥
ontology is TBox union of the other possibilis-
tic ontologies and the maximum selection of the pos-
sibilities between those axioms for the same concepts.
For an explicit explanation of the maximum alterna-
tive, considering the same concept
RightShoulder ⊑ ∃hasPosIn.V NOri3
has a possibility set to 0.9 in T O
π
1
being greater
than a possibility 0.3 of T O
π
2
, therefore, we in this
case select the concept of T O
π
1
with (max(α
i
, β
i
) =
max(0.9, 0.3) = 0.9) satisfied by Definition 5. Other
axioms are considered similar.
9 CONCLUSION
In this paper, we investigated a fragment of
lightweight description logic EL, named E L
+
⊥
, with
the possibility theory. This logic is suitable for ap-
plications such as biology and medicine. First, we
provided their syntax and semantics. Then, we stud-
ied the merging E L
+
⊥
possibility distributions using
the minimum operator. Furthermore, we defined the
An Application of Priority-Based Lightweight Ontology Merging
275

merging possibilistic E L
+
⊥
ontology using the same
operator.
Finally, we also represented a potential example
of merging the prioritized E L ontologies regarding
the dance domain. It would be a significant founda-
tion to build a universal application for Vietnamese
traditional dance management from many different
sources.
ACKNOWLEDGMENTS
This work was supported by ANR-22-CE23-0002
ERIANA and ANR CHAIRE IA BE4musIA.
REFERENCES
Baader, F., Brandt, S., and Lutz, C. (2005). Pushing the EL
Envelope. In IJCAI’05, page 364–369.
Baader, F., Brandt, S., and Lutz, C. (2010). Pushing the el
envelope further. CEUR Workshop Proceedings, 496.
Benferhat, S., Bouraoui, Z., and Loukil, Z. (2013). Min-
based fusion of possibilistic dl-lite knowledge bases.
In 2013 IEEE/WIC/ACM International Joint Confer-
ences on Web Intelligence (WI) and Intelligent Agent
Technologies (IAT), volume 1, pages 23–28. IEEE.
Benferhat, S., Cayrol, C., Dubois, D., Lang, J., and Prade,
H. (1993). Inconsistency management and prioritized
syntax-based entailment. In IJCAI, volume 93, pages
640–645.
Benferhat, S., Dubois, D., Kaci, S., and Prade, H. (2000).
A principled analysis of merging operations in pos-
sibilistic logic. In Proceedings of the Sixteenth con-
ference on Uncertainty in artificial intelligence, pages
24–31. Morgan Kaufmann Publishers Inc.
Benferhat, S., Dubois, D., and Prade, H. (1997). Syntactic
combination of uncertain information: A possibilistic
approach. In Qualitative and Quantitative Practical
Reasoning, pages 30–42. Springer.
Benferhat, S., Dubois, D., Prade, H., and Williams, M.-
A. (1999). A practical approach to fusing prioritized
knowledge bases. In Portuguese Conference on Arti-
ficial Intelligence, pages 222–236. Springer.
Benferhat, S. and Kaci, S. (2003). Fusion of possi-
bilistic knowledge bases from a postulate point of
view. International Journal of Approximate Reason-
ing, 33(3):255–285.
Delgrande, J. P., Dubois, D., and Lang, J. (2006). Iterated
revision as prioritized merging. KR, 6:210–220.
Dubois, D. and Prade, H. (2012). Possibility theory.
Springer.
Everaere, P., Konieczny, S., and Marquis, P. (2010). Dis-
junctive merging: Quota and gmin merging operators.
Artificial Intelligence, 174(12-13):824–849.
Giordano, L. and Dupr
´
e, D. (2020). An ASP approach
for reasoning in a concept-aware multipreferential
lightweight DL. Theory and Practice of Logic Pro-
gramming, 20:751–766.
Giordano, L., Gliozzi, V., Olivetti, N., and Pozzato, G. L.
(2009). Prototypical reasoning with low complex-
ity description logics: Preliminary results. In Pro-
ceedings of the 10th International Conference on
Logic Programming and Nonmonotonic (LPNMR’09),
pages 430–436.
Haret, A. and Woltran, S. (2019). Belief revision opera-
tors with varying attitudes towards initial beliefs. In
IJCAI’09, pages 1726–1733.
Hue, J., Papini, O., and Wurbel, E. (2007). Syntactic propo-
sitional belief bases fusion with removed sets. In EC-
SQARU’07, pages 66–77.
Kazakov, Y., Kr
¨
otzsch, M., and Simancık, F. (2003). The in-
credible elk: From polynomial procedures to efficient
reasoning with el ontologies. submitted to a journal.
Kazakov, Y., Kr
¨
otzsch, M., and Simancik, F. (2012). Prac-
tical reasoning with nominals in the el family of de-
scription logics. In KR.
Kazakov, Y., Kr
¨
otzsch, M., and Siman
ˇ
c
´
ık, F. (2014). The
incredible ELK: from polynomial procedures to effi-
cient reasoning with E L ontologies. J. Autom. Rea-
soning, 53(1):1–61.
Konieczny, S. and P
´
erez, R. P. (2002). Merging information
under constraints: a logical framework. Journal of
Logic and computation, 12(5):773–808.
Konieczny, S. and P
´
erez, R. P. (2011). Logic based merging.
Journal of Philosophical Logic, 40(2):239–270.
Lam, T.-L. (1994). Mua dan gian cac dan toc Viet Nam
(Vietnamese). Culture and nation publishing house,
Vietnam.
Patricia, E., Konieczny, S., and Marquis, P. (2008).
Conflict-based merging operators. In KR’08, pages
348–357.
Qi, G., Liu, W., and Bell, D. A. (2006). Merging stratified
knowledge bases under constraints. In AAAI, pages
281–286.
Tran, V.-S., Doan, T.-H., and Nguyen-Thi, M.-H. (2003).
Mua dan gian mot so dan toc vung Tay Bac (Viet-
namese). Culture and nation publishing house, Viet-
nam.
ICAART 2023 - 15th International Conference on Agents and Artificial Intelligence
276