Incident-Aware Distributed Signal Systems in Self-Organised Trafﬁc

Control Systems

Sven Tomforde

, Yanneck Ohl and Ingo Thomsen

Intelligent Systems, Kiel University, 24118 Kiel, Germany

Keywords:

Trafﬁc Management, Organic Trafﬁc Control, Progressive Signal Systems, Green Waves, Incident Detection,

Self-Organisation.

Abstract:

Trafﬁc congestion is a major contributor to carbon dioxide emissions and causes air pollution which poses

various health risks. In response to such challenges, trafﬁc management systems are becoming increasingly

intelligent and adaptive. Particularly self-organised approaches such as the Organic Trafﬁc Control (OTC)

system offer additional advantages such as efﬁciency, scalability, and robustness. In addition to the local and

trafﬁc-dependent switching of trafﬁc signals, a central task of such a system is the coordinated adaptation of

trafﬁc lights by means of Progressive Signal Systems. In this paper, we present a novel approach for estab-

lishing decentralised PSSs that takes into account recognised incidents and thus proactively ensures optimised

trafﬁc ﬂows. We develop three different strategies and evaluate them using realistic simulations.

1 INTRODUCTION

After a decline during the COVID crisis, the trafﬁc

demands in urban areas have increased again, and

congestion and trafﬁc disruption cause major eco-

nomic damage every year. Furthermore, it is often not

feasible to expand the existing infrastructure which

presents an additional challenge. Apart from a politi-

cally motivated reduction of trafﬁc volumes, the only

possible countermeasure is a more efﬁcient utilisation

of the existing infrastructure.

In addition to the trafﬁc-dependent and proactive

adaptation of trafﬁc lights or routing solutions, Pro-

gressive Signal Systems (PSS, also known as “green

waves”) are a key factor for optimisation. Currently

there are time-based static as well as centralised and

decentralised dynamic solutions. However, these are

not geared towards detected incidents within the un-

derlying inner-city road network.

Building on existing work on self-organised and

self-adaptive trafﬁc management – the OTC system,

(Sommer et al., 2016a) – this article explores a

novel approach to an incident-aware establishment

and maintenance of PSSs. We propose a correspond-

ing algorithm that can handle different levels of infor-

mation about incidents, and demonstrate that it can

https://orcid.org/0000-0002-5825-8915

https://orcid.org/0000-0002-0850-4786

improve trafﬁc ﬂow compared to conventional PSS

approaches.

The remainder of this paper is organised as fol-

lows: Section 2 provides a brief discussion of the

state-of-the-art. After that, Section 3 presents the de-

veloped approach for incident-aware PSS. Section 4

analyses the behaviour of the approach in close-to-

reality simulations and assesses the beneﬁt in com-

parison to alternatives. Finally, Section 5 summarises

the paper and gives an outlook on future work.

2 BACKGROUND

This section describes the underlying related work,

speciﬁcally in the context of self-organised trafﬁc

control, automated incident detection, and progres-

sive signal systems. It also introduces the OTC sys-

tem as the basis of this work.

2.1 Self-Organised Trafﬁc Control

Urban trafﬁc light control is usually done via traf-

ﬁc control centres, with SCOOT (Robertson and

Bretherton, 1991), SCATS (Sims and Dobinson,

1980), MOVA (Vincent et al., 1990), and UTOPIA/-

SPOT (Mauro and Taranto, 1990) as the most promi-

nent systems used world-wide. All of these ap-

Tomforde, S., Ohl, Y. and Thomsen, I.

Incident-Aware Distributed Signal Systems in Self-Organised Trafﬁc Control Systems.

DOI: 10.5220/0011705900003479

In Proceedings of the 9th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2023), pages 15-26

ISBN: 978-989-758-652-1; ISSN: 2184-495X

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

proaches establish a centralised control loop that col-

lects the current trafﬁc conditions and adapts the

switching policies of the distributed intersection con-

troller (IC). Typically, this adaptation is based on a

certain cost function including aspects such as the ex-

pected travel times, emissions, or public transport pri-

ority. An overview and comparison of approaches can

be found in (Studer et al., 2015).

These centralised approaches all are limited in

terms of efﬁciency, scalability, and robustness as all

information has to be passed to and collected by a one

central controller. It then has to conduct the optimisa-

tions and distribute the derived plans to the ICs.

As a response, self-adaptive and self-organised

(SASO) approaches with a local scope have been de-

veloped that perform decisions locally at each inter-

section controller and – in some cases – communi-

cate with each other to achieve coordinated decisions.

Examples include a multi-agent approach based on

fuzzy control as presented in (Gokulan and Srini-

vasan, 2010), a distributed W-learning concept to op-

timise a phase-oriented signal control as discussed

in (Dusparic and Cahill, 2009), or a model with pre-

dictive control as proposed by (Oliveira and Cam-

ponogara, 2010). The drawback of these approaches

compared to the centralised one is that they are mostly

of academic interest and just tested in simulations.

The third class of concepts is even more theoret-

ical as it eliminates the standard phase-based trafﬁc

signal switching schemes: A ﬂuid-dynamic model,

discussed in (Helbing et al., 2005), uses waiting ve-

hicles as pressure and counter-pressure for switching

trafﬁc lights policies. In contrast to the SASO con-

cepts above, these control systems cannot consider

further knowledge or coordinate their decisions as the

model primarily reacts to local queues.

2.2 Progressive Signal Systems

Some of the aforementioned trafﬁc control systems

possess abilities to determine coordination plans for

ICs, resulting in centrally planned PSS schemes. As

an alternative self-organised approaches have been

proposed. However, these are again mostly of an aca-

demic nature. One example presented in (Gershen-

son, 2007) is called “self-organising trafﬁc lights”

(SOTL). The approach does not explicitly establish

a PSS but relies on trafﬁc-responsive local controllers

that take into account the number of waiting cars or

the gaps between arriving vehicles. This behaviour

is similar to uncoordinated trafﬁc-adaptive controllers

(e.g. following the NEMA standard). Trafﬁc lights

keep a count κ of the number of cars waiting in front

of them. Each car is weighted by its waiting time and

as soon as κ reaches a certain threshold, the trafﬁc

light changes. The SOTL control method employs

several restrictions to avoid fast switching of traf-

ﬁc lights, the interruption of moving platoons, and

deadlocks caused by long platoons. Although there

is no explicit coordination, Gershenson describes the

observation of coordination effects similar to those

achieved by PSSs.

As an alternative, Bazzan described an approach

to distributed trafﬁc signal coordination in (Baz-

zan, 2005). Here, intersections are modelled as

individually-motivated agents. Each agent possesses

a set of predeﬁned control strategies to choose from.

The selection process is based on local events occur-

ring at the intersection as well as on the results of

“coordination games” that are played among neigh-

bouring agents. The principal applicability of this

approach is demonstrated in a simple scenario of an

arterial road consisting of ten intersections. Each in-

tersection agent has to choose between two strategies,

each of which favours one of the two directions over

the other. The distributed approach is compared to

a central controller that creates synchronised trafﬁc

lights in one of the arterial directions, based on de-

tector readings from the network. The agent-based

approach proves to be better in situations where the

ﬂow of trafﬁc in opposite directions is nearly equal.

An important difference between Bazzan’s approach

and the organic system presented here is that Bazzan

relies solely on the selection of predetermined strate-

gies while the approach presented here is able to gen-

erate new strategies dynamically.

2.3 Trafﬁc Incident Detection

Techniques for automatic recognition of incidents, ac-

cidents, and other road events, e.g. requiring emer-

gency responses, have been the focus of research for

more than three decades. Most of the resulting al-

gorithms rely on sensor data from loop detectors.

Chronologically, AID research started with the Stan-

dard Normal Deviate algorithm (Dudek et al., 1974),

subsequently followed by the California Algorithm

family (Payne, 1975; Payne and Tignor, 1978). These

techniques essentially follow a simple decision tree

structure and take thresholds into account.

Subsequently, approaches have been introduced

which are based on time series analysis (Ahmed

and Cook, 1980), identiﬁcation of low-volume

conditions (Dudek et al., 1975), ﬁltering and

smoothing-based algorithms (Stephanedes and Chas-

siakos, 1993), a dynamic-systems-model-based al-

gorithm (Willsky et al., 1980), correlation-analysis-

based approaches (Takaba and Matsuno, 1985), the

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

McMaster catastrophe theory-based algorithm (Gall

and Hall, 1989), and a mathematical trafﬁc-ﬂow-

model-based algorithm (Lin and Daganzo, 1997).

More recently, video-based approaches have been

outlined (Shehata et al., 2008) and combined with

semantic annotations (Kamijo et al., 2004). In ad-

dition to these infrastructure-based approaches for

estimating ﬂows, probe vehicles have been consid-

ered (Jenelius and Koutsopoulos, 2013). Some work

is especially dedicated to urban environments (Feng

et al., 2014) which may serve the incident detection.

However, these approaches all come with some

limitations: Either they are designed for highways

only or they are based on experienced travel times

through the underlying road network, and/or they do

not distinguish between different incident types (and

the corresponding reaction). Most importantly, there

is no integrated trafﬁc management solution that con-

siders detected incidents, an estimation of their sever-

ity and impact, or takes this information pro-actively

into account when, for instance, deciding about trafﬁc

control or progressive signal systems.

In response to these observations, we presented

a novel clustering-based approach for AID in urban

road networks that is based on standard loop detec-

tor technology again (Thomsen et al., 2021). Based

on the ICs’ responsibility zones (i.e. intersection area

and incoming sections equipped with induction loop

sensors), the controllers consider the time series of the

detector loop data. They then apply techniques such

as DBSCAN (Ester et al., 1996) to detect incidents

online within a certain time window. We showed that

appropriate detection accuracy is achieved for condi-

tions with high trafﬁc loads, while the approach still

suffers in weak load conditions.

2.4 Organic Trafﬁc Control

The Organic Trafﬁc Control (OTC) system (Proth-

mann et al., 2009) and its extensions serve as a ba-

sis for this work. The OTC system is a self-adaptive

and self-organised trafﬁc control system that decides

locally at each intersection about the behaviour of

the underlying trafﬁc light controller (TLC). Here,

“organic” follows the ideas of Organic Comput-

ing (M

uller-Schloer and Tomforde, 2017) and empha-

sises the transfer of principles from nature to technical

systems: The decentralised structure, the cooperation

of smaller, autonomous entities, as well as local adap-

tation and learning capabilities allow for high robust-

ness, scalability, and ﬂexibility.

Based on the Observer/Controller paradigm (Tom-

forde et al., 2011), the OTC system adapts the green

duration of trafﬁc lights using a phase-based ap-

proach and optimises this adaptation strategy at run-

time. This is achieved by means of reinforcement

learning and safety-oriented generation of novel be-

haviour within a simulation environment, see (Pro-

thmann et al., 2009). The adaptation process is per-

formed depending on the currently active cycle time

of the trafﬁc controller, i.e. an adapted control strat-

egy is active for three cycles (typically 60s to 120s)

before it can become subject to adaptations again.

The current trafﬁc ﬂows for all turning movements

passing the intersection (in

vehicles

/hour and estimated

from detector readings) are the basis for any adapta-

tion decision. The estimated waiting times are then

used as feedback to improve the behaviour over time.

OTC is further able to establish PSSs in a fully self-

organised manner (Tomforde et al., 2008) and to pro-

vide route recommendations to drivers which reﬂect

the current state of the trafﬁc network (Prothmann

et al., 2012).

Based on OTC, further contributions investigated

are robust trafﬁc demand prediction (Sommer et al.,

2013), integration of these predictions in the control

strategies, and infrastructure-based anticipatory route

guidance (Sommer et al., 2016b).

OTC is self-organised in a way that all nodes oper-

ate independently and collaborate to achieve system-

wide goals, such as reducing waiting times, number of

stops, emissions, etc. It is realised as a multi-layered

adaptation and learning system on top of a standard

TLC. Figure 1 illustrates the conceptual design.

Figure 1: Overview of the multi-layered OTC architecture.

Here, Layer 0 represents the System under Obser-

vation and Control (SuOC) which is the actual TLC

Incident-Aware Distributed Signal Systems in Self-Organised Trafﬁc Control Systems

and offers interfaces to detectors and neighbouring

nodes. The TLC (i.e. its green durations) is re-

conﬁgurable at runtime. This is done by the overly-

ing Layer 1 which assesses the environment (using

the sensors). Based on this observation, the controller

employs a Learning Classiﬁer System (LCS); in this

case a variant of Wilson’s XCS (Wilson, 1995). This

LCS chooses rules from a rule set to modify the trafﬁc

signalisation appropriately at runtime.

Finally, Layer 2 is activated when Layer 1 is con-

fronted with a situation for which no suitable rule or

only insufﬁcient knowledge exists. In this case, traf-

ﬁc simulation software (Aimsun Next, see (Aimsun,

2021)) is used to validate new rules which are gener-

ated by applying an evolutionary algorithm.

3 INCIDENT-AWARE

PROGRESSIVE SIGNAL

SYSTEMS

This section presents our novel incident-aware PSS

algorithm for self-adaptive and self-organised trafﬁc

control systems which is integrated into the OTC sys-

tem. To achieve this, we initially introduce the inci-

dent types under consideration, summarise the exist-

ing decentralised progressive signal system (DPSS)

algorithm that serves as a basis for this work, and de-

ﬁne the extension of this algorithm.

3.1 System Model and Incident Types

We assume regular urban road networks of varying

topology and decentralised nodes with intersection

controllers (ICs) that are responsible for controlling

the TLCs. Each node covers the area of the intersec-

tion as well as the incoming and outgoing sections

which are assumed to be equipped with detectors (e.g.

induction loops). Furthermore, each node has the ca-

pability to (a) communicate with the neighbours that

share its road segment as well as to (b) detect traf-

ﬁc incidents within the intersection, the incoming and

the outgoing sections. Here, we consider three groups

of possible static incidents as established in (Thomsen

and Tomforde, 2022):

• Section closure: Complete closing of the section

between two intersections in one direction

• Lane closure: Closing of one (or possibly more)

lanes of a multi-lane section

• Partial lane closure: Similar to a lane closure, but

limited to a segment of the section straight on)

Other types of incidents, e.g. both-way closures

of sections, a partial or a full blockage of an intersec-

tion or a technical defect (“loss of function”), will be

addressed in future work.

The incident detection mechanism employed by

the node is not further speciﬁed. It can be based on

machine learning technology as mentioned in Sec-

tion 2.3 or the approach from (Thomsen and Tom-

forde, 2022) with a possible extension for validation.

The only requirement is the ability to provide infor-

mation according to these knowledge levels (KL):

1. The IC is aware only of whether an incident oc-

curred in its sensor horizon or not.

2. It is additionally aware of the section or turning

where that incident occurred.

3. It further knows the incident type.

Based on these model assumptions, the objec-

tive of this work is to establish a fully decentralised

scheme for PSS that considers the uncertain incident

information available. As a result, we aim to improve

the trafﬁc ﬂow of the underlying road network.

3.2 The Basis: Decentralised

Progressive Signal Systems

The Decentralised Progressive Signal Systems

(DPSS) algorithm is performed by the local intersec-

tion controllers and follows a three-phased approach,

as outlined in (Tomforde et al., 2008):

1. Phase: Each intersection controller informs its

preferred predecessor that it would like to be its

successor in a PSS. Afterwards, each IC checks if

it was selected as a predecessor by its downstream

node. In that case, a partnership is established. Fi-

nally, each node knows it is part of a PSS and what

its predecessor and successor are.

2. Phase: The controllers agree on a common cycle

time. Each IC has a desired cycle time (DCT) and

keeps track of the agreed cycle time (ACT). The

DCT is the one currently active at the intersection

without coordination in a PSS. From the ﬁrst con-

troller to the last, the ACT is propagated through

the PSS, with each node updating the ACT to its

DCT if the local DCT is higher. After reaching

the last node, the same process is continued back

to the ﬁrst controller. As a result, all nodes agree

on the ACT – the common cycle time.

3. Phase: The offsets for the synchronised phases of

the trafﬁc controller are determined. These de-

pend on the predecessor’s starting time of the syn-

chronised phase, the travel time between sections,

the vehicle serving time and the nodes’ own start

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

time of the synchronised phase. For this, each

node propagates its parameters to its successor,

using the same echo algorithm as in phase 2.

3.3 Incident-Aware DPSS

In the following, we present our novel Incident-aware

DPSS (IA-DPSS) algorithm. It consists of four steps

and is performed periodically by each intersection

controller or as a response to incoming messages from

other controllers and local incident alerts. Steps 2, 3

and 4 correspond to the 3 phases of the DPSS already

outlined above.

Step 1: Incident-Aware Conditions

To achieve trafﬁc-ﬂow-based coordination, each con-

troller adapts the currently observed local streams

passing the turning movements. We refer to these ma-

nipulated trafﬁc streams as “synthetic streams”. The

measured trafﬁc ﬂow is artiﬁcially increased or de-

creased by a certain degree on the sections towards

the remaining possible neighbours (and possibly set

to zero in case a path to a successor is blocked by

an incident). The remaining neighbours are intersec-

tions reachable via an incident-free section. As an

alternative, we re-distribute the trafﬁc ﬂow based on

weights. This will be referred to as “weighted dis-

tribution” which are calculated by ﬁrst adding up the

total trafﬁc ﬂow f

between the remaining neighbours

and then dividing the section’s trafﬁc ﬂow f

by the

total ﬂow:

Another alternative is re-distributing the trafﬁc

ﬂow equally between all remaining neighbours. This

will be referred to as “equal distribution”. When no

re-distribution takes place, this is referred to as in-

cident ﬂow reduction. How these synthetic streams

are used depends on the knowledge levels (KL) intro-

duced in Section 3.1:

1. KL: The controller does not know the location.

Since waiting for sensor information to show an

abnormal trend would exhibit similar behaviour as

without incident awareness due to delayed statis-

tics, the node is excluded from DPSS calculation:

All synthetic streams at that node are set to zero.

2. KL: As no information regarding the incident type

and impact are available, a default is used. For

example, we estimate the averaged reduction of

capacity by 50% and therefore determine the syn-

thetic stream accordingly. Note that this is just a

default value. It could be learned through experi-

ence over time and therefore would be subject to

customisation by the local nodes.

3. KL: For section closures, the synthetic trafﬁc

streams over this section are set to zero. Option-

ally, the original ﬂows are distributed to the re-

maining open streams.

For lane closures, the reduction depends on the

number of lanes: r =

BlockedLanes

/TotalLanes. The

synthetic ﬂow is then f

= f × (1 − r). Again,

we optionally distribute uniformly the decreased

ﬂows to all remaining streams.

For partial lane closures, we decrease r by a

weight that is determined by the impact of the in-

cident (i.e. estimated length divided by the sec-

tion’s capacity).

Finally, for turning closures, we use the same for-

mula and calculate r for each outgoing section by

considering the turnings with incidents. In par-

ticular, we calculate r as the count of disturbed

turnings divided by the count of all turnings lead-

ing to this outgoing section. Again, a possible re-

distribution of reduced ﬂow values is considered.

Step 2: Partnerships

Each node determines the currently strongest trafﬁc

ﬂow running over its training movements. Let us

assume that node j determines the turning from up-

stream node i to downstream node k as its strongest

turning movement. For node j, the expected highest

beneﬁt lies in the coordination of the (longest) sig-

nal phase serving the selected turning from i to k with

the respective upstream intersection i. We call this

a “synchronised phase”. Consequently, node j sends

its desired predecessor i a message, asking it to be its

successor in a PSS. This is performed in parallel by

all nodes. As soon as all nodes have informed their

desired predecessor, they perform a local matching.

The local matching veriﬁes that the downstream

node k selected the node as the desired predecessor.

Then the partnership is conﬁrmed and other possible

registered nodes are rejected. For those nodes where

this rejection prohibits the ﬁrst choice, the process

checks for the second-best solution and performs the

same acknowledge/reject mechanism. As a result, all

nodes know if they are part of a PSS and who their

predecessor and successor are. Furthermore, the ﬁrst

and last nodes of the PSS know about their special

position as they have no predecessor or successor.

Incident-Aware Distributed Signal Systems in Self-Organised Trafﬁc Control Systems

Step 3: Common Cycle Time

Based on a short safety interval (usually 3s), the ﬁrst

node starts building the PSS which requires a com-

mon cycle time. Since this controls the capacity of the

node (i.e. longer cycle times correspond to higher ag-

gregated trafﬁc volumes passing the intersection), the

common cycle time follows the principle of the weak-

est link: Nodes have to identify the smallest possible

cycle time for all participants of the PSS. Each node

i keeps tracks of its own “desired cycle time” (DCT

)

and an “agreed cycle time” (ACT ). The desired cycle

time DCT

is the cycle time node i would prefer for

the current trafﬁc situation if it was not part of a PSS.

This can be retrieved from the learning component in

OTC or, if this is not active, the current cycle time.

The participating nodes determine an agreed cy-

cle time ACT . Since the DCT

is as short as possible,

due to the underlying objective to decrease averaged

waiting times at the nodes, the ACT is selected as the

maximum of all DCTs of the nodes i. A shorter ACT

might reduce the capacity of the most heavily used

node more than is acceptable, leading to rising queues

in its approaches.

A fully distributed echo algorithm determines

ACT : Initially, each node i stores its knowledge on

the agreed time locally as ACT

. The ﬁrst node in the

PSS updates its desired cycle time DCT

(by setting

ACT

:= DCT

) and sends ACT

to its successor in

the PSS. The succeeding nodes i, i = 2, ... ,n forward

their ACT

after updating it:

ACT

:= max{DCT

,ACT

i−1

}

= max{DCT

, max

j∈{1,...,i−1}

{DCT

}}

= max

j∈{1,...,i}

{DCT

The last node propagates the ACT

back to the ﬁrst

node, while each participant repeats the above pro-

cess. As a result, all nodes are aware of the most suit-

able ACT for the PSS.

Step 4: Offsets and Synchronisation

Finally, for the nodes respecting the ACT the offsets

as well as an appropriate signalisation can be deter-

mined. All nodes proportionally increase the green

durations of their signal phases until the sum of all

phase durations, including interphases which are kept

constant, corresponds to the ACT .

Naturally, the ﬁrst node has no offset restrictions.

For each successor node i, i = 2,.. .,n, the offset o

depends on:

Figure 2: Test environment: A 7-by-7 Manhattan-style net-

work. The green area marks the analysed junctions; those

outside are simulated but not analysed, to avoid simulation

artefacts. The sections marked red feature the incidents sim-

ulated in Section 4: The single incidents of the ﬁrst 3 exper-

iments are located in the left section. The additional one of

the combined experiment is placed in the right section.

• predecessor’s offset o

i−1

• start p

i−1

of the synchronised phase within the

predecessor’s TLC,

• time d

i−1,i

cars need to arrive from a predecessor,

• start p

of the synchronised phase within the

node’s own TLC, and ﬁnally,

• time q

needed to serve queued vehicles for the

synchronised phase.

All successors must know the absolute time s

when the ﬁrst node activates its TLC: the start time

for the PSS. Again, an echo algorithm is used by the

ﬁrst node. It informs its successor about the start

time s, its offset (without loss of generality o

= 0, the

ﬁrst nodes starts the PSS at time s) and the start p

of the synchronised phase in its TLC. The nodes i,

i = 2, ...,n, shift their signal plan by calculating their

own offset, relative to the ﬁrst PSS node:

= (o

i−1

+ p

i−1

+ d

i−1,i

− p

− q

) mod ACT.

Here, the time d

i−1,i

is assumed to be available

locally at each node for all its neighbours j (one of

which is node i − 1). This assumption is reasonable

since d

i−1,i

depends on the ﬁxed distance and usually

constant speed limits between nodes.

Furthermore, the current value of q

is a small con-

stant that will in the future be estimated based on local

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

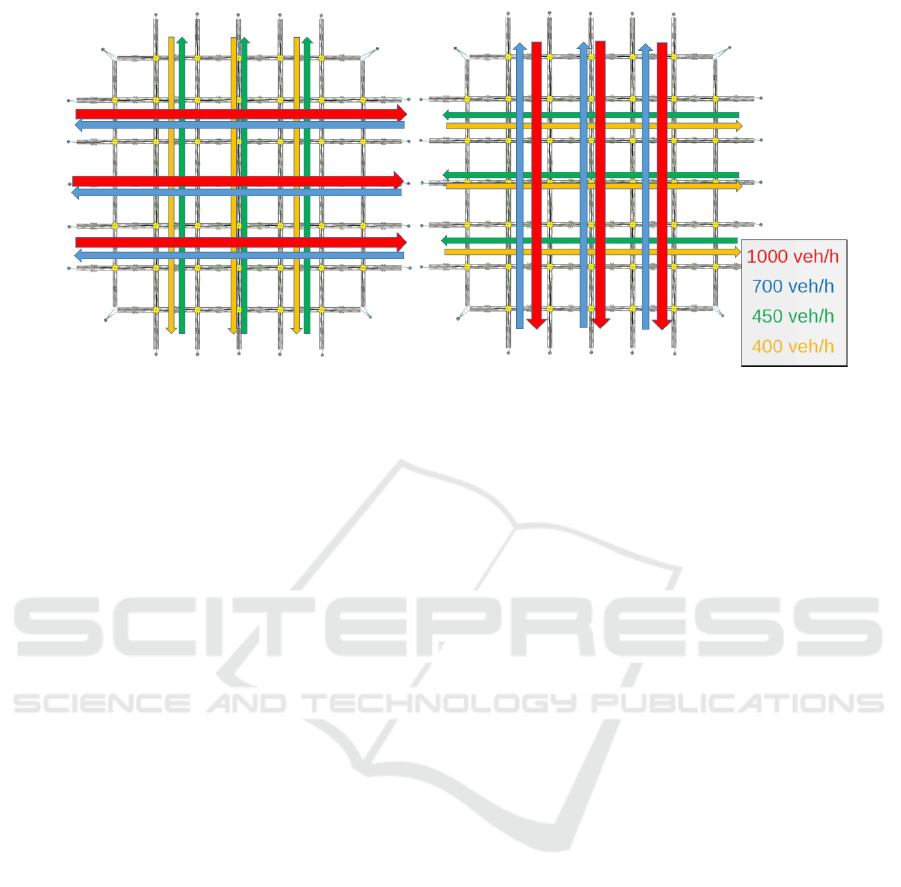
Figure 3: Simulated trafﬁc demands. The left graph visualises the demand during the 90 min of the ﬁrst half which has an

emphasis on a west-east direction. The right graph depicts the pronounced north-south demands during the second half.

trafﬁc. Once the offset calculation is ﬁnished, the val-

ues for s, o

and p

are forwarded to the successor in

the PSS until the last node is reached and the offset

calculation is completed. To avoid any violation of

legal requirements, the change not done immediately

but by using a statical handover signal plan, where

the phase order is kept and the durations are adapted

proportionally to ﬁll in the required offset.

Further Features

The changing trafﬁc conditions require a constant re-

assessment of the most promising PSS constellations.

To this end, the update mechanism from (Tomforde

et al., 2008) is reused. A global perspective on the

status of the trafﬁc conditions would allow for opti-

mal constellations, while our IA-DPSS is a heuris-

tic with local viewpoint (therefore, faster, more ro-

bust and scalable). Optimal constellations could be

achieved by taking a global perspective on the traf-

ﬁc, such as the hierarchical extension introduced in

(Tomforde et al., 2010) provides .

4 EVALUATION

4.1 Experimental Setup

To evaluate the IA-DPSS algorithm, we used the 7-

by-7 Manhattan-style network in Fig. 2 which was

simulated using Aimsun Next. This professional sim-

ulator was chosen since it provides close-to-reality

simulations with realistic results. Trafﬁc demands

have been deﬁned as shown in Fig. 3.

The experiments followed the same methodology

as in (Tomforde et al., 2008) and have a duration of

three hours, with an additional warm-up period of 15

min. All incidents occur 45 min after warm-up. OTC

serves as a basis for the implementation and analy-

sis of the behaviour. We compare the impact of the

different knowledge levels and investigate the beneﬁt

over a standard DPSS approach. All results are av-

eraged values over ﬁve runs of Aimsun experiments

with different random seeds.

4.2 Experimental Results

Experiment 1: Section Closure

First, we analyse the effect of one central section be-

ing closed by an incident. Figure 4 shows the increas-

ing number of stops during a 45 min closure: Com-

pared to the standard DPSS, all three IA-DPSS vari-

ants lead to more stops at the beginning of closure

as they react more efﬁciently to reroute the held back

trafﬁc. But after the new situation is established and

towards the end of the incident, the standard DPSS ex-

hibits the most stops per km and vehicle. Especially

after the incident, the update is less successful, result-

ing in a beneﬁt of about 5% for the IA-DSS variants.

When looking at the travel times, Fig. 4 illus-

trates how much the average travel time per car and

km increased: While the standard DPSS performs the

worst, KL 3 provides the highest beneﬁt, compared

to the other two levels and the reference. This is ex-

pected due to the more precise response. However,

the equal distribution strategy for KL 3 seems to be

less successful and should therefore not be used.

Incident-Aware Distributed Signal Systems in Self-Organised Trafﬁc Control Systems

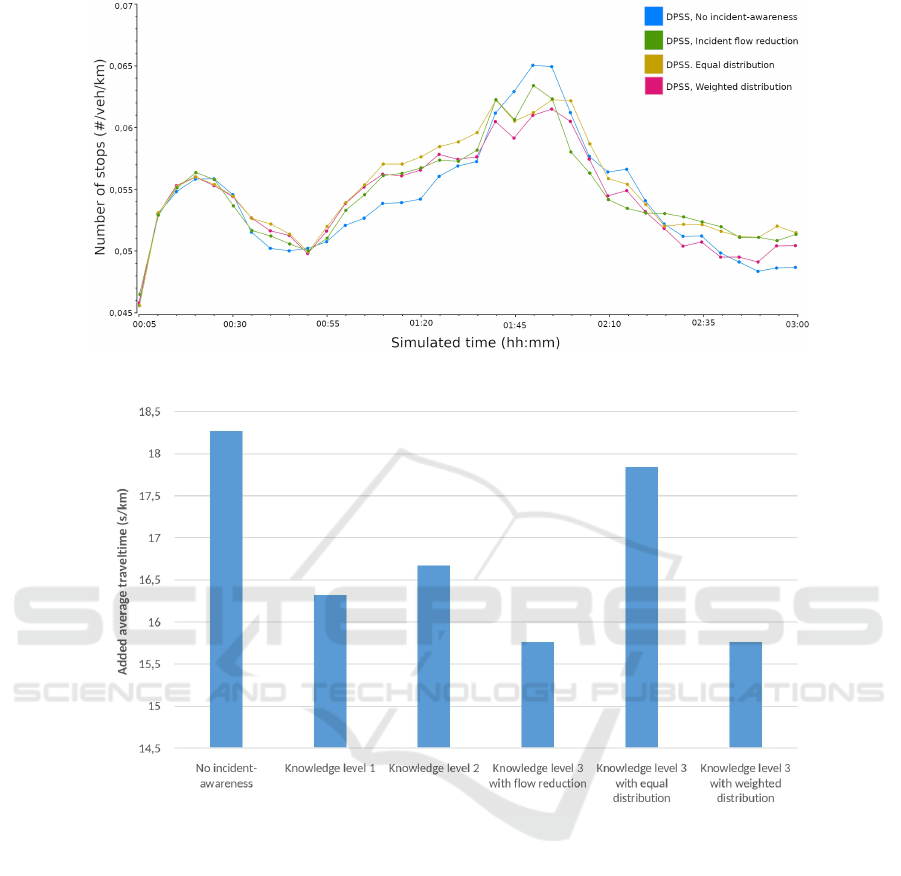
Figure 4: Average number of stops per car and kilometre with a section closure lasting from 0:45 to 1:50.

Figure 5: A comparison of the DPSS (with “no incident awareness”) and the different IA-DPSS variants regarding the average

time a vehicle takes longer per kilometre while the section closure in Fig. 4 is active.

Experiment 2: Lane Closure

Here, only one lane of the double-lane road is closed.

Generally, the number of stops for an 15 min clo-

sure is lower than the in case of the section closures

(Fig. 4), and all algorithms behave similarly at that

level. One exception is the IA-DPSS with weighted

distribution which reacts slightly faster but also with

stronger ﬂuctuations than the others.

While the number of stops does not give a clear

indication, Fig. 6 illustrates the roughly 1 to 2 sec-

onds of added average travel time in. Here, the IA-

DPSS algorithm exhibits an apparent beneﬁt when

compared to the standard DPSS.

Experiment 3: Partial Lane Closure

Similar to the lane closures, the general number of

stops is lower when compared to the section closures,

and none of the algorithms deviates signiﬁcantly dur-

ing the 15 min partial lane closures. But Fig. 7 in-

dicates that again one variant – IA-DPSS at KL 2 –

performs better the others and the standard DPSS.

Experiment 4: Multiple Incidents

Here, we simulate two simultaneous incidents which

are located at two different sections (see Fig. 2). The

best-performing IA-DPSS uses a combination of re-

duction factor for (partial) lane closures and weighted

distribution for section closures at KL 3. The com-

parison between the DPSS and the IA-DPSS in Fig. 8

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

Figure 6: Average added travel time per kilometre and cars for the DPSS and the IA-DPSS variants in case of simulated 15

min lane closure.

Figure 7: Average added travel time per km and car for the DPSS and the different IA-DPSS variants in case of a 15 min

partial lane closure.

shows that the averaged travel time after the incidents

have been removed increases for IA-DPSS, while it

is slightly lower beforehand. This is because waiting

times are only analysed as soon as the cars leave the

network – and the result of the IA-DPSS is a slightly

longer route due to avoidance of incident-regions. In

other words: Although the key metric is not reduced,

the desired effect has been achieved – longer incident

times would lead to higher beneﬁts. Figure 9 details

the results for the different incident types. Here, ho-

mogeneous incidents have a beneﬁt of 10% compared

to DPSS. On the other hand, heterogeneous incident

types still require more customisation.

5 CONCLUSIONS

In this work, we presented a fully distributed algo-

rithm for establishing progressive signal systems in

self-adaptive and self-organised trafﬁc control sys-

tems. The IA-DPSS is a four-phased algorithm that

adapts the local trafﬁc demand representation at each

intersection. It negotiates partnerships in a PSS,

ﬁnds the common cycle time for all nodes of a PSS,

and ﬁnally coordinates the signal plans by comput-

ing offsets. We analysed the behaviour in a 7-by-7

Manhattan-style network using close-to-reality simu-

lations in Aimsun Next and using the Organic Trafﬁc

Incident-Aware Distributed Signal Systems in Self-Organised Trafﬁc Control Systems

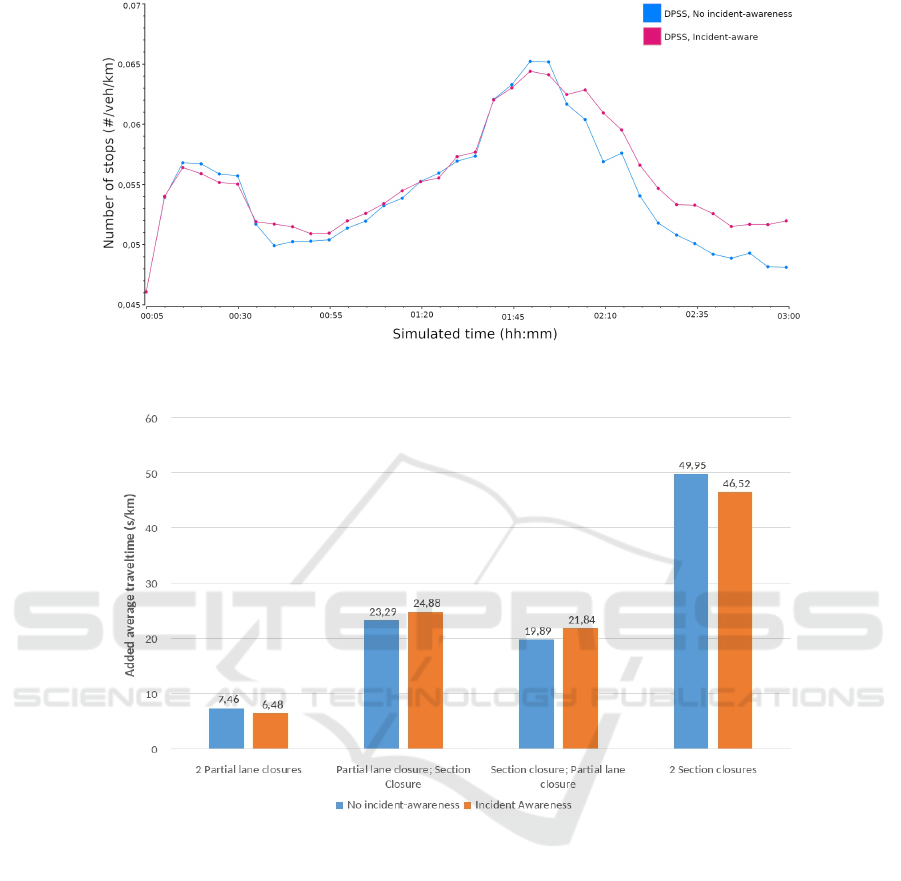
Figure 8: Average number of stops per car and kilometre for of the concurrent section and partial lane closure from 0:45 to

1:50. Here, the “incident aware DPSS” is a combination of algorithms which perform the best for these incident type.

Figure 9: The increase of the added averaged travel time per car per kilometre due to a combination of the two concurrent 45

min incidents in Fig. 8.

Control (OTC) system as a basis. We showed that,

depending on the levels of incident information avail-

able, a reduction of key ﬁgures such as the number of

stops of vehicles and added average travel times can

be achieved.

In future work, we will ﬁrst apply this approach

to less regular topology modelling in real city envi-

ronments, as done in previous work. We will also in-

vestigate the impact of more complex incident condi-

tions (i.e. interweaving and more heterogeneous) and

the mutual inﬂuences on the self-learning behaviour

of the underlying OTC system. From a machine learn-

ing perspective, we will also look into tuning the al-

gorithms. Thresholds and adapting weighting factors

of the IA-DPSS will be learned locally.

ACKNOWLEDGEMENTS

This research was supported by the Deutsche

Forschungsgemeinschaft, DFG, in the context of the

project “Zwischenfall-bewusstes resilientes Verkehrs-

management f

ur urbane Straßennetze (InTURN)” un-

der grant TO 843/5-1. We acknowledge this support.

REFERENCES

Ahmed, S. and Cook, A. (1980). Time series models for

freeway incident detection. Transp. Eng. J of the Am.

Soc. of Civ. Eng., 106(6):731–745.

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems

Aimsun (2021). Aimsun Next 20 User’s Manual, Aimsun

Next 20.0.3 edition.

Bazzan, A. L. (2005). A distributed approach for coordina-

tion of trafﬁc signal agents. Autonomous Agents and

Multi-Agent Systems, 10(2):131–164.

Dudek, C., Messer, C., and Nuckles, N. (1974). Incident

detection on urban freeways. Transp. Res. Rec., 495.

Dudek, C., Weaver, G., Ritch, G., and Messer, C. (1975).

Detecting freeway incidents under low-volume condi-

tions. Transp. Res. Rec., 533:34–47.

Dusparic, I. and Cahill, V. (2009). Using distributed w-

learning for multi-policy optimization in decentralized

autonomic systems. In Proc. of 6th Int. Conf. on Au-

tonomic Computing, pages 63–64. ACM.

Ester, M., Kriegel, H.-P., Sander, J., and Xu, X. (1996).

A density-based algorithm for discovering clusters in

large spatial databases with noise. In kdd, pages 226–

231. AAAI Press.

Feng, Y., Hourdos, J., and Davis, G. (2014). Probe vehicle

based real-time trafﬁc monitoring on urban roadways.

Transp. Res. Part C: Emerging Tech., 40:160–178.

Gall, A. and Hall, F. (1989). Distinguishing between inci-

dent congestion and recurrent congestion: a proposed

logic. Transportation Research Record.

Gershenson, C. (2007). Design and Control of Self-

organizing Systems. PhD thesis, Vrije Universiteit

Brussel.

Gokulan, B. and Srinivasan, D. (2010). Distributed geomet-

ric fuzzy multiagent urban trafﬁc signal control. IEEE

Trans. on Int. Transportation Sys., 11(3):714–727.

Helbing, D., L

ammer, S., and Lebacque, J. (2005). Self-

organized control of irregular or perturbed network

trafﬁc. Optimal control and dynamic games, pages

239–274.

Jenelius, E. and Koutsopoulos, H. (2013). Travel time esti-

mation for urban road networks using low frequency

probe vehicle data. Transp. Res. Part B: Methodolog-

ical, 53:64–81.

Kamijo, S., Harada, M., and Sakauchi, M. (2004). An in-

cident detection system based on semantic hierarchy.

In Proc. of 7th Int. Conf. on Int. Trans. Sys. (ITS’04),

pages 853–858. IEEE.

Lin, W. and Daganzo, C. (1997). A simple detection scheme

for delay-inducing freeway incidents. Transp. Res.

Part A: Policy and Practice, 31(2):141–155.

Mauro, V. and Taranto, C. D. (1990). Utopia. Control,

computers, communications in transportation.

uller-Schloer, C. and Tomforde, S. (2017). Organic

Computing-Technical Systems for Survival in the Real

World. Springer.

Oliveira, L. D. and Camponogara, E. (2010). Multi-agent

model predictive control of signaling split in urban

trafﬁc networks. Transp. Res. Part C: Emerging Tech.,

18(1):120–139.

Payne, H. and Tignor, S. (1978). Freeway incident-

detection algorithms based on decision trees with

states. Transportation Research Record.

Payne, H. J. (1975). Freeway incident detection based upon

pattern classiﬁcation. In Proc. of IEEE Conf. on Deci-

sion and Control, volume 14, pages 688–692. IEEE.

Prothmann, H., Branke, J., Schmeck, H., Tomforde, S.,

Rochner, F., H

ahner, J., and M

uller-Schloer, C.

(2009). Organic trafﬁc light control for urban road

networks. Int. J. Auton. Adapt. Commun. Syst., 2(3).

Prothmann, H., Tomforde, S., Lyda, J., Branke, J., H

ahner,

J., M

uller-Schloer, C., and Schmeck, H. (2012).

Self-organised routing for road networks. In Self-

Organizing Systems - 6th IFIP TC 6 International

Workshop, IWSOS 2012, Delft, The Netherlands,

March 15-16, 2012. Proceedings, pages 48–59.

Robertson, D. and Bretherton, D. (1991). Optimizing net-

works of trafﬁc signals in real time – the SCOOT

method. IEEE Trans. on Veh. Tech., 40(1):11–15.

Shehata, M., Cai, J., Badawy, W., Johannesson, R., and

Radmanesh, A. (2008). Video-based automatic inci-

dent detection for smart roads: The outdoor environ-

mental challenges regarding false alarms. IEEE Trans.

on Int. Transp. Sys., 9(2):349–360.

Sims, A. and Dobinson, K. (1980). The Sydney coordinated

adaptive trafﬁc (SCAT) system – Philosophy and ben-

eﬁts. IEEE Trans. on Veh. Tech., 29(2):130–137.

Sommer, M., Tomforde, S., and H

ahner, J. (2013). Using

a neural network for forecasting in an organic traf-

ﬁc control management system. In 2013 Workshop

on Embedded Self-Organizing Systems, ESOS’13, San

Jose, CA, USA, June 25, 2013.

Sommer, M., Tomforde, S., and H

ahner, J. (2016a). An Or-

ganic Computing Approach to Resilient Trafﬁc Man-

agement. In Autonomic Road Transport Support Sys-

tems, pages 113–130. Birkh

auser.

Sommer, M., Tomforde, S., and H

ahner, J. (2016b).

Forecast-augmented route guidance in urban trafﬁc

networks based on infrastructure observations. In

Proc. of VEHITS’16, pages 177–186.

Stephanedes, Y. and Chassiakos, A. (1993). Freeway inci-

dent detection through ﬁltering. Transp. Res. Part C:

Emerging Technologies, 1(3):219–233.

Studer, L., Ketabdari, M., and Marchionni, G. (2015). Anal-

ysis of adaptive trafﬁc control systems design of a de-

cision support system for better choices. J Civil Envi-

ron Eng, 5(195):2.

Takaba, S. and Matsuno, H. (1985). Trafﬁc incident detec-

tion using correlation analysis. In SCS 1985 Summer

Comp. Sim. Conf., pages 529–534.

Thomsen, I. and Tomforde, S. (2022). Intersection-centric

urban trafﬁc ﬂow clustering for incident detection in

organic trafﬁc control. In Proc. of VEHITS’22.

Thomsen, I., Zapfe, Y., and Tomforde, S. (2021). Urban

trafﬁc incident detection for organic trafﬁc control: A

density-based clustering approach. In Proceedings of

the 7th International Conference on Vehicle Technol-

ogy and Intelligent Transport Systems, VEHITS 2021,

Online Streaming, April 28-30, 2021, pages 152–160.

Tomforde, S., Prothmann, H., Branke, J., H

ahner, J., Mnif,

M., M

uller-Schloer, C., Richter, U., and Schmeck, H.

(2011). Observation and control of organic systems.

In Organic Computing—A Paradigm Shift for Com-

plex Systems, pages 325–338. Springer.

Tomforde, S., Prothmann, H., Branke, J., H

ahner, J.,

uller-Schloer, C., and Schmeck, H. (2010). Possi-

Incident-Aware Distributed Signal Systems in Self-Organised Trafﬁc Control Systems

bilities and limitations of decentralised trafﬁc control

systems. In Proc. of IJCNN’10, pages 1–9.

Tomforde, S., Prothmann, H., Rochner, F., Branke, J.,

ahner, J., M

uller-Schloer, C., and Schmeck, H.

(2008). Decentralised progressive signal systems

for organic trafﬁc control. In 2008 Second IEEE

International Conference on Self-Adaptive and Self-

Organizing Systems, pages 413–422. IEEE.

Vincent, R., Peirce, J., and Webb, P. (1990). Mova trafﬁc

control manual. MOVA reports.

Willsky, A., Chow, E., Gershwin, S., Greene, C., Houpt,

P., and Kurkjian, A. (1980). Dynamic model-based

techniques for the detection of incidents on freeways.

IEEE Transa. on Automatic Control, 25(3):347–360.

Wilson, S. W. (1995). Classiﬁer Fitness Based on Accuracy.

Evolutionary Computation, 3(2):149–175.

VEHITS 2023 - 9th International Conference on Vehicle Technology and Intelligent Transport Systems