Ultra-Low Power Electronic Circuits Inspired by Biological Genetic

Processes

Ilan Oren, Raghd Abu-Sinni and Ramez Daniel

Faculty of Bio-Medical Engineering, Technion - Israel Institute of Technology, Haifa 3200003, Israel

Keywords:

Subthreshold Electronic Circuits, Analog Design, Neural Network, Molecular Network, Bio-Inspired.

Abstract:

Neuromorphic engineering, inspired by principles and architecture of neuronal circuitries, enabled the design

of Artiﬁcial Neural networks (ANNs) for Intelligent systems. These systems perform very complex computa-

tion tasks, yet they consume signiﬁcant power. Thus, using artiﬁcial intelligence (AI) for applications where

only a small power source is available is very limited. While the neuronal networks in the brain can recognize

complex patterns and memorize enormous elements, molecular and protein networks can perform other com-

plex tasks such as adaptive immunity and cell differentiation at high energy efﬁciency. Here, we claim that a

bio-inspired computing platform mimicking molecular protein networks can lead to ultra-low power emergent

computation. Previously, we proposed a molecular-inspired computing model named Perceptgene that has the

attributes of learning and adaptivity as the neural network (Rizik et al., 2022). Similarities were found be-

tween equations describing biochemical reactions and transistor operation at subthreshold (Sarpeshkar, 2011)

enabling the design of Perceptgene with subthreshold electrical circuits. Thus, the subthreshold Perceptgene

circuits are expected to allow computing and learning capabilities at ultra-low power consumption.

1 INTRODUCTION

Biological neural systems are comprised of remark-

able parallel and distributed computing networks with

adaptive, self-repairing, and replicative capacities in

the performance of real-world tasks. Scientists and

engineers have been inspired to mimic these features

when designing artiﬁcial intelligence systems. Neu-

romorphic computing (Mead, 1990) applies abstract

models of neural systems, such as the perceptron

(Haykin, 2004), and uses microelectronics to build

artiﬁcial intelligent machines. Today, the world is in-

creasingly dependent upon this artiﬁcial intelligence

(AI) and machine learning (ML) systems in several

ﬁelds. Among these ﬁelds are health and ﬁnance, face

and object recognition, command of autonomous ve-

hicles, speech recognition, and natural language pro-

cessing. However, the power consumption of cur-

rent deep-learning machines and ‘layered neural net-

works’ is one of the most challenging limitations

of these systems. The steep increase in their en-

ergy consumption and the computing power required

for training them, which has grown 300,000-fold be-

tween 2012-18, are both unsustainable, putting sub-

stantial applications beyond the reach of all but well-

resourced organizations. While the brain can perform

sophisticated information processing by employing

complex neuronal circuit topologies with highly inter-

connected nodes, molecular biological systems con-

tain extensively noisy parts that collectively interact

to solve parallel tasks online with high energy efﬁ-

ciency. A single cell in the body, for example, per-

forms 10 million energy-consuming biochemical op-

erations per second on its noisy molecular inputs at

1pW of average power (Sarpeshkar, 2010). In this

study, we propose ultra-low power electronic cir-

cuits inspired by gene networks to demonstrate

the computational abilities of neuronal networks.

This approach relies on insights we have gained

that map neuronal networks to molecular biologi-

cal systems (biomorphic (Rizik et al., 2022) (Daniel

et al., 2013)) and then to electronic circuits (cyto-

morphic (Sarpeshkar, 2011) (Hanna et al., 2020) ),

as shown in Fig. 1. The proposed computational ap-

proach is realized by building subthreshold electronic

circuits mimicking molecular networks based on the

Perceptgene model [1]. We anticipate that subthresh-

old Perceptgene circuits will enable the implementa-

tion of an adaptive system with ultra-low power com-

putation abilities.

150

Oren, I., Abu-Sinni, R. and Daniel, R.

Ultra-Low Power Electronic Circuits Inspired by Biological Genetic Processes.

DOI: 10.5220/0011707800003414

In Proceedings of the 16th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2023) - Volume 1: BIODEVICES, pages 150-156

ISBN: 978-989-758-631-6; ISSN: 2184-4305

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

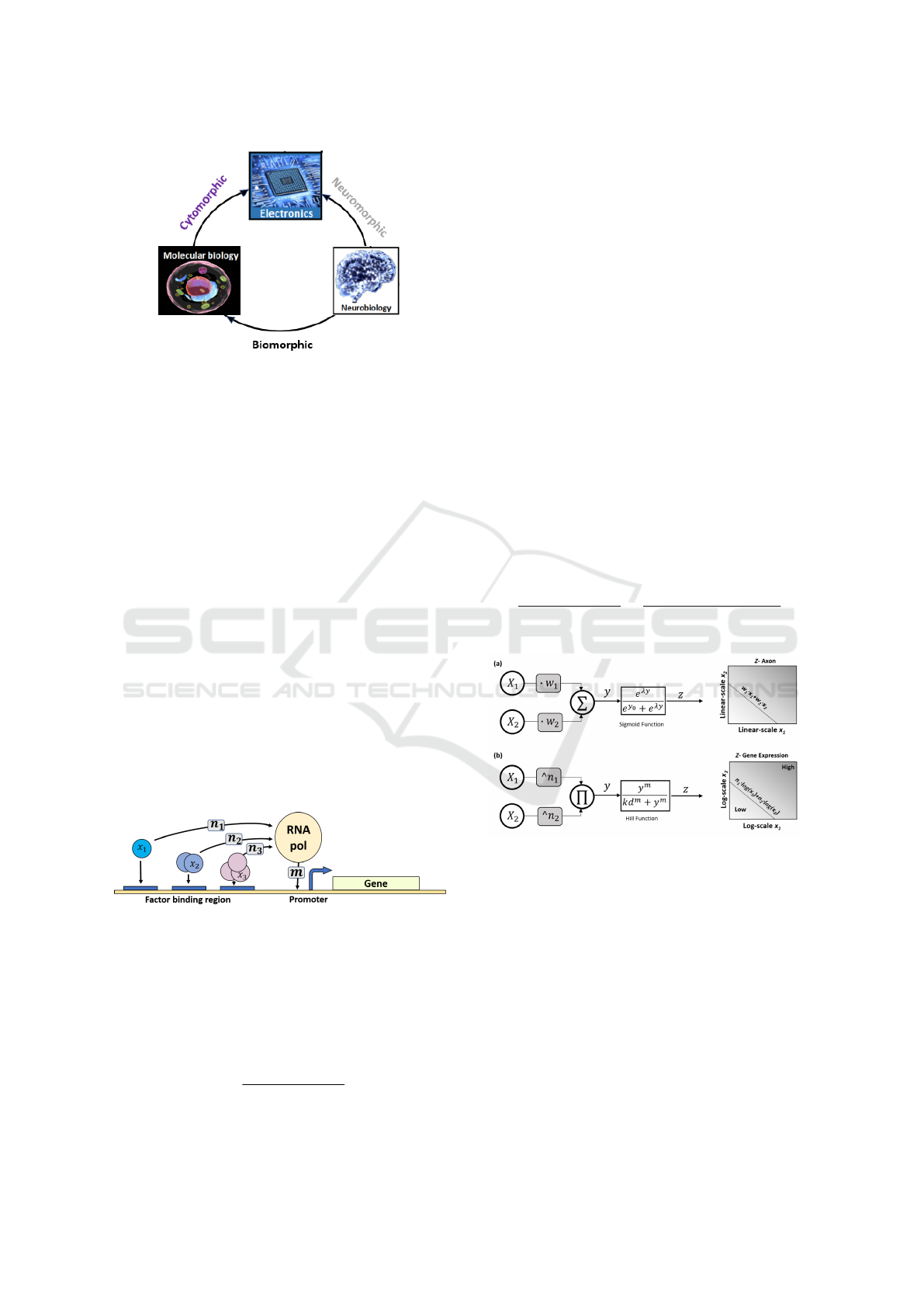
Figure 1: From Biomorphic to cytomorphic. Biomorphic:

implementation of neural networks into synthetic molecu-

lar networks. Cytomorphic: implementation of molecular

networks into electronics. Neuromorphic: implementation

of the neural network into electronics.

2 BIO-MOLECULAR ”NEURON”

Our neural model was inspired by combinatorial gene

regulation kinetics of promoter activation (Fig. 2) . A

combinatorial promoter is regulated by multiple tran-

scription factors x

, each transcription factor binds to

its designated region and afterward participates in re-

cruiting the RNA polymerase to form the activation

complex. In our model, several biological parame-

ters are involved, such as the biological cooperativ-

ity of proteins, the number of binding sites in the

promoter, the protein quaternary structure, and the

binding afﬁnities of protein-protein/protein-DNA re-

actions. In this process, multiple transcription factors

participate and bind upstream to a gene sequence. To-

gether they facilitate the binding of RNA polymerase

to the promoter region forming the activation complex

which initiates gene transcription.

Figure 2: Anatomy structure of operating principles of gene

regulatory network.

For a combinatorial activation, the relation be-

tween the transcription factors concentration and the

promoter transcription rate, under certain conditions

(Bintu, 2005), can be simpliﬁed and modeled as fol-

lows:

P =

(

∏

)

(

∏

)

+ kd

(1)

Where P is the activation rate, x

is the transcrip-

tion factor concentration, n

is the Hill coefﬁcient of

transcription factor i associated with the activation

complex formation, m is the Hill coefﬁcient for the

binding of the activation complex with the promoter

and kd is the dissociation constant for the complex

binding with the promoter.

By applying a logarithmic transform to Eq. 1, we

obtain a new abstract model analogous to the percep-

tron model that is used in artiﬁcial neural networks

(Fig. 3a). Similar to other artiﬁcial neuron models that

operate as binary classiﬁers, this model achieves clas-

siﬁcation via a weighted input integration followed by

a threshold activation for the output. However, three

notable differences exist. First, the weighing of the

inputs is done here according to a power law and not

multiplication. Second, the inputs are integrated via a

product rather than a summation. And third, the ac-

tivation function used for this model is the Hill equa-

tion instead of the standard logistic function. Inter-

estingly the perceptgene model can be viewed as a

perceptron (Fig. 3) with a log transform over its input

dynamic range, the proof is straightforward from the

following equality:

P =

(

∏

)

(

∏

)

+ kd

∑

Ln(x

)

∑

Ln(x

)

+ e

mLn(kd)

(2)

Figure 3: Abstract artiﬁcial intelligence models for (a) per-

ceptron inspired by neural networks: x

are the inputs, w

are

multiplicative weights, input integration is done via sum-

mation, and the activation function is the sigmoid function.

Depicted on the right is the resulting linear separable clas-

siﬁcation of the analog inputs x1 and x2 (b) perceptgene

inspired by genetic networks: x

are the inputs, n

are power

weights, input integration is done via a product, and the acti-

vation function is the Hill equation. Depicted on the right is

the resulting logarithmically separable classiﬁcation of the

analog inputs x1 and x2.

Ultra-Low Power Electronic Circuits Inspired by Biological Genetic Processes

151

3 PERCEPTGENE CIRCUIT

CONCEPT

Analogous to perceptron implementation using ana-

log linear circuits (e.g., resistors), we implement

the Perceptgene using analog logarithmic circuits.

Speciﬁcally, we use translinear analog circuits

(Gilbert, 1975) with MOSFET transistors operating

at the subthreshold region. The circuits implement

power-law and multiplication functions for the input

signals, while a nonlinear activation function circuit

generates the output result. The proposed analog cir-

cuit for implementing the Perceptgene model as can

be seen in Fig. 3b includes three subcircuits: 1. Power

circuit – to implement the power (n1, n2) function

over X1, X2 inputs 2. Multiplication circuit – to mul-

tiply the output of the power circuits 3. Activation

function – a decision-making circuit based on the Hill

equation

The analog subcircuits are translinear circuit that

operates at the subthreshold region. The operation at

the subthreshold region ensures that the current of the

transistors depends exponentially on the voltage be-

tween the gate and the source of the transistor (Eq. 3).

The translinear circuits follow the Trans Linear Prin-

ciple (TLP) which refers to the summation of volt-

ages with exponential dependency over closed loops.

On these circuits, the product of the currents through

the clockwise Translinear Elements (TEs) equals the

product of the currents through the counter-clockwise

TEs (Eq. 4). The usage of translinear subthreshold

circuits enables us to implement the arithmetic func-

tion needed for Perceptgene at ultra-low power.

Ids = I

· Exp

−V

)

(3)

Cw{π(I

)} = CCw{π(I

)} (4)

3.1 Multiplication Circuit

The purpose of the multiplication circuit is to imple-

ment the multiplication function between the outputs

of the power circuits. An illustration of the proposed

translinear subthreshold analog circuit for implement-

ing the multiplication can be viewed in Fig. 4. Since

all the transistors operate in the subthreshold region,

the current through them is exponentially inﬂuenced

by their gate-source voltage. According to KVL, the

voltages of the transistors sums up over a closed loop.

The log summation of the voltages over a closed-loop

turns into a multiplication of currents (Eq.5) as ex-

pected according to the TLP. Thus, for input currents

I1,I2, and a constant current I3 we get the required

functionality.

Figure 4: Multiplication subthreshold translinear circuit.

−V

= 0

ln(I1) +ln(I2) − ln(I3) − ln(I4) = 0

I4 =

I1 ∗ I2

(5)

Spice sweep simulations (Fig. 5) with I3=100pA

and a I1, I2 varying from 100pA to 500pA resulted

in the expected behavior of multiplication between I1

and I2.

Figure 5: Multiplication circuit simulations.

3.2 Power Circuit

The goal of the power circuit is to implement the

power (n1, n2) function over the input signals X1 and

X2. An illustration of the proposed translinear sub-

threshold analog circuit which implements the power

function can be viewed in Fig. 6.

The power circuit is similar to the multiplication

circuit except for the resistors (R1, R2) which are con-

nected to the device’s gates. These resistors are con-

nected as voltage dividers and thus deﬁne the Vgs of

the transistors (Eq. 6). The relation between these re-

sistors will be used to deﬁne the power constant n1,

n2 (Eq. 7)

BIODEVICES 2023 - 16th International Conference on Biomedical Electronics and Devices

152

Figure 6: Power subthreshold translinear circuit.

V gs = V ∗

R1 + R2

(6)

n =

R1 + R2

(7)

Due to the operation in the subthreshold region,

the current is an exponential function of the Vgs volt-

age which is set by the ratio of the resistors. Thus we

get a voltage that is a function of the power (n) of the

current (Eq. 8)

V = ln(Ids

) (8)

Summation of the voltages over a closed loop and

a constant reference current (I1, I3) will then give the

power (n) dependency between the input (I2) and the

output (I4) currents (Eq. 9) as required.

I4 = I1 ∗ (

)

I4 = (

) (9)

Spice sweep simulations (Fig. 7) with I3=200pA

, I1=100pA and Iin varying from 50pA to 500pA re-

sulted in the expected behavior of a power function

for different n values.

Figure 7: Power circuit simulations.

To insure minor currents through the voltage di-

viders the value of the resistors (R1,R2) should be

extremely high. The ability to design Giga ohms

pseudo-resistors using transistors was already demon-

strated ((Kassiri et al., 2013), (Puddu et al., 2016)).

Our implementation of the voltage dividers might also

include transistors or capacitors instead of resistors as

can be viewed in Fig. 8 and Fig. 9 below.

Figure 8: Transistors Voltage dividers.

The transistors implementation of the voltage di-

vider (Fig. 8) includes transistors that operate at a

subthreshold region and thus demonstrate huge resis-

tivity. For deep subthreshold or cut-off connectivity

where Vgs=0 the resistance can get to hundreds of

Giga Ohms. The sizes of these transistors which are

connected in series will deﬁne the exact amount of

voltage divider which is implemented. The main chal-

lenge of this implementation is its sensitivity due to

the exponential dependency of the current and thus

the resistance in threshold voltage Vt.

Figure 9: Capacitors Voltage dividers.

The capacitors implementation of the voltage di-

vider (Fig. 9) includes capacitors that are connected

in series. The capacitors are charged to different volt-

age values based on their capacitance thus creating

a voltage divider with 0 dc current as required. The

main challenge of this implementation is the need to

deal with the dynamic behavior of the divider which

might require extra switches for discharging the ca-

pacitors. On both implementations of the voltage di-

vider, the n power coefﬁcient of the circuit will be

tuned by changing the capacitor or transistor sizes.

3.3 Activation Function Circuit

The Activation Function (AF) Circuit is a decision-

making circuit implementing the Hill function (Eq. 1)

and it generates the result based on multiplication cir-

cuit output. The nonlinear activation function circuit

previously suggested in (Daniel et al., 2011) is based

on a differential ampliﬁer and 2 current mirrors as il-

lustrated in Fig. 10.

Due to the symmetry of the circuit and the current

Ultra-Low Power Electronic Circuits Inspired by Biological Genetic Processes

153

Figure 10: Activation function circuit.

mirrors, the ratio of the currents can be deﬁned by

(Eq. 10) The total current (It) of the differential pair

is the summation of the currents on its branches and

thus we get an output current (Eq. 11) which follow

the Hill equation.

(10)

I t = I2 + I4

I2 = It ∗

I1 + I3

(11)

The output current I2 is a nonlinear function of

input current I1. When operated on the log scale we

get the sigmoid activation function described in Eq.

12 below.

I2 = It ∗

Ln(I1)

+ e

Ln(I3)

(12)

Fig. 11 shows the spice simulation results of the

circuit. In that simulation, I1 varying from 10pA to

1nA (while It=500pA, I3=100pA) and the result in

the log domain shows the expected sigmoid behavior.

Figure 11: Activation circuit simulations.

3.4 Full Perceptgene Circuit

The circuits described in the previous sections were

integrated into the full Perceptgene circuit as can be

seen in Fig. 12 below. The full Perceptgene circuit

includes 2 power function circuits a multiplier and an

AF circuit. The 2 input currents Iin1 and Iin2 are be-

ing processed by the circuit to generate the output cur-

rent Iout. The Weights of the Perceptgene can be con-

ﬁgured by changing the voltage dividers values and

the Bias can be conﬁgured by changing the Iref cur-

rent of the multiplier.

Figure 12: Full Perceptgene circuit.

As expected, due to its subthreshold operation,

simulations of the circuit resulted in ultra-low power

consumption ranging from a few to hundred nano

Watts depending on the inputs and usage.

4 BASIC CLASSIFIER AND ANN

IMPLEMENTATION

To build an ANN network, the perceptgene circuit

needs to demonstrate its classiﬁcation capabilities.

Thus basic classiﬁers were implemented using a sin-

gle neuron ANN realized by perceptgene circuit (Fig.

13).

Figure 13: Single neuron classiﬁer.

The ﬁrst single perceptgene classiﬁers imple-

mented two inputs OR/AND logic functions. Those

functions were created by conﬁguring the weights

(R1, R2) and the bias (Irefm) of the perceptgene cir-

cuit. The following simulation results in Fig. 14 show

that the circuit function as AND classiﬁer when using

the correct weights.

Spice simulation results of a perceptgene circuit in

which the weights and bias were set to create an OR

BIODEVICES 2023 - 16th International Conference on Biomedical Electronics and Devices

154

Figure 14: Two inputs AND simulations.

function can be viewed in Fig. 15 below.

Figure 15: Two inputs OR simulations.

From a single perceptgene classiﬁer we move to

a multi-layer ANN implementation. An example of

such ANN can be viewed in Fig. 16. The three inputs

ANN includes three perceptgene cells organized in

two layers to implement the majority function when

the correct weights (n1-n8) are set. The majority

function is a logic function in which its output is

high when the majority of its inputs are high. Find-

ing the weights (n1-n8) which will enable the ANN

to execute the majority function required the use of

a Back-Propagation Gradient-Descend (BPGD) algo-

rithm. Due to differences between the perceptron and

the perceptgene a special version of the BPGD algo-

rithm was developed.

Figure 16: Three inputs Majority ANN.

In the Back-Propagation Gradient-Descend algo-

rithm, the inputs are fed to the ANN and the weights

are tuned based on the difference between the actual

result at its output vs. the expected result. The al-

gorithm search for the required weights of the ANN

which provide the minimum error as can be viewed in

Fig. 17.

The BPGD algorithm was tuned to operate in the

log domain to ﬁt the perceptgene operation. Thus the

LOG of the error is calculated as can be viewed in Eq.

13.

Error = 1/2 ∗ Log(

Out put

Actual

Out put

Expected

)

(13)

The tuned BPGD algorithm was used successfully

Figure 17: Gradient descends algorithm.

to build a few other multi-layer ANN which imple-

ments logic functions such as Muxes and full-adders.

5 CONCLUSION

We propose ultra-low power electronic circuits in-

spired by gene networks to demonstrate the compu-

tational abilities of neural networks. These circuits

were implemented using MOSFET devices operat-

ing at the sub-threshold region. Basic training abil-

ities for two and three inputs perceptgene networks

were demonstrated. This study presents an energy-

efﬁcient bio-inspired platform that allows ANN com-

puting with learning capabilities

ACKNOWLEDGEMENTS

We gratefully acknowledge the ﬁnancial support by

the Israel Ministry of Science (MOS) through grant

3-14364

REFERENCES

Bintu, L. (2005). Transcriptional regulation by numbers:

models. Curr Opin Genet.

Daniel, R., Rubens, J., Sarpeshkar, R., and Lu, T. (2013).

Synthetic analog computation in living cells. Nature.

Daniel, R., Woo, S., Turicchia, L., and Sarpeshkar, R.

(2011). Analog transistor models of bacterial genetic

circuits. IEEE biomedical circuits and systems con-

ference (BioCAS).

Gilbert, B. (1975). Translinear circuits: a proposed classiﬁ-

cation. Electron Lett.

Hanna, H., Danial, L., Kvatinsky, S., and Daniel, R. (2020).

Cytomorphic electronics with memristors for model-

ing fundamental genetic circuits. IEEE Transactions

on Biomedical Circuits and Systems.

Haykin, S. (2004). Neural networks: A comprehensive

foundation. Pearson Education.

Kassiri, H., Abdelhalim, K., and Genov, R. (2013). Low-

distortion super-gohm subthreshold-mos resistors for

cmos neural ampliﬁers. Biomedical Circuits and Sys-

tems Conference (BioCAS).

Ultra-Low Power Electronic Circuits Inspired by Biological Genetic Processes

155

Mead, C. (1990). Neuromorphic electronic systems. Proc

IEEE.

Puddu, R., Carboni, C., Bisoni, L., Barabino, G., D.Pani,

L.Raffo, and Barbaro, M. (2016). A precision pseudo

resistor bias scheme for the design of very large time

constant ﬁlters. IEEE Transactions on Circuits and

Systems.

Rizik, L., Danial, L., Habib, M., Weiss, R., and Daniel, R.

(2022). Synthetic neuromorphic computing in living

cells. Nature communications.

Sarpeshkar, R. (2010). “the big picture: Ultra-low power in-

formation processing in biology. In Ultra Low Power

Bioelectronics. Cambridge University Press.

Sarpeshkar, R. (2011). “cytomorphic electronics: cell-

inspired electronics for systems and synthetic biology.

In Ultra Low Power Bioelectronics. Cambridge Uni-

versity Press.

BIODEVICES 2023 - 16th International Conference on Biomedical Electronics and Devices

156