Time-Constrained, Event-Driven Coordination

of Composite Resources’ Consumption Flows

Zakaria Maamar

1 a

, Amel Benna

2 b

and Nabil Otsmane

College of Computing and IT, University of Doha for Science and Technology, Doha, Qatar

Department of Multimedia and Information Systems, CERIST, Algiers, Algeria

High School of Computer Science, Algiers, Algeria

Keywords:

Allen’s Time Algebra, Composite Resource, Consumption Flow, Event Driven, Time Constraint.

Abstract:

This paper discusses the composition of primitive resources in preparation for their run-time consumption by

business processes. This consumption is ﬁrst, subject to time constraints impacting the availability of primitive

resources and second, dependent on events impacting the selection of primitive resources. To address prim-

itive resources’ disparate time-availabilities that could lead to conﬂicts, a coordination approach is designed,

developed, and tested using Allen’s time algebra and a simulated dataset. The approach produces composite

resources’ consumption ﬂows on-the-ﬂy after discovering time relations between primitive resources that en-

sure their availabilities and hence, assignment to business processes. Implementation results demonstrate the

technical doability of the approach along with identifying time-related obstacles that could prevent primitive

resources’ availabilities. Solutions addressing these obstacles are also reported in the implementation results.

1 INTRODUCTION

In (Maamar and Al Khafajiy, 2021) and (Maamar

et al., 2021), we discuss the concepts of resource,

consumption of resource, consumption property, con-

sumption cycle, and disruption, and exemplify all

these concepts with cloud computing. The discus-

sions demonstrated the importance of a coordinated

consumption of resources in a multi-job environment

since the continued availability of resources is not

always guaranteed (Dimick, 2014); some are scare

while others decline. Example of resource would

be virtual machine, example of consumption prop-

erty would be limited-but-extensible, example of dis-

ruption would be urgent upgrade of a virtual ma-

chine, and, last but not least, example of job would

be order delivery. Assumption made in (Maamar and

Al Khafajiy, 2021) and (Maamar et al., 2021) is that

a job would consume one resource at a time, which is

not always the case in real life. A job like order deliv-

ery, again, would consume processing power/CPU to

run programs, storage capacity/database to store data,

and bandwidth/router to communicate data. By drop-

ping this assumption in the sense that a job would now

https://orcid.org/0000-0003-4462-8337

https://orcid.org/0000-0002-9076-5001

consume many resources, this means specializing re-

source into primitive and composite.

By analogy with tasks and component Web ser-

vices that are put together to form business pro-

cesses (Weske, 2012) and composite Web ser-

vices (Langdon, 2003), respectively, a composite re-

source would line up a set of primitive, and even

composite, resources that would be consumed accord-

ing to speciﬁc events that would arise and speciﬁc

functional and non-functional characteristics that jobs

would have. However, lining up several primitive

resources would require considering their respective

availability times. For instance, a primitive resource is

available between 2pm and 4pm, only, while another

is available after 10min from the complete consump-

tion of a group of primitive resources. How to coordi-

nate the consumption of composite resources accord-

ing to their primitive resources’ availability times is a

concern that we address in this paper.

In conjunction with achieving a time-constrained,

event-driven coordination of composite resources, the

impact of primitive resources’ consumption proper-

ties on composite resources’ availability times could

hinder this coordination. Specialized into unlimited,

limited, limited-but-extensible, shareable, and non-

shareable as per our work in (Maamar et al., 2016),

consumption properties could for instance, impose

Maamar, Z., Benna, A. and Otsmane, N.

Time-Constrained, Event-Driven Coordination of Composite Resources’ Consumption Flows.

DOI: 10.5220/0011711900003464

In Proceedings of the 18th International Conference on Evaluation of Novel Approaches to Software Engineering (ENASE 2023), pages 52-63

ISBN: 978-989-758-647-7; ISSN: 2184-4895

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

extending the availability times of some primitive re-

sources at the expense of others so that the consump-

tion of the composite resource as a whole completes

successfully. How to perform this extension without

initiating conﬂicts is another concern that we address

in this paper, as well.

To address both concerns, we resort to Allen’s

time algebra (Allen, 1983). The objective is to iden-

tify potential time-interval relations between the re-

spective availability times of primitive resources par-

ticipating in the same composite resource. Allen’s

algebra offers an exhaustive coverage of possible re-

lations between time intervals along with the possi-

bility of reasoning over these relations. Examples

of relations include equals, overlaps, starts, and dur-

ing. Our objective is to achieve a time-constrained,

event-driven coordination of composite resources that

would be sensitive to both availability times of and

consumption properties of primitive resources. Our

contributions are, but not limited to, (i) identiﬁca-

tion of potential time-interval relations between prim-

itive resources’ availability times using Allen’s time

algebra, (ii) analysis of the impact of consump-

tion properties on primitive resources’ availability

times, (iii) on-the-ﬂy deﬁnition of consumption ﬂows

of composite resources based on their primitive re-

sources’ availability times and consumption proper-

ties, and (iv) demonstration of consumption ﬂows

through a case study and system. The rest of this

paper is organized as follows. Section 2 is a sum-

mary of some related works. Section 3 deﬁnes the

concepts of resource and their consumption properties

and also refers to a running example used for illustra-

tion purposes. Section 4 provides a temporal analysis

of these consumption properties prior to detailing the

approach for coordinating the consumption of primi-

tive resources in Section 5. This approach’s technical

details and concluding remarks are reported in Sec-

tions 6 and 7, respectively.

2 RELATED WORK

In the research community, resource management in

business processes is commonly studied. In this sec-

tion, we discuss this management in terms of re-

source allocation and composition. In (Stefanini et al.,

2020), Stefanini et al. propose a process mining-

based approach to support resource planning of health

services. They combine techniques like time-driven

activity-based costing and process mining to identify

and analytically evaluate tasks, service times, and re-

source consumptions for speciﬁc medical conditions.

For the needs of process mining, the approach uses an

event log to estimate the expected resource consump-

tions of each medical intervention.

In (Maamar et al., 2022), Maamar et al. deﬁne

an approach for coordinating the consumption of re-

sources by business processes’ tasks. The approach

takes into account both resources’ properties like un-

limited and limited-but-extensible and tasks’ transac-

tional properties like pivot and compensatable. On

top of these properties, the approach adopts Allen’s

time algebra and uses historical details about past ex-

ecutions stored in an event log to coordinate resource

consumption. In (Arias et al., 2015), Arias et al. pro-

pose a process mining-based recommendation frame-

work to allocate resources to sub-processes instead

of individual tasks. The framework uses a set of

criteria related to resource’s capabilities, resource’s

workload, necessary expertise to perform tasks, and

event log that encompasses details about previous ex-

ecutions. Mixing these criteria allowed recommend-

ing the top-ranked resources to a sub-process based on

the best position algorithm (Akbarinia et al., 2011).

In (Park and Song, 2019), Park and Song

build upon the results of predictive process monitor-

ing to improve business processes especially resource

allocation. To optimize this allocation, the authors use

Long Short-Term Memory (LSTM) to predict the pro-

cessing time of each task and next task of an ongoing

process instance. These details (i.e., processing time

and next task) are exploited to allocate resources to

tasks thanks to a minimum cost and maximum ﬂow

algorithm. In (Sindhgatta et al., 2016), the authors

propose a context-based approach for making deci-

sions about resource allocation to tasks. The approach

relies on historical data, process context, and perfor-

mance of past instances all stored in an event log to

predict the performance of under-execution process

instances. Resources allocated to these instances are

taken care by k-Nearest Neighbor technique.

In (Zhao et al., 2016), Zhao et al. analyze re-

source allocation to a business process’s tasks as a

multi-criteria decision making problem. The rec-

ommendation of resources to a BP’s tasks considers

both resource characteristics and task preference pat-

terns established based on past executions. To un-

cover these patterns, the authors adopt an entropy-

based clustering ensemble method. In addition, they

provide dynamic resource allocation for concurrently

running process instances. In a recent work (Zhao

et al., 2020), Zhao et al. address the problem of hu-

man resources allocation using team faultlines. First,

resources’ characteristics are described from demo-

graphic and past execution perspectives. Then, this

faultline is identiﬁed and measured using various

characteristics and multiple subgroups. Finally, a

Time-Constrained, Event-Driven Coordination of Composite Resources’ Consumption Flows

neural network is used to achieve the allocation.

The paragraphs above reveal that resource alloca-

tion problem in business processes is timely based on

the different techniques that aim at optimizing this al-

location. Our approach is in line with what the re-

search community’s efforts with focus on resource

composition according to these resources’ time avail-

abilities and consumption properties. To synchro-

nize these availabilities along with these properties,

Allen’s time algebra is used permitting to form what

we refer to as consumption ﬂows.

3 BACKGROUND

This section deﬁnes the concept of resource, presents

a running example, and ﬁnally discusses consumption

properties of resources and Allen’s time Algebra.

Resource Deﬁnition. The concept of resource is

not new in the literature and has been adopted

in different domains like distributed artiﬁcial intel-

ligence (e.g., resource logic for multi-agent plan-

ning (de Weerdt and Clement, 2009)), service com-

puting (e.g., RDF for interoperability (Schreiber and

Raimond, 2014) and REST for building applica-

tions (Web, Intranet, and Web services) (Fielding,

2000)), cloud computing (abstracting hardware and

software (Mell and Grance, 2011)), and business pro-

cesses (persons/machines executing tasks (Fielding,

2000)). From a broad perspective, Baker et al. spe-

cialize resources into computational, consumed, and

produced, associating each type with a separate life-

cycle that would capture the resource’s behavioral

and operational characteristics (Baker et al., 2018).

In (Lucchim et al., 2008), Lucchim et al. consider re-

sources as “directly-accessible components handled

through a standard common interface”. The interface

could be a set of stateless operations like HTTP meth-

ods. Finally, Hofman adopts everything-as-a-resource

to build seamless interoperable platforms in the world

of IoT (Hofman, 2015). Each resource (e.g., truck and

smart object) has goals and capabilities and may have

an owner, user, and virtual representation.

Running Example. It is about John who is visiting

Melissa in Paris. One day they decide to meet in

a coffee shop, not far from Melissa’s ofﬁce. John

can reach the coffee shop by either taxi or bus. We

adopt Web services consuming on-premise and in-

the-cloud resources to suggest a high-level descrip-

tion of the job completing John scenario (Fig. 1).

At the hotel, John browses some transportation Web

sites about Paris. One running Itinerary WS and

hence, consuming processing power, proposes routes

between places. While checking the weather fore-

cast using Weather WS, Itinerary WS requests details

about the origin and destination places using Loca-

tion WS that accesses a dedicated database. Should

Weather WS return bad weather, Itinerary WS would

instruct Taxi WS to book a taxi for John. Otherwise,

Itinerary WS would send the location of both John’s

hotel and the coffee shop to Bus WS, which advises

about the bus numbers that John should ride. Potential

trafﬁc jams would make Bus WS interact with Traf-

ﬁc WS, should the bus numbers need to be adjusted.

Bus WS

Location WS

Weather WS

Taxi WS

Traffic WS

weather?

Itinerary WS

Component (WS) level

Resource level

Programs CloudsDatabasesServers

Figure 1: Speciﬁcation of the job handling John scenario.

From a consumption perspective, on-premise and

in-the-cloud resources would be associated with nec-

essary consumption properties as their owners see ﬁt.

For instance, databases could be non-shareable for

concurrent Web services so that consistency is en-

forced, and servers hosting virtual machines could

be limited-but-extensible for long-running Web ser-

vices so that a balanced load over the servers is main-

tained. Besides the consumption properties, the re-

sources could have availability times that need to

be considered, too. For instance, backup databases

are activated concurrently everyday after midnight for

3 hours, and servers hosting virtual machines are sus-

pended sequentially once a week for 2 hours for main-

tenance. Both consumption properties and availabil-

ity times of resources would have an impact on com-

pleting the job above.

Consumption Properties of Primitive Resources. In

compliance with our previous work on social co-

ordination of business processes (Maamar et al.,

2016), the consumption properties of a primitive re-

source (P R ) could be unlimited (u), shareable (s),

limited (l), limited-but-extensible (lx), and non-

shareable (ns). First, a primitive resource is limited

when its consumption is bound to an agreed-upon

time period (capacity, too, like 20 liters, but not con-

sidered in this work). Second, a primitive resource

is limited-but-extensible when its consumption con-

tinues to happen after extending the (initial) agreed-

upon time period. Finally, a primitive resource is non-

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

shareable when its concurrent consumption needs to

be coordinated (e.g., one at a time). A primitive re-

source is by default unlimited and/or shareable. The

set of all consumption cycles (CC) of the 5 properties

are captured into Fig. 2. However, only 2 consump-

tion cycles are listed for illustration purposes.

1. Unlimited property: P R .cc

: not-made-

available

start

−→ made available

waiting−to−be−bound

−→

not-consumed

consumption−approval

−→ consumed

no−longer−use f ul

−→ withdrawn.

2. Limited-but-extensible property: P R .cc

not-made-available

start

−→ made avail-

able

waiting−to−be−bound

−→ not-consumed

consumption−approval

−→ consumed

consumption−update

−→

done

renewable−approval

−→ made available. The

transition from done to made available allows a

resource to be regenerated for another cycle of

consumption.

Deﬁnition 1. A primitive resource P R is deﬁned

by the tuple < id, name, period, cp, cc

> where id

is the identiﬁer of the primitive resource, name is

the name of the primitive resource, period is the

availability-time interval [b, e] of the primitive re-

source where b and e stand for begin-time and end-

time, cp is the consumption property of the primi-

tive resource as either u, s, l, lx, or ns, and cc

the consumption cycle of the primitive resource ac-

cording to its consumption property and is deﬁned

by the tuple < S, T, S

active

>, i.e., cc

= s

trans

−→

i+1

trans

i+1

−→ s

i+2

. . . s

j−1

trans

j−1

−→ s

where S is the set

of states {s

} where s

is either not-made-available,

consumed, locked, etc. (Fig. 2), T is the set of tran-

sitions {trans

} where trans

is either consumption-

approval, consumption-update, etc. (Fig. 2), and

active

⊂ S is the set of states that have been enabled

since the activation of the consumption cycle. At ini-

tialization time, S

active

= {not-made-available}.

Allen’s time algebra. Table 1 presents some po-

tential relations (in fact, there exist 13) between time

intervals, i.e., pairs of endpoints, allowing to support

multiple forms of temporal reasoning like what to do

when 2 time intervals start/end together, when a time

interval falls into another time interval, etc. (Allen,

1983). In Allen’s time algebra, each relation is la-

beled as either distinctive, exhaustive, or qualita-

tive. Typical applications of Allen’s time algebra in-

clude planning and scheduling, natural language pro-

cessing, temporal databases, workﬂows, to cite just

some (Janhunen and Sioutis, 2019).

Table 1: Some Allen’s time-interval relations.

x y

time

x

y

x precedes y x equals y

x

y

time

y

x

time

x overlaps y x during y

4 TEMPORAL ANALYSIS OF

CONSUMPTION PROPERTIES

When tracking the consumption of a primitive re-

source (P R

) by a job (J

) from a time-interval

perspective, this consumption, that could happen

many times, i.e., 1[con

=1,...

]∗, would depend on the

primitive resource’s both consumption property and

availability-time interval and would allow to deﬁne

what we refer to as the job’s consumption-time inter-

vals (when the consumption has effectively occurred).

To track how a job consumes a primitive resource, we

proceed as follows:

1. Unlimited, limited, and limited-but-extensible

primitive resources, we associate them with

speciﬁc availability-time intervals, P R

[b, ∞[,

P R

[b, e], P R

[b, e 0[+δ]∗], where b, e, and δ

stand for begin-time, end-time, and extra-time (re-

peated but not indeﬁnitely), respectively.

2. Shareable and non-shareable primitive re-

sources, we either tolerate or not their con-

current consumption (con

, con

′

, . . . ) by

separate jobs (J

, J

, . . . ) during the respective

availability-time intervals of these primi-

tive resources, e.g., J

P R

con

, e

con

] ⊆

P R

[b, e] ∧ J

P R

con

′

, e

con

′

] ⊆ P R

[b, e] and

con

== b

con

′

3. Unlimited primitive resources, we allow them to

accommodate any job’s multiple consumption re-

quests (con

, con

, . . . ) during their availability-

time intervals.

To illustrate the 3 cases above, Table 2 refers to 3 jobs,

, J

, and J

, and their respective consumption of

resources for instance, J

’s con

, J

’s con

21,22

, and

’s con

31,32,33,34

. We now discuss the impact of lim-

ited and limited-but-extensible consumption proper-

ties on a primitive resource’s availability-time interval

using the same table.

1. Limited property means that a primitive re-

source’s availability-time interval that is set

Time-Constrained, Event-Driven Coordination of Composite Resources’ Consumption Flows

start

Locked

lock

consumption

approval

Unlocked

release

Not made

available

renewable approval

Made available

waiting

to be bound

Not consumed

consumption

update

consumption

rejection

Withdrawn

Done

consumption

completion

no-longer

useful

Initial state

End state

Entry-point state

Legend

consumption update

consumption

approval

Consumed

Figure 2: Primitive resource’s consumption cycle as a state diagram (Maamar et al., 2016).

Table 2: Availability-time interval versus Consumption-time interval.

b e

con 

11

con 

21

con 

31

con 

41

availability

time

consumption

time

con 

22

b e

con 

11

con 

21

con 

12

con 

31

con 

32

con 

33

con 

34

availability

time

consumption

time

extended

availability time

(a) limited P R (b) limited-but-extensible P R

at design-time, P R

[b, e], remains the same

at run-time despite the requests for additional

consumption that this primitive resource would

receive from the same jobs (after these jobs’

respective ﬁrst consumption). A job requesting

to consume a limited primitive-resource is con-

ﬁrmed iff the job’s ﬁrst consumption-time interval

falls into the primitive resource’s availability-time

interval (e.g., J

P R

con

, e

con

] ⊂ P R

[b, e] in

Table 2 (a) where b

con

> b and e

con

< e)

and, then, any additional consumption-

time intervals must fall into the primitive

resource’s same availability-time interval

(e.g., J

P R

con

, e

con

] ⊆ r

[b, e] in Table 2 (a)

where b

con

== e

con

and e

con

== e).

2. Limited-but-extensible property means that a

primitive resource’s availability-time interval that

is set at design-time, P R

[b, e], can be adjusted

at run-time, P R

[b, e 0[+δ]∗], so that the requests

for additional consumption that this primitive re-

source would receive from the same jobs (after

these jobs’ respective ﬁrst consumption) are ac-

commodated. A job requesting to consume a

limited-but-extensible primitive-resource is con-

ﬁrmed iff the job’s ﬁrst consumption-time inter-

val falls into the primitive resource’s availability-

time interval (e.g., J

con

, e

con

] ⊂ P R

[b, e]

in Table 2 (b) where b

con

> b and e

con

e) and, then, any additional consumption-

time intervals still fall into either the prim-

itive resource’s same availability-time interval

(e.g., J

P R

con

, e

con

] ⊂ P R

[b, e] in Ta-

ble 2 (b) where b

con

== e

con

and e

con

< e) or

the primitive resource’s extended availability-time

interval (e.g., J

P R

con

, e

con

] ⊂ P R

[e, e + δ]

in Table 2 (b) where b

con

== e

con

and e

con

e + δ).

5 CONSUMPTION OF

COMPOSITE RESOURCES

After deﬁning some concepts linked to the coordi-

nated consumption of composite resources, we now

discuss how these resources’ consumption ﬂows are

generated according to primitive resources’ availabil-

ity times and consumption properties.

5.1 Deﬁnitions

In preparation for deﬁning composite resources, we

deem necessary contrasting them with business pro-

cesses and composite Web services. On the one hand,

while a business process and composite Web service

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

have a process model and composition schema, re-

spectively, a composite resource also has a consump-

tion ﬂow. In addition, while the performance of a

business process and composite Web service is de-

pendent on their tasks’ and component Web services’

non-functional properties, respectively, the consump-

tion of a composite resource is also dependent on

their primitive resources’ availability-time intervals

and consumption properties. On the other hand, while

a business process’ process model and composite Web

service’s composition schema are known ahead of

time, a composite resource’s consumption ﬂow is

set on-the-ﬂy according to their primitive resources’

availability-time intervals and consumption proper-

ties and Allen’s time-interval relations that could vary

from one consumption cycle to another (begin and

end values assigned to time intervals vary per sce-

nario). Finally, the completion of business processes

and composite Web services depends on the availabil-

ity of composite resources that themselves depend on

the availability of primitive resources.

Deﬁnition 2. A composite resource C R is deﬁned

by the tuple < id, name, evt, {UPR}, C F > where

id is the identiﬁer of the composite resource, name

is the name of the composite resource, evt is the

name of the event that triggers the consumption of

the composite resource, UPR is an unordered set

of primitive resources {P R

} as per Deﬁnition 1,

and C F is the consumption ﬂow of the compos-

ite resource that is generated on-the-ﬂy based on

both the primitive resources’ availability-time in-

tervals/consumption properties and Allen’s appro-

priate time-interval relations between these primi-

tive resources. The consumption ﬂow is represented

as a set of couples {rel(P R

, P R

)} where rel ∈

{equals, starts, f inishes, overlaps, during}. More de-

tails are given in Section 5.2

5.2 Generation of Consumption Flows

Let us assume a job (J ) to carry out like in the run-

ning example. The generation of this job’s compos-

ite resource’s consumption ﬂow (C F ) would go over

identiﬁcation and adjustment stages (Fig. 3). Brieﬂy,

in the identiﬁcation stage, the designer deﬁnes Allen’s

time-interval relations that would connect the primi-

tive resources together based on these primitive re-

sources’ respective availability-time intervals. This

produces what we refer to as the composite resource’s

initial consumption ﬂow (I C F ). And, in the adjust-

ment stage, the designer assesses the impact of the

identiﬁed Allen’s time-interval relations on the primi-

tive resources’ consumption properties. This could re-

quire adjusting the availability-time intervals of these

primitive resources to enforce their concurrent/com-

posite consumption whenever deemed possible. The

assessment goes through several rounds until what we

refer to as the composite resource’s ﬁnal consumption

ﬂow (F C F ) is obtained.

Identiﬁcation Stage. As per Deﬁnition 2, the un-

ordered set of primitive resources (UP R ) that form

a composite resource are known based on the trig-

gered event of the job to complete. This set consti-

tutes an input to Algorithm 1 whose output is the com-

posite resource’s I C F . In I C F , the different primi-

tive resources are connected together through appro-

priate Allen’s time-interval relations, e.g., I C F =

{overlaps(P R

,P R

), ·· · , starts(P R

,P R

)}.

Adjustment Stage. The outcome of the identiﬁca-

tion stage that is I C F is processed according to the

following steps:

Step 1: parses the I C F to cluster the primitive re-

sources based on Allen’s time-interval relations.

The result are 5 clusters, C

rd=1···m

rt=1···5

, where a clus-

ter’s superscript (rd)

and subscript (rt) corre-

spond to the current number of round tracking

the progress of parsing the I C F and a numerical

value that is the time relation’s type, respectively.

For instance, C

is the cluster of all primitive re-

sources connected through equals at round 1 and

is the cluster of all primitive resources con-

nected through starts at round 3. It is worth noting

that some clusters could end-up empty depending

on the time-relation intervals included in I C F .

Step 2: ﬂushes UP R and generates a unique com-

posite resource, C R

i j

, for each Allen’s time-

interval relation included in the 5 clusters,

rt=1···5

, that illustrate a concurrent consumption

of primitive resources, namely equals, starts, ﬁn-

ishes, overlaps, and during. For instance, C R

is the composition of P R

and P R

at round 1.

Prior to inserting C R

i j

into the ﬂushed UP R

that will become an unordered set of composite

resources, CR

i j

’s availability-time interval needs

to be deﬁned ﬁrst, according to both Allen’s time-

interval relation of the cluster and the consump-

tion properties and availability-time intervals of

the primitive resources in the cluster as well and

second, in a way that the concurrent consumption

of the primitive resources is maintained.

• Equals(P R

, P R

): whether P R

and P R

are limited or limited-but-extensible, C R

i j

’s

availability-time interval is the availability-

time interval of any primitive resource, for in-

The maximum value, m, is known after completing the

adjustment stage.

Time-Constrained, Event-Driven Coordination of Composite Resources’ Consumption Flows

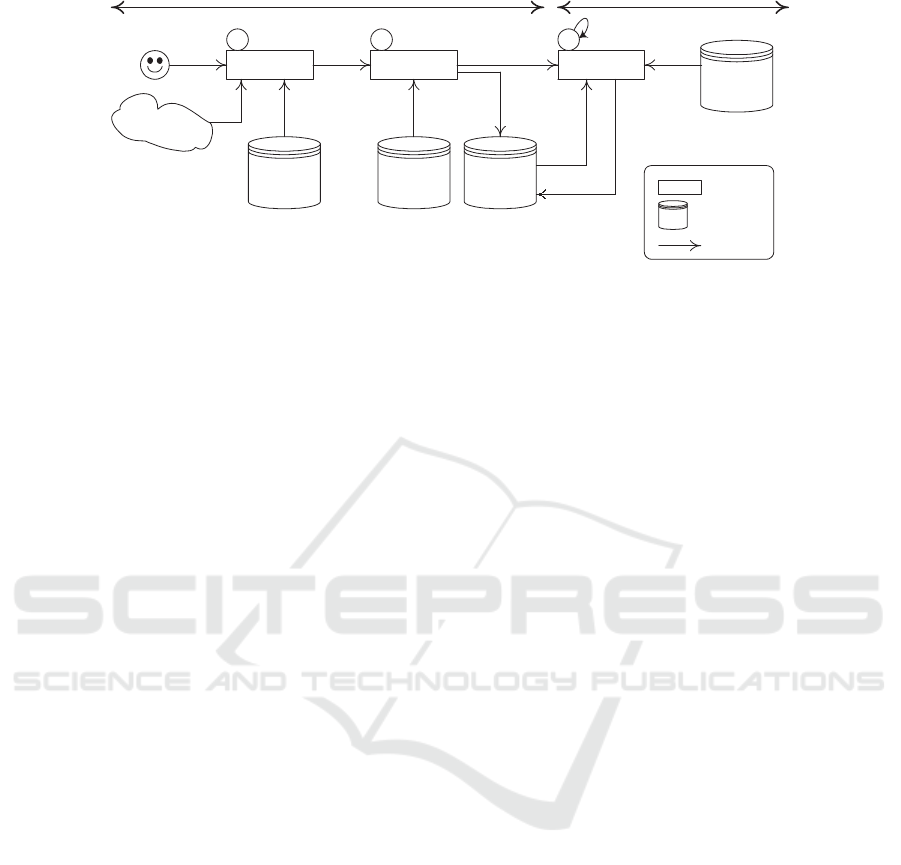
Identification stage

Selection

invoke

Designer

1

Adjustment

stage

Connection

notify

Connected

primitive

resources

Time-

interval

relations

input

output

Job to

complete

input

Analyzer

enact

Primitive

resources

(availability-time

intervals)

Primitive

resources

(consumption

properties)

input

output

2

Module

Repository

Interaction

Legend

3

Figure 3: Modules, repositories, and interactions in the generation of consumption ﬂows

stance [b

, e

• Starts(P R

, P R

– Limited property (Table 3-Case a): C R

i j

’s

availability-time interval is set as follows:

begin-time of any primitive resource and end-

time of PR

since it has the ﬁrst end-time, for

instance [b

, e

– Limited-but-extensible property (Table 3-

Case b): C R

i j

’s availability-time interval is

set as follows: begin-time of any primitive re-

source and end-time of P R

that has the last

end-time, for instance [b

, e

]. At the same

time, P R

’s end-time is extended to match

P R

’s end-time, e

+ δ == e

• Finishes(P R

, P R

- Limited property: CR

i j

’s availability-time

interval is set as follows: begin-time of P R

that has the last begin-time and end-time of

any primitive resource.

- Limited-but-extensible property: C R

i j

’s

availability-time interval is set as follows:

begin-time of PR

that has the last begin-time

and end-time of any primitive resource.

• During(P R

, P R

- Limited property: CR

i j

’s availability-time

interval is set as follows: begin-time of P R

that has the last begin-time and end-time of

P R

again that has the ﬁrst end-time.

- Limited-but-extensible property: C R

i j

’s

availability-time interval is set as follows:

begin-time of P R

that has the last begin-

time and end-time of P R

that has the last

end-time. At the same time, P R

’s end-

time is extended to match P R

’s end-time,

+ δ == e

• Overlaps(P R

, P R

- Limited property: CR

i j

’s availability-time

interval is set as follows: begin-time of P R

that has the last begin-time and end-time of

P R

that has the ﬁrst end-time.

- Limited-but-extensible property: C R

i j

’s

availability-time interval is set as follows:

begin-time of P R

that has the last begin-

time and end-time of P R

again that has the

last end-time. At the same time, P R

’s end-

time is extended to match P R

’s end-time,

+ δ == e

Step 3: increments the number of round by 1,

runs Algorithm 1 again with UP R as an un-

ordered set of composite resources, and goes

back to Step 1 until the 4 clusters, except

for equals, become empty, i.e., C

rt=2···5

φ. Should the condition hold for the 4 clus-

ters, then the composite resource’s F C F is de-

picted in C

linked to equals, e.g., F C F =

{equals(C R

, C R

) ∪ equals(C R

, C R

) ∪

equals(C R

, C R

), . . . }. All the composite re-

sources will have the same interval.

5.3 Illustration

With respect to the running example, the Web

services consume different resources like vir-

tual machines for processing and databases for

storage. To illustrate the generation of a con-

sumption ﬂow, we assume an UP R consisting

of 4 primitive resources, P R

1..4

, all limited,

having each an availability-time interval, for

instance [2,5], [3,6], [2,5], and [3,5], respectively.

We proceed with rolling out the identiﬁca-

tion and adjustment stages. After completing

Algorithm 1, I C F = {overlaps(P R

,P R

equals(P R

,P R

), overlaps(P R

,P R

starts(P R

,P R

), ﬁnishes(P R

,P R

ﬁnishes(P R

,P R

)}. Then, the ﬁnal inter-

val would be [3,5].

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

Input: UP R : {P R

, e

]}

i=1,n

: unordered set of primitive

resources

Output: I C F : initial consumption ﬂow of a composite

resource

1 begin

2 Initialize I C F to φ;

3 Initialize Concurrency to true;

4 foreach i ∈ [1, n-1] do

5 foreach j ∈ [i + 1, n] do

6 if Concurrency == true then

7 if e

== b

then

8 I C F = φ; Concurrency ← f alse;

break;

9 end

10 if b

== e

then

11 I C F = φ; Concurrency ← f alse;

break;

12 end

13 if b

> b

and e

< b

then

14 I C F = φ; Concurrency ← f alse;

break;

15 end

16 if e

> b

and e

< b

then

17 I C F = φ; Concurrency ← f alse;

break;

18 end

19 if (e

== e

andb

== b

) then

20 I C F = I C F ∪ equals(P R

, P R

);

break;

21 end

22 if b

== b

and e

> e

then

23 I C F = I C F ∪ starts(P R

, P R

);

break;

24 end

25 if b

== b

and e

< e

then

26 I C F = I C F ∪ starts(P R

, P R

);

break;

27 end

28 if e

== e

and b

< b

then

29 I C F =

I C F ∪ f inishes(P R

, P R

);

break;

30 end

31 if e

== e

and b

> b

then

32 I C F =

I C F ∪ f inishes(P R

, P R

);

break;

33 end

34 if b

< b

and e

< e

then

35 I C F = I C F ∪ during(P R

, P R

);

break;

36 end

37 if b

< b

and e

> b

then

38 I C F =

I C F ∪ overlaps(P R

, P R

);

break;

39 end

40 if e

> b

and e

> e

then

41 I C F = I C F ∪ during(P R

, P R

);

break;

42 end

43 if e

> b

and e

< e

then

44 I C F =

I C F ∪ overlaps(P R

, P R

);

break;

45 end

46 end

47 end

48 end

49 return IC F

50 end

Algorithm 1: Initial consumption-ﬂow development.

Table 3: Deﬁnition of a composite resource’s availability-

time interval because of starts.

PR 

j

b 

j

e 

j

trim

CR 

ij

b 

i

e 

i

PR 

i

b 

i

e 

i

Case a

PR 

j

b 

j

e 

j

extend

PR 

i

b 

i

e 

i

CR 

ij

b 

i

e 

j

Case b

6 IMPLEMENTATION

This section discusses ﬁrst the system implementing

the approach for composing primitive resources and

then, the experiments to test and evaluate this system.

6.1 Overview

To demonstrate the technical doability of on-the-ﬂy

development of consumption ﬂows of composite re-

sources, a system whose main graphical user inter-

face is shown in Fig. 4, was implemented using multi-

ple languages, tools, and technologies. This includes

Java, NodeJS (a back-end JavaScript runtime environ-

ment), Spring boot (a Java-based open source frame-

work to build and deploy Web applications), Gradle (a

tool for automating software build), ReactJS (a front-

end JavaScript library to build user interfaces), JSON

(an open standard for data format and interchange),

Visual Studio Code (an open source lightweight-code

editor for JavaScript and TypeScript languages), and

Postman (a platform for testing components repre-

sented as API endpoints). Classes in the system

are primitiveResource, compositeResource, relation-

Allen, and consumptionFlowGenerator implementing

the model-view-presenter architectural pattern. The

development and experimentation of the system took

place on top of an 11

Generation Intel 4 Cores

i5 Processors@4.2GHZ, 16GB RAM desktop.

To use the system, a designer stores necessary de-

tails about jobs to complete using primitive resources

into JSON ﬁles and then, uploads these ﬁles into the

system as per Fig. 4. In this ﬁgure, “All are con-

current”, “Part are concurrent”, and “Both” (not-

considered further) indicate possible scenarios to test

as per the next paragraphs.

Time-Constrained, Event-Driven Coordination of Composite Resources’ Consumption Flows

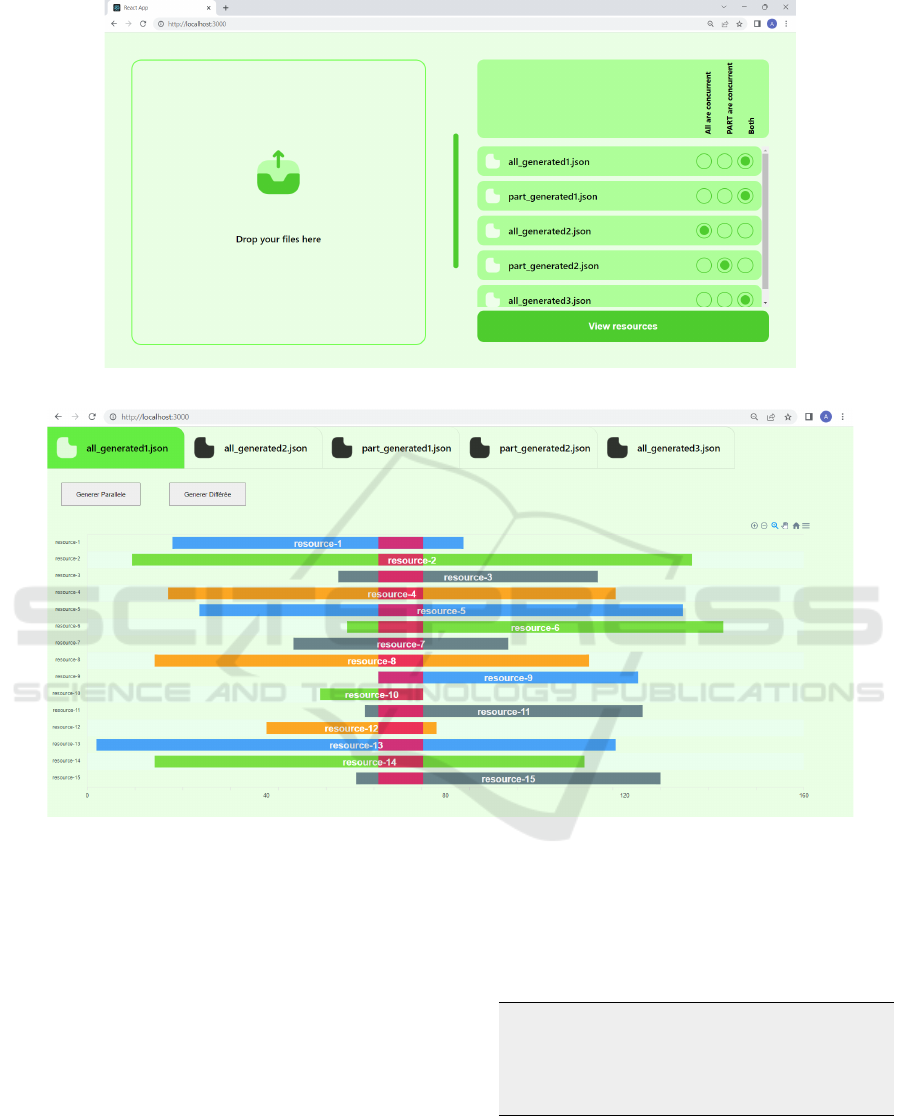
Figure 4: System’s main GUI.

Figure 5: Representation of scenario 1’s resources’ availability-time intervals.

6.2 Tests and Evaluation

Due to the unavailability of datasets that would cater

for our needs, we generated 2 separate datasets con-

taining each 15, 150, 1500, 15000, and 150000 primi-

tive resources along with their respective availability-

time intervals. The scenarios that were tested and

evaluated are as follows.

Scenario 1 (”All are concurrent”) targets a con-

sumption ﬂow that features concurrent consumption

of all primitive resources (Fig. 5). The dataset of this

scenario, i.e., UP R formatted as per Listing 1, is

the result of Algorithm 2 whose inputs are a given

time interval ([b, e]) and a number of primitive re-

sources (n). To deﬁne each primitive resource’s

availability-time interval in the dataset, generateInter-

val function uses a randomize function twice where

genBegin and genEnd are pseudo-random numbers

with 0 ≤ genBegin ≤ b, e ≤ genEnd ≤ max, and max

is an arbitrary value like (b +e).

Listing 1: Excerpt of scenario 1-related dataset in JSON.

1 [{" id " : 2 , " n a me " : " re so ur c e - 3 " , " b e gi n T i m e " : 5 6 ,"

en d T i me " : 11 4 , " sh a re a bl e ": fa ls e },

2 . ..

3 {" id " : 1 3 , " n am e " : " r eso ur ce - 1 4 " , " b e gi n Ti m e " : 1 5 , "

en d T i me " : 11 1 , " sh a re a bl e ": fa ls e }]

A graphical representation of Listing 1 is shown in

Fig. 5 after setting the number of primitive resources

to 15. Some Allen’s time relations in this representa-

tion include during between resource-1 and resource-

2, and overlaps between resource-4 and resource-5.

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

Input: b: begin-time interval, e: end-time

interval, n: number of primitive resources

to generate

Output: UP R : set of primitives resources

1 begin

2 Initialize UP R to φ;

3 foreach i ∈ [1, n] do

4 generateInterval(b,e,b +

e,genBegin,genEnd);

5 UP R = UP R ∪

createResource(genBegin,genEnd);

6 end

7 return UP R

8 end

Algorithm 2: Dataset generation for scenario 1.

After completing the identiﬁcation and adjustment

stages, [65,75] is the common availability-time in-

terval (Fig. 5:red band) ensuring the concurrent con-

sumption of all the primitive resources. Using the sys-

tem, the designer can check the availability-time in-

terval of each primitive resource, zoom in/out the dis-

played results, and save these results in formats like

csv and png.

Scenario 2 (”Part are concurrent”) targets a con-

sumption ﬂow that features both concurrent and se-

quential consumption of primitive resources (Fig. 6).

This scenario whose dataset is formatted as per List-

ing 2 required adjusting Algorithm 1 in a way that

meets and precedes time-relations were supported this

time. To generate the second dataset, Algorithm 2 is

used again after adjusting randomize function where

a start time is generated ﬁrst subject to satisfying

0 ≤ genBegin < e. Then, an end time that satis-

ﬁes genBegin < genEnd ≤ max is generated based on

this start time.

Listing 2: Excerpt of scenario 2-related dataset in JSON.

1 [{" id " : 0 , " n a me " : " re so ur c e - 1 " , " b e gi n T i m e " : 2 5 ,"

en d T i me " : 93 , " sh a re a bl e " : fa l s e },

2 . ..

3 {" id " : 1 4 , " n am e " : " r eso ur ce - 1 5 " , " b e gi n Ti m e " : 5 4 , "

en d T i me " : 55 , " sh a re a bl e " : fa l s e }]

A graphical representation of Listing 2 is given in

Fig. 6 where 15 primitive resources are included again

with a maximum number among these resources

to consume concurrently and the rest sequentially.

Some Allen’s time relations include meets between

resource-2 and resource 11, and overlaps between

resource-12 and resource-9. After completing the

identiﬁcation and adjustment stages, Fig. 6:red band

indicates the availability-time interval for consuming

each resource in the ﬁnal consumption ﬂow. The de-

signer can roll the mouse over the red band to check

when the consumption of a primitive resource will ef-

fectively occur. All the consumption whether sequen-

tial or concurrent will fall into [28,100] interval. Dur-

ing this interval, several gaps like ]39,54[ and ]55, 62[

can be noticed where no consumption will happen.

Outside these gaps, other availability-time intervals

like [28, 39] and [54, 55] will correspond to consump-

tion.

Testing both scenarios was done in compliance

with unit testing in test-driven development (Beck,

2003) where for each test an output result is compared

to an expected output to verify the correctness of this

result. In conjunction with this testing, we evaluated

the creation time of a composite resource’s ﬁnal con-

sumption ﬂow (F C F ) per scenario (Table 4). This

time increases as the number of primitive resources

increases too with scenario 2 requiring more process-

ing than scenario 1.

Table 4: Creation time of a composite resource’s F C F .

F C F creation time (ms)

# of resources Scenario 1 Scenario 2

15 4 6

150 6 750

1500 80 2522

15000 10040 25540

7 CONCLUSION

This paper presented an approach for coordinating the

consumption of primitive resources subject to con-

sumption properties and time availabilities. These

properties included unlimited, limited, limited-but-

extensible, shareable, and non-shareable impacting

their assignments to user-related jobs. The assign-

ments are also dependent on time periods dictating

when a primitive resource is available for use. Multi-

ple primitive resources means multiple separate time-

availabilities that raise different coordination chal-

lenges. To tackle these challenges, Allen’s time alge-

bra was used establishing time relations between time

availabilities like overlaps, meets, and during. The

paper also presented a system demonstrating the tech-

nical doability of a time-constrained, event-driven co-

ordination of composing primitive resources. In term

of future work, we would like to examine the impact

of failures on primitive resources’ time availabilities.

Could these availabilities be adjusted when a primi-

tive resource has a limited consumption-property, for

example? Another future work is to assess the im-

pact of transactional properties like pivot, retriable,

and compensatable on primitive resources’ availabil-

ity times and hence, integration into composite re-

sources.

Time-Constrained, Event-Driven Coordination of Composite Resources’ Consumption Flows

Figure 6: Representation of scenario 2’s resources’ availability-time intervals.

REFERENCES

Akbarinia, R., Pacitti, E., and Valduriez, P. (2011). Best Po-

sition Algorithms for Efﬁcient Top-k Query Process-

ing. Information Systems, 36(6).

Allen, J. (1983). Maintaining Knowledge about Temporal

Intervals. Communications of the ACM, 26(11).

Arias, M., Rojas, E., Munoz-Gama, J., and Sep

ulveda, M.

(2015). A Framework for Recommending Resource

Allocation based on Process Mining. In Proceedings

of the 13th International Business Process Manage-

ment Workshops held in conjunction with BPM’2015,

Innsbruck, Austria.

Baker, T., Ugljanin, E., Faci, N., Sellami, M., Maamar,

Z., and Kajan, E. (2018). Everything as a Re-

source: Foundations and Illustration through Internet-

of-Things. Computers in Industry, 94.

Beck, K. (2003). Test-driven Development - by Example.

Addison-Wesley Signature Series. Addison-Wesley.

de Weerdt, M. and Clement, B. (2009). Introduction to

Planning in Multiagent Systems. Multiagent Grid Sys-

tems, 5(4).

Dimick, D. (2014). As World’s Population Booms, Will

its Resources be Enough for Us? https://tinyurl.com/

5an3dhez.

Fielding, R. (2000). Architectural Styles and the Design

of Network-based Software Architectures. PhD thesis,

University of California, Irvine.

Hofman, W. (2015). Towards a Federated Infrastruc-

ture for the Global Data Pipeline. In Proceedings

of the 14th IFIP WG 6.11 on Open and Big Data

Management and Innovation held in conjunction with

I3E’2015, Delft,The Netherlands.

Janhunen, T. and Sioutis, M. (2019). Allen’s Interval Alge-

bra Makes the Difference. CoRR, abs/1909.01128.

Langdon, C. S. (2003). The State of Web Services. IEEE

Computer, 36(7).

Lucchim, R., Millot, M., and Elfers, C. (2008). Resource

oriented Architecture and REST: Assessment of Im-

pact and Advantage on INSPIRE. JRC Scientiﬁc and

Technical Reports EUR 23397 EN - 2008, JRC Euro-

pean Commission.

Maamar, Z. and Al Khafajiy, M. (2021). Cloud-Edge Cou-

pling to Mitigate Execution Failures. In Proceedings

of SAC’2021, South Korea (online).

Maamar, Z., Faci, N., Sakr, S., Boukhebouze, M., and Bar-

nawi, A. (2016). Network-based Social coordination

of Business Processes. Information Systems, 58.

Maamar, Z., Sellami, M., and Masmoudi, F. (2021). A

Transactional Approach to Enforce Resource Avail-

abilities: Application to the Cloud. In Proceedings

of RCIS’2021, Cyprus (online).

Maamar, Z., Yahya, F., and Benammar, L. (2022). On the

Use of Allen’s Interval Algebra in the Coordination

of Resource Consumption by Transactional Business

Processes. In Proceedings of ENASE’2022, Portu-

gal (online).

Mell, P. and Grance, T. (2011). The NIST Deﬁnition of

Cloud Computing. Technical Report 800-145, Na-

tional Institute of Standards and Technology (NIST).

Park, G. and Song, M. (2019). Prediction-based Re-

source Allocation using LSTM and Minimum Cost

and Maximum Flow Algorithm. In Proceedings of

ICPM’2019, Aachen, Germany,.

Schreiber, G. and Raimond, Y. (2014). RDF 1.1 Primer.

Technical report, World Wide Web Consortium.

Sindhgatta, R., Ghose, A. K., and Dam, H. K. (2016).

Context-aware Analysis of Past Process Executions to

Aid Resource Allocation Decisions. In Proceedings

of CAiSE’2016, Ljubljana, Slovenia.

ENASE 2023 - 18th International Conference on Evaluation of Novel Approaches to Software Engineering

Stefanini, A., Aloini, D., Benevento, E., Dulmin, R., and

Mininno, V. (2020). A Data-driven Methodology

for Supporting Resource Planning of Health Services.

Socio-Economic Planning Sciences, 70.

Weske, M. (2012). Business Process Management Archi-

tectures. In Business Process Management. Springer.

Zhao, W., Liu, H., Dai, W., and Ma, J. (2016). An Entropy-

based Clustering Ensemble Method to Support Re-

source Allocation in Business Process Management.

Knowledge and Information Systems, 48(2).

Zhao, W., Pu, S., and Jiang, D. (2020). A Human Resource

Allocation Method for Business Processes using Team

Faultlines. Applied Intelligence, 50(9).

Time-Constrained, Event-Driven Coordination of Composite Resources’ Consumption Flows