Recommendation Model for an After-School E-learning Mobile

Application

Ana

elle Badier, Mathieu Lefort and Marie Lefevre

Univ Lyon, UCBL, CNRS, INSA Lyon, LIRIS, UMR5205, F-69622 Villeurbanne, France

Keywords:

Adaptive Learning, Recommendation System, Educational Mobile Application, After-School Learning.

Abstract:

In this article we present a learning resources recommendation system for an after-school educational mobile

application. The goal of our system is to recommend relevant content among the learning resources available

in the application to ﬁt student needs and to encourage autonomous learning. The system is based on a graph

of key notions to structure the application learning resources. We use the Item Response Theory method to

evaluate the student knowledge and ﬁlter the most relevant resources to study depending on three learning

strategies: revision, continuation and deepening. The resources ﬁltered by the selected strategy, are ranked

mainly based on a pedagogical score. The system has been implemented for the Mathematics subject and

analysed for middle and high-school students in real-life conditions. In Fall 2022, we recorded the learning

traces of 1458 students that interacted with the system. By analysing experts opinions, logs and students

feedback, we can conclude that our system is pedagogically relevant, appreciated and used by students.

1 INTRODUCTION

The rise of e-learning applications for several decades

now led to new ways of learning. Students tends

to learn more and more by themselves, looking for

extra-class learning content. We are working with an

after-school e-learning mobile application that pro-

vides courses and quizzes for all grade levels from

middle school to university. This e-learning system

is organized into subjects, containing chapters. In-

side each chapter there are between 1 and 5 small

courses and between 1 and 4 multiple-choice quizzes

of 5 questions each. In this context, our goal is to

recommend content suited for each student, within a

platform accessible to many proﬁles. This application

gathers students, who mostly work with the applica-

tion in small working sessions (less than 5 minutes),

and not regularly. Our research question is the fol-

lowing : How to mobilize the learning resources of

the application across different grade levels to of-

fer relevant recommendations ?

In the next section we present the scientiﬁc work

related to our subject and highlight the particularities

of our context. In a third part, we describe our con-

tribution that proposes a recommendation system that

meets the particularities presented in section 2. Then

(section 4), based on experts reviews, learning traces

analysis and students feedbacks, we show that the sys-

tem that was tested in the real context of use validates

the relevance of our recommendation model and give

us elements to improve our system. We discuss our

implementation choices and results in section 5.

2 RELATED WORKS

As we are working with a mobile application, our

context is quite similar to the MOOCs platforms,

characterized by high attrition rates (Reich, 2014),

but our learners use our app as an extra and not as

their main support to learn. Thus, our application is a

micro-learning tool (Nikou and Economides, 2018).

According to systematic reviews (Vaidhehi and

Suchithra, 2018), recommendation systems in educa-

tion are essentially based on content and on learner

modeling (including hybrid strategies). (Guruge

et al., 2021) listed several methods used in recom-

mender systems, such as collaborative, content-based

ﬁltering, or data mining technics. To provide rec-

ommendations and adapt to the users, some sys-

tems are based on the concept of ”Zone of Proximal

Development” (ZPD) developed by (Vygotski

ı and

Cole, 1978). It consists on evaluating the knowledge

level of a student to recommend slightly more difﬁ-

cult learning content, to make the students progress.

(Baker et al., 2020) used a ZPD-based recommenda-

Badier, A., Lefort, M. and Lefevre, M.

Recommendation Model for an After-School E-learning Mobile Application.

DOI: 10.5220/0011717800003470

In Proceedings of the 15th International Conference on Computer Supported Education (CSEDU 2023) - Volume 2, pages 80-87

ISBN: 978-989-758-641-5; ISSN: 2184-5026

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

tion system and proved its positive effects on learning.

This method requires to evaluate the student level.

Several systems are using the Bloom’s competencies

taxonomy (Bloom, 1956) to adapt to learner’s com-

petencies. The Knowledge Tracing Models (Corbett

and Anderson, 1994) are widely used to infer compe-

tencies and model the level of knowledge of a student

(Vie and Kashima, 2019). These models aim to pre-

dict the outcomes of students over questions. Using

statistics, the Item Based Theory (IRT) (Baker, 2001)

is a method used to evaluate the latent level of compe-

tency of a given student. The use of IRT for intelligent

tutoring systems have been studied by (Wauters et al.,

2021).

Recommendation systems can be developed to

help students to solve a precise task in one particu-

lar topic for example to learn programming languages

(Branth

ome, 2022). In our case, we want to use our

recommendation system for different subjects, there-

fore we are not based on didactic. Other intelligent

tutoring systems are based on online resources (Da-

her et al., 2018). The content is usually structured

with ontological methods thanks to descriptive meta-

data and hyperlinks references (Nguyen et al., 2014)

and can be organised in knowledge graphes (Rizun,

2019). Our system must be suitable for several sub-

jects, but we do not have as many resources as the

web-based systems and we cannot beneﬁt from the

meta-data description of learning resources (De Maio

et al., 2012). However, we adapted some methods

previously described as IRT that we use to evaluate

the knowledge of a student but also to describe the

difﬁculty level of our resources.

The system we present in the following section

is designed to handle a voluntary, irregular and au-

tonomous use with limited and internal resources.

Due to our context, existing methods are not directly

applicable and some criteria for evaluating recom-

mender systems (Erdt et al., 2015) cannot be used

neither, as the measure of effects on learning. Indeed,

this measure can only be calculated if we master the

complete learning cycle to be sure that the learning

gain is due to our system. However, as we provide an

extra-curricular application, the learning takes place

through the app and outside the app. Therefore, we

will only use the evaluation criteria of recommender

systems that apply to our context of out of school, free

and voluntary learning (section 4).

3 RECOMMENDATION MODEL

Our strategy is to recommend a small list of chap-

ters, ranked by relevancy, and to let the ﬁnal choice

to the student. Our system orients the learner from

one chapter to another across several grade levels.

The recommendation process is represented on Fig-

ure 1. Firstly, we organise our learning materials in

a notions graph (section 3.1). We use IRT to select a

recommendation strategy to ﬁlter our resources (sec-

tion 3.2). We ﬁnally build a pedagogical score to rank

the preﬁltered resources and recommend the more rel-

evant to the student (section 3.3).

3.1 Notions Graph of Ressources

Our learning resources are chapters that include

multiple-choice quizzes, small courses and summary

cards for each chapter called ”the Essentials”. We or-

ganize our chapters in a notions graph by tagging it

with prerequisite and expected notions. We call no-

tion a piece of knowledge useful to understand the

current chapter. A notion is labelled as prerequisite if

the learner must already understand part of the con-

cept described by the notion to master the current

chapter. The notion is expected if the chapter strat-

egy is either to discover this notion, or to go further

with more difﬁcult questions on this notion. Thus a

chapter can be tagged with the same notion as prereq-

uisite and expected if this chapter enables the learner

to acquire a deeper knowledge on this notion.

The tags were applied by the experts, i.e. the

designers of the pedagogical resources according to

the ofﬁcial French education program. 244 different

notions have been applied on the 1 601 mathemat-

ics learning resources. These notions can be general

such as Triangle, Division or more speciﬁc like Fer-

mat Theorem. Our chapters are hence linked to each

others through the different grade levels. An extract

of this notion graph is represented on Figure 2.

3.2 Strategies Based on IRT

Because of our context, it is difﬁcult to know the pre-

cise need of a student, so we decide to apply a recom-

mendation strategy depending on how well students

master the chapter they just ﬁnished. Three strategies

are deﬁned : revision, continuation and deepening.

This level of mastery is not deﬁned by the aver-

age success score, because each quiz was created by

a different teacher and they can be of varying levels

of difﬁculty. Furthermore, the multiple-choice format

makes it possible to guess the good answer by random

choice. To deﬁne the student level on each chapter,

we use IRT to estimate the latent learner mastery of

the notions required in the chapter. IRT is not used

here as it is often the case in the literature, to build

computerized-adaptive tests, but we directly use the

Recommendation Model for an After-School E-learning Mobile Application

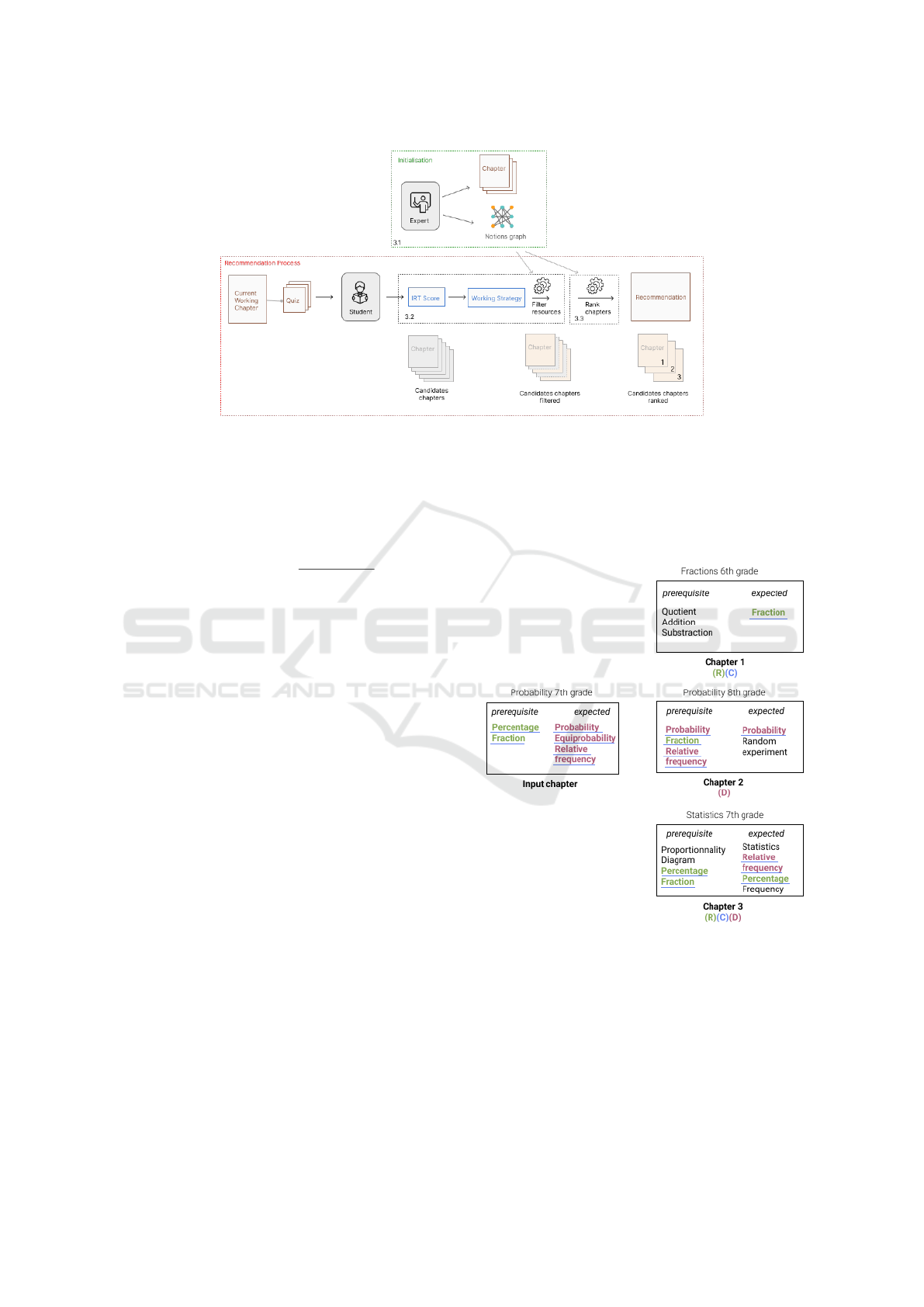
Figure 1: Recommendation workﬂow combining an initialisation step to build a notions graph (done only once), a ﬁltering

step based on IRT to choose among three recommendation strategies and a ranking step relying on a pedagogical score.

student estimated ability level θ to assign each student

a level of mastery at the end of each quiz.

We use the 3 parameters version of the IRT model

that includes a guessing parameter:

P(θ) = c + (1 − c)

1 + e

−a(θ−b)

(1)

with θ the ability level, a the discrimination, b the

difﬁculty and c the guessing parameters.

Firstly, we collected all the previous answers

given by all students that have used the application.

Using the mirt R package, we compute for each ques-

tion the parameters a, b and c, i.e the item characteris-

tics. To compute the θ value of the quiz for a new stu-

dent, we use the IRT property of local independence

of the items (Baker, 2001) and apply the conditional

probability formula with independent events. Given

a sequence of answers correctness for a quiz (for ex-

ample seq = {true, f alse, f alse,true,true}), and the

items characteristics, we can compute P(seq|θ)

P(Seq|θ) =

∏

i=1

(true/ f alse|θ) (2)

with P

(θ) computed from equation 1 with corre-

sponding item parameters.

We can then use the iterative procedure based on

the maximum likelihood described by (Baker, 2001)

and assign to the learner the θ value that maximises

P(Seq|θ) for a given answers sequence. From this θ

we want to select a recommendation strategy for the

learner at the end of a quiz. To do so, we simulate

all the possible combinations for a 5-questions quiz

(Q1: correct, Q2: incorrect, etc...), and for each series

we got a θ score. We split this range [θ

min

,θ

max

] into

3 equal ranges assigned to one different strategy. By

splitting the whole range of simulated-θ in 3 groups

and not using a clustering method on the students col-

lected data, we make the strategy attribution indepen-

dent of the level of the whole group of learners.

Figure 2: Example of chapters in the notion graph with

corresponding recommendation strategies. Green notions

are the notions in common with the prerequisite notions

of the input chapter, pink notions are the notions in com-

mon with the expected notions, underlined blue notions are

all notions in common with the input chapter. R:revision,

C:continuation, D:deepening.

For the revision strategy (assigned to IRT-group

low students, R on Figure 2) we focus on the prereq-

uisite notions of the input chapter that are supposed

not sufﬁciently mastered: we retain all the chapters

CSEDU 2023 - 15th International Conference on Computer Supported Education

of lower or equal grade level than the input chapter,

tagged with the input chapter prerequisite notions (in

green on Figure 2). From this example, if the student

ends the chapter Probability from 7th grade, we will

keep the candidate chapter 1, labelled with the input

chapter prerequisite Fraction and the candidate chap-

ter 3 for the Percentage and Fraction notions. Chapter

candidate 2 will not be preﬁltered because it targets

a higher grade level. The continuation strategy (as-

signed to IRT-group medium students, C on Figure 2)

pre-ﬁlters all the chapters linked to the input chap-

ter by a prerequisite or expected tag (both green and

pink notions on Figure 2) of level equal or just one

year below the input chapter. On Figure 2, chapters 1

and 3 will be selected because chapter 2 does not ﬁt

the level criterion. The deepening strategy (assigned

to IRT-group high students, D on Figure 2) selects all

the chapters of higher or equal level which notions in-

clude the input chapter expected notions. On the ex-

ample presented on Figure 2, chapters 2 and 3 will be

selected because of the notions Probability and Rela-

tive frequency. Chapter 1 has none of the input chap-

ter expected notions, and won’t pass the level crite-

rion anyway. The choose of notions type to preﬁlter

is discussed in section 5.

Having ﬁltered our chapters with these 2 criteria

(notion type and grade level), we ﬁnally recommend

the more relevant chapters, according to the pedagog-

ical score described on subsection 3.3.

3.3 Pedagogical Ranking

The aim of this step is to rank chapters by pedagogical

relevance, to recommend resources that are related to

the input chapter, i.e the chapter the student is work-

ing on. The pedagogical relevance score takes into

account 2 components: the shared notions with the

input chapter (similarity score) and the distance to the

academic level of this chapter.

score

peda

= score

similarity

∗ (1 − penalty

distance

) (3)

The similarity score is calculated by taking into

account the shared notions (considering prerequi-

site and/or expected depending on the previously se-

lected strategy) between the available chapters and

the input chapter. To do so, we use the cosine

similarity method to compute the similarity between

chapters notions, previously vectorized using the

Term-Frequency Inverse-Document-Frequency (TF-

IDF) index. This vectoring method is used to take into

account the precision of the notions afﬁxed (the more

generic concepts will have less weight in the similar-

ity index than the precise ones) and the number of

notions assigned to each chapter.

The second criterion is the level grade distance

between the input chapter grade and the others (For-

mula 4), which is an indirect indicator of the chap-

ter difﬁculty. As the French national education pro-

grams are structured by cycles, the distance penalty is

chosen in such a way as to penalise an ”inter-cycle”

distance (from 7th to 6th grade) more than an ”intra-

cycle” distance (from 8th to 7th grade). Considering

the input chapter grade level L

, and a candidate chap-

ter grade level L

, if L

and L

belong to the same cy-

cle, we apply the intra-cycle coefﬁcient. Otherwise,

we apply the inter-cycle coefﬁcient.

penalty

distance

c ∗ |L

− L

max

+ 1

(4)

with D

max

the maximum distance between range

levels (7 for now since the notions graph is build

from 7th to 13th grade) and c = 0.25 if we are in

intra-cycle, c = 0.75 elsewhere.

With the second criterion, two chapters having

the same similarity score regarding the shared notions

will be ranked to recommend the chapter whose grade

level is the closest to the input chapter. As a sec-

ond consequence, if a chapter A has a similarity score

slightly lower than a chapter B, chapter A may still

have a higher pedagogical score if its grade level is

closest to the input chapter than chapter B grade level.

4 SYSTEM EVALUATION

4.1 Expert’s Validation

The pedagogical relevance of our recommendations

was surveyed by 5 mathematics teachers from differ-

ent schools via a survey. We present to them a simu-

lated use case: an imaginary student ends one chapter,

and is assigned to a given strategy. We repeat this case

for 8 chapters, for each of the 3 strategies. Thus, each

expert evaluated 24 use cases, divided into 2 proto-

cols (i.e 4 different chapters with the 3 strategies are

presented for each protocol).

• In the ﬁrst protocol, the teachers were asked to

propose themselves a recommendation among the

inner-app content, that was compared to the rec-

ommendation proposed by the system.

• In the second protocol, the other 4 of the 8 chap-

ters not presented previously are presented to each

expert for the 3 strategies. The teachers were

asked to rate the recommendations proposed by

the system on a 4-points Lickert scale between

”highly irrelevant” and ”perfectly suitable” and to

explain their decision.

Recommendation Model for an After-School E-learning Mobile Application

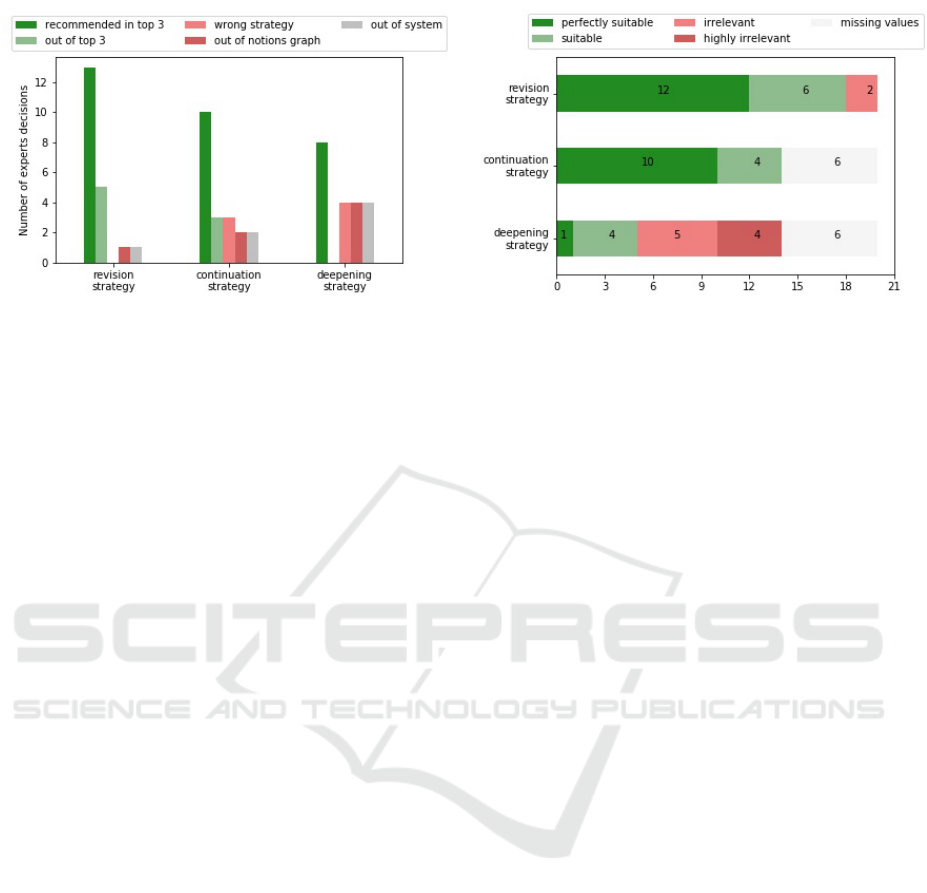
Figure 3: Results of protocol 1. Position of experts recom-

mended chapters regarding our system, depending on the

selected strategy.

The results of the protocol 1 are shown in Figure 3.

Among the 102 mathematics chapters available in the

application for middle school and high-school grade

levels, the expert’s recommended chapters were also

recommended by the system in 51.7% of the cases

(31 cases out of 60). In 35% of the cases, their rec-

ommended chapters were in the top 1 for our system.

8 chapters (13.3%) recommended by the experts were

associated to the input chapter in the notions graph

but not selected in the 3 most relevant. In 7 cases

(11.7%), the experts recommendation was labeled as

”wrong strategy” : they recommended a lower grade-

level chapter for a high-group student, or more than 1

grade-level lower chapter for a medium-group student

which was not a possibility we had considered, but it

was consistent with our notions graph. For other 7

cases, the recommended chapters were not in the no-

tions graph. This limitation is discussed in section 6.

7 cases are labeled as ”out of system”: the experts

recommended to retry the same chapter, or to go back

working on a previously missed chapter instead of

starting to study next grade level content, possibilities

not handled by the system. The deepening strategy is

the one on which the experts most disagreed : 2 of

the experts argued that it would be too difﬁcult for the

student, or do not want the student to look ahead to

the coming year by themselves.

The results of the protocol 2 are given in Figure 4.

6 cases, tagged as missing values, were not answered

by 2 of the 5 experts. The experts mostly agreed with

the recommendation provided by the system for the

revision and continuation strategies (32/34 of rated

chapters from protocol 2 were evaluated as suitable

or perfectly suitable), however they would have rec-

ommended something else for the deepening strategy.

2 of the 5 experts rated all the high-group students

cases recommendations at 1 and 2. They argued that

it would be better to recommend for high-level stu-

Figure 4: Results of protocol 2. Experts validation of

system’s recommended chapters depending on the selected

strategy.

dents to practice more exercises from the same chap-

ter but with more difﬁcult questions : trying higher

grade chapters would be too difﬁcult. As the number

of chapters and quizzes is limited in the application (4

quizzes of 5 questions each), this solution is unfortu-

nately not applicable in our context. For some cases,

the teacher validated the system recommendations ar-

guing ”The recommended chapter was in this grade

level before the last educational reform, this makes

sense”. This validation encouraged us to recommend

chapters across different level grades. These expert’s

comments in the survey assess that our recommenda-

tions are pedagogically relevant for most of the pre-

sented cases. However, the deepening strategy seems

to be more problematic.

4.2 Real Life Experimentation

4.2.1 Implementation Design and Speciﬁcities

Our recommendation model have been implemented

in the mobile application for Mathematics, and was

made available for all the users during 1 month since

their ﬁrst login to the app. The in-app recommenda-

tion interface is presented on Figure 5. We present

to each student 3 recommended chapters and 1 Es-

sential. The Essential is chosen from the student cur-

rent grade level, the most similar to the current chap-

ter according to the notions graph. The chapters rec-

ommendations are delivered from the previously de-

scribed model. The scores of the chapters that were

already studied by the learner, and those who were al-

ready recommended by the system are penalised by

the app in order to keep novelty in the recommenda-

tions. However, it only penalises a small number of

chapters and does not change the pedagogical rele-

vance previously established.

CSEDU 2023 - 15th International Conference on Computer Supported Education

Figure 5: Recommendation interface (translated from

French). The shared notions are displayed in orange. The

grade level of the chapter is written in parenthesis. The sys-

tem recommends 3 chapters (personalized) and one Essen-

tial (common to all learners).

4.2.2 Analysis of the Students Learning Traces

The system was tested in real-life conditions, that

is with students working by themselves, whenever

they wanted without control on their time spent us-

ing the app. We analysed the learning traces collected

during 3 months of experiment: from September to

November 2022. We implemented a tracking system

to record interactions between the learner and the sys-

tem. These data are kept for internal analysis only and

deleted after 3 years according to the European pri-

vacy data protection. To analyse our results, we are

using these terms:

• A working session is deﬁned by all the activities

recorded on the application for one student be-

tween opening and closing of the application; a

student can have several working sessions for 1

day.

• A working session is a Mathematics Active Ses-

sion (MAS) if the student started at least 1 Mathe-

matics quiz in this working session.

• A recommendation is chosen if the student selects

one of the suggested contents (chapters or essen-

tial), regardless of the time spent on this resource.

We collected the learning traces of 1458 students that

used the application for studying Mathematics during

at least 1 Maths Active Session on the 3 months ex-

periment. The number of recommendations chosen

by the students, sorted by grade level is represented

on Figure 6.

Figure 6: Distribution of students, by grade level and by

number of chapters recommended chosen.

Among these 1458 students, 28.9% (421 students)

chose at least 1 recommendation and 11.5% (167 stu-

dents) chose at least 2 recommendations. The distri-

bution of these 1458 students among grade levels is

the following : 14.6% (213) are in 8th grade, 34.5%

(503) in 9th grade, 28.6% (417) in 10th grade, Fig-

ure 6: Distribution of students, by grade level and by

number of chapters recommended chosen 8.8% (129)

in 11th grade, 12.3% (179) in 12th grade and 1.2%

(17) in other grades. From those who chose at least 1

recommendation (421 students), 16.4% (69) were 8th

grade students, 36.3% (153) were 9th grade students

and 27.6% (116) were 10th grade students. These re-

sults indicate that we manage to keep some students

from different level grades using several times our

recommendations. Students grade-level distribution

also shows that our recommendations seems attrac-

tive for several grade levels.

4.2.3 Learner’s Evaluation

We collected the student’s evaluations on this rec-

ommendation system through an online survey ﬁlled

by 49 students of middle school and high school

grade, from different institutions at the end of the 3-

months experiment. The aim of this survey was to get

the user-centered indicators (Erdt et al., 2015). We

wanted to evaluate their perceived usefulness, expec-

tation and satisfaction regarding the coherence of the

recommendations with the chapter studied and difﬁ-

culty level. The survey contained 4 4-points Likert

scale questions (Figure 7), one multi-choices question

and one open-ended question.

Among the 49 students answers, 11 (22%) never

seen the recommendations (i.e they never used the app

to study Mathematics), 25 (51%) already followed

a recommendation, and 12 never followed a recom-

mendation (24%). We removed the 11 students that

never viewed any recommendation from the follow-

ing results analysis. Students mostly found the rec-

Recommendation Model for an After-School E-learning Mobile Application

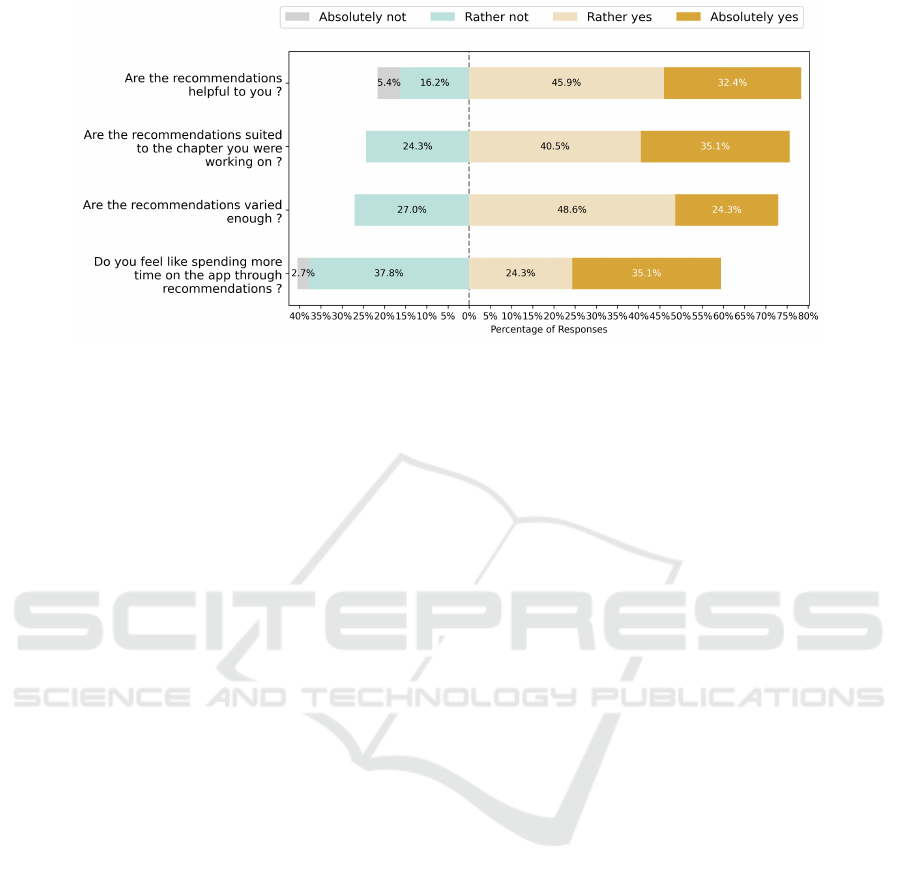
Figure 7: Likert-scale results of students survey answers.

ommendations helpful (78.3%) and adapted (75.6%)

to the chapter they were working on. Fewer think the

recommendations are varied enough (72.9%), which

can be explained by the low number of resources

in the application. For 22 students (59.4%), these

recommendations seem to be a motivating factor to

spend more time working on the application. A multi-

choices question asked about the perceived difﬁculty

of the recommendations: 32 found the recommended

chapters difﬁculty appropriated, 5 too easy and 3 too

difﬁcult. An optional open-ended question asked the

learner’s criteria to decide to choose a recommenda-

tion. The given answers were: the grade level dis-

played in parenthesis and perceived difﬁculty, the per-

ceived usefulness and if the recommended chapter

was already studied in class or not.

5 DISCUSSION

5.1 Implementation Choices

Notions Graph Exploration. We organized our

learning resources inside a notions graph, and decided

to look at all the notions in the candidates chapter

for the recommendation, and to not explore the no-

tions graph linearly. If we take the example of the

input chapter on Figure 2, for a student having difﬁ-

culties on this chapter, we had different choices. As

the percentage notion is a prerequisite notion maybe

not mastered enough, we could ﬁlter all the chapters

of lower grade level where percentage is an expected

notion to ensure the notion will be mastered at the end

of the recommended chapter, or ﬁlter all the chapters

where it is a prerequisite notion, to reinforce the mas-

tery of this notion by using it in a different context. As

these two options can be justiﬁed, we decided to con-

sider all the chapters of lower grade having a notion

in common with the prerequisite notion of the input

chapter, no matter of its type. We could separately

test these two hypothesis in a future work.

IRT-Driven Strategies. We choose to split the θ

range in three equal groups based on the simulated re-

sults, but could have decided to restrict the deepening

strategy for the students that obtained any ﬁxed arbi-

trary value or to extend the revision strategy for those

whose θ is below any other arbitrary value. We chose

this option as it does not add hyper-parameters to the

model and allow us to gather ﬁrst data to analyze, and

further improve our model.

Recommendation Design. We choose to recommend

only the three best chapters to the student. We wanted

to let the student choose among several possibili-

ties but within a small number of chapters to get all

the recommendations displayed on the mobile screen.

Moreover, with the limited number of available re-

sources, the chapters ranked more than top-3 would

be less relevant. We displayed the grade-level of the

recommended chapter, which can bias the student’s

decision as it has be shown in section 4.2.3. Like the

displayed of the graph notions in orange, we wanted

to make the system as transparent as possible.

5.2 Results Discussion

Learning Traces Analysis. We decided to label a

working session as maths active (MAS) based on the

criterion of 1 quiz started, and to assign a strategy

based on quizzes results. We could have chosen oth-

ers criteria such as time spent studying a Mathemat-

ics chapter, or the number of course read. We choose

quizzes because in our context, our students mostly

use the application to try quizzes, hence they are more

representative of student’s activity on the application.

CSEDU 2023 - 15th International Conference on Computer Supported Education

Learner’s Evaluation. Most of students declared

that the recommendations were helpful and suited

(section 4.2.3), however we did not observed higher

following rates in learning analysis. The survey was

proposed to all students having faced the recommen-

dation system however only 49 answered. It can be

explained because most students do not use the ap-

plication regularly and may not accessed the survey.

That highlights the difﬁculty of developing a recom-

mendation system and ﬁnding an evaluation criteria

for this context.

6 CONCLUSION

We propose a recommendation system to improve

navigation in a mobile application through different

chapters and different grade levels. This system relies

on a notions graph to link chapters, uses IRT method

to assign each student a working strategy (revision,

continuation or deepening) to ﬁlter content and build

a pedagogical score to rank chapters by relevancy. It

is designed for a micro-learning use and to encourage

autonomous learning through the different grade lev-

els. The system is currently implemented and used

by students. Pedagogical experts approved the rec-

ommendation made for the revision and continuation

strategies, and the users evaluated the system as help-

ful and suitable. Interviewing more experts will help

to consolidate our ﬁndings and to perform some sta-

tistical analysis on the given marks. The deepen-

ing strategy seems to be more debatable mainly ex-

plained by the reluctance (of experts and students) on

the use and role of an extracurricular application to

discover coming years program. Concerning the ex-

perts recommendations not preﬁltered by the system

or those not in top three (Figure 4), we could look

for a method to enhance or correct our notions graph.

We assume that some students reject the recommen-

dation because their were assigned to the wrong strat-

egy. Analysis of students behaviour from learning

traces will give the possibility to improve the system

to deﬁne the best strategy for each learner. We aim

to analyse deeper how learners use our recommenda-

tions, to consider students choices to improve the sys-

tem knowledge, and to try our system on other sub-

jects.

REFERENCES

Baker, F. B. (2001). The Basics of Item Response Theory.

ERIC Clearinghouse on Assessment and Evaluation.

Baker, R., Ma, W., Zhao, Y., Wang, S., and Ma, Z. (2020).

The results of implementing zone of proximal devel-

opment on learning outcomes. In The 13th Interna-

tional Conference on Educational Data Mining.

Bloom, B. (1956). Taxonomy of educational objectives: The

classiﬁcation of educational goals.

Branth

ome, M. (2022). Pyrates: A Serious Game De-

signed to Support the Transition from Block-Based to

Text-Based Programming. Educating for a New Fu-

ture: Making Sense of Technology-Enhanced Learn-

ing Adoption, 13450:31–44.

Corbett, A. T. and Anderson, J. R. (1994). Knowledge trac-

ing: Modeling the acquisition of procedural knowl-

edge. User Modeling and User-Adapted Interaction.

Daher, J. B., Brun, A., and Boyer, A. (2018). Multi-source

Data Mining for e-Learning. In 7th International Sym-

posium “From Data to Models and Back (DataMod)”.

De Maio, C., Fenza, G., Gaeta, M., Loia, V., Orciuoli, F.,

and Senatore, S. (2012). RSS-based e-learning rec-

ommendations exploiting fuzzy FCA for Knowledge

Modeling. Applied Soft Computing, 12(1):113–124.

Erdt, M., Fernandez, A., and Rensing, C. (2015). Evaluat-

ing Recommender Systems for Technology Enhanced

Learning: A Quantitative Survey. IEEE Transactions

on Learning Technologies, 8(4):326–344.

Guruge, D. B., Kadel, R., and Halder, S. J. (2021). The State

of the Art in Methodologies of Course Recommender

SystemsA Review of Recent Research. Data, 6(2):18.

Nguyen, C., Roussanaly, A., and Boyer, A. (2014). Learn-

ing Resource Recommendation: An Orchestration of

Content-Based Filtering, Word Semantic Similarity

and Page Ranking. In 9th European Conference on

Technology Enhanced Learning, EC-TEL 2014.

Nikou, S. and Economides, A. (2018). Mobile-Based

micro-Learning and Assessment: Impact on learning

performance and motivation of high school students.

Journal of Computer Assisted Learning, 34(3).

Reich, J. (2014). MOOC Completion and Retention in the

Context of Student Intent. Educause Review.

Rizun, M. (2019). Knowledge Graph Application in Educa-

tion: A Literature Review. Acta Universitatis Lodzien-

sis. Folia Oeconomica, 3(342):7–19.

Vaidhehi, V. and Suchithra, R. (2018). A Systematic Review

of Recommender Systems in Education. International

Journal of Engineering & Technology, 7:188.

Vie, J.-J. and Kashima, H. (2019). Knowledge Tracing Ma-

chines: Factorization Machines for Knowledge Trac-

ing. In Proceedings of the AAAI Conference on Artiﬁ-

cial Intelligence.

Vygotski

ı, L. S. and Cole, M. (1978). Mind in Society:

The Development of Higher Psychological Processes.

Harvard University Press.

Wauters, K., Desmet, P., and den Noortgate, W. V. (2021).

Adaptive item-based learning environments based on

the item response theory: Possibilities and challenges.

Journal of Computer Assisted Learning, 26(6).

Recommendation Model for an After-School E-learning Mobile Application