An Evaluation of Malware Triage Similarity Hashes

Haoping Liu

, Josiah Hagen

, Muqeet Ali

and Jonathan Oliver

TrendMicro Research, U.S.A.

The University of Queensland, Australia

Keywords: Malware Triage, Similarity Hashes, Approximate Matching.

Abstract: Detection of polymorphic malware variants is crucial in cyber security. Searching and clustering are crucial

tools for security analysts and SOC operators in malware analysis and hunting. Similarity hashing generates

similarity digests based on binary files, allowing for the calculation of similarity scores, saving time and

resources in malware triage operations. In this paper, we compare the accuracy and run time of TLSH and

LZJD algorithms, both based on windows-based malware samples. TLSH is widely used in industry, while

LZJD is newly developed and released in academia. TLSH hashes skip-n-grams into a histogram, providing

distance scores based on histogram similarity, while LZJD converts byte strings into sub-strings, providing

similarity scores between the sets. Our experiments show that TLSH performs slightly better than LZJD in

detection rate, but vastly outperforms LZJD in index and search time.

1 INTRODUCTION

The Security Operations Center (SOC) is the core of

a company, responsible for detecting, analyzing, and

fixing security threats. As threats evolve, it's crucial

for the SOC to keep pace. During investigations, SOC

analysts may encounter suspicious files or

executables. Understanding the origin and intent of

potential malware provides valuable information to

guide further investigation and action. Malware

analysis techniques equip analysts with the necessary

tools to uncover critical insights.

Static and dynamic analysis technologies are

effective in detecting polymorphic malware.

However, they are vulnerable to evasions and become

less efficient as malware evolves. Extracting features

also consumes a lot of computing resources and time

per sample, making it difficult to keep pace with the

daily influx of malware. Currently, the most widely

used in malware triage are similarity hashing (Li,

Sundaramurthy, Bardas, & Ou, 2015) (Pagani,

Dell'Amico, & Balzarotti, 2018) (Oliver, Ali, &

Hagen, 2020) (Cooley, et al., 2021), import hashing

(Fireeye, 2014) (Naik, Jenkins, Savage, & Yang,

2020) and YARA rules (Naik, Jenkins, Savage, &

Yang, 2019). Accuracy and response time in

matching samples of a method are the primary

challenges in the triaging process.

Contributions. I This paper aims to address concerns

about the detection efficiency and effectiveness of

two similarity hashes, which both handle byte-stream

data but lack cross-comparison.

2 BACKGROUNDS: TLSH AND

LZJD

Cryptographic hashes like SHA1 or SHA256 are used

for precise file or byte-stream matching. Hash-based

filtering involves hashing two data objects and

comparing the results. Cryptographic hashes only

provide binary answers, while similarity hashes offer

a probabilistic answer as a measure of similarity or

distance. The aim of similarity hashing is to enable

approximate matching and support similarity search

and classification. This paper provides a high-level

overview of the design and operation of evaluated

tools, while the finer details can be found in

referenced publications.

2.1 TLSH

TLSH (Trend Micro Locality Sensitive Hash) is a

locality sensitive hash which produces a fixed-length

hash digest based on the input bytes (Oliver, Cheng,

& Chen, 2013). The standard TLSH hash (which is

Liu, H., Hagen, J., Ali, M. and Oliver, J.

An Evaluation of Malware Triage Similarity Hashes.

DOI: 10.5220/0011728500003467

In Proceedings of the 25th International Conference on Enterprise Information Systems (ICEIS 2023) - Volume 1, pages 431-435

ISBN: 978-989-758-648-4; ISSN: 2184-4992

 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)

431

used throughout in this paper) produces a digest 70

characters in length. The TLSH hash digest has the

property that two similar inputs would produce a

similar hash digest, based on statistical features of the

input bytes (Oliver & Hagen, 2021). The hash digest

is a concatenation of the digest header and digest

body. The following steps are involved in

computation of the standard TLSH hash:

• All 3-grams from a sliding window of 5 bytes

are used to compute an array of bucket counts,

which are used to form the digest body.

• Based on the calculation of bucket counts (as

calculated above) the three quartiles are

calculated (referred to as q1, q2, and q3

respectively).

• The digest body is constructed based on the

values of the quartiles in the array of bucket

counts, using two bits per 128 buckets to

construct a 32-byte digest.

• The digest header is composed of a checksum,

the logarithm of the byte string length and a

compact representation of the histogram of

bucket counts using the ratios between the

quartile points for q1:q3 and q2:q3

Two different TLSH hash digests are compared using

the TLSH distance. The TLSH distance of zero

represents that the files are likely identical, and scores

greater than that indicate the greater degrees of

dissimilarity (please see the original paper for more

details on the computation of the distance).

2.2 LZJD

Lempel-Ziv Jaccard Distance or LZJD algorithm

(Raff

& Nicholas, 2017)

. The inspiration of LZJD come

from the Normalized Compression Distance, which

measures the ability to compress two inputs into a

similar output using the same compression technique.

This has a long history of use in data mining, and

LZJD applies this approach to determine malware

similarity. First, the Lempel-Ziv Set algorithm

coverts a byte sequence into a set of byte sub-

sequences which is previously seen sequences in the

set. Initially, the set is empty, and then the following

process is repeated from the beginning of the byte

stream until the end of the stream is reached:

beginning with a sub-sequence of length 1, if this sub-

sequence has not been seen, then add it to the set and

the pointer move to the end of current sub-sequence

and next desired sub-sequence length reset to one. If

the sub-sequence has been seen before, it increases

next desired sub-sequence length by one to

incorporate the next byte.

LZJD only compares a small portion of the set to

speed up the process even more. To approximate the

distance by using min-hashing to create a compact

representation of the input string. Use this

approximation to reduce time and memory

requirements for computing LZJD. Moreover, there

is around 3% approximation error by selecting

minimum k = 1024 hashes from the set. The steps of

procedure to compare byte sequences are following:

• Covert byte sequence 𝐵



into many unique sub-

sequences using Lempel-Ziv Set Algorithm

• Hash these unique sub-sequences into a set 𝐶



integers via hash functions.

• Sort integers set and keep k=1024 smallest

values

• Calculate the Jaccard distance between two set

of smallest values.

𝐴𝑝𝑝𝑟𝑜𝑥𝑖𝑚𝑎𝑡𝑒 𝐿𝑍𝐽𝐷𝐵



, 𝐵



≈1 − 𝐽(𝐶





, 𝐶





)

We can interpret the LZJD score as a rough measure

of byte similarity. For example, consider two inputs

A and B. A score of 0.75 means that, for all sub-

strings shared between the LZSet(A) and LZSet(B),

75% of them could be found in both files. This can be

loosely interpreted as saying that A and B share 75%

of their byte strings (Raff & Nicholas, 2017).

3 EXPERIMENTS SETUPS

Dataset. Our evaluation uses real malware files

obtained from the MalwareBazaar website

(MalwareBazaar, n.d.). The 5138 Windows-based

malware samples, belonging to 20 families, come

from this source. The training set uses April 2022

collected files, while the testing set consists of

samples from May 1st, 2022.

Classifier. We employ the Nearest Neighbors

classifier with KD Tree indexing. The principle is to

identify the closest predefined number of training

samples to the new point and predict its label. This

paper uses radius-based neighbor learning instead of

k-nearest neighbor learning. The number of training

samples is based on the local density of points within

a set radius. Any metric measure can be used for

distance, but standard Euclidean distance is the most

common. In this case, we use TLSH and LZJD

distance scores as the distance metric.

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

432

3.1 Evaluation Procedure

To evaluate, we first need to understand the output of

each tool. TLSH provides a distance score of 0 to 300,

with a lower score indicating higher skip n-gram byte

similarity. LZJD only offers a similarity score of 0 to

1, where a higher score means higher substring

similarity. To make them comparable, we created a

LZJD distance function by reversing its similarity

score by multiplying by 100. Both tools now have

distance scores as output, which we use in our

experiments. The threshold value of the distance

score in the nearest neighbors' algorithm affects the

classification performance results.

3.2 Evaluation Metrics

We split the predictions into three categories: Correct,

Incorrect, and Inconclusive:

• Correct: The cluster is correctly labeled, and

the prediction matches the true label.

• Inconclusive: The sample or cluster lacks a

label, resulting in a "I don't know" answer to a

distance query.

• Incorrect: The cluster labeling is inconsistent,

and the prediction does not match the true label.

Finally, we consider two basic measurements,

detection rate and error rate:

Detection Rate refers to the ratio of correct

detections among all samples in the testing set.

Detection Rate = Correct / N, where N = Correct +

Incorrect + Inconclusive

Error Rate reflects the incorrect predictions made by

each approach in the testing set. In practical terms,

inconclusive results cannot lead to any conclusions.

Error Rate = Incorrect / (Correct + Incorrect)

4 EXPERIMENTAL RESULTS

We analyzed the distribution of distance scores for

three categories: correct, incorrect, and inconclusive.

The distance score is a crucial tunable parameter in

nearest neighbors' classification, and we aim to

demonstrate the distribution of distance scores under

real-world data to assess their usefulness and efficacy.

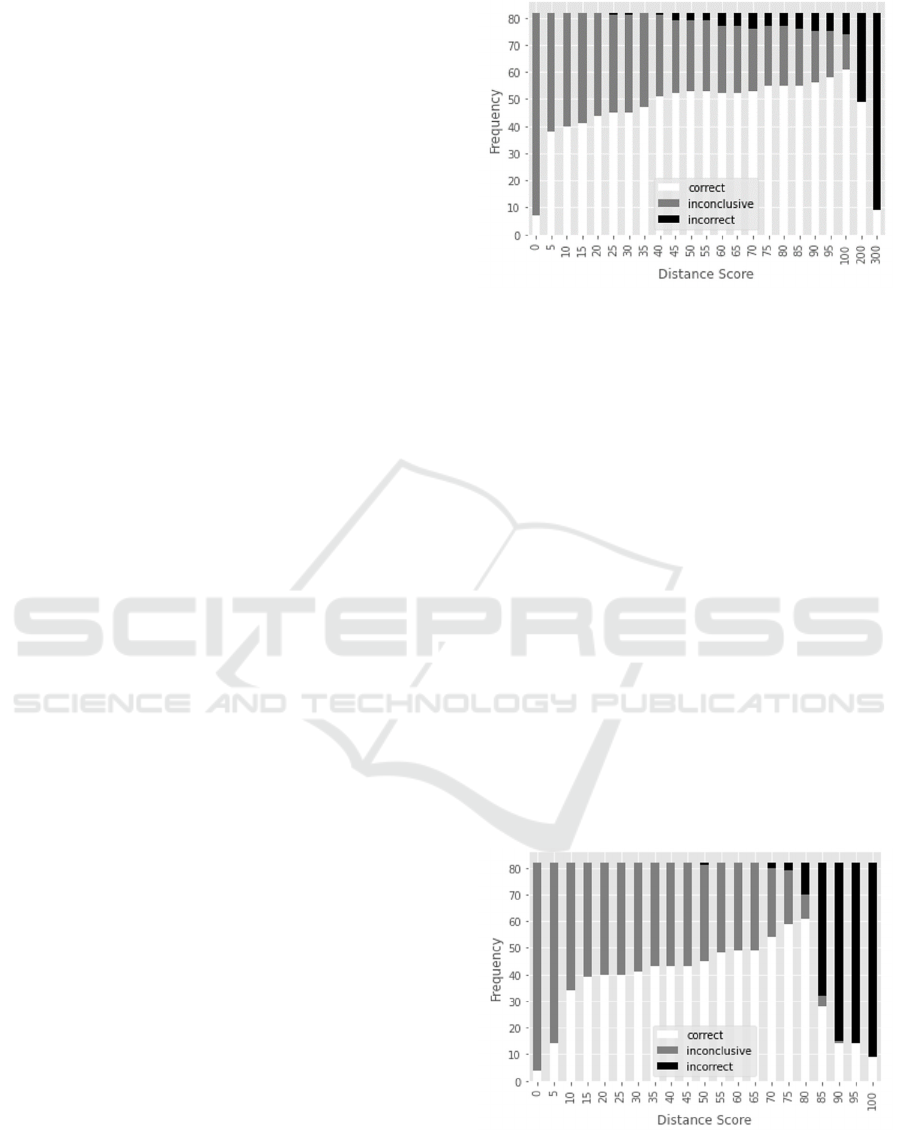
Figure 1: Experiments of TLSH distance score distribution.

4.1 TLSH Distance Scores Distribution

We analyzed all files with TLSH distance scores

between 0 and 300. As shown in Figure 1, we

observed that incorrect predictions were not present

when the distances were less than or equal to 20,

resulting in a zero Error Rate. However, as the

distance parameter increased, the Error Rate

increased as well. Conversely, the Detection Rate also

increased with a larger distance, reflecting a trade-off

between a higher Error Rate and increased Detection

Rate.

4.2 LZJD Distance Scores Distribution

We studied all files with LZJD distance scores

between 0 and 100. As shown in Figure 2, there were

no incorrect predictions until the distance parameter

was raised to 50. However, the number of incorrect

predictions increased significantly when the distance

score reached 85 or higher.

Figure 2 : Experiments of LZJD distance score distribution.

An Evaluation of Malware Triage Similarity Hashes

433

4.3 Detection Rate and Error Rate

Table 1: TLSH and LZJD detection and error rate.

TLSH LZJD

score

Detection

rate

Error

rate

score

Detection

rate

Error

rate

10 48.78% 0.00% 10 41.46% 0.00%

20 53.66% 0.00% 20 48.78% 0.00%

30 54.88% 2.17% 30 50.00% 0.00%

40 62.20% 1.92% 40 52.44% 0.00%

50 64.63% 5.36% 50 54.88% 2.17%

60 63.41% 8.77% 60 59.76% 0.00%

70 64.63% 10.17% 65 59.76% 0.00%

80 67.07% 8.33% 70 65.85% 3.57%

90 68.29% 11.11% 75 71.95% 4.84%

100 74.39% 11.59% 80 74.39% 16.44%

150 69.51% 22.97% 85 34.15% 64.10%

200 59.76% 40.24% 90 17.07% 82.72%

250 14.63% 85.37% 95 17.07% 82.93%

300 10.98% 89.02% 100 10.98% 89.02%

Observations from the table are as follows:

• TLSH and LZJD have different score ranges,

with TLSH up to 300 and potentially over 1000,

while LZJD is limited to 0-100.

• Both TLSH and LZJD have low error rates,

gradually increasing with the increase of the

distance parameter.

• LZJD has a lower error rate compared to TLSH,

but also a lower detection rate.

• TLSH has better detection rate than LZJD at all

reasonable thresholds but has a smaller number

of errors.

• LZJD has zero error rate at thresholds <= 65

(except 50), with best detection rate at threshold

= 65 with zero error rate.

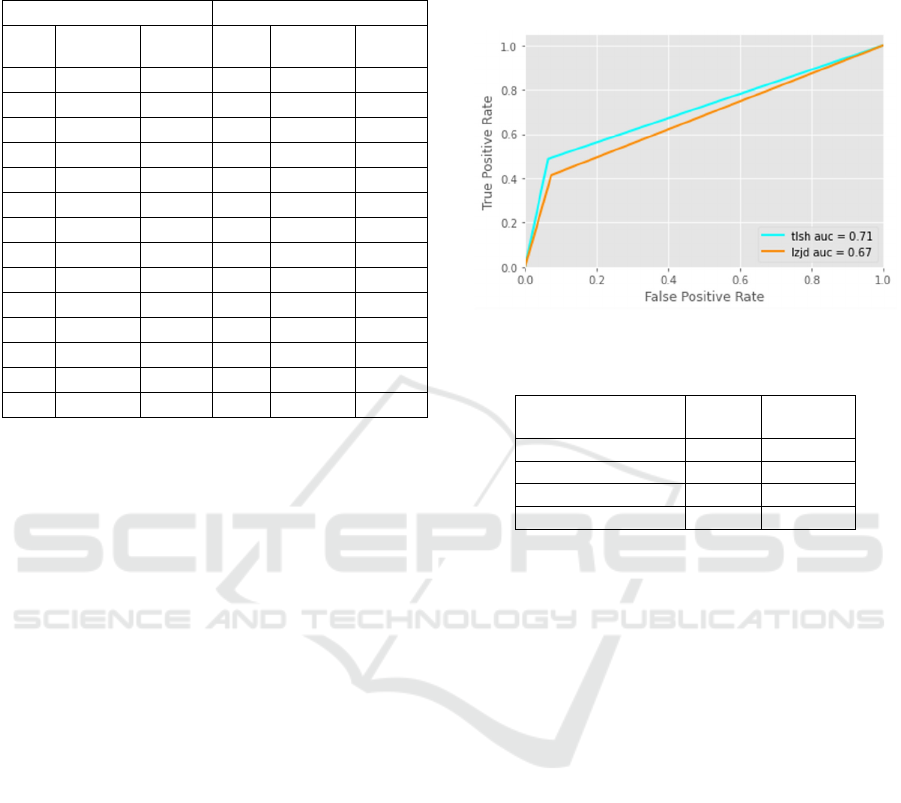
4.4 ROC Metric

We took the false positive and true positive rates for

two of We used false positive and true positive rates

of two schemes to plot a ROC curve, including

inconclusive as a false positive when the classifier

fails to predict. As shown in Fig. 3, the ROC curve

reveals that TLSH has slightly higher Area Under the

Curve (AUC) compared to LZJD.

4.5 Runtime Performance

Our experiment was conducted on a commodity 4-

core machine with 64 GB memory and Intel Core i7

6820HQ series processor (with a core turbo clock

speed of 2.7 GHz). We tested both similarity hash

tools and Table 1 shows the total runtime from

indexing to prediction. LZJD is large runtime

overhead.

Figure 3: ROC Curve of TLSH and LZJD.

Table 2: Comparison of runtime time for TLSH and LZJD.

Index & Search Time

(seconds)

TLSH LZJD

Average

0.894 167.458

Median

0867 166.022

Min

0.822 158.415

Max

1.092 183.519

5 CONCLUSIONS

The results indicate that both methods have strong

predictive abilities. TLSH outperforms LZJD in

indexing and searching time for malware triage due

to its shorter digests. TLSH compresses binary data

effectively while retaining meaningful information,

whereas its short digests conserve disk space,

memory and computing resources during index

creation and distance calculation.

REFERENCES

Cooley, R., Cutshaw, M., Wolf, S., Rita, F., Haile, J., &

Borowczak, M. (2021). Comparing Ransomware using

TLSH and @DisCo Analysis Frameworks. IEEE

International Conference on Big Data. Orlando, FL,

USA: IEEE International Conference on Big Data.

Fireeye. (2014). Tracking Malware with Import Hashing.

Retrieved from https://www.mandiant.com/resour

ces/tracking-malware-import-hashing

Li, Y., Sundaramurthy, S., Bardas, A., & Ou, X. (2015).

Experimental study of fuzzy hashing in malware

clustering analysis. 8th Workshop on Cyber Security

Experimentation and Test (CSET 15). Washington,

ICEIS 2023 - 25th International Conference on Enterprise Information Systems

434

D.C.: 8th Workshop on Cyber Security

Experimentation and Test.

MalwareBazaar. (n.d.). Retrieved from https://bazaar.

abuse.ch/

Naik, N., Jenkins, P., Savage, N., & Yang, L. (2019).

Triaging Ransomware using Fuzzy Hashing, Import

Hashing and YARA Rules. IEEE International

Conference on Fuzzy Systems (FUZZ-IEEE). New

Orleans: IEEE International Conference on Fuzzy

Systems (FUZZ-IEEE).

Naik, N., Jenkins, P., Savage, N., & Yang, L. (2020).

Fuzzy-Import Hashing: A Malware Analysis Approach.

IEEE International Conference on Fuzzy Systems

(FUZZ-IEEE). Glasgow, UK: IEEE International

Conference on Fuzzy Systems (FUZZ-IEEE).

Oliver, J., & Hagen, J. (2021). Designing the Elements of a

Fuzzy Hashing Scheme. 19th International Conference

on Embedded and Ubiquitous Computing (EUC).

Shenyang, China: IEEE 19th International Conference

on Embedded and Ubiquitous Computing (EUC).

Oliver, J., Ali, M., & Hagen, J. (2020). HAC-T and Fast

Search for Similarity in Security. International

Conference on Omni-layer Intelligent Systems (COINS).

Barcelona, Spain.

Oliver, J., Cheng, C., & Chen, Y. (2013). Tlsh – a locality

sensitive hash. Fourth Cybercrime and Trustworthy

Computing Workshop. Sydney, Australia: Fourth

Cybercrime and Trustworthy Computing Workshop.

Pagani, F., Dell'Amico, M., & Balzarotti, D. (2018).

Beyond Precision and Recall: Understanding Uses (and

Misuses) of Similarity Hashes in Binary Analysis.

Proceedings of the Eighth ACM Conference on Data

and Application Security and Privacy. New York:

Proceedings of the Eighth ACM Conference on Data

and Application Security and Privacy.

Raff, E., & Nicholas, C. (2017). An Alternative to NCD for

Large Sequences, Lempel-Ziv Jaccard Distance. the

23rd ACM SIGKDD International Conference. Halifax,

Canada: Proceedings of the 23rd ACM SIGKDD

International Conference on Knowledge Discovery and

Data Mining.

Raff, E., & Nicholas, C. K. (2017). Lempel-Ziv Jaccard

Distance, an Effective Alternative to Ssdeep and

Sdhash. Digital Investigation. Digital Investigation.

An Evaluation of Malware Triage Similarity Hashes

435